Numerical Stability and Performance of Semi-Explicit and Semi-Implicit Predictor–Corrector Methods
Abstract
:1. Introduction
2. Materials and Methods
2.1. Semi-Explicit and Semi-Implicit ABM Methods
2.1.1. General Description of Semi-Explicit and Semi-Implicit BDF (PEC) Methods
2.1.2. Semi-Explicit ABM Method
2.1.3. Semi-Implicit ABM Method
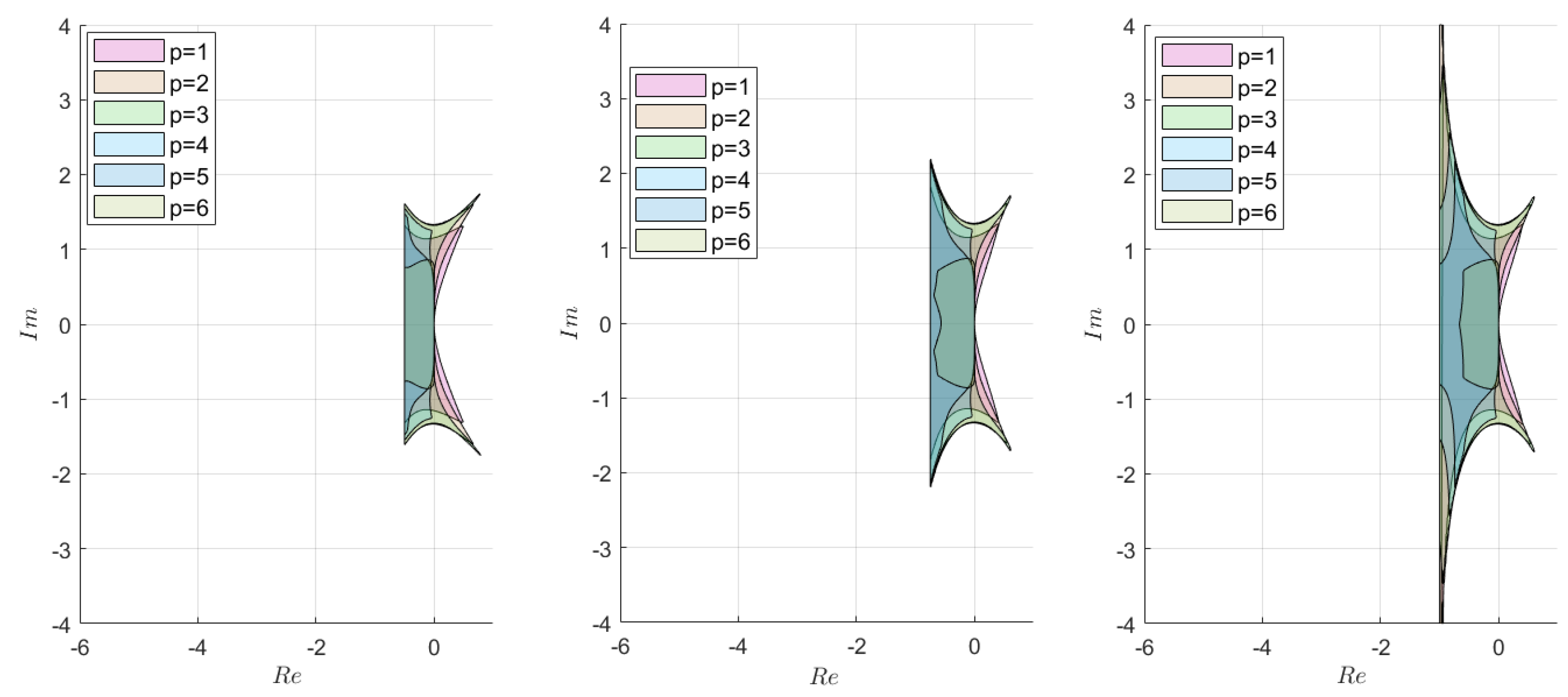
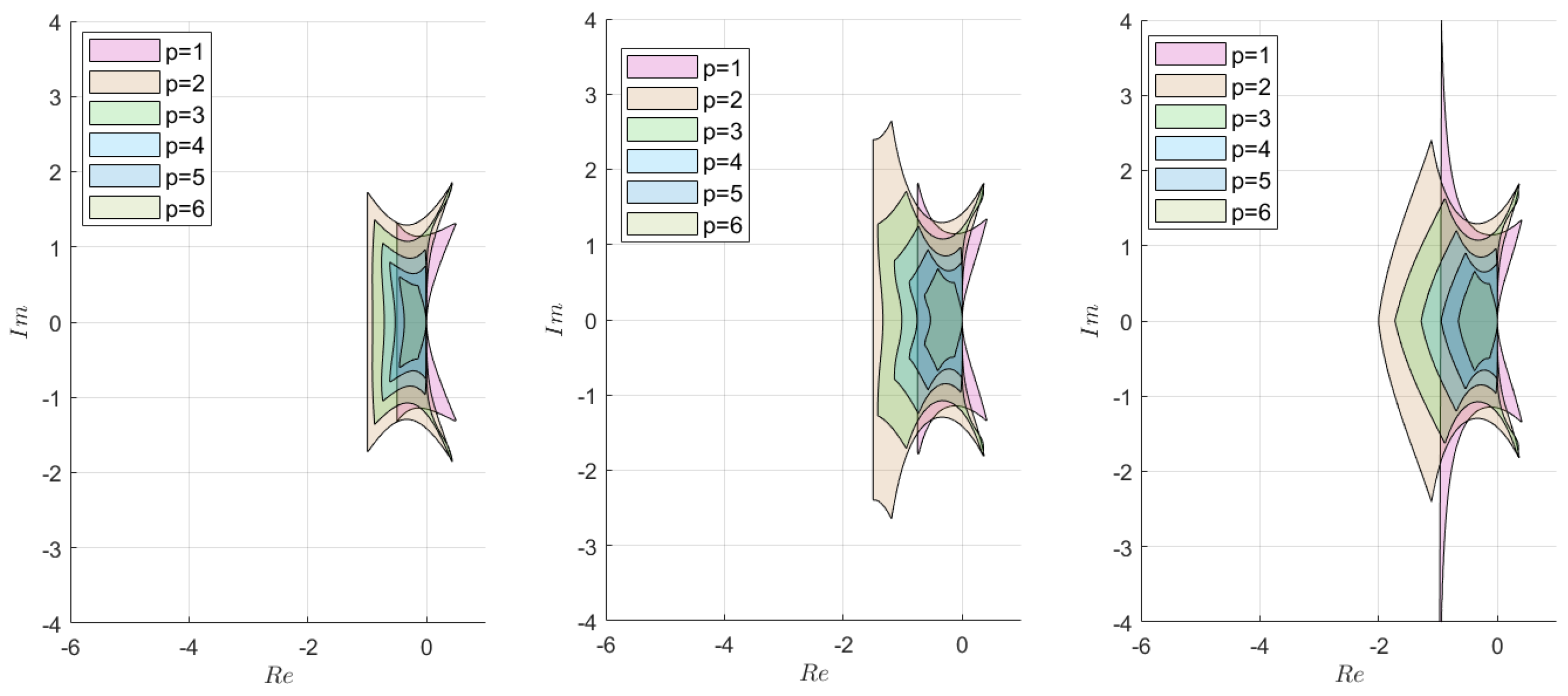
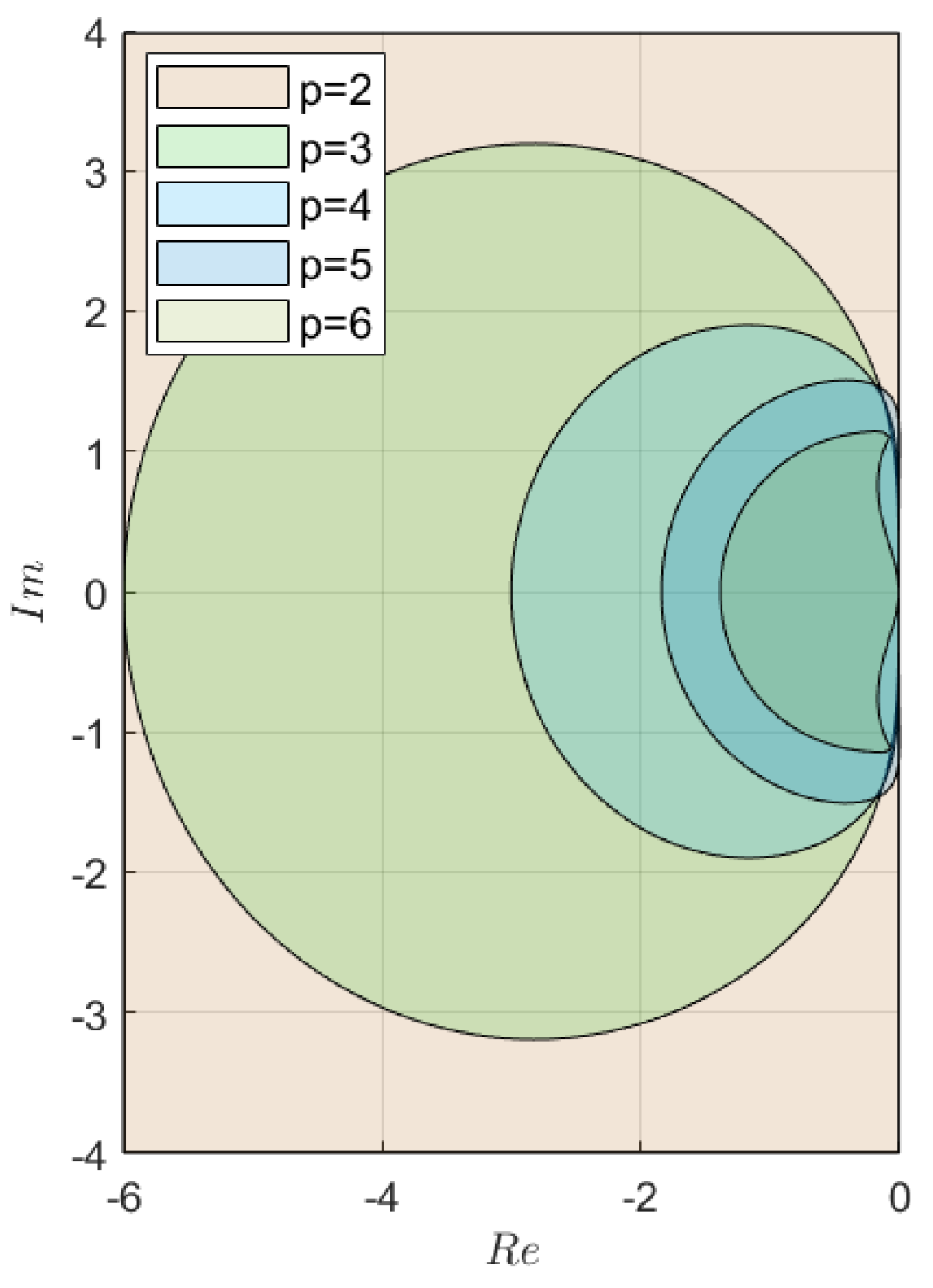
2.2. Stability Analysis
2.2.1. Semi-Explicit ABM Method
2.2.2. Semi-Implicit ABM Method
2.2.3. Semi-Explicit BDF (PEC) Method
2.2.4. Semi-Implicit BDF (PEC) Method
2.3. Test Problem for Estimating Method Stability
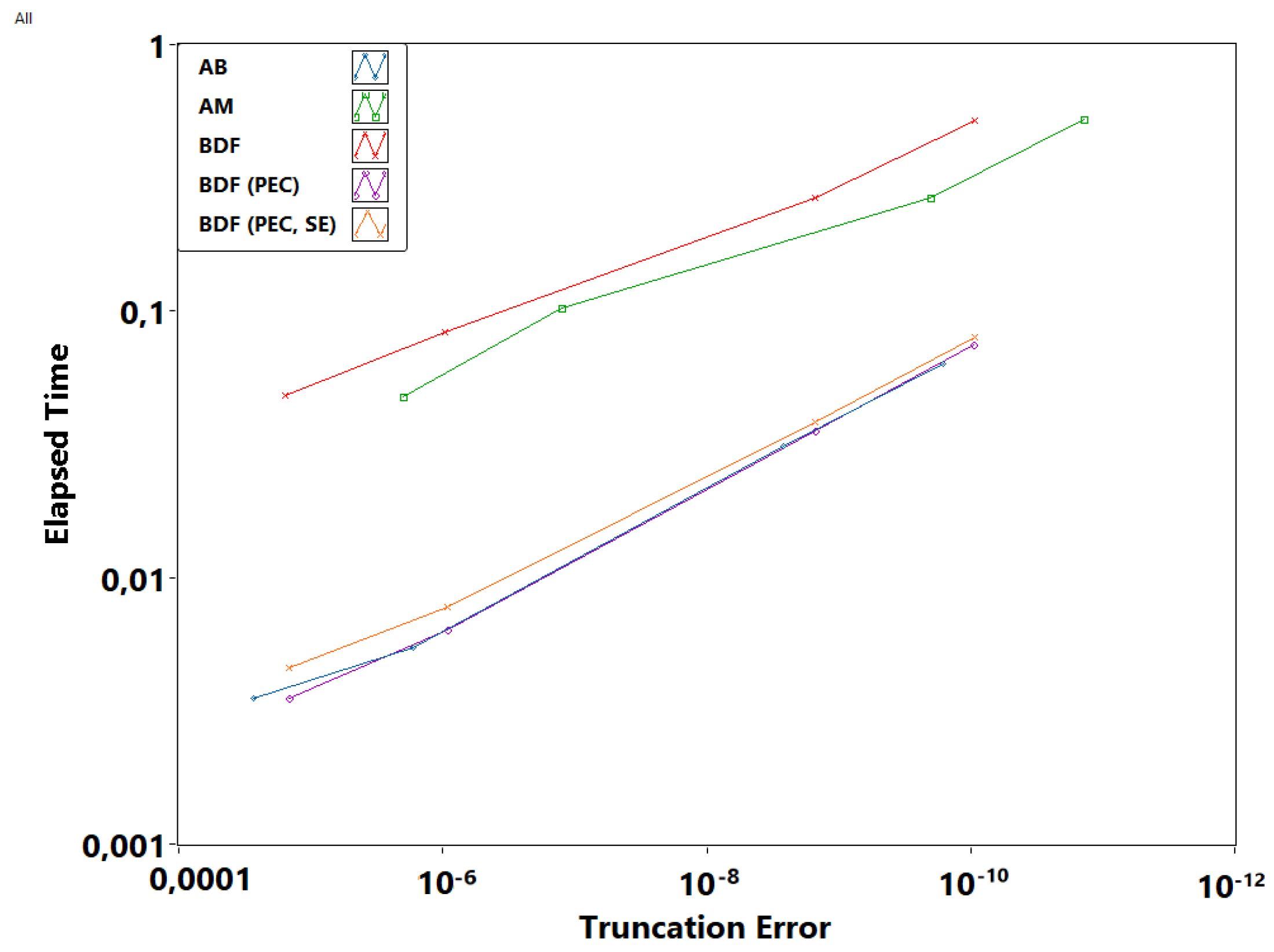
2.4. Test Problems for Estimating Method Performance
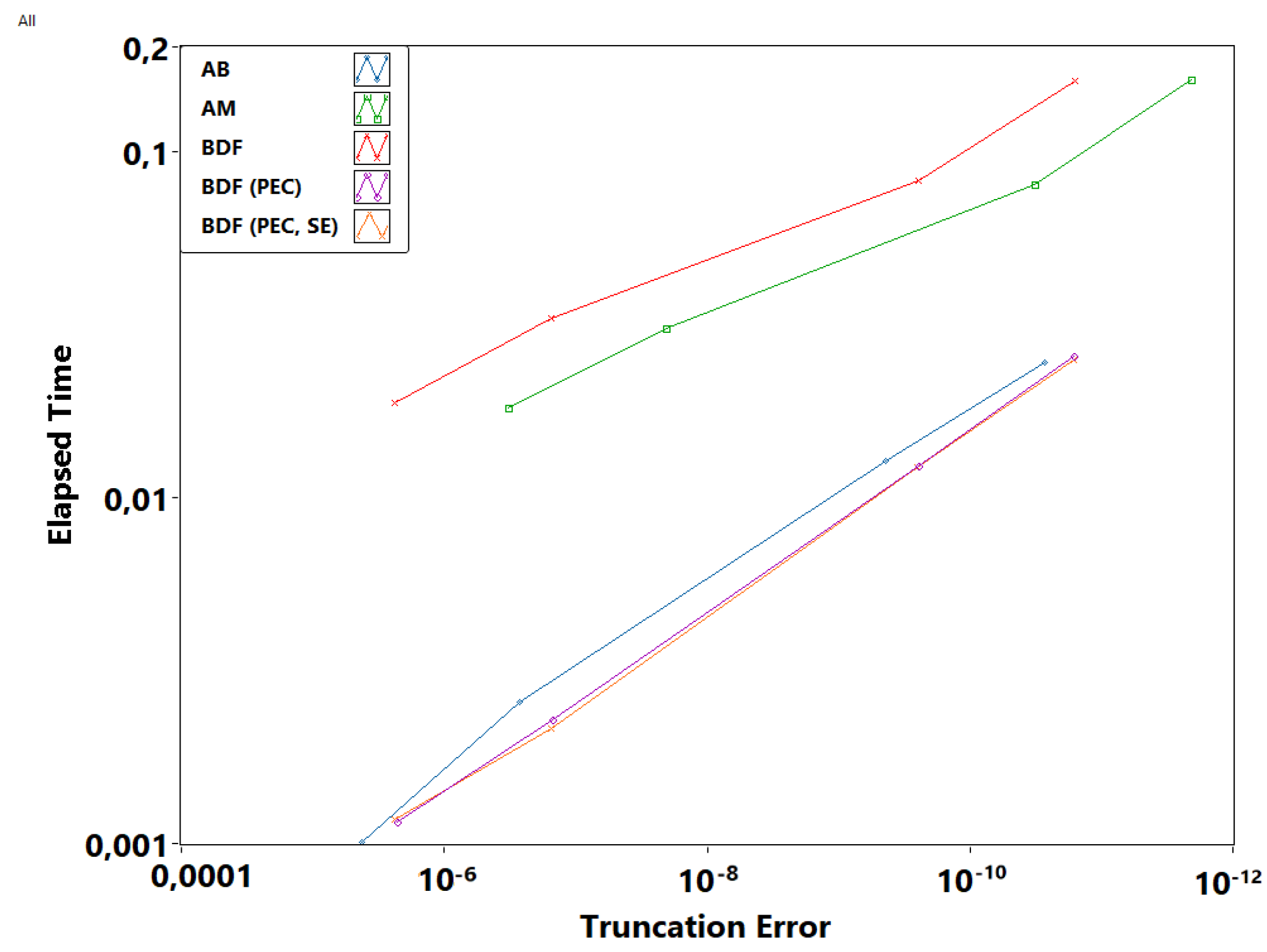
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ODE | Ordinary differential equations |
| BDF | Backward differentiation formula |
| SIRK | Singly implicit Runge–Kutta |
| DIRK | Diagonally implicit Runge–Kutta |
| ABM | Adams–Bashforth–Moulton |
| AM | Adams–Moulton |
References
- Awrejcewicz, J. Ordinary Differential Equations and Mechanical Systems; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Cardelli, L.; Tribastone, M.; Tschaikowski, M. From electric circuits to chemical networks. Nat. Comput. 2020, 19, 237–248. [Google Scholar] [CrossRef]
- Cardelli, L. From Processes to ODEs by Chemistry. In Proceedings of the Fifth IFIP International Conference On Theoretical Computer Science—TCS 2008, IFIP International Federation for Information Processing, Milano, Italy, 7–10 September 2008; Ausiello, G., Karhumäki, J., Mauri, G., Ong, L., Eds.; Springer: Boston, MA, USA, 2008. [Google Scholar]
- Polynikis, A.; Hogan, S.J.; Di Bernardo, M. Comparing different ODE modelling approaches for gene regulatory networks. J. Theor. Biol. 2009, 261, 511. [Google Scholar] [CrossRef] [PubMed]
- Keeling, M.; Rohani, P. Modeling Infectious Diseases in Humans and Animals; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Hairer, E.; Nørsett, S.P.; Wanner, G. Solving Ordinary Differential Equations I: Nonstiff Problems, 2nd ed.; Springer: Berlin, Germany, 1993; pp. 427–429. [Google Scholar]
- Jafari, H.; Ganji, R.M.; Nkomo, N.S.; Lv, Y.P. A numerical study of fractional order population dynamics model. Results Phys. 2021, 27, 104456. [Google Scholar] [CrossRef]
- Faleichik, B.V. Minimal residual multistep methods for large stiff non-autonomous linear problems. J. Comput. Appl. Math. 2019, 389, 112498. [Google Scholar] [CrossRef]
- Karimov, A.I.; Butusov, D.N.; Tutueva, A.V. Adaptive explicit-implicit switching solver for stiff ODEs. In Proceedings of the IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), St. Petersburg and Moscow, Russia, 1–3 February 2017; pp. 440–444. [Google Scholar]
- Lopez, S. A predictor-corrector time integration algorithm for dynamic analysis of nonlinear systems. Nonlinear Dynynamics 2020, 101, 1365–1381. [Google Scholar] [CrossRef]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Problems, 2nd ed.; Springer: Berlin, Germany, 1993; pp. 91–100, 128–130. [Google Scholar]
- Rauber, T.; Rünger, G. Parallel Implementations of Iterated Runge-Kutta Methods. Int. J. Supercomput. Appl. High Perform. Comput. 1996, 10, 62–90. [Google Scholar] [CrossRef]
- Liu, C.; Wu, H.; Feng, L.; Yang, A. Parallel Fourth-Order Runge-Kutta Method to Solve Differential Equations. In Proceedings of the ICICA 2011: Information Computing and Applications, Qinhuangdao, China, 28–31 October 2011; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2011; Volume 7030. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Tutueva, A.; Karimov, T.; Butusov, D. Semi-Implicit and Semi-Explicit Adams-Bashforth-Moulton Methods. Mathematics 2020, 8, 780. [Google Scholar] [CrossRef]
- Cellier, F.E.; Kofman, E. Continuous System Simulation; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Tutueva, A.; Butusov, D. Stability Analysis and Optimization of Semi-Explicit Predictor–Corrector Methods. Mathematics 2021, 9, 2463. [Google Scholar] [CrossRef]
- Butusov, D.; Karimov, A.; Andreev, V.; Ostrovskii, V. Semi-Explicit Composition Methods in Memcapacitor Circuit Simulation. Int. J. Embed. Real-Time Commun. Syst. 2019, 10, 37–52. [Google Scholar] [CrossRef]
- Rössler, O.E. An equation for continuous chaos. Phys. Lett. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Posch, H.A.; Hoover, W.; Vesely, F.J. Canonical dynamics of the Nosé oscillator: Stability, order, and chaos. Phys. Rev. A 1986, 33, 4253–5265. [Google Scholar] [CrossRef]
- van der Pol, B. The nonlinear theory of electric oscillations. Proc. Inst. Radio Eng. 1934, 22, 1051–1086. [Google Scholar] [CrossRef]
- Zhang, A.; Ganji, R.M.; Jafari, H.; Ncube, M.N.; Agamalieva, L. Numerical Solution of Distributed-Order Integro-Differential Equations. Fractals 2021. [Google Scholar] [CrossRef]
- Kadkhoda, N.; Jafari, H.; Ganji, R.M. A numerical solution of variable order diffusion and wave equations. Int. J. Nonlinear Anal. Appl. 2021, 12, 27–36. [Google Scholar]




| 1 | 0 | 0 | 0 | 0 | 0 |
| 3/2 | −1/2 | 0 | 0 | 0 | 0 |
| 23/12 | −16/12 | 5/12 | 0 | 0 | 0 |
| 55/24 | −59/24 | 37/24 | −9/24 | 0 | 0 |
| 1901/720 | −2774/720 | 2616/720 | −1274/720 | 251/720 | 0 |
| 4277/1440 | −7923/1440 | 9982/1440 | −7298/1440 | 2877/1440 | −475/1440 |
| −1 | 0 | 0 | 0 | 0 | 0 |
| −4/3 | 1/3 | 0 | 0 | 0 | 0 |
| −18/11 | 9/11 | −2/11 | 0 | 0 | 0 |
| −48/25 | 36/25 | −16/25 | 3/25 | 0 | 0 |
| −300/137 | 300/137 | −200/137 | 75/137 | −12/137 | 0 |
| −360/147 | 450/147 | −400/147 | 225/147 | −72/147 | 10/147 |
| 1 | 2/3 | 6/11 | 12/25 | 60/137 | 60/147 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beuken, L.; Cheffert, O.; Tutueva, A.; Butusov, D.; Legat, V. Numerical Stability and Performance of Semi-Explicit and Semi-Implicit Predictor–Corrector Methods. Mathematics 2022, 10, 2015. https://doi.org/10.3390/math10122015
Beuken L, Cheffert O, Tutueva A, Butusov D, Legat V. Numerical Stability and Performance of Semi-Explicit and Semi-Implicit Predictor–Corrector Methods. Mathematics. 2022; 10(12):2015. https://doi.org/10.3390/math10122015
Chicago/Turabian StyleBeuken, Loïc, Olivier Cheffert, Aleksandra Tutueva, Denis Butusov, and Vincent Legat. 2022. "Numerical Stability and Performance of Semi-Explicit and Semi-Implicit Predictor–Corrector Methods" Mathematics 10, no. 12: 2015. https://doi.org/10.3390/math10122015
APA StyleBeuken, L., Cheffert, O., Tutueva, A., Butusov, D., & Legat, V. (2022). Numerical Stability and Performance of Semi-Explicit and Semi-Implicit Predictor–Corrector Methods. Mathematics, 10(12), 2015. https://doi.org/10.3390/math10122015









