A New Kantorovich-Type Rational Operator and Inequalities for Its Approximation

Abstract

We introduce a new Kantorovich-type rational operator. We investigate inequalities estimating its rates of convergence in view of the modulus of continuity and the Lipschitz-type functions. Moreover, we present graphical comparisons exemplifying concretely its better approximation for a certain function. The results of the paper are crucial by means of possessing at least better approximation results than an existing Kantorovich-type rational function.

1. Introduction

In 1975, Balázs [1] introduced the following rational function for any real function v on $\left[0,\infty \right)$ and sequences of real numbers $a_n$ and $b_n$ such that $b_n=n{a}_n$ by

$${\mathcal{R}}_n\left(v;x\right)=\frac{1}{{\left(1+a_{n}x\right)}^n}\sum _{k=0}^{n}v\left(\frac{k}{b_n}\right)\left(\genfrac{}{}{0pt}{}{n}{k}\right){\left(a_{n}x\right)}^k,n\in \mathbb{N},$$

(1)

and he investigated its approximation properties by choosing $b_n=n^{2/3}$ for functions such that $v\left(x\right)=O\left(e^{\sigma x}\right),x\to \infty$ for some $\sigma \in \mathbb{R}.$ In 1985, Balázs and Szabados [2] improved its approximation properties under more restrictive cases such that $a_n=n^{\zeta -1}$, $b_n=n^{\zeta }$, $0<\zeta <\frac{2}{3}$. Moreover, Balázs [3] studied these operators on all the real axis. Totik [4] investigated the saturation properties of Balázs–Szabados operators, and Abel and Veccia [5] obtained a Voronovskaja type result. Agratini [6] studied Bernstein type rational functions by choosing a strictly decreasing positive real sequence $\left(a_n\right)$ such that ${\lim }_{n\to \infty }{a}_n=0$ as follows:

$${\mathcal{L}}_n\left(v;x\right)=\frac{1}{{\left(1+a_{n}x\right)}^n}\sum _{k=0}^{n}v\left(\frac{k}{n{a}_n}\right)\left(\genfrac{}{}{0pt}{}{n}{k}\right){\left(a_{n}x\right)}^k,n=1,2,\dots ,$$

(2)

where v is continuous on $\left[0,\infty \right)$ satisfying a certain growing condition.

The Kantorovich extension of the operator ${\mathcal{R}}_n$ defined by (1) was given by Agratini [7] in 2001 by

$${\mathcal{K}}_n\left(v;x\right)=n{a}_n\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)\frac{{\left(a_{n}x\right)}^k}{{\left(1+a_{n}x\right)}^n}\underset{\frac{k}{n{a}_n}}{\overset{\frac{k+1}{n{a}_n}}{\int }}v\left(t\right)dt,$$

(3)

where $x\ge 0$, $n\in \mathbb{N}$, v is a measurable function on $\left[0,\infty \right)$ and bounded on each compact subinterval of $\left[0,\infty \right)$, $a_n$ is a real sequence for $n=1,2,\dots$. In [8], Agratini studied the Kantorovich operator defined by (3) under the condition such that $a_n=n^{\zeta -1}$, $0<\zeta <1$. For some other Kantorovich-type rational operators, one can see the references [9,10,11,12,13].

Recently, a new generalized Bernstein-type rational function [14] has been introduced by

$$R_n^G\left(v;x\right)=\sum _{k=0}^{n}v\left(\frac{k}{{\tau }_n}\right)\left(\genfrac{}{}{0pt}{}{n}{k}\right)\frac{{\left({\sigma }_n\right)}^{n-k}{\left({\rho }_{n}x\right)}^k}{{\left({\sigma }_n+{\rho }_{n}x\right)}^n},$$

(4)

where $x\ge 0$, $n\in \mathbb{N}$, v is a continuous function on $\left[0,\infty \right)$, ${\rho }_n$, ${\sigma }_n$, and ${\tau }_n$ are non-negative sequences of real numbers, satisfying ${\tau }_n=n{\rho }_n$, and its approximation properties have been investigated under the following conditions:

$$\underset{n\to \infty }{\lim }{\rho }_n=0,\underset{n\to \infty }{\lim }{\sigma }_n=1,\underset{n\to \infty }{\lim }{\tau }_n=\infty .$$

(5)

The operator $R_n^G$ is reducible to (1) and (2) when ${\rho }_n=a_n$, ${\sigma }_n=1$ and ${\tau }_n=n{a}_n,$ and it has at least better approximation than the operator ${\mathcal{R}}_n$ defined by (1) (see [14]).

In this paper, we initially introduce a Kantorovich-type operator of the generalized rational function defined by (4), which is a generalization of the operator ${\mathcal{K}}_n$ defined by (3). Secondly, we investigate its Korovkin-type local and global approximation properties. Lastly, we present some graphical comparisons of the new Kantorovich-type rational operator with the operator ${\mathcal{K}}_n$ defined by (3). The results of the paper is crucial by means of possessing at least better approximation results than those existing for the Kantorovich-type operator ${\mathcal{K}}_n$ defined by (3).

2. Definition of Kantorovich-Type Operator

In this part, we constitute a new Kantorovich-type operator including the operator ${\mathcal{K}}_n$ defined by (3), and we present some auxiliary results.

Definition 1.

Let v be a real-valued measurable function on $\left[0,\infty \right)$ and bounded on each compact subinterval of $\left[0,\infty \right)$. A new Kantorovich-type rational operator of the generalized rational function given in (4) is defined by

$$K_n^G\left(v;x\right)={\tau }_n\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)\frac{{\left({\sigma }_n\right)}^{n-k}{\left({\rho }_{n}x\right)}^k}{{\left({\sigma }_n+{\rho }_{n}x\right)}^n}\underset{\frac{k}{{\tau }_n}}{\overset{\frac{k+1}{{\tau }_n}}{\int }}v\left(t\right)dt,$$

(6)

where $x\ge 0$, $n\in \mathbb{N}$, ${\rho }_n$, ${\sigma }_n$ and ${\tau }_n$ are non-negative sequences of real numbers such that ${\tau }_n=n{\rho }_n$, satisfying (5). The operator $K_n^G$ is a linear positive operator, satisfying the property:

$$\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)\frac{{\left({\sigma }_n\right)}^{n-k}{\left({\rho }_{n}x\right)}^k}{{\left({\sigma }_n+{\rho }_{n}x\right)}^n}=1.$$

(7)

When ${\rho }_n=a_n$, ${\sigma }_n=1$ and ${\tau }_n=n{a}_n$, the operator $K_n^G$ is reduced to the operator ${\mathcal{K}}_n$ defined by (3). Therefore, the Kantorovich-type operator $K_n^G$ is a generalization of the operator ${\mathcal{K}}_n$ defined by (3).

Lemma 1.

We have the following results for the operator $K_n^G$:

$$K_n^G\left(1;x\right)=1,$$

(8)

$$K_n^G\left(t;x\right)=\frac{x}{{\sigma }_n+{\rho }_{n}x}+\frac{1}{2{\tau }_n},$$

(9)

$$K_n^G\left(t^2;x\right)=\frac{\left(1-\frac{1}{n}\right)x^2}{{\left({\sigma }_n+{\rho }_{n}x\right)}^2}+\frac{2x}{{\tau }_n\left({\sigma }_n+{\rho }_{n}x\right)}+\frac{1}{3{\left({\tau }_n\right)}^2}.$$

(10)

Proof. 

By (7), we obtain

$$\begin{array}{ccc}\hfill K_n^G\left(1;x\right)& =& {\tau }_n\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)\frac{{\left({\sigma }_n\right)}^{n-k}{\left({\rho }_{n}x\right)}^k}{{\left({\sigma }_n+{\rho }_{n}x\right)}^n}\underset{\frac{k}{{\tau }_n}}{\overset{\frac{k+1}{{\tau }_n}}{\int }}1dt\hfill \\ & =& 1.\hfill \end{array}$$

By (7) and ${\tau }_n=n{\rho }_n$, we calculate

$$\begin{array}{ccc}\hfill K_n^G\left(t;x\right)& =& {\tau }_n\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)\frac{{\left({\sigma }_n\right)}^{n-k}{\left({\rho }_{n}x\right)}^k}{{\left({\sigma }_n+{\rho }_{n}x\right)}^n}\underset{\frac{k}{{\tau }_n}}{\overset{\frac{k+1}{{\tau }_n}}{\int }}tdt\hfill \\ & =& {\tau }_n\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)\frac{{\left({\sigma }_n\right)}^{n-k}{\left({\rho }_{n}x\right)}^k}{{\left({\sigma }_n+{\rho }_{n}x\right)}^n}\frac{2k+1}{2{\left({\tau }_n\right)}^2}\hfill \\ & =& \frac{x}{{\sigma }_n+{\rho }_{n}x}\sum _{k=0}^{n-1}\left(\genfrac{}{}{0pt}{}{n-1}{k}\right)\frac{{\left({\sigma }_n\right)}^{n-1-k}{\left({\rho }_{n}x\right)}^k}{{\left({\sigma }_n+{\rho }_{n}x\right)}^{n-1}}+\frac{1}{2{\tau }_n}\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)\frac{{\left({\sigma }_n\right)}^{n-k}{\left({\rho }_{n}x\right)}^k}{{\left({\sigma }_n+{\rho }_{n}x\right)}^n}\hfill \\ & =& \frac{x}{{\sigma }_n+{\rho }_{n}x}+\frac{1}{2{\tau }_n}.\hfill \end{array}$$

Similarly, we obtain

$$\begin{array}{ccc}\hfill K_n^G\left(t^2;x\right)& =& {\tau }_n\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)\frac{{\left({\sigma }_n\right)}^{n-k}{\left({\rho }_{n}x\right)}^k}{{\left({\sigma }_n+{\rho }_{n}x\right)}^n}\underset{\frac{k}{{\tau }_n}}{\overset{\frac{k+1}{{\tau }_n}}{\int }}{t}^{2}dt\hfill \\ & =& {\tau }_n\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)\frac{{\left({\sigma }_n\right)}^{n-k}{\left({\rho }_{n}x\right)}^k}{{\left({\sigma }_n+{\rho }_{n}x\right)}^n}\frac{3k^2+3k+1}{3{\left({\tau }_n\right)}^3}\hfill \\ & =& \frac{\left(1-\frac{1}{n}\right)x^2}{{\left({\sigma }_n+{\rho }_{n}x\right)}^2}\sum _{k=0}^{n-2}\left(\genfrac{}{}{0pt}{}{n-2}{k}\right)\frac{{\left({\sigma }_n\right)}^{n-2-k}{\left({\rho }_{n}x\right)}^k}{{\left({\sigma }_n+{\rho }_{n}x\right)}^{n-2}}\hfill \\ & & +\frac{x}{{\tau }_n\left({\sigma }_n+{\rho }_{n}x\right)}\sum _{k=0}^{n-1}\left(\genfrac{}{}{0pt}{}{n-1}{k}\right)\frac{{\left({\sigma }_n\right)}^{n-1-k}{\left({\rho }_{n}x\right)}^k}{{\left({\sigma }_n+{\rho }_{n}x\right)}^{n-1}}\hfill \\ & & +\frac{x}{{\tau }_n\left({\sigma }_n+{\rho }_{n}x\right)}\sum _{k=0}^{n-1}\left(\genfrac{}{}{0pt}{}{n-1}{k}\right)\frac{{\left({\sigma }_n\right)}^{n-1-k}{\left({\rho }_{n}x\right)}^k}{{\left({\sigma }_n+{\rho }_{n}x\right)}^{n-1}}\hfill \\ & & +\frac{1}{3{\left({\tau }_n\right)}^3}\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)\frac{{\left({\sigma }_n\right)}^{n-k}{\left({\rho }_{n}x\right)}^k}{{\left({\sigma }_n+{\rho }_{n}x\right)}^n}\hfill \\ & =& \frac{\left(1-\frac{1}{n}\right)x^2}{{\left({\sigma }_n+{\rho }_{n}x\right)}^2}+\frac{x}{{\tau }_n\left({\sigma }_n+{\rho }_{n}x\right)}+\frac{x}{{\tau }_n\left({\sigma }_n+{\rho }_{n}x\right)}+\frac{1}{3{\left({\tau }_n\right)}^2}\hfill \\ & =& \frac{\left(1-\frac{1}{n}\right)x^2}{{\left({\sigma }_n+{\rho }_{n}x\right)}^2}+\frac{2x}{{\tau }_n\left({\sigma }_n+{\rho }_{n}x\right)}+\frac{1}{3{\left({\tau }_n\right)}^2}.\hfill \end{array}$$

□

3. A Korovkin-Type Approximation Result

In this section, we give local and global approximation results for the Kantorovich-type operator defined by (6).

Theorem 1.

Let $K_n^G$, $n\in \mathbb{N}$, be Kantorovich-type operator defined by (6). If $v\in C\left(\left[0,r\right]\right)$, then $K_n^G(v;.)$ converges to v uniformly on $\left[0,r\right]\subset \left[0,\infty \right)$, $r>0$, for each $v\in C\left(\left[0,r\right]\right)$.

Proof. 

The proof is obtained from well-known Bohman–Korovkin theorem in [15]. By (8) of Lemma 1, we have

$$\underset{n\to \infty }{\lim }{∥K_n^G\left(e_0;.\right)-e_0(.)∥}_{\left[0,r\right]}=0.$$

(11)

By (9) of Lemma 1, we write

$$\begin{array}{ccc}\hfill \left|K_n^G\left(e_1;x\right)-e_1\left(x\right)\right|& =& \left|\frac{x}{{\sigma }_n+{\rho }_{n}x}+\frac{1}{2{\tau }_n}-x\right|\hfill \\ & =& \frac{\left|\left(1-{\sigma }_n\right)x-{\rho }_n{x}^2\right|}{\left|{\sigma }_n+{\rho }_{n}x\right|}+\frac{1}{2{\tau }_n}\hfill \\ & \le & \frac{\left|1-{\sigma }_n\right|r+{\rho }_n{r}^2}{{\sigma }_n}+\frac{1}{2{\tau }_n}.\hfill \end{array}$$

(12)

Under the condition (5), from (12), we obtain

$$\underset{n\to \infty }{\lim }{∥K_n^G\left(e_1;.\right)-e_1\left(.\right)∥}_{\left[0,r\right]}=0.$$

(13)

By (10) of Lemma 1, we calculate

$$\begin{array}{ccc}\hfill \left|K_n^G\left(e_2;x\right)-e_2\left(x\right)\right|& =& \left|\frac{\left(1-\frac{1}{n}\right)x^2}{{\left({\sigma }_n+{\rho }_{n}x\right)}^2}+\frac{2x}{{\tau }_n\left({\sigma }_n+{\rho }_{n}x\right)}+\frac{1}{3{\left({\tau }_n\right)}^2}-x^2\right|\hfill \\ & \le & \left|\frac{-{\left({\rho }_n\right)}^2{x}^4-2{\sigma }_n{\rho }_n{x}^3+\left(1-{\left({\sigma }_n\right)}^2-\frac{1}{n}\right)x^2}{{\left({\sigma }_n+{\rho }_{n}x\right)}^2}\right|\hfill \\ & & +\left|\frac{2x}{{\tau }_n\left({\sigma }_n+{\rho }_{n}x\right)}\right|+\frac{1}{3{\left({\tau }_n\right)}^2}\hfill \\ & \le & \frac{{\left({\rho }_n\right)}^2{r}^4}{{\left({\sigma }_n\right)}^2}+\frac{2{\rho }_n{r}^3}{{\sigma }_n}+\frac{\left|1-{\left({\sigma }_n\right)}^2-\frac{1}{n}\right|r^2}{{\left({\sigma }_n\right)}^2}+\frac{2r}{{\tau }_n{\sigma }_n}\hfill \\ & & +\frac{1}{3{\left({\tau }_n\right)}^2}.\hfill \end{array}$$

(14)

Under condition (5), from (14), we get

$$\underset{n\to \infty }{\lim }{∥K_n^G\left(e_2;.\right)-e_2\left(.\right)∥}_{\left[0,r\right]}=0.$$

(15)

From (11), (13), and (15), the hypotheses of Korovkin theorem are satisfied, which completes the proof. □

4. Rates of Convergence

Now, we estimate the rate of convergence by means of the first and second modulus of continuity and Lipschitz-type functions.

By $C_{\mathcal{B}}\left(\left[0,\infty \right)\right)$ is denoted the space of real-valued continuous and bounded functions on $\left[0,\infty \right)$.

For any $\varsigma >0$, the modulus of continuity of $v\in C_{\mathcal{B}}\left(\left[0,\infty \right)\right)$ is defined as

$$\omega \left(v;\varsigma \right)=\underset{0<s<\varsigma }{\sup }\underset{x\in \left[0,\infty \right)}{\sup }\left|v\left(x+s\right)-v\left(x\right)\right|,$$

(16)

which satisfies the following inequality:

$$\omega \left(v;\kappa \varsigma \right)\le \left(\kappa +1\right)\omega \left(v;\varsigma \right),$$

(17)

for $\kappa >0$, and ${\lim }_{\varsigma \to 0^{+}}\omega \left(v;\varsigma \right)=0$, when v is uniformly continuous [16].

Theorem 2.

If $v\in C_{\mathcal{B}}\left(\left[0,\infty \right)\right)$, then

$$\left|K_n^G\left(v;x\right)-v\left(x\right)\right|\le 2\omega \left(v;\sqrt{{\varsigma }_n^x}\right),$$

where

$$\begin{array}{ccc}\hfill {\varsigma }_n^x& :& =\frac{{\left({\rho }_n\right)}^2{x}^4}{{\left({\sigma }_n+{\rho }_{n}x\right)}^2}+\frac{2{\rho }_n\left({\sigma }_n-1\right)x^3}{{\left({\sigma }_n+{\rho }_{n}x\right)}^2}+\frac{\left({\left({\sigma }_n-1\right)}^2-\frac{1}{n}\right)x^2}{{\left({\sigma }_n+{\rho }_{n}x\right)}^2}\hfill \\ & & +\frac{2x}{{\tau }_n\left({\sigma }_n+{\rho }_{n}x\right)}-\frac{x}{{\tau }_n}+\frac{1}{3{\left({\tau }_n\right)}^2}.\hfill \end{array}$$

(18)

Proof. 

Let $v\in C_{\mathcal{B}}\left(\left[0,\infty \right)\right)$. By (17), we have

$$\left|v\left(t\right)-v\left(x\right)\right|\le \left(1+\frac{\left|t-x\right|}{\varsigma }\right)\omega \left(v;\varsigma \right).$$

(19)

Applying the operator $K_n^G$ to (19), and using the Cauchy–Schwarz inequality, we obtain

$$\begin{array}{ccc}\hfill \left|K_n^G\left(v;x\right)-v\left(x\right)\right|& \le & K_n^G\left(\left|v\left(t\right)-v\left(x\right)\right|;x\right)\hfill \\ & \le & \omega \left(v;\mu \right)\left(1+\frac{1}{\varsigma }{K}_n^G\left(\left|t-x\right|;x\right)\right)\hfill \\ & \le & \omega \left(v;\mu \right)\left(1+\frac{1}{\varsigma }\sqrt{K_n^G\left({\left(t-x\right)}^2;x\right)}\right).\hfill \end{array}$$

(20)

By (8)–(10) of Lemma 1, we calculate

$$\begin{array}{ccc}\hfill K_n^G\left({\left(e_1-x\right)}^2;x\right)& =& \frac{{\left({\rho }_n\right)}^2{x}^4}{{\left({\sigma }_n+{\rho }_{n}x\right)}^2}+\frac{2{\rho }_n\left({\sigma }_n-1\right)x^3}{{\left({\sigma }_n+{\rho }_{n}x\right)}^2}+\frac{\left({\left({\sigma }_n-1\right)}^2-\frac{1}{n}\right)x^2}{{\left({\sigma }_n+{\rho }_{n}x\right)}^2}\hfill \\ & & +\frac{2x}{{\tau }_n\left({\sigma }_n+{\rho }_{n}x\right)}-\frac{x}{{\tau }_n}+\frac{1}{3{\left({\tau }_n\right)}^2}.\hfill \end{array}$$

(21)

By replacing $\varsigma =\sqrt{K_n^G\left({\left(e_1-x\right)}^2;x\right)}=:\sqrt{{\varsigma }_n^x}$, the proof is completed. □

For $v\in C_{\mathcal{B}}\left(\left[0,\infty \right)\right)$, the Petree’s K-functional is defined as

$$K_2\left(v;\varsigma \right)=\underset{u\in C_{\mathcal{B}}^{\left(2\right)}\left(\left[0,\infty \right)\right)}{\inf }\left\{{∥v-u∥}_{\infty }+\varsigma {∥u^{″}∥}_{\infty }\right\},$$

(22)

where ${∥.∥}_{\infty }$ is the supremum norm on $C_{\mathcal{B}}\left(\left[0,\infty \right)\right)$ and

$$C_{\mathcal{B}}^{\left(2\right)}\left(\left[0,\infty \right)\right):=\left\{u\in C_{\mathcal{B}}\left(\left[0,\infty \right)\right):u^{\prime },u^{″}\in C_{\mathcal{B}}\left(\left[0,\infty \right)\right)\right\}.$$

We have the following inequality (see p. 192 in [17]):

$$K_2\left(v;\varsigma \right)\le C{\omega }_2\left(v;\sqrt{\varsigma }\right),$$

(23)

where

$${\omega }_2\left(v;\sqrt{\varsigma }\right)=\underset{0<s<\sqrt{\varsigma }}{\sup }\underset{x\in \left[0,\infty \right)}{\sup }\left|v\left(x+2s\right)-2v\left(x+s\right)+v\left(x\right)\right|.$$

(24)

Theorem 3.

If $v\in C_{\mathcal{B}}\left(\left[0,\infty \right)\right)$, then there exists a $c_0>0$, such that

$$\left|K_n^G\left(v;x\right)-v\left(x\right)\right|\le c_0\left\{{\omega }_2\left(v;\sqrt{{\varsigma }_n^x}\right)+\sqrt{{\varsigma }_n^x}\right\},$$

where $x\ge 0$, ${\varsigma }_n^x$ is given as in (18).

Proof. 

Let $v\in C_{\mathcal{B}}\left(\left[0,\infty \right)\right)$. For any $u\in C_{\mathcal{B}}^{\left(2\right)}\left(\left[0,\infty \right)\right)$, by Langrange form of Taylor theorem, we can write

$$u\left(t\right)-u\left(x\right)=u^{\prime }\left(x\right)\left(t-x\right)+R_1\left(t\right),$$

(25)

where $R_1\left(t\right)=\frac{u^{″}\left({\xi }_L\right)}{2!}{\left(t-x\right)}^2$ is the remainder term for some real number $x<{\xi }_L<t$ such that ${\lim }_{t\to x}{R}_1\left(t\right)=0$ and ${\lim }_{t\to x}\frac{R_1\left(t\right)}{t-x}=0$.

Applying the operator $K_n^G$ to (25), we obtain

$$\begin{array}{ccc}\hfill \left|K_n^G\left(u;x\right)-u\left(x\right)\right|& \le & \left|u^{\prime }\left(x\right)\right|K_n^G\left(\left|t-x\right|;x\right)+K_n^G\left(\left|R_1\left(t\right)\right|;x\right)\hfill \\ & \le & {∥u^{\prime }∥}_{\infty }{K}_n^G\left(\left|t-x\right|;x\right)+\frac{1}{2}{∥u^{″}∥}_{\infty }{K}_n^G\left({\left(t-x\right)}^2;x\right).\hfill \end{array}$$

(26)

In (26), by using the Cauchy–Schwarz inequality, we get

$$\left|K_n^G\left(u;x\right)-u\left(x\right)\right|\le {∥u^{\prime }∥}_{\infty }{\left(K_n^G\left({\left(t-x\right)}^2;x\right)\right)}^{1/2}+\frac{1}{2}{∥u^{″}∥}_{\infty }{K}_n^G\left({\left(t-x\right)}^2;x\right).$$

(27)

For $v\in C_{\mathcal{B}}\left(\left[0,\infty \right)\right)$, we can write

$$\begin{array}{ccc}\hfill \left|K_n^G\left(v;x\right)-v\left(x\right)\right|& \le & \left|K_n^G\left(\left(v-u\right);x\right)-\left(v-u\right)\left(x\right)\right|+\left|K_n^G\left(u;x\right)-u\left(x\right)\right|\hfill \\ & \le & K_n^G\left(\left|v-u\right|;x\right)+\left|\left(v-u\right)\left(x\right)\right|+\left|K_n^G\left(u;x\right)-u\left(x\right)\right|\hfill \\ & \le & {∥v-u∥}_{\infty }{K}_n^G\left(1;x\right)+{∥v-u∥}_{\infty }+\left|K_n^G\left(u;x\right)-u\left(x\right)\right|.\hfill \end{array}$$

(28)

Because $u\in C_{\mathcal{B}}^{\left(2\right)}\left(\left[0,\infty \right)\right)$, there exists a $c_1>0$ such that ${∥u^{\prime }∥}_{\infty }=c_1.$ Therefore, applying (27) to (28), by (21) and (22), we obtain

$$\begin{array}{ccc}\hfill \left|K_n^G\left(v;x\right)-v\left(x\right)\right|& \le & 2{∥v-u∥}_{\infty }+\frac{1}{2}{∥u^{″}∥}_{\infty }{K}_n^G\left({\left(t-x\right)}^2;x\right)\hfill \\ & & +{∥u^{\prime }∥}_{\infty }{\left(K_n^G\left({\left(t-x\right)}^2;x\right)\right)}^{1/2}\hfill \\ & \le & 2K\left(v;{\varsigma }_n^x\right)+c_1\sqrt{{\varsigma }_n^x}.\hfill \end{array}$$

(29)

Lastly, applying (23) to (29), we acquire

$$\left|K_n^G\left(v;x\right)-v\left(x\right)\right|\le c_2{\omega }_2\left(v;\sqrt{{\varsigma }_n^x}\right)+c_1\sqrt{{\varsigma }_n^x},$$

where $c_2>0$. Choosing $c_0=\max \left\{c_1,c_2\right\}$, we obtain the desired result. □

Let $A\subseteq \left[0,\infty \right)$ and $\varphi \in \left(0,1\right]$. For $v\in C_{\mathcal{B}}\left(\left[0,\infty \right)\right)$, a class of Lipschitz-type functions denoted by $Li{p}_{M_v}\left(A,\varphi \right)$ is defined as follows:

$$\left|v\left(t\right)-v\left(x\right)\right|\le M_v{\left|t-x\right|}^{\varphi },$$

(30)

where $t\in \overline{A}$, $x\ge 0$, $M_v$ is a constant, and $\overline{A}$ is the closure of A in $\left[0,\infty \right)$.

Theorem 4.

If $v\in Li{p}_{Mv}\left(A,\varphi \right)$, then we have the following inequality:

$$\left|K_n^G\left(v;x\right)-v\left(x\right)\right|\le M_v\left\{{\left(\sqrt{{\varsigma }_n^x}\right)}^{\varphi }+2{\left(d\left(x,A\right)\right)}^{\varphi }\right\},$$

where $A\subset \left[0,\infty \right)$, $x\in \left[0,\infty \right)$ and $\varphi \in \left(0,1\right]$, ${\varsigma }_n^x$ is given as in (18), and $M_v$ is a constant depending on v.

Proof. 

Let $x\in \left[0,\infty \right)$ and $y\in \overline{A}$. For $v\in Li{p}_{M_v}\left(A,\varphi \right)$, we can write

$$\begin{array}{ccc}\hfill \left|K_n^G\left(v;x\right)-v\left(x\right)\right|& \le & K_n^G\left(\left|v-v\left(y\right)\right|;x\right)+K_n^G\left(\left|v\left(x\right)-v\left(y\right)\right|;x\right)\hfill \\ & \le & M_v\left\{K_n^G\left({\left|t-y\right|}^{\varphi }.1;x\right)+K_n^G\left({\left|x-y\right|}^{\varphi };x\right)\right\}\hfill \\ & =& M_v\left\{K_n^G\left({\left|t-y\right|}^{\varphi }.1;x\right)+{\left|x-y\right|}^{\varphi }{K}_n^G\left(1;x\right)\right\}.\hfill \end{array}$$

(31)

In (31), from Hölder’s inequality for $a=\frac{2}{\varphi }$ and $b=\frac{2}{2-\varphi }$ such that $\frac{1}{a}+\frac{1}{b}=1$, we obtain

$$\begin{array}{ccc}\hfill \left|K_n^G\left(v;x\right)-v\left(x\right)\right|& \le & M_v\left\{{\left(K_n^G\left({\left|t-x\right|}^{\varphi a};x\right)\right)}^{1/a}{\left(K_n^G\left(1^b;x\right)\right)}^{1/b}+2{\left(d\left(x,A\right)\right)}^{\varphi }\right\}\hfill \\ & =& M_v\left\{{\left(K_n^G\left({\left(t-x\right)}^2;x\right)\right)}^{\varphi /2}+2{\left(d\left(x,A\right)\right)}^{\varphi }\right\}\hfill \\ & =& M_v\left\{{\left(\sqrt{{\varsigma }_n^x}\right)}^{\varphi }+2{\left(d\left(x,A\right)\right)}^{\varphi }\right\},\hfill \end{array}$$

which completes the proof. □

Remark 1.

In Theorems 2–4, ${\varsigma }_n^x$ is depend on x and choosing of ${\rho }_n$, ${\sigma }_n$, and $\left({\tau }_n\right)$. ${\rho }_n$, ${\sigma }_n$, and $\left({\tau }_n\right)$ must be non-negative real sequences satisfying ${\varsigma }_n^x\ge 0$. Otherwise, these theorems become invalid. For example, if ${\sigma }_n\ge 1$ and ${\left({\sigma }_n-1\right)}^2\ge \frac{1}{n}$, then ${\varsigma }_n^x\ge 0$. This is not only possible condition such that ${\varsigma }_n^x\ge 0$.

5. Some Comparisons

In this section, we present an example demonstrating concretely the approximation of the operator $K_n^G.$

Example 1.

Let v be a real-valued function on $\left[0,\infty \right)$ such that $v\left(x\right)=x^4{e}^{4x}$.

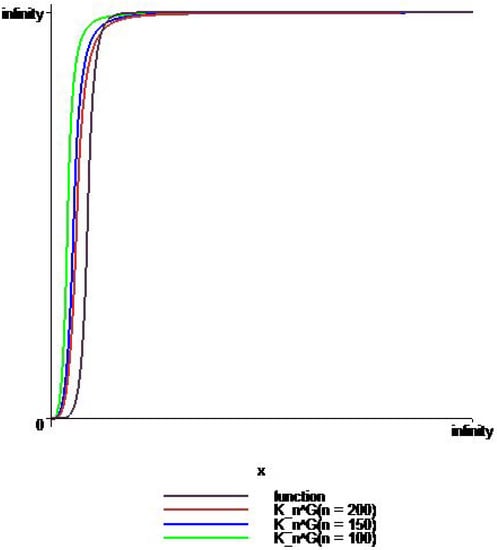
In Figure 1, we compare the approximation of $K_n^G\left(v;x\right)$ to $v\left(x\right)$ on $\left[0,\infty \right)$ for increasing value of n by choosing ${\rho }_n=n^{-1/20}$ such that ${\tau }_n=n{\rho }_n$, i.e., ${\tau }_n=n^{19/20}$ and ${\sigma }_n=1-50n^{-1}$. We see that the approximation of the operator $K_n^G$ becomes better for the increasing value of n.

Figure 1. Approximation by $K_{200}^G\left(v;x\right)$ (orange), $K_{150}^G\left(v;x\right)$ (blue), and $K_{100}^G\left(v;x\right)$ (green) to $v\left(x\right)$ (violet) on $\left[0,\infty \right)$ for ${\rho }_n=n^{-1/20}$, such that ${\tau }_n=n{\rho }_n$, i.e., ${\tau }_n=n^{19/20}$ and ${\beta }_n=1-50n^{-1}$.

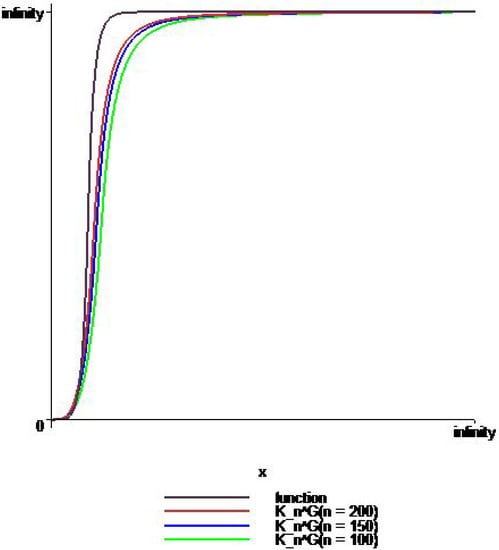
In Figure 2, we compare the approximation of $K_n^G\left(v;x\right)$ to $v\left(x\right)$ on $\left[0,\infty \right)$ for increasing value of n by choosing ${\rho }_n=n^{-1/20}$, such that ${\tau }_n=n{\rho }_n$; i.e., ${\tau }_n=n^{19/20}$ and ${\sigma }_n=1+50n^{-1}$. Similarly, we see that the approximation of the operator $K_n^G$ becomes better for increasing value of n.

Figure 2. Approximation by $K_{200}^G\left(v;x\right)$ (orange), $K_{150}^G\left(v;x\right)$ (blue), and $K_{100}^G\left(v;x\right)$ (green) to $v\left(x\right)$ (violet) on $\left[0,\infty \right)$ for ${\rho }_n=n^{-1/20}$, such that ${\tau }_n=n{\rho }_n$, i.e., ${\tau }_n=n^{19/20}$ and ${\beta }_n=1+50n^{-1}$.

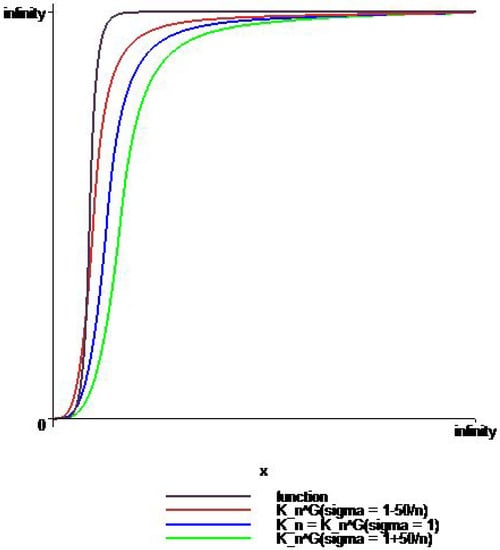
In Figure 3, we compare the approximation of $K_{200}^G\left(v;x,{\sigma }_n^1\right)$, $K_{200}^G\left(v;x,{\sigma }_n^2\right)={\mathcal{K}}_{200}\left(v;x\right)$ and $K_{200}^G\left(v;x,{\sigma }_n^3\right)$ to $v\left(x\right)$ on $\left[0,\infty \right)$ by choosing ${\rho }_n=n^{-1/20}$, such that ${\gamma }_n=n{\rho }_n$, i.e., ${\tau }_n=n^{19/20}$, and ${\sigma }_n^1=1-50n^{-1}$, ${\sigma }_n^2=1$ and ${\sigma }_n^3=1+50n^{-1}$, which satisfies the opportunity of comparison the operator $K_n^G$ with the operator ${\mathcal{K}}_n$ defined by (3). We can see that $K_n^G$ has at least better approximation than ${\mathcal{K}}_n.$

Figure 3. Comparison of the approximations by $K_{200}^G\left(v;x,{\sigma }_n^1=1-50n^{-1}\right)$ (orange), $K_{200}^G\left(v;x,{\sigma }_n^2=1\right)={\mathcal{K}}_{200}\left(v;x\right)$ (blue), and $K_{200}^G\left(v;x,{\sigma }_n^3=1+50n^{-1}\right)$ (green) to $v\left(x\right)$ (violet) on $\left[0,\infty \right)$.

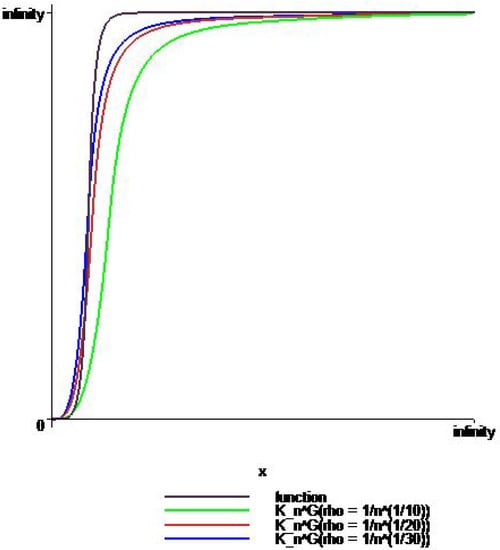
In Figure 4, we compare the approximation of $K_{200}^G\left(v;x,{\rho }_n^1\right)$, $K_{200}^G\left(v;x,{\rho }_n^2\right)$, and $K_{200}^G\left(v;x,{\rho }_n^3\right)$ to $v\left(x\right)$ on $\left[0,\infty \right)$ by choosing ${\sigma }_n=1-50n^{-1}$, ${\rho }_n^1=n^{-1/30}$, ${\rho }_n^2=n^{-1/20}$, and ${\rho }_n^3=n^{-1/10}$, such that ${\tau }_n^i=n{\rho }_n^i$ for $i=1,2,3$. We have better approximation for ${\rho }_n^1=n^{-1/30}$ than the others.

Figure 4. Comparison of the approximations by $K_{200}^G\left(v;x,{\rho }_n^1=n^{-1/30}\right)$ (blue), $K_{200}^G\left(v;x,{\rho }_n^2=n^{-1/20}\right)$ (orange) and $K_{200}^G\left(v;x,{\rho }_n^3=n^{-1/10}\right)$ (green) to $v\left(x\right)$ (violet) on $\left[0,\infty \right)$.

6. Conclusions

In this study, we have introduced a new Kantorovich-type rational operator reducible to the Kantorovich-type rational operator defined by (3), and we have been obtained its rates of convergence. The exemplifying application of this operator has demonstrated that the new Kantorovich-type rational operator has at least better approximating results depending on choice of the sequences ${\rho }_n$, ${\sigma }_n$, and the fuction v than the existing Kantorovich-type operator defined by (3) (see Figure 3). Obtainig a general result for the better approximation for the new Kantorovich-type rational operator and the Kantorovich-type rational operator defined by (3) is an open problem for future work motivated by this study.