Analysis of a Class of Stochastic Animal Behavior Models under Specific Choice Preferences
Abstract
:1. Introduction and Preliminaries
- We propose a general functional equation with more than two options, focusing on food location and the chosen side;
- Our proposed model generalizes many models in the existing literature and opens a new avenue of research within mathematical psychology and learning theory;
- We also discuss Hyers–Ulam and Hyers–Ulam–Rassias stability for the proposed system;
- We present some examples to show the importance of our results within this field of study.
2. Main Results
- Let be a class containing all continuous real-value functions satisfying and where and with . There is also a subset of , such that is a Banach space (for details, see [17]);
- Let be contraction mappings with contractive coefficients , respectively, with ;
- Let be a non-expansive mapping with for and ;
- The mappings satisfy the following conditions:for all with and where ;
- Let be a fixed function. Then, for every that satisfies , there is a unique , such that and for ;
- Let . Then, for every that satisfies , there is a unique , such that and for .
- Let be contraction mappings with contractive coefficients , respectively, with .
- Points exist such that and .
3. Stability Analysis
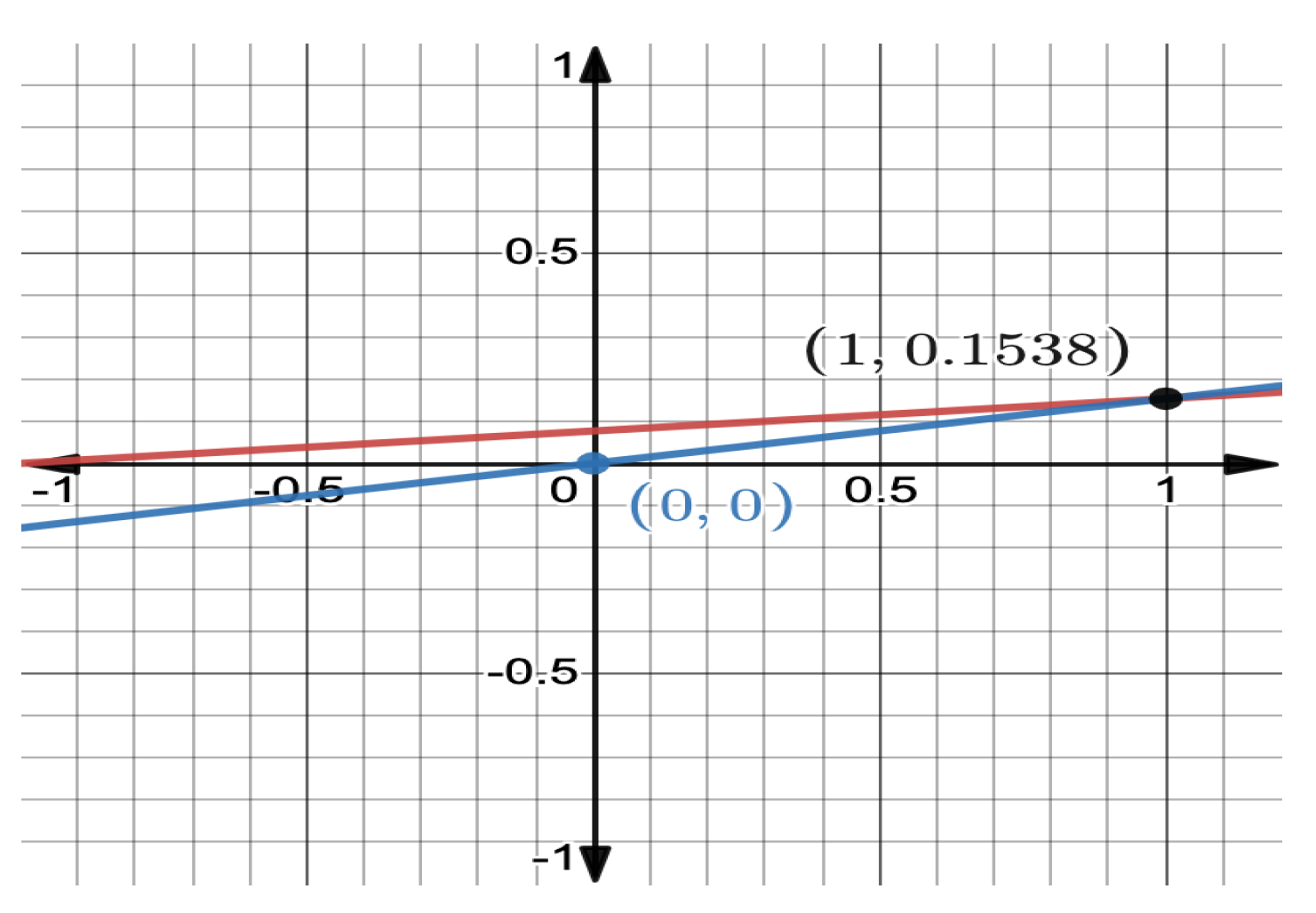
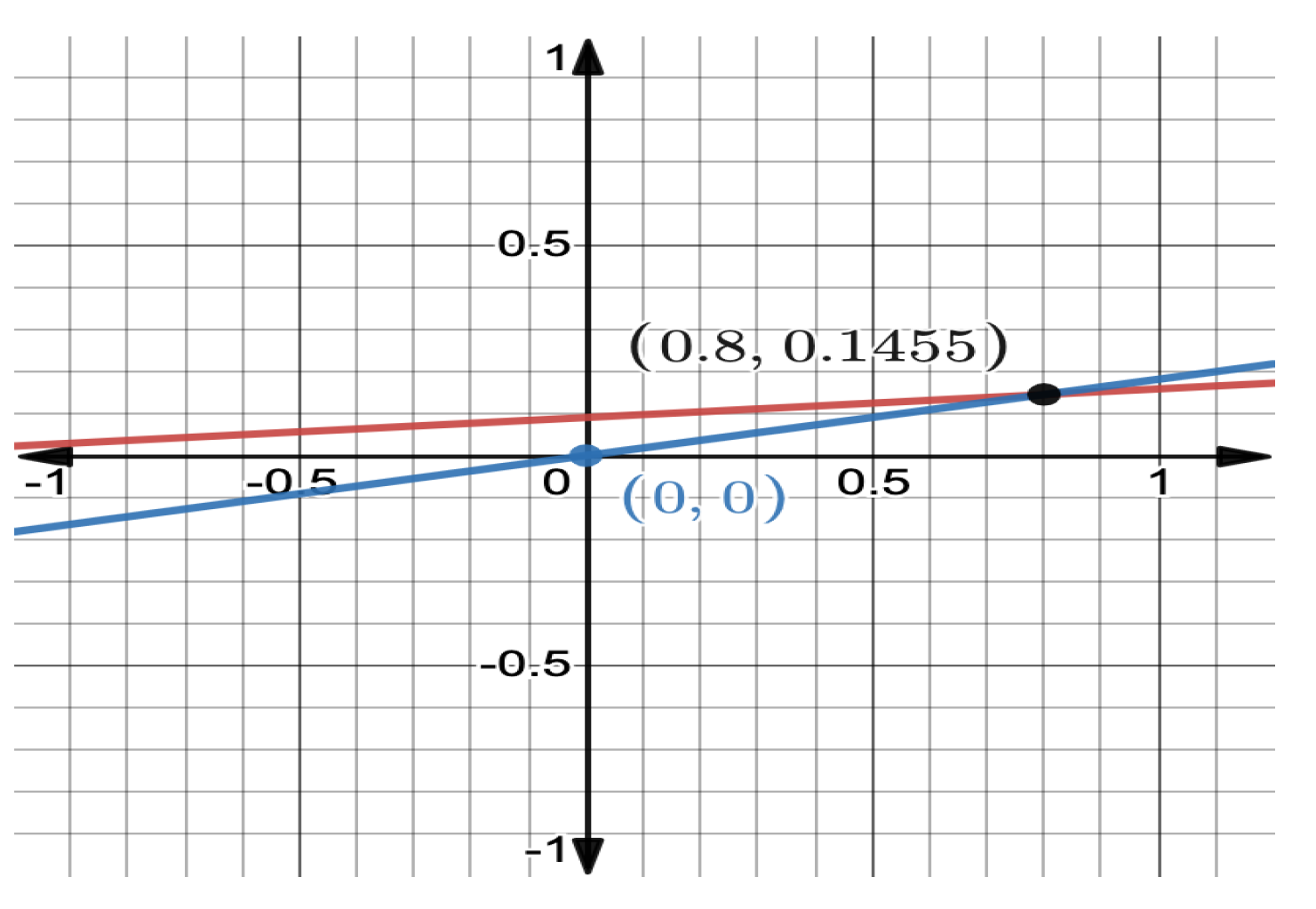
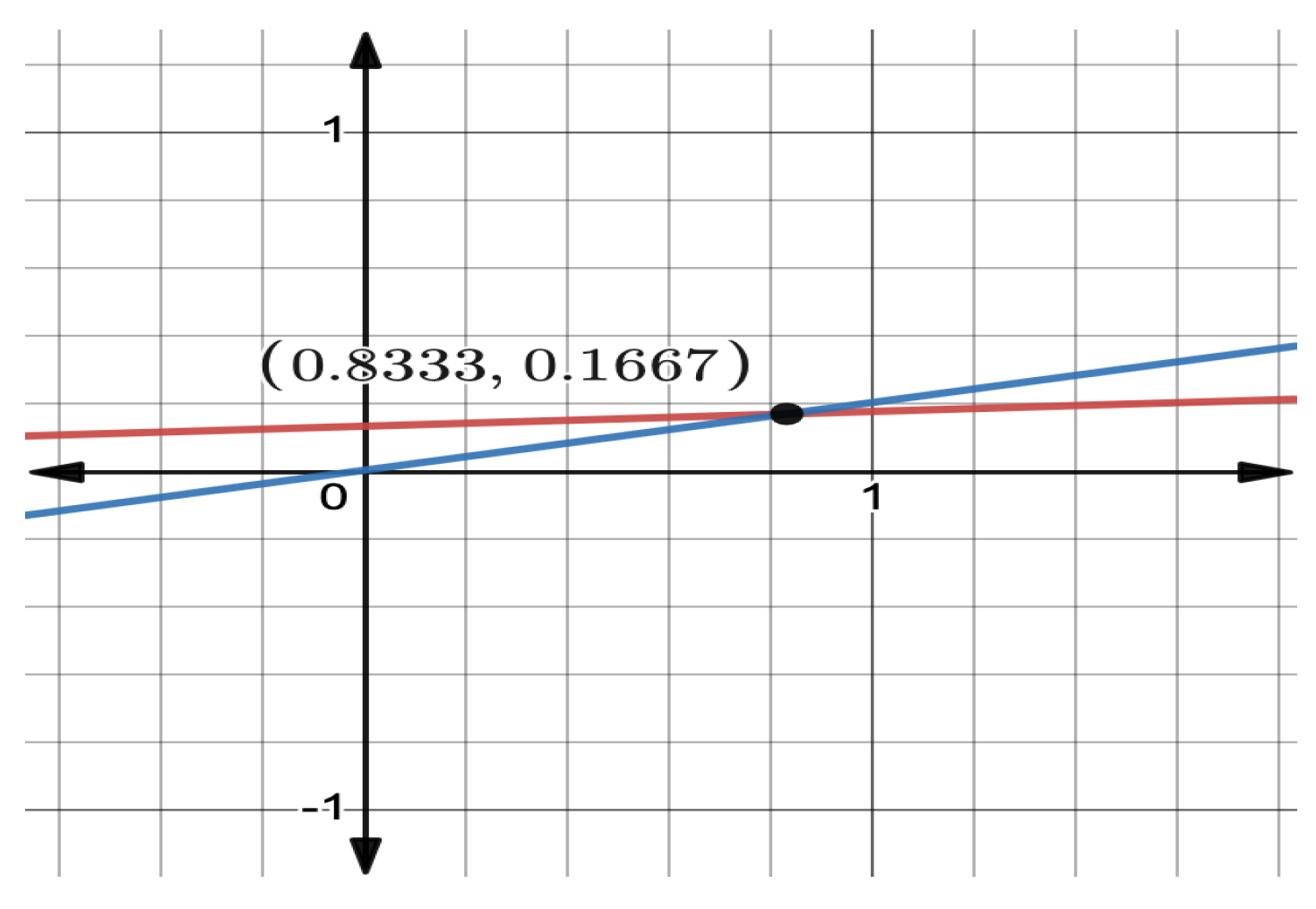
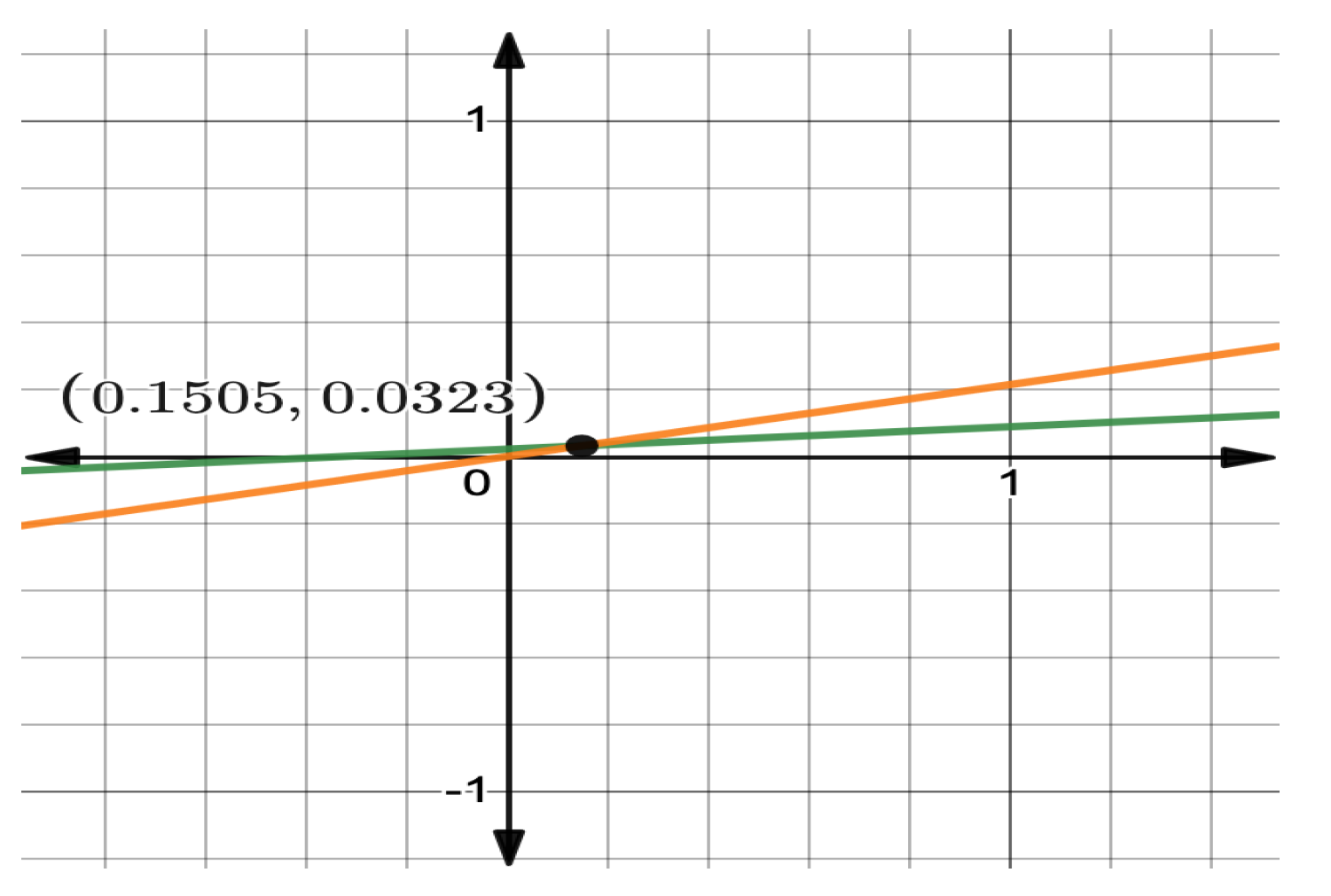
4. Some Illustrative Examples
5. Conclusions
- Is there another method for establishing the conclusions of Theorems 2 and 3?
- Is it possible to prove Theorem 2 without using Condition ?
- What would happen if an animal did not react to any particular trial?
- Can we extend the proposed approach to discuss the behavior of animals in situations with more than four choices?
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brenner, S. The genetics of Caenorhabditis elegans. Genetics 1974, 77, 71–94. [Google Scholar] [CrossRef] [PubMed]
- Broom, D.M.; Fraser, A.F. Domestic Animal Behaviour and Welfare, 5th ed.; Gutenberg Press: Tarxien, Malta, 2015. [Google Scholar]
- Marchant-Forde, J.N. The science of animal behavior and welfare: Challenges, opportunities, and global perspective. Front. Vet. Sci. 2015, 2, 16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fatjó, J.; Bowen, J. Behavior and medical problems in pet animals. Adv. Small Anim. Care 2020, 1, 25–33. [Google Scholar] [CrossRef]
- Berger-Tal, O.; Saltz, D. Conservation Behavior, Applying Behavioral Ecology to Wildlife Conservation and Management; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Luce, R.I.; Suppes, P. Preference, utility and subjective probability. In Handbook of Mathematical Psychology; Luce, R.D., Bush, R.I., Galanter, E., Eds.; Wiley: New York, NY, USA, 1965; Volume 111. [Google Scholar]
- Gamson, W.A. Experimental studies of coalition formation. In Advances in Experimental Social Psychology; Berkowitz, L., Ed.; Academic Press: New York, NY, USA, 1964; Volume 1. [Google Scholar]
- Gamson, W.A. An Experimental test of a theory of coalition formation. Am. Sociol. Rev. 1961, 26, 565–573. [Google Scholar] [CrossRef]
- Estes, W.K. Toward a statistical theory of learning. Psychol. Rev. 1950, 57, 94–107. [Google Scholar] [CrossRef] [Green Version]
- Estes, W.K.; Straughan, J.H. Analysis of a verbal conditioning situation in terms of statistical learning theory. Exp. Psychol. 1954, 47, 225–234. [Google Scholar] [CrossRef] [PubMed]
- Bush, A.A.; Wilson, T.R. Two-choice behavior of paradise fish. J. Exp. Psych. 1956, 51, 315–322. [Google Scholar] [CrossRef] [PubMed]
- Bush, R.; Mosteller, F. Stochastic Models for Learning; Wiley: New York, NY, USA, 1955. [Google Scholar]
- Gerlai, R.; Hogan, J.A. Learning to find the opponent: An ethological analysis of the behavior of paradise fish (Macropodus opercularis) in intra- and interspecific encounters. J. Comp. Psychol. 1992, 106, 306–315. [Google Scholar] [CrossRef]
- Warren, J.M. Reversal learning by paradise fish (Macropodus opercularis). J. Comp. Physiol. Psychol. 1960, 53, 376–378. [Google Scholar] [CrossRef]
- Turab, A.; Ali, W.; Park, C. A unified fixed point approach to study the existence and uniqueness of solutions to the generalized stochastic functional equation emerging in the psychological theory of learning. AIMS Math. 2022, 7, 5291–5304. [Google Scholar] [CrossRef]
- Epstein, B. On a difference equation arising in a learning-theory model. Israel J. Math. 1966, 4, 145–152. [Google Scholar] [CrossRef]
- Turab, A.; Sintunavarat, W. Corrigendum: On analytic model for two-choice behavior of the paradise fish based on the fixed point method, J. Fixed Point Theory Appl. 2019, 21:56. J. Fixed Point Theory Appl. 2020, 22, 82. [Google Scholar] [CrossRef]
- Turab, A.; Sintunavarat, W. On the solution of the traumatic avoidance learning model approached by the Banach fixed point theorem. J. Fixed Point Theory Appl. 2020, 22, 50. [Google Scholar] [CrossRef]
- Berinde, V.; Khan, A.R. On a functional equation arising in mathematical biology and theory of learning. Creat. Math. Inform. 2015, 24, 9–16. [Google Scholar] [CrossRef]
- Turab, A.; Sintunavarat, W. On the solutions of the two preys and one predator type model approached by the fixed point theory. Sadhana 2020, 45, 211. [Google Scholar] [CrossRef]
- Istrăţescu, V.I. On a functional equation. J. Math. Anal. Appl. 1976, 56, 133–136. [Google Scholar] [CrossRef]
- Schein, E.H. The effect of reward on adult imitative behavior. J. Abnorm. Soc. Psychol. 1954, 49, 389–395. [Google Scholar] [CrossRef]
- Miller, N.E.; Dollard, J. Social Learning and Imitation; Yale University Press: New Haven, CT, USA, 1941. [Google Scholar]
- Schwartz, N. An experimental Study of Imitation. The Effects of Reward and Age. Ph.D. Thesis, Radcliffe College, Cambridge, MA, USA, 1953. [Google Scholar]
- Grant, D.A.; Hake, H.W.; Hornseth, J.P. Acquisition and extinction of a verbal conditioned response with differing percentages of reinforcement. Exp. Psychol. 1951, 42, 1–5. [Google Scholar] [CrossRef]
- Humphreys, L.G. Acquisition and extinction of verbal expectations in a situation analogous to conditioning. Exp. Psychol. 1939, 25, 294–301. [Google Scholar] [CrossRef]
- Jarvik, M.E. Probability learning and a negative recency effect in the serial anticipation of alternative symbols. Exp. Psychol. 1951, 41, 291–297. [Google Scholar] [CrossRef]
- Turab, A.; Park, W.G.; Ali, W. Existence, uniqueness, and stability analysis of the probabilistic functional equation emerging in mathematical biology and the theory of learning. Symmetry 2021, 13, 1313. [Google Scholar] [CrossRef]
- Turab, A.; Brzdęk, J.; Ali, W. On solutions and stability of stochastic functional equations emerging in psychological theory of learning. Axioms 2022, 11, 143. [Google Scholar] [CrossRef]
- Turab, A.; Sintunavarat, W. On the solution of Bush and Wilson’s stochastic model for two-choice behavior of the paradise fish approached by the fixed-point method. In Proceedings of the Seventh International Conference on Mathematics and Computing, Shibpur, India, 2–5 March 2021; Advances in Intelligent Systems and Computing; Giri, D., Choo, K.K.R., Ponnusamy, S., Meng, W., Akleylek, S., Maity, S.P., Eds.; Springer: Cham, Switzerland, 2022; Volume 1412. [Google Scholar] [CrossRef]
- Debnath, P. A mathematical model using fixed point Theorem for two-choice behavior of rhesus monkeys in a noncontingent environment. In Metric Fixed Point Theory. Forum for Interdisciplinary Mathematics; Debnath, P., Konwar, N., Radenović, S., Eds.; Springer: Singapore, 2021. [Google Scholar] [CrossRef]
- Aydi, H.; Karapinar, E.; Rakocevic, V. Nonunique fixed point theorems on b-metric spaces via simulation functions. Jordan J. Math. Stat. 2019, 12, 265–288. [Google Scholar]
- Karapinar, E. Recent advances on the results for nonunique fixed in various spaces. Axioms 2019, 8, 72. [Google Scholar] [CrossRef] [Green Version]
- Alsulami, H.H.; Karapinar, E.; Rakocevic, V. Ciric type nonunique fixed point theorems on b-metric spaces. Filomat 2017, 31, 3147–3156. [Google Scholar] [CrossRef]
- Lakzian, H.; Gopal, D.; Sintunavarat, W. New fixed point results for mappings of contractive type with an application to nonlinear fractional differential equations. J. Fixed Point Theory Appl. 2016, 18, 251–266. [Google Scholar] [CrossRef]
- Baradol, P.; Gopal, D.; Radenović, S. Computational fixed points in graphical rectangular metric spaces with application. J. Comput. Appl. Math. 2020, 375, 112805. [Google Scholar] [CrossRef]
- Banach, S. Sur les operations dans les ensembles abstraits et leur applications aux equations integrales. Fund. Math. 1922, 3, 133–181. [Google Scholar] [CrossRef]
- Ahmad, J.; Ullah, K.; Arshad, M.; de la Sen, M.; Ma, Z. Convergence results on Picard-Krasnoselskii hybrid iterative process in CAT(0) spaces. Open Math. 2021, 19, 1713–1720. [Google Scholar] [CrossRef]
- Srivastava, J. Introduction of new Picard–S hybrid iteration with application and some results for nonexpansive mappings. Arab. J. Math. Sci. 2022, 28, 61–76. [Google Scholar] [CrossRef]
- Almusawa, H.; Hammad, H.A.; Sharma, N. Approximation of the fixed point for unified three-step iterative algorithm with convergence analysis in Busemann spaces. Axioms 2021, 10, 26. [Google Scholar] [CrossRef]
- Rassias, T.M. On the stability of the linear mapping in Banach spaces. Proc. Am. Math. Soc. 1978, 72, 297–300. [Google Scholar] [CrossRef]
- Hyers, D.H. On the stability of the linear functional equation. Proc. Nat. Acad. Sci. USA 1941, 27, 222–224. [Google Scholar] [CrossRef] [Green Version]
- Ulam, S.M. A Collection of the Mathematical Problems; Interscience Publ.: New York, NY, USA, 1960. [Google Scholar]
- Aoki, T. On the stability of the linear transformation in Banach spaces. J. Math. Soc. Jpn. 1950, 2, 64–66. [Google Scholar] [CrossRef]
- Hyers, D.H.; Isac, G.; Rassias, T.M. Stability of Functional Equations in Several Variables; Birkhauser: Basel, Switzerland, 1998. [Google Scholar]
- Bae, J.H.; Park, W.G. A fixed point approach to the stability of a Cauchy-Jensen functional equation. Abst. Appl. Anal. 2012, 2020, 205160. [Google Scholar] [CrossRef]
- Gachpazan, M.; Bagdani, O. Hyers-Ulam stability of nonlinear integral equation. Fixed Point Theory Appl. 2010, 2010, 927640. [Google Scholar] [CrossRef] [Green Version]
- Morales, J.S.; Rojas, E.M. Hyers-Ulam and Hyers-Ulam-Rassias stability of nonlinear integral equations with delay. Int. J. Nonlinear Anal. Appl. 2011, 2, 1–6. [Google Scholar]
- Turab, A.; Ali, W.; Nieto, J.J. On a unique solution of a T-maze model arising in the psychology and theory of learning. J. Funct. Spaces 2022, 2022, 6081250. [Google Scholar] [CrossRef]
- Maze Basics: T Maze. Available online: https://conductscience.com/maze/maze-basics-t-maze-test/ (accessed on 25 May 2022).
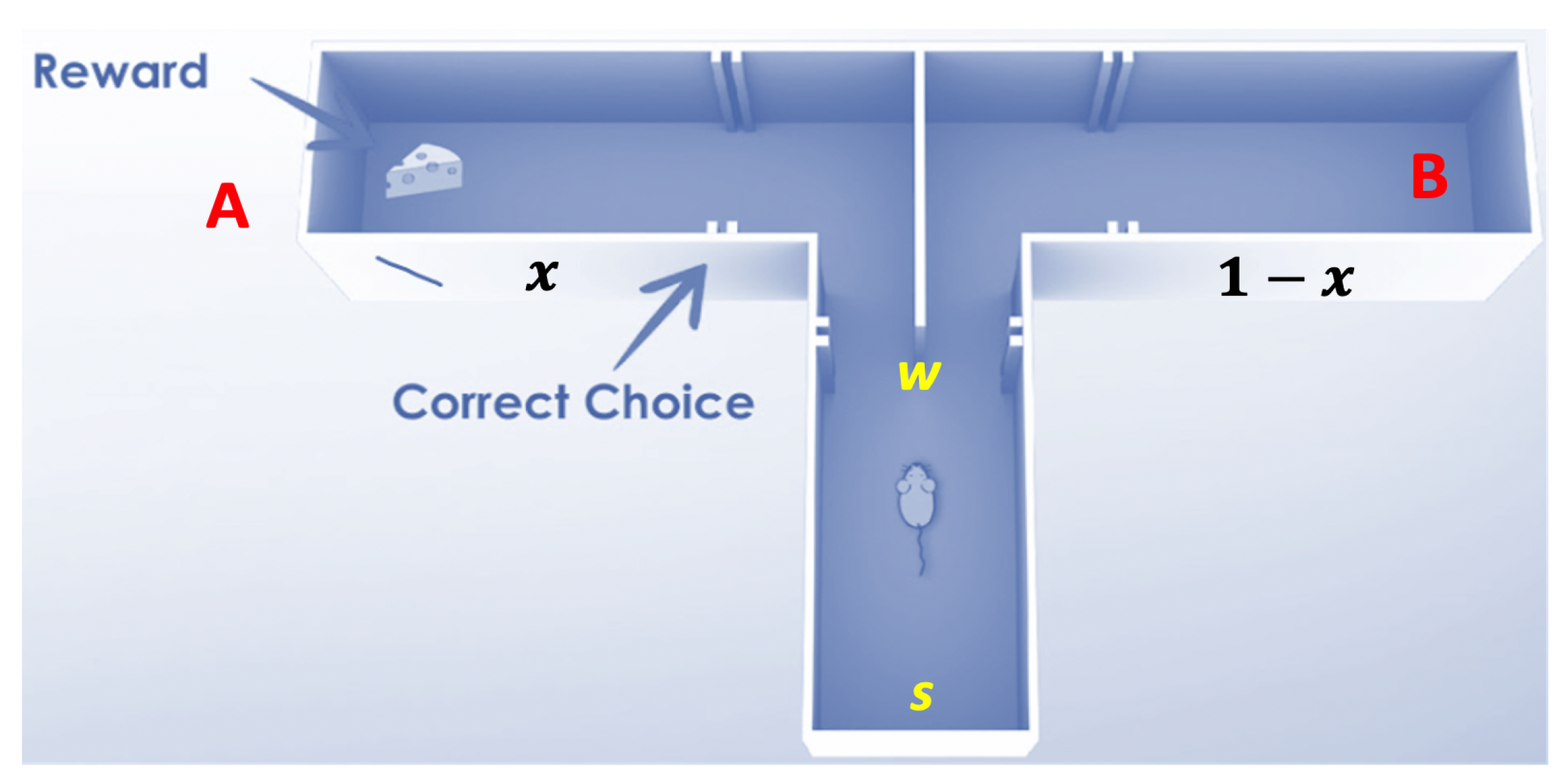
| Placement of Food | Side Chosen by Rat | Probability of Occurrence |
|---|---|---|
| A: Left Side | Left Turn (Food Side) | |
| A: Left Side | Right Turn (Non-Food Side) | |
| B: Right Side | Right Turn (Food Side) | |
| B: Right Side | Left Turn (Non-Food Side) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turab, A.; Mlaiki, N.; Fatima, N.; Mitrović, Z.D.; Ali, W. Analysis of a Class of Stochastic Animal Behavior Models under Specific Choice Preferences. Mathematics 2022, 10, 1975. https://doi.org/10.3390/math10121975
Turab A, Mlaiki N, Fatima N, Mitrović ZD, Ali W. Analysis of a Class of Stochastic Animal Behavior Models under Specific Choice Preferences. Mathematics. 2022; 10(12):1975. https://doi.org/10.3390/math10121975
Chicago/Turabian StyleTurab, Ali, Nabil Mlaiki, Nahid Fatima, Zoran D. Mitrović, and Wajahat Ali. 2022. "Analysis of a Class of Stochastic Animal Behavior Models under Specific Choice Preferences" Mathematics 10, no. 12: 1975. https://doi.org/10.3390/math10121975
APA StyleTurab, A., Mlaiki, N., Fatima, N., Mitrović, Z. D., & Ali, W. (2022). Analysis of a Class of Stochastic Animal Behavior Models under Specific Choice Preferences. Mathematics, 10(12), 1975. https://doi.org/10.3390/math10121975








