A Probabilistic Chaotic Image Encryption Scheme
Abstract
:1. Introduction
2. Related Work
| Algorithm 1: Wu et al.’s encryption scheme | |
Data: Color plain image P of size | |
Data: Secret key | |
Result: Cipher image | |
 | |
- The scheme is insecure against chosen-plain image attack.
- The secret key of the scheme is insensitive to all of its parameters.
- The scheme is lossy. The first pixel of the plain image cannot be recovered because , and are not part of the secret key.
- The scheme requires the parameters , and d to satisfy the restrictive conditions expressed in Equation (3).
3. The Chaotic Engine
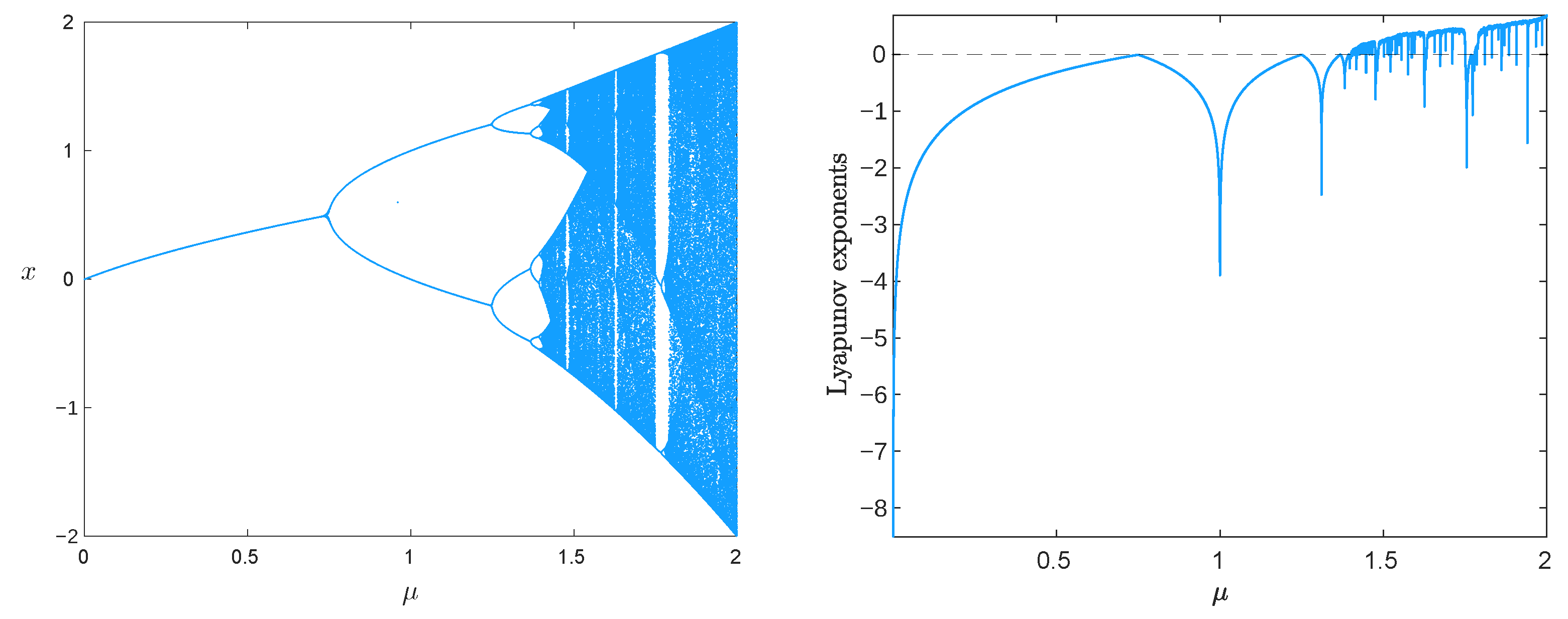
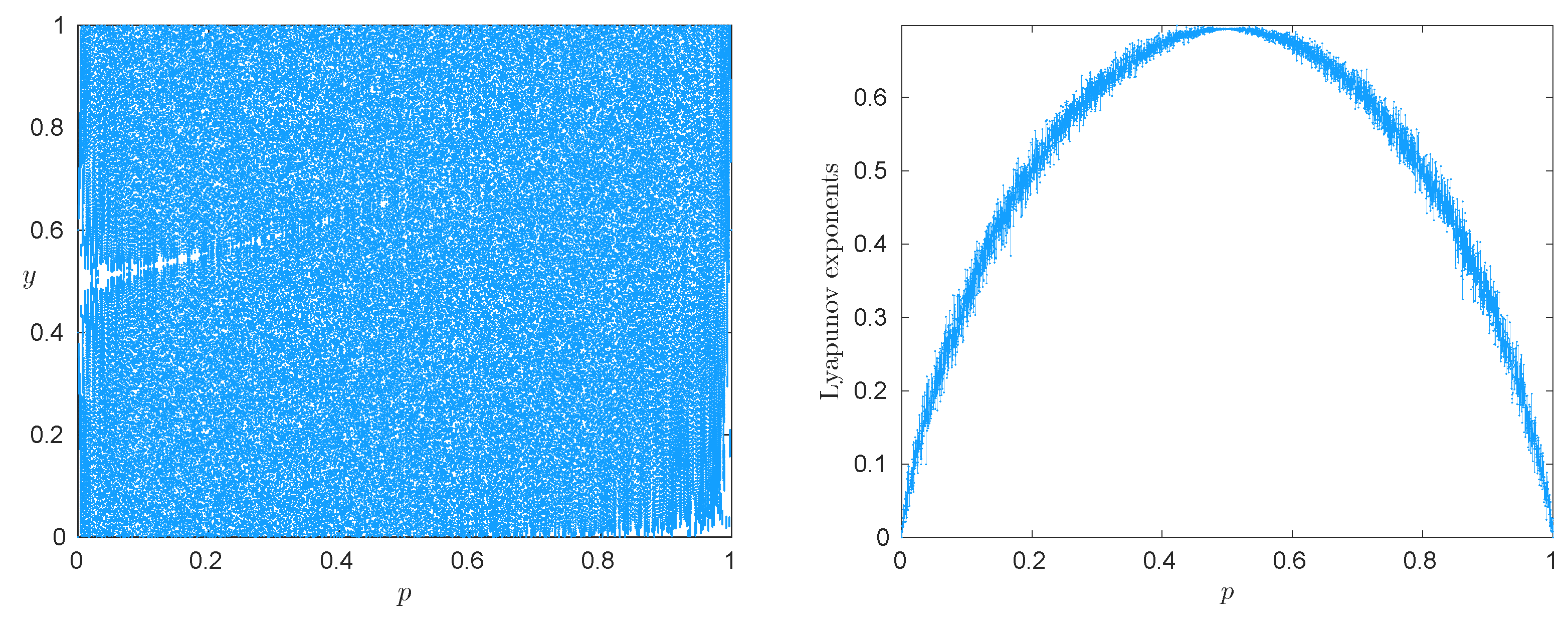
3.1. The Quadratic Map
3.2. The Skew-Tent Map
| Algorithm 2: The chaining algorithm (Rule C) | |
Data: Initial states and control parameters from secret key | |
Data: Number of elements ℓ | |
Result: Pseudorandom sequence of length ℓ | |
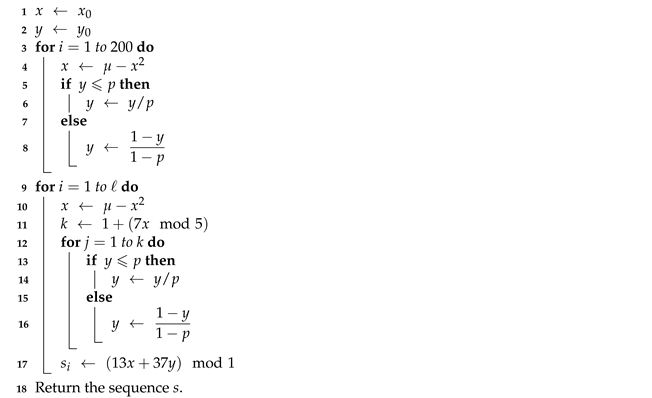 | |
4. The Proposed Scheme
| Algorithm 3: The (lossless) encryption scheme | |
Data: Plain image P of size | |
Data: Secret key | |
Data: Random number | |
Result: Cipher image | |
| 1 | |
| 2 | Preprocess(P)
|
| 3 | , where is the number of rounds
|
| 4 | Mask(), where is the number of rounds
|
| 5 | |
| 6 | Return the cipher image obtained by reshaping to size |
4.1. The Preprocessing Phase
4.2. The Permutation Phase
| Algorithm 4: The permutation phase of the proposed scheme | |
Data: Padded input image of size | |
Data: Number of rounds | |
Data: Initial states , and control parameters , p from secret key | |
Result: Shuffled image | |
 | |
4.3. The Masking Phase
| Algorithm 5: The masking phase of the lossless encryption scheme | |
Data: Shuffled image of size | |
Data: Initial states , and control parameters , from secret key | |
Data: Number of rounds | |
Result: Masked image | |
 | |
| Algorithm 6: The unmasking phase of the lossless decryption scheme | |
Data: Masked image of size | |
Data: Initial states , and control parameters , from secret key | |
Data: Number of rounds | |
Result: Unmasked image | |
 | |
| Algorithm 7: The masking phase of the lossy encryption scheme | |
Data: Shuffled image of size | |
Data: Initial states , and control parameters , from secret key | |
Data: Number of rounds | |
Result: Masked image | |
 | |
| Algorithm 8: The unmasking phase of the lossy decryption scheme | |
Data: Masked image of size | |
Data: Initial states , and control parameters , from secret key | |
Data: Number of rounds | |
Result: Unmasked image | |
 | |
4.4. Efficiency of the Proposed Scheme
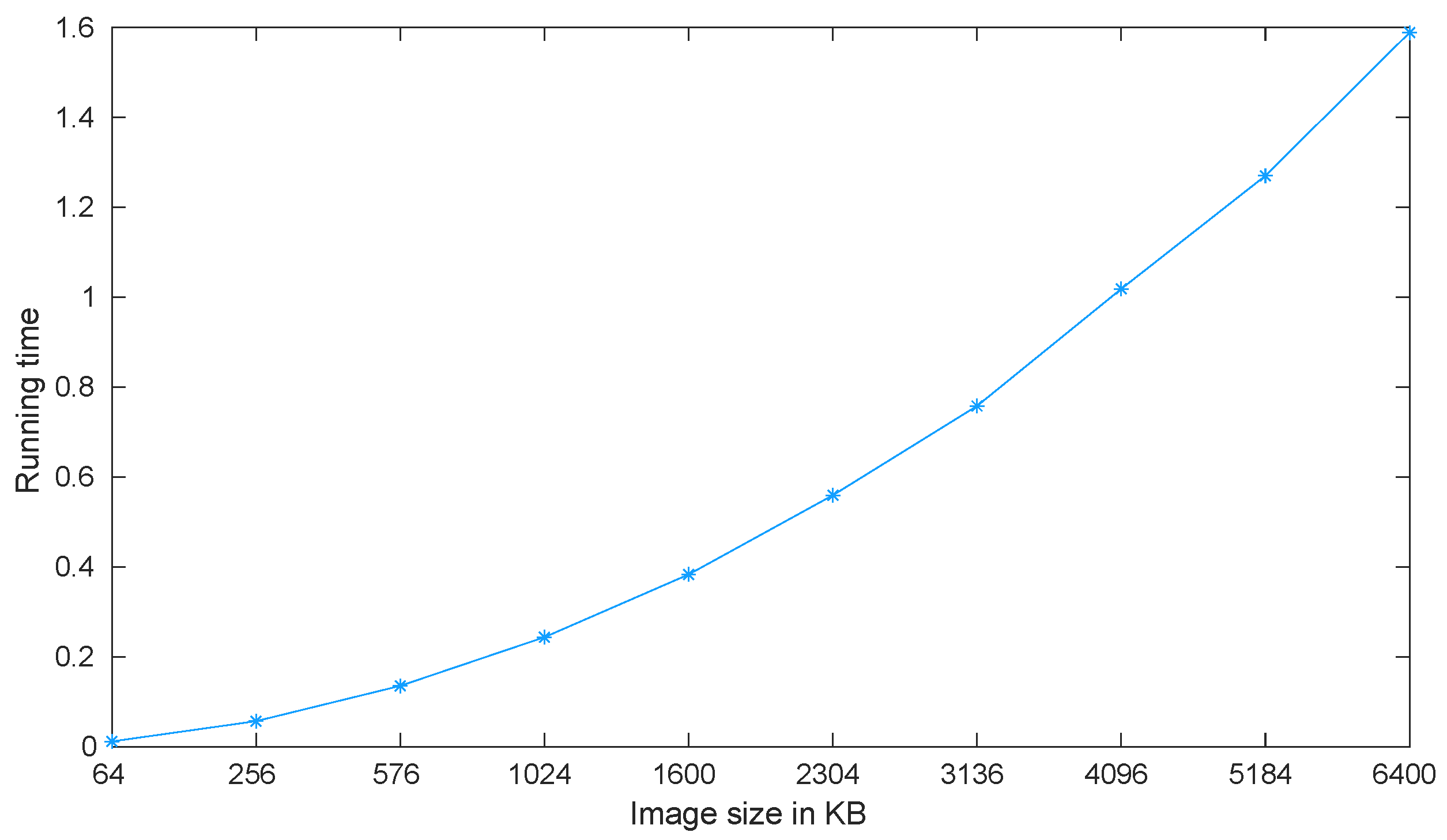
4.5. Running Speed
5. Statistical Analysis
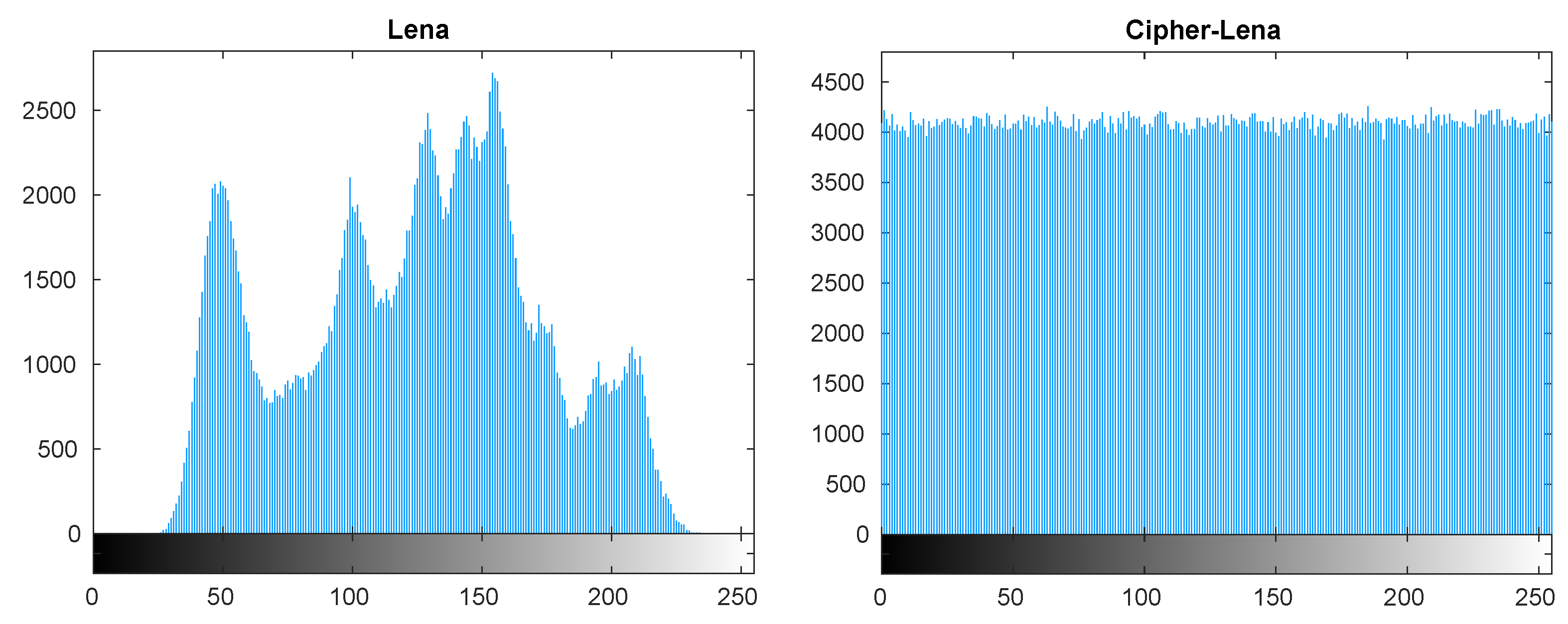
5.1. Histogram Analysis
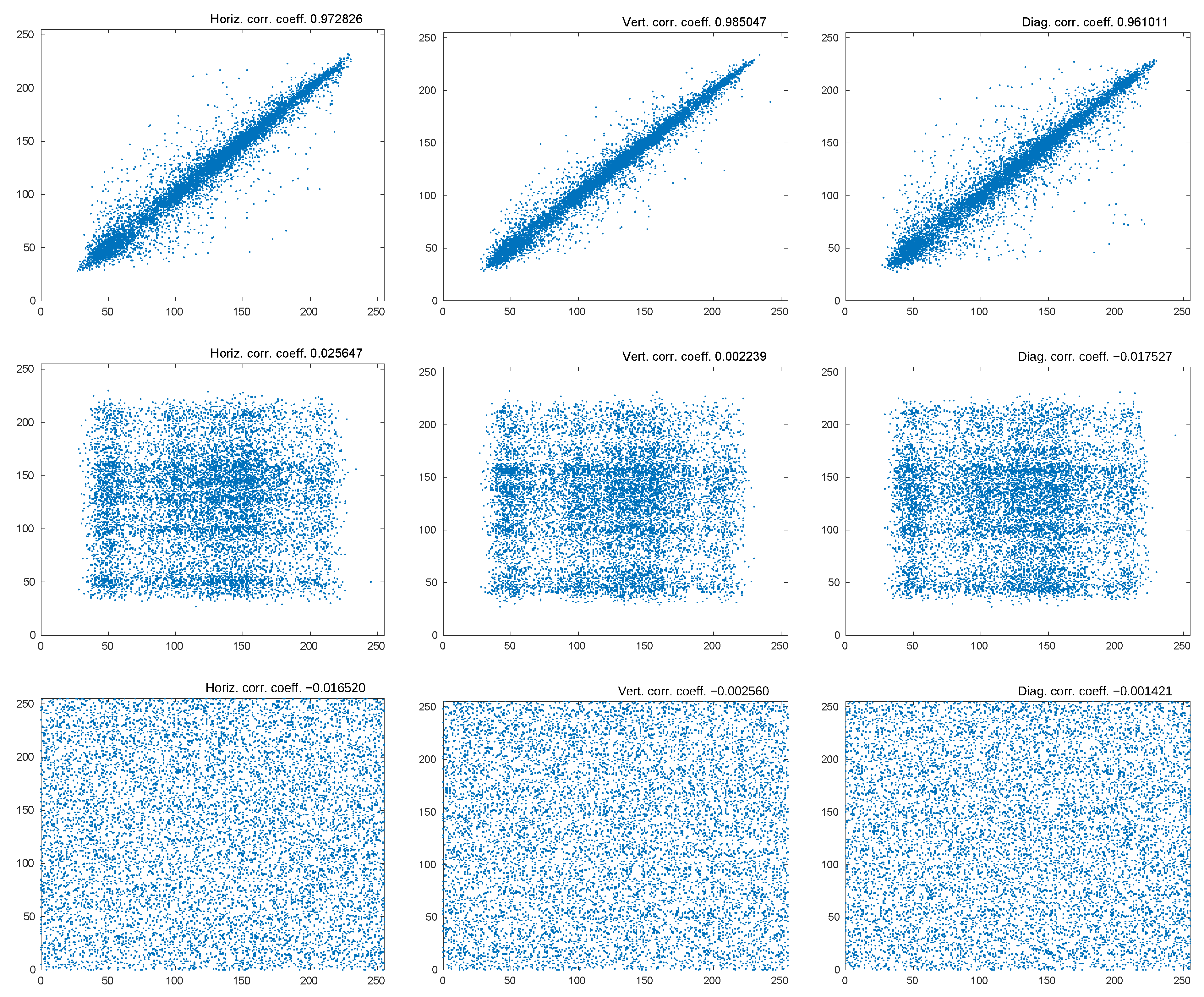
5.2. Correlation Analysis
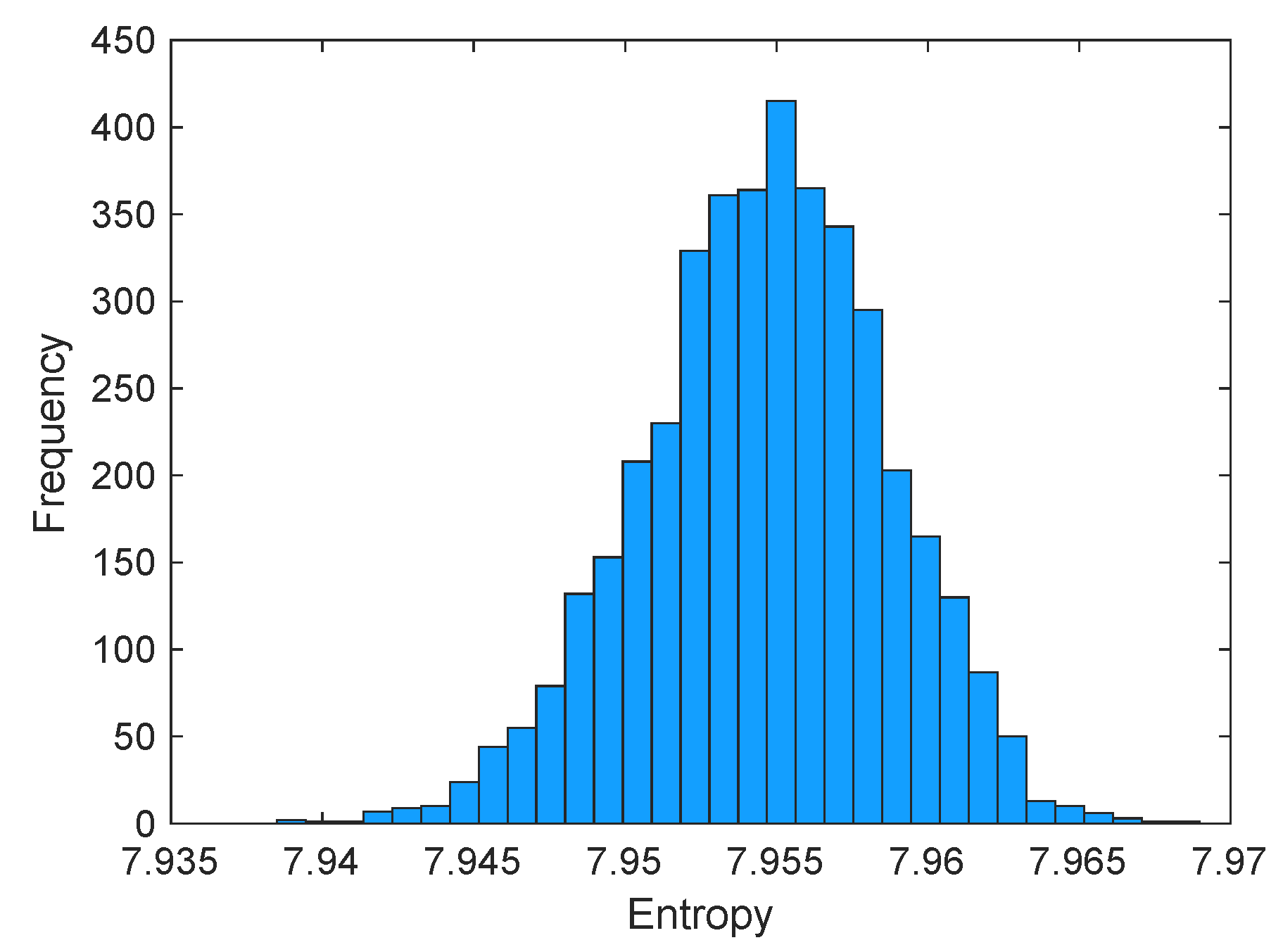
5.3. Entropy Analysis
5.4. Randomness Analysis
6. Security Analysis
6.1. Key Space
6.2. Differential Analysis
6.3. Key Sensitivity Analysis
6.4. Robustness to Common Attacks
6.5. Robustness against Common Image Processing Operations
6.5.1. Cropping
6.5.2. Noise Addition
6.5.3. JEPG Compression
7. Comparison with Existing Work
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fridrich, J. Symmetric ciphers based on two-dimensional chaotic maps. Int. J. Bifurc. Chaos 1998, 8, 1259–1284. [Google Scholar] [CrossRef]
- Chen, G.; Mao, Y.; Chui, C.K. A symmetric image encryption scheme based on 3D chaotic cat maps. Chaos Solitons Fractals 2004, 21, 749–761. [Google Scholar] [CrossRef]
- Behnia, S.; Akhshani, A.; Mahmodi, H.; Akhavan, A. Chaotic cryptographic scheme based on composition maps. Int. J. Bifurc. Chaos 2008, 18, 251–261. [Google Scholar] [CrossRef]
- Ye, R. A novel chaos-based image encryption scheme with an efficient permutation-diffusion mechanism. Opt. Commun. 2011, 284, 5290–5298. [Google Scholar] [CrossRef]
- Kanso, A.; Ghebleh, M. A novel image encryption algorithm based on a 3D chaotic map. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2943–2959. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X.; Kadir, A. Image encryption using DNA complementary rule and chaotic maps. Appl. Soft Comput. 2012, 12, 1457–1466. [Google Scholar] [CrossRef]
- Song, C.Y.; Qiao, Y.L.; Zhang, X.Z. An image encryption scheme based on new spatiotemporal chaos. Opt.-Int. J. Light Electron Opt. 2013, 124, 3329–3334. [Google Scholar] [CrossRef]
- Wang, X.; Liu, L.; Zhang, Y. A novel chaotic block image encryption algorithm based on dynamic random growth technique. Opt. Lasers Eng. 2015, 66, 10–18. [Google Scholar] [CrossRef]
- Rehaman, A.; Liao, X.; Kulsoom, A.; Abbas, S.A. Selective encryption for gray images based on chaos and DNA complementary rules. Multimed. Tools Appl. 2015, 74, 4655–4677. [Google Scholar] [CrossRef]
- Souyah, A.; Faraoun, K.M. An image encryption scheme combining chaos-memory cellular automata and weighted histogram. Nonlinear Dyn. 2016, 86, 639–653. [Google Scholar] [CrossRef]
- Xu, L.; Li, Z.; Li, J.; Hua, W. A novel bit-level image encryption algorithm based on chaotic maps. Opt. Lasers Eng. 2016, 78, 17–25. [Google Scholar] [CrossRef]
- Rehman, A.; Liao, X.; Kulsoom, A.; Ullah, S. A modified (Dual) fusion technique for image encryption using SHA-256 hash and multiple chaotic maps. Multimed. Tools Appl. 2016, 75, 11241–11266. [Google Scholar] [CrossRef]
- Belazi, A.; Abd El-Latif, A.A.; Belghith, S. A novel image encryption scheme based on substitution-permutation network and chaos. Signal Process. 2016, 128, 155–170. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, B.; Hu, Y.; Ran, Y. A novel color image encryption scheme using rectangular transform-enhanced chaotic tent maps. IEEE Access 2017, 5, 6429–6436. [Google Scholar]
- Wang, X.; Zhu, X.; Wu, X.; Zhang, Y. Image encryption algorithm based on multiple mixed hash functions and cyclic shift. Opt. Lasers Eng. 2018, 107, 370–379. [Google Scholar] [CrossRef]
- Nardo, L.G.; Nepomuceno, E.G.; Arias-Garcia, J.; Butusov, D.N. Image encryption using finite-precision error. Chaos Solitons Fractals 2019, 123, 69–78. [Google Scholar] [CrossRef]
- Wang, J.; Liu, L. A Novel Chaos-Based Image Encryption Using Magic Square Scrambling and Octree Diffusing. Mathematics 2022, 10, 457. [Google Scholar] [CrossRef]
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Menezes, A.J.; Van Oorschot, P.C.; Vanstone, S.A. Handbook of Applied Cryptography; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Daemen, J.; Rijmen, V. Reijndael: The Advanced Encryption Standard. Dr. Dobb’s J. Softw. Tools Prof. Program. 2001, 26, 137–139. [Google Scholar]
- Solak, E.; Cokal, C.; Yildiz, O.T.; Biyikoğlu, T. Cryptanalysis of Fridrich’s chaotic image encryption. Int. J. Bifurc. Chaos 2010, 20, 1405–1413. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Zou, L.; Song, A.; He, Z. On the security of 3D Cat map based symmetric image encryption scheme. Phys. Lett. A 2005, 343, 432–439. [Google Scholar] [CrossRef]
- Li, C.; Arroyo, D.; Lo, K.T. Breaking a chaotic cryptographic scheme based on composition maps. Int. J. Bifurc. Chaos 2010, 20, 2561–2568. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Wang, C.; Chen, H. A hyper-chaos-based image encryption algorithm using pixel-level permutation and bit-level permutation. Opt. Lasers Eng. 2017, 90, 238–246. [Google Scholar] [CrossRef]
- Kulsoom, A.; Xiao, D.; Abbas, S.A.; Rehman, A.U. An efficient and noise resistive selective image encryption scheme for gray images based on chaotic maps and DNA complementary rules. Multimed. Tools Appl. 2016, 75, 1–23. [Google Scholar] [CrossRef]
- Zhu, C.; Sun, K. Cryptanalyzing and improving a novel color image encryption algorithm using RT-enhanced chaotic tent maps. IEEE Access 2018, 6, 18759–18770. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, C.; Li, W.; Li, H.; Feng, W.; Qian, K. Image encryption algorithm with circle index table scrambling and partition diffusion. Nonlinear Dyn. 2021, 103, 2043–2061. [Google Scholar] [CrossRef]
- Hua, Z.; Zhu, Z.; Chen, Y.; Li, Y. Color image encryption using orthogonal Latin squares and a new 2D chaotic system. Nonlinear Dyn. 2021, 104, 4505–4522. [Google Scholar] [CrossRef]
- Gao, X.; Mou, J.; Xiong, L.; Sha, Y.; Yan, H.; Cao, Y. A fast and efficient multiple images encryption based on single-channel encryption and chaotic system. Nonlinear Dyn. 2022, 108, 613–636. [Google Scholar] [CrossRef]
- Wang, X.; Guan, N.; Zhao, H.; Wang, S.; Zhang, Y. A new image encryption scheme based on coupling map lattices with mixed multi-chaos. Sci. Rep. 2020, 10, 9784. [Google Scholar] [CrossRef]
- Crampin, M.; Heal, B. On the chaotic behaviour of the tent map. Teach. Math. Appl. Int. J. IMA 1994, 13, 83–89. [Google Scholar] [CrossRef]
- Michaels, A.J. Quantitative comparisons of digital chaotic circuits for use in communications. In Proceedings of the Joint INDS’11 & ISTET’11, Klagenfurt, Austria, 25–27 July 2011; pp. 1–8. [Google Scholar]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Hasler, M.; Maistrenko, Y.L. An introduction to the synchronization of chaotic systems: Coupled skew tent maps. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 1997, 44, 856–866. [Google Scholar] [CrossRef]
- Li, Y.; Xiao, D.; Deng, S.; Han, Q.; Zhou, G. Parallel Hash function construction based on chaotic maps with changeable parameters. Neural Comput. Appl. 2011, 20, 1305–1312. [Google Scholar] [CrossRef]
- Ghebleh, M.; Kanso, A.; Noura, H. An image encryption scheme based on irregularly decimated chaotic maps. Signal Process. Image Commun. 2014, 29, 618–627. [Google Scholar] [CrossRef]
- Kanso, A.; Ghebleh, M.; Noura, H. A variant of Baptista’s encryption scheme. Secur. Commun. Netw. 2015, 8, 3701–3712. [Google Scholar] [CrossRef]
- Ghebleh, M.; Kanso, A. A novel secret image sharing scheme using large primes. Multimed. Tools Appl. 2018, 77, 11903–11923. [Google Scholar] [CrossRef]
- Ghebleh, M.; Kanso, A. A novel efficient image encryption scheme based on chained skew tent maps. Neural Comput. Appl. 2019, 31, 2415–2430. [Google Scholar] [CrossRef]
- Kanso, A.; Ghebleh, M.; Alazemi, A. Efficient Image Encryption Scheme Based on 4-Dimensional Chaotic Maps. Informatica 2020, 31, 793–820. [Google Scholar] [CrossRef]
- Gilmore, R.; Lefranc, M. The Topology of Chaos; Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Chen, G.; Mou, X. On the dynamical degradation of digital piecewise linear chaotic maps. Int. J. Bifurc. Chaos 2005, 15, 3119–3151. [Google Scholar] [CrossRef] [Green Version]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E.; Leigh, S.; Levenson, M.; Vangel, M.; Banks, D.; Heckert, A.; et al. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. NIST Special Publication 800-22 Revision 1a 2010. Available online: https://nvlpubs.nist.gov/nistpubs/legacy/sp/nistspecialpublication800-22r1a.pdf (accessed on 19 January 2022).
- Diffie, W.; Hellman, M. New directions in cryptography. IEEE Trans. Inf. Theory 1976, 22, 644–654. [Google Scholar] [CrossRef] [Green Version]
- Shannon, C. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Noonan, J.P.; Agaian, S. NPCR and UACI randomness tests for image encryption. Cyber J. Multidiscip. J. Sci. Technol. J. Sel. Areas Telecommun. (JSAT) 2011, 1, 31–38. [Google Scholar]
- Farajallah, M.; El Assad, S.; Deforges, O. Fast and secure chaos-based cryptosystem for images. Int. J. Bifurc. Chaos 2016, 26, 1650021. [Google Scholar] [CrossRef] [Green Version]

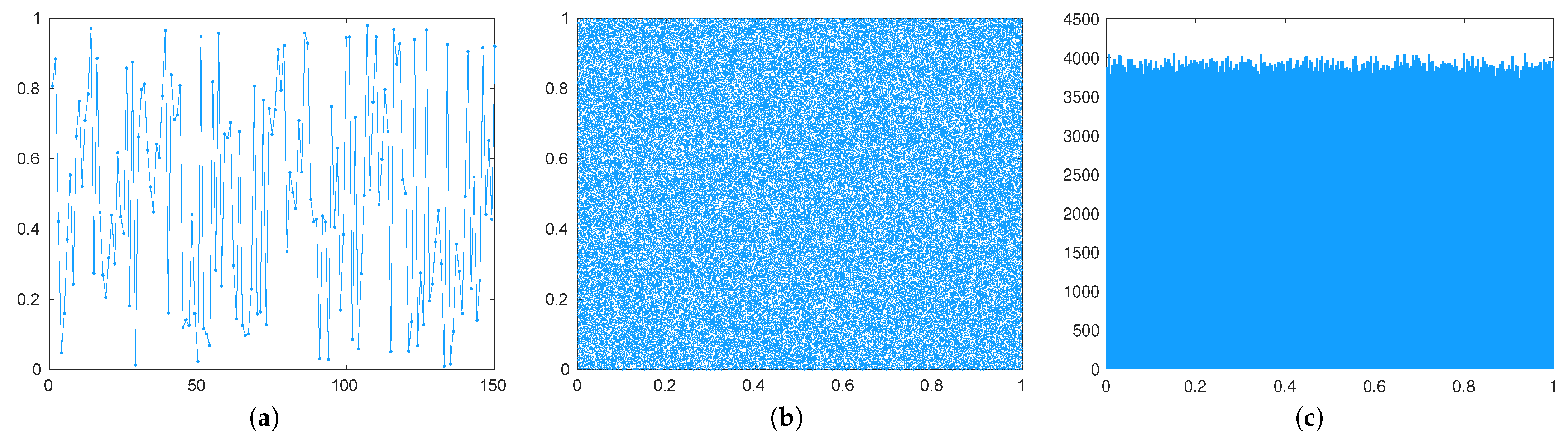






| Statistical Test | p-Value | Result |
|---|---|---|
| Frequency | ||
| Block-Frequency | ||
| Cumulative-Sums (Forward) | ||
| Cumulative-Sums (Reverse) | ||
| Runs | ||
| Longest-Runs | ||
| Rank | ||
| FFT | ||
| Non-Overlapping-Templates | ||
| Overlapping-Templates | ||
| Universal | ||
| Approximate Entropy | ||
| Random-Excursions | ||
| Random-Excursions Variant | ||
| Serial 1 | ||
| Serial 2 | ||
| Linear-Complexity |
| Image | Size | Time (s) | Speed (MB/s) |
|---|---|---|---|
| Color Lena | |||
| Lena | |||
| Baboon | |||
| Elaine | |||
| Blank |
| Image | Horizontal Correlation | Vertical Correlation | Diagonal Correlation |
|---|---|---|---|
| Color Lena | |||
| Shuffled color Lena | |||
| Cipher color Lena | |||
| Lena | |||
| Shuffled Lena | |||
| Cipher Lena | |||
| Baboon | |||
| Shuffled Baboon | |||
| Cipher Baboon | |||
| Elaine | |||
| Shuffled Elaine | |||
| Cipher Elaine | |||
| Blank | |||
| Shuffled Blank | |||
| Cipher Blank |
| Image | Plain Image Blocks | Cipher Image Blocks | ||||||
|---|---|---|---|---|---|---|---|---|
| Whole Image | Whole Image | |||||||
| Color Lena | 7.705492 | 7.596513 | 7.672054 | 7.730098 | 7.951841 | 7.986445 | 7.996513 | 7.999112 |
| Lena | 7.445507 | 7.249355 | 7.329093 | 7.300183 | 7.999401 | 7.861393 | 7.962324 | 7.990425 |
| Baboon | 7.386544 | 7.530603 | 7.459901 | 7.370083 | 7.849006 | 7.964011 | 7.990541 | 7.999232 |
| Elaine | 7.212572 | 7.363777 | 7.429946 | 7.502942 | 7.862744 | 7.965494 | 7.990723 | 7.999788 |
| Blank | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 7.868534 | 7.965741 | 7.991261 | 7.999953 |
| Random | 7.847664 | 7.962963 | 7.990915 | 7.999328 | 7.856857 | 7.962767 | 7.989938 | 7.999321 |
| Statistical Test | Cipher Meaningful Image | Cipher Blank | ||
|---|---|---|---|---|
| p-Value | Result | p-Value | Result | |
| Frequency | ||||
| Block-Frequency | ||||
| Cumulative-Sums (Forward) | ||||
| Cumulative-Sums (Reverse) | ||||
| Runs | ||||
| Longest-Runs | ||||
| Rank | ||||
| FFT | ||||
| Non-Overlapping-Templates | ||||
| Overlapping-Templates | ||||
| Universal | ||||
| Approximate Entropy | ||||
| Random-Excursions | ||||
| Random-Excursions Variant | ||||
| Serial 1 | ||||
| Serial 2 | ||||
| Linear-Complexity | ||||
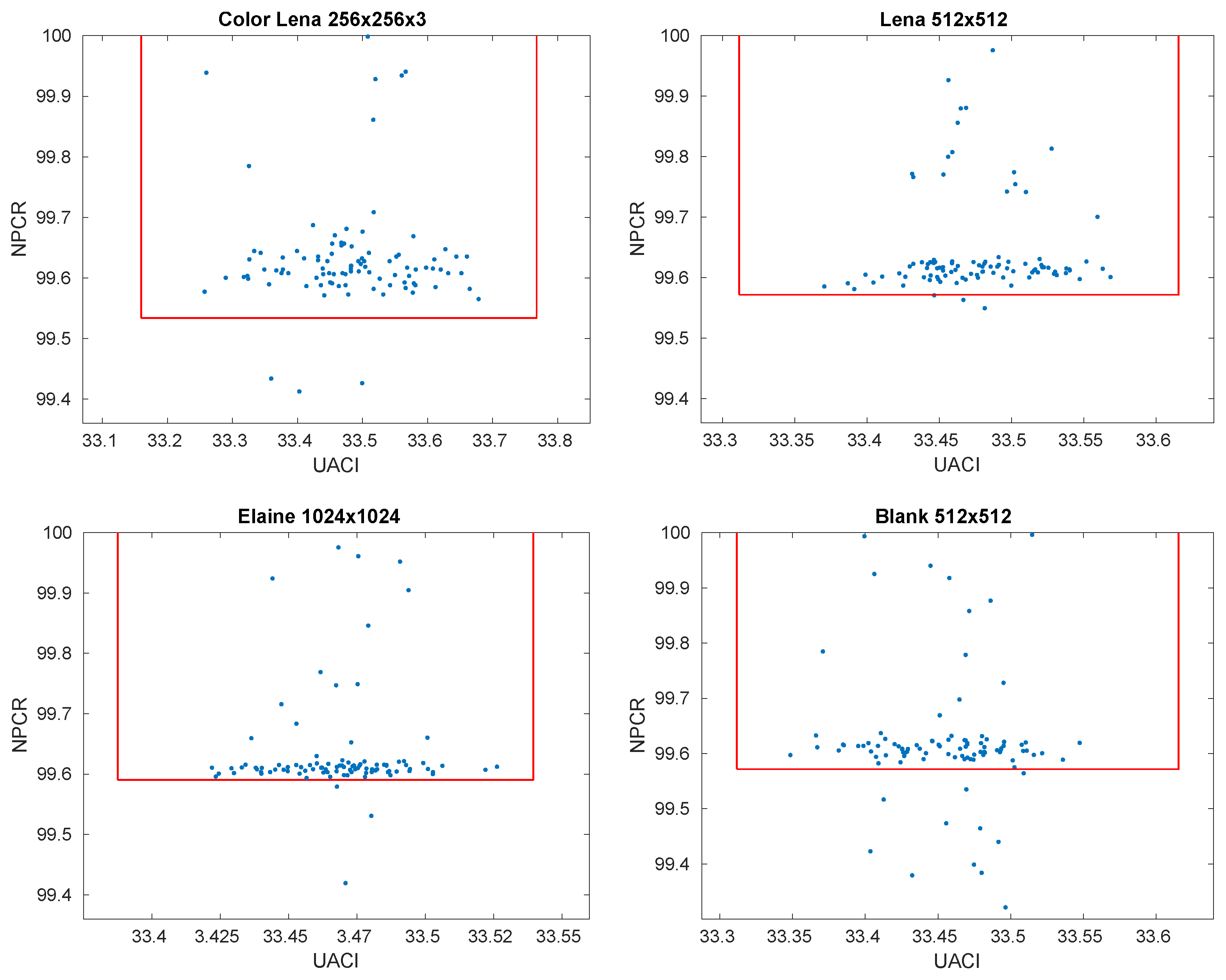
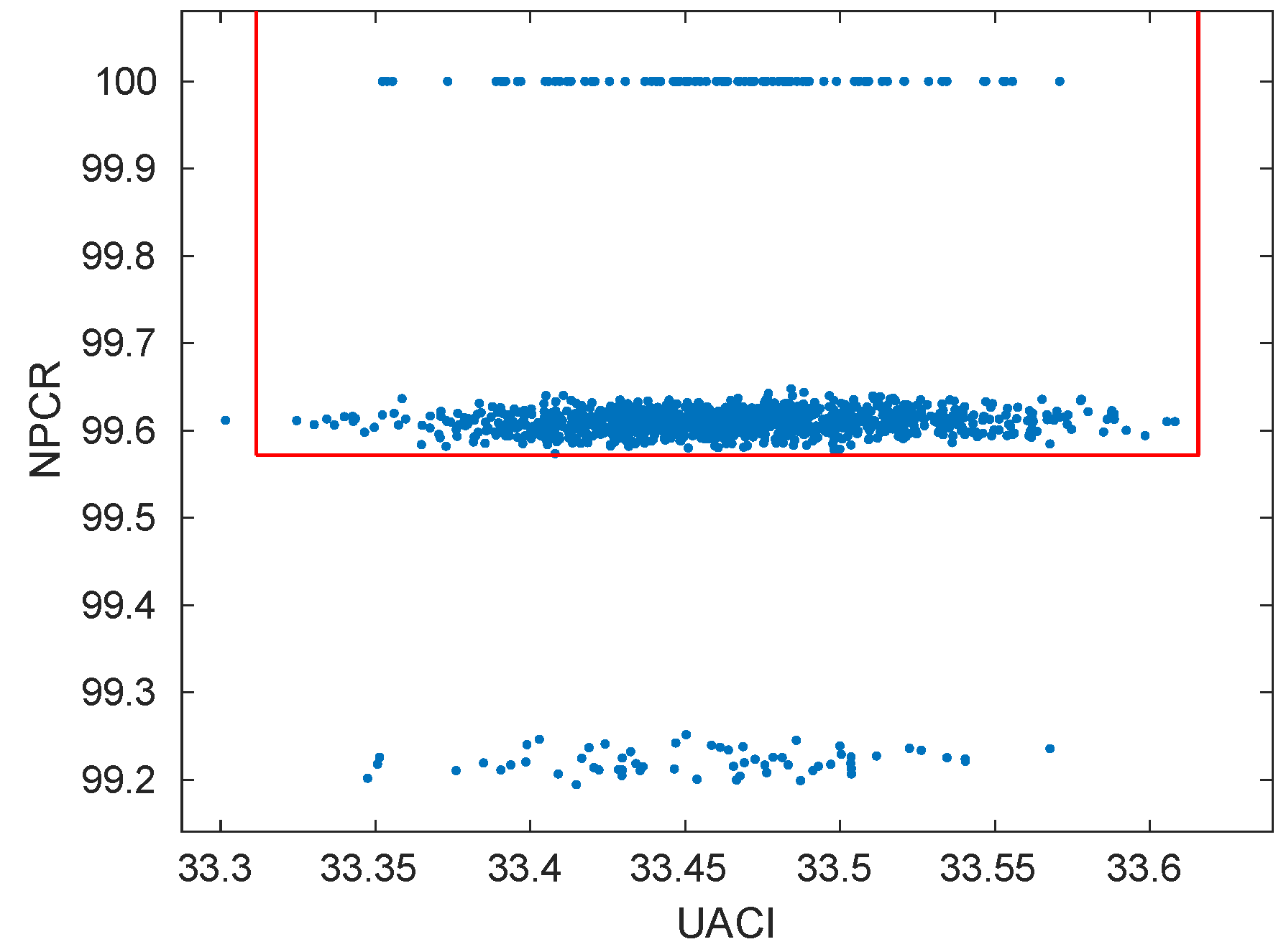
| Measure | Image Size | 0.001–Level |
|---|---|---|
| NPCR | ||
| UACI | ||
| Image | Mean NPCR | Mean UACI |
|---|---|---|
| Cipher color Lena | ||
| Cipher Lena | ||
| Cipher Baboon | ||
| Cipher Elaine | ||
| Cipher Blank |
| Image Pair | NPCR | UACI |
|---|---|---|
| and | ||
| and |
| Noise | PSNR |
|---|---|
| Salt and pepper (density ) | |
| Speckle (density ) | |
| Gaussian (mean 0 and variance ) | |
| Poisson |
| JPEG Quality Factor | PSNR |
|---|---|
| 80 | |
| 60 | |
| 40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanso, A.; Ghebleh, M.; Bou Khuzam, M. A Probabilistic Chaotic Image Encryption Scheme. Mathematics 2022, 10, 1910. https://doi.org/10.3390/math10111910
Kanso A, Ghebleh M, Bou Khuzam M. A Probabilistic Chaotic Image Encryption Scheme. Mathematics. 2022; 10(11):1910. https://doi.org/10.3390/math10111910
Chicago/Turabian StyleKanso, Ali, Mohammad Ghebleh, and Mazen Bou Khuzam. 2022. "A Probabilistic Chaotic Image Encryption Scheme" Mathematics 10, no. 11: 1910. https://doi.org/10.3390/math10111910
APA StyleKanso, A., Ghebleh, M., & Bou Khuzam, M. (2022). A Probabilistic Chaotic Image Encryption Scheme. Mathematics, 10(11), 1910. https://doi.org/10.3390/math10111910





