Evaluation of Magnetohydrodynamics of Natural Convective Heat Flow over Circular Cylinder Saturated by Nanofluid with Thermal Radiation and Heat Generation Effects
Abstract
:1. Introduction
2. Fundamental Governing Equations
Assumptions for the Problem
3. Solution Approach
4. Outcomes and Discussions
5. Conclusions
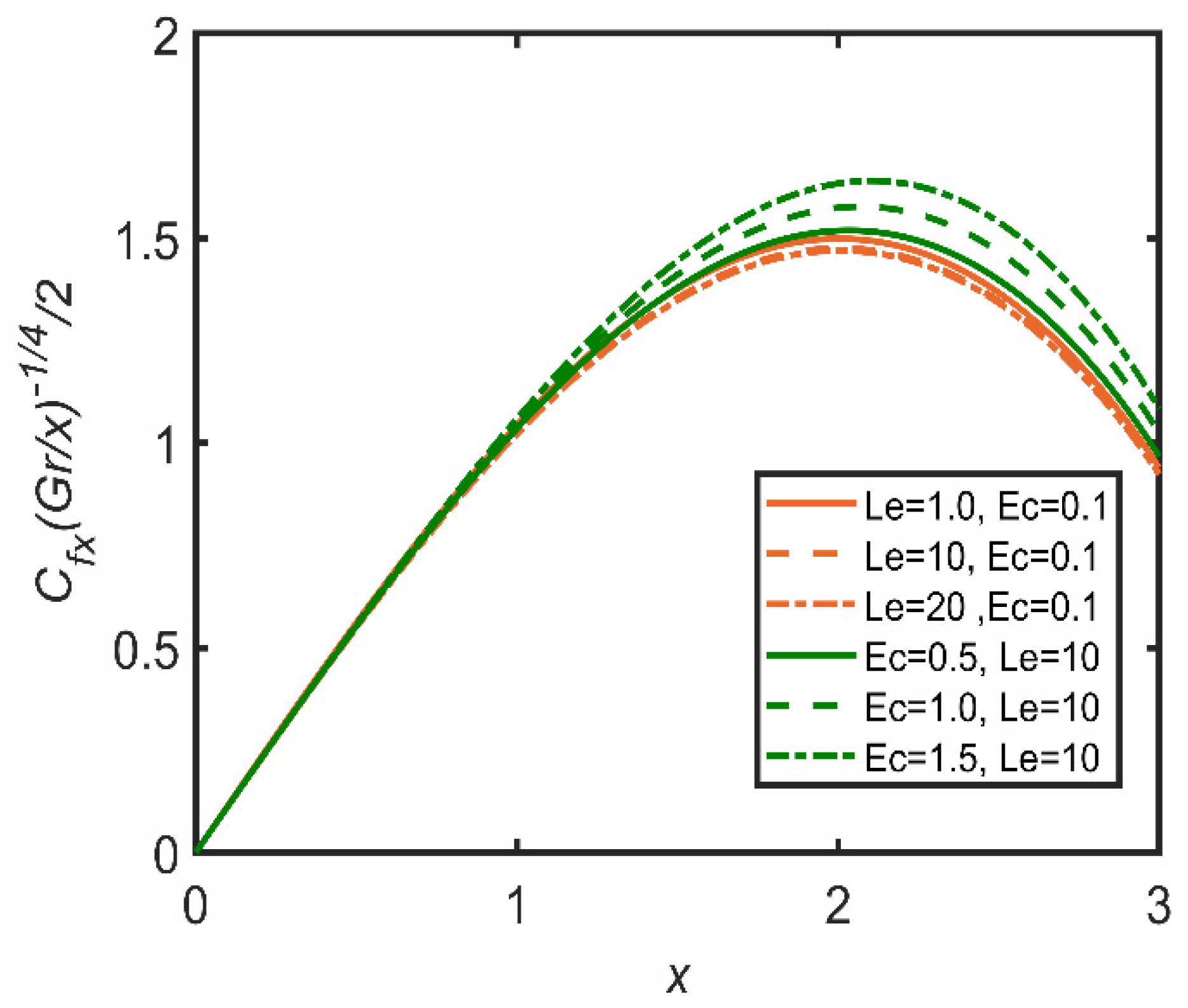
- It can be predicted from the graph that the Eckert number increases; then, the Nusselt number increases, but the Sherwood number decreases. This effect is due to the increases in the volume of the nanofluid particles and in the Nusselt number. Furthermore, it does not affect the velocity, concentration, or temperature profile;
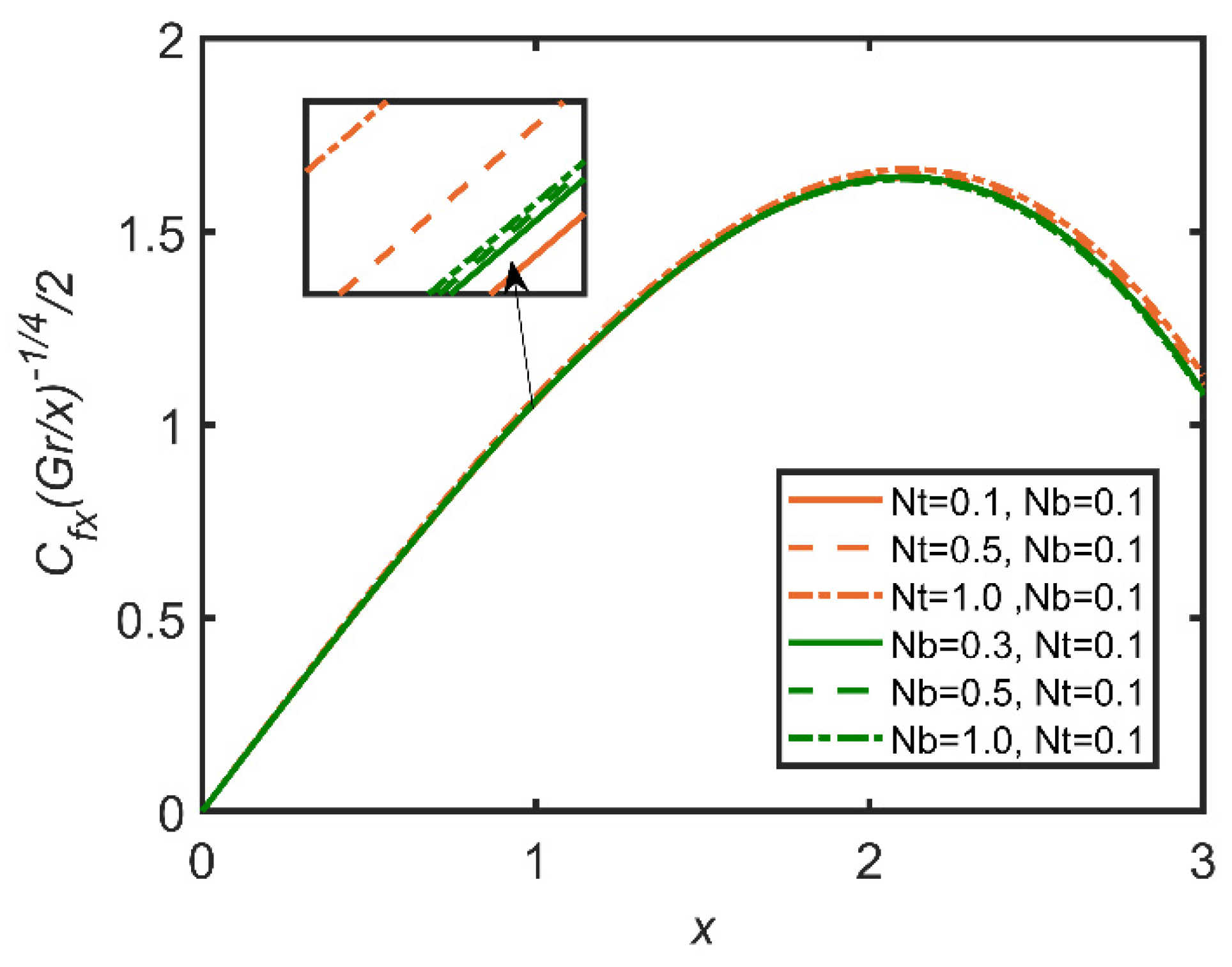
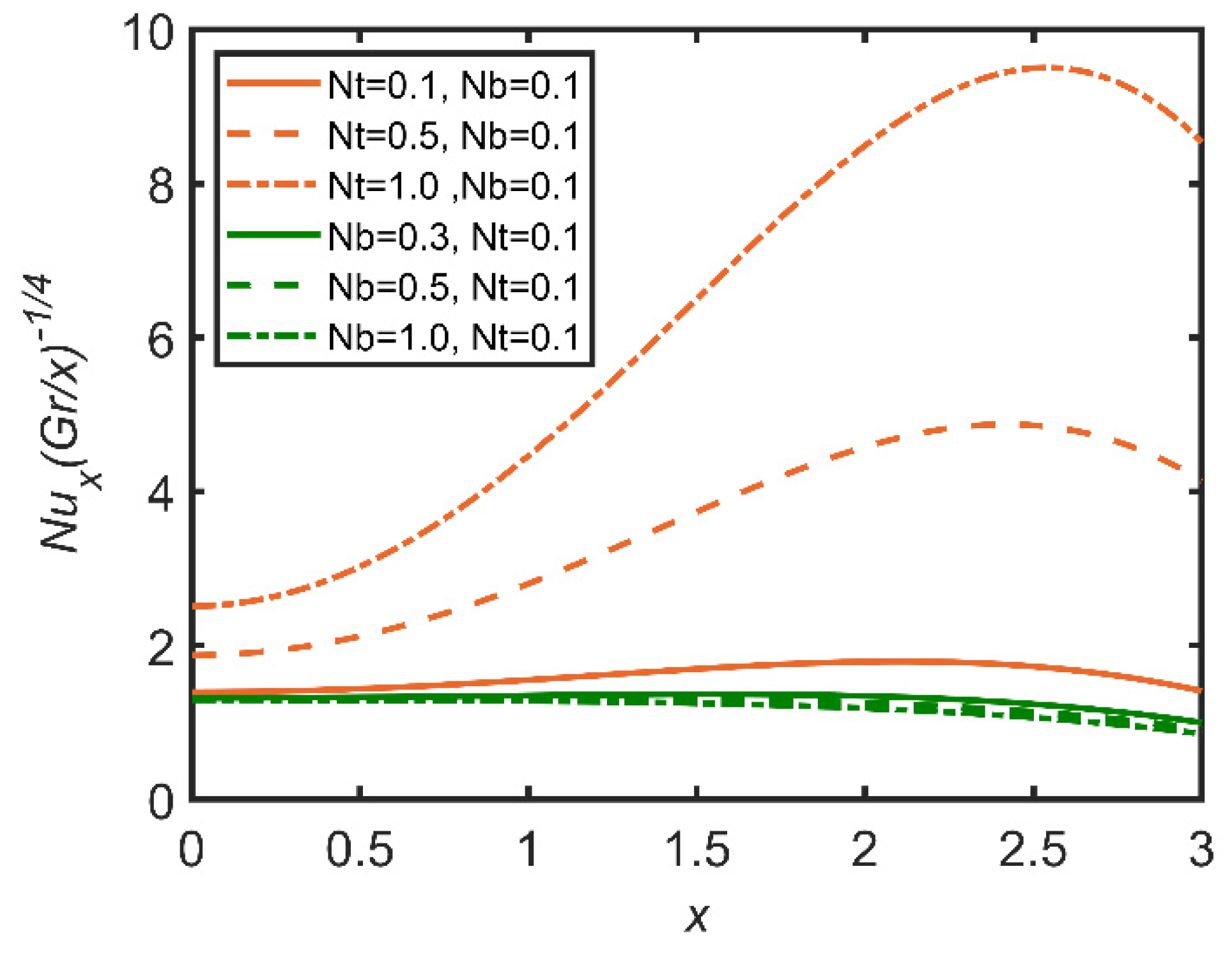
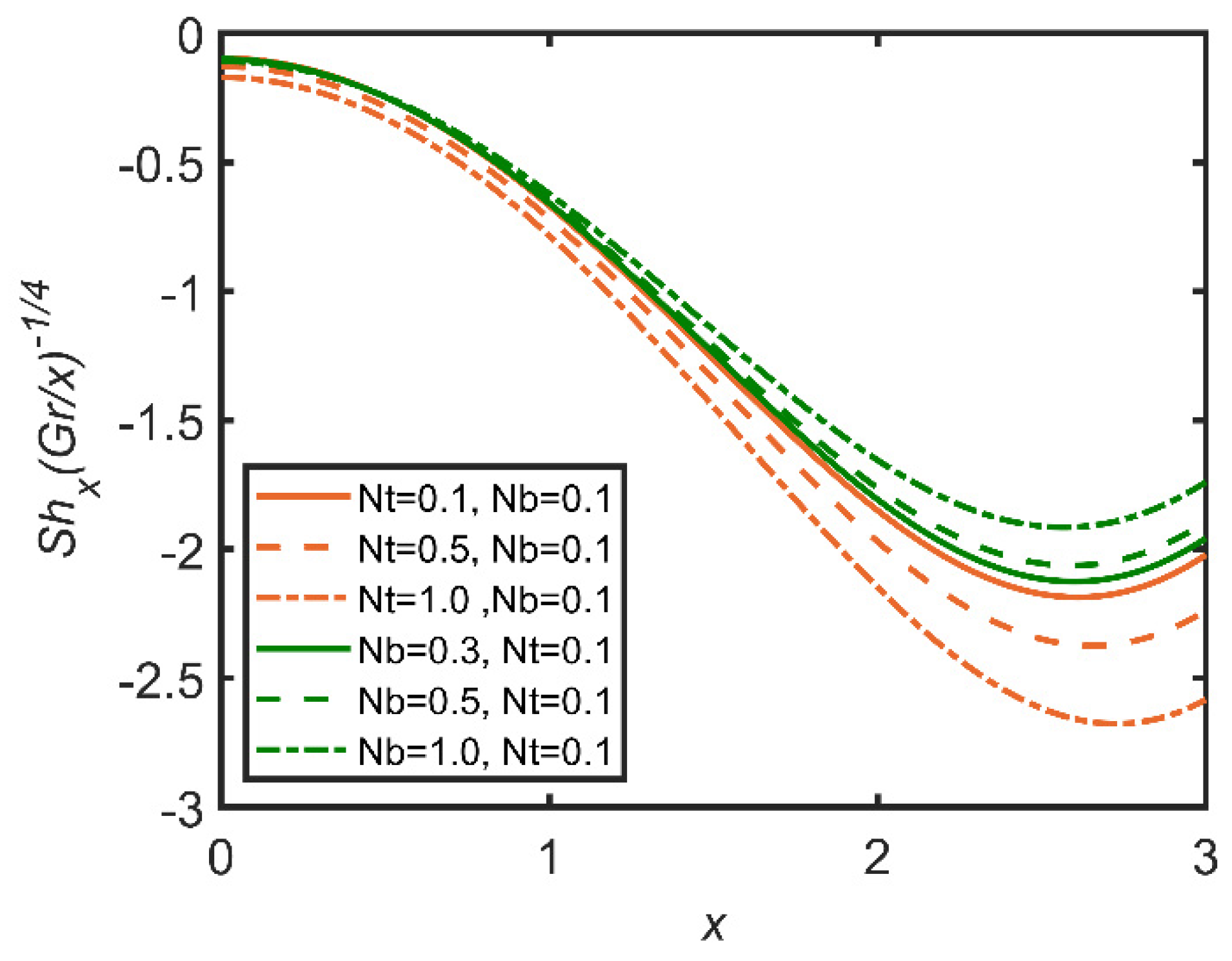
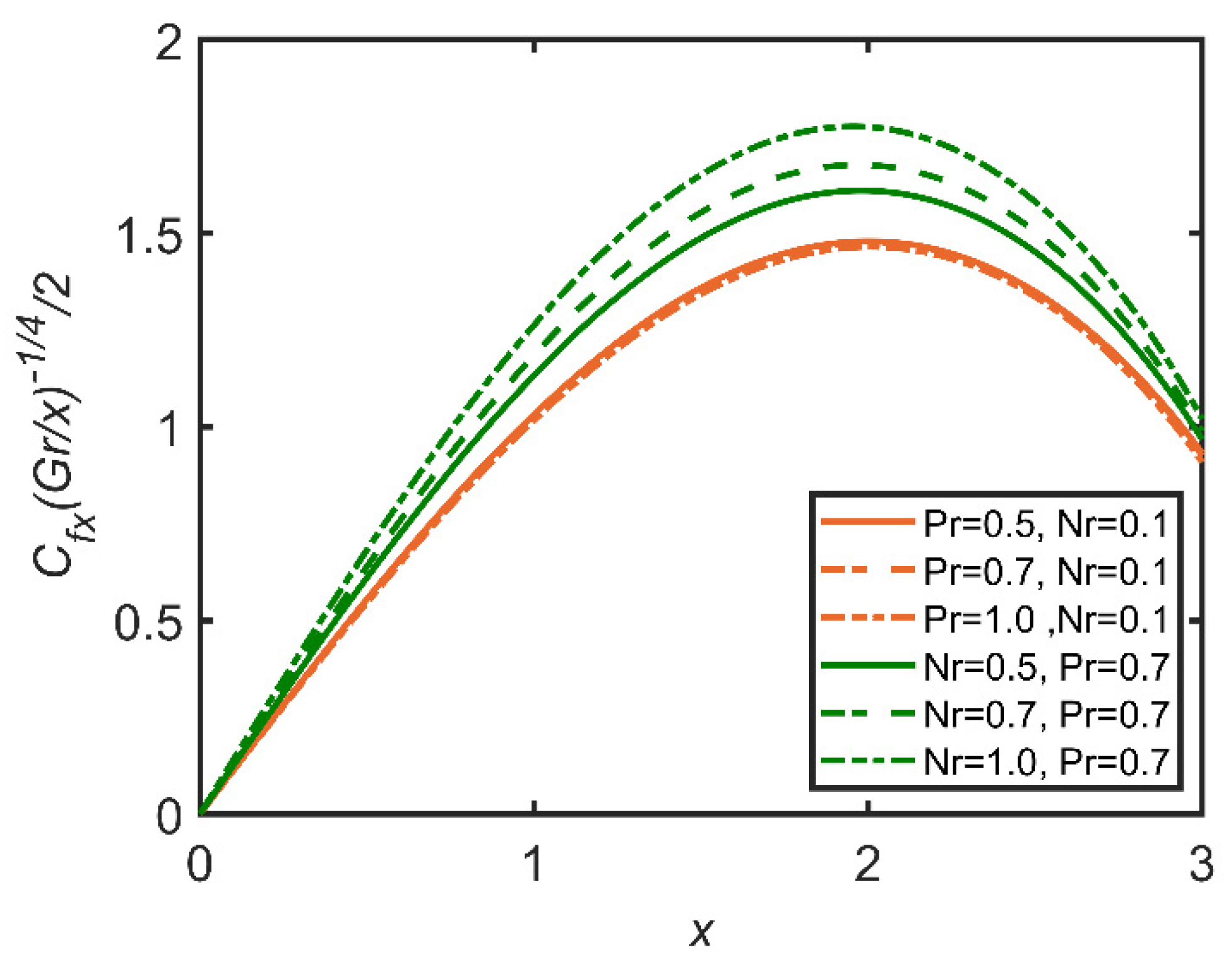
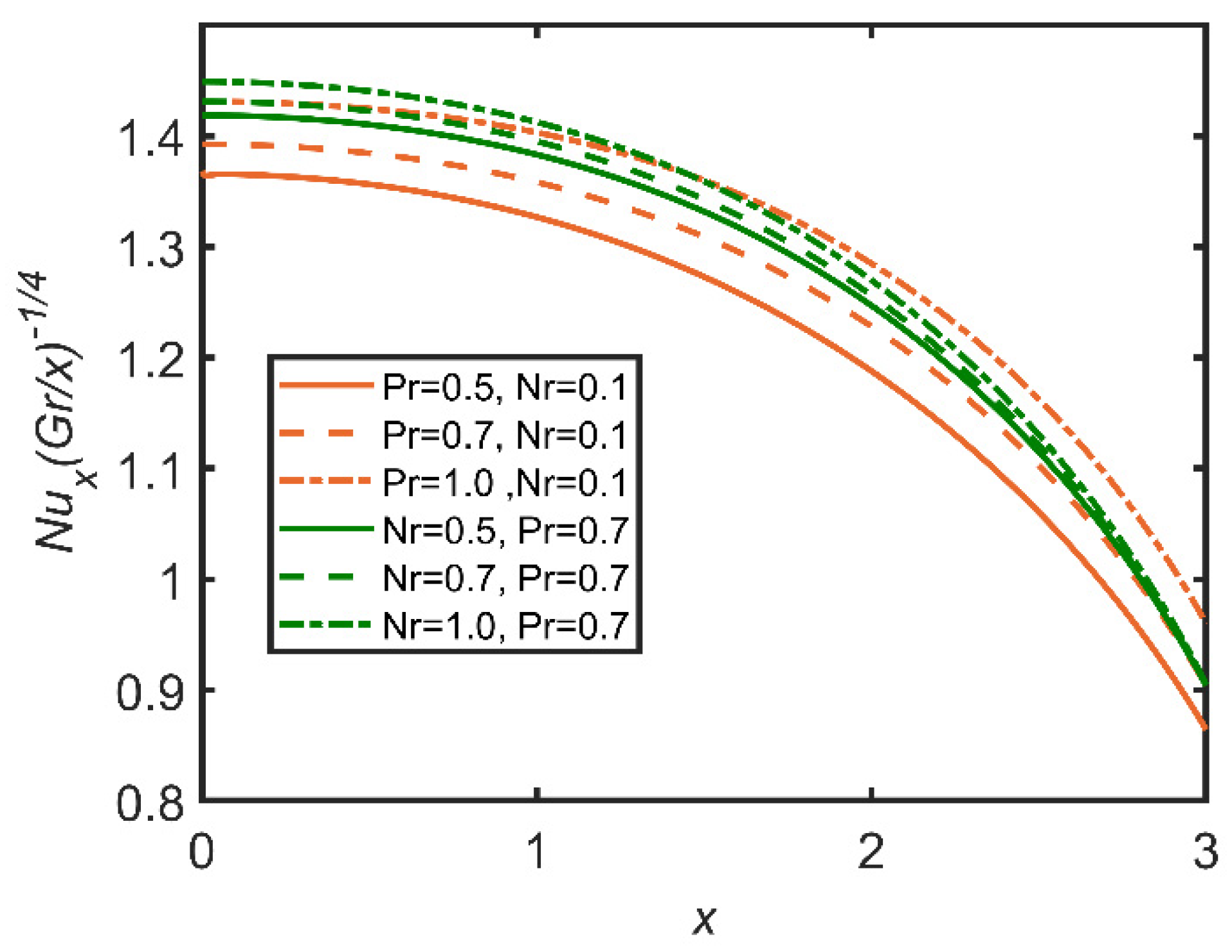
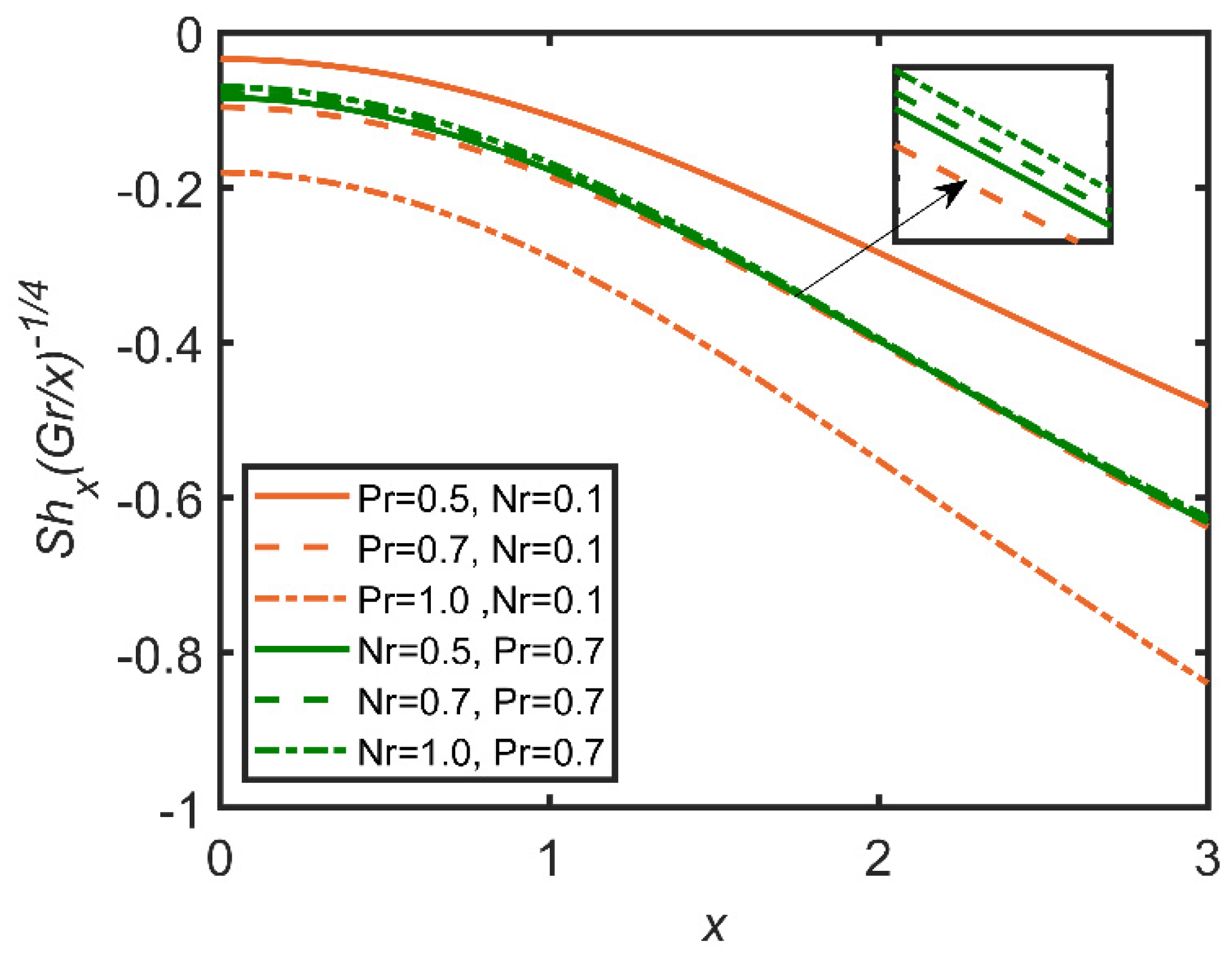
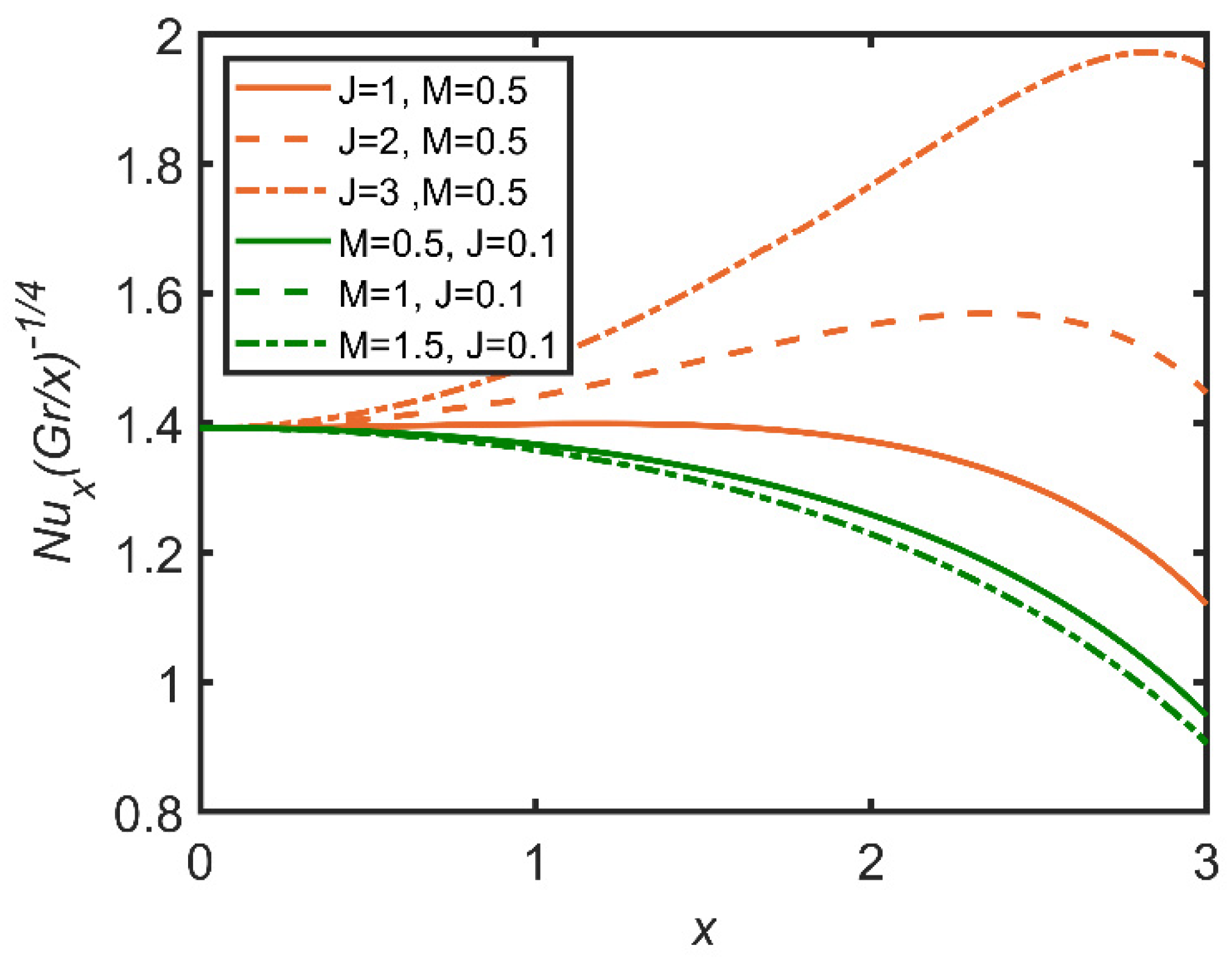
- The increases in Brownian motion and buoyancy ratio increase the Nusselt number due to an increase in the volume ratio of the nanoparticles, and rate of heat transfer is enhanced by the increase in the mass ratio;
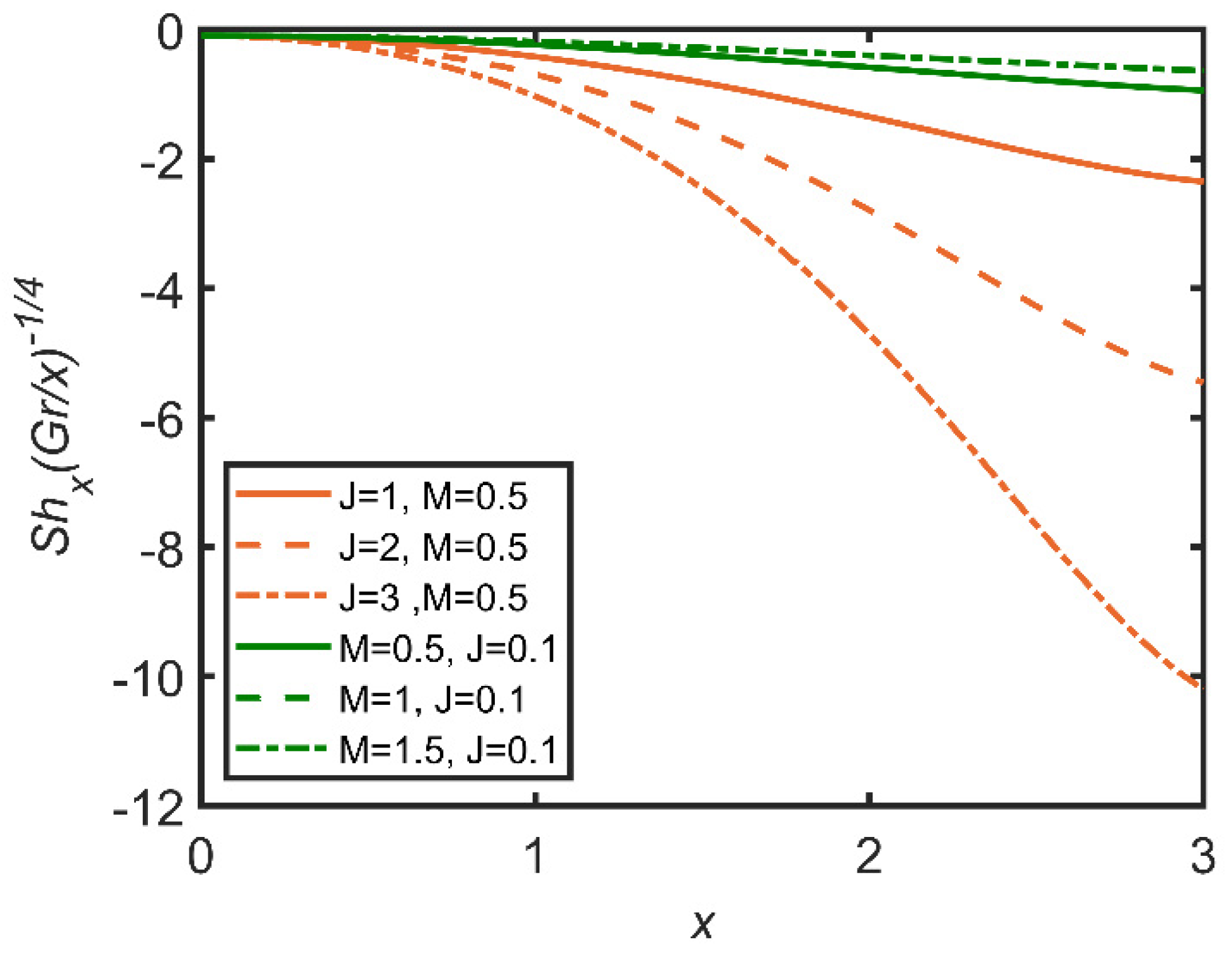
- The magnetic parameter reduces the Sherwood number and the Nusselt number due to the effects of the movement of the nanoparticles, which is reduced with the increase in the magnetic parameter;
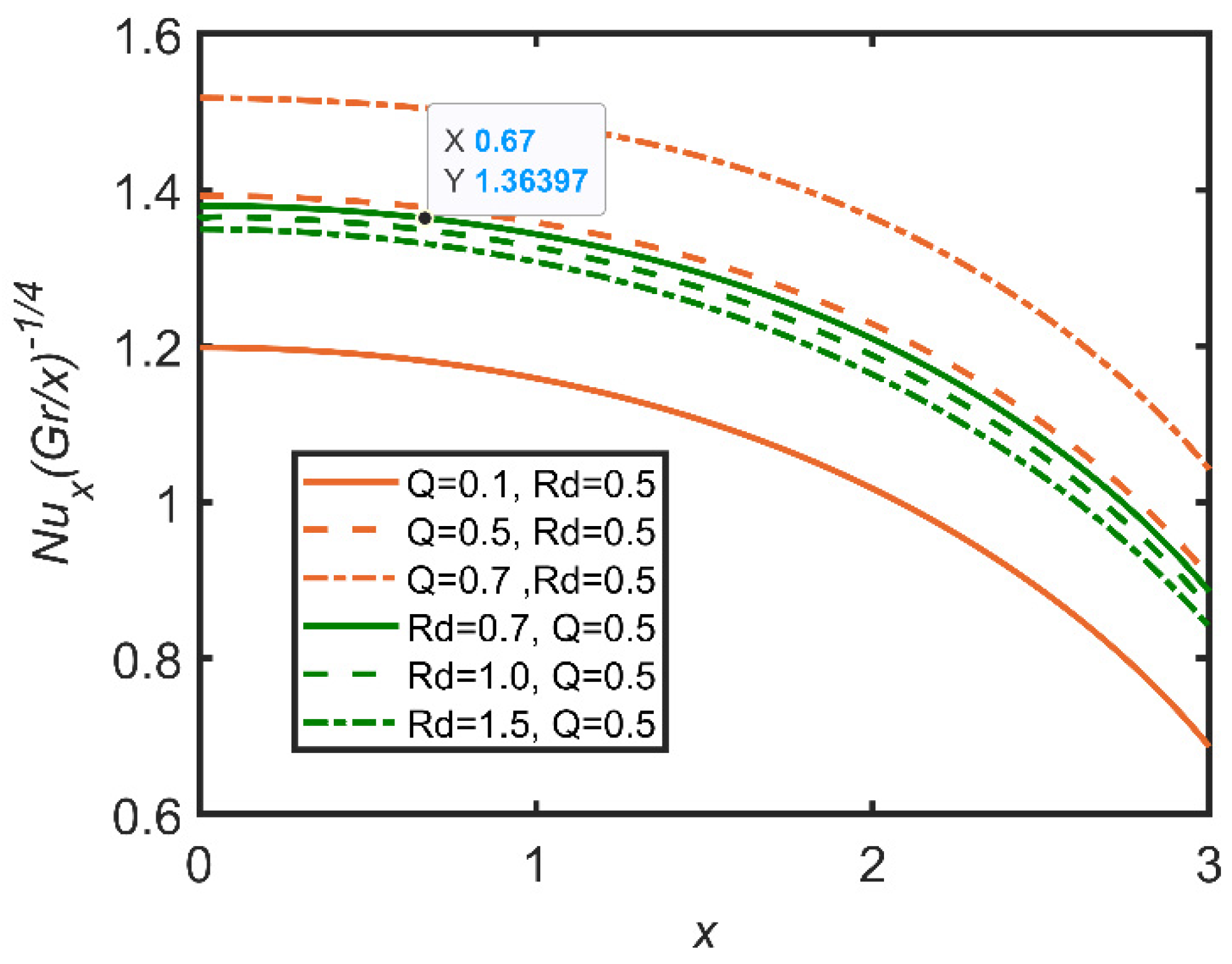
- Heat generation also decreases the Nusselt number, as the rate of heat transfer is reduced due to the reduction in the temperature difference between the wall of the cylinder and the nanofluid.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| k | Thermal conductivity (W/mK) |
| DB | Brownian diffusion coefficient (m2/s) |
| a | Radius of the horizontal circular circle (m) |
| Velocity of the fluid at the boundary layer (m/s) | |
| Le | Lewis number (dimensionless number) |
| g | Acceleration due to gravity (m/s2) |
| Gr | Grashof number (dimensionless number) |
| Dimensional and components of velocity (dimensionless number) | |
| u, v | Dimensionless x and y components of velocity (dimensionless number) |
| Nb | Brownian motion parameter (kgm3/s4) |
| Dr | Thermophoretic diffusion coefficient (m2/s K) |
| T | Temperature of the fluid in the boundary layer (K) |
| Temperature of the ambient fluid (K) | |
| Cartesian coordinates (dimensionless number) | |
| x, y | Coordinates in the direction along and normal to surface (dimensionless number) |
| Nu | Local Nusselt Number (dimensionless number) |
| f | Dimensionless stream function (dimensionless number) |
| Nt | Thermophoresis parameter (kgm3/s4K) |
| Nr | Buoyancy ratio (dimensionless number) |
| Pr | Prandtl number (dimensionless number) |
| U | Reference velocity (m/s) |
| Cp | Specific heat term at constant pressure (J/kg⋅K) |
| Local skin friction coefficient (dimensionless number) | |
| Tw | Temperature at the surface (K) |
| Radiative heat flux (w/m2) | |
| C | Nano particle volume fraction (dimensionless number) |
| Nano fluid volume fraction outside the boundary layer (dimensionless number) | |
| Heat flux at the surface (W/m2) | |
| Nanoparticle-concentration expansion coefficient outside the boundary layer (mol/m3) | |
| Rd | Radiation parameter (W/m2) |
| Strength of magnetic field (A/m) | |
| Source term of heat generation (J) | |
| Ec | Eckert number (dimensionless number) |
| J | Joule heating parameter (A2.ohm.s) |
| M | Magnetic parameter (dimensionless number) |
| Q | Heat generation parameter (J) |
| Greek Symbols | |
| α | amplitude of the wavy surface (m) |
| β | volumetric coefficient of thermal expansion (1/K) |
| μ | viscosity of the fluid (kg/m s) |
| ψ | stream function (dimensionless number) |
| σ(x) | surface profile function (dimensionless number) |
| σ | Stefan Boltzman constant ((W/m 2 K 4) |
| η | non-dimensional similarity variable (dimensionless number) |
| τ | shear stress (N/m2) |
| reference kinematic viscosity (m2/s) | |
| θ | dimensionless temperature function (dimensionless number) |
| dynamic viscosity of the ambient fluid (N s/m2) | |
| f | non-dimensional nanoparticle volume fraction (dimensionless number) |
| ρ | density of the fluid (kg/m3) |
| nanoparticle mass density (kg/m3) | |
| fluid velocity outside the boundary layer (m/s) | |
| fluid density (kg/m3) | |
| electrical conductivity (S/m) | |
| scattering coefficient (1/m) | |
| heat capacity of the fluid (J/kg K) | |
| αr | Rosseland mean extinction coefficient (1/m) |
Appendix A
Appendix B
References
- Blasius, H. Grenzschichten in Flüssigkeiten Mit Kleiner Reibung; Druck von BG Teubner: Leipzig, Germany, 1907. [Google Scholar]
- Merkin, J.H. Free convection boundary layers on cylinders of elliptic cross section. J. Heat Transf. 1977, 99, 453–457. [Google Scholar] [CrossRef]
- Merkin, J.H. Mixed convection from a horizontal circular cylinder. Int. J. Heat Mass Transf. 1977, 20, 73–77. [Google Scholar] [CrossRef]
- Pop, I.; Ingham, D.B. Convective Heat Transfer: Mathematical and Computational Modelling of Viscous Fluids and Porous Media; Elsevier: Oxford, UK, 2001. [Google Scholar]
- Mohamed, M.K.A.; Noar, N.; Salleh, M.Z.; Ishak, A. Free convection boundary layer flow on a horizontal circular cylinder in a nanofluid with viscous dissipation. Sains Malays. 2016, 45, 289–296. [Google Scholar]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab. (ANL): Argonne, IL, USA, 1995. [Google Scholar]
- Zokri, S.M.; Arifin, N.S.; Kasim, A.R.M.; Salleh, M.Z. Free convection boundary layer flow of Jeffrey nanofluid on a horizontal circular cylinder with viscous dissipation effect. J. Adv. Res. Micro Nano Eng. 2020, 1, 1–14. [Google Scholar]
- Hassan, M.; Ellahi, R.; Zeeshan, A.; Bhatti, M.M. Analysis of natural convective flow of non-Newtonian fluid under the effects of nanoparticles of different materials. Proceedings of the Institution of Mechanical Engineers. Part E J. Process Mech. Eng. 2019, 233, 643–652. [Google Scholar] [CrossRef]
- Nisa, Z.U.; Hajizadeh, A.; Nazar, M. Free convection flow of nanofluid over infinite vertical plate with damped thermal flux. Chin. J. Phys. 2019, 59, 175–188. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Waheed, A.; Shehzad, N.; Sait, S.M. Natural convection nanofluid flow with heat transfer analysis of carbon nanotubes–water nanofluid inside a vertical truncated wavy cone. Math. Methods Appl. Sci. 2021. [CrossRef]
- Mourad, A.; Aissa, A.; Mebarek-Oudina, F.; Al-Kouz, W.; Sahnoun, M. Natural convection of nanoliquid from elliptic cylinder in wavy enclosure under the effect of uniform magnetic field: Numerical investigation. Eur. Phys. J. Plus 2021, 136, 429. [Google Scholar] [CrossRef]
- Eastman, J.A.; Choi, S.; Li, S.; Yu, W.; Thompson, L.J. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl. Phys. Lett. 2001, 78, 718–720. [Google Scholar] [CrossRef]
- Das, S.K.; Putra, N.; Thiesen, P.; Roetzel, W. Temperature dependence of thermal conductivity enhancement for nanofluids. J. Heat Transf. 2003, 125, 567–574. [Google Scholar] [CrossRef]
- Hossain, M.A.; Alim, M.A. Natural convection-radiation interaction on boundary layer flow along a thin vertical cylinder. Heat Mass Transf. 1997, 32, 515–520. [Google Scholar] [CrossRef]
- Hossain, M.; Kutubuddin, M.; Pop, I. Radiation-conduction interaction on mixed convection from a horizontal circular cylinder. Heat Mass Transf. 1999, 35, 307–314. [Google Scholar] [CrossRef]
- Elbashbeshy, E.M.; Emam, T.G.; Sayed, E.A.A. Effect of thermal radiation on free convection flow and heat transfer over a truncated cone in the presence of pressure work and heat generation/absorption. Therm. Sci. 2016, 20, 555–565. [Google Scholar] [CrossRef]
- Zeeshan, A.; Shehzad, N.; Abbas, T.; Ellahi, R. Effects of radiative electro-magnetohydrodynamics diminishing internal energy of pressure-driven flow of titanium dioxide-water nanofluid due to entropy generation. Entropy 2019, 21, 236. [Google Scholar] [CrossRef] [Green Version]
- Vajravelu, K.; Hadjinicolaou, A. Heat transfer in a viscous fluid over a stretching sheet with viscous dissipation and internal heat generation. Int. Commun. Heat Mass Transf. 1993, 20, 417–430. [Google Scholar] [CrossRef]
- Molla, M.M.; Hossain, M.A.; Paul, M.C. Natural convection flow from an isothermal horizontal circular cylinder in presence of heat generation. Int. J. Eng. Sci. 2006, 44, 949–958. [Google Scholar] [CrossRef]
- Molla, M.M.; Paul, S.C.; Hossain, M.A. Natural convection flow from a horizontal circular cylinder with uniform heat flux in presence of heat generation. Appl. Math. Model. 2009, 33, 3226–3236. [Google Scholar] [CrossRef]
- Cheng, C.-Y. Natural convection heat transfer from a horizontal isothermal elliptical cylinder with internal heat generation. Int. Commun. Heat Mass Transf. 2009, 36, 346–350. [Google Scholar] [CrossRef]
- Mohamed, M.K.A.; Sarif, N.M.; Kasim, A.R.M.; Noar, N.; Salleh, M.Z.; Ishak, A. Effects of viscous dissipation on free convection boundary layer flow towards a horizontal circular cylinder. ARPN J. Eng. Appl. Sci. 2016, 11, 7258–7263. [Google Scholar]
- Hossain, M.; Das, S.; Pop, I. Heat transfer response of MHD free convection flow along a vertical plate to surface temperature oscillations. Int. J. Non-Linear Mech. 1998, 33, 541–553. [Google Scholar] [CrossRef]
- Wilks, G. Magnetohydrodynamic free convection about a semi-infinite vertical plate in a strong cross field. Z. Angew. Math. Phys. ZAMP 1976, 27, 621–631. [Google Scholar] [CrossRef]
- Azim, N.; Chowdhury, M. MHD-conjugate free convection from an isothermal horizontal circular cylinder with joule heating and heat generation. J. Comput. Methods Phys. 2013, 2013, 180516. [Google Scholar] [CrossRef] [Green Version]
- Azim, N. Effects of viscous dissipation and heat generation on MHD conjugate free convection flow from an isothermal horizontal circular cylinder. SOP Trans. Appl. Phys. 2014, 1, 1–11. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Study of natural convection MHD nanofluid by means of single and multi-walled carbon nanotubes suspended in a salt-water solution. IEEE Trans. Nanotechnol. 2015, 14, 726–734. [Google Scholar] [CrossRef]
- Nazeer, M.; Ali, N.; Javed, T. Numerical simulations of MHD forced convection flow of micropolar fluid inside a right-angled triangular cavity saturated with porous medium: Effects of vertical moving wall. Can. J. Phys. 2019, 97, 1–13. [Google Scholar] [CrossRef]
- Hobiny, A.; Alzahrani, F.; Abbas, I.; Marin, M. The effect of fractional time derivative of bioheat model in skin tissue induced to laser irradiation. Symmetry 2020, 12, 602. [Google Scholar] [CrossRef]
- Marin, M.; Othman, M.; Abbas, I. An extension of the domain of influence theorem for generalized thermoelasticity of anisotropic material with voids. J. Comput. Theor. Nanosci. 2015, 12, 1594–1598. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Marin, M.; Zeeshan, A.; Abdelsalam, S.I. Recent trends in computational fluid dynamics. Front. Phys 2020, 8, 593111. [Google Scholar] [CrossRef]
- Marin, M.; Florea, O. On temporal behaviour of solutions in thermoelasticity of porous micropolar bodies. An. Univ. Ovidius Constanta-Ser. Mat. 2014, 22, 169–188. [Google Scholar] [CrossRef] [Green Version]
- Abouelregal, A.E.; Marin, M. The Response of Nanobeams with Temperature-Dependent Properties Using State-Space Method via Modified Couple Stress Theory. Symmetry 2020, 12, 1276. [Google Scholar] [CrossRef]
- Zeeshan, A.; Majeed, A.; Akram, M.J.; Alzahrani, F. Numerical investigation of MHD radiative heat and mass transfer of nanofluid flow towards a vertical wavy surface with viscous dissipation and Joule heating effects using Keller-box method. Math. Comput. Simul. 2021, 190, 1080–1109. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akram, J.; Zeeshan, A.; Alhodaly, M.S.; Marin, M. Evaluation of Magnetohydrodynamics of Natural Convective Heat Flow over Circular Cylinder Saturated by Nanofluid with Thermal Radiation and Heat Generation Effects. Mathematics 2022, 10, 1858. https://doi.org/10.3390/math10111858
Akram J, Zeeshan A, Alhodaly MS, Marin M. Evaluation of Magnetohydrodynamics of Natural Convective Heat Flow over Circular Cylinder Saturated by Nanofluid with Thermal Radiation and Heat Generation Effects. Mathematics. 2022; 10(11):1858. https://doi.org/10.3390/math10111858
Chicago/Turabian StyleAkram, Javed, Ahmed Zeeshan, Mohammed Sh. Alhodaly, and Marin Marin. 2022. "Evaluation of Magnetohydrodynamics of Natural Convective Heat Flow over Circular Cylinder Saturated by Nanofluid with Thermal Radiation and Heat Generation Effects" Mathematics 10, no. 11: 1858. https://doi.org/10.3390/math10111858
APA StyleAkram, J., Zeeshan, A., Alhodaly, M. S., & Marin, M. (2022). Evaluation of Magnetohydrodynamics of Natural Convective Heat Flow over Circular Cylinder Saturated by Nanofluid with Thermal Radiation and Heat Generation Effects. Mathematics, 10(11), 1858. https://doi.org/10.3390/math10111858







