Abstract
This paper addresses a problem faced by maintenance service providers: performing maintenance activities at the right time on geographically distributed machines subjected to random failures. This problem requires determining for each technician the sequence of maintenance operations to perform to minimize the total expected costs while ensuring a high level of machine availability. To date, research in this area has dealt with routing and maintenance schedules separately. This study aims to determine the optimal maintenance and routing plan simultaneously. A new bi-objective mathematical model that integrates both routing and maintenance considerations is proposed for time-based preventive maintenance. The first objective is to minimize the travel cost related to technicians’ routing. The second objective can either minimize the total preventive and corrective maintenance cost or the failure cost. New general variable neighborhood search (GVNS) and variable neighborhood descent (VND) algorithms based on the Pareto dominance concept are proposed and performed over newly generated instances. The efficiency of our approach is demonstrated through several experiments. Compared to the commercial solver and existing multi-objective VND and GVNS, these new algorithms obtain highly competitive results on both mono-objective and bi-objective variants.
Keywords:
time-based maintenance; vehicle routing problem; random failures; multi-objective optimization; variable neighborhood descent; general variable neighborhood search MSC:
90-08; 90-10; 90B06; 90C27; 90C29
1. Introduction
Large-scale systems are essential to today’s industry, such as aeronautics, railways, telecommunications, etc. The management of such systems is often complicated and requires an adapted maintenance strategy. Maintenance is indeed a vital primary service in industries, especially when failures are likely to impact personnel safety and cause important environmental damages. It can also have a major impact on profitability.
Maintenance aims to retain equipment in its operating condition or restore it to a previous state enabling its required functions. To perform maintenance activities, it is crucial to effectively manage a crew of operators and sequence their visits over a planning horizon. Two main categories of maintenance can be distinguished [1]:
- (1)
- Corrective Maintenance (CM) that is performed after the failure. It includes actions such as repair or replacement.
- (2)
- Preventive Maintenance (PM), which occurs before the failure and intends to reduce the risks of unforeseen breakdowns. It can itself be divided into two categories:
- 1.
- Time-Based Maintenance (TBM) that includes the periodic replacement and the age replacement policy (ARP).
- 2.
- Condition-Based Maintenance (CBM) that is based on the inspection of the unit or system before the intervention.
In the first case of TBM, the preventive replacement is performed at regular time intervals. For the ARP, the unit is replaced depending on its age or its remaining useful life [1]. CBM is based on the inspection of the unit or system before the intervention. It focuses on predicting the health condition of the system using information collected from sensors.
The companies mainly outsource their maintenance operations to a service provider. This maintenance provider is required to ensure good quality maintenance services at the lowest overall cost. Figuring out the right time and manner to carry out the maintenance are therefore major concerns. The planning of maintenance operations on geographically dispersed machines subjected to random failures is, therefore, a complex problem faced by service providers. In the industry, machines are exposed to random failures that can lead to significant penalties. The opportune maintenance times are sometimes defined by the equipment manufacturer, but more often, the companies entrust their maintenance providers to define the maintenance schedule. The service provider tries to reduce the number of maintenance operations as much as possible, which can be accomplished by maximizing the periods between two successive visits to the same machine. At the same time, he seeks to avoid the huge costs resulting from carrying out corrective maintenance operations on broken machines. The challenge is therefore finding the optimal number of visits to perform maintenance operations. Mathematical maintenance policies are used to develop an effective preventive maintenance plan. The objective of such policies is to design a maintenance schedule including both preventive replacement and corrective replacement. The maintenance models dealing with these policies are probabilistic due to the uncertainty of the mechanism that causes failure. When machines are geographically distributed, it is necessary to sequence the visits and determine the best routing–maintenance policy. Cost, availability, reliability, and maintainability are the benchmarks for evaluating maintenance decisions, similar to cost, quality, and time objectives in logistics. The maintenance company would be interested in finding the best compromise between services and maintenance costs on one hand and operational and transport costs on the other hand. The objective is to jointly consider the technical aspects of maintenance and the organizational aspects of operations management. To consider these two aspects, many works in the literature consider both maintenance and routing problems [2,3,4,5]. To handle this optimization problem, it is necessary to simultaneously investigate the maintenance scheduling and vehicle routing problem (VRP). The vehicle routing problem with time windows (VRPTW) has been widely used in the literature as the main variant of VRP for planning and scheduling maintenance operations [4,5,6,7].The problem addressed in this paper consists of determining the best routing maintenance policy when planning operators’ schedules to perform maintenance operations on geographically distributed machines subjected to random failures.
Herein, the main contributions of this work are summarized as follows.
- (1)
- A new bi-objective model is proposed, aiming to minimize both maintenance and transport costs in the case of time-based preventive maintenance. The first objective minimizes the total travel cost related to technicians’ routing. The second objective can either minimize the total preventive and corrective maintenance cost or the failure cost. A penalty cost is incurred when the maintenance activities are performed after the optimal time interval. The present paper comes with the novelty of introducing a nonlinear and uncertain failure cost that uses information from equipment degradation. Moreover, the failure and maintenance costs adopted have not been used in a multi-objective study with the routing objective. We also include a continuous-time for the last restoration in the second objective of the model.
- (2)
- Variable Neighborhood Descent and General Variable Neighborhood Search variants have been designed and implemented to solve the mono-objective and the bi-objective problems. The proposed multi-objective VND and GVNS algorithms are based on the Pareto dominance strategy and start with a unique initial solution. The algorithm MOVND/P is designed to be an intensified local search component of the GVNS algorithms, whereas MOVND/PI and MOGVNS/P are intended to solve the multi-objective problem. They use a proposed multi-objective best improvement strategy called MOBI/P and new adaptations of VNS mechanisms in the multi-objective context.
- (3)
- Extensive experiments demonstrated that the proposed algorithms outperformed the literature algorithms. We also test some other GVNS variants for comparison reasons. An analysis is conducted to clearly show the differences between the performance of the algorithms proposed and the literature algorithms. It permits measuring the influence of the proposed mechanisms to improve the results.
This study will be presented as follows: Section 2 sets a summary of the corresponding literature. Section 3 delineates the problem and sets out its mathematical formulation. A description of the proposed solution approaches and their implementation details are given in Section 4. Section 5 then presents experimental results. At last, Section 6 lays out concluding observations and perspectives for upcoming research.
2. Literature Review
The majority of existing studies tackling routing and maintenance problems dealt separately with each of them. Two principal research streams can be distinguished in the literature:
- First stream: The routing is used to schedule maintenance operations.
- Second stream: Maintenance and routing are viewed as an integrated problem by considering both their specific features.
The first stream of research includes workforce scheduling problems that are particularly useful in reality and affect many organizations. Indeed, the workforce cost constitutes one of the highest costs in any organization. The major problems addressed in the first stream are technician routing and scheduling problem (TRSP) [8], technician and task scheduling problem (TTSP) [7], service technician routing and scheduling problem (STRSP) [6], and workforce scheduling and geographically distributed asset maintenance problems (GDMP) [2]. Cordeau et al. [7] proposed a mixed-integer linear program and a solution approach for the ROADEF 2007 challenge. This challenge tackled the specific features of the TTSP in a large telecommunications company. A constructive heuristic was proposed to generate a feasible solution by defining teams and assigning tasks. An adaptive large neighborhood search metaheuristic is then used to solve the problem in the improvement phase. Each technician is specialized in different tasks with different skill levels. He is able to execute tasks requiring lower levels than his as well. Skills requirements and a time window characterize each maintenance task. An outsourcing budget, as well as task priorities, are considered. Kovacs et al. [6] introduced the service technician routing and scheduling problem. Their model minimized routing and outsourcing costs by considering skills and team-building constraints. They used an adaptive large neighborhood search algorithm to solve the problem. They also proposed to select destroy–repair operator pairs and adapted the adaptive mechanism consequently. Pillac et al. [8] dealt with the dynamic technicians routing and scheduling problem (DTRSP). The assignment of technicians with adequate skills, spare parts, and tools to tasks is realized to minimize the overall cost. To handle more requests, technicians can replenish tools and spares at the depot at any time. The authors proposed a re-optimization approach for the periodic problem. This approach relies on a parallel adaptive neighborhood search (RpALNS) algorithm, which generates a new route each time a request arrives. The suggested parallelization scheme distributes the computational effort among the different processors. Their metaheuristic has achieved the same performances as the state-of-the-art results for the dynamic vehicle routing problem with time windows. Çakırgil et al. [9] studied the multi-skill workforce scheduling and routing problem for an electricity company. Different skills requirements and priorities characterize the maintenance operations, and teams of technicians need to be formed to perform them. A mixed-integer programming model was proposed to complete higher priority tasks earlier and minimize total costs. The authors proposed a two-stage matheuristic based on the variable neighborhood search to solve the bi-objective problem.
The second stream of research is concerned with the combination of maintenance and routing characteristics. Workforce scheduling is not the only problem dealt with in this case since other maintenance problems are taken into account. Reliability analysis can be included to design solutions that assign technicians at the right time to perform maintenance operations. Workforce costs and maintenance costs are both dealt with in this case. Lopez-Santana et al. [4] proposed a mathematical model called the combined maintenance and routing (CMR) and a two-phase procedure to solve it. In the first phase, a maintenance model is solved to determine the optimal times to perform preventive maintenance operations, their frequency, and their time windows while minimizing the total expected maintenance cost. The output data of the maintenance model is then considered in a second phase as the input data of the routing model that schedules maintenance operations for each technician. The maintenance model is again solved using the updated start times of preventive operations obtained by the routing model to connect the two problems. This procedure is repeated until meeting the stopping criterion. The nonlinear and convex maintenance cost of the objective function is approximated using a piecewise linear function, and the problem is solved for small instances using a commercial solver. Jbili et al. [3] modeled an integrated strategy of vehicle routing and maintenance. They considered vehicles used in transcontinental transportation that are subject to random failures on the road. These failures have to be repaired, which may take random durations that induce delays. A policy consisting of replacing the critical component when arriving at selected customers is adopted. A mathematical model is proposed to determine the optimal routing and sequence of PM actions simultaneously. The objective is to minimize the total expected cost per unit time. It considers the reliability of the vehicle, maintenance (PM operations and minimal repairs), transportation costs, and finally, maintenance durations and penalties incurred by late arrivals. A genetic algorithm is then proposed to solve large instances. Chen et al. [2] studied the maintenance of gully pots or storm drains. They modeled a multi-period VRP, which considers the risk impact of gully pot failure and its failure behavior each day. The risk impact is estimated using meteorological information. A risk-driven analysis is adopted to evaluate maintenance actions. They focused on two factors: parked cars and gully pots status information. The latter has been proven to be the dominant factor that may negatively affect the scheduling of maintenance actions. Rashidnejad et al. [5] presented a bi-objective multi-period model of preventive maintenance planning in geographically dispersed systems through prognostic information and remaining useful life (RUL) called the integrated vehicle routing problem with time windows and maintenance scheduling (IVRPTW-MS). The first objective minimizes the total cost composed of the performing maintenance cost, the expected failure cost, and the travel cost, whereas the second objective minimizes the unavailability of the assets. The authors used fixed costs and did not include corrective maintenance. They used a non-dominated sorting genetic algorithm II (NSGA-II) to solve this NP-hard problem.
There is a relatively small amount of research combining preventive and corrective maintenance strategies since most of the papers examined dealt only with preventive scheduling, apart from [2,4]. Moreover, they did not consider the uncertainty of the breakdowns and did not deal with a multi-objective perspective. Papers that considered random breakdowns among those examined are [3,4]. The multi-objective formulation is considered in [5,9]. Analyzing the previous problems emphasizes the need to propose solutions to the real problem that includes the following realistic features: large scale, uncertainty, the combination of both corrective and preventive maintenance, and finally, routing of technicians in a multi-objective perspective. To the best of our knowledge, no previous study investigated these features together. These aspects make the NP-hard optimization problem even more challenging. Therefore, heuristic-based approaches are necessary for large instances since exact methods are practically limited. Due to their success in solving many mono-objective combinatorial problems, VND and GVNS algorithms were extended in several studies to deal with multi-objective optimization problems. However, most of these extensions do not question the utility of using properties working well for evolutionary algorithms such as dealing with a population of solutions, aggregation, etc. They also do not propose a specific local search strategy for multi-objective optimization apart from Paquette et al. [10]. Instead, most literature algorithms apply mono-objective local searches by dealing with each objective separately [11] or use previously proposed local search strategies [12,13] such as Pareto local search [13].
The present paper comes with the novelty of exploring the combination of vehicle routing and maintenance problems in a unique bi-objective model and proposes novel VND and GVNS algorithms to solve it. This paper proposes a bi-objective model for the joint maintenance and routing problem. The first objective minimizes the total travel cost and the penalty cost. The second objective can be minimizing the total preventive and corrective maintenance cost. This cost was proposed by Lopez-Santana et al. [4] in their single objective model. The paper also introduces a nonlinear and uncertain failure cost that uses information from equipment degradation, with the routing model as a second objective. The maintenance hypothesis of renewal theory is considered on both costs through a continuous time for the last restoration. Penalties for late arrivals are also associated with the second considered objective. Moreover, the failure and maintenance costs adopted have not been used in a multi-objective study with the routing objective. The workforce cost and the maintenance cost represent the highest costs in a plant. Failing to optimize these costs together can lead to a serious loss for the manufacturing company and reduce its profitability. The maintenance and transport are support processes often outsourced due to their importance. They are directly linked for a service provider to the production of its service. This model simultaneously optimizes these costs in an organization, making it appropriate for real-world situations. Maintenance service providers can use this model to provide the best services to their customers whenever the maintenance strategy adopted by those customers is time-based maintenance, including preventive and corrective maintenance. The previous research gaps of the problem in the literature are therefore filled. To solve the integrated maintenance and routing problem efficiently, multi-objective new adaptations of the variable neighborhood descent and the general variable neighborhood search algorithms are proposed. This paper describes the design of the improvement method, the new best improvement strategy proposed MOBI/P, the acceptance criterion, the stopping criterion, and the approach adopted to reduce the computational time. The paper finally presents an analysis to demonstrate the efficiency and novelty of the proposed mechanisms compared to the literature. This work differs from the literature since it proposes novel adaptations of VND and GVNS algorithms to solve multi-objective problems. Indeed, it does not use the existing local search strategies but a new one called MOBI/P. Moreover, the VND algorithm, which is to be used as an intensification algorithm, is designed to be far faster than the GVNS algorithm. In addition, these algorithms include more design features to lead to better solutions than the literature.
3. Problem Definition and Formulation
We consider a set of machines that are located in dispersed customers’ sites. They are subjected to random breakdowns due to the failure of a critical component. For each machine and at regular time intervals, preventive maintenance (PM) interventions are scheduled. A PM operation has a cost and lasts a duration . Each preventive operation must be performed within its corresponding time window. However, if it is not possible due to the high workload of technicians, late arrivals are then allowed. Hence, technicians can arrive at an operation i following the end of its time window . A penalty cost is incurred in this case. On the other hand, a team of technicians has to wait until the earliest time to start an operation i. Teams of technicians are available to perform both preventive and corrective maintenance. They perform corrective maintenance (CM) operations when machines unexpectedly break down. In this case, the machine stays in a failure state until the arrival of the teams of technicians for a certain time . The unit waiting cost for each operation is . A CM operation has a cost and lasts a duration . A minimized number of vehicles among the available ones must be determined and used for all operations to reduce transport costs. The Node 0 is considered the departure point of maintenance teams, and the Node is considered the final destination. We denote by the set of all nodes of the PM operations related to all machines, and by , the set of all locations (operations nodes plus the depots). Each team of technicians has to perform the maintenance operations at the customers’ sites. Thus, the model could be defined as a directed complete graph , where with and as the sets of origin and destination vertices. The following assumptions are considered:
- All maintenance teams have the same skills and qualifications to do the maintenance operations.
- It is considered that the random variable of the time to failure for each machine follows a Weibull distribution whose shape and scale parameters are, respectively, and , . Any other distribution resulting from the historical data of machine failures can be applied.
- We suppose to deal with the third part of the bathtub curve. This part features the wear-out life of the machine when the failure rate is an increasing function of age or usage. Indeed, the wear-out is the phenomenon accelerating the risk of failure over time.
- All costs related to the maintenance and penalties are known and constant.
- The duration of PM and CM tasks are known and constant.
- After each PM or CM operation, a machine is considered in a state similar to a new one.
- The mean time of the CM operation is superior to the mean time of the PM operation.
- The cost of a CM operation is superior to the cost of a PM operation.
- Each PM operation must be performed in its associated time window. However, if it is not possible, we allow a team of technicians to arrive following the end of its time window. In this case, a penalty cost is added to the total cost.
- The failure of a machine is generally due to the failure of its critical components.
- Failures of individual machines are statistically independent.
- A machine can have several maintenance operations over the planning horizon.
- In case of failure, before the beginning of the next PM operation, the customer must wait for the team of technicians to perform a CM operation instead. The team is not rescheduled based on this new situation.
- The travel times are deterministic and satisfy the triangle inequality.
3.1. Notation of the Joint Maintenance Scheduling and Workforce Routing Problem
The notations below are employed throughout the paper.
3.1.1. Sets
- : set of machines.
- : set of PM operations ().
- : set of all vertices including the PM operations, departure depot 0 and destination depot .
- : set of origin nodes.
- : set of destination nodes.
- : set of technicians’ teams or vehicles.
- : set of arcs linking nodes.
3.1.2. Maintenance Parameters
- : total preventive maintenance operation (PM) cost of machine m.
- : total corrective maintenance operation (CM) cost of machine m.
- : unit waiting cost. This cost can be interpreted as the production loss cost per unit time incurred by the customer for this machine m.
- : service time of PM operation of machine m.
- : service time of CM operation of machine m.
- : mean time to failure of the machine m given that the failure occurred before the optimal PM period for machine m, .
- : waiting time before starting a CM operation on machine m. It is the time waited before the arrival of the technicians to perform a CM operation when the machine m suddenly breaks down.
- : the total cost per unit time if the PM operation is performed when the machine m is of age .
- : random variable of the time to failure of machine m.
- : shape parameter of the Weibull distribution of machine m.
- : scale parameter of the Weibull distribution of machine m.
- : cumulative distribution function of t. It represents also the probability of failure of machine m in the interval .
- : density function of the Weibull distribution of t of machine m.
- : the percentage of time of delaying or advancing a PM operation.
- H: length of the planning horizon.
3.1.3. Routing Parameters
- : travel time associated to the arc .
- : routing cost associated to the arc .
- : earliest time to start a PM operation i.
- : latest time to start a PM operation i.
- c: penalty cost per unit time for arriving after the deadline associated to PM operation.
- K: number of teams of technicians.
- B: large number.
3.1.4. Variables
- : binary decision variable that takes the value one if the technicians’ teams k travels through arc and 0 otherwise.
- : arrival time of the team of technicians k to the maintenance operation i.
- : penalty variable that measures the total time in excess of the latest permitted time to start the service by the team of technicians k. .
- : time of the last restoration (renewal) previous to the i-th PM operation performed by the team of technicians k. It is the previous start time of the operation on the same machine.The variables of the maintenance model that are constant input parameters for the routing one are defined as follows:
- : optimal PM period for machine m.
- : frequency of PM operations of machine m. It is the number of PM operations of the machine m on the planning horizon.
- : execution time of operation i.
- n: number of PM operations to perform in the planning horizon.
3.2. The Description of the General Approach
The maintenance model is solved to determine the optimal time for each maintenance operation i that minimizes the total maintenance cost. The optimal date to perform a PM operation i is used to determine the durations for the PM operations, the total number of operations n and a time window interval [, ] that minimizes the total maintenance cost. The above steps have been adopted by Lopez-Santana et al. [4]. We then solve the defined joint maintenance and routing model that minimizes the routing and the maintenance costs or the routing and the failure costs. Penalties for late arrival are considered in both cases. In the first case, the maintenance cost is minimized considering the workforce routing constraints that incorporate maintenance requirements (maintenance time windows, etc.). Integrating technical maintenance requirements with transport management is the first merit of the approach. In the second case, the failure cost is minimized to reduce the risk of failures. However, the optimal time chosen must be within a time window that minimizes the total maintenance cost. This latter case considers three objective requirements simultaneously while the minimization of maintenance cost is included in time windows constraints. Expressing some objectives of optimization problems as constraints reduces the problem complexity as adopted in [14]. The second merit of our approach is integrating several maintenance strategies. Indeed, the chosen optimal time reduces the risk of failures, the maintenance cost, and the travel cost (risk-based maintenance, etc.). The outputs of the problem are shown in Figure 1. The workforce routing constraints influence the time to perform maintenance operations, the time of the last restoration that depends on that latter in the combined model, and the waiting time. All the variables are interconnected. Therefore, it is essential to model an integrated problem and to solve it using multi-objective optimization.
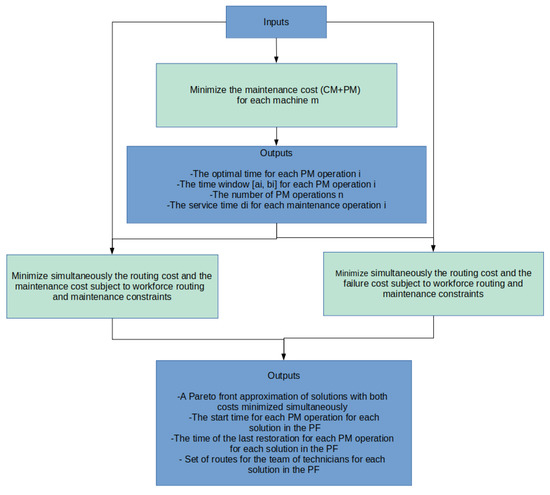
Figure 1.
The general approach.
3.3. The Maintenance Model
The decision model to determine the optimal interval between PM operations is referred to as the maintenance model. It is used when the aim of performing maintenance activities is to minimize the total related maintenance costs of preventive and corrective maintenance operations. The optimal period to perform a PM operation is determined for each machine m with the frequency of PM operations in the planning horizon.
In the following, we define the main terms employed in the maintenance decision model. The probability of failure in the interval of machine m, where is the probability’s notation, is:
The model generally applied by researchers in the literature to settle optimal times to carry out PM operations in the case of periodic preventive maintenance is defined in [15]. Given a machine m, we seek the optimal time to execute PM operations that minimizes the total maintenance cost :
The terms and refer, respectively, to the total expected cost of a cycle and the expected cycle length for a machine m.
Lopez-Santana et al. [4] propose an extended maintenance cost which includes the waiting cost expression in addition to the PM and CM durations. These service times cannot be negligible when the systems under study are large-scale.
represents the expected time to failure of machine m assuming the failure happens before .
According to Lopez-Santana [4], the waiting time of an operation i undertaken by the teams of technicians k is the difference between the technicians arrival time to the PM task and the mean time to failure :
The values of are needed to compute the waiting times. They are also the outputs of the routing model. Consequently, the number of obtained is equal to the number of PM operations to be performed for the machine m in the planning horizon. Since the maintenance model takes only one value, Lopez-Santana et al. [4] consider the average value of all , where i refers to the PM operations related to the machine m to update the waiting time and iterate the procedure. However, the values of are unknown before solving the routing model. Therefore, we suppose a PM operation will be scheduled at . This approximation has also been used by [16].
The waiting time is therefore defined as follows:
The maintenance cost per time unit for a machine m at the time is finally equal to:
This nonlinear equation without constraints is solved to obtain the optimal period for each machine m, argmin .
The frequency of a PM operation on the planning horizon H can be obtained as follows:
The frequency of a PM task is the number of times it is realized in the horizon. Considering a frequency of a machine m, the PM operations need to be performed at times , , ,..., . The execution date of an operation o corresponding to machine m is equal to which represents the execution date of an operation i and is obtained as follows:
The time window of PM tasks associated with a machine are obtained using the time window of the PM period of machine m on the first cycle. is determined using the percentage of time of postponing or preempting a PM task that we can tolerate. The cost stays relatively low and close to the minimal value in this interval. can be expressed as follows:
where and correspond to the lower and upper bound of the time window of machine m and its associated operation o. Each machine m can have operations in the horizon, . All operations for all machines are indexed by i. For each machine m, we can associate an operation i with and (). The interval is determined as follows:
3.4. The Joint Maintenance Scheduling and Workforce Routing Model
As mentioned previously, a machine has to undergo a number of operations within the time horizon. They are indexed by . In this case, the parameters related to operations i related to the same machine m are equal to the parameters of this machine m. , and are, respectively, equal to , and . This way, the values of the operations parameters in the routing model are obtained from the maintenance parameters. The mathematical model of the integrated maintenance scheduling and routing problem can be formulated as follows.
s.t.
The first objective function regards the transport of technicians. The second objective function deals with maintenance. It equals either or :
The objective function (23) minimizes the total travel cost related to technicians routing as well as the penalty cost of not respecting the operations time windows upper bounds. The objective function (24) minimizes the failure cost, the waiting cost, and the penalty cost. Minimizing the machines probability of failure is equivalent to maximizing machines reliability. The objective function (25) minimizes the total expected maintenance cost and the penalty cost incurred for arriving after the deadline associated to PM operations. The penalty term is intended to ensure that the time windows are respected. Therefore, it is considerably small compared to the first term of the objectives whether it is the routing, failure, or maintenance cost and does not increase the correlation between the objectives. The constraints (15) and (16) indicate that each PM operation has to be executed exactly once by one team of technicians. Constraints (17) ensure that the entry of a team of technicians to node i is mandatorily followed by their leaving. Constraints (18) make sub-tours impossible. The purpose of constraints (19) is ensuring that each PM operation is carried out within its time window. Note that we assume and represents the maximum time of arrival to the depot. It is permitted to arrive after the deadline . A penalty is then calculated. Constraints (20) determine the number of vehicles needed and that minimizes the total costs. Constraints (21) ensure that there are different teams of technicians in the different tours. They also ensure that every tour starts at the depot. Finally, the constraints (22) impose domain conditions on the variables.
3.5. The Novelty of the Proposed Model
Several multi-objective or bi-objective models have been proposed for the maintenance scheduling and workforce routing problem. However, adopting the failure and maintenance costs as the second objective with the routing cost has never been proposed to date in the literature to the best of our knowledge. The second objective function of the model can either be minimizing the total preventive and corrective maintenance cost and the penalty cost (25) or minimizing the failure cost with the penalty cost (24). In both costs related to maintenance, the time of the last restoration previous to the i-th PM operation performed by the team of technicians k, is used to verify the hypothesis of the renewal theory. Including this time in the objectives functions is a novel aspect of the model. The definition of the failure cost itself and its possible use is another novelty of the proposed model.
- The Failure Cost: The second objective function minimizes the failure cost and the penalty cost. The aim is to maximize machines reliability. The uncertainty aspect is integrated into the failure cost function by incorporating the probability of failure and the reliability of each machine. In the second objective function, we have used the probability of failure, , for each operation to utilize information from equipment degradation and hence consider failure risks in technicians’ assignment to tasks. It includes direct costs (failure cost) and indirect costs (production losses) illustrated by the waiting time. During that time, the failed machines were out of order and were not used by the organization for production activities. Losses are, therefore, supported by the company. When we multiply it by the waiting cost per unit time, we obtain a cost that can be interpreted as the production loss incurred by the organization due to this machine failure. The failure cost is beneficial in industries where breakdowns are hazardous and influence safety. This term is nonlinear and includes a random variable. It is equal, in the case of the Weibull distribution, to:
- The Maintenance Cost: The objective function minimizes the total expected maintenance cost with the penalty cost. The maintenance cost balances both preventive and corrective maintenance to find the least cost considering the two strategies.
- The Task Duration: The duration of the maintenance operation i is probabilistic. It is simplified in the model as proposed by [4] to be deterministic. Its real expression proposed by [4] is:
4. Proposed Multi-Objective Algorithms
The proposed mathematical model is a mixed integer nonlinear program (MINLP) which cannot be solved by commercial solvers in a reasonable time when applied to large-scale instances. VRPTW is NP-hard [5], and the classical maintenance scheduling problem using operations research techniques is NP-hard as well [5]. Naturally, the combined problem is an NP-hard problem.
The following section presents an adaptation of variable neighborhood descent (VND) and general variable neighborhood search (GVNS) to the multi-objective context to solve the proposed bi-objective combined maintenance and routing problem. At first, the method adopted is explained, and multi-objective notions used in this paper are defined; then the solution representation is shown. Next, the functions used by the algorithms and neighborhood structures are presented. Finally, the proposed multi-objective algorithms are described, as well as their novelty compared to the literature. The proposed algorithms extend single objective variable neighborhood descent (VND) and general variable neighborhood search (GVNS) proposed by Mladenovic and Hansen [17] to solve multi-objective problems. The algorithm MOVND/P is designed to be an intensification local search component of the GVNS algorithms, whereas MOVND/PI and MOGVNS/P are intended to solve the multi-objective problem. They use the Pareto dominance strategy and start with a unique initial solution. They also incorporate novel proposed strategies. Additionally, they all use a novel multi-objective best improvement strategy called MOBI/P. The other GVNS variants aim to measure the impact of the inclusion of a decomposition strategy on the algorithms. MOGVNS/D uses a weighted sum method instead of the Pareto dominance concept and a population of solutions, whereas MOGVNS/CDP tests the use of a population of solutions with MOGVNS/P.
4.1. Pareto Optimality
- Pareto Optimal Dominance: “The solution s dominates another solution ” is denoted by that is ensured if these both conditions are verified and where k is the number of objectives.
- Pareto Optimal Dominance Negation: “The solution s does not dominate another solution ” is denoted by
- Pareto Weakly Dominance: “The solution s weakly dominates another solution ” is denoted by if
- Incomparable Solutions: Two solutions s and are incomparable if they are equally good. This means neither solution dominates the other and is denoted by and
4.2. Solution Representation and Constraints Handling
A solution is represented as a set of K tours, where each tour is a permutation of PM operations. All the constraints considered are hard apart from verifying the upper bounds of the time windows. We allow the arrival of a team to an operation after the latest permitted time defined by its time window. We therefore accept only feasible solutions. Figure 2 shows the solution representation that was used in our implementation and the results for one instance when minimizing only the first objective (the routing cost). The solution that minimizes this cost is composed of two routes (two vehicle are therefore needed). Each route is composed of three tasks in the specified order. Section 3.4 explicitly indicates how the three objective costs are evaluated and how the start time is calculated . For instance, five machines are being considered. Each machine has one operation, apart from machine three that has two operations: three and four. The renewal time for all operations apart from four is therefore zero. The renewal time for task four related to machine three is in route two. It is equal to the start time of task three associated with the same machine, and that precedes task four. The data of this specified instance is detailed in [18].
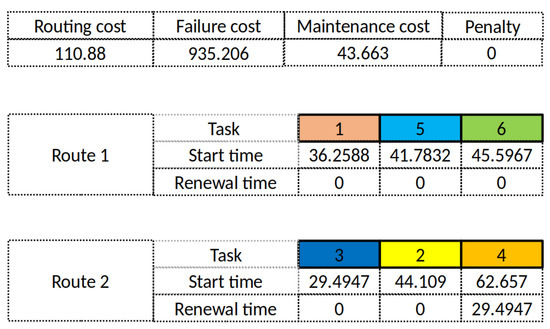
Figure 2.
Solution representation of the result minimizing the routing cost for the instance Re/6/2/80/80/0.07/2 (time in hours).
4.3. Initial Population Generation
We use a weighted aggregation of the two objectives when generating an initial solution. The weighted sum method is used in MOGVNS/D to evaluate and compare solutions. In contrast, the other proposed algorithms (MOVND/P, MOVND/PI, MOGVNS/P, and MOGVNS/CDP) use a multi-objective evaluation and can therefore start with any weightless solution. The weighted sum method is a linear combination of weights. The evaluated function using this method is:
The algorithms start with initial solutions constructed using the best insertion heuristic. This latter calculates the minimum insertion cost for each operation that has to be inserted in the solution. The insertion cost of an operation i represents the difference between the cost solution with and without operation i. At each iteration of the heuristic, the operation with the minimum insertion cost is inserted at its best position in the current solution. The process stops when all the operations are inserted. The proposed algorithms, MOGVNS/CDP and MOGVNS/D deal with a population of solutions. Each population individual is generated using the best insertion heuristic and specific weighted sum method. The detailed procedure is described in Algorithm 1. In decomposition approaches, each population individual is associated with a subproblem. It is necessary to decompose the multi-objective problem effectively to reach the maximum parts of the Pareto front. Subproblems are defined in our case by firstly generating the weights. These weights (or search directions) are chosen to explore different directions. The best insertion heuristic is then used to construct each population’s individual using these weights.
| Algorithm 1: GenerateInitialPopulation. |
| Data: M: population parameter |
| Result: : a population of initial solutions |
 |
4.4. Local Search Procedure and Neighborhood Structures
Our VNS and VND algorithms rely on the set of the neighborhood structures used and particularly on the sequence of their execution. The neighborhood structures are classified and then applied from the best to the least performing [17]. This work adopts the following sequence of neighborhood structures: the swap, the insert, the 2-opt*, and the 2-opt operators. We use approximately the same order as the literature for VRP problems [19,20]. The results of our previous work [18] show that with well-chosen operators, the GVNS algorithm is an effective method to solve the single objective version of our problem. Its general structure can be applied to improve other methods performance [21]. Preliminary tests were realized using a steepest descent heuristic (best improvement local search) to verify this order. The semi-randomization and the randomization of the operators have been tested in both shaking and VND phases. They worsen the solutions obtained. In this study, we have used the classical BA strategy for the mono-objective GVNS and a novel proposed BA strategy, the MOBI/P, for the multi-objective algorithms to obtain a complete Pareto front. In our Pareto-based algorithms, a solution is considered better than an other solution s if it dominates it or if it is incomparable to it. In other words, if after applying a move operator or and , the solution is considered as a new efficient solution and the set A is updated by means of the method. The intra-route moves are used on a single route, while inter-route moves intervene on multiple routes. We examine in the neighborhood exploration all possible positions for each operator. The three first neighborhood structures are inter-routes, and the 2-opt is an intra-route operator. The insert and 2-opt* procedure may modify the number of operations in each route as well as their order. Here’s a description of the different possible moves:
- The swap move exchanges two operations either in the same route or between different routes.
- The insert move deletes an operation from its position and inserts it in another position that can be in the same route or in a different route.
- The 2-opt* operator generates a neighboring solution by removing arcs and belonging to two distinct routes and reconnecting arcs and . It withdraws two edges from a route and replaces them with two other edges to form new routes. This operator is therefore inter-route.
- The 2-opt operator removes arcs and from a route and links arcs and in the same route. This operator is the same as a reverse operator that reverses the elements between i and . This operator is intra-route since it intervenes on arcs belonging to the same route.
4.5. Updating Non-Dominated Solutions Set
The addSolution method described in Algorithm 2 is used to update the set of non-dominated solutions in the archive A [12,22]. This method uses Pareto dominance to evaluate solutions.
| Algorithm 2: addSolution. |
| Data: A: a set of non-dominated solutions; |
| s: a starting solution; |
| Result: A: updated archive; |
| : a boolean equal to true if s is added to the archive A; |
 |
4.6. Multi-Objective Variable Neighborhood Descent Based on Pareto Dominance (MOVND/P)
The multi-objective variable neighborhood descent based on Pareto dominance is an adaptation of the variable neighborhood descent algorithm (VND) to solve our multi-objective problems. It is called MOVND/P. This algorithm has been designed primarily as a multi-objective local search component and an intensification algorithm. Its goal is to improve the performance of other algorithms. This algorithm is based on the general principle of exploring several neighborhoods when there is still an improvement and is inspired by the single objective VND.
Algorithm 3 describes the proposed MOVND/P algorithm. At each iteration and while the archive is still improving (steps 6–28), the current neighborhood of s is entirely explored with a novel multi-objective best improvement strategy called MOBI/P. This MOBI/P procedure tests if each neighbor of s is non-dominated with the best solution found so far in the neighborhood of s. This best solution changes during the search. The MOBI/P strategy is very impactful since it allows the search to be more efficient and diversified and enables the algorithm to converge rapidly. All non-dominated solutions by the best solution found so far in the neighborhood of s are then stored in the set P (step 11).
Each point in P generated with the MOBI/P procedure that is not in the archive A is evaluated to enter this latter or not (steps 13–19). The solution x is included in the archive A if it is non-dominated by s and replaces the current solution s. This replacement of the current solution s by a solution that dominates it or that is incomparable to it is another new feature used. It can be noticed in line 15 and is directly inspired by a single-objective local search.
The counterAISecond measures if some solutions have been added to the archive from the previous iteration to the next iteration. It is incremented in line 17. The aim is to continue running the algorithm while there is still an improvement. The counterAISecond precisely measures if there is an improvement compared to the counter of the previous iteration counterAISecondPrevIt. There is, however, a stopping condition on the number of iterations to avoid large computational time.
We define a new multi-objective neighborhood change procedure. In our case, we say that a neighborhood improves the archive A if all the solutions returned in P are non-dominated by the solutions in A. An improvement means that all new points have been added to the archive A. This is recorded using the counter , which is incremented at each improvement.
A new characteristic was also incorporated in the neighborhood change procedure. In our algorithm, we stay in the improving neighborhood if all the solutions in P are non-dominated by s but also when did not reach . The last part of the condition is required to avoid not exploring the other neighborhoods when the first neighborhood is constantly improving. We can obtain an efficient mix between staying in the best neighborhood and exploring the different neighborhoods.
| Algorithm 3: Multi-objective VND based on Pareto Dominance (MOVND/P). |
| Data: : number of neighborhood structures; |
| : initial solution; |
| Result: A: a set of potentially efficient solutions; |
 |
4.7. Multi-Objective Variable Neighborhood Descent Based on Pareto Dominance Improved (MOVND/PI)
The multi-objective variable neighborhood descent improved based on Pareto dominance (MOVND/PI) presented in Algorithm 4 is an improvement of our Algorithm 3 presented in Section 4.6. The improved algorithm can be used to solve multi-objective problems but is not intended to be a local search component such as the previous algorithm. We allow it, therefore, to consume more computational time through a more sophisticated selection criterion. The new solution s for the following iteration is randomly chosen from the set of non-dominated solutions A among solutions that have not been previously explored in the search. The aim of this criterion is to avoid the intensification of a point already visited and exploited. The algorithm, therefore, does not include the line 16 of the Algorithm 3 to select a solution for the next iteration. The only criteria here to continue running the algorithm is the maximum number of iterations.
| Algorithm 4: Multi-objective VND based on Pareto Dominance Improved (MOVND/PI). |
| Data: : number of neighborhood structures; |
| : initial solution’ |
| Result: A: a set of potentially efficient solutions; |
 |
4.7.1. Multi-Objective General Variable Neighborhood Search Based on Pareto Dominance (MOGVNS/P)
Algorithm 5 describes the GVNS-based algorithm proposed. At each iteration of MOGVNS/P and while the archive is still improving (steps 7–33), a shaking procedure is applied on the current solution s to obtain . The shaking procedure selects a random solution from the current kth neighborhood of the current solution s (). The aim of this phase is to diversify the search process. This perturbation is applied times.
An intensification step is then applied to the perturbed solution using the MOVND/P described in Section 4.6. The non-dominated solutions obtained by MOVND/P are stored and returned in the set (step 16). All the solutions of the set are compared to s to update the archive A using the function addSolution. The improvement of the archive A while exploring is recorded using and from one iteration to the other such as in the MOVND/P algorithm.
We stay in the same neighborhood if all solutions in are added to the archive (steps 25–29). The multi-objective neighborhood change procedure is the same as defined in MOVND/P and MOVND/PI.
In this algorithm, and differently from MOVND/P, the non-dominated solutions in the archive A are used to restart the current solution s. Indeed, the new solution s for the next iteration is randomly chosen from the archive A among solutions that have not been already explored.
The step-by-step procedure of MOGVNS/P can be summarized as follows. First, an initial solution is constructed using the best insertion heuristic and is added to the archive of efficient solutions A. The main procedure is then repeated while there is still an improvement of the archive A and while not reaching a maximum number of iterations . It is composed of the following steps: the exploration of the neighborhood structures while and a random selection in the archive A for the next iteration of the algorithm. The neighborhood exploration phase is composed of four steps. It starts with a shaking procedure to perturb the current solution, followed by an intensification phase using the MOVND/P algorithm to generate the Pareto front . Next, a test is applied to verify that the points in are non-dominated by s to enter the set of efficient solutions A or not. Finally, the decision to stay in the improving neighborhood or explore other neighborhoods is made. Counters are used throughout the algorithms to define stopping criteria, including counters that record the improvement of the archive A.
| Algorithm 5: Multi-objective GVNS based on Pareto Dominance (MOGVNS/P). |
| Data: : number of neighborhood structures in MOGVNS/P; |
| : number of neighborhood structures in MOVND/P; |
| Result: A: a set of potentially efficient solutions; |
 |
4.7.2. Multi-Objective General Variable Neighborhood Search Based on Pareto Dominance and Decomposition (MOGVNS/CDP)
Algorithm 6 extends the MOGVNS/P by starting with a population of initial solutions rather than a single solution. The population is generated using the population generation procedure previously presented in Algorithm 1. The chosen weights in each solution aim to guide the search process in different directions. For each individual in the population, the MOGVNS/P algorithm is used to obtain the non-dominated solutions. The algorithm is therefore based on Pareto dominance. The population of solutions aims to introduce more diversity in the search process by exploring different regions. The drawback of this method is that it can be more time-consuming since we start from a population of solutions.
| Algorithm 6: Multi-objective GVNS based on Pareto Dominance and Decomposition (MOGVNS/CDP). |
| Data: : number of neighborhood structures in MOGVNS/P; |
| : number of neighborhood structures in MOVND/P; |
| vector of empty solutions; |
| M: population parameter; |
| Result: A: a set of potentially efficient solutions; |
 |
4.8. Multi-Objective General Variable Neighborhood Search Based on Decomposition (MOGVNS/D)
Algorithm 7 combines the general structure of the classical aggregation-based method, decomposition algorithms, and GVNS algorithm. It divides the multi-objective problem into mono-objective problems based on aggregation through different weight vectors. The proposed algorithm here is called MOGVNS/D. It uses the single objective local search VND to solve the scalar subproblems.
The single objective VND applies a weighted sum function to evaluate and compare solutions. Given a solution s, the weighted sum function associated to a solution and weight vector is calculated as follows: with l = 2, 3. The initial population is generated using the procedure described in Algorithm 1. Compared to the previous ones based on Pareto dominance, the main drawback of this method is that the Pareto front returned is an approximation of the supported efficient solutions. It can also be time-consuming since we start from a population of solutions. On the other hand, this algorithm is easily convertible to the single objective GVNS algorithm since it is based on aggregation.
4.9. Novelty in the Proposed Algorithms
4.9.1. Novelty among Acceptance Strategies in Multi-Objective Optimization
Several authors have proposed and used several adaptations for the first-accept (FA) and best-accept (BA) in the multi-objective optimization. Therefore, we analyze and review the existing ones and the proposed method hereafter.
- First-Accept based on Pareto dominance: This procedure consists of accepting the first solution that is non-dominated by s. It has been used by Cota et al. [12].
- Best-Accept based on Pareto dominance PLS: Paquete et al. [10] proposed Pareto local search to apply the BA strategy in the multi-objective context. All the neighborhood of s is explored, and the new solution is accepted if it is not dominated by any solution in the set of efficient solutions.
- Best-Accept based on Pareto dominance MOBI/P: We use in this paper a novel best-accept strategy for multi-objective optimization called Multi-objective Best Improvement strategy based on Pareto dominance (MOBI/P). This procedure tests if each neighbor of s is non-dominated with the best solution found so far in the neighborhood of s. This best solution changes during the search. If the new solution dominates this best solution, it replaces it, and so on until exploring all the neighborhoods and retaining a unique last best solution that is the most converging. Choosing the last best solution permits a translation in the Pareto front, ensuring diversification if the new solution is incomparable with the best solution or more convergence if it dominates it. Moreover, it is faster compared to the PLS strategy since we avoid comparing each solution in the neighborhood to each solution in the archive as in PLS.
Algorithm 7: Multi-objective General Variable Neighborhood Search based on Decomposition (MOGVNS/D). Data: kmax: number of neighborhood structures in MOGVNS/P; lmax: number of neighborhood structures in MOVND/P; pop: vector of M + 1 empty solutions; M: population parameter; Result: A: a set of potentially efficient solutions; 
- Best-Accept for each objective separately: This procedure consists of applying a single objective local search but for each objective separately. Duarte et al. [11] use VND-1 (respectively, VND-2) to improve the value of f1 (respectively, f2) regardless of the value of f2 (respectively, f1) in a bi-objective problem. The final local optimum is then tested to enter the archive or not.Combination between the FA and BA strategy in PLS: Dubois-Lacoste et al. [13] propose an alternative to accept only dominating solutions to speed up the search. They suggest switching to the criteria adopted in PLS of accepting non-dominated solutions if such solutions are no longer found. The authors also proposed an alternative strategy. It consists of using the first-improvement technique to converge first to a good approximation of the Pareto front until all solutions in the archive are flagged as visited. Afterward, one can move to the PLS best improvement strategy to complete the archive with the remaining neighbors.
4.9.2. Novelty in the Design of the Multi-Objective Algorithms
We consider an improvement if all the solutions explored have been added to the archive. This procedure is different than the definition of improvement proposed by [11], where improving means at least one new point has been added to the archive A.
Likewise, we stay in the improving neighborhood if all the solutions explored are non-dominated by s but also when a defined counter does not reach a maximum number of iterations. This last condition is required to avoid not exploring the other neighborhoods when the first neighborhood is constantly improving. In the literature, if there is an improvement, the exploration continues in the same neighborhood structure [11]. Queiroz and Mundim [23] propose to change the neighborhood systematically at each iteration in an adapted template from [11] to reduce the computational time.
The proposed algorithms use the MOBI/P procedure above as a multi-objective best improvement strategy, whereas there are several different FA and BA accept strategies in the literature.
5. Computational Experiments
This section presents computational experiments carried out to measure the performance of the proposed algorithms. We present the results of the mono-objective problem using the GVNS algorithm and the results of the multi-objective problem using the proposed algorithms MOVND/P, MOVND/PI, and MOGVNS/P. The results of the other proposed variants, MOGVNS/CDP and MOGVNS/D, are also shown to demonstrate the performance of the three aforementioned algorithms. In addition, CPLEX results are reported for the mono-objective problem. Heuristic Pareto fronts are also provided for comparison to our multi-objective problem. The maintenance model without constraints was solved using Python 3.6. The joint maintenance scheduling and workforce routing model was then solved using C++. This work has been compiled with GCC 7.4 in a Linux environment. To solve the MILP using an exact method, the concert technology library of CPLEX 12.10.0 version with default settings in C++ has been used. Experiments were conducted using the CALCULCO computing platform in an AMD EPYC 7702 with 2CPU, 2 gigahertz, and 1 core was dedicated to each instance. All methods are run using the same machine to avoid bias.
5.1. Instances Description
We use two sets of instances. The first one, denoted by Re, is inspired by industrial reality. In the Re instances, large and short maintenance durations are considered ( and go from 0.5 to 48 h). We set the shape the parameter of deleted Weibull distribution to consider the wear-out period of the machine’s life. These machines are, therefore, old. Short (27 km) and long distances (up to 500 km) are considered. The speed is fixed to 60 km/h, as adopted in real-world scenarios. The horizon is set to H = 101 h for n = 12 and H = 80 h for n = 6. The penalty cost is fixed to c = 10. This cost is high enough to produce the desired effect of penalizing the objective functions whenever multiplied by the penalty variables. The depot time window is the interval between the lower bound = 0 and the upper bound . For this class of instances, . These data are shown in [18]. There are six machines that may need more than one maintenance task in the planning horizon in the class of instances Re. The travel time and distance between the same machine operations are naturally zero. The number of available vehicles is initially fixed to 4 for and 2 for . We note that in some obtained solutions, we can use fewer vehicles than those available. The second set is derived from the well-known Solomon benchmark. These benchmark problems are available on Solomon’s web page http://web.cba.neu.edu/msolomon/problems.htm (accessed on 29 April 2022). We used the first 10, 25, 50 machines of Solomon’s classes of instances. The number of operations used in these instances varies from 23 to 91 operations, and the number of vehicles ranges from 5 to 35. This latter can also be reduced during the search.
Solomon’s instance are classified in three groups:
- R: randomly distributed locations.
- C: geographically clustered locations.
- RC: partially randomly distributed and partially clustered locations.
There are six Solomon’s classes with different locations coordinates: C101, C201, R101, R201, RC101, RC201. The unitary speed is adopted. For each of these six classes, we consider the horizon H = 100 h with a latest arrival time at the depot = 200 h and H = 200 h with = 400 h. The opening time is = 0. The maintenance parameters were generated as described in [4]: , , , , , and . Only the parameter is generated differently compared to the one described in [4] so that it can be closer to reality. The continuous uniform distribution has been used to generate the random information. In the instances sets, the percentage of time windows tolerance is set to . It is inspired by the values usually used in large-scale industries that consider a restricted time window. Another significant time windows tolerance is considered .
5.2. Numerical Results for the Mono-Objective Problem
5.2.1. Parameter Setting and Performance Metrics
To set the algorithm parameters, we have run several preliminary tests. We noticed that a high value of the shaking parameter and a high number of iterations have a negative impact on the computational time. The retained parameters for the maximum number of iterations is for the routing objective (23) and the maintenance objective (25), where the symbol E stands for the whole experiments parts of the integer portion of the number. For the failure objective (24), this parameter is . The diversification parameter in the shaking phase is set to three. We compare the results of the CPLEX solver and our mono-objective GVNS algorithm for the routing objective function (23). In the CPLEX columns, we report the objective value, the CPU time, and whether the solution is optimal, feasible, or not found after 96 h of execution. In the GVNS algorithm, we indicate, respectively, the maximum, minimum, and average values for five runs. We also provide the corresponding maximum, minimum, and CPU time.
The pseudo-code of mono-objective GVNS and VND are shown in [18]. The mono-objective GVNS can directly be obtained with MOGVNS/D when the initial population is reduced to one individual. The gap between the objective value of our metaheuristic and the CPLEX solution is calculated as follows:
This gap represents the percent decrease of the cost objective when the GVNS algorithm is used in comparison to the use of the CPLEX solver. It is the case whenever the CPLEX solver only found a feasible penalized solution, and the gap is different from zero.
The percent decrease of CPU time when using the GVNS algorithm compared to the CPLEX solver is given by:
5.2.2. Test Results
The results of the GVNS and CPLEX solver for the routing objective are represented in Table 1. Bold values are the minimum objective values obtained by either the GVNS or the solver. Whenever a number in the improvement column is bold, there is an improvement.

Table 1.
Results of mono-objective GVNS for the routing objective.
The quality of the initial solution obtained with the best insertion heuristic considerably reduces the CPU time since we start from a reduced objective compared to random initial solutions. The impact of good initial solutions on the CPU time is illustrated in [18]. Indeed, providing a well-chosen starting solution positively influences the execution time and helps to improve the final solution quality rapidly. Optimizing the failure cost requires more iterations to reach high-quality solutions than optimizing the routing cost or the maintenance cost.
For small instances (less than 26 operations) of Solomon’s class C, both CPLEX and GVNS were able to solve the problem optimally. However, the GVNS algorithm consumed less CPU time than CPLEX for most of the instances. When the number of operations increases to more than 34, some optimums were obtained for class C, R, or RC instances. For these instances, CPLEX returns mostly either feasible solutions or optimal solutions but after a very long CPU time (more than 48 h). In many instances, CPLEX fails to find optimal solutions after one week. In most cases, the GVNS algorithm improves the objective value of feasible solutions obtained by CPLEX. The Gap of GVNS for most instances is . The algorithm is also very robust since the difference between the maximum, minimum, and average values is very small, almost negligible.
For the 47 tested instances, CPLEX returned either feasible or optimal values for 29 instances and failed to obtain any feasible solution for the remaining 18 instances, even after a week of execution. For the 29 instances for which we obtained either feasible or optimal solutions using CPLEX, the average gap or objective improvement of GVNS over CPLEX is 18.47%. The average improvement of CPU is 32.81%. When removing the four Re instances for which the number of operations is inferior to 12, we obtain an average objective improvement in favor of GVNS equal to 21.42 % and an average improvement of the CPU is 77.96%. The gap value is 0 for 17 instances among 29 instances solved. Therefore, the proposed GVNS found the optimums in these instances. The GVNS algorithm improves the CPLEX results on 11 instances out of the 29 instances for which CPLEX returns either feasible or optimal solutions. However, it obtains a slightly worse value for only one instance. The average gap for the 12 instances where the gap is different from 0 is 44.61%. This means that when the gap is different from zero (meaning only a feasible solution is found), GVNS finds a better objective value than CPLEX with a percentage of 44.61%. The average percent decrease of CPU time when using GVNS compared to CPLEX is 85.73% in this case.
Our GVNS algorithm outperforms CPLEX in terms of running time, the longest CPU time being only 3 h (10,906.1 s) compared to the maximum CPU time reached by CPLEX of 95.53 h (343,932 s).
5.3. Numerical Results for the Multi-Objective Problem
5.3.1. Parameter Setting and Performance Metrics
There are two stopping conditions for the MOVND/P, MOVND/PI and MOGVNS/P: the maximum number of iterations and the stopping criterion related to the neighborhood change . The value of these parameters has been fixed according to the number of operations n. For the MOVND/P algorithm, the maximum number of iterations is . The second defined stopping criterion related to the neighborhood change is . Similarly, for MOGVNS/P these parameters are and . For MOVND/PI, these values are and . For the algorithm MOGVNS/D, in the multi-objective case. The algorithm also repeats the instructions until there is no improvement for each individual of the population. For the mono-objective case, as mentioned previously, the stopping criterion is a maximum number of iterations that equals for the routing objective and the maintenance objective and for the failure objective. MOGVNS/CDP calls MOGVNS/P and has, therefore, the same values as this latter for and . The population size parameter equals .
In mono-objective optimization, it is simple to evaluate the quality of a solution. It is a more difficult task in multi-objective optimization since the output is represented by sets of trade-off solutions, potentially incomparable in terms of Pareto dominance. Consequently, we use several indicators to measure the quality of an approximation of the Pareto front involving several criteria such as solution quality, computational effort, robustness, and other factors. The indicators assess solution quality and computational effort. The CPU indicator evaluates the time needed for the algorithm to return a final Pareto front. The quality indicators that we used are the number of non-dominated solutions and the hypervolume indicator to measure coverage and assess the front returned convergence.
The hypervolume (HV) indicator is a metric that measures the size of the space covered. It assesses the space enclosed by all the solutions of the objective space. The HV of an estimated Pareto front is the sum of the hypercubes that each set of solutions contains. It shows the distribution of solutions along the Pareto front. The larger the HV indicator is, the better the Pareto front is.
The reference point is chosen to be dominated by all solutions of the Pareto front. In this section, the reference point used is since we seek to minimize costs. and are, respectively, the maximum values of the first objective (routing cost) and the second objective, either failure or maintenance cost in the Pareto front identified by the mono-objective GVNS. The size of a rectangular area enclosed by a solution is where l = 2,3. The hypervolume is the sum of the areas formulated as follows:
where l = 2,3, and p is the number of solutions in the Pareto front A.
Our bi-objective algorithms based on VND and GVNS frameworks were compared to those of [11]. Algorithms in [11] were run for a longer time to have a complete Pareto front and meaningful results. For a fair comparison, all methods were run on the same machine in the computing platform.
The improvement of our algorithms over the literature algorithm is evaluated using a percent increase of the HV indicator and the number of non-dominated points when using the proposed algorithms PA compared to the comparison algorithms CA of [11].
It is also evaluated using the percent decrease of the CPU time of the proposed algorithms PA over the comparison algorithms CA.
5.3.2. Test Results
Tests are realized over small, medium, and large instances. Small instances include 6 and 12 PM operations. The number of operations varies between 23 and 34 for medium-sized instances and between 52 and 73 for large-sized instances. The indicators assessed are the hypervolume (HV) to measure the convergence and coverage of the solutions in the Pareto front obtained, the number of non-dominated points (NDP), and the CPU time in seconds.
Comparison with the Literature
Table A1 and Table A2 show the results of the proposed variable neighborhood descent algorithms, MOVND/P, MOVND/PI, and the results of the MOVND suggested by [11]. Furthermore, Table A1 details the results for the maintenance cost as a second objective, whereas Table A2 shows the results when the failure cost is the second objective of the problem.
Some results that were not displayed in detail are also reported here for the tested instances: the average percent improvement of HV (IHV), NDP (INDP), and CPU (ICPU). They are summarized in Table 2. There is an improvement for bold numbers. When the maintenance cost is the second objective considered, both MOVND/P and MOVND/PI have better average values than the MOVND of [11] on all the considered quality indicators. Indeed, the average percent improvement of MOVND/P compared to MOVND [11] of the hypervolume (IHV) and the number of non-dominated points (INDP) is, respectively, and . These two indicators improved slightly; however, the CPU time decreased considerably by . The second proposed algorithm, MOVND/PI, considerably outperforms the MOVND of the literature [11] for the 46 instances tested. Indeed, the hypervolume and the number of non-dominated points increased, respectively, by an average of and , which is a considerable improvement. However, the CPU decreased by only . Despite the minor improvement for the CPU time, the other coverage and convergence indicators are considerably improved. We also measure this improvement for the proposed VND algorithms over MOVND of the literature [11] for the instances without the four small instances Re. For the 42 derived from Solomon’s instances, the improvement of the indicators HV, NDP, and CPU of MOVND/P is, respectively, , , and . The improvement of the same indicators for MOVND/PI becomes , , and .

Table 2.
Comparisonbetween the proposed algorithms and the literature algorithms.
We consider the failure cost as a second objective with the routing one. The average percent improvement of the indicators of MOVND/P in comparison to MOVND of the literature [11] is considerable, and the values of HV, NDP, and CPU indicators equal, respectively, , , and . The average percent improvement of HV for MOVND/PI compared to MOVND of the literature is . The number of non-dominated points NDP increased by . However, the improvement of the CPU is . When the four small instances Re are deleted to consider only instances generated from Solomon’s set, the improvement of the indicators stays considerable for both algorithms. The values of HV, NDP, and CPU indicators improved by, respectively, , , and for MOVND/P and by , , and for MOVND/PI. The quality indicators are improved, and the CPU time of our algorithms is considerably less.
We can conclude that all the indicators were improved for both failure cost and maintenance cost as the second objective. There is a slight improvement for the HV and NDP indicator for MOVND/P for the maintenance cost and a considerable improvement in the CPU time that has decreased. On the other hand, MOVND/PI improves the HV and NDP indicators considerably with only a tiny improvement in the CPU time. The results of the failure cost as a second objective demonstrated a considerable improvement for all the quality and time indicators for both MOVND/P and MOVND/PI algorithms.
Table A3 illustrates the results of the comparison between our proposed MOGVNS/P and MOGVNS of the literature suggested by [11]. When the maintenance cost is the second objective, the average percent improvement of HV when using MOVGVNS/P is . The number of non-dominated points NDP increased by an average of . The computational time CPU of MOVGVNS/P decreased by . When the failure cost is the second objective, the average percent improvement of HV of MOVGVNS compared to MOGVNS of the literature is . The number of non-dominated points NDP increased by . The running time is reduced by . All the indicators have been improved. We can conclude that the MOGVNS/P algorithm considerably outperforms the literature algorithm in all the assessed indicators for both second objectives.
We fixed a time limit to one week to have all the instances. We have therefore tested the MOGVNS of the literature for fewer instances since it consumes more time.
Comparison between the Proposed Algorithms
Table A4 and Table A5 present the results of the three indicators measuring the quality of the solutions obtained and the time to get those solutions for the proposed MOGVNS/P, MOGVNS/CDP, and MOGVNS/D algorithms. The last study aims to compare the performance of the algorithms presented and discuss their difference. When the maintenance cost is the second objective, and for the 46 tested instances, MOGVNS/P outperforms in average MOGVNS/CDP in the three indicators HV, number of NDP, and CPU with, respectively, 2.42%, 1.92%, and 24.73%. MOGVNS/P is better on average than the decomposition-based algorithm MOGVNS/D in the indicators HV, the number of NDP, and CPU with, respectively, 574.41%, 573.14%, and 19.92%. The MOGVNS/P improves MOVND/PI on the indicators HV and NDP by about 25.87% and 26.90%. However, MOGVNS/P consumes more time (−706.20%) than MOVND/PI. In the opposite direction, the MOVND/PI improves MOGVNS/P by −0.38%, −0.23%, and 65.74%. Therefore, we can conclude that MOVND/PI has similar performance for the HV and NDP indicators and is far faster than MOGVNS/P. When the failure cost is the second objective and for the 46 instances tested, MOGVNS/P outperforms on average MOGVNS/CDP in the three indicators HV, the number of NDP, and CPU with, respectively, , , and . The MOGVNS/P is better than MOGVNS/D in the indicators HV, NDP, and CPU with , , and . The MOGVNS/P improves MOVND/PI on the three indicators HV, NDP, and CPU by about 22.02%, 21.75%, and −387.50%. The HV and NDP indicators are improved; however here again, MOGVNS/P consumes more time than MOVND/PI when the failure cost is considered. In the opposite sense, the MOVND/PI improves MOGVNS/P by −7.55%, −7.41%, and 70.87%. We can conclude from this study that MOGVNS/P is better in all indicators compared to MOGVNS/CDP and MOGVNS/D. Moreover, MOVND/PI has approximately the same performance as MOGVNS/P, but it is considerably faster.
The convergence of the proposed algorithms for all the instances tested can be discussed from the HV results of Table 2. The improvement for the HV indicator of MOGVNS/P over MOGVNS/CDP is slight. The two algorithms therefore have similar convergence and coverage performance. They also have approximately the same number of non-dominated points NDP. The mono-objective GVNS, whose results are presented in Section 5.2.2 obtains a solution with the optimal cost found by the solver or a solution with a better objective value than the feasible solution returned by the solver. Therefore, the GVNS algorithm converges. The algorithm MOGVNS/D uses the same components (neighborhood structures, etc.) as the GVNS algorithm and an aggregated function to evaluate solutions. It therefore has the same convergence as the other GVNS algorithms. However, the set of efficient solutions returned includes only supported solutions, which explains its weak performance in the HV and NDP indicators compared to MOGVNS/P. Figure 3 illustrates for a given instance of 52 operations that MOGVNS/D has a good convergence but returned an incomplete Pareto front. MOVND/P is designed to be an intensification algorithm. It is a main component of MOGVNS/P and MOGVNS/CDP. It therefore has less convergence than the latter two. MOGVNS/P outperforms MOVND/PI in the HV and NDP indicators. MOGVNS/P also takes more time. Therefore, the convergence and the coverage of MOGVNS/P are better than those of MOVND/PI. The MOGVNS/P algorithm also returns more non-dominated points than MOVND/PI. This is shown in Figure 3. We can conclude that all the algorithms converge; however, the convergence of the GVNS algorithms is better than the convergence of VND-based algorithms. All the GVNS algorithms proposed in this paper have the same convergence as MOGVNS/P but differ only in terms of coverage.
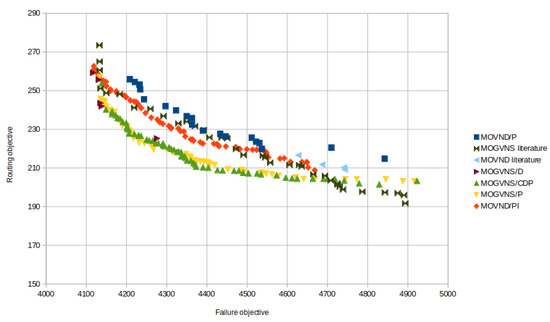
Figure 3.
Pareto fronts of the different algorithms for the instance C201/25/18/100/200/0.30 and the failure cost as second objective (52 operations).
Discussion of the Results
In conclusion, the proposed algorithms MOVND/P, MOVND/PI, and MOGVNS/P have a better performance compared to the MOVND, and MOGVNS of [11]. One reason can be that the VND used by [11] first tries to improve each objective separately independently from the other using a single objective evaluation. As a result, the algorithms are not totally based on Pareto dominance. The method we used to fully explore the neighborhoods MOBI/P is also very impactful in improving solution quality and reducing computational time. We also force the exploration of all the neighborhoods with specific stopping criteria, while in [11], staying in the same neighborhood is necessary when it still improves. MOGVNS/P has a similar performance as MOGVNS/CDP. However, the latter consumes more time since MOGVNS/CDP is the same as MOGVNS/P applied to a population of solutions instead of one initial solution. The shaking procedure is also a better perturbation than the method we used to generate the initial population and is sufficient to diversify the search. The importance of the shaking procedure also appears when comparing the performance between MOGVNS/P and MOVND/PI. MOGVNS/P outperforms for the quality indicators MOVND/PI. MOGVNS/P is far better than MOGVNS/D for all quality indicators since the latter algorithm returns only supported solutions. All methods have a good convergence towards a good Pareto front. The methods differ in the coverage and convergence indicator, the number of non-dominated solutions, and the computational time. Our best algorithms are MOGVNS/P and MOVND/PI.
Figure 3 illustrates the Pareto front obtained on the instance C201/25/18/100/200/0.30. For this specific instance, MOGVNS/P and MOGVNS/CDP have good performance over all other algorithms. MOVND/P and MOVND/PI are better than the MOVND proposed in the literature. Moreover, MOVND/PI is also better than MOGVNS in the literature. MOGVNS/D returns an incomplete Pareto front but has a good convergence. This instance can represent the results of the performance of all the algorithms on average. The proposed MOGVNS/P algorithm has better convergence compared to MOVND/PI. The average percent results obtained in Table 2 show the same performance. However, the results of MOVND/PI, on average, are close to those of MOGVNS/P, although it is less converging.
6. Conclusions
In this paper, we address a joint maintenance and workforce routing problem. We propose a novel bi-objective mathematical model that aims to minimize both maintenance and transport costs in the case of time-based preventive maintenance. The set of machines is supposed to be geographically distributed and subject to non-deterministic failures. The joint maintenance and routing problem’s objective is to simultaneously determine the optimal times to perform preventive maintenance operations on each machine and find the optimal sequence of these operations that simultaneously minimizes the maintenance and routing cost.
There are many contributions to this paper. We first propose a nonlinear stochastic failure cost that uses information from equipment degradation. It includes direct costs (failure cost) and indirect costs (production losses) illustrated by the waiting time. This objective is particularly valuable for industries where failures seriously influence personnel safety and cause environmental damage. We also investigate another maintenance cost previously proposed in the literature that aims to balance both preventive and corrective costs related to maintenance operations. For the first time, a bi-objective approach is proposed to deal with this problem, where we associate either the failure cost or the maintenance cost with the routing cost. Both costs also consider the time of the last restoration. The proposed model considers maintenance operations time windows, penalties related to late arrival, and maintenance costs under uncertainty which are interesting features of real industrial problems. New adaptations of variable neighborhood descent and general variable neighborhood search frameworks called respectively MOVND/P, MOVND/PI, and MOGVNS/P are proposed to deal with combinatorial multi-objective optimization problems, and this problem, particularly. To obtain high-quality solutions, we describe how to design the improvement method, the acceptance criterion, the stopping criterion, and the neighborhood change procedure. These algorithms are based on the Pareto dominance concept and use a new multi-objective best improvement strategy called MOBI/P. We test a pure decomposition approach. The resultant algorithm, MOGVNS/D, decomposes the problem into several scalar subproblems and uses the weighted sum method to evaluate the solutions. This algorithm is easily convertible to a mono-objective general variable neighborhood search. Finally, we test the use of a population of solutions with MOGVNS/P. The resulting variant is called MOVNS/CDP.
Several numerical experiments have been performed to validate our proposals. First, the mathematical model and the proposed algorithms were evaluated on randomly generated instances. For the single objective variant of the problem, the computational results for the linear routing objective indicate that the GVNS significantly outperforms the results of the commercial solver CPLEX in terms of solution quality and CPU time. The obtained results also demonstrate that MOVND/P, MOVND/PI, and MOGVNS/P outperform existing MOVND and MOGVNS in the literature for all indicators measuring convergence and coverage in less computational time. Compared to the other proposed MOGVNS variants, MOGVNS/P is significantly better than MOGVNS/D for all the quality and time indicators since the latter algorithm returns only supported solutions. MOGVNS/P slightly outperforms MOGVNS/CDP in less computational time. Moreover, MOVND/PI and MOGVNS/P have almost similar performances with a time advantage in favor of MOVND/PI.
Future research will include exploring the integration of other maintenance strategies with the routing problem to reduce maintenance costs and improve the quality of maintenance services. It will also be promising to test the hybridization of local search and population-based methods to solve the problem.
Author Contributions
Conceptualization, L.D.; methodology, L.D.; software, L.D.; validation, L.D., A.K., R.B., R.N.G., C.F.; formal analysis, L.D.; investigation, L.D.; data curation, L.D.; writing—original draft preparation, L.D.; writing—review and editing, L.D.; visualization, L.D.; supervision, A.K., R.B., R.N.G., C.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the PhD research scholarship grant number 1INSEA2018 of the Centre National pour la Recherche Scientifique et Technique (CNRST), Morocco and the joint PhD research scholarship of the Université du Littoral Côte d’Opale (ULCO), France.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
Acknowledgments are addressed to the Centre National pour la Recherche Scientifique et Technique (CNRST), Morocco and the Université du Littoral Côte d’Opale (ULCO), France for the research scholarship provided. Acknowledgments are also addressed to the anonymous referees for the valuable comments that significantly improved the paper. Experiments presented in this paper were carried out using the CALCULCO computing platform, supported by SCOSI/ULCO (Service Commun du Système d’Information de l’Université du Littoral Côte d’Opale).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Comparison of the Proposed Algorithms with the Literature

Table A1.
Results of MOVND/P, MOVND/PI and MOVND literature for the maintenance cost as a second objective.
Table A1.
Results of MOVND/P, MOVND/PI and MOVND literature for the maintenance cost as a second objective.
| n | MOVND/P | MOVND/PI | MOVND Literature | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HV () | NDP | CPU (s) | HV () | NDP | CPU (s) | HV () | NDP | CPU (s) | ||
| 6 | 0.0003 | 5 | 0.05 | 0.0003 | 5 | 0.2 | 0.0003 | 4 | 0.04 | |
| 12 | 0.0485 | 8 | 1.22 | 0.0666 | 11 | 4.47 | 0.0843 | 14 | 5.36 | |
| 6 | 0.0007 | 4 | 0.06 | 0.0007 | 7 | 0.21 | 0.0002 | 1 | 0.03 | |
| 12 | 0.0479 | 5 | 1.22 | 0.0670 | 4 | 4.48 | 0.0572 | 6 | 4.01 | |
| 23 | 1.24 | 4 | 19.47 | 2.49 | 8 | 133.15 | 3.11 | 10 | 116.31 | |
| 23 | 1.55 | 5 | 23.72 | 0.31 | 1 | 5.87 | 0.93 | 3 | 86.28 | |
| 26 | 12.97 | 9 | 23.83 | 12.97 | 9 | 209.43 | 5.77 | 4 | 130.84 | |
| 54 | 562.34 | 16 | 533.78 | 1581.59 | 45 | 6428.67 | 667.78 | 19 | 8932.8 | |
| 24 | 4.10 | 4 | 15.71 | 5.77 | 4 | 142.89 | 3.07 | 3 | 40.64 | |
| 52 | 386.17 | 11 | 609.31 | 1097.39 | 32 | 5450.49 | 702.11 | 20 | 9680.37 | |
| 34 | 6.39 | 2 | 55.92 | 3.19 | 1 | 26.76 | 6.40 | 2 | 281.41 | |
| 68 | 951.51 | 12 | 1091.67 | 2140.90 | 27 | 17,624.5 | 475.75 | 6 | 21,268.8 | |
| 34 | 17.17 | 2 | 91.98 | 6.17 | 2 | 26.74 | 9.27 | 3 | 417.44 | |
| 65 | 897.63 | 14 | 1242.88 | 1987.66 | 31 | 14,485.9 | 769.37 | 12 | 19,628.2 | |
| 33 | 17.17 | 3 | 55.66 | 7.22 | 2 | 24.26 | 7.24 | 2 | 276.07 | |
| 62 | 1011.35 | 15 | 677.4 | 2292.50 | 34 | 10,612.2 | 1348.52 | 20 | 13,304 | |
| 33 | 6.59 | 2 | 68.92 | 6.57 | 2 | 24.24 | 3.30 | 1 | 121.77 | |
| 60 | 1227.72 | 21 | 1032.7 | 2104.66 | 36 | 8961.95 | 876.78 | 15 | 9027.58 | |
| 23 | 5.41 | 19 | 22.12 | 9.97 | 35 | 132.91 | 4.56 | 16 | 147.47 | |
| 23 | 1.42 | 5 | 20.67 | 5.41 | 19 | 126.2 | 2.85 | 10 | 99.42 | |
| 26 | 29.05 | 17 | 35.08 | 42.94 | 31 | 209.26 | 18.01 | 13 | 150.65 | |
| 54 | 548.34 | 16 | 590.27 | 2296.17 | 67 | 6034.47 | 274.17 | 8 | 8805.36 | |
| 24 | 3.93 | 4 | 9.73 | 19.66 | 20 | 154 | 12.78 | 13 | 92.96 | |
| 52 | 445.82 | 13 | 357.9 | 3223.72 | 94 | 5141.7 | 1097.37 | 32 | 17,867.8 | |
| 34 | 15.71 | 5 | 61.06 | 6.28 | 2 | 26.77 | 18.85 | 6 | 340.59 | |
| 68 | 938.94 | 12 | 743.79 | 4616.59 | 59 | 18,565.4 | 2660.35 | 34 | 54,171.9 | |
| 34 | 8.99 | 3 | 52.73 | 35.96 | 12 | 564.07 | 29.97 | 10 | 425.77 | |
| 65 | 1008.25 | 16 | 904.88 | 3150.85 | 50 | 15,022.9 | 441.12 | 7 | 32,633.30 | |
| 33 | 10.66 | 3 | 96.33 | 3.55 | 1 | 24.27 | 21.32 | 6 | 454.34 | |
| 62 | 863.89 | 13 | 609.68 | 3322.72 | 50 | 11,081.2 | 1727.76 | 26 | 22,870.20 | |
| 33 | 25.77 | 8 | 73.56 | 22.55 | 7 | 502.72 | 22.55 | 7 | 429.36 | |
| 60 | 345.92 | 6 | 464.33 | 2882.67 | 50 | 9104.31 | 1787.19 | 31 | 20,760.4 | |
| 52 | 294.75 | 17 | 1242.3 | 346.77 | 20 | 11,082 | 294.75 | 17 | 18,586.1 | |
| 58 | 464.93 | 13 | 1868.44 | 434.22 | 12 | 14,898.9 | 289.48 | 8 | 20,384.3 | |
| 54 | 158.07 | 6 | 1092.76 | 447.88 | 17 | 11,487.4 | 342.48 | 13 | 23,556.1 | |
| 73 | 690.09 | 10 | 1395.12 | 3795.37 | 55 | 49,525.1 | 1587.10 | 23 | 64,858.6 | |
| 72 | 871.90 | 14 | 1719.02 | 2366.54 | 38 | 47,512.1 | 1556.88 | 25 | 86,544.6 | |
| 71 | 860.73 | 11 | 1957.61 | 2112.70 | 27 | 43,173.4 | 1095.45 | 14 | 39,987.6 | |
| 72 | 604.69 | 8 | 3235.91 | 982.63 | 13 | 45,042.6 | 755.85 | 10 | 86,450.6 | |
| 52 | 260.40 | 32 | 2103.68 | 398.74 | 49 | 10,837.7 | 195.29 | 24 | 34,088.3 | |
| 58 | 569.45 | 16 | 1129.3 | 1530.41 | 43 | 15,580.8 | 284.73 | 8 | 19,984.4 | |
| 54 | 234.59 | 9 | 616.88 | 1172.96 | 45 | 12,336.6 | 781.95 | 30 | 23,290.3 | |
| 73 | 1570.12 | 23 | 2435.37 | 3618.16 | 53 | 49,447 | 2457.47 | 36 | 149,979 | |
| 72 | 430.94 | 7 | 1366.78 | 4063.01 | 66 | 46,973.4 | 1785.15 | 29 | 150,895 | |
| 71 | 1547.50 | 20 | 1715.48 | 5493.56 | 71 | 44,989.6 | 1934.23 | 25 | 80,095.2 | |
| 72 | 820.64 | 11 | 2227.89 | 2909.57 | 39 | 46,574.3 | 2685.58 | 36 | 130,648 | |

Table A2.
Results of MOVND/P, MOVND/PI and MOVND literature for the failure cost as a second objective.
Table A2.
Results of MOVND/P, MOVND/PI and MOVND literature for the failure cost as a second objective.
| n | MOVND/P | MOVND/PI | MOVND Literature | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HV () | NDP | CPU (s) | HV () | NDP | CPU (s) | HV () | NDP | CPU (s) | ||
| 6 | 0.0034 | 5 | 0.06 | 0.0004 | 5 | 0.21 | 0.0004 | 4 | 0.04 | |
| 12 | 0.0909 | 8 | 1.22 | 0.1117 | 10 | 4.45 | 0.1008 | 9 | 4.05 | |
| 6 | 0.0015 | 4 | 0.06 | 0.0015 | 4 | 0.21 | 0.0004 | 1 | 0.03 | |
| 12 | 0.0671 | 5 | 1.22 | 0.1174 | 7 | 4.48 | 0.1001 | 6 | 3.64 | |
| 23 | 5.31 | 9 | 15.1 | 5.31 | 9 | 135.19 | 5.30 | 9 | 64.05 | |
| 23 | 1.76 | 3 | 14 | 6.45 | 11 | 128.08 | 3.52 | 6 | 43.86 | |
| 26 | 18.79 | 7 | 31.58 | 18.79 | 7 | 213.73 | 10.74 | 4 | 103.54 | |
| 54 | 1231.33 | 18 | 559.09 | 3899.40 | 57 | 6678.62 | 1983.79 | 29 | 8206.33 | |
| 24 | 5.77 | 3 | 16.77 | 5.77 | 3 | 13.77 | 5.77 | 3 | 37.4 | |
| 52 | 865.32 | 13 | 551.99 | 2196.74 | 33 | 5780.61 | 532.46 | 8 | 10,127.5 | |
| 34 | 42.19 | 8 | 86.95 | 116.43 | 22 | 657.07 | 52.88 | 10 | 1166.9 | |
| 68 | 4066.99 | 29 | 2002.37 | 21,038.07 | 150 | 18,851.9 | 3786.48 | 27 | 33,391.7 | |
| 34 | 63.14 | 12 | 94.28 | 52.66 | 10 | 647.3 | 21.05 | 4 | 452.07 | |
| 65 | 4361.90 | 38 | 1034.57 | 15,726.16 | 137 | 15,669.4 | 918.13 | 8 | 33,337.7 | |
| 33 | 55.46 | 9 | 127.03 | 67.90 | 11 | 565.16 | 43.13 | 7 | 881.1 | |
| 62 | 3657.44 | 30 | 707.27 | 9510.84 | 78 | 11,472.4 | 4023.34 | 33 | 15,830.2 | |
| 33 | 32.66 | 6 | 59.1 | 10.86 | 2 | 65.87 | 27.21 | 5 | 453.44 | |
| 60 | 1566.20 | 15 | 685.66 | 3445.64 | 33 | 9295.29 | 1252.91 | 12 | 18,024.7 | |
| 23 | 13.77 | 25 | 29.48 | 18.73 | 34 | 132.67 | 8.81 | 16 | 86.21 | |
| 23 | 5.49 | 10 | 16.25 | 10.44 | 19 | 125.59 | 8.22 | 15 | 116.21 | |
| 26 | 7.82 | 3 | 31.54 | 49.50 | 19 | 210.47 | 23.42 | 9 | 155.62 | |
| 54 | 806.57 | 12 | 384.27 | 4571.50 | 68 | 6545.2 | 537.50 | 8 | 10,506 | |
| 24 | 24.09 | 13 | 32.81 | 27.79 | 15 | 154.49 | 12.95 | 7 | 160.28 | |
| 52 | 1308.52 | 20 | 641.11 | 5038.12 | 77 | 5401.41 | 261.65 | 4 | 5892.46 | |
| 34 | 72.90 | 14 | 147.27 | 156.51 | 30 | 642.17 | 104.19 | 20 | 906.05 | |
| 68 | 2914.36 | 21 | 1139.92 | 9306.64 | 67 | 19,275.6 | 6387.17 | 46 | 55,910.8 | |
| 34 | 55.75 | 10 | 77.69 | 117.96 | 23 | 658.76 | 77.96 | 14 | 911.04 | |
| 65 | 2934.54 | 25 | 880.81 | 12,567.23 | 111 | 15,819.6 | 1173.17 | 10 | 26,295.3 | |
| 33 | 54.65 | 9 | 95.43 | 158.08 | 26 | 579.12 | 30.29 | 5 | 445.19 | |
| 62 | 3137.26 | 26 | 976.83 | 9533.74 | 79 | 10,722.8 | 3378.24 | 28 | 25,547.6 | |
| 33 | 32.19 | 6 | 114.38 | 32.13 | 6 | 543.16 | 16.07 | 3 | 348.52 | |
| 60 | 1654.22 | 16 | 917.79 | 5377.30 | 52 | 8604.74 | 929.90 | 9 | 17,975.6 | |
| 52 | 247.51 | 10 | 519.16 | 544.52 | 22 | 11,468.7 | 321.76 | 13 | 9274.35 | |
| 58 | 1011.13 | 20 | 1644.54 | 1769.47 | 35 | 16,796.7 | 859.45 | 17 | 22,559.4 | |
| 54 | 300.01 | 8 | 489.9 | 450.04 | 12 | 11,983.4 | 375.00 | 10 | 13,677 | |
| 73 | 5556.85 | 61 | 2423.77 | 24,150.22 | 265 | 48,796.8 | 4281.01 | 47 | 187,668 | |
| 72 | 4314.09 | 51 | 2484.2 | 20,134.71 | 238 | 45,927.8 | 5412.29 | 64 | 154,388 | |
| 71 | 6007.16 | 57 | 1913.23 | 14,228.34 | 135 | 44,609.6 | 2107.10 | 20 | 28,488 | |
| 72 | 1199.78 | 12 | 1645.21 | 1199.79 | 12 | 45,741 | 899.84 | 9 | 42,006.1 | |
| 52 | 350.15 | 30 | 1882.84 | 735.40 | 63 | 11,110 | 46.67 | 4 | 13,236 | |
| 58 | 548.26 | 11 | 876.11 | 3489.58 | 70 | 16,929.4 | 1246.10 | 25 | 24,077.3 | |
| 54 | 409.33 | 11 | 630.19 | 1228.07 | 33 | 12,909.9 | 669.76 | 18 | 20,636.9 | |
| 73 | 4336.84 | 48 | 1873.73 | 13,106.60 | 145 | 48,922.1 | 4876.02 | 54 | 230,071 | |
| 72 | 6785.69 | 81 | 3001.99 | 13,665.38 | 163 | 46,528.3 | 921.47 | 11 | 209,551 | |
| 71 | 5012.31 | 48 | 2224.24 | 12,745.50 | 122 | 44,825 | 3446.74 | 33 | 103,688 | |
| 72 | 1089.28 | 11 | 1673.89 | 5447.25 | 55 | 47,334.7 | 3169.18 | 32 | 95,318.4 | |

Table A3.
Results of MOGVNS literature and improvement of MOGVNS/P over the MOGVNS of the literature [11].
Table A3.
Results of MOGVNS literature and improvement of MOGVNS/P over the MOGVNS of the literature [11].
| n | The Maintenance Objective | The Failure Objective | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MOGVNS Literature | Improvement of MOGVNS/P | MOGVNS Literature | Improvement of MOGVNS/P | ||||||||||
| Over MOGVNS Literature (%) | Over MOGVNS Literature (%) | ||||||||||||
| HV (×1010) | NDP | CPU (s) | IHV | INDP | ICPU | HV (×1010) | NDP | CPU (s) | IHV | INDP | ICPU | ||
| 23 | 2.49 | 8 | 292.92 | 62.52 | 62.50 | −93.80 | 7.66 | 13 | 291.07 | −30.76 | −30.77 | 25.46 | |
| 23 | 0.93 | 3 | 158.81 | −33.08 | −33.33 | −35.97 | 3.52 | 6 | 146.89 | 100.04 | 100.00 | −87.10 | |
| 26 | 10.09 | 7 | 638.24 | 42.86 | 42.86 | 45.60 | 18.79 | 7 | 762.43 | −14.29 | −14.29 | 53.43 | |
| 54 | 843.52 | 24 | 253,456 | 108.33 | 108.33 | 85.62 | 2736.29 | 40 | 328,945 | 62.51 | 62.50 | 89.62 | |
| 24 | 3.07 | 3 | 438.08 | 33.34 | 33.33 | 68.18 | 5.77 | 3 | 270.76 | 33.33 | 33.33 | −24.74 | |
| 52 | 912.74 | 26 | 288,684 | 7.70 | 7.69 | 94.81 | 1464.39 | 22 | 285,426 | 145.47 | 145.45 | 89.27 | |
| 34 | 3.20 | 1 | 1294.75 | 199.70 | 200.00 | 59.75 | 95.23 | 18 | 8911.06 | 72.29 | 72.22 | 69.82 | |
| 34 | 6.18 | 2 | 2827.07 | 0.09 | 0.00 | 68.17 | 63.15 | 12 | 8289.31 | 150.18 | 150.00 | 62.83 | |
| 33 | 7.24 | 2 | 1846.61 | 0.09 | 0.00 | 71.40 | 61.75 | 10 | 8152.01 | 90.10 | 90.00 | 66.10 | |
| 62 | 1618.23 | 24 | 521,083 | 20.83 | 20.83 | 94.71 | 5242.74 | 43 | 682,100 | 79.09 | 79.07 | 90.13 | |
| 33 | 3.30 | 1 | 1174.53 | 200.25 | 200.00 | 59.59 | 21.78 | 4 | 5799.4 | 0.04 | 0.00 | 83.40 | |
| 60 | 1520.17 | 26 | 501,547 | 215.39 | 215.38 | 89.74 | 2928.86 | 24 | 484,991 | 14.10 | 33.33 | 95.00 | |
| 23 | 4.84 | 18 | 401.75 | 147.06 | 133.33 | −156.04 | 7.15 | 13 | 418.21 | 277.19 | 276.92 | −99.83 | |
| 23 | 5.13 | 18 | 365.8 | 33.34 | 33.33 | −145.15 | 7.68 | 14 | 350.3 | 43.09 | 42.86 | −5.53 | |
| 26 | 24.93 | 18 | 856.62 | 55.56 | 55.56 | −78.38 | 23.42 | 9 | 1009.15 | 355.96 | 355.56 | −75.78 | |
| 54 | 1268.02 | 37 | 401,784 | 86.49 | 86.49 | 90.30 | 2621.15 | 39 | 351,411 | 97.49 | 97.44 | 90.52 | |
| 24 | 16.71 | 17 | 712.62 | 52.94 | 52.94 | −15.28 | 16.66 | 9 | 790.65 | 122.38 | 122.22 | −17.34 | |
| 52 | 1474.66 | 43 | 351,203 | 42.93 | 53.49 | 95.26 | 2355.18 | 36 | 317,681 | 75.02 | 75.00 | 92.68 | |
| 34 | 15.71 | 5 | 5142.73 | 80.02 | 80.00 | 63.00 | 78.19 | 15 | 13,043.5 | 260.37 | 260.00 | 59.06 | |
| 34 | 23.97 | 8 | 7247.38 | 25.00 | 25.00 | 78.59 | 66.84 | 12 | 10,749.3 | 175.16 | 175.00 | 79.46 | |
| 33 | 17.77 | 5 | 5546.07 | −20.03 | −20.00 | 88.04 | 97.18 | 16 | 7944.16 | 25.13 | 25.00 | 74.25 | |
| 33 | 22.55 | 7 | 5212.09 | 57.14 | 57.14 | 79.06 | 37.51 | 7 | 5000.94 | 57.41 | 57.14 | 63.73 | |
| 52 | 329.43 | 19 | 351,203 | 10.53 | 10.53 | 91.65 | 396.01 | 16 | 336,779 | 93.75 | 93.75 | 90.98 | |
| 58 | 361.85 | 10 | 891,106 | −50.00 | −50.00 | 97.02 | 1213.34 | 24 | 801,339 | 62.50 | 62.50 | 93.07 | |
| 54 | 342.49 | 13 | 466,326 | −23.08 | −23.08 | 93.54 | 712.53 | 19 | 567,144 | 10.53 | 10.53 | 91.68 | |
| 54 | 729.82 | 28 | 701,594 | 3.58 | 3.57 | 94.44 | 1116.37 | 30 | 833,222 | 20.01 | 20.00 | 91.00 | |
Appendix B. Comparison between the Proposed Algorithms

Table A4.
Results of MOGVNS/P, MOGVNS/CDP and MOGVNS/D for the maintenance cost as a second objective.
Table A4.
Results of MOGVNS/P, MOGVNS/CDP and MOGVNS/D for the maintenance cost as a second objective.
| n | MOGVNS/P | MOGVNS/CDP | MOGVNS/D | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HV () | NDP | CPU (s) | HV () | NDP | CPU (s) | HV () | NDP | CPU (s) | ||
| 6 | 0.0003 | 5 | 0.61 | 0.0003 | 5 | 0.69 | 0.0002 | 3 | 2.17 | |
| 12 | 0.0909 | 15 | 22.72 | 0.0784 | 13 | 23.76 | 0.0181 | 3 | 64.39 | |
| 6 | 0.0007 | 4 | 0.58 | 0.0010 | 6 | 0.69 | 0.0005 | 3 | 2.37 | |
| 12 | 0.0862 | 9 | 19.37 | 0.0766 | 8 | 21.64 | 0.0190 | 2 | 49.14 | |
| 23 | 4.04 | 13 | 567.69 | 4.35 | 14 | 540.53 | 1.55 | 5 | 963.5 | |
| 23 | 0.62 | 2 | 215.94 | 1.86 | 6 | 301.86 | 1.24 | 4 | 995.92 | |
| 26 | 14.41 | 10 | 347.19 | 14.41 | 10 | 543.16 | 2.88 | 2 | 1540.26 | |
| 54 | 1757.32 | 50 | 36,453.2 | 1476.15 | 42 | 32,099.8 | 140.58 | 4 | 21,119.6 | |
| 24 | 4.10 | 4 | 139.39 | 4.10 | 4 | 451.88 | 1.02 | 1 | 814.02 | |
| 52 | 983.00 | 28 | 14,984.4 | 1954.68 | 57 | 29,964.8 | 140.42 | 4 | 14,866 | |
| 34 | 9.60 | 3 | 521.14 | 3.20 | 1 | 1425.67 | 3.20 | 1 | 4394.02 | |
| 68 | 1506.65 | 19 | 20,893 | 1982.43 | 25 | 38,759.2 | 158.59 | 2 | 55,887.3 | |
| 34 | 6.19 | 2 | 899.84 | 12.38 | 4 | 1100.96 | 3.10 | 1 | 4236.49 | |
| 65 | 2821.33 | 44 | 47,265.5 | 1538.86 | 24 | 39,607.3 | 320.60 | 5 | 50,983.9 | |
| 33 | 7.25 | 2 | 528.11 | 7.25 | 2 | 1435.14 | 3.62 | 1 | 2839.68 | |
| 62 | 1955.35 | 29 | 27,539.3 | 3169.04 | 47 | 46,969.1 | 337.13 | 5 | 33,062.7 | |
| 33 | 9.89 | 3 | 474.6 | 6.60 | 2 | 1363.49 | 6.60 | 2 | 4309.18 | |
| 60 | 4794.41 | 82 | 51,475.7 | 1871.00 | 32 | 32,881.3 | 116.93 | 2 | 29,448.2 | |
| 23 | 11.97 | 42 | 1028.66 | 12.25 | 43 | 1012.73 | 1.71 | 6 | 1255.38 | |
| 23 | 6.84 | 24 | 896.75 | 10.55 | 37 | 916.97 | 1.99 | 7 | 1230.12 | |
| 26 | 38.78 | 28 | 1528.05 | 40.17 | 29 | 1676.91 | 5.54 | 4 | 1407.87 | |
| 54 | 2364.74 | 69 | 38,991.2 | 2707.43 | 79 | 41,306.1 | 274.17 | 8 | 33,123.8 | |
| 24 | 25.56 | 26 | 821.53 | 31.46 | 32 | 1169.56 | 5.90 | 6 | 872.48 | |
| 52 | 2107.70 | 66 | 16,633 | 1920.48 | 56 | 32,819.2 | 240.06 | 7 | 18,837.8 | |
| 34 | 28.28 | 9 | 1902.74 | 21.99 | 7 | 3817.55 | 12.57 | 4 | 4957.75 | |
| 68 | 3599.37 | 46 | 33,302.6 | 5242.55 | 67 | 78,662.6 | 391.23 | 5 | 65,550.5 | |
| 34 | 29.97 | 10 | 1551.54 | 56.94 | 19 | 3758.07 | 14.98 | 5 | 4040.9 | |
| 65 | 3339.90 | 53 | 80,219.7 | 3217.40 | 52 | 41,885.8 | 315.09 | 5 | 42,049.4 | |
| 33 | 14.21 | 4 | 663.56 | 28.44 | 8 | 1989.76 | 7.11 | 2 | 4935.93 | |
| 62 | 2694.57 | 51 | 53,688.2 | 2923.98 | 44 | 61,284.6 | 398.72 | 6 | 40,465.1 | |
| 33 | 35.43 | 11 | 1091.48 | 25.77 | 8 | 3174.47 | 9.67 | 3 | 4613.12 | |
| 60 | 4669.82 | 81 | 31,113.3 | 2479.05 | 43 | 59,595.3 | 461.22 | 8 | 27,920.8 | |
| 52 | 364.11 | 21 | 29,319.5 | 260.08 | 15 | 28,688.7 | 86.69 | 5 | 56,155.4 | |
| 58 | 180.92 | 5 | 26,547.2 | 578.96 | 16 | 55,461.7 | 108.55 | 3 | 57,331.8 | |
| 54 | 263.46 | 10 | 30,138.6 | 289.80 | 11 | 30,350.5 | 131.73 | 5 | 42,786.6 | |
| 73 | 2691.29 | 39 | 143,386 | 3312.35 | 48 | 160,197 | 138.00 | 2 | 74,408.6 | |
| 72 | 2491.10 | 40 | 156,440 | 1992.88 | 32 | 247,398 | 186.83 | 3 | 79,235.2 | |
| 71 | 1486.71 | 19 | 19,687.1 | 1799.71 | 23 | 106,481 | 234.74 | 3 | 68,235.6 | |
| 72 | 1133.81 | 15 | 89,683 | 1133.80 | 15 | 55,479.2 | 302.33 | 4 | 81,787 | |
| 52 | 598.30 | 47 | 48,933.3 | 415.00 | 51 | 78,190.2 | 56.96 | 7 | 43,388.3 | |
| 58 | 1921.90 | 54 | 103,540 | 1743.90 | 49 | 103,414 | 177.95 | 5 | 58,642.1 | |
| 54 | 755.93 | 29 | 39,023.7 | 1251.16 | 48 | 45,827.1 | 156.39 | 6 | 56,019.9 | |
| 73 | 4573.85 | 67 | 193,702 | 6485.25 | 95 | 258,245 | 477.87 | 7 | 143,966 | |
| 72 | 3016.52 | 49 | 138,179 | 3570.61 | 58 | 253,926 | 345.06 | 5 | 88,666.5 | |
| 71 | 3404.46 | 44 | 62,050.9 | 4487.63 | 58 | 220,287 | 524.99 | 7 | 83,348.4 | |
| 72 | 2238.12 | 30 | 98,068 | 2536.52 | 34 | 149,601 | 447.63 | 6 | 77,137.2 | |

Table A5.
Results of MOGVNS/P, MOGVNS/CDP and MOGVNS/D for the failure cost as a second objective.
Table A5.
Results of MOGVNS/P, MOGVNS/CDP and MOGVNS/D for the failure cost as a second objective.
| n | MOGVNS/P | MOGVNS/CDP | MOGVNS/D | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HV () | NDP | CPU (s) | HV () | NDP | CPU (s) | HV () | NDP | CPU (s) | ||
| 6 | 0.0005 | 6 | 0.59 | 0.0004 | 5 | 0.65 | 0.0002 | 3 | 2.43 | |
| 12 | 0.1698 | 15 | 15.71 | 0.1907 | 17 | 24.67 | 0.0339 | 3 | 60.23 | |
| 6 | 0.0018 | 5 | 0.59 | 0.0018 | 5 | 0.71 | 0.0011 | 3 | 2.32 | |
| 12 | 0.1172 | 7 | 19.9 | 0.1005 | 6 | 18.95 | 0.0333 | 2 | 45.58 | |
| 23 | 5.31 | 9 | 216.96 | 10.61 | 18 | 981.69 | 2.36 | 4 | 1085.69 | |
| 23 | 7.04 | 12 | 274.83 | 2.93 | 5 | 573.82 | 2.93 | 5 | 1293.41 | |
| 26 | 16.10 | 6 | 355.05 | 24.15 | 9 | 1021.91 | 13.42 | 5 | 1627.55 | |
| 54 | 4446.77 | 65 | 34,139.1 | 5092.48 | 74 | 34,088.1 | 478.86 | 7 | 25,013.6 | |
| 24 | 7.69 | 4 | 337.74 | 3.89 | 2 | 475.76 | 5.77 | 3 | 993.2 | |
| 52 | 3594.67 | 54 | 30,615.3 | 2942.53 | 44 | 29,954.2 | 399.40 | 6 | 20,716.7 | |
| 34 | 164.07 | 31 | 2689.1 | 217.78 | 40 | 5828.58 | 31.76 | 6 | 5327.16 | |
| 68 | 18,654.84 | 133 | 93,925.7 | 15,409.97 | 109 | 90,059.7 | 1262.27 | 9 | 64,565 | |
| 34 | 158.00 | 30 | 3081.38 | 200.01 | 37 | 4998.82 | 36.84 | 7 | 5065.3 | |
| 65 | 15,381.74 | 134 | 74,284 | 21,163.04 | 183 | 87,084 | 1033.06 | 9 | 60,050.9 | |
| 33 | 117.39 | 19 | 2763.77 | 120.11 | 19 | 4822.82 | 43.24 | 7 | 4516.16 | |
| 62 | 9389.07 | 77 | 67,295.3 | 10,924.15 | 89 | 63,118.8 | 853.54 | 7 | 29,063.3 | |
| 33 | 21.79 | 4 | 962.57 | 55.62 | 10 | 3642.36 | 16.33 | 3 | 4058.1 | |
| 60 | 3341.87 | 32 | 24,243.6 | 4940.53 | 47 | 47,436.3 | 313.30 | 3 | 36,816.5 | |
| 23 | 26.99 | 49 | 835.69 | 31.05 | 54 | 1032.43 | 3.86 | 7 | 1339.66 | |
| 23 | 10.99 | 20 | 369.67 | 16.10 | 28 | 838.58 | 2.75 | 5 | 1098.4 | |
| 26 | 106.78 | 41 | 1773.90 | 95.24 | 36 | 1755.06 | 13.02 | 5 | 2057.67 | |
| 54 | 5176.53 | 77 | 33,325.1 | 7161.20 | 106 | 42,890.5 | 201.54 | 6 | 31,026.5 | |
| 24 | 37.05 | 20 | 927.78 | 39.34 | 21 | 1098.54 | 12.97 | 7 | 1200.75 | |
| 52 | 4122.09 | 63 | 23,267.9 | 4268.45 | 65 | 24,749.7 | 196.19 | 6 | 20,101 | |
| 34 | 281.77 | 54 | 5339.7 | 203.74 | 38 | 5483.74 | 36.52 | 7 | 4909.06 | |
| 68 | 8193.86 | 59 | 31,630.7 | 10,913.77 | 78 | 67,300.9 | 1111.17 | 8 | 72,624 | |
| 34 | 183.93 | 33 | 2207.54 | 250.89 | 44 | 5704.28 | 39.03 | 7 | 6199.63 | |
| 65 | 11,274.87 | 96 | 80,442.8 | 11,462.14 | 97 | 82,898.8 | 822.02 | 7 | 53,859.1 | |
| 33 | 121.61 | 20 | 2045.54 | 161.47 | 26 | 2161.36 | 30.40 | 5 | 4634.17 | |
| 62 | 14,242.86 | 118 | 70,866.5 | 11,046.54 | 91 | 75,571.3 | 361.91 | 6 | 43,626.3 | |
| 33 | 59.04 | 11 | 1814.02 | 38.31 | 7 | 2147.76 | 21.47 | 4 | 4423.04 | |
| 60 | 5687.61 | 55 | 24,037.7 | 7904.99 | 76 | 52,829.2 | 310.14 | 6 | 37,858.9 | |
| 52 | 767.28 | 31 | 30,374.4 | 691.19 | 27 | 65,021.6 | 173.26 | 7 | 36,495 | |
| 58 | 1971.71 | 39 | 55,556.1 | 1996.60 | 39 | 114,965 | 353.90 | 7 | 58,048.8 | |
| 54 | 787.57 | 21 | 47,186.4 | 416.12 | 11 | 21,047.7 | 187.51 | 5 | 45,972.9 | |
| 73 | 17,862.57 | 196 | 218,379 | 21,549.32 | 232 | 291,184 | 820.01 | 9 | 157,945 | |
| 72 | 16,413.05 | 194 | 212,096 | 17,552.03 | 204 | 287,891 | 761.31 | 9 | 152,872 | |
| 71 | 9064.57 | 86 | 139,083 | 14,973.80 | 140 | 254,233 | 737.76 | 7 | 101,806 | |
| 72 | 1999.65 | 20 | 124,109 | 2228.21 | 22 | 108,438 | 499.90 | 5 | 77,240.8 | |
| 52 | 548.62 | 47 | 66,374.2 | 916.12 | 76 | 81,434.6 | 70.02 | 6 | 45,062.4 | |
| 58 | 2193.46 | 44 | 101,037 | 3329.42 | 66 | 125,092 | 249.18 | 5 | 68,694.4 | |
| 54 | 1339.74 | 36 | 75,004.4 | 1838.22 | 49 | 77,837.6 | 297.70 | 8 | 59,965.1 | |
| 73 | 13,650.66 | 151 | 304,359 | 13,525.98 | 147 | 295,760 | 813.41 | 9 | 221,425 | |
| 72 | 8549.00 | 102 | 98,438.4 | 13,032.20 | 153 | 301,157 | 838.35 | 10 | 176,422 | |
| 71 | 11,283.23 | 108 | 197,350 | 9114.36 | 86 | 231,112 | 940.41 | 9 | 176,085 | |
| 72 | 4456.75 | 45 | 3502.3 | 5715.83 | 57 | 14,995.39 | 594.30 | 6 | 132,318 | |
References
- Dohi, T.; Kaio, N.; Osaki, S. Preventive Maintenance Models: Replacement, Repair, Ordering, and Inspection. In Handbook of Reliability Engineering; Hoang, P., Ed.; Springer: London, UK, 2003; pp. 349–366. [Google Scholar]
- Chen, Y.; Polack, F.; Cowling, P.; Mourdjis, P.; Remde, S. Risk Driven Analysis of Maintenance for a Large-scale Drainage System. In Proceedings of the 5th ICORES, Rome, Italy, 23–25 February 2016; pp. 296–303. [Google Scholar]
- Jbili, S.; Chelbi, A.; Radhoui, M.; Kessentini, M. Integrated strategy of Vehicle Routing and Maintenance. Reliab. Eng. Syst. Saf. 2018, 170, 202–214. [Google Scholar] [CrossRef]
- López-Santana, E.; Akhavan-Tabatabaei, R.; Dieulle, L.; Labadie, N.; Medaglia, A.L. On the combined maintenance and routing optimization problem. Reliab. Eng. Syst. Saf. 2016, 145, 199–214. [Google Scholar] [CrossRef]
- Rashidnejad, M.; Ebrahimnejad, S.; Safari, J. A bi-objective model of preventive maintenance planning in distributed systems considering vehicle routing problem. Comput. Ind. Eng. 2018, 120, 360–381. [Google Scholar] [CrossRef]
- Kovacs, A.A.; Parragh, S.N.; Doerner, K.F.; Hartl, R.F. Adaptive large neighborhood search for service technician routing and scheduling problems. J. Sched. 2012, 15, 579–600. [Google Scholar] [CrossRef]
- Cordeau, J.F.; Laporte, G.; Pasin, F.; Ropke, S. Scheduling technicians and tasks in a telecommunications company. J. Sched. 2010, 13, 393–409. [Google Scholar] [CrossRef]
- Pillac, V.; Guéret, C.; Medaglia, A.L. A Fast Reoptimization Approach for the Dynamic Technician Routing and Scheduling Problem. In Recent Developments in Metaheuristics. Operations Research/Computer Science Interfaces Series; Amodeo, L., Talbi, E.G., Yalaoui, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; Volume 62. [Google Scholar]
- Çakırgil, S.; Yücel, E.; Kuyzu, G. An integrated solution approach for multi-objective, multi-skill workforce scheduling and routing problems. Comput. Oper. Res. 2020, 118, 104908. [Google Scholar] [CrossRef]
- Paquete, L.; Chiarandini, M.; Stützle, T. Pareto local optimum sets in the biobjective traveling salesman problem: An experimental study. In Metaheuristics for Multiobjective Optimisation; Springer: Berlin/Heidelberg, Germany, 2004; pp. 177–199. [Google Scholar]
- Duarte, A.; Pantrigo, J.J.; Pardo, E.G.; Mladenovic, N. Multi-objective variable neighborhood search: An application to combinatorial optimization problems. J. Glob. Optim. 2015, 63, 515–536. [Google Scholar] [CrossRef]
- Cota, L.P.; Guimarães, F.G.; Ribeiro, R.G.; Meneghini, I.R.; de Oliveira, F.B.; Souza, M.J.; Siarry, P. An adaptive multi-objective algorithm based on decomposition and large neighborhood search for a green machine scheduling problem. Swarm Evol. 2019, 51, 100601. [Google Scholar] [CrossRef]
- Dubois-Lacoste, J.; López-Ibáñez, M.; Stützle, T. Anytime pareto local search. Eur. J. Oper. Res. 2015, 243, 369–385. [Google Scholar] [CrossRef]
- Dahite, L.; Kadrani, A.; Benmansour, R. Optimization models for train load and transport planning problems. In MATEC Web of Conferences 2018; EDP Sciences: Les Ulis, France, 2018; Volume 200. [Google Scholar]
- Tsang, A.H.C. Condition-based maintenance: Tools and decision making. J. Qual. Maint. Eng. 1995, 1, 3–17. [Google Scholar] [CrossRef]
- Fontecha, J.E.; Akhavan-Tabatabaei, R.; Duque, D.; Medaglia, A.L.; Torres, M.N.; Rodríguez, J.P. On the preventive management of sediment-related sewer blockages: A combined maintenance and routing optimization approach. Water Sci. Technol. 2016, 74, 302–308. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Hansen, P.; Mladenovic, N. A Tutorial on Variable Neighborhood Search. Les Cah. GERAD ISSN 2003, 711, 2440. [Google Scholar]
- Dahite, L.; Kadrani, A.; Benmansour, R.; Guibadj, R.N.; Fonlupt, C. Optimization of Maintenance Planning and Routing Problems. In Lecture Notes in Computer Science, Proceedings of the International Conference on Variable Neighborhood Search, ICVNS 2019, Rabat, Morocco, 3–5 October 2019; Benmansour, R., Sifaleras, A., Mladenović, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 12010, p. 12010. [Google Scholar]
- Chen, P.; Huang, H.K.; Dong, X.Y. Iterated variable neighborhood descent algorithm for the capacitated vehicle routing problem. Expert Syst. Appl. 2010, 37, 1620–1627. [Google Scholar] [CrossRef]
- Rezgui, D.; Bouziri, H.; Aggoune-Mtalaa, W.; Siala, J.C. An Evolutionary Variable Neighborhood Descent for Addressing an Electric VRP Variant. In Proceedings of the International Conference on Variable Neighborhood Search, ICVNS 2018, Sithonia, Greece, 4–7 October 2018; Sifaleras, A., Salhi, S., Brimberg, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 11328. [Google Scholar]
- Dahite, L.; Guibadj, R.N.; Fonlupt, C.; Kadrani, A.; Benmansour, R. A Semi Adaptive Large Neighborhood Search for the Maintenance Scheduling and Routing Problem. In Proceedings of the 2021 7th International Conference on Optimization and Applications (ICOA), Wolfenbüttel, Germany, 19–20 May 2021; pp. 1–6. [Google Scholar]
- Lust, T.; Teghem, J. Two-phase Pareto local search for the biobjective traveling salesman problem. J. Heuristics 2010, 16, 475–510. [Google Scholar] [CrossRef]
- Queiroz, T.A.D.; Mundim, L.R. Multiobjective pseudo-variable neighborhood descent for a bicriteria parallel machine scheduling problem with setup time. Int. Trans. Oper. Res. 2020, 27, 1478–1500. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).