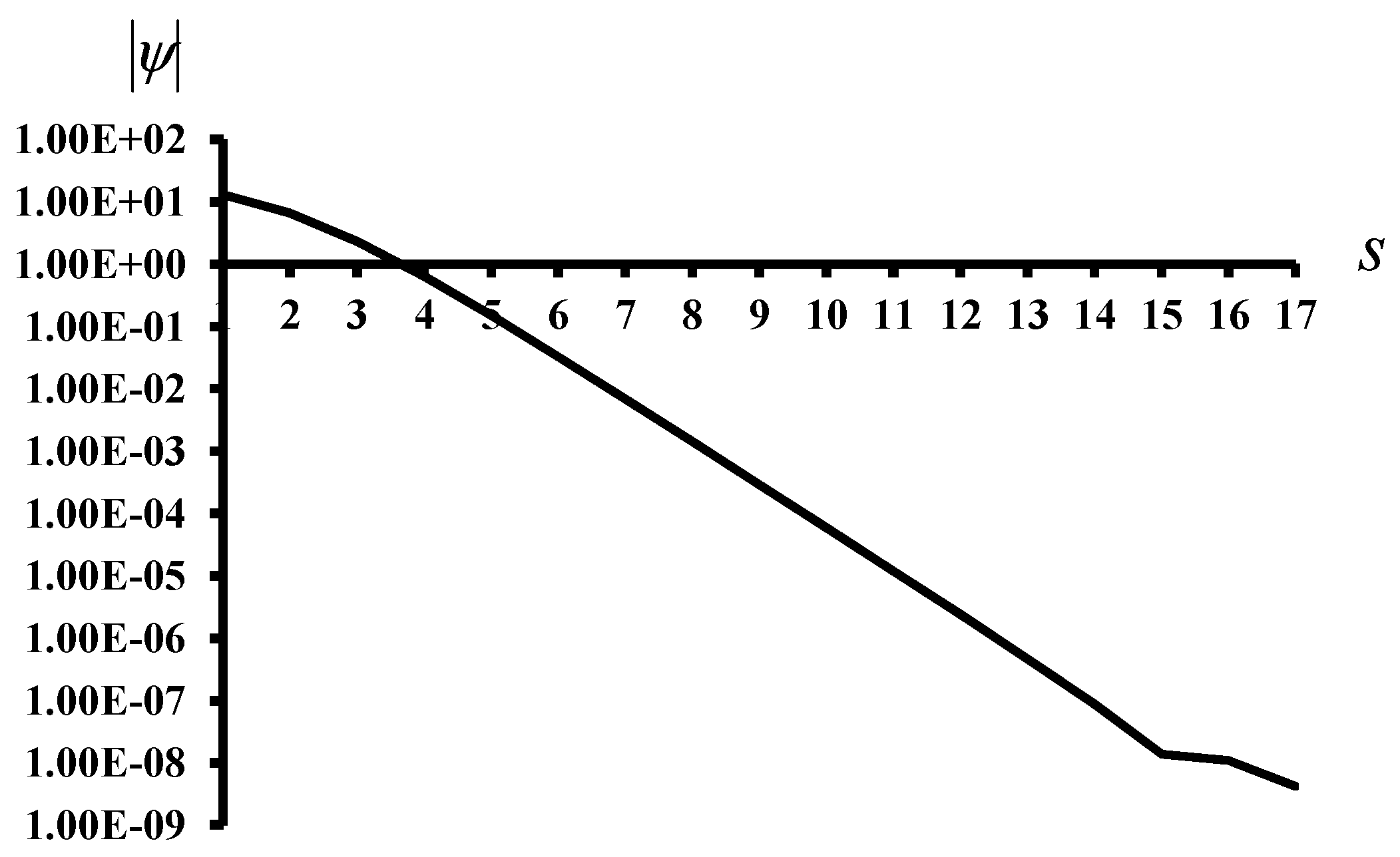A Nikaido Isoda-Based Hybrid Genetic Algorithm and Relaxation Method for Finding Nash Equilibrium

Abstract

Nash Equilibrium (NE) plays a crucial role in game theory. The relaxation method in conjunction with the Nikaido–Isoda (NI) function, namely the NI-based relaxation method, has been widely applied to the determination of NE. Genetic Algorithm (GA) with adaptive penalty is introduced and incorporated in the original NI-based relaxation method. The GA enhances the capability in the optimization step for computing the optimum response function. The optimization of the non-convex and non-concave NI function is made possible by GA. The proposed method thus combines the advantageous feature of the GA in its optimization capability and that of the relaxation method in its implementation simplicity together. The applicability of the method is shown through the illustrative examples, including the generalized Nash Equilibrium problem with nonlinear payoff functions and coupled constraints, the game with multiple strategic variables for individual players, and the non-differentiable payoff functions. All test example results suggest the appropriate crossover and mutation rate to be 0.05 and 0.002 for use in GA. These numbers are closed to the recommended values by DeJong. The proposed method shows its capability of finding correct NEs in all test examples.

1. Introduction

The determination of Nash Equilibrium (NE) is the subject of interest in game theory. Among the NE finding methods, the relaxation method that is applied in conjunction with the Nikaido–Isoda (NI) function [1], referred to as the NI-based relaxation method, has been widely recognized [2]. Further improvement includes the NI-based relaxation method with inexact line search [3] and the gradient-based NI function [4].

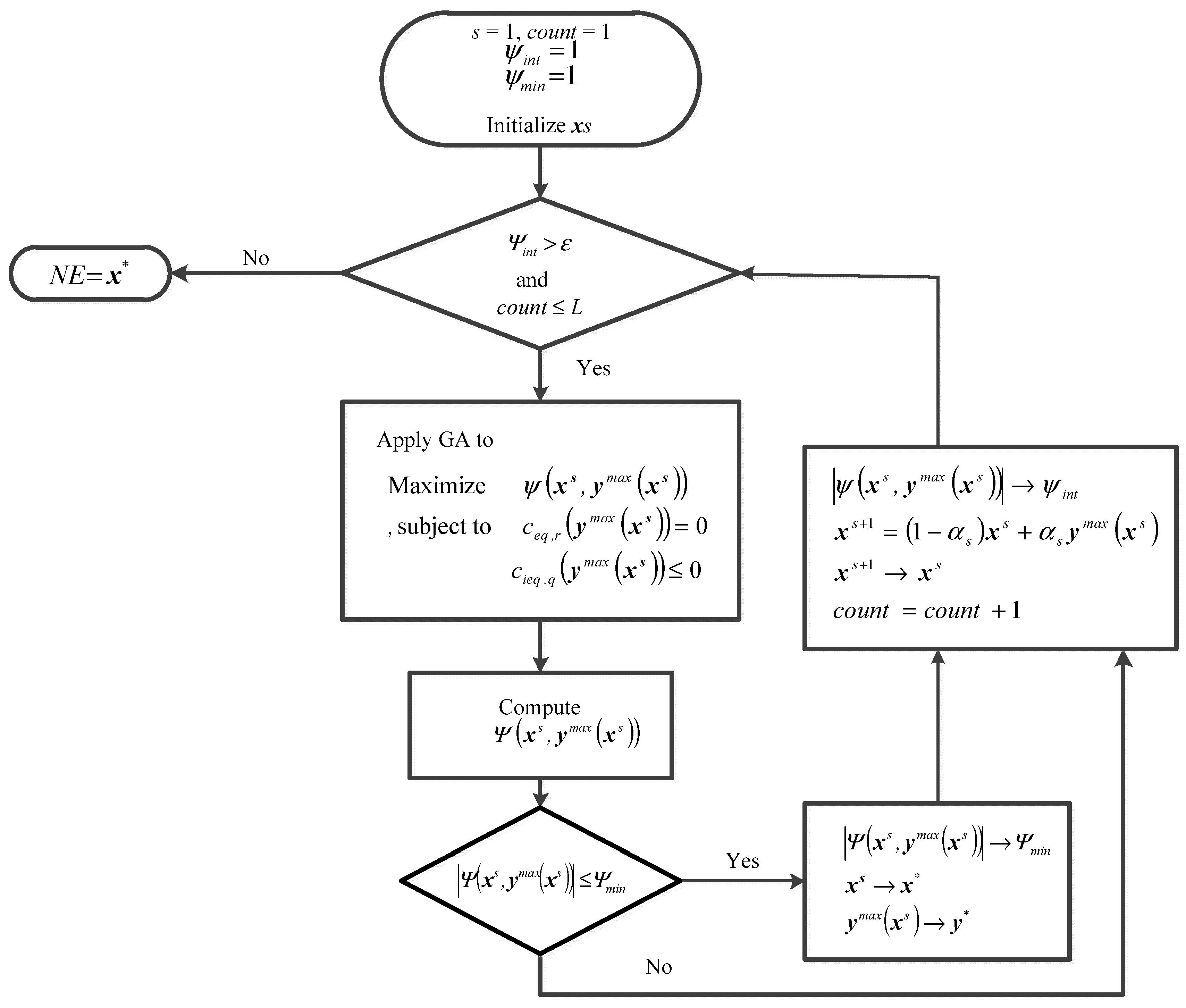
The NI-based relaxation method and its variants have the virtue of its conceptual simplicity. The method consists of two steps, namely the optimization and relaxation. Given the present actions of all players, the optimal actions that create the improvement in the payoffs are obtained from the optimization step. The new actions that replace the present ones are defined as the weighted combination of the optimal and present actions via the relaxation algorithm in the second step. The procedure repeats both steps until the value of NI function becomes zero. The actions that result in the zero NI function value are taken as the NE. Regarding the relaxation algorithm, it is proved to converge to an NE for a wide class of problems [5,6]. The optimal actions are generally derived in an analytical form. However, when the NI function is highly non-linear, the analytical form of the optimal actions may not be obtained. Without the optimal actions, the relaxation step cannot be processed.

To extend the relaxation method to the case of the non-differentiable NI function, the methodologies that can solve the optimization problems with non-differentiable objective functions are used. It was discussed that analytical methods are not able to handle complicated or non-differentiable payoff functions while mathematical programming approaches may not reach the NE point, due to not being reliable due to their dependence on initial searching points [7]. Meta-heuristic algorithms are more effective in dealing with non-differentiable, non-linear, complex payoff functions from their fundamental procedures [7]. Accordingly, the evolutionary computation was proposed for finding the NE points [8]. The so-called Nash dominance concept was defined and has been directly used or modified in later research [7,9,10]. The concept was implemented in Non-dominated Sorting Genetic Algorithm II (NSGAII) [11] with changing from the Pareto dominance to the defined Nash dominance. Other Nash dominance concept-based algorithms include Nash Domination Evolutionary Multiplayer Optimization (NDEMO) [9] and co-evolutionary approach [10,12]. NDMO employed Differential Evolution (DE) as its optimizer in conjunction with Nash dominance sorting. NDEMO was applied to transportation systems management electricity markets. The co-evolutionary approach was applied for strategic bidding in competitive electricity markets. Genetic Algorithm (GA) and DE were both used in that work in which a non-convex, non-smooth, bi-level optimization problem was solved. The co-evolutionary approach was later combined with a ranking technique called Nash non-dominated sorting (NNDS) for the determination of NE [12]. Genetic Algorithm (GA) and DE were again utilized as optimization tools. Instead of checking the Nash Equilibrium condition based on the Nash dominance concept, the NI function was employed for the purpose [7]. However, the new actions were still created by the evolutionary algorithm DE. The use of the NI function shows shorter runtimes than the Nash dominance sorting. Most recently, Nash Equilibrium sorting Genetic Algorithm (NESGA) was introduced to identify NE [13]. The fitness assignment was based on sorting. The methodology solved a combinatorial game problem. Around the same time, a heuristic algorithm, namely a distributed algorithm was developed to solve non-smooth aggregative games [14]. Nevertheless, the distributed algorithm imposed many mathematical assumptions and therefore was limited to the shown aggregative games.

The motivation of this work is to extend the NI-based relaxation method with its simplicity of implementation to a novel method that can cope with non-linear, non-differentiable, and combinatorial forms of payoff and NI functions. GA has such desired properties. GA is a derivative-free algorithm and is applicable to continuous as well as combinatorial optimization problems [15]. Fundamentally, GA can be used for solving non-differentiable objective functions [13] as well as non-convex and non-concave optimization problems [16,17,18]. One real-world application is the portfolio optimization with typical transaction costs [19]. Considering the potential of GA in detecting the NE from the afore-reviewed literature and its ability in solving non-linear, non-differentiable, and combinatorial forms of payoff and NI functions, GA will be employed in the present paper as the optimization tool. The GA is also combined with an adaptive penalty scheme [20] and makes the proposed hybrid GA and relaxation method applicable to the general Nash Equilibrium problem as well.

The novelty of this paper is it is the first time that presents an NI-based hybrid GA and relaxation method for finding Nash Equilibrium. The proposed method utilizes the straightforward computation of the NI function, which has significantly less complication than the dominance evaluation and sorting of those GA/DE-extended literature methods. Consequently, the contribution of the paper is providing a simple but effective computational method for detecting the NE in generalized Nash Equilibrium problems. The presented method thus combines the advantageous feature of the GA in its optimization capability and the implementation simplicity of the relaxation method together.

The comparison of the literature and presented method is summarized in

Table 1. Comparison of methods for finding NE.

Method	Check of Nash Equilibrium Condition	Creation of New Actions	Ability to Solve Generalized Nash Problems	Hardship in Implementation
Evolutionary Computation [8]	Nash Non-Dominated Sorting	Evolutionary Algorithm (NSGAII)	Not Addressed	High
NDEMO [9]	Nash Dominance Sorting	Evolutionary Algorithm (DE)	Applicable	High
NIDE [7]	Nikai–Isoda Function Computation	Evolutionary Algorithm (DE)	Not Addressed	Moderate
Co-evolutionary Approach [10,21]	Nash Non-Dominated Sorting	Co-evolutionary Algorithm (GA and DE)	Applicable	High
NESGA [13]	Sorting of Payoff Function Values	Evolutionary Algorithm (GA)	Not Addressed	High
Distributed Algorithm [14]	Payoff Function Evaluation and Sorting	Dynamic Equations	Limited to An Equality Constraint	High
NI-based Hybrid GA and Relaxation Method (Proposed Method)	Nikai–Isoda Function Computation	Relaxation Method	Applicable	Low

.

It is noted that there are more than 110 meta-heuristic algorithms (see e.g., [21,22]) that can be used instead of GA. As mentioned before, this is an initiative paper on combining a meta-heuristic with a relaxation method to obtain a simple method for tackling the problem of non-regular payoff and NI function. The comparison of the optimization algorithms is thus beyond the scope of the paper.

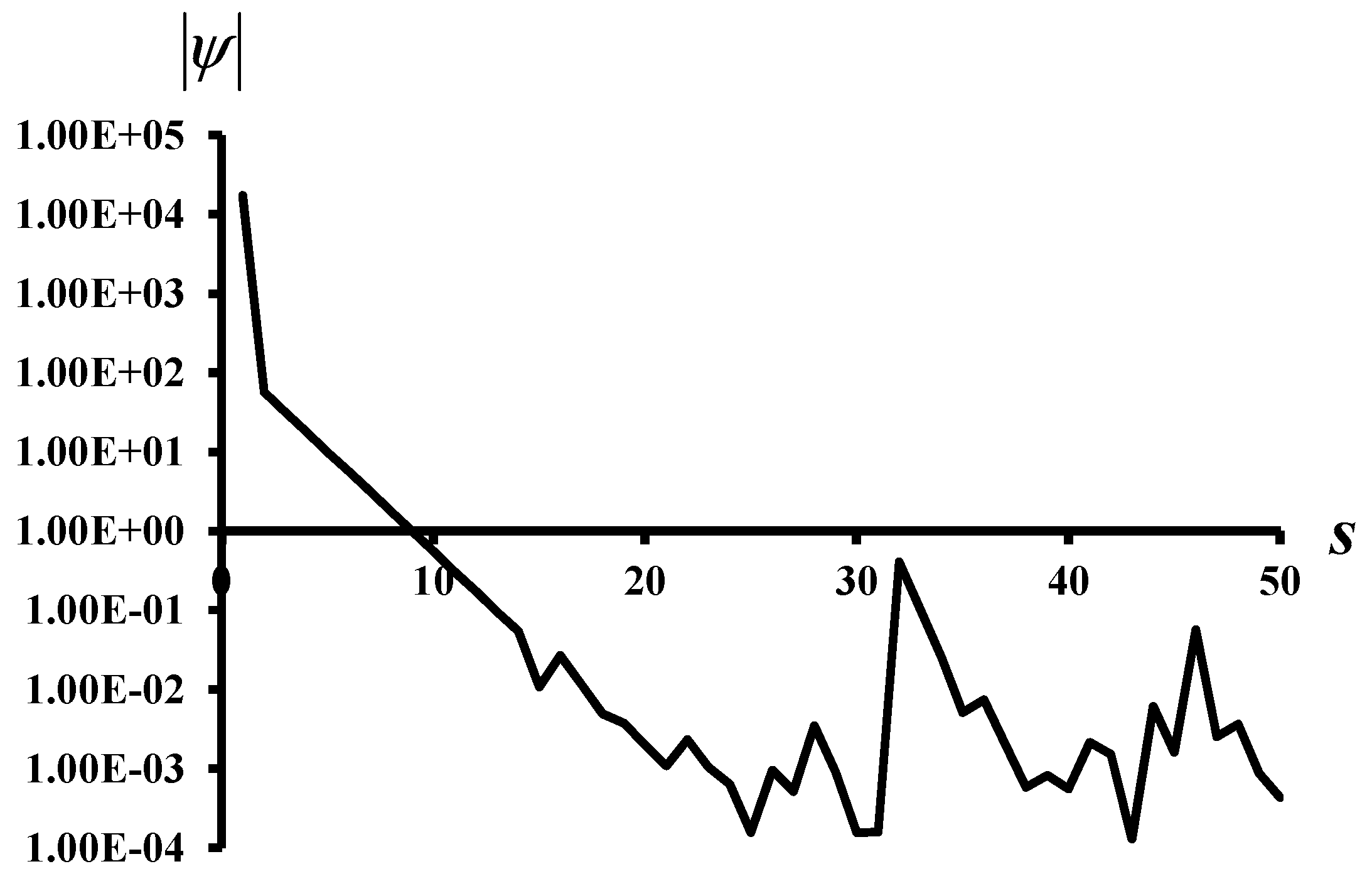
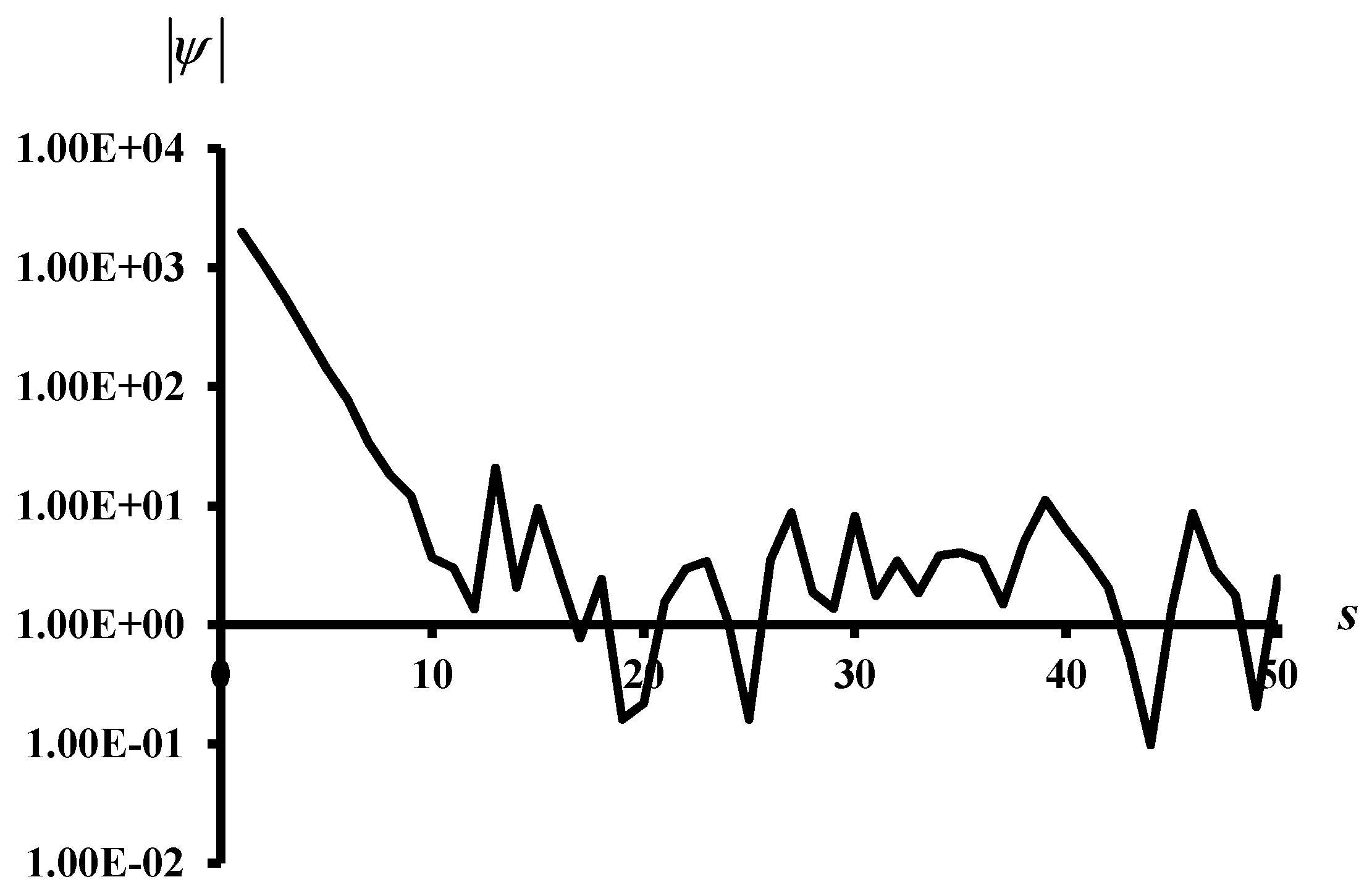
The applicability of the proposed method is shown through the illustrative examples. These examples include the generalized Nash Equilibrium problem with nonlinear payoff functions and coupled constraints, the game with multiple strategic variables for individual players, and the non-differentiable payoff functions. The results are compared with those from the literature and some meta-heuristic algorithms, such as DE, Gravitational Search Algorithm—GSA [23], Inclined Planes System Optimization Algorithm—IPO [24], and the most recent algorithms including Capuchin Search Algorithm—CSA [25] as well as the distributed algorithm [14]. The proposed method shows its capability of finding correct NEs in all test examples.

The structure of the paper is as follows. After this introduction, the fundamental concept is described. The details of the proposed method are next explained. The application of the method is demonstrated via the numerical examples. The conclusions are made at the end.

2. Problem Formulation

2.1. Definitions

Consider a game of n players. Each player takes an individual action, which is represented by a vector x_i in the Euclidean space ${\mathit{R}}^{m_i}$. All players take a collective action $x=\left(x_1,....,x_n\right)\in R^{m_1}\times \cdots \times R^{m_n}$. Let $X_i\subseteq R^{m_i}$ be an action set of player i, and ${\varphi }_i:X_i\to R$ be the corresponding payoff function. Let $X$ be the collective action set. By definition, $X\subseteq X_1\times \cdots \times X_n\subseteq R^{m_1}\times \cdots \times R^{m_n}=R^m$. Let $x=\left(x_1,....,x_n\right)$ and $y=\left(y_1,....,y_n\right)$ be elements of the collective action set $X_1\times \cdots \times X_n$. An element $\left(y_i|x\right)\equiv \left(x_1,....,x_{i-1},y_i,x_{i+1},\dots ,x_n\right)$ of the collective action set is interpreted as a collection of actions when the i-th player tries y_i, while the remaining players still keep $x_j,j=1,\dots ,i-1,i+1,\dots ,n$.

Definition 1.

A point $x^{\ast }=\left(x_1^{\ast },....,x_n^{\ast }\right)$ is called the Nash Equilibrium point [1] if, for each i,

$${\varphi }_i\left(x^{\ast }\right)=\underset{\left(x_i|x^{\ast }\right)\in X}{max}{\varphi }_i\left(x_i|x^{\ast }\right)$$

(1)

Definition 2.

The NI function $\Psi :\left(X_1\times \cdots \times X_n\right)\times \left(X_1\times \cdots \times X_n\right)\to R$ is defined as [1]

$$\Psi \left(x,y\right)={\displaystyle \sum _{i=1}^n\left[{\varphi }_i\left(y_i|x\right)-{\varphi }_i\left(x\right)\right]}$$

(2)

Note that

$$\Psi \left(x,x\right)=0$$

(3)

Each summand of the NI function represents the improvement in payoff that a player will receive when the player changes the action from x_i to y_i, while all other players continue playing according to x. That means that one player changes the action, while the others do not. Thus, the function represents the sum of these improvements in the payoff. Note that the maximum value of this function is always nonnegative for a given x. Furthermore, the function is nonpositive for all feasible when it is a NE, since no player can improve his payoff at equilibrium. In consequence, each summand can be at most zero at the NE [1].

Definition 3.

An element, $x^{\ast }\in X$, is referred to as a Nash Equilibrium point [26], if

$$\underset{y\in X}{max}\Psi \left(x^{\ast },y\right)=0$$

(4)

In addition to the payoff functions, the action spaces of each player may depend on the actions chosen by all other players. This type of problem is referred to as the generalized Nash Equilibrium problem. The dependency among different players’ actions is generally represented by a set of equality constraints,

$$c_{eq,r}\left(x\right)=0(r=1,\dots ,N_{eq})$$

(5)

and a set of inequality constraints,

$$c_{ieq,q}\left(x\right)\le 0(q=1,\dots ,N_{ieq})$$

(6)

where N_eq and N_ieq are the number of the equality and inequality constraints, respectively. Consequently, the NE needs to satisfy not only the condition (4), but also the constraints (5) and (6).

2.2. NI-Based Relaxation Method

The NI-based relaxation method starts from determining the optimum response function Z(x):

$$Z\left(x\right)=\underset{y\in X}{\arg \max }\Psi \left(x,y\right);x,Z\left(x\right)\in X$$

(7)

Let y that is corresponding to Z(x) be denoted by y^max(x). In case of the generalized Nash Equilibrium problem, y^max(x) must fulfill all constraint requirements (5) and (6). The optimum response function returns the set of players’ actions whereby the players all try to unilaterally maximize their respective payoffs. By playing actions y^max(x) rather than x, the players approach the equilibrium.

The relaxation algorithm is applied next. The relaxation algorithm follows

$$x^{s+1}=\left(1-{\alpha }_s\right)x^s+{\alpha }_s{y}^{max}\left(x^s\right),s=1,2,\dots$$

(8)

where $0\le {\alpha }_s\le 1$. Assigning x^s to the NI function (2), the optimum response function $y^{max}\left(x^s\right)$ is obtained from solving the optimization problem (7). $y^{max}\left(x^s\right)$ is then input into (8) and results in x^s+1, which is successively used in the NI function (2). The procedure repeats until the condition (4) is satisfied, i.e.,

$$\Psi \left(x^t,y^{max}\left(x^t\right)\right)=0$$

(9)

The x^t is the NE. There are two remarks regarding the determination of the NE. First, it can be difficult to attain the zero value of the NI function. In practice, the procedure is allowed to stop when

$$\left|\Psi \left(x^t,y^{max}\left(x^t\right)\right)\right|\le \epsilon$$

(10)

ε is the tolerance and has a small value close to zero. Second, the determination of y^max(x) is normally carried out in analytical manners. However, when the NI function is complicated, the analytical form of the optimum response function may not be possible to obtain. The next section explains an alternative method of obtaining $y^{max}\left(x^s\right)$, from which its numerical value is computed instead of deriving the closed form solution.

3. NI-Based Hybrid Genetic Algorithm and Relaxation Method

3.1. Methodological Concept

The previous application of the relaxation method relies only on the close form solution of y^max(x) [2,3]. This section proposes a method for determining the numerical value y^max(x). The so-called Genetic Algorithm (GA) is applied for this purpose. Let ${\Psi }_{min}$ be the minimum value of the NI function during the computational procedure, ${\Psi }_{int}$ be the intermediate value during the computation loop, count be the counter of computation loop, and L be the maximum number of computation loop. The NI-based hybrid GA and relaxation method has the following steps:

• Starting with s = 1, initialize x^s which satisfies the constraints (5) and (6). Then initialize ${\Psi }_{min}$ and ${\Psi }_{int}$ to large values compared to ε, e.g., equal to 1.
• While ${\Psi }_{int}>\epsilon$ and $count\le L$, perform steps 3 to 7.
• Using GA, compute $y^{max}\left(x^s\right)$ from the constrained optimization problem:
  Maximize

  $$\Psi \left(x^s,y^{max}\left(x^s\right)\right)$$

  (11)
  subject to

  $$c_{eq,r}\left(y^{max}\left(x^s\right)\right)=0(r=1,\dots ,N_{eq})$$

  (12)

  $$c_{ieq,q}\left(y^{max}\left(x^s\right)\right)\le 0(q=1,\dots ,N_{ieq})$$

  (13)
• Compute $\Psi \left(x^s,y^{max}\left(x^s\right)\right)$, if $\left|\Psi \left(x^s,y^{max}\left(x^s\right)\right)\right|\le {\Psi }_{min}$:
  • Assign $\left|\Psi \left(x^s,y^{max}\left(x^s\right)\right)\right|$ to ${\Psi }_{min}$.
  • Assign $x^s$ to x^* and $y^{max}\left(x^s\right)$ to y^*.
• Assign $\left|\Psi \left(x^s,y^{max}\left(x^s\right)\right)\right|$ to ${\Psi }_{int}$.
• Compute $x^{s+1}=\left(1-{\alpha }_s\right)x^s+{\alpha }_s{y}^{max}\left(x^s\right)$ and assign $x^{s+1}$ to $x^s$.
• Compute count = count + 1.

After the computational procedure terminates, the NE is equal to x^*. The procedure of the NI-based hybrid GA and relaxation method is summarized in Figure 1. The GA is described in the following section.

3.2. Genetic Algorithm (GA)

GA is a stochastic search technique that has a population-based nature. The algorithm comes from the concept of natural selection. GA has randomized operators in its exploring and exploiting strategy [27]. Various optimization problems were successfully solved by GA (see, for example [28,29]). The use of the population and stochastic transition scheme reduces the probability of getting local optima. GA does not require mathematical assumptions and makes use of only numerical values of the objective function. Consequently, the algorithm is applicable to non-differentiable functions. Yet, the algorithm is easy to understand and thus simple for implementation.

The computational procedure starts with a random sampling of a set of the population, i.e., trial solution set. Each element in the population is encrypted as a chromosome. The goodness of a chromosome to be the solution is measured through a fitness function. Each chromosome is selected for further reproduction based on its fitness. The offspring undergoes the cross-over and mutation to yield new chromosomes [27]. The new chromosomes form a new population generation. The evolution repeats again until the termination condition is satisfied. Normally, a prescribed number of generations is used as a termination condition.

In the present paper, the design variable of the GA procedure is $y^{max}\left(x^s\right)$, to which a simple binary for the real value is applied for its encryption to become a chromosome. Given x^s, the fitness function $F\left(y^{max}\left(x^s\right)\right)$ of a chromosome is

$$F\left(y^{max}\left(x^s\right)\right)=\{\begin{array}{cc}\Psi \left(x^s,y^{max}\left(x^s\right)\right)& ,y^{max}\left(x^s\right)\mathrm{is}\mathrm{feasible}\\ \Psi \left(x^s,y^{max}\left(x^s\right)\right)-{\displaystyle \sum _{r=1}^{N_{eq}}{\lambda }_r{v}_r\left(y^{max}\left(x^s\right)\right)}-{\displaystyle \sum _{q=1}^{N_{ieq}}{\kappa }_q{u}_q\left(y^{max}\left(x^s\right)\right)}& ,y^{max}\left(x^s\right)\mathrm{is}\mathrm{infeasible}\end{array}$$

(14)

$$v_r\left(y^{max}\left(x^s\right)\right)=max\left(c_{eq,r}^2\left(y^{max}\left(x^s\right)\right),0\right)$$

(15)

$$u_q\left(y^{max}\left(x^s\right)\right)=max\left(c_{ieq,q}{y}^{max}\left(x^s\right),0\right)$$

(16)

Since original GA was created for non-constrained optimization problems. Accordingly, an adaptive penalty scheme was used for handling the constraints [20,30]. The adaptive penalty scheme proves its excellency in handling a variety of constrained optimization problems [31,32]. Based on the adaptive penalty scheme, the penalty parameters are given by

$${\lambda }_r=\left|max\left[{\Psi }^{inf}\left(x^s,y^{max}\left(x^s\right)\right)\right]\right|\frac{\langle v_r\rangle }{{\displaystyle \sum _{jeq=1}^{N_{eq}}{\left[\langle v_{jeq}\rangle \right]}^2}}$$

(17)

$${\kappa }_q=\left|max\left[{\Psi }^{inf}\left(x^s,y^{max}\left(x^s\right)\right)\right]\right|\frac{\langle u_q\rangle }{{\displaystyle \sum _{leq=1}^{N_{ieq}}{\left[\langle u_{leq}\rangle \right]}^2}}$$

(18)

$max\left[{\Psi }^{inf}\left(x^s,y^{max}\left(x^s\right)\right)\right]$ is the maximum of the objective function values in the current population in the infeasible region. $v_r$ is the violation magnitude of the r-th equality constraint. $\langle v_r\rangle$ is the average of $v_r$ over the current population. ${\lambda }_r$ is the penalty parameter for the r-th equality constraint defined at each generation. $u_q$ is the violation magnitude of the q-th inequality constraint. $\langle u_q\rangle$ is the average of $u_q$ over the current population. ${\kappa }_q$ is the penalty parameter for the q-th inequality constraint defined at each generation. The fulfillment of the equality constraint can be made less strict by alternatively using

$$v_r\left(y^{max}\left(x^s\right)\right)=max\left(c_{eq,r}^2\left(y^{max}\left(x^s\right)-\varsigma \right),0\right)$$

(19)

where $\varsigma >0$ is the tolerance of deviation from zero and $\varsigma \to 0$.

After obtaining the fitness of chromosomes, the well-known reproduction process, namely the roulette wheel selection [27,29] is applied. The j-th chromosome is reproduced with the probability of

$$P_j=\frac{F_j}{{\displaystyle \sum _{u=1}^{N_{\mathrm{Pop}}}{F}_u}}$$

(20)

in which N_Pop is the population size. The fitness value F_j is obtained from (20). Two-point crossover and binary mutation are then applied to the reproduced chromosomes to result in the new population generation [27]. The whole procedure is to be explained through the use of numerical examples in the following section.

4. Illustrative Examples

The following GA parameters are used in all examples. The population size is 500. DeJong [33] suggested the crossover rate to be 0.6 and the mutation rate to be 0.001. The suggested mutation and crossover rate have been found in many GA applications [34]. All combinations of the mutation rates of 0.0005, 0.001, 0.0015, as well as 0.002 and the crossover rates of 0.5, 0.6, and 0.7 are employed herein. Ten runs of GA are carried out for each parameter combination. The mutation and crossover rate that yields the best result for each example is reported in the example. The computation is performed using Intel(R) Core(TM) i5-2430M CPU @ 2.40GHz with installed RAM 4.00 GB. The system type is a 64-bit operating system, x64-based processor.

4.1. River Basin Pollution Game

This exemplified game [35] considers three players. Each player is engaged in paper pulp producing at a chosen level x_j. The players must meet environmental conditions set by a local authority. Pollutants may be expelled into the river, where they disperse. Two monitoring stations l = 1, 2 are located along the river, at which the local authority has set maximum pollutant concentration levels.

The revenue for player j is

$$R_j\left(x\right)=\left[d_1-d_2\left({\displaystyle \sum _{i=1}^3{x}_i}\right)\right]x_j$$

(21)

with expenditure

$$F_j\left(x\right)=\left(c_{1j}+c_{2j}{x}_j\right)x_j$$

(22)

The payoff for the player j is thus

$${\varphi }_j\left(x\right)=\left[d_1-d_2\left({\displaystyle \sum _{i=1}^3{x}_i}\right)-\left(c_{1j}+c_{2j}{x}_j\right)\right]x_j$$

(23)

The emission constraint imposed by the local authority at location l is

$$q_l\left(x\right)={\displaystyle \sum _{j=1}^3{u}_{jl}{e}_j{x}_j}\le K_l;l=1,2$$

(24)

The economic constants d₁ and d₂ determine the inverse demand law and are equal to 3.0 and 0.1, respectively. The values of c_1j and c_2j are given in Table 1, and K_l = 100 (l = 1, 2). u_jl are the decay and transportation coefficients from player j to location l. e_j is the emission coefficient of player j, which is also given in

Table 2. Parameters for the river basin pollution game.

Player j	c1j	c2j	ej	uj1	uj2
1	0.10	0.01	0.50	6.5	4.853
2	0.12	0.05	0.25	5.0	6.250
3	0.15	0.01	0.75	5.5	3.750

[35].

This game is a generalized Nash Equilibrium problem in which the solution is required to satisfy the imposed constraints apart from minimizing the NI function. The NI function corresponding to the prescribed payoffs is

$$\begin{array}{ll}\psi \left(x,y\right)=& \left[d_1-d_2\left(y_1+x_2+x_3\right)-\left(c_{11}+c_{21}{y}_1\right)\right]y_1+\\ & \left[d_1-d_2\left(x_1+y_2+x_3\right)-\left(c_{12}+c_{22}{y}_2\right)\right]y_2+\\ & \left[d_1-d_2\left(x_1+x_2+y_3\right)-\left(c_{13}+c_{23}{y}_3\right)\right]y_3-\\ & \left[d_1-d_2\left({\displaystyle \sum _{i=1}^3{x}_i}\right)-\left(c_{1j}+c_{2j}{x}_j\right)\right]x_j\end{array}$$

(25)

The NI-based hybrid GA and relaxation method is employed to determine the NE. ${\alpha }_s=1$ is assigned to the relaxation algorithm and ensured the constraint satisfaction of $x^{s+1}$. The convergence tolerance for the solution ε is set to be 1.0 × 10⁻⁴. The evolution of the NI function value is plotted in Figure 2.

The obtained NE is compared to the literature [35] in

Table 3. The NE for the river basin pollution game.

Pulp Producing Level	The Proposed Method	[Krawczyk and Uryasev, 2000] [35]
x1	21.570	21.140
x2	15.860	16.030
x3	2.440	2.728

.

The best solution is obtained using the crossover rate of 0.05 and the mutation rate of 0.002. The adaptive penalty scheme in GA handles the constraint in an automatic manner without the assumption of the equal burden of satisfying constraints as in the previous work [35]. As is known, the equilibrium with coupled constraints can be a multiple equilibrium and depends on how the burden of satisfying the constraints is to be distributed among the players [36]. A priori fixing of burden may lead to local optima. The population-based search of GA and the adaptive penalty scheme as used here reduces the possibility of being trapped in the local optima and makes the solution satisfy constraints at the same time.

4.2. Electricity Market Game

Consider an electricity market using the IEEE 30-bus system [26]. In this case study, it is assumed that there are three generating companies and each of them possesses several generating units, as shown in

Table 4. IEEE 30-bus system market data.

Company #	Generator #	${\mathit{P}}_{\mathit{g}}^{\mathit{m}\mathit{i}\mathit{n}}$ (MW)	${\mathit{P}}_{\mathit{g}}^{\mathit{m}\mathit{a}\mathit{x}}$ (MW)	${\mathit{P}}_{\mathit{C}}^{\mathit{m}\mathit{i}\mathit{n}}$ (MW)	${\mathit{P}}_{\mathit{C}}^{\mathit{m}\mathit{a}\mathit{x}}$ (MW)
1	1	0	80	0	80
2	2	0	80	0	130
	3	0	50
3	4	0	55	0	125
	5	0	30
	6	0	40

[37]. P_g and P_C are the power generation of a unit and a company, respectively.

The cost of a generating unit i is of the type

$$C_i\left(P_{gi}\right)=\left(c_i/2\right)P_{gi}^2+d_i{P}_{gi}+e_i$$

(26)

whose coefficients are given in

Table 5. Generating units cost coefficients.

Generator #	${\mathit{c}}_{\mathit{i}}$ [$/MW2h]	${\mathit{d}}_{\mathit{i}}$ [$/MWh]	${\mathit{e}}_{\mathit{i}}$ [$/h]
1	0.04	2	0
2	0.035	1.75	0
3	0.125	1	0
4	0.0166	3.25	0
5	0.05	3	0
6	0.05	3	0

[37].

The standard loading condition of the IEEE 30-bus system in a selected interval is supposed to be

$$P_{load}\left(p\right)=189.2-0.5p$$

(27)

p is the electricity price. The payoff made by company j that owns ngj generating unit is

$$\begin{array}{ll}{\varphi }_j\left(P_{gj}\right)& =p{\displaystyle \sum _{j=1}^{ngj}{P}_{gj}}-{\displaystyle \sum _{j=1}^{ngj}{C}_j}\left(P_{gj}\right)\\ & =\left(378.4-2{\displaystyle \sum _{i=1}^{ng}{P}_{gi}}\right){\displaystyle \sum _{j=1}^{ngj}{P}_{gj}}\\ & -{\displaystyle \sum _{j=1}^{ngj}\left(\frac{c_j}{2}\right)P_{gj}^2+d_j{P}_{gj}+e_j}\end{array}$$

(28)

subject to the boundary constraints $P_{mingj}\le P_{gj}\le P_{maxgj}$. The NI function for (28) is

$$\begin{array}{ll}\psi \left(P_{gj},y_j\right)=& \left\{[378.4-2\left(y_1+P_{g2}+\cdots +P_{g6}\right)]y_1-\left(\frac{c_1}{2}{y}_1^2+d_1{y}_1+e_1\right)\right\}\\ & -\left\{[378.4-2\left(P_{g1}+P_{g2}+\cdots +P_{g6}\right)]P_{g1}-\left(\frac{c_1}{2}{P}_{g1}^2+d_1{P}_{g1}+e_1\right)\right\}\\ & +\{[378.4-2\left(P_{g1}+y_2+y_3\cdots +P_{g6}\right)]\left(y_2+y_3\right)\\ & -\left(\frac{c_2}{2}{y}_2^2+d_2{y}_2+e_2\right)-\left(\frac{c_3}{2}{y}_3^2+d_3{y}_3+e_3\right)\}\\ & -\{[378.4-2\left(P_{g1}+P_{g2}+P_{g3}\cdots +P_{g6}\right)]\left(P_{g2}+P_{g3}\right)\\ & -\left(\frac{c_2}{2}{P}_{g2}^2+d_2{P}_{g2}+e_2\right)-\left(\frac{c_3}{2}{P}_{g3}^2+d_3{P}_{g3}+e_3\right)\}\\ & +\{[378.4-2\left(P_{g1}+\cdots +y_4+y_5+y_6\right)]\left(y_4+y_5+y_6\right)\\ & -\left(\frac{c_4}{2}{y}_4^2+d_4{y}_4+e_4\right)-\left(\frac{c_{\backslash 5}}{2}{y}_5^2+d_5{y}_5+e_5\right)-\left(\frac{c_{\backslash 6}}{2}{y}_6^2+d_6{y}_6+e_6\right)\}\\ & -\{[378.4-2\left(P_{g1}+\cdots +P_{g4}+P_{g5}+P_{g6}\right)]\left(P_{g4}+P_{g5}+P_{g6}\right)\\ & -\left(\frac{c_4}{2}{P}_{g4}^2+d_4{P}_{g4}+e_4\right)-\left(\frac{c_{\backslash 5}}{2}{P}_{g5}^2+d_5{P}_{g5}+e_5\right)-\left(\frac{c_{\backslash 6}}{2}{P}_{g6}^2+d_6{P}_{g6}+e_6\right)\}\end{array}$$

(29)

It is noted that the NI function is complicated. Another characteristic is that while most games contain only one strategic variable for each player, some players of this game have more than one strategic variable. The company #1 owns one generator, the company #2 owns two generators, and the company #3 owns three generators. In other words, there are two and three strategic variables for the company #2 and #3, respectively. The two characteristics of the complicated NI function and multiple strategic variables make the close-form derivation of $y^{max}\left(x^s\right)$ not tractable. The determination of NE using the proposed NI-based hybrid GA and relaxation method with ${\alpha }_s=0.5$ is then performed. The convergence tolerance for the solution ε is set to be 1.0 × 10⁻⁴. The evolution of NI function value is plotted in Figure 3. The search terminates after the maximum number of loops, 50, is reached. The values of the strategic variables that yield the minimum NI function, ${\psi }_{min}=1.3\times {10}^{-4}$, are taken as the NE. The obtained NE is compared to the literature [38] in

Table 6. The NE for the electricity market game.

Power Generation Unit	The Proposed Method (MW)	(Contreras et al., 2004) [38] (MW)
$P_{g1}$	46.66	46.66
$P_{g2}$	32.15	32.16
$P_{g3}$	15.01	15
$P_{g4}$	22.13	22.13
$P_{g5}$	12.35	12.33
$P_{g6}$	12.31	12.33

.

The best solution is obtained using the crossover rate of 0.05 and the mutation rate of 0.0015. While the original NI-based relaxation method [38] requires the concavity-convexity property in the NI function, the employed GA has no computational limitation with respect to the requirement. This is due to the capability of the GA in solving non-convex and non-concave optimization problems, see e.g., [19].

4.3. Nash–Cournot Aggregative Game of Power Generation Firms

Consider five power generation firms [14]. The communication among the firms is delineated by an undirected ring graph. The power generation firm $i\in \left\{1,\dots ,5\right\}$ has the following payoff function:

$${\varphi }_i\left(P_i\right)=P_{i}p\left(\sigma \right)-c_i\left(P_i\right)$$

(30)

All the firms subject to

$${\displaystyle \sum _{i=1}^5{P}_i}={\displaystyle \sum _{i=1}^5{d}_i}$$

(31)

and

$$P_{imin}\le P_i\le P_{imax}$$

(32)

The payoff is in M$. P_i is the output power of firm i in MW, d_i is the local demand in MW, and P_imin and P_imax are the upper and lower bounds of the output power P_i, respectively. $p\left(\sigma \right)$ is the electricity price and is defined by

$$p\left(\sigma \right)=p_0-a\left({\displaystyle \sum _{i=1}^5{P}_i}\right)$$

(33)

$p_0=10$ and a = 0.001. $c_i\left(P_i\right)$ is the generation cost and has the following form:

$$c_i\left(P_i\right)={\alpha }_i+{\beta }_i\left|P_i-{\varsigma }_i\right|+{\gamma }_i{P}_i^2$$

(34)

where ${\alpha }_i,{\beta }_i,{\gamma }_i$, and ${\varsigma }_i$ are the characteristic parameters of firm i. All of the parameters are shown in

Table 7. Characteristic parameters of all firms.

Parameter	Firm 1	Firm 2	Firm 3	Firm 4	Firm 5
${\alpha }_i$	5	8	6	9	7
${\beta }_i$	12	10	11	11	13
${\gamma }_i$	2	1	3	1.5	0.5
${\varsigma }_i$	25	48	15	30	45
di	45	35	25	40	30
Pimin	20	45	10	20	25
Pimax	37	55	25	33	40

[14].

The NI function corresponding to the payoff function is

$$\begin{array}{ll}\psi \left(P,y\right)=& y_1\left[p_0-a\left(y_1+P_2+P_3+P_4+P_5\right)\right]-\left({\alpha }_1+{\beta }_1\left|y_1-{\varsigma }_1\right|+{\gamma }_1{y}_1^2\right)\\ & -\left\{P_1\left[p_0-a\left(P_1+P_2+P_3+P_4+P_5\right)\right]-\left({\alpha }_1+{\beta }_1\left|P_1-{\varsigma }_1\right|+{\gamma }_1{P}_1^2\right)\right\}\\ & +y_2\left[p_0-a\left(P_1+y_2+P_3+P_4+P_5\right)\right]-\left({\alpha }_2+{\beta }_2\left|y_2-{\varsigma }_2\right|+{\gamma }_2{y}_2^2\right)\\ & -\left\{P_2\left[p_0-a\left(P_1+P_2+P_3+P_4+P_5\right)\right]-\left({\alpha }_2+{\beta }_2\left|P_2-{\varsigma }_2\right|+{\gamma }_2{P}_2^2\right)\right\}\\ & +y_3\left[p_0-a\left(P_1+P_2+y_3+P_4+P_5\right)\right]-\left({\alpha }_3+{\beta }_3\left|y_3-{\varsigma }_3\right|+{\gamma }_3{y}_3^2\right)\\ & -\left\{P_3\left[p_0-a\left(P_1+P_2+P_3+P_4+P_5\right)\right]-\left({\alpha }_3+{\beta }_3\left|P_3-{\varsigma }_3\right|+{\gamma }_3{P}_3^2\right)\right\}\\ & +y_4\left[p_0-a\left(P_1+P_2+P_3+y_4+P_5\right)\right]-\left({\alpha }_4+{\beta }_4\left|y_4-{\varsigma }_4\right|+{\gamma }_4{y}_4^2\right)\\ & -\left\{P_4\left[p_0-a\left(P_1+P_2+P_3+P_4+P_5\right)\right]-\left({\alpha }_4+{\beta }_4\left|P_4-{\varsigma }_4\right|+{\gamma }_4{P}_4^2\right)\right\}\\ & +y_5\left[p_0-a\left(P_1+P_2+P_3+P_4+y_5\right)\right]-\left({\alpha }_5+{\beta }_5\left|y_5-{\varsigma }_5\right|+{\gamma }_5{y}_5^2\right)\\ & -\left\{P_5\left[p_0-a\left(P_1+P_2+P_3+P_4+P_5\right)\right]-\left({\alpha }_5+{\beta }_5\left|P_5-{\varsigma }_5\right|+{\gamma }_5{P}_5^2\right)\right\}\end{array}$$

(35)

where $P={\left[\begin{array}{ccccc}{P}_1& P_2& P_3& P_4& P_5\end{array}\right]}^T$ and $y={\left[\begin{array}{ccccc}{y}_1& y_2& y_3& y_4& y_5\end{array}\right]}^T$.

Obviously, $c_i\left(P_i\right)$ is a non-differentiable function [39,40]. Consequently, the payoff function and the NI function are also non-differentiable and the derivative-based optimization is not possible. The derivative-free GA is used for computing the optimum response function $y^{max}\left(x^s\right)$. The determination of NE using the proposed NI-based hybrid GA and relaxation method with ${\alpha }_s=0.5$ is then performed. The convergence tolerance for the solution $\epsilon$ is set to be 1.0 × 10⁻⁴.

The evolution of the NI function value is plotted in Figure 4. The search terminates after the maximum number of loops, 50, is reached. The values of the strategic variables that yield the minimum NI function, ${\psi }_{min}=9.78\times {10}^{-2}$, are taken as the NE. The results are shown in

Table 8. The NE for the Nash–Cournot game of power generation firms.

Firm i	Output Power Pi (MW)
1	28.51
2	54.66
3	18.84
4	32.99
5	40.00

.

The best solution is obtained using the crossover rate of 0.07 and the mutation rate of 0.002. The results are close to those in Figure 1 from the distributed algorithm [14]. The distributed algorithm is specifically designed for this aggregative game and thus has a limited application when it is compared with the proposed NI-based hybrid GA and relaxation method. Furthermore, the present example shows for the first that the concept of NI function is applicable to a non-differentiable payoff function having the absolute value function.

4.4. Game with Local Optima

Consider a two-player game with non-concave payoff functions [7]:

$${\varphi }_1\left(x_1,x_2\right)=21+x_{1}sin\left(\pi x_1\right)+x_1{x}_{2}sin\left(\pi x_2\right)$$

(36)

$${\varphi }_2\left(x_1,x_2\right)=21+x_{2}sin\left(\pi x_2\right)+x_1{x}_{2}sin\left(\pi x_1\right)$$

(37)

$x_i\in \left[0,7.5\right]$; $\left(i=1,2\right)$.

The NI function corresponding to the payoff functions is:

$$\psi \left(x,y\right)={\varphi }_1\left(y_1,x_2\right)+{\varphi }_2\left(x_1,y_2\right)-{\varphi }_1\left(x_1,x_2\right)-{\varphi }_2\left(x_1,x_2\right)$$

(38)

The NI function contains several local optima. The determination of NE using the proposed NI-based hybrid GA and relaxation method with the standard value of ${\alpha }_s=0.5$ is then performed. The evolution of the NI function value is plotted in Figure 5. The search terminates after the convergence tolerance is satisfied. The values of the variables that yield the minimum NI function, ${\psi }_{min}=4.2\times {10}^{-9}$, are taken as the NE. Since there is a reference solution from the DE-based method [7,41], the comparison with other heuristic algorithms is done in this example. Three additional algorithms called the Gravitational Search Algorithm (GSA) [23,42], the Inclined Planes System Optimization Algorithm (IPO) [24,43], and the Capuchin Search Algorithm (CSA) [25,44] are performed for comparison. All computational programs were coded by the inventors of those three algorithms [25,45,46]. The convergence tolerance is for checking the NE, and therefore, it is the same for all algorithms. The convergence tolerance for the solution ε is set to be 1.0 × 10⁻⁸.

The parameters used by DE, GSA, IPO, and CSA are shown in

Table 9. Parameters used by DE.

Parameter	Value
Population size	50
Maximum number of iterations	400
Probability of crossover	0.35
Mutation factor	0.45
Termination tolerance	0.0001

,

Table 10. Parameters used by GSA.

Parameter	Value
Population size	50
Maximum number of iterations	1000
Number of runs	30
G0	100
α	20
K0	50 and is decreased linearly to 1

,

Table 11. Parameters used by IPO.

Parameter	Value
Population size	50
Maximum number of iterations	1000
Number of runs	30
c1	0.72
c2	2.76
shift1	72.47
shift2	188.51
scale1	0.04
scale2	0.82

and

Table 12. Parameters used by CSA.

Parameter	Value
Population size	30
Maximum number of iterations	1000
Number of runs	30
Velocity control constant	1
Inertia parameter	0.7
Balance factor	0.7
Elasticity factor	9

, respectively.

The result comparison is reported in

Table 13. The NE for the Nash–Cournot game of power generation firms.

Variable	Proposed Method	DE [7]	GSA [23]	IOP [24]	CSA [25]
$x_1$	6.611808827	6.61	6.611799888	3.2143	13.47359735
$x_2$	6.611804039	6.61	6.611801489	3.2143	14.982799

. The best solution by the present method is obtained using the crossover rate of 0.05 and the mutation rate of 0.002. The results of GA are significantly the same as those from the literature for DE and GSA, while IPO and CSA cannot detect the NE. This affirms the capability of GA as an optimizer on finding the NE, similar to previous research [7,8,9,10,12,13].

It is, however, not claimed that GA is the best method. It is indeed known that the GA solution is the NE because it satisfies the optimality condition, i.e., the zero or near-zero value of the NI function. Therefore, GA proves to be effective in itself without the necessity of comparing it with the other algorithms when using the NI function as a measure of reaching NE.

5. Conclusions

A Nikaido–Isoda (NI)-based hybrid Genetic Algorithm (GA) and relaxation method for finding Nash Equilibrium (NE) is proposed. The method combines the capability of the GA in optimizing non-convex and non-concave problems together with the implementation simplicity of the relaxation method. The adaptive penalty scheme is incorporated in the GA that the proposed method is applicable to the generalized Nash Equilibrium problem as well. The examples of the method applicability include the generalized Nash Equilibrium problem with nonlinear payoff functions and coupled constraints, the game with multiple strategic variables for individual players, and the non-differentiable payoff functions. All test example results suggest the appropriate crossover and mutation rate to be 0.05 and 0.002 for use in GA. These numbers are close to the recommended values by DeJong [33]. With respect to the performance in detecting the NE, the proposed method shows its capability of finding correct NEs in all test examples.

Future research should include the comparative study of meta-heuristic algorithms for use as alternative tools in the optimization step of this hybrid method. Another research direction is to apply the proposed method to the game problems with combinatorial payoff functions.