Introducing Tables to Second-Grade Elementary Students in an Algebraic Thinking Context
Abstract
:1. Introduction
2. Functional Thinking and Representations
3. Tabular Representations
4. Research Objectives
5. Materials and Methods
5.1. Participants and School
5.2. Data Collection
5.2.1. Interview 1
5.2.2. Interview 2
5.3. Data Analysis
- Recognise tables as elements for recording data in different functional contexts functional (yes/no)
- Organise data in the tables during the tasks:
- Did they place data in the appropriate column and row? (yes/no)
- Did they write in or complete the table headings? (yes/no)
- 3.
- Identify structures:
- Did they relate the values of each variable (numbers or quantities) in the two columns to the variables involved, identifying the regularities between them? (yes/no)
- Were the structures correctly identified? (yes/no)
6. Results
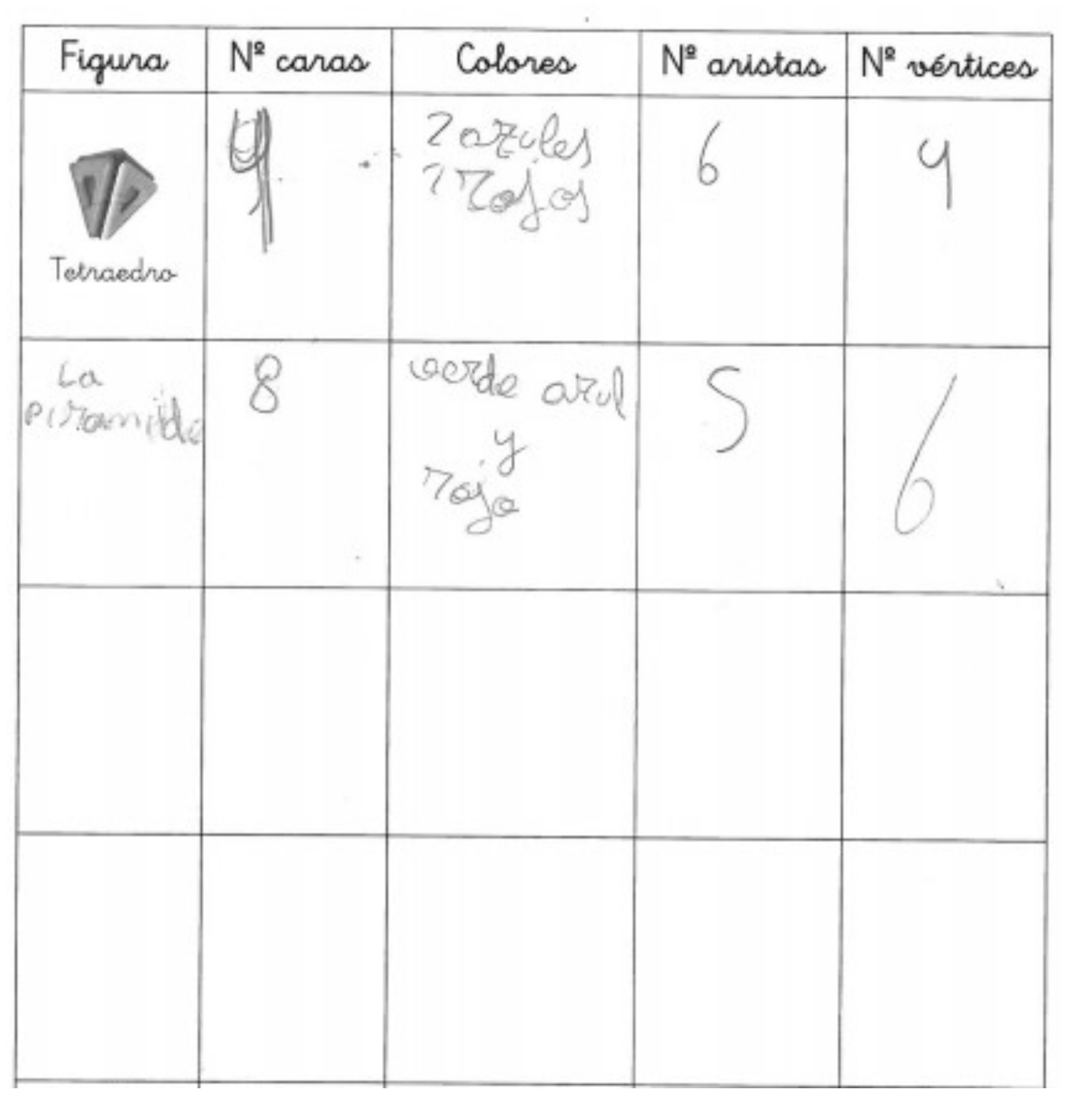
6.1. Tables as a Means to Record Data
6.2. Data Organisation in Tables
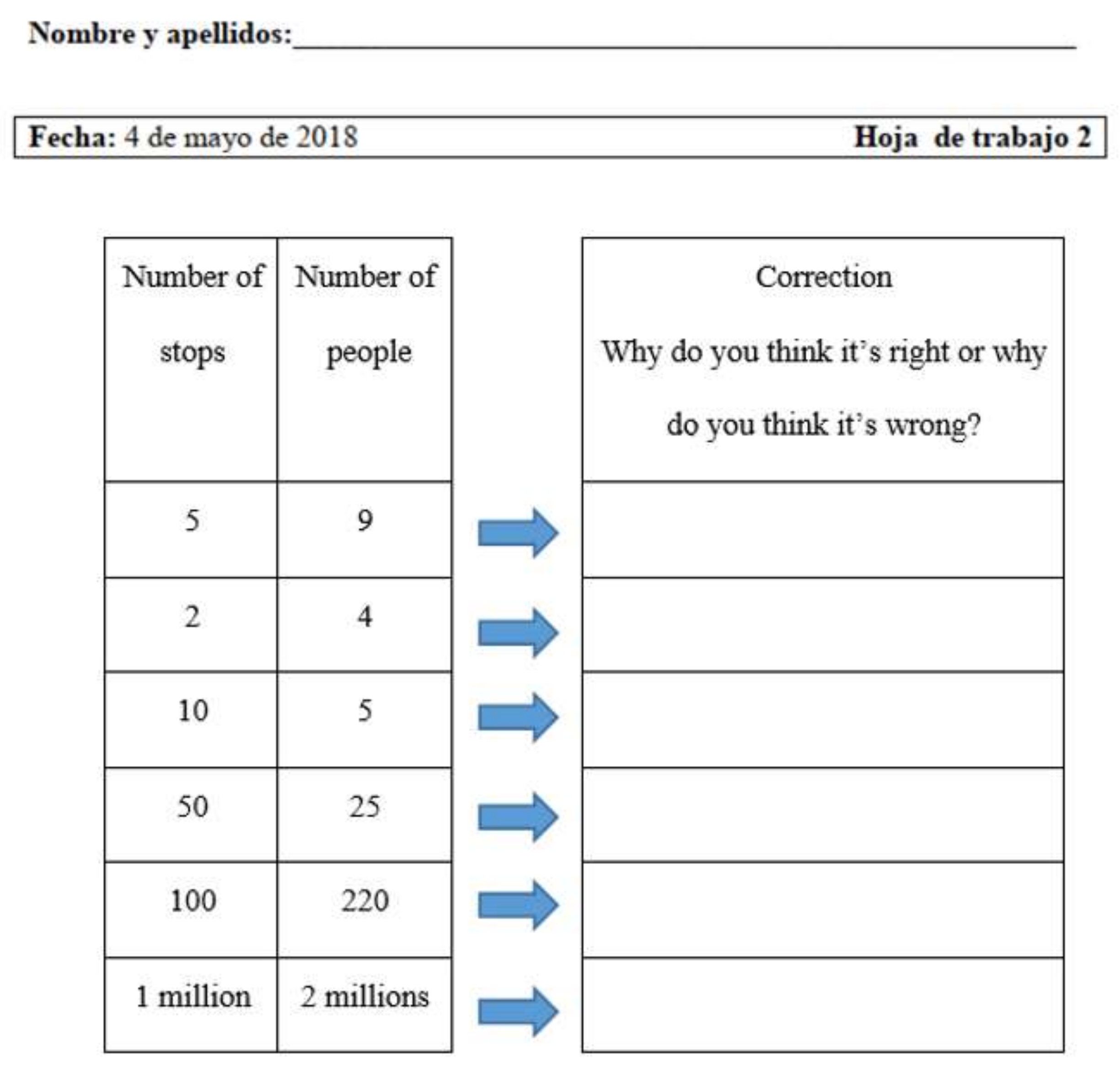
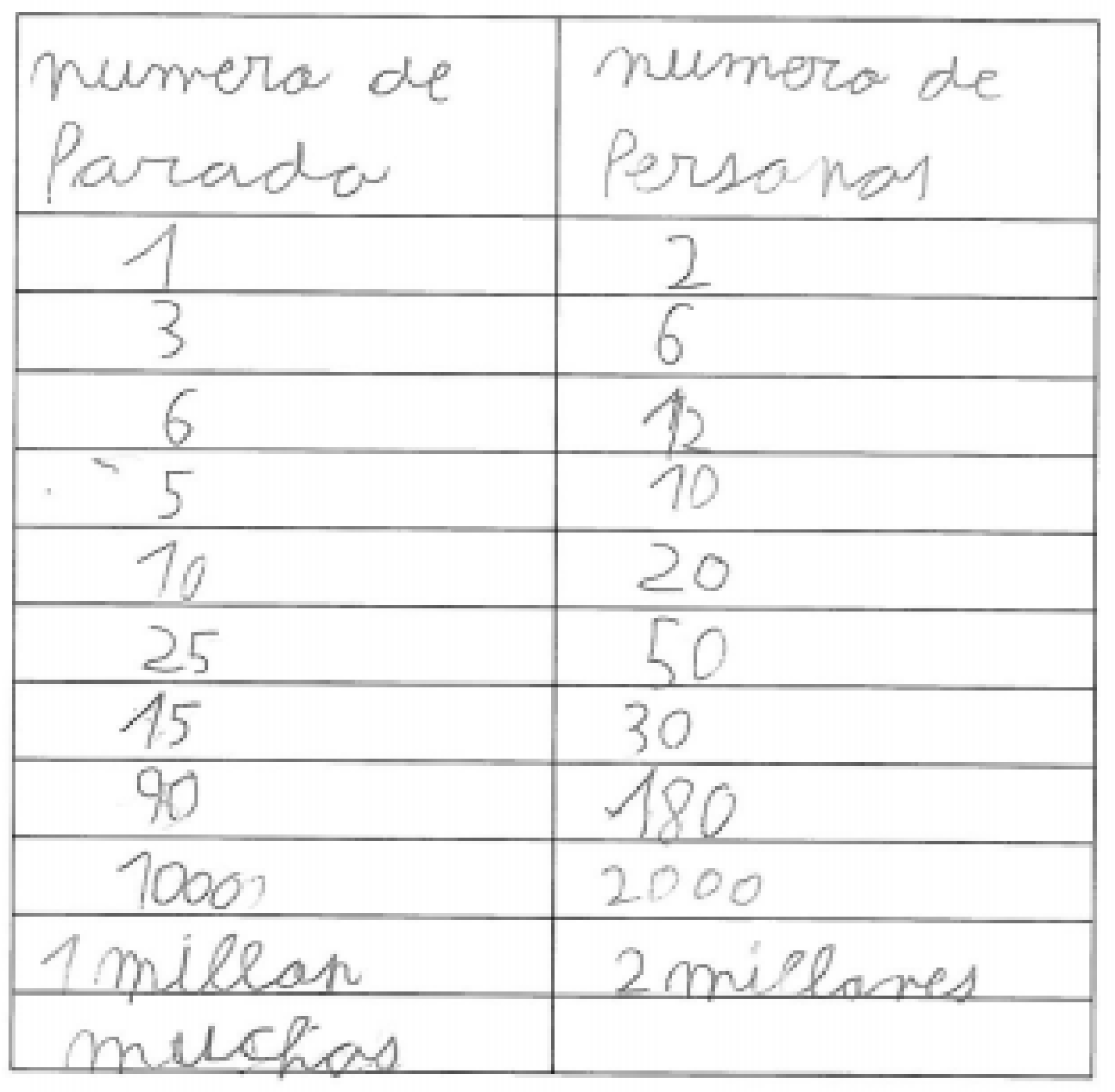
- Interviewer (I): “When the train stops once, how many people get on?”.
- All: “Two” (in unison).
- I: “If two people board every time the train stops, how can we show that on the table?”.
- Darío: “Putting half of the word here and the other half there” (pointing to the two column headings).
- I: “Which half-word do we write in, Darío? Let us see, write down whatever you want”.
- Darío: “Hmmmm (thinking). I do not know”.
- Alba: “Yes, you can, but I do not know where”.
- Ángel: “I do not think you can”.
- 9.
- I: “OK, no problem. Let’ us try something. Let us write number of stops here in this space (heading for left column). Now we are going to try to show that the train stops once and two people get on”.
- 10.
- All: (Still writing nothing)
- 11.
- I: “How could we show that the train stops once?”.
- 12.
- Lola: “Writing it down?”.
- 13.
- I: ‘Yes, but how? What should we write? Any ideas?”.
- 14.
- All: (Shaking their heads no.)
- 15.
- I: “Well, we could write in a ‘1′ under where it says number of stops? The train stops once and two people board each time it stops. We write in the number of people in the second column next to the 1. If the train stops three times, for instance, we write that down underneath the 1”.
6.3. Identification of Structures
- 16.
- I: “If the train stops three times how many people get on?”
- 17.
- All: “6”.
- 18.
- I: “Why 6?”.
- 19.
- Ángel: “Because 2 plus 2 is and 2 more make 6”.
- 20.
- I: “And how did you do that, Ángel?”.
- 21.
- Ángel: “Well, I multiplied 2 times 3”.
- 22.
- I: “And why did you multiply times 2? What is 2 here?”.
- 23.
- Ángel: “Well, the number of stops”.
- 24.
- I: “Well, let us see, when the train stops three times (pointing to the stops column), how many people (pointing to the number of people column) boarded?”.
- 25.
- All: “6” (all write in 6 in the respective cell).
- 26.
- I: “Alba, can you explain why the answer is 6?”.
- 27.
- Alba: “Because if the train stops three times six people would get on. I multiplied 3 times 2”.
- 28.
- I: “And why times 2, Alba?”.
- 29.
- Alba: “Because 2 means two people”.
- 30.
- I: “Good, now let us think about what happens if the train stops, let us say six times”.
- 31.
- Lola: “Twelve would get on”.
- 32.
- Ángel: “Twelve” (answering a little later).
- 33.
- I: “And now how did you get that answer?”.
- 34.
- Ángel: “Multiplying 6 times 2”.
- 35.
- Darío and Lola: “Multiplying times 2”.
- 36.
- Darío: “Yeah, you always need to multiply”.
- 37.
- I: “Then we can show that in the table: if the train stops six times (pointing to the stops column), what number should we put here?” (pointing to the number of people column).
- 38.
- All: (Writing 12 in the respective cell).
- 39.
- I: “Fine. Now if the train stopped five times, how many of Elsa’s friends could have boarded?”.
- 40.
- All: Ten (answering quickly at the same time; Darío and Alba write the number into the table, now unaided by the interviewer).
- 41.
- I: “OK, and if the train stops ten times?”.
- 42.
- Darío: “Well, it picks up 20 people”.
- 43.
- Ángel and Alba: “20” (answering after Darío).
- 44.
- Ángel: “Now it is 10 times 2”.
- 45.
- I: “If the train can carry however many people we want… It is Elsa’s train. For instance, Alba, if the train stops one million times, how many people can board?”.
- 46.
- Darío: “Well, two million” (answering quickly).
- 47.
- Alba: (No answer).
- 48.
- Darío: “But teacher, how do you write one million?”.
- 49.
- I: “You can write it out in words, Darío, no problem”.
- 50.
- Darío: (Writes “one million” in words in the table).
- 51.
- I: “Now let us suppose the train stops a lot of times, I do not know how many, but a lot. In the number of stops column we are going to write in ‘lots’, in words”.
- 52.
- All: (Three students write in “lots” in the respective cell).
- 53.
- I: “Good. If the train stops lots of times, how many people can board?”.
- 54.
- Ángel: “Nine hundred thousand?”.
- 55.
- Lola: (Raises her hands to her head, thinking)
- 56.
- Ángel: ‘Lots”.
- 57.
- I: “Not so sure. And if it stops an infinity of times?”.
- 58.
- Darío: “Oof, one trillion or one hundred thousand trillion”.
- 59.
- I: “Why, Darío?”.
- 60.
- Darío: “Because lots of stops can be a trillion”.
- 61.
- I: “I am going to ask one more question… These numbers (pointing to the number of stops column), what did we say they are?”.
- 62.
- All: (In unison) “Number of stops”.
- 63.
- I: “Very good. And these?” (pointing to the number of people column).
- 64.
- All: (In unison) ”Number of people”.
- 65.
- I: “OK, can we explain to a classmate or to one another how we can figure out the number of people that can be on the train when it stops lots of times? How can we figure that out?”.
- 66.
- Darío: “You always need to multiply, like before”.
- 67.
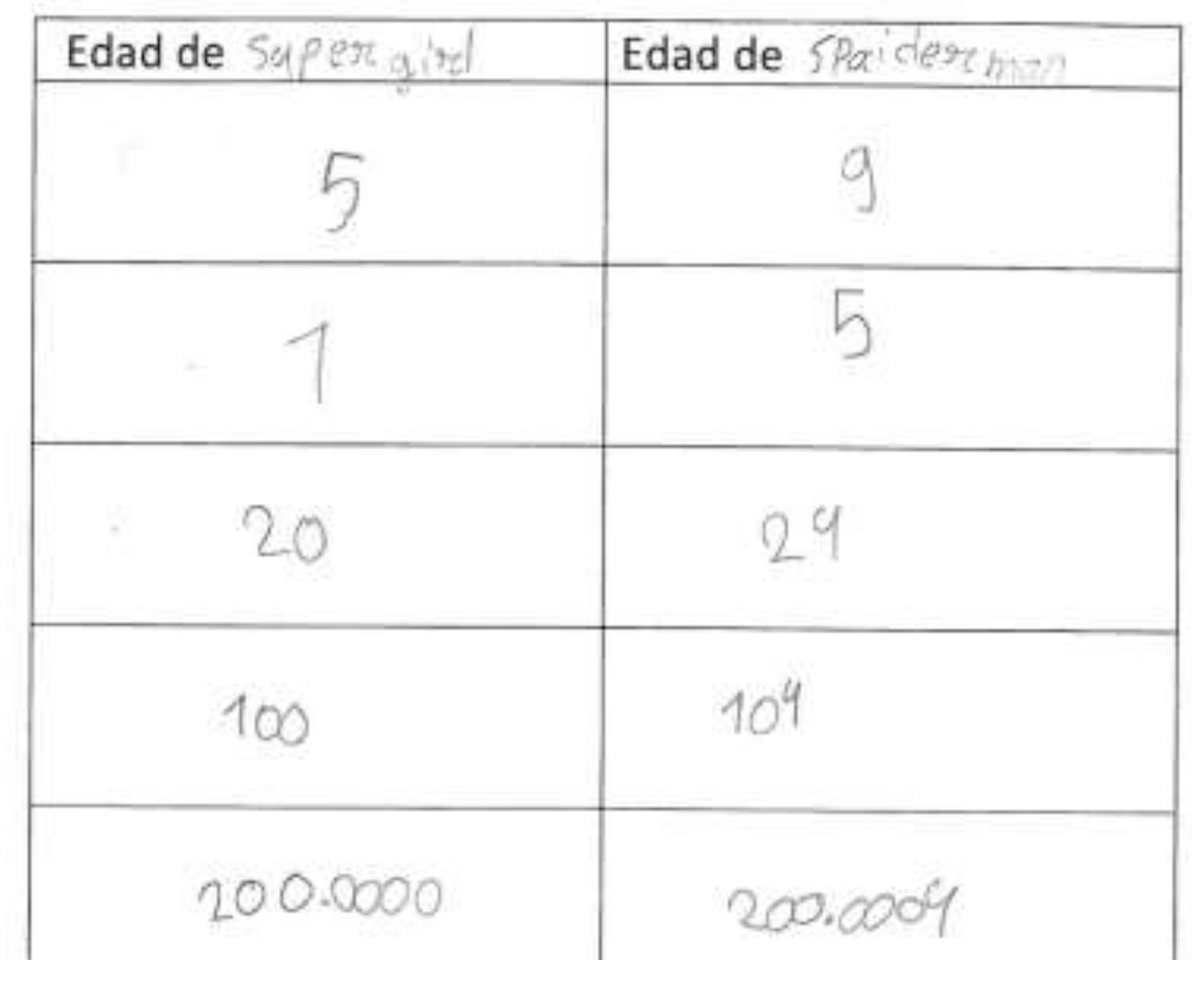
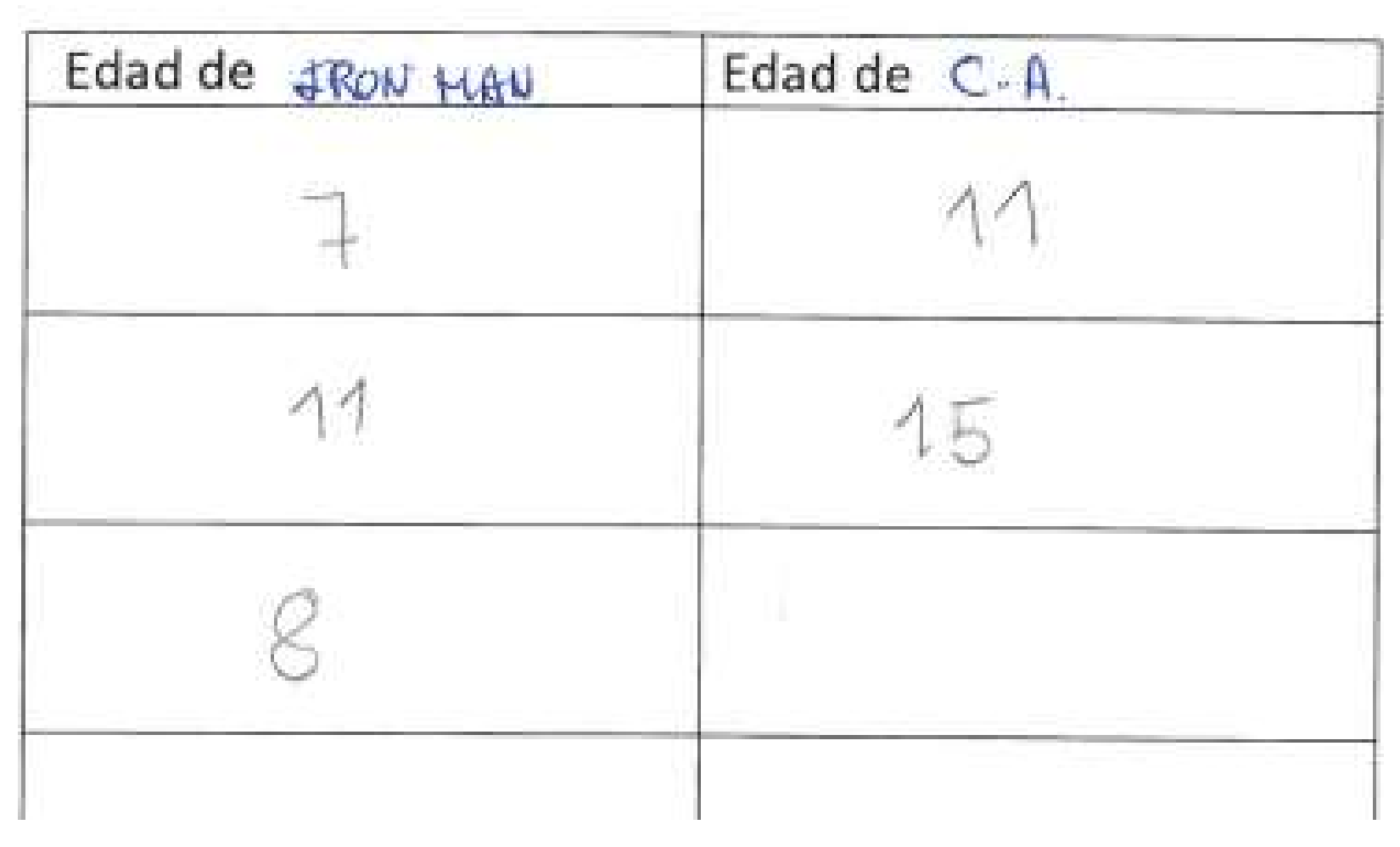
- I: “Could you tell me how much older Captain America will be when Iron Man is many years old?”.
- 68.
- Darío: “He would be many plus 4”.
- 69.
- I: “And when Iron Man is infinite years old, how old will Captain America be?”.
- 70.
- Darío: “Well, infinite plus 4”.
- 71.
- I: “How would you explain to friends what they have to do to figure out Captain America’s age?”.
- 72.
- Darío: “As always, adding 4. Captain America was born 4 years before”.
7. Discussion and Conclusions
8. Patents
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Duval, R. The cognitive analysis of problems of comprehension in the learning of mathematics. Edu. Stud. Math. 2006, 61, 103–131. [Google Scholar] [CrossRef]
- Rico, L. Sobre las nociones de representación y comprensión en la investigación en educación matemática (On the notions of representation and understanding notions in mathematics education research). PNA 2009, 4, 1–14. [Google Scholar]
- Castro, E.; Castro, E. Representaciones y modelización (Representations and modeling). In La Educación Matemática en la Enseñanza Secundaria; Rico, L., Ed.; Horsori: Barcelona, Spain, 1997; pp. 95–124. [Google Scholar]
- Henriques, A.; Ponte, J. As representações como suporte do raciocínio matemático dos alunos quando exploram atividades de investigação (Representations as a tool to support students’ mathematical reasoning when exploring investigation activities). Bolema 2014, 28, 276–298. [Google Scholar] [CrossRef] [Green Version]
- NCTM. Principios e Normas Para a Matemática Escolar; APM: Lisboa, Portugal, 2007. [Google Scholar]
- Martínez, M.; Brizuela, B.M. A third grader’s way of thinking about linear function tables. J. Math. Behav. 2006, 25, 285–298. [Google Scholar] [CrossRef]
- Gabucio, F.M.a.r.t.í.; EEnfedaque, J.; Gilbert, S.; Konstantinidou, A. Niveles de comprensión de las tablas en alumnos de primaria y secundaria. Cult. Edu. 2010, 22, 183–197. [Google Scholar] [CrossRef]
- Martí, E. Tables as cognitive tools in primary education. In Representational Systems and Practices as Learning Tools in Different Fields of Learning; Andersen, C., Scheuer, N., Echeverría, P., Teubal, E., Eds.; Sense Publishers: Barcelona, Spain, 2009; pp. 133–148. [Google Scholar]
- Leinhardt, G.; Zaslavsky, O.; Stein, M.K. Functions, graphs, and graphing: Tasks, learning, and teaching. Review Edu. Res. 1990, 60, 1–64. [Google Scholar] [CrossRef]
- Nemirovsky, R.; Tierney, C.; Wright, T. Body motion and graphing. Cogn. Instruct. 1998, 16, 119–172. [Google Scholar] [CrossRef]
- Brizuela, B.M.; Lara-Roth, S. Additive relations and function tables. J. Math. Behav. 2002, 20, 309–319. [Google Scholar] [CrossRef]
- Cañadas, M.C.; Molina, M. Una aproximación al marco conceptual y principales antecedentes del pensamiento funcional en las primeras edades (An approach to the conceptual framework and main antecedents of functional thinking in the early ages). In Investigación en Educació;n Matemática. Homenaje a Luis Rico; Castro, E., Lupiáñez, J.L., Ruíz, J.F., Torralbo, M., Eds.; Editorial Comares: Granada, Spain, 2016; pp. 209–218. [Google Scholar]
- Blanton, M.; Kaput, J. Elementary grades students’ capacity for functional thinking. In Proceedings of the 28th International Conference for the Psychology of Mathematics Education, Bergen, Norway, 14–18 July 2004; Hoines, M., Fuglestad, A., Eds.; Bergen University College: Bergen, Norway, 2004; Volume 2, pp. 135–142. [Google Scholar]
- Blanton, M.; Levi, L.; Crites, T.; Dougherty, B. Developing Essential Understanding of Algebraic Thinking for Teaching Mathematics in Grades 3–5; NCTM: Reston, VA, USA, 2011. [Google Scholar]
- Doorman, M.; Drijvers, P. Algebra in functions. In Secondary Algebra Education; Drijvers, P., Ed.; Sense Publishers: Rotterdam, The Netherlands, 2011; pp. 119–135. [Google Scholar]
- Carraher, D.W.; Schliemann, A. Powerful ideas in elementary school mathematics. In Handbook of International Research in Mathematics Education, 3rd ed.; English, L., Kirshner, D., Eds.; Routledge: Amsterdam, The Netherlands, 2016; pp. 191–218. [Google Scholar]
- Pinto, E.; Cañadas, M.C. Estructuras y generalización de estudiantes de tercero y quinto de primaria: Un estudio comparativo [Structures and generalisation in third and fifth year of primary school: A comparative study]. In Investigación en Educación Matemática XXI; Muñoz-Escolano, J.M., Arnal-Bailera, A., Beltrán-Pellicer, P., Callejo, M.L., Carrillo, J., Eds.; SEIEM: Zaragoza, Spain, 2017; pp. 407–416. [Google Scholar]
- Torres, M.D.; Cañadas, M.C.; Moreno, A. Estructuras, generalización y significado de letras en un contexto funcional por estudiantes de 2º de primaria. In Investigación en Educación Matemática XXII; Rodríguez-Muñiz, L.J., Rodríguez, L.M., Aguilar-González, A., Alonso, P., García, F.J.G., Bruno, A., Eds.; SEIEM: Gijón, Spain, 2018; pp. 574–583. [Google Scholar]
- Mason, J.; Stephens, M.; Watson, A. Appreciating mathematical structure for all. Math. Edu. Res. J. 2009, 21, 10–32. [Google Scholar] [CrossRef] [Green Version]
- Torres, M.D.; Moreno, A.; Cañadas, M.C. Generalization process by second grade students. Mathematics 2021, 9, 1109. [Google Scholar] [CrossRef]
- Strother, S. Algebra Knowledge in Early Elementary School Supporting Later Mathematics Ability. Ph.D. Thesis, University of Louisville, Louisville, KY, USA, 2011. [Google Scholar]
- Warren, E.; Miller, J.; Cooper, T.J. Exploring young students’ functional thinking. PNA 2013, 7, 75–84. [Google Scholar] [CrossRef]
- Radford, L. The seen, the spoken and the written: A semiotic approach to the problem of objectification of mathematical knowledge. Learn. Math. 2002, 22, 14–23. [Google Scholar]
- Carraher, D.; Martinez, M.; Schliemann, A. Early algebra and mathematical generalization. Int. J. Math. Edu. (ZDM) 2008, 40, 3–22. [Google Scholar] [CrossRef]
- Cañadas, M.C.; Fuentes, S. Pensamiento funcional de estudiantes de primero de educación primaria: Un estudio exploratorio [Functional thinking in first-year primary teacher students: An exploratory study]. In Investigación en Educación Matemática XIX; Fernández, C., Molina, M., Planas, N., Eds.; SEIEM: Alicante, Spain, 2015; pp. 211–220. [Google Scholar]
- Radford, L. Gestures, speech, and the sprouting of signs: A semiotic-cultural approach to students’ types of generalization. Math. Think. Learn. 2003, 5, 37–70. [Google Scholar] [CrossRef]
- Kaput, J. Representation systems and mathematics. In Problems of Representation in the Teaching and Learning of Mathematics; Janvier, C., Ed.; Lawrence Erlbaum Associated: Mahwah, NJ, USA, 1987; pp. 19–26. [Google Scholar]
- Campbell-Kelly, M.; Croarken, M.; Flood, R.; Robson, E. (Eds.) . The history of Mathematical Tables. From Summer to Spreadsheets; Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Martí, E.; Garcia-Milà, M.; Teberosky, A. Notational strategies for problem solving in 5 to 7 year olds. Eur. J. Develop. Psychol. 2005, 2, 364–384. [Google Scholar] [CrossRef]
- Morales-Moreno, Y.; Martí, E. Uso de notaciones y teoría de la mente en niños de 3 a 6 años [Use of notations and theory of mind in 3 to 6 year-old children]. Infancia Aprendizaje 2004, 27, 289–305. [Google Scholar] [CrossRef]
- Brizuela, B.M.; Alvarado, M. First graders’ work on additive problems with the use of different notational tools. Revista IRICE 2010, 21, 37–43. [Google Scholar]
- Molina, M.; Castro, E.; Molina, J.L.; Castro, E. Un acercamiento a la investigación de diseño a través de los experimentos de ense- ñanza. Enseñanza Ciencias 2011, 29, 75–88. [Google Scholar] [CrossRef] [Green Version]
- Kelly, A.E.; Lesh, R.A. Research Design in Mathematics and Science Education; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 2000. [Google Scholar]
- Cañadas, M.C.; Castro, E. A proposal of categorisation for analysing inductive reasoning. PNA 2007, 1, 67–78. [Google Scholar] [CrossRef]
- Torres, M.D.; Cañadas, M.C.; Moreno, A. Estructuras y representaciones de alumnos de 2º de primaria en una aproximación funcional del pensamiento algebraico [Second graders’ structures and representations used in a functional approach of algebraic thinking]. In Investigación en Educación Matemática XXIII; Marbán, J.M., Arce, M., Maroto, A., Muñoz-Escolano, J.M., Alsina, Á., Eds.; SEIEM: Valladolid, Spain, 2019; pp. 573–582. [Google Scholar]
- Kozulin, A. Psychological Tools; Harvard University Press: Cambriege, MA, USA, 1998. [Google Scholar]
- Pincheira Hauck, N.G.; Alsina, À. Hacia una caracterización del álgebra temprana a partir del análisis de los currículos contemporáneos de Educación Infantil y Primaria. Educación Matemática 2021, 33, 153–180. [Google Scholar] [CrossRef]





| Context | Function |
|---|---|
| Session 1: Ball machine | y = x + 3 |
| Session 2: Amusement park 1 | y = x + 3 |
| Session 3: Amusement park 2 | y = 2x + 1 |
| Session 4: Birthday | y = 2x |
| Session 5: Introduction to tables | N/A |
| Interview 1: Train stops | y = 2x |
| Interview 2: Superhero ages | y = x + 4 |
| Structures | |||
|---|---|---|---|
| Function | Student | Particular Case | General Case |
| y = 2x | Ángel | y= 2x | NR |
| Lola | y= 2x | NR | |
| Darío | y= 2x | y = 2x | |
| Alba | y= 2x | NR | |
| Structures | |||
|---|---|---|---|
| Function | Student | Particular Case | General Case |
| y = x + 4 | Ángel | y = x + 4 | y = x + 4 |
| Lola | y = x + 4 | y = x + 4 | |
| Darío | y = x + 4 | y = x + 4 | |
| Alba | y = x + 4 y = x + x | NR | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torres, M.D.; Brizuela, B.M.; Cañadas, M.C.; Moreno, A. Introducing Tables to Second-Grade Elementary Students in an Algebraic Thinking Context. Mathematics 2022, 10, 56. https://doi.org/10.3390/math10010056
Torres MD, Brizuela BM, Cañadas MC, Moreno A. Introducing Tables to Second-Grade Elementary Students in an Algebraic Thinking Context. Mathematics. 2022; 10(1):56. https://doi.org/10.3390/math10010056
Chicago/Turabian StyleTorres, María D., Bárbara M. Brizuela, María C. Cañadas, and Antonio Moreno. 2022. "Introducing Tables to Second-Grade Elementary Students in an Algebraic Thinking Context" Mathematics 10, no. 1: 56. https://doi.org/10.3390/math10010056
APA StyleTorres, M. D., Brizuela, B. M., Cañadas, M. C., & Moreno, A. (2022). Introducing Tables to Second-Grade Elementary Students in an Algebraic Thinking Context. Mathematics, 10(1), 56. https://doi.org/10.3390/math10010056






