1. Introduction
Ramanujan [
1] gave a list of infinite series identities of the form
for
where
are singular values that correspond to elliptic curves with complex multiplication, and
are explicit algebraic numbers. Below is an example of one identity from Ramanujan’s list,
Here,
denotes the rising factorial
In fact, the following similar identity was given earlier by Bauer [
2],
Proofs of these formulas were first given by J. Borwein and P. Borwein [
3] and D. Chudnovsky and G. Chudnovsky [
4]. Both approaches rely on the arithmetic of elliptic integrals of the first and second kind, including the Legendre relation at singular values. Finding new formulas for
using various techniques has been an active research area. We refer interested readers to two survey papers, one by Baruah, Berndt, and Chan [
5] and another by Zudilin [
6], as well as a list of conjectures due to Z.-W. Sun [
7]. One of the motivations for studying Ramanujan formulas for
is to efficiently compute the decimal digits of
In 1997, van Hamme discovered several surprising
adic analogues of Ramanujan formulas for
[
8]. For each prime
he conjectured
where
is the Legendre symbol.
The congruence (1.1) was first proved by Mortenson using hypergeometric evaluation identities [
9]. This method is dependent upon the availability of such corresponding identities. Later, Equation (
1.1) was also established by Zudilin using the techniques of Wilf and Zeilberger [
10], which, unfortunately, are not easy to use in general. Motivated by work of Mortenson [
9] as well as by McCarthy and Osburn [
11], the third author proved congruence (1.2) [
12]. Recently, Z.-W. Sun has given a refinement of congruence (1.1) modulo
by adding a factor involving Euler numbers [
13].
It is interesting to note that both Equations (1.1) and (1.2) hold modulo with either or for the limit of summation. However, this is not true modulo for either Equation (1.2) or Sun’s refinement of Equation (1.1).
In this paper, we prove a general result on Ramanujan type congruences modulo
under further assumptions. In
Section 2, we introduce necessary notation and state our main result. Our method relies on the arithmetic and geometry of elliptic curves, which includes Picard–Fuchs equations, formal expansions of the invariant differentials of elliptic curves, the Chowla–Selberg formula for periods of elliptic curves with complex multiplication, as well as Atkin and Swinnerton–Dyer congruences and results due to Katz. In
Section 3, we review a method to prove Ramanujan type formulas for
utilizing Picard–Fuchs equations associated to families of elliptic curves, originating in the work of Chowla and Selberg [
14]. In
Section 4 we discuss arithmetic of certain families of elliptic curves. We conclude in
Section 5 with the proof of our result.
2. Statement of Results
For
r a nonnegative integer and
, the hypergeometric series
is defined by
which converges for
. We write
to denote the truncation of the series after the
term.
For
let
denote the following families of elliptic curves parameterized by
t,
There are in fact many ways to choose such models. Recall that an elliptic curve over a number field is said to have complex multiplication (CM) if its endomorphism ring over is an order of an imaginary quadratic field.
For
t such that
has CM, let
, and write
. We note that
is determined up to a choice of square root, but we will see this does not affect our conclusion. Assume
for any embedding. Then there is a Ramanujan type formula
for some unique algebraic numbers
depending on
d and
. To be more explicit,
a can be computed from a so-called singular value function [
3]. Specific choices of CM values of
as well as the corresponding constants
can be derived from various data given by the Borweins [
3].
Theorem 1. For , let such that is totally real, the elliptic curve has complex multiplication, and for an embedding of to . For each prime p that is unramified in and coprime to the discriminant of such that can be embedded in (and we fix such embeddings), thenwhere is the Legendre symbol, and , equaling 1
if and only if is ordinary modulo p. Remark 1. In fact, Zudilin conjectured the above to be true modulo when .
Remark 2. Our conclusion in Theorem 1 also holds for totally real singular moduli with
. In either case, the values of
a are predicted by the Chowla–Selberg formula [
14]. See work of Guillera and Zudilin for existing “divergent” Ramanujan type supercongruences [
15].
Remark 3. When
, there is an underlying
surface
described by the equation
When
, this manifold is related to the one-parameter family of elliptic curves of the form
via the so-called Shioda–Inose structure [
16]. The arithmetic relation between
and
is obtained by Ahlgren, Ono, and Penniston [
17]. The
invariant of
is
In fact,
is isomorphic to
as above. In the next section, we will use the curve
to demonstrate some basic ingredients.
Moreover, we obtain the following supercongruence. The case for
was proved by Kibelbek, Long, Moss, Sheller and Yuan [
18].
Theorem 2. With notation and assumptions as in Theorem 1,Here when has supersingular reduction at p, and otherwise where is the unit root of the geometric Frobenius at p acting on the first cohomology of the elliptic curve . 5. Proof of Theorems 1 and 2
Results of Atkin, Swinnerton-Dyer and Katz
Atkin and Swinnerton-Dyer [
29] proved the following. Let
be a nonsingular elliptic curve over a totally real field. Let
be any prime such that
can be embedded in
and
E has good reduction modulo
Let
ξ be any local uniformizer of
E at infinity over
that is a formal power series of
with coefficients in
that starts with
. Then the holomorphic differential
has coefficients in
Moreover, for the coefficient
of the differential, the following congruence holds for all
,
where we define
when
n is not a positive integer. Note that the assumption of
E being defined over a totally real field is necessary to conclude that the last coefficient is
p. Otherwise, it is only determined up to a ± sign. Atkin and Swinnerton-Dyer’s result inspired the work of Cartier [
30] and Katz [
31]. Here we shall use Katz’s approach with a slight generalization using the approach outlined by Stienstra and Beukers [
24] so that the base ring is not restricted to
.
Throughout this section, we assume that E is an elliptic curve defined over a number field by a cubic equation in terms of x and y with identity . We further assume that E has CM by an order of an imaginary quadratic field . The endomorphism ring of is denoted by R.
Choose some prime
p such that
can be embedded into
and such that
p is unramified in
. We extend the
adic valuation of
to
so that
and let
. The ring
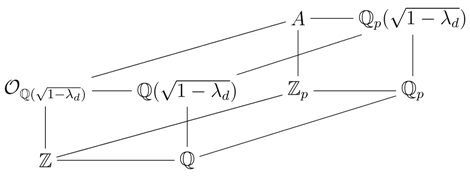
A is a local ring with maximal ideal
. This information can be organized in the following diagram.
Note that
A is the ring of Witt vectors of
. Let
σ be the nontrivial automorphism on
lifted from the Frobenius automorphism
on
. It satisfies the relation
for all
. If
,
σ is simply the identity map on
. Otherwise,
σ is conjugation, mapping
to
. We further assume that
E has a model over
A and has good reduction modulo
. From Katz we know the de Rham cohomology space
is isomorphic to
Further details are given by Katz [
31]. Both eigenfunctions
ω and
ν of the endomorphism ring
R, as discussed earlier, in
can be embedded in
under our assumption. We choose a local uniformizer
ξ of
E over
A near
that is a formal power series of
starting with
. Using expansion at infinity with
ξ to get
, consisting of formal differentials of
E of the form
, where
. By formal integration, these differentials will be represented as
in
. Below, we assume
with coefficients in
A. Under this notation, any degree–
p Frobenius lifting Φ of
from
to
A acts semi-linearly, which sends the class represented by
to the class represented by
Let
be the cohomology group defined from a subcomplex of the de Rham complex of
E with respect to the divided power ideal
. To be more precise,
is isomorphic to
In this space, the class representing
ω is annihilated by
where
. By comparison between étale and crystalline cohomologies,
is related to the local Hasse–Weil zeta function of
E over
K and, consequently,
. It follows that
For simplicity, we assume that
and
are both 1 after normalization.
Proposition 16. With notation and assumptions as above, if under the choice of the local uniformizer there exists a degree p (resp. ) Frobenius lifting Φ
that commutes with the induced action of R on in the ordinary (resp. supersingular case) thenwhere and it is 1 if and only if , i.e.,
p is ordinary. Proof. Recall that
. When
p is ordinary,
i.e.,
, and Φ commutes with
R, then
ω and
ν are eigenfunctions of Φ with eigenvalues
π and
, which are the two roots of
. In particular,
is the unit root in
A and
(See work of Katz [
32] for further details.) From comparing the
pth coefficients of
, we conclude that
Similarly, we have
and thus
Multiplication by
p on both sides gives
.
In the supersingular case,
. We first assume that there is a lifting
of
which stabilizes the
A–submodule of
generated by
ω and
ν. Assume that the matrix of Φ under the basis consisting of
ω and
ν is
. In particular,
. We now determine
M modulo
. Assume that
, then
are nonzero modulo
as well. Otherwise, the determinant cannot be
p. As both
u and
w are units, one can choose a different basis such that the matrix becomes diagonal modulo
With determinant
p, one of the eigenvalues is a unit, contradicting the fact that the trace is 0 modulo
. Thus in fact
and
. In this case,
This implies
w is a unit and
and the desired result follows, namely
In fact, such a lift
exists by adding any
p-torsion of the elliptic curve to
, which allows us to solve
. Here Φ is the degree–
Frobenius lifting that commutes with
R under our assumption. Both
ω and
ν are eigenfunctions of Φ with the same eigenvalue
. The corresponding field extension is ramified. However, using the corresponding maximal ideal, the above argument shows that
lies in the maximal ideal. Hence, our claim follows.
☐
The following lemma is an immediate consequence of the fact that the Euler numbers , for .
Lemma 17. Let . Then for any odd prime p coprime to d,when andwhen Consequently, we have the following truncated version of Clausen’s formula.
Lemma 18. Let , p be an odd prime coprime to d, and . Then Proof. The Clausen formula can be also stated as
Note that both hand sides are polynomials of degree no larger than
. In fact, modulo
, the polynomial on the right has only degree
. It suffices to prove the
kth coefficient on the left hand side is also 0 modulo
when
, which follows from Lemma 17. ☐
We now prove Theorems 1 and 2.
Proof of Theorems 1 and 2. Let
be the local uniformizer of the elliptic curve. As discussed in
Section 3.4, we assume
for some constant
under our assumptions. So
with
and
can be computed accordingly. Note that the leading coefficients of both
ω and
ν are 1.
Let
. Then
, as a function on the elliptic curve, has its zeros and poles supported at the 2-torsion points of the elliptic curve. Consequently, in the ordinary case the multiplication by
π map,
, is a degree-
p rational function of
t, where
π is the non-unit root of
as discussed in Proposition 16. As
π is in the ring of integers of the CM quadratic field that contains the endomorphism ring
R,
π commutes with
R. The formal power series
is the formal logarithm of the formal group arising from the elliptic curve, which is of height 1 when modulo
due to the ordinary assumption. (The unfamiliar reader is encouraged to consult work of Stienstra and Beukers [
24] for a reference on this terminology.) Therefore,
for some
that can be computed explicitly. For further details, consult papers of Kibelbek
et al. [
18] and Coster
et al. [
33]. If we replace
ξ by
, then
, which allows us to apply Proposition 16. As computed by Kibelbek
et al., this change of variable corresponds to the quartic twists for both cases that we discussed in 4.3. Recall that in
Section 4.2, after applying the corresponding quartic twist, we find that the constant term is
p from the oddness conclusion stated as Lemma 15. Similarly, for
, the zeros and poles of
locate at the 3-torsion points of the elliptic curve. From the theory of elliptic functions, one can show that the multiplication by
π map on
t, likewise a degree–
p rational map of
t, after a similar quartic twisting, can be used as the Frobenius map in Proposition 16. For
, it follows from
, the monodromy group for
is an index-6 supergroup of the monodromy group for
, which is
(see Remark 7). In each case, we need to replace
ξ by
to use Proposition 16 and
. In conclusion, we have
for the ordinary case. Now we relate
to our theorems.
We first prove Theorem 2. The case of
was proved by Kibelbek
et al. [
18]; we handle the cases
here. When
p is supersingular, the claim follows from Lemma 18. Let
p be ordinary. Recall that
as in Lemma 12. One can use the same formula to compute
. In particular,
for
. Let
or
. By comparing the
th coefficients of
we have
for some
, where
with
ε a forth root of unity and
. Meanwhile, for both
and
,
are hypergeometric series in
t that terminate before the
pth term. By the formula given in Lemma 12, the previous two lemmas, and the
p-adic analysis given by the third author [
12],
for some
when
. Thus
, which implies
The claim of Theorem 2 follows from Lemma 18. The ordinary case of Theorem 1 also follows.
To conclude the supersingular case for Theorem 1, we note that the multiplication by map on results in a degree– rational map on t, which can be used for Proposition 16 after the same quartic twist as the ordinary case. ☐