“How Real People Really Need Mathematics in the Real World”—Authenticity in Mathematics Education

Abstract

This paper discusses authenticity from the perspective of mathematics education. Often, school mathematics offers students inauthentic word problems, which don’t show the authentic usefulness of mathematics in real life. In some tasks, authentic aspects are combined with inauthentic ones (e.g., an authentic context, but the question is artificial and different from what people within that context would ask). Several studies show that students are more motivated by authentic questions than by authentic contexts. Embedding these findings, I discuss issues associated with defining authenticity in education. A first issue is that philosophers use the term to characterize a person’s existential expressions (e.g., being true to oneself), whereas in education, we use the term for learning environments, artefacts, etc. Second, some researchers define authentic learning environments according to criteria (being open to different approaches, simulate a real-life activity, etc.), but I will illustrate that inauthentic activities can comply with such criteria as well. Alternatively, I suggest using the term for separate aspects in a learning environment (contexts, questions, etc.), and define authenticity as a social construct rather than as a subjective perception. In this way, a community (teachers, students, out-of-school experts) can reach agreement on the nature of this characteristic. For an aspect to be authentic, it needs to have: (1) an out-of-school origin and (2) a certification of originality (e.g., by bringing artifacts physically into a classroom or by testimony of an expert). This approach is illustrated by a study on students’ project work during an excursion to a mathematics research workplace.

1. Introduction—Authenticity as a Noun to Critique Word Problems in Mathematics Education

This paper in the Special Issue on Authentic Learning edited by Jurgen Schulte comes from an outsider. I am a researcher of neither Science Education nor of Higher Education. My research pertains to a theory-heavy discipline, in which learning is traditionally organized in teacher-structured environments: mathematics. For many students, already in lower secondary schools, the relevance of mathematics is not apparent, and the question “why do we have to learn this?” is frequently asked [1]. From the 1980’s onwards, researchers started to analyze shortcomings in mathematics education, and the terms authentic and authenticity entered the research discourse. For example, Kaiser [2] writes on German mathematics classes: “... it is typical for German mathematics teaching that real-world examples discussed in lessons are not authentic real-world problems, but made to illustrate mathematical contents. Therefore, these examples give a quite artificial and far from reality impression” (p. 253).

In this contribution to the Special Issue, I will highlight some of the discussions in mathematics education research, as these may broaden and deepen discussions on authenticity in theory-heavy courses in Science Education.

In mathematics education, the term authenticity plays an important role in critiquing practices, in which mathematics is seemingly related to real life. How can a theory-heavy subject like mathematics be connected to real life? A typical way in which this is done is through word problems. A word problem is a narrative that describes an artificial, pseudo-realistic situation, and ends with a question for a number. Here is an example of such a typical word problem:

Farmer Alfred has three times as many chickens as cows. Altogether, there are 60 legs in the barn. How many cows does farmer Alfred have?

The curricular intention of word problems is to train students in the area of arithmetic and algebra (take x for the number of cows, etc.). Additionally, such word problems are thought to offer variety in activities, to motivate, and to show how mathematical techniques can be applied in contexts. However, these problems have been found to be problematic in many ways. First, word problems disregard common sense, because when it comes to finding the number of cows on a farm, one usually asks the farmer, counts, or guesses rather than using the sum of legs. Second, the imposed algebraic solution approach disregards a variety of non-algebraic solution methods. Without variable x, one can reason that for each cow there are three chicken; so, one cow (4 legs) and three chicken (6 legs) make a group of 10 legs. With a total of 60 legs, there must be six of such 10-leg-groups, thus 6 cows. It remains to be noted, that in all these approaches, we disregard real life by assuming that not one animal misses a leg and that the insects in the barn are ignored.

The epistemological issue at stake is that that all over the world, during approximately ten years in their school careers, students are made to solve many such word problems. Rather than learning that mathematics is about reasoning, creativity, and collaboration, and that mathematics is useful for solving authentic real life problems, this imprinting practice makes students learn that mathematics is for inauthentic situations; that mathematical tasks contain added artificial complexities (sum of legs); that mathematical problems have one, and only one, answer; that the answer in mathematics is always a number and not a range of answers, an estimate or an essay containing a reasoning; and that there is just one algebraic approach to solve the problem [3,4,5,6,7,8]. In fact, word problems are inauthentic and prevent students from experiencing the authentic usefulness of mathematics. Therefore, it is no wonder that many students perceive mathematics as alien, that they don’t understand it, and that they drop it as soon as possible [9,10].

The problem with traditional practices is that they aren’t easily changed, in particular if these have a history that goes back more than two thousand years. In antique times, mathematical word problems were recreational challenges among leisurely adults. The oldest known source describing a mathematical word problem is the Rhind Papyrus (around 1650 BC), in which a puzzle is given of how to divide 700 loaves of bread into 4 sets that have proportion ⅔:½:⅓:¼ [11]. The oldest known collection of mathematical word problems is from Metrodorus (around 500 A.D.) [12]. Also, the first, medieval mathematical textbooks for common people (not written in Latin or Greek) contained artificial word problems [13]. Reasons for including word problems into mathematical textbooks were to make the concepts and algorithms more meaningful and concrete, and to link these to real life, but the didactic approach—which surely had good intentions—developed into a school culture, in which inauthenticity and repetitiveness became mainstream. This approach has detrimental effects on students’ attitudes and beliefs in mathematics, and consequently, on achievements, and to analyze the school culture, researchers of mathematics education used terms such as inauthentic, pseudo-realistic, artificial, constructed, deviating from out-of-school practices, distorting out-of-school practices, and dressed-up mathematical problems. Several questions popped up. The main question was how to improve mathematics education; in particular, how authentic real life problems could be connected to the teaching and learning of mathematics, and what such education would look like. Underlying questions were whether adding authenticity would lead to better performance, and, at a more theoretical level, what the concept of authenticity embraces.

2. Authenticity and Its Complex Relation to Performances and Attitudes in Mathematics

When secondary school students are asked which situations or contexts they are interested in, they mention sports, smart phones, climate, environment, and extra-terrestrial life; boys’ interests are more technical, mechanical, electrical, spectacular, violent, and explosive, whereas girls indicate a stronger interest in health, medicine, beauty, the human body, ethics, aesthetics, wonder, and the paranormal [14,15]. However, when a mathematical task is set in such a context, for example to calculate the diagonal of an authentic table tennis table, students neither perform better than they would on an abstract mathematical task on the diagonal of a rectangle, nor do they indicate interest in such a mathematical table tennis task [16]. An explanation for this apparent contradiction is offered in [17]. In this study, 14-year old students in Albania were interviewed on their motivation for doing mathematical tasks that had either an abstract, or an authentic context. For example, students had to calculate the perimeter of an abstract rectangle, and they also had to calculate the perimeter of a rectangular market place in their home town (the Mother Teresa Piazza in Shkodra), of which authentic measures were given. The students indicated that they disliked the task with the authentic situation, because the perimeter of the market place was something they would never need; the task with the authentic context showed them more clearly the uselessness of mathematics; the authentic context made mathematics worse.

There is also research showing that students can become highly motivated when authentic resources are used in mathematical tasks. I led research in Mozambique, in which we designed geometry lessons starting from authentic hand-made baskets, fish traps, and drums, as well as statistics lessons starting from genuine newspaper articles [18]. We brought the resources physically into the classroom, demonstrating true authenticity, and the students showed a high appreciation for seeing a connection between mathematics and out-of-school life. In this study, we also observed that the authentic artifacts were not educational in themselves. For example, basket users and basket makers would neither pose questions about the surface area in cm², nor would they answer these using mathematical formulas. It is an educational designer who creates such area tasks with educational aims in mind, and in the design process, questions can become inauthentic. Thus, we observed the combination of authentic resources and inauthentic activities.

From the above, we see that, first, authentic contexts do not imply authentic questions (questions that real people within the context would pose). Second, authentic contexts can, but don’t necessarily improve students’ motivation or performance in mathematics education. This means that we need to clarify what makes a question authentic. A question is authentic if it is one that people within the context would ask. In other words, it is a question which relates to an authentic problem for the people in the context. However, when an authentic context is offered to students together with an authentic question, this authenticity may not be obvious to the students. Thus, a task designer has to anticipate on how students can recognize the authenticity of context and question, and whether they will know about the people in the task context.

There is research on making students answer a task in a way which is comparable to how real people in real life carry out a task. This research focuses on the effects of a more authentic answer format. I will summarize two unrelated, but similar experimental studies, in which the effects of the answer format were compared between an experimental and a control group [19,20]. Both were based on the following bus problem:

How many buses are needed for a school excursion with 360 children, while each bus has 48 seats?

This task has a ‘realistic’ (imaginable) context, as many students will be able to picture the situation even if they never organized an excursion themselves. When given to students in grade 6, a large majority answers: 7.5 or 7R24 (7 with remainder 24) [19,20]. These students perceive it as a traditional word problem and respond to the surface cues. They carry out the required calculations without further thinking, because they have been drilled to pick the numbers from the text, perform a calculation, to disregard real-life considerations (wouldn’t the bus company have smaller buses as well?), and neglect the meaning of the answer in light of its context. In its short, one-sentence format, this bus problem lacks authenticity as the text lacks credible details, such as the name of the school, the destination of the excursion, date, time, what bus company, and so forth. Therefore, the following two classroom experiments were enlightening. In the experiment by Palm, the students in the experimental group were asked to fill in an order sheet from an imaginary bus company [20]. So, students had to put their names, addresses, and the number of buses needed. The sheet had to be completed with a signature, implicitly asking students to approve of their own answer. In the second experiment, the students in the experimental group were asked to make a phone call to the bus company with a real telephone in the classroom (the bus company was simulated by an actor in the classroom next door) [19]. In both studies, the students in the experimental condition answered the question by rounding off to 8, realizing that there was an integer needed when ordering buses. The answer format that simulated the ordering of buses in real life assisted the students in being aware of the round number of buses, and significantly outperformed the students in the control group. It remains to be noted that in the two studies, the task context was inauthentic—there was neither an authentic school excursion happening nor did the bus company authentically exist. However, the activity (filling in an order form, or phoning a fictitious bus company) was authentic, as it was the same as people in the context would have to do.

Thus, we see that authenticity can pertain to different aspects in a task. Above, we saw that a context can be inauthentic, whereas the task question can be authentic. Second, the authenticity of the question (a question asked by people in the context) and the authenticity of the answer format (the way students will answer) may be more important to students’ performance and motivation than the authenticity of the context. Third, we saw that tasks can simulate real-life activities, whereby students copy these activities as if in a role play. I will turn to a discussion of simulations (e.g., flight simulators) and how these are (in-)authentic in the next paragraph, but first, I turn to the question: what can count as authentic in mathematics education?

3. Issues in Defining Authenticity in Education

A first issue that blurs the definition of authenticity in education is that philosophers (e.g., Martin Heidegger, Søren Kierkegaard) and psychologists (e.g., Donald Winnicott, Susie Orbach) have used the term to characterize a person’s existential feelings or expressions. They describe a person to be authentic when he/she is true to him/herself, as opposed to being superficial, fake, or following others. In this perspective, being authentic means having one’s own norms, and going against conventions. Used in this way, authenticity is a subjective perception of an individual who judges the appearances, expressions, or work of others. Such a subjective judgement is a personal interpretation, to which some can agree and others can disagree. Using the term authenticity in this way may be valuable in the teaching and learning of Arts and Humanities, but this definition is unsuitable when we want to characterize learning environments, artefacts, tasks, questions, and so forth. In those cases, we want a community of various people (students, teachers, researchers, out-of-school stakeholders) to agree that something is authentic or not. Thus, we need to define authenticity as a social construct.

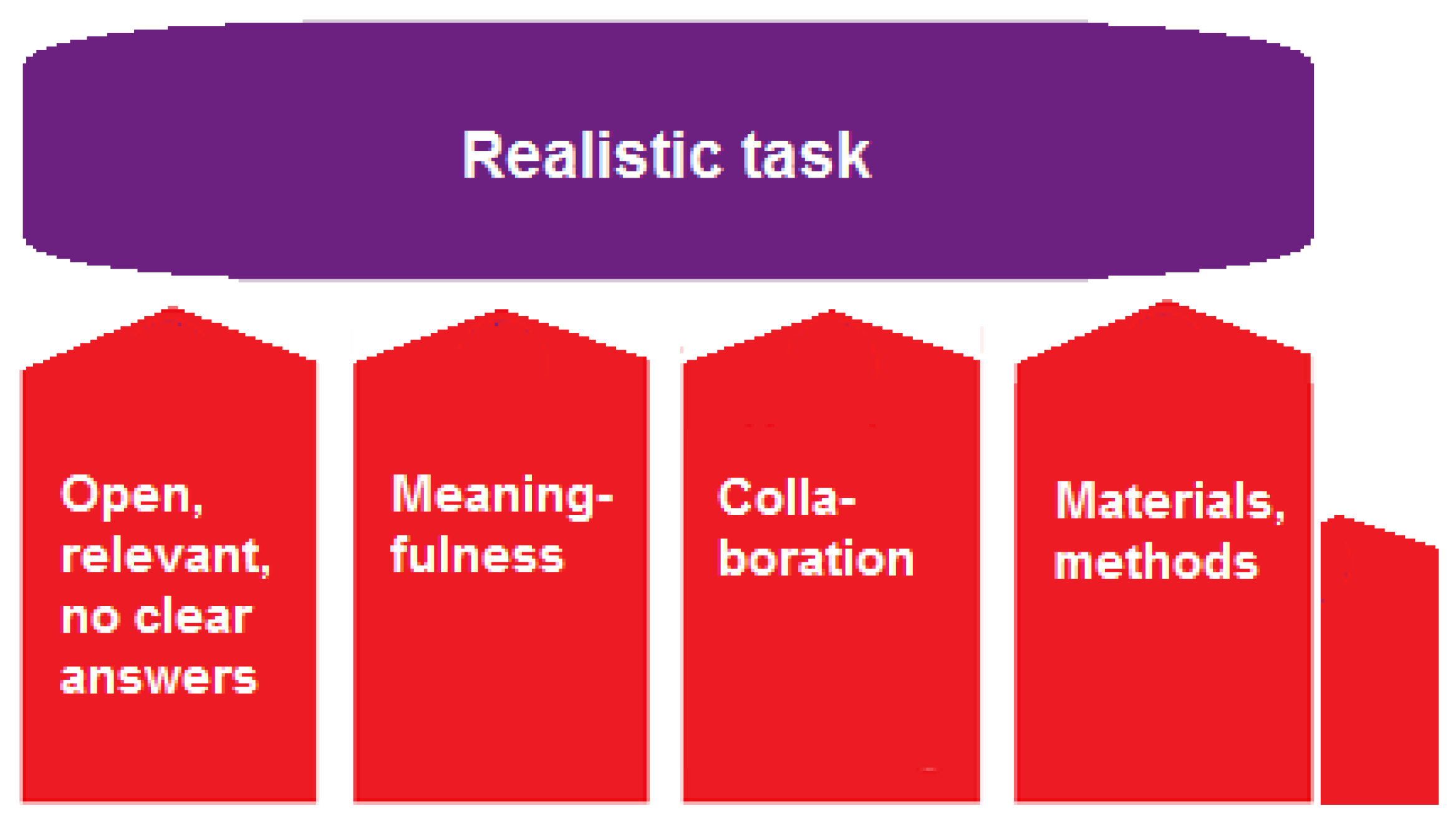
In an attempt to define authenticity for mathematics learning environments, a number of researchers decided to start from lists of components that together define an authentic activity, an authentic task, or authentic learning. For example, Heck [21] referred to authentic student research projects if: (1) students work on self-selected, challenging, messy, ill-defined, open-ended problems rooted in a real life situation; (2) students do not follow some standard recipes, but examine their problem from different perspectives, using a variety of resources and high-order skills; (3) a broad range of competencies is required to make the project a success, and one of these abilities is making use of ICT for information gathering, data processing, and reporting; (4) students’ work is open-ended in the sense that there are multiple methods to obtain possible or even competing answers; (5) it offers students the opportunity to be in contact with contemporary, cross-disciplinary research, and to learn about the nature of mathematics and science; (6) students disclose their own understanding through a portfolio, a report, or a presentation.

Palm [22] made a different list and defined authenticity in tasks according to the aspects of the event (might the event occur in real life?), the question (might the question be posed in that event?), the purpose, the information/data (are the data corresponding to real life data?), the presentation of the task, the solution strategies, the circumstances of the students’ activity, and the solution requirements.

So, these and other researchers make lists, from which they define authenticity. However, it is possible that a constructed, inauthentic task can comply with the criteria. Being “rooted in real life” as Heck notes, or “data that correspond to real data” as Palm proposes, gives room to a task designer to de-authenticate certain aspects. A designer does this for good reasons, for example, to make the task more comprehensible, better fitting a limited time frame, better fitting students’ levels, or physically feasible within the school environment. In Heck’s research, students remained within the school environment and mathematically modeled the bungee jump from the school stairways by a Barbie-doll. This was an exciting task, which fulfilled the list of criteria, but it wasn’t an authentic bungee jump with all the risks involved. If it had been, a miscalculation would lead to someone smashing his head on the floor. Also, in Palm’s research on the bus problem for which the students filled in the order form to a fictitious bus company, it is hard to see this as an authentic task, as there are neither real buses nor any real students going on a day-out. Such tasks can be indicated as realistic, in the sense that students can realize that a similar and more serious activity is done in real life. One can say that these tasks simulate (copy) real life, and thus, these are pseudo-authentic. Figure 1 illustrates how researchers start from a list of certain characteristics to define a class of tasks. The foundation and pillars differ between researchers, and also, these can be adapted and refined according to a task designer’s preference.

Realistic tasks can be very effective and motivating. The principles on which they are designed ensure openness in the tasks, and give room to students’ creativity, collaboration, inquiry, and so forth. However, for defining authentic tasks, or authentic learning environments, these definitions are built on the assumption that authenticity is a term that can be applied holistically to a complete task (or to a complete learning environment). Yet, as we saw in the previous paragraph, a task can have some aspects that are authentic and others that are inauthentic. When using holistic terminology such as ‘authentic student projects’, ‘authentic enquiry’, or ‘authentic assessment’, the question then is: how much correspondence with reality is sufficient to qualify for authenticity? 80%? Three out of five criteria? Or in other words: what essential aspects can, and what cannot be cut out for the sake of education? Could there exist some half-baked authenticity?

There is another issue in defining complete tasks holistically as authentic. To hammer the point home, I will use an example from vocational education and not from mathematics education. In the training of airplane pilots, flight simulators are crucial tools. Externally, these are containers standing on poles that enable the simulator to shake. Inside the container is a copied cockpit with seats, steering rudders, engine throttles, and many instrument panels, keyboards, displays and signals, radio and navigation equipment, and so forth. Such details make the simulator resemble an original cockpit, but it remains a simulator, that is: it is not the real thing, but a copy. When a candidate sits there, he/she sees through the windows a number of panels on which a realistic horizon is projected. To ‘add authenticity’, a candidate is requested to dress in full pilot gear. According to some authors (e.g., [23]), a flight simulator is an ‘authentic learning environment’ because it simulates a real plane with sufficient accuracy. Nevertheless, flight simulators do not fly and there is not one account of a fatal accident with flight simulators. What flight simulators clearly distinguish from real planes is that a candidate has no responsibility over lives or material. Thus, in such a learning environment, an essential aspect has been cut out for educational purposes: the responsibility over material and lives. If the environment were authentic, this professional responsibility would be an integral part of the task. However, for educational purposes, we prefer to offer students some de-authentication to ensure that students have safe, yet resourceful environments to learn in [24].

The same holds for authentic mathematical tasks. For example, mathematicians in the car industry have the task of calculating the amount of paint needed for the cars that are produced in a factory. This is an authentic task in the car industry. This industrial task was used to design a mathematics task for grade 10 students, the Porsche Task [25]. The task asked students to calculate the amount of paint needed for an authentic Porsche 911.

Students were given the authentic measures of that car, see Figure 2. After the students had found their way to an answer, it turned out that their calculation method by segmenting the car’s surface into triangles was authentic as well. The teacher checked with the mathematicians in the factory, who confirmed that they also partitioned into triangles. However, there was quite a difference between the authentic task of the mathematicians in the industry and the task for the students: the students had absolutely no urge for correctness of the calculation, but for getting praise from their teacher. The students weren’t in an internship in the factory and they weren’t responsible for a correct answer. If an industrial mathematician makes an error, this can have repercussions in the factory (incorrect stock) or with the consumers (rusting cars). So, in education, we don’t offer fully-authentic tasks, because we want to allow students to commit errors. In removing this responsibility from the original task, we remove authenticity., and the task is no longer holistically authentic.

So, we see several issues. A first issue is that we cannot use the term in the psychological and philosophical tradition to subjectively characterize a person being true to him/herself, as we need a term to characterize learning environments, artefacts, etc. Second, lists of criteria to define authenticity can yield realistic, pseudo-authentic, or even inauthentic tasks. And third, in educational settings, task designers want to allow students to make errors, they remove responsibility, and thereby de-authenticate a task. The question then remains: aren’t we throwing away the baby with the bathwater, when authenticity seemingly cannot exist in learning environments? Aren’t there some ways to use the terms “authenticity” and “authentic“ constructively for tasks?

4. Defining Authenticity as a Social Construct

According to dictionaries (e.g., Webster’s Online Dictionary), authentic means genuine, known to be true, being of undisputed origin. Often, the term is illustrated with the archaeological example of found artifacts by amateurs. These are considered authentic when they truthfully originate from human activities in the past. In the discipline of archeology (but also in law courts, in historical research, etc.), the term authentic is used to make a contrast to being a copy, such as imitations and forgeries. Also, authenticity is a binary qualification: an artifact is either authentic or not; one cannot say that an artifact is ‘more authentic than another’. However, it is possible that an artifact’s authenticity ‘cannot (yet) be established’, but this doubt does not render the artifact ‘slightly authentic’. To establish authenticity and to agree over this across a community, there is a need for trust and truthfulness in the judgement. Therefore, some kind of certification is needed, for example an acknowledged expert can label an artifact as authentic or not. If a layman finds an antique object in his/her backyard, she/he will not be considered sufficiently competent to establish authenticity, and one will need an expert to do so.

Thus, we see that in archeology, authenticity is constructed through a ritual to establish truthfully authenticity. Through this ritual, authenticity becomes a social construct in order for a community to agree on the label of being authentic, and making this judgement independent of an individual’s subjective perception. This means that authenticity becomes objective, although—of course—the expert can make errors and be overruled by another expert. Being authentic is a property of an artifact; to establish this property, certain evidence that is acceptable to the wider community (students, teachers, parents, etc.) needs to be given. The certification in the Porsche Task consisted of the original fact sheet from the factory (see Figure 2), and the original brand and type of the car were retained. The certification of the authentic artifacts in the Mozambique study, see above, consisted of bringing the artefacts physically into the classroom. The certification of the authentic rectangular Mother Teresa Piazza in Shkodra (Albania) was through the use of the original name in the familiar environment of the students. On some occasions, certification isn’t given. It is possible that a task designer has to change the name of an original brand to avoid copyright issues. Also, an artefact used in a classroom task can be authentic, yet students are unaware of this. In such cases, a teacher can be the expert who provides evidence of authenticity, but evidence can also be provided by videos, photos, or other additional information.

Using the term authenticity as a social construct, that is, in alignment with the archeology definition, implies that we can no longer use it for complete tasks, because the educational setting will require adaptations or de-authentications, in the same way as with the flight simulator. A flight-simulator is not an authentic airplane (but an effective learning environment); the horizon seen inside is not authentic (but realistic). Still, a flight simulator can contain authentic instruments that originate from a real plane, candidates wear authentic pilot’s uniforms, and a flight simulator can use authentic software, which is exactly the one used in reality. Also, the training activities can be authentic, being exactly identical to activities in reality. Applying this view on authenticity in mathematics education, a task can ask students to work with authentic data, with authentic software (the original software that mathematical researchers use), and so forth. Some aspects in a task or learning environment can be authentic while others aren’t. In many cases, if a task designer includes authentic aspects into a task, this will lead the task to be more open, have room for students’ creativity, collaboration, inquiry, and so forth. See Figure 3 for an illustration.

Considering authenticity as a social construct, for an aspect in education to be considered as authentic it requires:

• an out-of-school origin;
• a certification of provenance.

The out-of-school origin ensures that the artifact originally didn’t have an educational purpose. The certification can be given physically, or through media (photo, video, newspaper reports, etc.). Certification can also be given by a professional working in the workplace, from which the artifact originates, by stakeholders (e.g., villagers explaining environmental problems). Also, it is possible that a student in the classroom has the out-of-school expertise to testify to the authenticity of an aspect in a task [26].

5. Some Examples of Authenticity in Mathematics Education

In a theory-heavy discipline such as mathematics, there are many ways to innovate instruction by including authentic aspects, some of which comply more with traditional classroom practices than others. The word problems with artificial contexts and strange complexities (number of legs in a barn) can well be replaced by tasks with authentic contexts (the rectangular Mother Teresa Piazza in Shkodra, Albania), but if such a context is used to ask questions unrelated to the problems of people in that context, the authenticity is like a wolf in sheep’s clothing. It preserves conservative learning environments.

An important move towards reforming mathematics education and including authentic aspects into tasks was the idea that there are many problems in real life in which mathematics is needed. Such problems are known as mathematical modelling problems [27]. From the 1970’s onwards, modelling activities entered tertiary mathematics education, a movement that started in engineering studies [27,28,29]. From the 1990’s onwards, they entered primary and secondary mathematics education [30,31]. Modelling problems start from a realistic, and not necessarily authentic, situation, but a distinction point is that they contain a question that people in such a context authentically can face. Examples are choice problems (e.g., buying an electric or a fossil fuel car), optimization problems (e.g., lowest CO₂ emission), and prediction problems (e.g., determining bottle necks in traffic intensity). These problems can be workplace problems, consumer problems, environmental problems, scientific research problems, and so forth. A special category of such modelling problems are Fermi problems, also known as back-of-the envelope-problems, which are magnitude problems (e.g., estimating the height of a building, or the number of people in a concert hall) that require calculations based on intelligent assumptions and estimations. Research has established that when comparing between students who learn mathematics under the traditional approach and students who learn mathematics through a modelling approach, there is no significant difference in achievement on traditional tasks, but the latter group outperforms the first when it comes to using their mathematical knowledge flexibly in new situations [32,33,34].

More recently, modelling projects entered mathematics education, whereby students work for more than a few hours on a large, often authentic problem. At universities, we see how undergraduates can successfully engage in authentic modelling research to experience what authentic research entails [35]. Also at lower levels, we see modelling projects. For example, in a Danish primary school, the students worked on a project task called “your mathematical mornings” for hours on to find out, for example, how long the line of toothpaste would be if one completely squeezed an authentic, new tube [36]. And at a Norwegian primary school, a mathematics teacher gave her grade 6 students on Monday morning a problem to design a parc in their home city to accommodate fruit trees, play grounds, and parking places. A city planner visited the classroom to explain that this is authentic work done by city planners (a certification of authenticity). The students worked for a full week, and on Friday, the students held a “mathematics conference” to present their findings [37].

From my own research, I will present here details from a project carried out with senior secondary school students [38], and below I will include interview data not published before. The project is organized at a university in The Netherlands. There, the department of mathematics offers school excursions for a full day (10:00–15:00 h) to give secondary school students a sense of how mathematics is authentically used to solve society’s problems. The project centered on research done by members of the research group Discrete Mathematics and Optimization to assist the National Dutch Railway Company in creating a more efficient time table. The researchers used Graph Theory to model the railway network in order to identify bottlenecks. By making students travel to the campus, they encountered authentic professors, researchers, and university students in authentic university halls and laboratories. Clearly, the secondary school students were not taken to a theatre, in which a play was performed by actors.

After a short welcome, the problem of the railway company was presented through a live video connection with the Railway Control Room by a railway manager. He explained the urge of the railway company to collaborate with research mathematicians. So, the professional certified the origins of the timetable problem. Thereafter, the students’ task was to create a railway timetable for the province of North Holland, a region close to Amsterdam. So, rather than have a guided tour and lectures, the students were made to solve the problem themselves! The students were introduced to the authentic mathematical symbols and techniques that the researchers used. In this excursion, a few aspects were de-authenticated. First, the students used software that was specially designed for the excursion, but it was explained to the secondary school students that the mathematicians had to create their own software as part of the research on the bottlenecks. Also, the task given to the students, which was to find a timetable for the province of North Holland, was inauthentic, because it was a reduced problem for pedagogical reasons, and the students merely simulated the researchers’ work. The original work was far more complex and could not be covered in the time span of the excursion. Also, students did not need to report back solutions to the railway company in such a way that their solution would be implemented. If they made errors, it did not have consequences for the company or for the passengers. However, we discovered an unexpected authentic aspect: the ‘researcher’s frustration’, that is: students worked for a long time on the problem without finding a reasonable solution, and they discovered that the problem was far more complex than anticipated. The authenticity of this experience was certified by the university researcher who accounted for his own frustrations and his need for perseverance while doing research.

After the excursion, short interview were administered with two randomly-selected students and the teacher. Not wanting to impose the term “authenticity”, I asked them to point out the difference between normal mathematics lessons and this excursion. Here are excerpts of their answers:

Student H:

For me the most important difference between normal lessons at school and this with the railways is that in school you work from a book and do exercises, whereas here you get kind of … an applied introduction and I like this better because you see how mathematics is used. And you really do something with it and we, ourselves … are dealing with it. At school, you don’t get to see what you can do with mathematics in the [makes gesture of quotation marks] “real” world.

Student A:

For me the difference between normal mathematics at school and here at the university is here you work so much longer on a topic and for hours on... and so you can dig deeper and also go broader. What I like is that you get to see how mathematics is applied... like this with the railways. They [the railway company] really need mathematics to plan things. In normal lessons at school you don’t get the picture on what you can use it for.

Teacher:

This offers something extra to normal education. Here you have the videoconferencing, something we can never organize at school. Also, these are topics that appeal to the students, in particular to those who take Advanced Mathematics. And they get connected to the university. (...) Also, what is nice about this day, is that you work for a full day on a complex problem. And that it is a problem with which real people work, and on which people really need to think about.

In these interview excerpts, we see that all interviewees use the term real (really do something with mathematics, mathematics in the real world, they really need mathematics to plan things, a problem with which real people work, a problem on which people really need to think about), without being prompted to do so. They could choose their words freely. From what they say, it is clear that for the respondents, the term real refers to people, artifacts, and problems that exist in out-of-school, real life. This can be interpreted as the interviewees referring to authenticity. It can also be noted that they referred to separate aspects, and not holistically to the excursion.

The above example, but also other project tasks within mathematical modelling education, from primary to undergraduate level, illustrate that a theory-heavy subject like mathematics can be well connected to real-life problems, and that classroom activities can include many different authentic aspects. There is still much research needed, both in the design, implementation and effects regarding performance and motivation, but there are good reasons to believe that mathematical modelling tasks do a better job than the inauthentic word problems that have dominated mathematics education for many centuries.

6. Discussion, Conclusions, Recommendations

In this contribution to the Special Issue on Authentic Learning, I gave an outsider’s perspective coming from a theory-heavy discipline, mathematics. For centuries, the teaching in this discipline has had a tradition of connecting to real-life through utterly inauthentic word problems. Based on progressive intervention studies, in which mathematical modelling is an integral part of mathematics education, I make a case for not defining authentic learning holistically, but rather, for judging separate aspects in education for their authenticity, whether these be contexts, questions, activities, artifacts, or anything else. I used the term ‘aspect’ because other terms (element, part) have more dualistic connotations. ‘Aspects’ can have any grain-size, and can overlap mutually.

Important authentic aspects that contribute to better connecting a theory-heavy discipline to real life are the question and the activities generated by the question. If a question addresses a problem that people really have in a certain context, this motivates students to work. However, if students aren’t informed about the importance of the question or the activity to certain people, the task can remain meaningless. To inform them about the authenticity was termed ‘certification’ in this paper. It was observed that mathematical tasks can contain many different authentic aspects: authentic symbols (the original ones used by Newton, or by researchers at a university), authentic research experiences (working for a long time and not finding an answer), authentic objects (original newspaper articles, information sheets from factories), and authentic applicability of mathematics to authentic problems (graph theory and it’s applicability to the railway company’s timetable problem).

The many different authentic aspects cannot be added together to make a task, as a whole, authentic. In this paper, I explained that responsibility is an important aspect of the tasks in work places, whereas in educational settings, we want students to be able to make errors without major consequences. Therefore, task designers reduce authentic aspects into inauthentic ones: activities from the real world are downsized or simplified to match the educational setting, which is framed by time constraints, cognitive constraints, organizational constraints, and so forth. This reduction serves educational purposes, which are to offer students experiences and give them a ‘feel’ of what real professionals do with real mathematics in the real world. Not everything can or needs to be authentic in education. If all aspects of a learning environment were authentic, the students would take up the full task of a professional. This would mean that mathematical errors would have serious consequences, such as railway accidents or profit loss for an industrial company.

Often, tasks with many authentic aspects will be strongly related to the work of professionals. This may be related to an educational vision on the preparation of students for the work force. However, students are also to become critical consumers, or citizens worried about plastic pollution or CO₂ emissions. It is important for task designers to keep a broad focus on the broad interest of the variety of students.

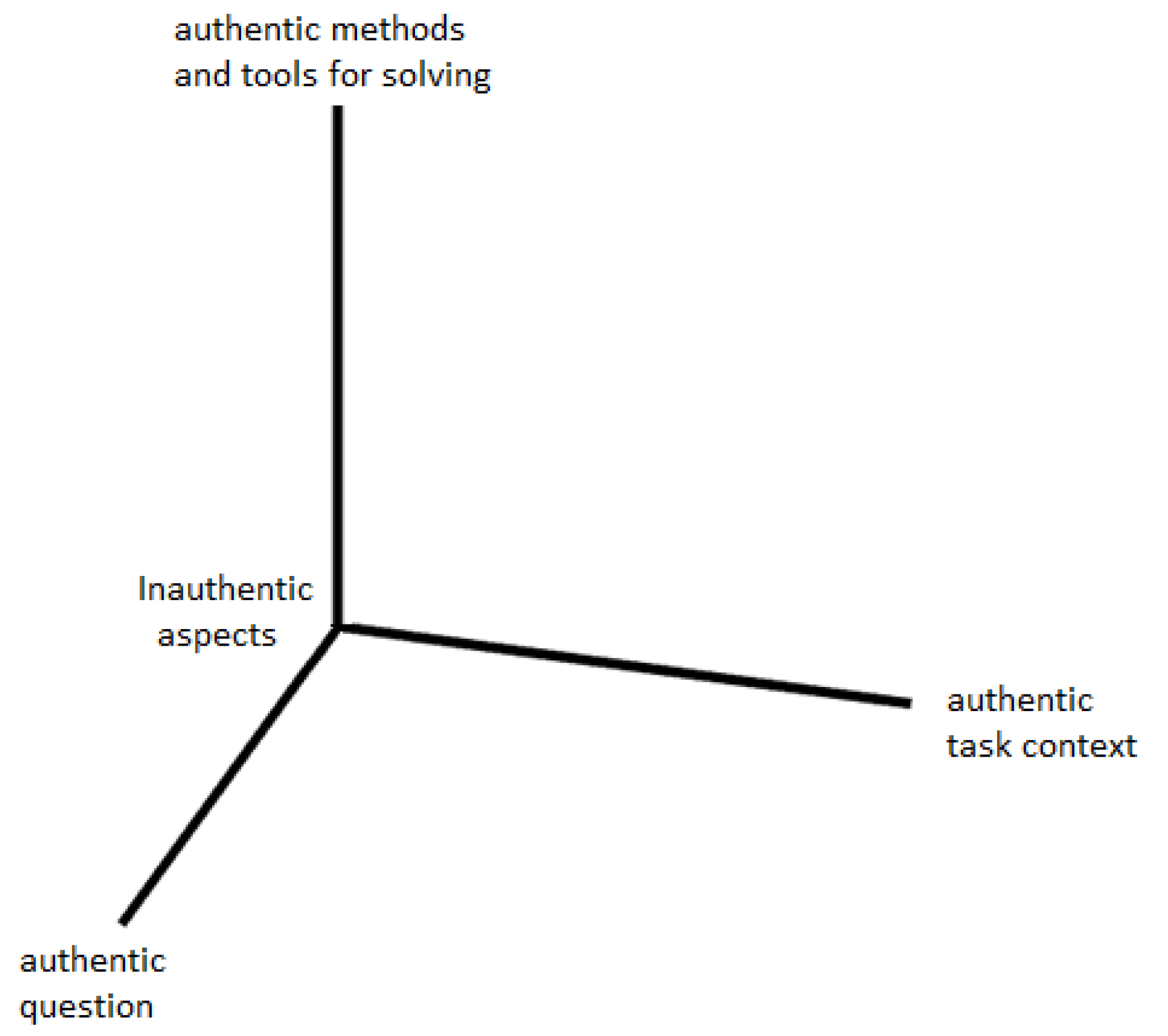
In this paper, I have given reasons to take authenticity as a social construct, which aligns with the meaning of authenticity in other domains (archeology, law, history). Taken this way, authenticity is independent of subjective perceptions and does not apply to how an individual expresses him/herself. The social construction happens by verifying an out-of-school origin and whether this origin can be certified. Often the certification will consist of testimony by an expert, such as the video conferencing with the Railway Company’s control room. In educational settings, it can occur that the authenticity is not made explicit to students. Teachers and task designers may not always be aware of the importance of the certification. It serves to show students that the learning activities are strongly related to out-of-school life. I consider this certification of authentic aspects an important point in the design of learning environments. One can choose to take a set of aspects (e.g., task context, question and solution methods & tools) and categorize tasks according to the authenticity of these aspects, see Figure 4. This can be a tool for the analysis of tasks in future research. However, it remains to be noted that there are probably many aspects that can be authentic, and thus, the three dimensions depicted in the figure do not cover the many different authentic aspects that could be part of a task. For example, in the study on the Railway Timetable Project (see Supplementary Materials), we discovered the authentic researcher’s frustration which the students experienced after having worked intensely for a long time on the problem without finding a reasonable solution. Researchers of authenticity in education may only find news types of authentic aspects if they keep their options open.