1. What Are “Myths”?
Though learning mathematics is a global occupation of children, the myths that surround that learning vary among different cultures and countries. Even in one country, numerous myths impact teaching and learning. In a discussion of myths about the “achievement gap”—a topic often discussed in the United States—Singham describes a myth as “a belief whose truth or reality is accepted uncritically” [
1] (p. 586). Such beliefs may be entirely invisible to the holder because they are embedded in the culture, and they can be expected to differ by culture (see, e.g., [
2]). In the United States, for example, mathematical achievement is often attributed to “aptitude,” the (fixed) ability to achieve. US culture tacitly accepts that some children “have” mathematical minds and some do not; effort can grow either group, but their upper limits are fixed. Not all cultures believe that (see, e.g., [
3]). Yet despite research (e.g., Dweck [
4,
5]) that convincingly disputes this “fixed mindset,” and even despite teachers’ increasing awareness and discussion of this research, the belief that talent must be found and nourished but cannot be made is resilient in the United States.
Another assumption that appears commonly in mathematics education literature (at least in the US) is that real-world applications make mathematics more meaningful to children. This is “accepted uncritically” in at least the sense that (as far as the authors have been able to find) no research scientifically shows that it is true. Nor, for that matter, is “real world” well defined; the real worlds of children and adults are not likely the same. The real world of a child may be more about imagination and personal challenge, about puzzling out the world and about intellectual and social play than it is about how much carpet Felicia needs for her bedroom.
This article is a conceptual piece. It describes classroom phenomena that expose two myths in mathematics education—ideas that are taken almost for granted in the US—in a way that we have not seen discussed in the literature, even though the myths themselves
are recognized. One myth deals with the order in which mathematical topics must be learned; the other is about the perception of topics as units—a collection of information, ideas, techniques, and skills to be learned together more or less at one time (as in one single lesson or one three-week unit or one course). We hope the ideas will also encourage research that might lead to the kind of transformational thinking Kuhn [
6] described as a “paradigm shift,” altering our myths and allowing us to more effectively teach mathematics.
2. Introduction
It is reasonable to expect that certain mathematical facts and ideas must be mastered before others can sensibly be approached. After all, it is hard to multiply if you cannot add, a broad understanding of fractions would seem to require at least some proficiency with operations (especially multiplicative) on whole numbers, fractions are seen as foundational for success in algebra (e.g., [
7]), and so on.
No serious mathematics educators (that we know of) believe that such a sequencing of ideas is strictly linear like a railroad track. But time is linear, so curriculum developers, standards-writers, teacher educators, and teachers need guidance suggesting a reasonable order in which to sequence lessons and materials. Research using inference from the logical structure of mathematics and empirical study of student learning has generated such trajectories (e.g., [
8,
9,
10,
11]).
By “inference from the logical structure of mathematics,” we mean, for example, that learning and applying the distributive property of multiplication over addition would seem necessarily to come after learning to add and multiply. Such an assumption would hardly seem to need empirical study, but that logical inference, we will argue later, is actually not correct. Similarly, because empirical studies of student learning inevitably exist in a cultural and methodological context, so do the research results; one could, for example, expect studies of children’s acquisition of algebraic ideas and skills to suggest different learning trajectories in Russia and the United States because of differences in children’s early school experiences and even differences in cultural expectations.
The most nuanced, and perhaps the most helpful, trajectories are more like networks than railroads (see, e.g., [
8]) but, in implementation, linearization still happens (because time and page order are linear), and some kind of sequence ultimately gets imposed on learning. Traditions build up and familiar sequences get canonized, leading to a more rigid image of sequential order than originally intended. The result is what Aungst calls “a false assumption: that mathematics is a fixed, linear sequence of skills that must be acquired … building block by building block” [
12] (pg xvii). So the myth has an explainable origin; moreover, it is clear that the myth was identified long before us. What we present here is a less-discussed kind of classroom evidence that shows how far out of the reasonably expected sequence some mathematical ideas naturally develop. This kind of data might change how teachers view the ways children can learn. It might also alert researchers to patterns in learning that are, at least in part, artifacts of how students are already being taught, rather than facts about cognitive development or a necessary (or even optimal) order for learning. Without care, claims about optimal order explain (perhaps thereby institutionalizing) what exists rather than revealing new possibilities. Xenofontos [
2], in a different context, refers to such institutionalizing as “unconsciously [contributing] to the preservation and reproduction of […] existing beliefs.”
What can and cannot be learned at particular ages and stages is always measured in some context—perhaps a laboratory setting with a particular methodology, or perhaps by observing what children do typically know at particular ages, in which the context is the natural experiment of typical instructional techniques and sequences—so understanding the data requires sorting out the influence of the context. Contexts are complicated. A measurement that is intended to indicate what a student can understand at a particular point in time can be an artifact of the form in which prior learning took place or of the way current understanding is assessed, and thus may not be a reliable measure of built-in cognitive necessity. This recognition—that our picture of children’s cognition can be an artifact of how it is studied—is not new. For example, in 1982, Margaret Donaldson [
13] showed that a large part of what is still taken for granted as young children’s lack of conservation of number can be attributed to their interpretation of language in context: slight changes in the way questions are posed show that little ones conserve better than is often reported! The fact that her work is not new is evidence of how resilient myths can be.
Even identical tasks presented in identical ways can be experienced differently, leading to different results, depending on events that took place beforehand. See, for example, the welter of research on priming, and Brown and Day [
14] on stereotype threat. In fact, just priming a teacher to expect certain children to “bloom” can affect their performance [
15].
Poor performance on items that teachers (or curriculum designers) think are prerequisite can lead them to slow down or delay instruction, reducing what students get to see and learn, some of which might well support the missing “prerequisites.” For example, when people believe fraction proficiency is not just useful for but prerequisite to the learning of algebra, they are less likely to envision ways that algebraic ideas might be used to build fraction proficiency. Yet, at least two current curricula, one at elementary [
16,
17] and one at middle- or high-school [
18,
19], do just that. In a similar way, the authors (and, we suspect, the readers, too) regularly watch kids prescreened in whole number calculation and, on the basis of speed alone, sorted into groups that determine what the students are even exposed to. In truth, calculation proficiency may, by itself, be causative, not just predictive, of future achievement in mathematics—in other words, a genuine prerequisite. Alternatively, the link to future achievement might be the changed expectations and pace of teaching that follow students’ poor performance on skills that are not actually prerequisite, but are thought to be. This is why serious researchers rarely claim that proficiency at A must be achieved before attempting B. But simplified (or out-of-date) residues of research do give that impression, narrowing what teachers, administrators, and students expect is doable, narrowing what curriculum designers create, and consequently limiting students’ progress in, or even exposure to, mathematics. For the purposes of this article, we will refer to this as the “Myth of Priority.”
A second myth, distinct but related, is that topics are unitary things. Again, this is grounded in a reasonable and useful place. It’s useful to have names for mathematical sub-disciplines, and terms for distinct mathematical ideas, processes, and objects. It makes sense to carve the massive scope of mathematics into huge segments like arithmetic, algebra, analysis, or topology and then, within those, to smaller chunks (topics, ideas, operations, etc.) like addition, multiplication, and fractions. Teachers and other mathematics educators recognize that understanding of mathematical ideas and proficiency in using them evolve over time—even educated and mathematically thoughtful adults can gain new insights into basic ideas and procedures—so having a topic named “fractions” or “algebra” should not fool anyone into thinking that all of it can or should be learned at one time.
But having a name for a topic does invite a kind of myth of unity that is evidenced in questions like “When should algebra be taught?” Despite awareness of the many algebras that follow Algebra 1, and despite discussions of early algebra, the question “when should algebra be taught” reflects an underlying image not of the various bits and pieces commonly aggregated under the title “algebra,” but of a unitary subject, Algebra-The-Course, that is commonly taught in ninth grade, or perhaps eighth, or perhaps started in seventh and spread over two years. (There are alternatives to this unitary view. There are even a few curricula built on the premise that the logic and even language of algebra can begin in first grade and build systematically, with a respectable amount of “Algebra 1” content learned well by grade 5. See, e.g., [
16,
20] and consider also the extent and variety of work on early algebra, e.g., [
21,
22,
23].) This casual image of a unitary algebra is in conflict with what we all know, but it is powerful, giving a sense that the topic has a distinct beginning and a scope and an end.
Researchers and teachers know differently—division and fractions-the-subject may evolve through a variety of ideas beginning with young children sharing a favorite cookie—but it’s easy to slip into questions like “When are students ready for x?” and think of x not as a micro-step, but a whole topic like fractions or algebra. For the purposes of this article, we will refer to this as the “Myth of Unity.” In fact, the “When are students ready …” question reflects both myths—unity and priority.
3. Myth of Priority: Evidence from the Classroom
Most babies crawl before they walk and walk before they run. But that is a statistical statement, not a developmental necessity.
Common wisdom tells teachers to introduce arithmetic first and algebra later. Reality is not so simple. Some algebraic ideas—for instance, those about the properties of binary operations apart from the numbers these operations may combine—develop naturally before children learn arithmetic. In fact, they must develop before arithmetic can make sense [
24] (p. 549).
Fraction errors like 1/4 + 2/4 = 3/8 are commonly cited and studied because they are so commonly seen in classrooms. This error is also a good example of what we would call an artifact of presentation. The first author asked a similar question of a kindergartener, “What’s five eighths plus five eighths?” and got a happily chirped response “Ten ayfs!” then a pause, and “What’s an ayf?” Third graders, who have heard of eighths, can also respond correctly to the verbal question as long as they are not seduced by the written form, which pulls for a very different behavior, more like “add everything in sight.” In a similar way, little children will hear two-hundred plus three-hundred and know that they make five-hundred but may not know what to do with the written versions.
Second graders who know that half of eight is four will spontaneously say, with no coaching or instruction, that half of eighty is forty. It just sounds right. The activity is entirely verbal. The teacher speaks a strategically chosen number—four, forty, eighty, six, two-hundred, sixty, eight, four, forty, eight, forty (a single even digit times 1, 10, or 100)—and children halve it. To keep kids’ cognitive focus on the patterns they hear, the teacher deliberately avoids distracting extra verbiage: no explaining, not even saying “now give half of,” just saying the number. The kids are enacting a function.
After a bit of play—frankly just drill, but in short, lively, playful bursts, a minute or two per day for a few days—to let the children feel fluent, seven-year-olds love trying half of eight-hundred-six, and even those who have done nothing like this before pretty readily say four-hundred-three, although the effort (cognitive load; see, e.g., [
25]) of holding 806, 800, 6, 400, and 3 in working memory and picking out the two to say out loud can lead to slips like four-hundred-six.
Interestingly, this move from stating half of small numbers like 6 and 8 to becoming quite proficient at halving numbers like forty-eight or eighty-six (when presented and responded to verbally) can take as little as ten minutes with no instruction and, amazingly, with nearly no feedback on the correctness of the answers.
“Nearly” no feedback, but some. The very first time second graders try to give half of forty-eight after hearing the teacher say forty and eight alternatively a couple of times, roughly half the class will respond correctly and perhaps half will slip, often enough saying twenty-eight. The feedback “I heard twenty-four and twenty-eight; one of those is correct! Would you like another problem?” often gets an enthusiastic “Yes.” They are second graders and proud of this fancy arithmetic they are doing. Then more of them get half of sixty-four right. That feedback is useful, despite the fact that it didn’t say which of the answers was correct because it affirms that one of those answers was correct. The ayfs are a hint that children already have much of the logical underpinning for this task, and the non-randomness of second graders’ wrong answers suggests slips in keeping track of the many parts of the mental calculation—keeping the parts in working memory and tracking what one is doing are two elements of what is broadly called “executive function” [
26]—rather than mathematical misconceptions that require knowledge or conceptual intervention [
18]. Affirming that one answer is correct is a huge piece of information because it lets the children focus on the part of the two responses that differed, gives them a bit of extra time to sort out what they’ve done, and assumes that they can sort it out themselves. The intervention they got was space, a chance to sort out and rehearse ideas that they already have (evidenced by the ayfs, and so on). Following up with other interesting but still “easy” numbers like four-hundred-six or six-thousand-eight or even eight-hundred-twelve lets children focus on the key idea. Keeping it “easy” is not just to assure success (a good thing, but not the point here) but to keep the focus on the idea (a more explicit, but still intuitive, sense of the distributive property) and not camouflage that idea in tough arithmetic.
All of these—the ten ayfs, the five-hundred, and the rapid acquisition of halving of two digit numbers in which both digits are even—are evidence of a cognitive predisposition, the equivalent of the distributive property of multiplication over addition, before children have even learned what multiplication is.
The logic the children are using is essentially linguistic, with potential for wild errors. (Children use linguistic pattern to derive non-names like tenteen and eleventeen. Similarly, taking half of eighty by linguistic analogy to eight and four could suggest that half of eighteen is fourteen. One kindergartener we know concluded, after learning from her brother that “five times five is twenty-five” but having no mathematical idea what that meant, that six times six is twenty six!). But linguistic sense-making is standard equipment in young children and is mostly quite serviceable, even for number names. After all, numbers are not born with names; humans named them, and the naming reflects numerical relationships and structure. Six, sixty, six-hundred; thirty-six, forty-six, fifty-six. Details differ across languages, of course, but children use the structure they hear, and teaching can take advantage of that logic.
When children have learned enough to know that five eights has a numeric value—either by knowing a multiplication fact or by thinking of adding—they can then take a step beyond what their logic already made available to them: five eights plus two eights should be seven eights, just as five cows plus two cows is seven cows. Spoken, that statement feels entirely natural. By contrast, if children encounter the distributive property for the first time in a written form like
it is nearly opaque. The chances are that even you, despite being mathematically literate and already knowing the property, skipped past that long string of symbols, taking what we wrote for granted, without reading closely enough to notice whether or not we had made a typing error. Processing that string of symbols takes focus and effort and is therefore unlikely to be the optimal way to introduce the distributive property to an eight-year-old. Too much mental effort will have already been used up just decoding the string to have enough left for thinking about the core idea!
The Common Core State Standards—a system of mathematics standards that has become the basis for many US states’ own standards—does not mandate any particular method by which the distributive property (or any other mathematical content) should be taught, but the symbol string shown above is how the standards illustrate the property that should be taught in third grade. That has left some teachers and administrators assuming it is the idea, not just a way to express that idea. Of course, at some point, the written form does need to be learned, but here, we will plead priority’s case: vocabulary to name ideas (and written forms to express them) sensibly come after students have the ideas to name and express. Once students are clear about what is being said—five eights plus two eights must be seven eights—and can use that idea (entirely in their heads or with only enough pencil scratching to help them keep track), only then might a written form be useful. Third graders are not yet fully fluent readers of prose, let alone mathematical text. While they are just beginning to learn mathematical ideas, or are just beginning to make intuitive ones explicit, word problems and symbolic formulations can be camouflage and extra cognitive load. Children need space for acquiring the idea and space to solidify it. Then, text or symbols can help express and refine it.
So, what about priority? We have argued both pro and con. On the one hand, we talked about a structured, verbal-first, easy-number-first, activity with vocabulary and writing coming last. Deliberate priority. On the other hand, we have presented evidence that children apparently naturally develop and use the distributive property of multiplication before they have multiplication itself. Not the expected priority.
The logical order for learning mathematics can be quite different from the logical order one sees in the structure of the fully developed discipline. For learning, we would argue that order be driven not by topic but by mathematical ways of thinking for children to hone and turn into habits—mathematical habits of mind [
24]. Priority—what comes early and what comes later—is determined by understanding children’s early intuitions as independently as possible from early teaching—ideas, for example, represented by the ayfs—and refining their ideas in an environment that stretches and extends their thinking. Of course things must be learned “in order,” because the one-way-arrow of time gives us no alternative. So the myth of priority is only a myth that order is immutable for some particular topics defined in ways adults already understand them. Not only can children implicitly use the distributive property before they know how to multiply, in some real sense they must; the cognitive precursor of the distributive property—the intuitive use—seems essential before even addition can make sense. We would never call the summing of two eggs and three eggs to get five eggs a case of “factoring out eggs” or using the distributive property—it’s just kindergarten addition—but it is structurally the same as summing 2
x + 3
x to get 5
x, or factoring out
x to get (2 + 3)
x. The conventional written form does not look the same, but it sounds the same, and that language-logic makes sense to kids. The logic is there before the particular facts, and way before the notation. Exercising that logic first gives kids a hook on which to hang the formalizations. (See related ideas in [
27].)
Mathematics-the-discipline has a hierarchical structure—each new idea is built on a logical foundation of others. That establishes a logical priority, though the structure is a network not a railroad track. However, assumptions about pedagogical priority based on the structure of mathematics can create barriers to children’s learning, as can using statistical prevalence to make claims about cognitive necessity. While we (one of the authors and a huge team of others) were building a comprehensive K–5 curriculum [
28,
29,
30], many teachers and district coordinators told us not to mix addition with subtraction, and that if we did so, they would separate them—seeing two numbers and reporting their sum must come first. Missing addend problems were also “known” to be too hard. But classroom observations showed that when problems are presented as puzzles to figure out, not as notation on paper, children “subtract” and “find missing addends” quite early (see, e.g., [
20,
30]) and more readily see the connection between addition and subtraction. Kindergarten children who have become comfortable with counting objects reliably to five and are can reliably set out five pennies are also pretty reliable at reporting how many of those pennies have been covered with a napkin. The research-based claims were absolutely correct, given the kind of prior teaching the students had experienced and the nature of the assessment/research tasks they had been given. The kindergarten children with pennies and napkins might be counting on (e.g., seeing the three pennies and touching the napkin twice as they count “four, five”) or adding—they might not be “subtracting” as such—but certainly showed that the kind of thinking required for missing addend problems isn’t alien to them. They had the cognitive ability; suitable activities could tap it, practice it, and extend it. The penny-and-napkin activity practiced the sums in a novel context that children find appealing. It also gave them a firm logical foundation on which to build ideas of subtraction. Though a solid understanding of subtraction does require a solid understanding of addition, they can grow together. Withholding such puzzles from children who are not yet proficient with sums up to five unnecessarily holds them back in both addition and subtraction.
4. Myth of Unity
We have argued that the Distributive Property is not a lesson or even a unit. Parts of it seem to be an early and natural development in child cognition, existing before addition is learned. Its intuitive parts can be exercised and become more comfortable and conscious through doubling and halving before introducing multiplication-the-topic; the concept of doubling and halving seems to mature earlier than, and be good grounding for, general multiplication.
In the same way, second graders’ developable proficiency with halving and doubling can be a valuable foundation for fraction addition and fraction multiplication long before they are ready for the full-blown topics of Multiplication, let alone Fractions, and even though fraction arithmetic requires at least some skill with all four basic whole-number operations. Halving/doubling experience builds intuition and logic that can be formalized later, mitigating some canonical errors.
Thinking without the fetters imposed by an image of unity—the notion that a topic must wait in its entirety because parts of it must wait—loosens up the possibilities for teaching “algebra.” For one thing, algebra-the-course comprises many things. Two of them are (1) using algebraic notation as a shorthand for describing patterns that the child can already describe with words and examples and (2) using that notation as a tool for deriving things (e.g., numbers) that the child does not already know. The first is essentially a language-learning act, and young children are way better language learners than older children and adults. The second is a logical-analytic act and requires a fair amount of tracking of manipulations without the aid of semantic support—an executive-function-heavy “system two” act (see, e.g., [
31])—that is understandably less common in young children, and therefore less easy to “scale up” to general classroom use. (Important caveat: this does not mean that children cannot; it means that with the instructional experiences children generally get, at least in the United States, most children do not.) But why keep these two elements of algebra together as one unitary Algebra? The first, the use of algebraic notation as language, is tractable in first and second grade (see, e.g., [
16,
17,
20]).
Figure 1 shows an example of using algebraic notation as language for describing pattern in the second grade. For the moment, ignore the last column of the table-like puzzle. The rest of this input-output table is a type of activity that might be seen in many curricula, presented as a puzzle in which children are invited to induce a rule. They look for clues about what is going on, see that the rule is apparently “subtract 8,” and fill the empty cells accordingly.
When second grader Michelle explained how she had finished quickly, she said she figured out the pattern by noticing the “28, 20” column first, then the “10, 2” column (because she was so familiar with the pairs that make 10), and then the “8, 0” column. In her words, this pattern was clearly “take away eight.” And then, looking at the teacher with a grin as if the teacher had made some cosmic mistake by leaving the “answer” on the page, she pointed to the last column that says “
n,
n − 8,” and said “Besides, it says so right there!” Her classroom teachers had never even mentioned those symbols, nor any like them, nor had her parents, so how did she know that is what the last column meant? Michelle had figured out the pattern exactly as she said, using the numbers. From that, she inferred the meaning of “
n,
n − 8.” That is how young children learn nearly all their language: they hear (or later, read) a new word in a context that gives them a theory about its meaning. With enough experience (sometimes surprisingly little), they get it. Had Michelle seen “
n,
n − 8” without the context of the table, or with no confirming data in the table, she would not have known what it meant, but once she got the idea from the table, the symbols even look like what she inferred they meant, confirming her inference. (Related ideas are in [
21,
27] and in other work by these authors.)
Puzzles (like
Figure 1) and “tricks” (see below and
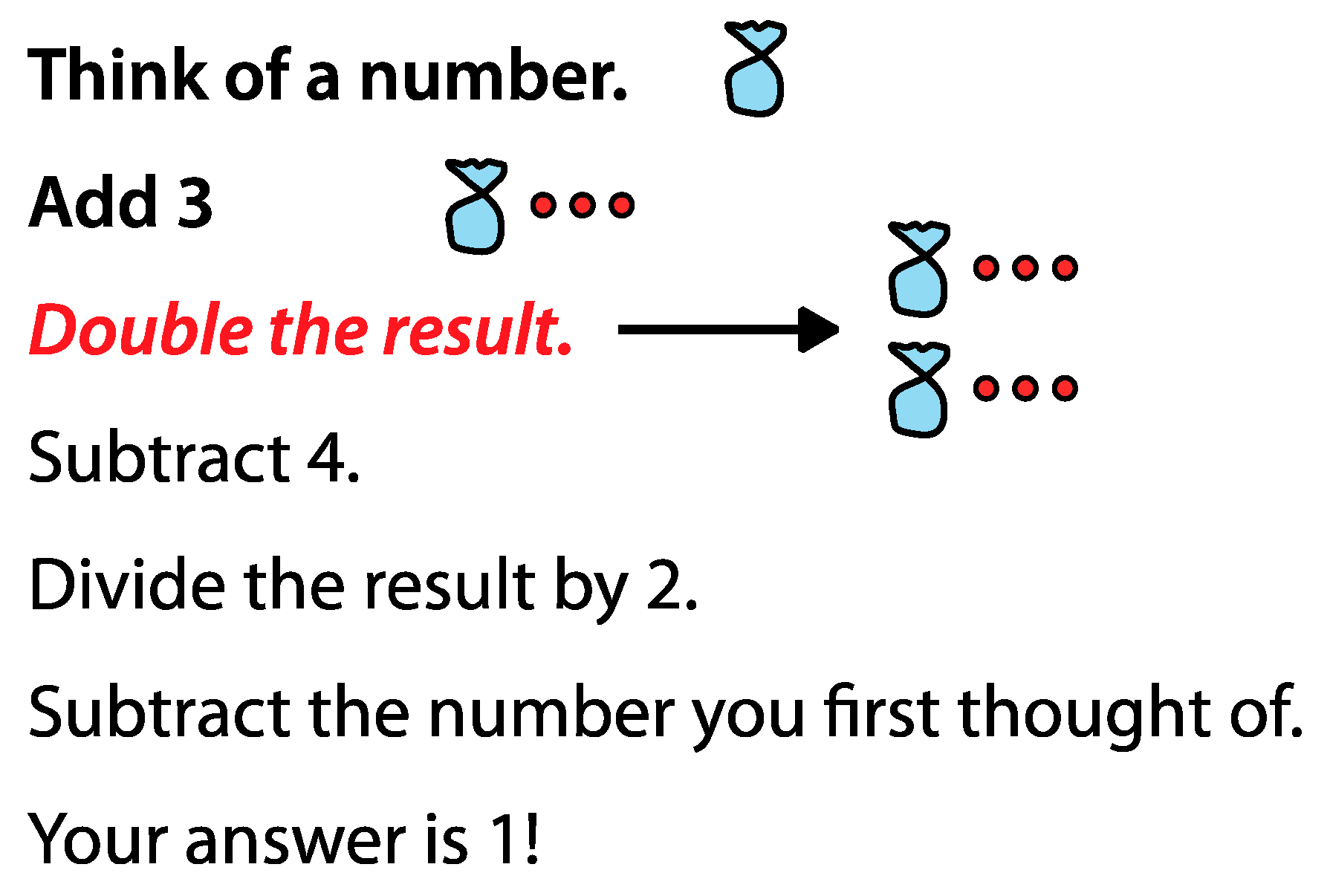
Figure 2) pull for thought and interest. Fourth graders, after the initial and highly motivating surprise and delight of a number trick like the following, can work through the logic (and get another dose of surprise and delight) by using images as temporary precursors (for only about a week!) of standard algebraic notation.
Initially, the entire trick is presented orally; the children think of a small number and do the arithmetic in their heads. After the students’ delight, the teacher redoes the trick and, for the first two steps, uses the image of a bag or bucket “to contain the secret number” and extra “marbles” (or grapes or…) for what is to be added (
Figure 2). After seeing the teacher’s image for “add three,” the children are asked what picture should be drawn to represent “double the result,” the next step. Most respond “two bags and six,” which is yet another piece of evidence that the distributive property is well established, even if children cannot yet express or apply it in conventional notation.
Children need practice drawing the pictures and working the arithmetic on other puzzles. Then the teacher “gets lazy” and does not want to draw pictures. So, with a new trick, the teacher writes the words the kids say (e.g., “two bags and six”) rather than drawing the pictures that those words describe. That’s hardly less tedious, so the teacher then just abbreviates the exact words the children used—“2 b + 6” instead of “two bags and six”—way easier than either pictures or words.
This entry into algebraic notation—using algebraic language as a “pattern indicator” and deriving its structure as a natural abbreviation of the children’s own language—was proposed by W. W. Sawyer [
32] and applied in a beautiful and formerly well-used elementary text series [
20]. It is further elaborated in [
18,
28,
29] and used in the algebra curriculum [
19]. It uses abstractions as all language does, but children are great language learners and abstracters. Teachers already widely use letters as pattern indicators anyway, in a different context, with notations like ABBABB indicating patterns like ∇∆∆∇∆∆.
Having first used algebra as a language for expressing what is happening in this puzzle, fourth graders can then take the next step: using what they have encoded to derive things that they did not know. If, for example, the teacher stops in the midst of doing the trick and ask the secret-keeper what number she has just calculated, children can use the pictures to figure out the secret-keeper’s secret number (the number “in the bag”). After some experience figuring out the secret number using the pictures and seeing how shorthand like 2 b + 6 is just a way to describe those pictures, fourth and fifth graders can become quite adept at thinking “if two bags plus 6 is 10, then the two bags themselves must be 4, so your secret number must be 2!”.
Michelle’s second grade induction of the meaning of n − 8 and the fourth graders’ “invention” of a way to solve 2 b + 6 = 10 are not all the content of Algebra 1, but they comprise a significant part that is completely accessible well before a thorough study of Algebra 1 content makes sense, and they are completely consistent with what those children are to be practicing anyway. They are grade level mathematics but done in a way that works toward and facilitates a subject that will be deepened later. They foreshadow and prepare, rather than leaving Algebra 1 to be a shocking new departure from anything that has been seen before. Parts of Algebra 1 must wait for an older child with more mathematical knowledge and skill, but there is no reason to hold back the parts that don’t require that wait. Thinking this way no longer treats algebra as an indivisible unit. As we said earlier, everyone knows that algebra has parts, but questions about when “it” should be taught betray an underlying image, despite our knowledge, of a single “it,” a single course.
Tall and Vinner’s [
33] notion of “concept definition” and “concept image” helps explain the apparent paradox. For our purposes here, “concept definition” can be thought of as the formal mathematical definition of the concept (Tall and Vinner are more nuanced). “Concept image” is “the total [personal] cognitive structure that is associated with the concept, which includes all the mental pictures and associated properties and processes. It is built up over the years through experiences of all kinds, changing as the individual meets new stimuli and matures” [
33] (p. 152).
Tall and Vinner’s original examples, and much of the subsequent work using their ideas, dealt with advanced mathematics, but their insight is evidenced even in elementary school math. When a child (or adult!) refers to ∇ as an “upside-down triangle,” that description might flag a misconception, but it might equally come from someone fully aware of the precise mathematical definition, adding extra detail to their communication. Even in that latter case, though, it suggests that they have, and expect the listener to have, a concept image of a triangle ∆ that includes, along with required features, a favored “right side up” orientation.
Here is a second example from grades 4–8 mathematics. As a heuristic for deciding whether to use multiplication or division in a word problem, teachers often suggest that children ask themselves whether they expect the result to be bigger or smaller. That implicitly invokes a concept image that multiplication “makes things bigger,” despite the knowledge that even second graders have that multiplication by 0 and 1 do not make things bigger, and that children must relearn when they are multiplying by numbers between 0 and 1, and relearn again when they multiply by negative numbers [
34]. That particular persistent image is not a “myth” about mathematics in the sense this series of articles addresses, but it is evidence of the tenacity with which things that we all know are not true can nevertheless take hold of our thinking.
The relevance of concept image to the myth of unity is that, though we all know that algebra (or fractions or whatever) contains many distinct ideas and bits of knowledge, technique and skill (its concept “definition”) the power of the concept image of algebra can still unify everything into a single package, algebra-the-course, rather than algebra-the-collection-of-ways-of-thinking-and-bits- of-knowledge-and-technique. Being guided by the unitary image hides opportunities that the more flexible concept definition provides. This image leads people to ask when to teach algebra (or …) rather than to ask which component parts fit best at what time. One consequence is the unnecessary delay of ideas that young children can find totally sensible.
5. Other Advantages of Not Being Constrained by These Myths
Treating algebraic “facts” such as the distributive property not as a unit but as the culmination and formalization of a spectrum of experiences, ideas and skills helps educators avoid the trap of teaching the same thing every year. In the US, it is not uncommon to see nearly identical lessons on the distributive property for 8- through 12-year-olds, maybe just with different arithmetic. Though images may supplement the presentation, the property is taught as if it
is the long string of symbols. Thinking about the development of understanding makes it possible to foreshadow ideas in earlier grades and then solidify and formalize later. Ideas ripen over calendar time. When those ideas are firm, more can be done with them, including vocabulary, formalization and use as building blocks for other ideas. Trying to do this all at once begets a canonical formulation of symbols, steps and rules that is more efficient, but less durable, than giving students experiences that let them build their logic and sort out some confusions themselves. The “efficient” presentation tends to last a few days and then fade [
35], requiring yet another lesson typically in much the same form. Students struggle each time if the presentations never allow the time and experience to build the ideas behind the symbols or, far better, recognize that one already had those ideas for years and is now learning only a conventional notation and more generalized application for them.
Seeing through the myths lets us teach ideas from algebra (or multiplication or fractions or whatever) to children who are ready for some but not all of the disparate features of the topic; it provides a richer, more engaging repertoire for teaching even “standard” material and suggests experiences and a structure that can be smooth, coherent, age-appropriate, faithful to mathematics, and foreshadowing future learning. Kindergarten students may identify how many fingers “they don’t see” as a way to practice addition to five and later to ten, and that approach moves them closer to subtraction. Second graders who take half of various numbers are, in effect, multiplying by ½ “before they are ready,” before any notion of division (let alone with large numbers) was learned or even possible for them. Second graders understand n − 8 as a pattern indicator to express things they do already know. Fourth graders use algebra as a language to record and understand a trick they love; after building comfort with that, they use the algebra to derive information that they do not already know (the secret number); and then they learn how to devise their own simple tricks. Students enter later grades with a firm understanding of the logic behind the distributive property, which they can then formalize (with that algebraic language they have been using for a while) rather than struggling through the camouflage of a string of factors and terms that obscure the logic and teach students that the distributive property (which they long knew) is incomprehensibly obscure.
Finally, research can address new phenomena. Much research has gone into understanding what causes the difficulties so many American students have with algebra; it often identifies the culprit as some weakness in one or more pre-algebra skills (often fractions). Because schooling is a huge and complex system, it is harder to explore completely different trajectories for the early grades, such as the Davydov curriculum [
16,
17] or the applications of Sawyer’s ideas [
18,
19,
20,
24,
28,
29,
30,
32], even as we see successful international examples of such trajectories (and others). Research based on very different approaches might well develop different pictures of the possible trajectories and interventions.