1. Introduction
Students with disabilities are frequently framed as a “problem” within educational research. Often this framing goes unnoticed, as disability is automatically assumed to be a problematic condition, rather than one aspect of natural human diversity. One way this “problem” is often framed is as an achievement gap. Students with a variety of disabilities underperform relative to peers without disabilities on mathematics assessments, and these gaps widen over time [
1]. When discussing students with disabilities, we include the full range of disabilities that are part of the natural human condition, both disabilities that are primarily cognitive such as autism, specific learning disabilities and intellectual disabilities, as well as other biological and physical differences, such as cerebral palsy or blindness. For students with cognitive disabilities, the problem is often framed as a cognitive deficit. For learning disabilities (LD), for example, scholars have argued that cognitive deficits, such as difficulties with working memory or weak computational skills, interfere with higher achievement in mathematics [
2]. Thus, the problem is located within individual students.
Another way the problem can be framed is through limited access to standards-based mathematics, which includes both conceptual and procedural instruction [
3]. Students with disabilities are offered fewer opportunities to engage in meaningful mathematics, as their curriculum have historically focused on procedural rather than conceptual instruction, a pattern that continues in current U.S. educational practices [
4]. For example, Jackson and Neel [
5] found that students in general education classrooms spent significantly more time engaged in conceptual work in mathematics (61% observed time), while students in segregated special education settings at the same school spent far less time engaging in conceptual mathematics (19% of observed time). If students with disabilities are not offered instructional opportunities at the same conceptual level as their non-disabled peers, the reason for achievement differences may be this lack of access.
While both achievement and access for students with disabilities are indeed critical issues in current mathematics education, we focus this paper on a possible underlying issue: the mathematics educational research divide for those with disabilities, primarily situated in the field of special education, and those without disabilities, primarily situated in the field of mathematics education. In so doing, we intentionally frame the problem as not located within the individual students with disabilities, or even in the classrooms in which they are educated. We ask instead how educational research itself contributes to these gaps in achievement and access for students with disabilities in mathematics. Hence, we frame current academic research on mathematics, in the fields of both mathematics education and special education, as the problem to be analyzed.
In this paper, we present a recently completed analysis of mathematics educational research published between 2013 and 2015 [
6,
7], with a particular focus on problem solving. We first describe current issues for students with disabilities in mathematics followed by a description of our conceptual framework, disability studies in mathematics education. We then describe the relevant historical development of two distinct research traditions: mathematics education and special education. After describing our methods, we present an analysis of our findings on problem solving. We closely analyze how conceptualizations of students with disabilities are constructed within the current research in the area of problem solving. Finally, we describe the implications of our study for mathematics educational research.
2. Conceptual Framework
Activists with disabilities pioneered the academic field of disability studies, advocating replacement of the medical model of disability with the social model [
8]. While individuals may have cognitive or physical differences, disability is created through society's response to these differences. Hence, the response to difference is not cure or remediation of the individual, but to understand how unjust social systems create or exacerbate differences. Applied to schools, disability studies in education (DSE) examines disability in schools as a social construction that results in social exclusion and oppression, as students with disabilities are routinely excluded from the educational opportunities presented to students without disabilities [
9]. To be clear, we do not argue that disability does not exist, as we recognize the significant biological differences between those with disabilities and those without disabilities. Those differences can and should be the focus of some educational research. Much more work needs to be done on how schools and classrooms further exacerbate differences between students through differential access to certain types of curriculum, or segregation into difference types of learning environments. In short, we understand disability as both biological and cultural.
Disability studies has long engaged in critical analysis of the role of higher education, academia, and other institutions in constructing disability. As Linton [
10] (pp. 2–3) noted,
Disability studies has arisen in the past twenty years to focus an organized critique on the constricted, inadequate, and inaccurate conceptualizations of disability that have dominated academic inquiry. Above all, the critique includes a challenge to the notion that disability is primarily a medical category. Consequently, disability studies contests the current academic division of labor in which the study of the phenomenon rests in the specialized applied fields (rehabilitation, special education, health, and so on) and the rest of the academy is largely exempt from meaningful inquiry into the subject of disability.
Linton called for a reframing of the “problem” of students with disabilities, with a focused critique of bifurcated academic realms, in which the study of disability is clustered into specific “applied” fields. Following this argument, we question why mathematics educational research that includes students with disabilities should be primarily in special education, “exempting” the field of mathematics education from addressing disability.
For researchers in both academic fields, the disability studies in mathematics education (DSME) framework [
11] may be useful to advance meaningful inquiry. DSME draws from critical mathematics education and disability studies in reimagining the structures and processes of teaching and learning mathematics and disrupting traditional notions of disability (e.g., relying on working memory deficits to explain errors in number calculation). DSME positions students with disabilities (and all students) as representative of the diversity of human experiences for which all educational environments should be designed. In drawing on critical mathematics education, DSME foregrounds social and political aspects of the learning of mathematics and how students and teachers operate in a social system rife with hegemonic power [
12]. Such foregrounding is intended to: (1) develop within individuals a political awareness of individual’s positions in a system (e.g., classroom, school, or community); and (2) motivate individuals to enact change toward advancing social justice [
13]. In addition, DSME extends conventional mathematics educational research by involving students with disabilities and their families by surfacing and questioning power differentials. In turn, action towards more just practices is led first and foremost by students with disabilities where their lived experiences and voices are privileged in research. This process includes challenging “hegemonic narratives about who can do mathematics and to reconstruct the role of mathematics in the struggle to empower learners whose mathematical powers have been underdeveloped” [
13] (p. 425). Indeed, with DSME, regardless of academic discipline, mathematics educational researchers have an additional tool to conduct socially just research and to advocate for students with disabilities.
From a critical perspective, analysis of the historical roots of current ideologies and epistemologies is necessary to understand the current state of mathematics educational research. We next present an analysis of the development of two academic fields, mathematics education and special education, making note of both similarities and differences in how these two fields have conceptualized mathematics and mathematics learning, including approaches to problem solving.
2.1. Historical Roots of Mathematics Education
The fields of mathematics education and special education both share similar roots in the behaviorist movement [
14]. Thorndike and colleagues argued in 1923 that mathematics was best learned through structured associations, with carefully sequenced drills [
15]. In the behavioral movement led by Skinner in the 1950s, learning mathematics was assumed to entail learning procedures for solving computational problems; success was defined as speed and efficiency in solving these problems. An emphasis on what is measurable created an affinity between behaviorist theories of learning and methodologies that measure such learning precisely, such as randomized controlled experiments [
16].
Mathematics education shifted dramatically as a result of the cognitive revolution [
17]. Formulated as a challenge to the pure exteriority of the behaviorists, cognitive theories focused attention on internal processes of the mind. There are two main cognitive perspectives: (1) information processing; and (2) constructivism. Information processing (IP) focuses on how the brain makes sense of information, using a computer as the dominant metaphor [
18]. Mathematics learning is understood as a matter of processing and storing information in short-term or long-term memory. Newell and Simon [
19] were influenced by the work of Polya in problem solving [
20]. IP has contributed to understanding problem solving as a generalized cognitive process, including analysis of meta-cognition. IP also focuses on the role of long-term and short-term memory, attention and visual processing [
14]. IP focuses on general processes in mathematics learning, not on specific mathematical content areas. Strategic instruction, a major aspect of information processing, has researched the general heuristics through which students solve word problems [
21]. According to a review of IP research [
18], IP typically uses experimental quantitative methodologies to understand human processing.
The second major theory in the cognitive revolution was constructivism, which became the dominant force in mathematics education by the 1990s [
14]. According to Thompson [
22] (p. 96), constructivism is an “epistemological stance regarding the nature of human knowledge.” Learning is understood as individually constructed through experience, built always on previous understandings. Central concepts are schemas, assimilation and disequilibrium. Confrey and Kazak [
23] described several strands of constructivism: research on problem solving [
24,
25], research on student misconceptions [
26], and theories of cognitive development in mathematics [
27]. Constructivism has brought with it attention to qualitative research methodologies, focused on detailed analysis of individual mathematical thinking.
Like many other fields in education, mathematics education took a social turn [
28], beginning in the 1990s. From the sociocultural perspective, learning is understood as situated in contexts, and mediated by tools that include mathematical discourse. Important strands of sociocultural theory as applied to mathematics educational research include activity theory and/or cultural historical activity theory [
29], situated cognition [
30], and distributed cognition [
31]. Socially constructed entities such as the culture within a mathematics class are conceptualized as communities of practice [
32], activity systems [
29], and/or figured worlds [
33]. Identity is a key theoretical construct, produced through participation in cultural contexts and practices [
29]. Analysis of learning from a sociocultural perspective has tended to focus on learning as mediated by tools, including discourse, and tends to be qualitative analysis of individuals and/or groups.
The final movement in mathematics education is sociopolitical [
12,
34]. Researchers using a sociopolitical lens analyze mathematical learning in its broader contexts. Analysis may use critical mathematics to analyze the cultural production of mathematics education in particular political contexts. According to Valero [
34], sociopolitical analysis expands analysis of what matters in mathematics to broader cultural spheres, such as race, class and gender. In addition, she notes that sociopolitical work must also be critical, or actively seek to disrupt power inherent in taken-for-granted social systems. We include feminist and poststructuralist critique in mathematics education in this category. This movement is still emergent in mathematics education. Methods in sociopolitical analysis include both qualitative and quantitative methods. Thus far, calls for sociopolitical equity in mathematics education rarely include a focus on disability. For example, a special issue on equity and sociopolitical perspectives from a prominent journal in mathematics educational research, the
Journal of Research in Mathematics Education, published in 2013 did not include any articles focused on students with disability [
12].
2.2. Historical Roots of Special Education
While behaviorist approaches in the field of mathematics education have become significantly less prevalent in mathematics education since the 1970s [
35], mathematics educational research in the field of special education continues to be heavily influenced by behaviorist theories of learning [
14,
16]. By the end of the 1980s, special education had also taken up central concepts from information processing such as metacognition, processing, attention and memory. Swanson [
36] argued for information processing to become the dominant learning theory in special education, particularly to understand students with learning disabilities. Focused on general cognitive processes such as metacognition and general heuristics for problem solving, strategic instruction [
37] has become central in mathematics educational research for students with disabilities.
The field of special education has tended to distrust constructivism as a theoretical approach [
14], although there has been some recent shift in this area. Critiques from special education scholars about constructivist mathematics tend to assume that teachers teaching from a constructivist view of learning will never be explicit with students, drawing a contrast between “explicit” instruction and “reform” mathematics [
38]. In the past, some special education researchers have argued further that constructivist theories of learning are inappropriate to use with students with disabilities because of this lack of explicit instruction. A leading scholar in mathematics educational research, Jitendra et al. [
38] (p. 271), described in 2013 an “inquiry-based approach” as “counter-intuitive in meeting the instructional needs of students at risk for MD [mathematics difficulties]”. At the same time, special education has increasingly included aspects of constructivism as part of a “cognitive” approach that includes information processing [
39].
2.3. Research on Problem Solving
Research on problem solving has been a prominent feature of the cognitive revolution, influenced by both theories of constructivism and information processing. According to Schoenfeld [
40] (pp. 87–88)., a mathematical problem is: “(a) a task in which a student is interested and engaged for which he wants to obtain a resolution; and (b) for which the student does not have a readily accessible means by which to achieve that resolution.” Research in problem solving tends to describe a distinction between non-trivial problems and word problems, the former being problems that do not have a single, obvious answer and the latter known as exercises, often found at the end of chapters in mathematics textbooks. Problem solving from the constructivist perspective is inherently non-routine, asking students to think creatively, and often collaboratively, about solving problems [
41]. In contrast, solving word problems in school is characterized as memorizing a procedure and replicating it. Engaging in this kind of procedural problem solving can lead students to believe that mathematics is a series of short word problems or computation problems, affecting their ability to engage in sustained problem solving for more complex problems [
42].
2.4. Neuroscience and Education
As the discipline of cognitive neuroscience has developed, fueled by rapid advances in brain imaging, a gap has emerged between cognitive neuroscience and educational research [
43]. Partially, this gap comes from a lack of collaboration between educational research and cognitive neuroscience [
44]. Special education, in contrast, with its continued close collaboration with experimental psychology and embrace of the medical model, has utilized cognitive neuroscience. The last twenty years has seen significant collaboration between cognitive psychology and neuroscience to develop significant new understandings of learning disabilities such as dyslexia [
45]. Studies of brain imaging are central to current research on mathematical learning disabilities, or dyscalculia [
46]. A significant amount of that research is focused on identifying core deficits of students identified with dyscalculia. Critiques from scholars in the field of mathematics education on the use of cognitive neuroscience include a narrow focus on the elementary aspects of mathematics and a disconnect between cognitive neuroscience and established research in mathematics education [
47].
We designed our research to provide an understanding of the current state of mathematics educational research on problem solving for students with and without disabilities. The data we used for the current study are drawn from a larger study in which we analyzed 1461 mathematics educational research studies across three years [
6]. The larger study was guided by two previously published research reviews. The first was a review of over ten years of educational research in mathematics between the years of 1982 and 1998 [
48], which found that most research on disability was published in special education and psychology journals. In the second review, van Garderen and colleagues [
39] analyzed 50 articles published in mathematics education compared to mathematics research published in special education. Classifying studies based on behaviorist, cognitivist (which included constructivist and information processing), or sociocultural learning theories, the authors found that the field of mathematics education only included students with disabilities in one article from their sample. While 80% of articles in the field of mathematics education were classified as sociocultural, only 12.5% of the special education articles were sociocultural. In addition, the authors reported that the approach to learning in special education research was cognitivist (47.5%) and behaviorist (40%). In our larger study we expanded the work of van Garderen and colleagues from 50 to 1461 articles published across three years [
6]. Of these 1461 articles, 149 focused on problem solving, which are the focus of our current study. Our research questions are: (1) How does current mathematics educational research on problem solving differ for students with and without disabilities? (2) How are students with and without disabilities conceptualized as problem-solvers in this research?
3. Methods
In order to answer our questions, we drew data from a larger study where we conducted a content analysis of research articles published between 2013 and 2015 that focused on mathematics and PK-12 education [
6,
7]. Both authors coded data. In the larger study, we limited the sample to education research articles published in peer-reviewed journals in English between 2013 and 2015 that included mathematics. We found articles through searches of educational databases (ERIC, JSTOR, and PsychINFO) looking for descriptors and keywords of mathematics, math, and numeracy. In addition, we did a hand search through all journals mentioned in an analysis of equity in research published by Lubienski and Bowen [
48]. To insure that we found all the relevant studies that included disability, we also searched in all databases for combinations of
mathematics,
math, and
numeracy in combination with various terms for disabilities (IDEA categories). We included articles that were published in a wide variety of journals, including mathematics education, special education, psychology and general education journals. We limited our search by reading the title, abstract and keywords to only include: (1) research reports published in peer-reviewed academic journals in English; (2) published between 2013 and 2015; (3) articles needed to be focused on mathematics (mentioning math, mathematics or numeracy in the title or abstract); and (4) participants were either teachers of mathematics, or students at the prekindergarten to 12th grade levels. We excluded editorials, book reviews and introductions to special issues, and research written for practitioner audience. In total, 633 articles were excluded based on the focus of their journals as either practitioner-oriented or focused on adult or post-secondary learners. A further 1134 articles were excluded based on the criteria above, with a total of 1767 articles excluded. The outcome of this search was 1461 articles. We coded articles as including disability if they referenced disability, or a particular disability explicitly in the title, abstract or keywords. We also included articles that referenced “mathematical difficulties” if that article included students with disabilities in their sample, or prominently referenced disability. All of these articles were read in full to determine eligibility. To address our research questions on problem solving, we drew from these 1461 articles the ones that included the keywords problem solving, or word problems in the title, abstract, or keywords. The final data set for this analysis was 149 articles.
The first stage of research involved general coding based on the title, abstract and keywords for each article. We coded for academic field of the journal, methodology of article, participant focus, equity groups mentioned (such as race or disability), mathematical content focus, and theoretical orientation. Some articles did not present enough information in the title, abstract or keywords for us to code, particularly in methodology and pedagogy. In some categories, it was possible to be coded for more than one content area or theoretical orientation. Inter-rater reliability of coding between the two researchers was 94.6%.
Coding the articles for theoretical underpinnings was a critical part of our investigation since we were interested in whether or not students with disabilities were understood differently in the research literature. However, this was a complex task. Following a historical account of special education and mathematics education by Woodward [
14], we first identified behaviorist, information processing, constructivist and sociocultural as pedagogical theories that have influenced both the fields of mathematics education and special education, beginning with Woodward’s description of the differences between these categories as coding indicators. We added two additional categories: (a) sociopolitical [
12] to capture an emerging focus in mathematics education on analysis of wider contexts and processes that affect classrooms and learning; and (b) medical. We added the category of medical because we found a significant number of research articles that understood learning as mediated or controlled by psychometric data, often using cognitive neuroscience.
Articles could be coded for more than one theoretical perspective. Additional information, including specific keywords used to code, is described in
Table 1 and additional publications [
6]. We recognize the limitations of this particular analysis, particularly that we determined these categorizations through the title, abstract, and keywords alone, which meant that we did not assign a code to all articles.
After coding for all of these categories in the larger set of 1461 articles, we conducted a deeper analysis of a subset of the 149 articles on problem solving. Specifically, our analysis involved categorizing the articles within specific theoretical orientation (i.e., medical, behavioral, information processing, constructivist, sociocultural, and sociopolitical). We then explored possible themes across these articles.
Our study has several limitations. First, while we analyzed current research (2013–2015), our results may not generalizable outside this range. Other researchers [
39,
47] have conducted similar analysis in mathematics education research collectively covering the period between 1984 and 2008. Thus, while there are similarities in findings between our study and these previous studies, the differences in methods and depth of analysis employed prevents us from claiming we are replicating or continuing the work of those authors. Second, we only included research published in English. Third, coding from only the title, abstract, and keywords provides a snapshot of the research article, particularly in the area of methodology and theoretical orientation.
4. Findings
Of the total of 149 problem solving articles, 113 did not include disability (the No-Disability Set) and 36 (24%) did include disability (the Disability Set). In much of the analysis that follows, we compare these two sets to see how research on these two sets differs. Compared to the larger data set (N = 1461) in which 12% of the articles included disability, the problem solving set had a higher proportion of articles with a focus on disability (24%). As we will describe, research on problem solving for one specific disability category, learning disabilities, is a prominent area of academic research in special education, and may account for the greater proportion of articles in this category. In this section, we present general findings in the problem solving set, followed by a deeper analysis of several articles within this set that demonstrate larger themes.
Comparing the Disability Set to the No-Disability Set, we found similar patterns as with our overall data [
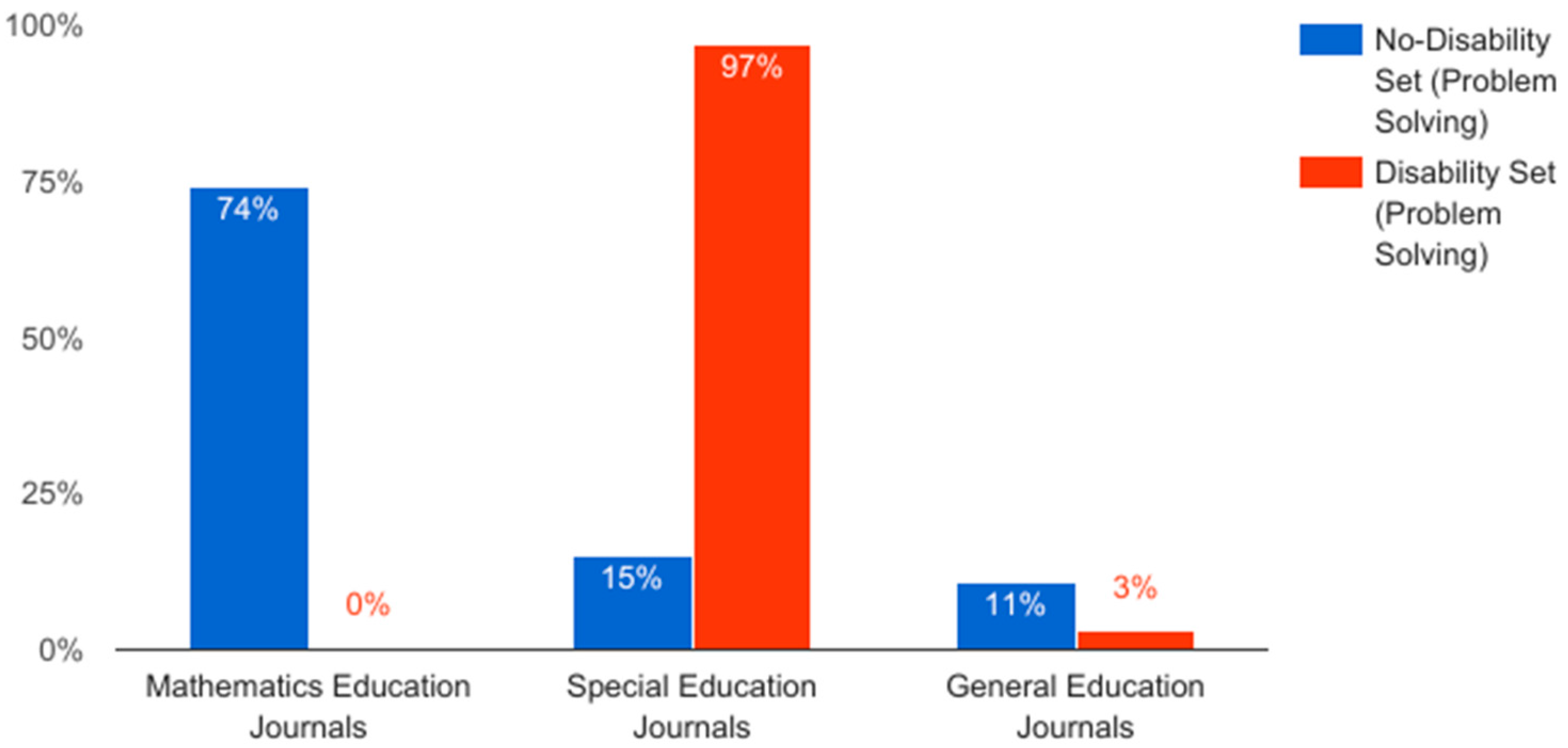
6]: research involving disability was published in psychology and special education journals, while absent as a primary focus from mathematics educational journals (
Figure 1). Indeed, mathematics education journals did not publish any articles on problem solving with a focus on disability from 2013 to 2015. The 36 articles that included a focus on disability were overwhelmingly published in psychology or special education journals (97%) with one (3%) published in general education research journals, and none in mathematics education journals.
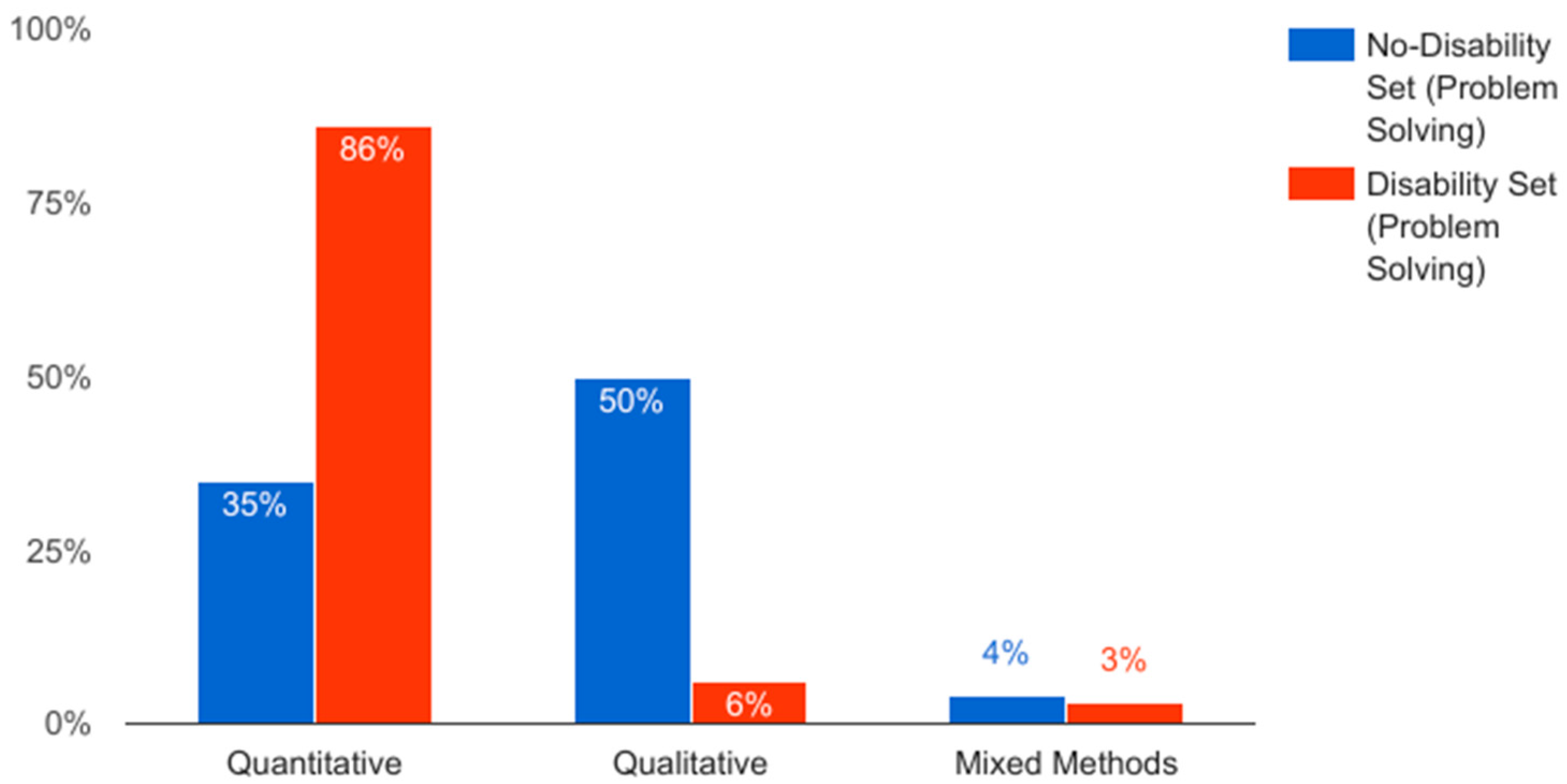
Articles that included a focus on disability were also more likely to use quantitative methods, while articles that did not include disability used both quantitative and qualitative methods (
Figure 2). In this problem solving data set, 35% of the empirical articles in the No-Disability Set used quantitative methods, while 50% used qualitative methods and 4% used mixed methods, in contrast to the Disability Set where 86% was quantitative, 6% qualitative, and 3% mixed methods.
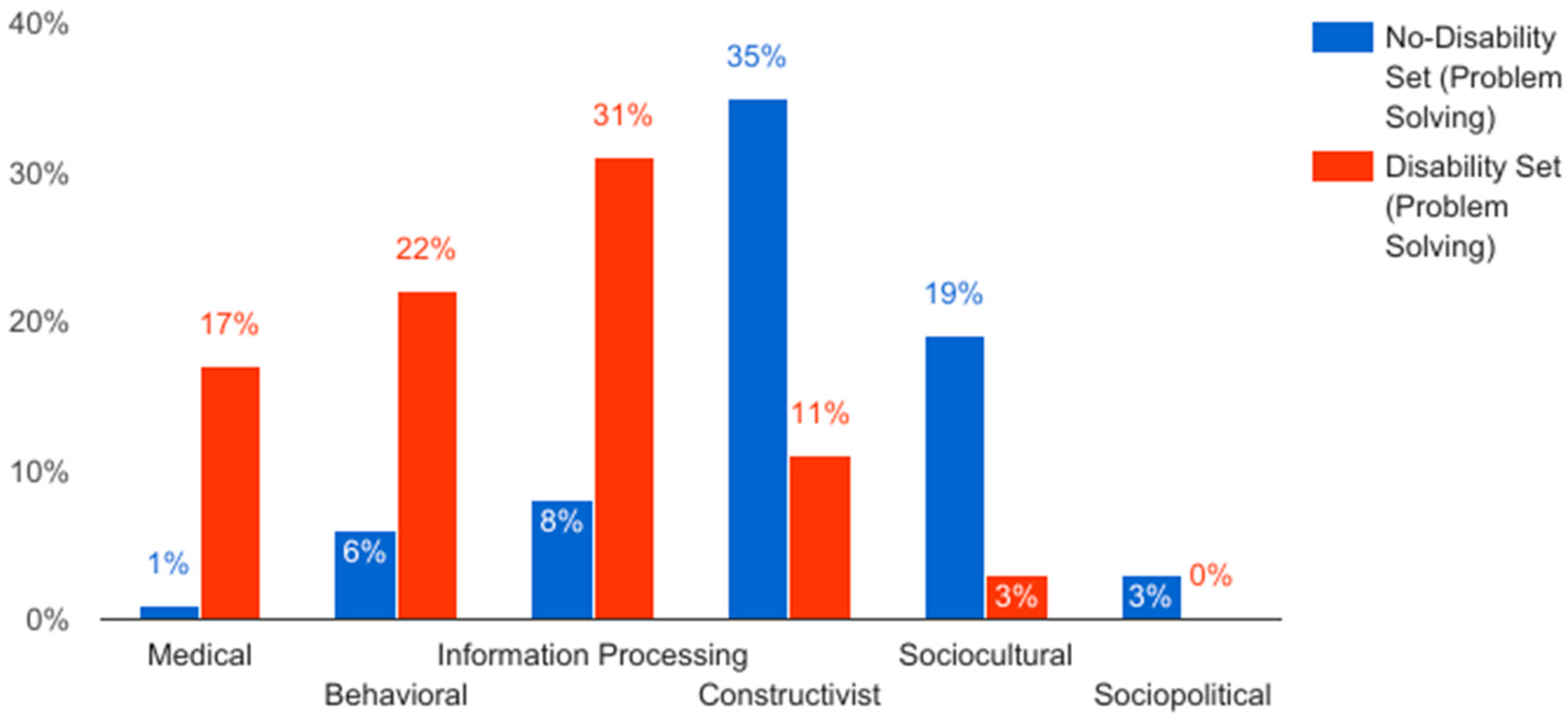
The theoretical orientations of the research also reflected our larger findings [
6], with some shifts (
Figure 3). The No-Disability Set was most influenced by constructivism, with 35% of articles coded as constructivist. For students without disabilities, problem solving was primarily understood through constructivist theory. We identified more use of information processing approaches in the Disability Set of articles as compared to the full data set. For the Disability Set, information processing, particularly in the form of schema-based instruction, was most prevalent at 31%. The second most prevalent theoretical orientation was behaviorist approaches at 22%, followed by articles that were based on a medical perspective (17%).
In the following section, we will describe our analysis of the problems solving articles within each theoretical orientation (i.e., medical, behavioral, information processing, constructivist, sociocultural, and sociopolitical). We will then describe two themes that emerged across the articles: (1) the use of schema-based instruction, which was primarily applied to students with disabilities; and (2) problem posing, which was primarily applied to students without disabilities.
4.1. Medical Theoretical Orientation
We have defined medical theoretical orientation as a focus on biology in relation to mathematics learning, including understanding disability as a primarily medical condition. For example, these articles have described mathematics instruction interventions, as “treatments” [
49]. Other studies investigated the relationship between cognitive sub skills, such as working memory or phonological processing, and problem solving [
50]. Bae et al. [
51] compared the ability to solve mathematics word problems of typically developing students compared to students with autism spectrum disorder. The article begins by listing the diagnostic criteria for autism spectrum disorder, and situates the analysis in the differences between autistic students and non-autistic students. For example, the authors analyzed working memory capacity as a possible determinant of word problem solving ability. In addition, particular cognitive processes are analyzed through a diagnostic lens (those who do and do not qualify for autism). In turn, there is no individual analysis of students, but a quantitative aggregation of testing data, separated into the categories of the disabled or the non-disabled. The majority of the problem solving articles integrate cognitive neuroscience in either methods or relevant literature. Almost all articles that were coded as having a medical pedagogical orientation were focused on disability (6 out of 7). A medical theoretical orientation was included in 17% of the articles on problem solving for students with disabilities, while only 1% of the non-disability articles used this perspective.
4.2. Behavioral Theoretical Orientation
Some of the articles (
n = 15) took a behavioral perspective on problem solving. In this approach, successful problem solving results from students replicating a series of scripted behaviors to solve mathematical problems, using direct instruction [
39]. By following and demonstrating these processes, students learn to solve problems successfully. For example, Freeman-Green et al. [
21] (2015) described an intervention using a scripted problem solving routine called SOLVE. They found that explicit instruction in this problem solving routine was effective in increasing the problem solving skills of six secondary students with learning disabilities. Similar to several other studies in our sample, this study integrated behavioral theories of learning (explicit instruction), with metacognitive processes influenced by information processing (strategic instruction). We coded this article as both. The overlap between these categories was prominent in our analysis, particularly when we read the full text of problem solving articles in the Disability Set. Eight of the articles in the Disability Set were coded as behavioral, which was 22% of the set. Seven of the articles in the No-Disability Set were coded as behavioral, representing 6% of those articles.
4.3. Informational Processing Theoretical Orientation
An example of information processing approaches to problem solving is schema-based instruction. In one example, Jitendra and colleagues [
38] studied the effects of schema-based instruction in word problems for third–grade students at risk for mathematical difficulties, which was defined as students who scored below 40% on a standardized mathematics assessment. Schema-based instruction focuses on developing student understanding of underlying sematic structures of word problems. While these theories of problem types are also used in constructivist mathematics approaches, notably Cognitively Guided Instruction [
52], Jitendra and colleagues [
38] integrated schema theory with a behaviorist approach to pedagogy, namely explicit instruction. In this case, what is made explicit is the schema (or problem types) of each word problem and the steps to follow to solve the problems. The researchers used an intervention group, which received schema-based instruction, and a control group, which received instruction based on standards-based curriculum program adopted by the school. They found that the intervention group outscored students in the control group in two assessments of word problem solving, however, these gains were not maintained. Information processing was the largest category of theoretical orientations in the Disability Set of problem solving articles, representing 31% of the Disability Set of articles (
n = 11). In the non-Disability Set, information processing represented 8% of problem solving articles (
n = 9).
4.4. Constructivist Theoretical Orientation
The largest pedagogical orientation category in the entire data set of problem solving articles was constructivist, with 43 total articles. Forty of those articles were in the No-Disability Set, while three were in the Disability Set. Thirty-five percent of No-Disability Set articles on problem solving were coded as constructivist, compared to 11% of Disability Set articles. As we will discuss in depth, a common approach used in this set of articles was
problem posing. Problem posing is understood as a creative process in which an individual makes meaning of mathematical problems. Bonotto [
53] reported on a study in which students in an Italian elementary school were provided with artifacts, such as a list of discounts for visiting an amusement park, and were asked to develop problems based on the context. The analysis of the students’ generated problems focused on whether or not they were able to pose viable mathematical problems, as well as the creativity of their posed problems.
Only a small number of articles with a constructivist orientation to pedagogy in problem solving included disability (3 out of 43). Hunt and Vasquez [
54] conducted research with three students with learning disabilities, developing an intervention to increase students’ understanding of ratio. The intervention consisted of individualized tutoring, based on an instructional trajectory developed from research on the development of multiplicative thinking in the area of ratio [
55]. Students were encouraged to make sense of problems and develop their own strategies; the researchers scaffolded learning through both interaction and problem choice. They reported that all three students developed more sophisticated strategies around ratio during the intervention, although the initial baseline of one student was unstable which impacted analysis of that student’s growth. They noted that the “results from this study suggest the potential power of instruction that begins with a respect of how students approach solving mathematics problems and then adds meaningful teacher supports and prompts” [
54] (p. 189). Indeed, Hunt and Vasquez’s work involved a characteristically constructivist approach: the focus was on close attention to student’s mathematical thinking, with an assumption that instruction should build on student prior conceptions and students should choose their own strategies. Similarly, Powell et al. [
56] used constructivist research on student conceptions of the equal sign [
57] to design an intervention for students with mathematical disabilities. Indeed, these two studies demonstrate work across boundaries. Both studies grounded their interventions in mathematics education research, but used single subject methodologies that allowed for close analysis of student thinking and were quantifiable. Of note, both studies were published in special education journals, demonstrating a crossing of the research divide.
4.5. Sociocultural Theoretical Orientation
Highlighting the role of discourse, language and other semiotic systems in mediating mathematical thought, sociocultural theories focus on the interactional aspects of learning, whether between two people, within a mathematics classroom, or in wider cultural contexts [
58]. Sociocultural theories often deal with the identity development of individuals as deeply influenced by their participation in contexts. In coding this sample of articles on problem solving, we found 23 articles that used this lens to examine problem solving. Nineteen percent of the No-Disability Set (
n = 22) was coded under sociocultural, compared to 3% of the Disability Set (
n = 1). Francisco [
59], for example, analyzed in detail the collective problem solving of a group of high school students. The unit of analysis was not individual problem solving, but that of a group. In another study, Verzosa and Mulligan [
60] studied how students in the Philippines solved word problems, providing an intervention that focused on supporting the students in making meaning of problems both in their own language and in English, the mandated language of instruction. The study included a constructivist component, focused on close analysis of student learning. Moreover, the authors attended to multiple contextual layers: students solving problems in English when they had very little exposure to the language, even socially, as well as how student beliefs and motivation affected their choice of strategies during problem solving. In both studies, problem solving was understood as a collective product of group engagement in discourse.
4.6. Sociopolitical Pedagogical Orientation
We found few examples (3) of sociopolitical research in this problem solving set, all within the No-Disability Set. Birky et al. [
61] studied an exceptional African-American female middle school mathematics teacher, with an understanding of how she situated her own work in the political context of African-Americans in an inequitable U.S. school system. The authors focused on her mathematical teaching, as well as how her mathematical teaching was connected to the larger political context. We did not find a study in our sample that used a sociopolitical perspective on the problem solving of students with disabilities.
4.7. Word Problems and Problem Posing
After initial analysis, we chose to take a deeper look at two themes emerging from the initial exploration of the articles. We noticed that problem posing was a theme within the No Disability Set, while not present in the Disability Set. We also noticed that schema-based instruction was a theme within the No Disability Set, but with much more restrictive representation in the No-Disability Set. The research on students with disabilities was more focused on students solving word problems, which are typically associated with procedural problem solving. Twenty-five percent of articles in the No-Disability Set used the term word problems, while 56% of the articles in the Disability Set used the term word problems.
Much of the research in word problem solving for students with disabilities used the schema-based approach. Children in these studies were given “explicit instruction” on the problem types in a scripted intervention. Jitendra et al. [
38] (p. 257) made a clear distinction between the two pedagogies, “standards-based instruction is characterized by an inquiry-based, student-directed approach, whereas SBI [Schema Based Instruction] incorporates an explicit, teacher-mediated approach.” (The researchers used research in mathematics education and psychology to create a replicable procedure for solving word problems based on determining the problem type, using a pre-determined representation (or graphic organizer) for each problem type, and then to create an equation, and then solve. The intervention consisted of teacher modeling of these procedures, and then guided student practice. Over time, the scaffolds were faded so that students would be increasingly independent in their ability to identify problem schemas, represent information, and solve the problem. Problem solving here does not follow the definition presented by Schoenfeld [
40]; students are engaged in repetitive practice rather than creatively experimenting to find an answer. Not only was student learning scripted, but teacher actions were even more so. Intervention studies such as Jitendra et al. [
38] are designed around scripted teacher work so that fidelity in the intervention can then be verified and replicated in other settings. Both teaching and learning are not seen as creative, unique acts, but as aiming towards reproducible data. In studies based on the schema-based instruction, there was no analysis of individual student mathematical thinking. The data were reported at the group level, and was comprised of aggregated scores on assessments.
A subset of the non-disability research, but not present in the Disability Set, was research on problem posing. We found 11 studies of problem posing, 9 of which were included in a special issue of
Educational Studies in Mathematics, a leading mathematics education journal. In that issue, problem posing was defined as a process in which students used their experiences to “construct personal interpretations of concrete situations and from these situations formulate meaningful (i.e., non-trivial) mathematical problems” [
62] (p. 119). All of the problem posing articles in our sample that could be coded for methodology (
n = 7) were coded as qualitative.
Problem-posing research was focused on teachers as well as students. Teachers in this set of articles were understood as learners with their own set of understandings and motivations. Ticha and Hospesova [
63] analyzed the problem posing of pre-service teachers around fractions. Teaching itself was conceptualized as complex work, as “dynamic,” requiring “the ability to act adequately, to respond to situations and stimuli that come up during lessons, and to capitalize on these in order to improve the quality of their students’ education” [
63] (p. 134). According to Ticha and Hospesova, when pre-service teachers have the opportunity both to pose problems, and then to reflect on those problems collectively, they gain a deeper understanding of both the mathematical content and relevant pedagogical concerns.
One consistent theme in the problem posing literature in our sample was the connection between problem posing, creativity, and mathematical giftedness. Van Harpen and Presmeg [
62], for example, made these connections explicit as they sought to understand how problem posing is connected to high ability in mathematics. Considering that more than one article connected problem posing to mathematical giftedness, and that none of the articles focused on disability, we wonder how creativity in mathematics may be constructed to exclude learners with disabilities. Do articles that seek to understand the relationship between problem posing and mathematical ability further deny access to those who are not currently seen as mathematically able? Are students with disabilities not seen as competent to make sense of their worlds using mathematics? On the one hand, the literature on word problems solved through explicit schema-based instruction was almost exclusively applied to students with disabilities. On the other hand, the literature on problem posing was almost exclusively applied to students without disabilities. Thus, we derive that within the general category of research on problem solving, students with disabilities are less likely to be researched as meaning makers and were more likely to be asked to work procedurally from a more limited set of strategic options compared to students without disabilities.
One article on problem posing challenged this deficit framing of students. While disability was not a focus of this article, Bonotto [
53] did mention within the text of the article how the use of artifacts in authentic problem posing connected to learner’s experience was particularly useful for the students who had experienced prior difficulties in mathematics that were included in the study. One student, described by Bonotto [
53] (p. 45) as “less able,” declared the use of the amusement park flyer as “not a problem. Problems are full of words, and I can never do them because I do not understand very much. I can do these though because anyone can read prices on a flyer.” Another student, described as having “learning difficulties,” engaged in problem posing around restaurant menus, remarked that, “This is easier than the problems in the book because we already know how things work at a restaurant.” Both students’ statements contrast problem posing with school math, in which they solve word problems in the book. These student comments suggest that those who have had difficulties with school mathematics can successfully engage in real-world problem solving connected to artifacts that resonate with their experiences.
Taken together, these articles on schema-based word problem solving instruction and problem posing highlight the very different theoretical and methodological parameters around research in mathematics for those with, and those without, disabilities. We do not suggest that schema-based instruction is not an appropriate pedagogical or methodological approach. We believe this research is crucial to providing viable intervention options for educating a wider range of students in problem solving. Rather, we question why there is currently such a limited repertoire of research in problem solving for students with disabilities. While we hope that schema-based instructional research continues, we deeply believe that students with disabilities are a heterogeneous group and research needs to explore multiple avenues for their mathematical education, most critically their inclusion in standards-based instruction.
5. Discussion
In this article we sought to address the research questions: (1) How does current educational research on problem solving in mathematics differ for students with and without disabilities? (2) How are students with and without disabilities conceptualized as problem-solvers in current educational research? Based on the larger analysis of research published between 2013 and 2015, there was a substantial difference between educational research focused on learners with disabilities, and that which was focused on those without disabilities [
6]. For those with disabilities, mathematical learning was understood primarily from medical, behavioral and information processing perspectives, the research was predominantly quantitative, and rarely focused on the teacher. For those without disabilities, mathematical learning was understood primarily through constructivist, sociocultural, and sociopolitical perspectives, the research was both quantitative and qualitative, and almost 40% of the research was focused on the role of the teacher in learning.
The findings were similar when we focused in this article on the subset of articles on problem solving. In these articles, the research methods were even more disparate: while almost all research on problem solving that included students with disabilities was quantitative (86%), only 35% of research on students without disabilities was quantitative. Instead, 50% of problem solving research on students without disabilities was qualitative, compared to only 6% of research on students with disabilities. Problem solving, then, is studied in very different ways for learners with and without disabilities. Students without disabilities are studied through close analysis of mathematical thinking, often individual. Students with disabilities are most often studied through aggregate test scores, in groups, with little or no analysis of individual thinking.
Having worked with both students with and without disabilities in mathematics for many years, we find this glaring disparity in research methods puzzling, as we know that students with disabilities are an extremely heterogeneous group, even when broken up into disability categories. Students with mathematical learning disabilities, for example, often have particularly unique ways of approaching mathematics, yet research on these students is typically not sensitive to individual differences, instead seeking to understand all individuals with a single disability as a unified group. Research by Hunt and Empson [
55] and Lewis [
64] from our large data set challenges these boundaries, paying close attention to the unique thinking of individual students with learning disabilities.
While we found these few examples of constructivist learning theory being applied to students with disabilities, we found very little research that used sociocultural approaches to understand the mathematical learning of students with disabilities. How might it shift understandings of learners with disabilities to understand problem-solving as collective, instead of individualized, as researchers like Francisco [
59] did with students without disabilities? While not within our set of problem solving articles, we did find a small set of research in the data set that used sociocultural analysis to better understand how disability is produced in mathematics classrooms. Heyd-Metzuyanim [
65] analyzed the co-construction of learning disabilities in mathematics through analysis of interaction between a mathematics teacher and a student. Lambert [
66] analyzed how disability and ability in mathematics were constructed differently by teachers based on different pedagogies; disability shifted in contexts, produced through interaction within particular pedagogical structures. These studies suggest connections between sociocultural analysis and disability studies, as well as possibilities for further explorations.
We also found a research divide when we compared the theoretical orientation of problem solving research for those with and without disabilities. The mathematical problem solving of students with disabilities was primarily understood through medical, behavioral, and informational processing approaches. The mathematical problem solving of students without disabilities was primarily understood through constructivist and sociocultural approaches. In problem solving, this meant that students with disabilities were in many cases being asked to follow set procedures to solve word problems, while students without disabilities were more likely to be understood as creative, unique problem solvers who engaged in both solving and posing mathematical problems.
We argue that the existence of this research divide in methodologies and theoretical orientations, historically in the development of each academic field, continually reinscribes an assumption that students with disabilities are not doers and thinkers of mathematics. Learners with disabilities are understood through a medical model that seeks to identify psychometric deficits that can inform remediation. These remediations are typically designed through a behaviorist lens, focusing on simplifying mathematics by breaking mathematics into tasks, teaching students procedures. Policy initiatives such as Response to Intervention (RTI) ask that interventions to be evidence-based, yet the definition of evidence privileges particular quantitative methodologies.
Assumption that certain learners need rigid, narrow pedagogies, while others can handle real meaning making is the core assumption that needs to be challenged. We assert that as long as this research divide is unchallenged, such assumptions will continue. The field of mathematics education will continue to defer research involving students with disabilities to another field (e.g., special education), not make explicit disability issues in research, and/or explicitly exclude disability. In one article from the sample, Múñez et al. [
67] (p. 341) describe their participants as follows, “Participants were 50 students from a public secondary school in a middle-class suburb. We excluded from the analyses 1 student who was diagnosed with language/learning problems.” There is no further discussion of why disability excludes this student from participation, leaving us to assume that these mathematics education researchers, like many others, simply assume that individuals with disabilities are so qualitatively different than those without disabilities that they should not be studied together. What is so inherently exclusionary about disability that it is the only routinely excluded demographic category in mathematical research?
6. Conclusions
Currently, despite widespread policy language calling for increased access and achievement for “all learners,” the field of mathematics education rarely includes students with disabilities. Instead, almost all mathematics educational research on students with disabilities is conducted within the academic field of special education. The mathematics learning of students with disabilities is understood through a narrow set of methodologies and pedagogies, limiting these students’ access to standards-based mathematics in classrooms. The research divide constructs and reifies what many consider to be a “common sense” assumption: children with and without disabilities are different, and should be educated differently in mathematics. The pedagogical and methodological divides that separate research in mathematics on students with and without disabilities are a critical issue for mathematics education because they justify deficit constructions of students with disabilities, construct students with disabilities as passive rather than active learners of mathematics, and limit our understanding of how contexts shape learning for all students.
Different kinds of research ask different questions. Does it matter that we only ask certain questions about the mathematical learning of students with disabilities? As mathematics education researchers, we must honor our long-standing commitment to equity for marginalized groups of students. Both activists and academics in the disability rights movement increasingly demand that diversity include disability [
68]. While mathematics educational researchers bring an arsenal of conceptual and theoretical tools to their work, DSME provides an additional framework that shifts perception of disability from a deficit orientation toward one focused on difference and uniqueness. Thus, we seek a deeper analysis of disability in mathematics through these lenses, including analysis of how disability intersects with race and genders [
69]. We call on all mathematics educational researchers to include students with disabilities in research, not as passive subjects, but as active constructors of meaning.
We call for including disability, not only to improve the lives of those with disability, but aslo to advance the fields of mathematics education and special education. As de Freitas and Sinclair [
70] have suggested, mathematics educational researchers could benefit from more deeply considering the perspective of learners with disabilities, as exploring the mathematical world through these diverse learners can help us better understand the relationship between embodiment and knowing in mathematics. We believe that shifting mathematics research towards learners with disabilities will allow the educational field to rethink assumptions that privilege the mythical “normal” mathematical learner.
The borders between these academic fields police a distinction between students without disabilities and those with disabilities, who are not recognized as competent and able mathematics learners. These learners are separated from inquiry and problem solving pedagogy and curriculum, which can affect not only learning, but also identity development, or who students with disabilities are learning to become in mathematics. Non-disabled peers also stand to academically and socially benefit as classrooms shift to recognize and develop a wider range of mathematical competencies and perspectives. Deficit-based assumptions about the mathematical meaning-making potential of students with disabilities must be challenged by mathematics educational research.