1. Introduction
Technology has become an important component of teaching and learning, particularly in mathematics, yet its effectiveness varies. As educators advocate for purposeful use of technology [
1,
2,
3], it is critical to investigate children’s interactions with technology to inform classroom practice, educational research, and technology design. Educational technology offers teachers and students a broad array of representations of mathematics and mathematical learning opportunities [
2,
4], and some types of educational technology can have equalizing effects on achievement across demographic groups [
5]. Researchers have begun to investigate touchscreen technology use in mathematics, including evaluating app content and quality [
6,
7,
8,
9], influences of multi-touch apps on learning outcomes [
10,
11] and experiences [
12,
13,
14], and ways children access app affordances [
15,
16]. However, less research has examined characteristics of both children and apps that contribute to this activity, alongside patterns that emerge in these interactions. Therefore, this study focuses on fifth grade (10–11 year-old) children’s interactions with touchscreen mathematics apps, in particular how attribute modification is relevant to this activity. Understanding these characteristics and patterns may inform design, implementation, and research concerning educational technology.
The paper begins with pertinent theoretical and empirical background, including Artifact-Centric Activity Theory, educational technology in mathematics education, attributes, and attribute modification. Next, the paper describes the iterative qualitative methodology used during the study. Results focus on evidence of patterns of attribute modification. The discussion and conclusion contextualize these results in theory and empirical research while offering applications for research, design, and practice involving educational technology within and beyond mathematics education. Together, this supports the assertion that attributes of people and technology, along with ways to encourage appropriate attribute modification, are relevant when designing, implementing, and researching educational technology.
2. Background
This study is grounded in Artifact-Centric Activity Theory and builds on research on educational technology, with a particular focus on attributes and attribute modification.
2.1. Theoretical Framework: Artifact-Centric Activity Theory
Artifact-Centric Activity Theory (ACAT) frames the interactions involved in learning mathematics while using technology [
17,
18]. ACAT stems from Artifact Theory, which asserts that activity is the continuously developing interaction between subject and object [
19]. Objects populate the world and exist independent of humans, having “objective” (i.e., widely accepted) meanings. However, humans that interact with the objects produce an image (e.g., opinion, understanding) of the object via activity that may not be consistent with the objective meaning. Subjects have needs to fulfill, including learning (e.g., developing understandings and skills), which requires interacting with objects. These interactions are activities, which are ways of relating subject to object, and changes in these activities and their outcomes provide evidence of learning. For example, two children (i.e., subjects) are learning about subtraction (i.e., object). The widely accepted, socioculturally constructed meaning of subtraction can be depicted with the equation
x − y = (
x − y). However, the children have different understandings (i.e., images) of subtraction. One child may consider subtraction to be ‘taking away’. The other child may believe it to be a simplified way to represent counting backwards. Engaging with subtraction may lead the children to change their images (i.e., the children may learn). Activity Theory is useful for understanding human interactions with objects in the world (e.g., human-computer interaction) and for designing these objects, as it places these interactions in the context of activities [
20].
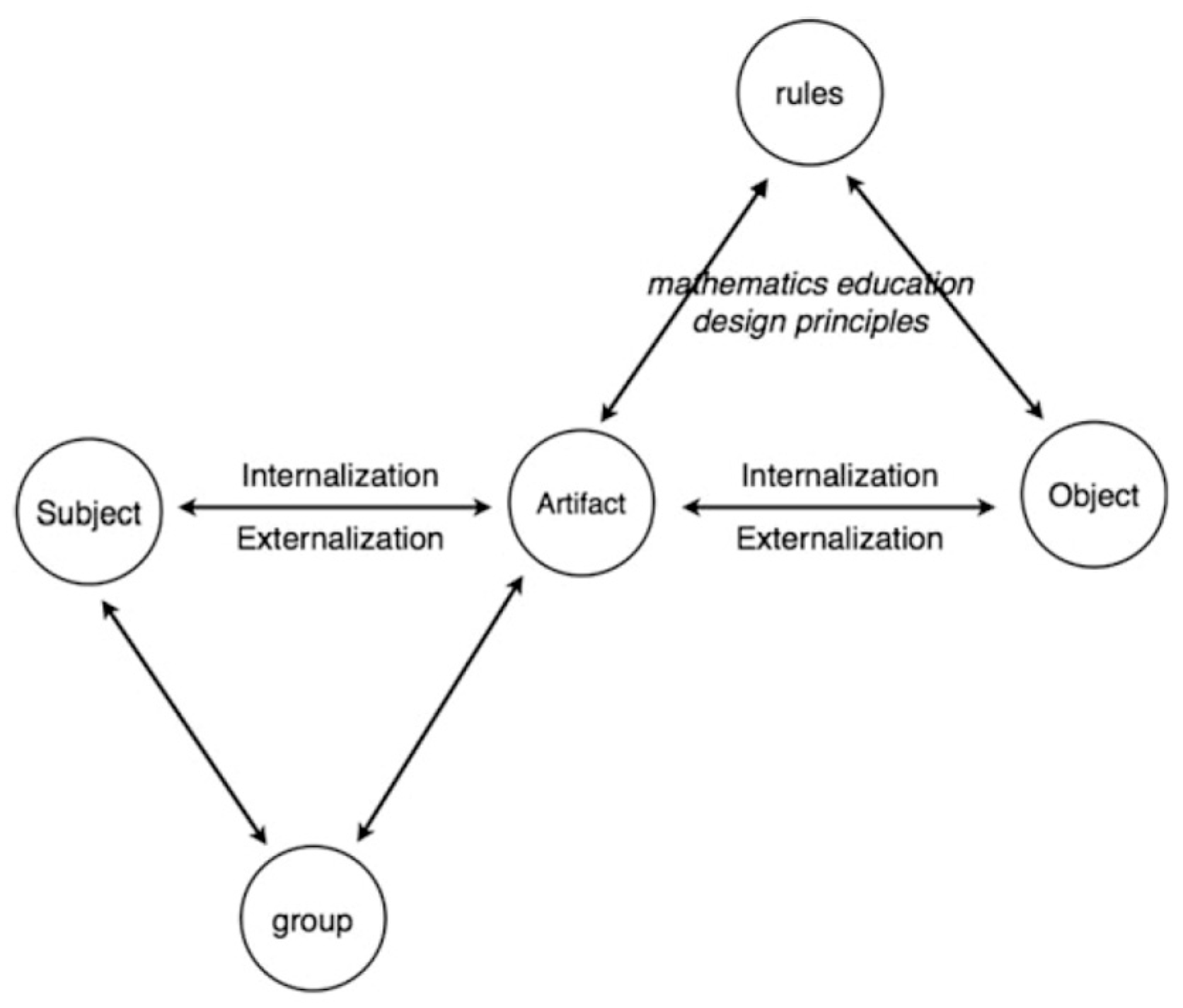
Extending Activity Theory, ACAT accounts for the subject (e.g., student), group (e.g., other people), artifact (e.g., iPad app), object (e.g., the mathematics), and rules (e.g., systems from relevant disciplines) (see
Figure 1). ACAT focuses on an artifact, rather than an instrument, as an artifact can be a physical thing, whereas an instrument includes the ways a subject uses the thing for a specific task. Developing an instrument from an artifact is instrumental genesis [
21], a process organized with support from others via instrumental orchestration [
22]. Although these processes may occur during the interactions, identifying the central component of the framework as an artifact permits ACAT greater applicability for contexts in which a subject is not present (e.g., designing an artifact in relation to object and rules, before it becomes an instrument).
The main axis of ACAT is the activity between a subject (e.g., child) and an object (e.g., mathematics), mediated by an artifact (e.g., mathematics app) [
17,
18]. The presence of the artifact at the center of the axis focuses attention on its role as mediator between subject and object. The subject’s use of an artifact influences their activity as they externalize mental representations using the artifact and internalize knowledge interpreted from the representations provided by the artifact in response to their actions. Changes in the activity and the subject’s externalized representations provide evidence of learning. The artifact externalizes the object as it reflects the designer’s knowledge, as the designer creates the artifact according to their knowledge of the object. The lower left triangle of ACAT accounts for the role of the group (e.g., classroom peers, teacher) in the subject-artifact relationship, which acknowledges instrumental genesis and involves instrumental orchestration that occur in settings where others are present. The upper right triangle of ACAT accounts for the role of the rules (e.g., design considerations from mathematics, technology, etc.) in the artifact–object relationship, which acknowledges considerations of what one wishes the subject to learn and what knowledge and skills will be required for interacting with the artifact.
Continuing the subtraction example, the children are now using cubes, six of which are in a row. The ‘counting backwards’ child sequentially points to individual cubes, saying “6… so 5, 4, 3, 2… 2.” In response, the ‘taking away’ child pushes aside four cubes, explaining, “right—six take away four is two.” The cubes mediate the children’s exploration of subtraction (i.e., artifact mediates subject-object activity). The children interact with each other and develop ways to use the cubes (i.e., role of group). The cubes have been designed to be easily manipulable pieces that can be used to represent many mathematical concepts, including subtraction (i.e., role of rules). Through this activity, the children adapt their understandings of subtraction (i.e., they learn). However, the meaning each assigns to the object may still differ from the objective meaning.
2.2. Educational Technology in Mathematics Learning
Technology plays an increasingly prominent role in learning mathematics, with apps for touchscreen tablets (e.g., iPads) becoming a growing presence in mathematics classrooms. In the context of ACAT, educational technology, such as mathematics apps, are artifacts, mediating the activity between the child (i.e., subject) and the mathematics (i.e., object). However, few mathematics apps are effective in supporting students’ development of mathematics knowledge [
8], as the vast majority of apps involve little more than passive, repetitive practice [
7]. However, some apps feature virtual manipulatives, which are “an interactive, technology-enabled visual representation of a dynamic mathematical object, including all of the programmable features that allow it to be manipulated, which presents opportunities for constructing mathematical knowledge” [
23] (p. 13). Virtual manipulatives provide categories of affordances that support learning [
24,
25] and can positively influence learning outcomes [
10,
26]. Research indicates that when students used virtual manipulatives to learn fraction concepts, fewer demographic characteristics (e.g., English Language Learner status, socio-economic status) predicted performance than when students did not use virtual manipulatives to learn the same content [
5].
Experiences with technology vary based on characteristics of the subjects [
15] and the artifacts [
27]. For example, educational technology often includes scaffolding to support completion of tasks that would otherwise be too difficult [
28], and some technology progressively adjusts scaffolding in accordance with the amount of support the user needs [
29,
30]. However, users do not always perceive or use aspects of technology as designers intended, though signifiers (e.g., labels) may help advertise these potential actions [
31]. Furthermore, children do not spontaneously reflect on their strategies or actions when interacting with technology, often repeating the same strategies whether or not they are successful or efficient [
12]. Thus, researchers recognize the importance of multiple types of scaffolding, both within the technology and from an external expert (e.g., teacher) [
32]. Most prior research primarily focused on outcomes of interacting with mathematics apps, but researchers have begun examining the activity itself [
13,
14], opening the door to identify characteristics and patterns present in such activity.
2.3. Attributes
Characteristics of people or things are “attributes” [
33], which form the basis of interactions with technology [
34,
35]. Applied to the context of ACAT, subjects (i.e., children), artifacts (i.e., apps), and objects (i.e., mathematics) have attributes that contribute to the activity. In this context, the focus is on attributes of the subject and the artifact because the artifact mediates the activity and represents only certain attributes of the object chosen by the designers of the artifact. Subjects and artifacts have multiple categories of attributes. Both subjects and artifacts have content attributes and technological attributes, while subjects have personal attributes and artifacts have structural attributes [
34,
35]. Aligning with the importance of the object in ACAT and for practical classroom applications, this classification structure places object-related (i.e., educational content) attributes as equal to the other categories. Many alternative structures de-emphasize these attributes, implicitly spreading them across multiple categories (e.g., challenge, learning performance) (cf. [
36,
37,
38]). The scope of this study does not extend to detailed description of specific attributes, attributes of rules or groups, or comparison to alternative attribute classifications.
Content attributes concern representations of the object, which in this context are mathematical attributes [
34,
35]. For subjects, mathematical attributes include prior knowledge pertaining to the object and its representations (e.g., comparison of integers, symbolic form, number line). For artifacts, mathematical attributes include representations of the object (e.g., integers on a number line). Additional evidence of content attributes of artifacts [
39,
40] and subjects [
41,
42] is present in other literature. Technological attributes concern the physical interactions with the technology [
34,
35]. For subjects, technological attributes include those involved in physically coordinating input (e.g., familiarity with a gesture, motor coordination). For artifacts, technological attributes include those involved in recognizing the input (e.g., scope of acceptable gestures for a particular function). Further evidence of technological attributes of artifacts [
36,
43,
44] and subjects [
6,
45] is present in other literature.
Subjects and artifacts each have an additional, unique category of attributes: personal and structural, respectively [
34,
35]. Personal attributes are characteristics of a subject’s personality that influence the activity, including affect and goals (e.g., goal of speed vs. accuracy). Structural attributes are non-content presentation features, including feedback and scaffolding (e.g., “Solution” scaffold revealing a worked example). Further evidence of personal attributes of subjects [
46,
47] and structural attributes of artifacts [
38,
48,
49] is present in other literature.
Through the lens of ACAT, one can apply these attribute types to an example from activity involving with Motion Math: Zoom, an app used in this study. The app presents a number line showing 0–40 by intervals of ten and requires the child to find where “15” fits (artifact mathematical attributes: number line, intervals of ten). The child identifies that the place for 15 will be within 10–20 (subject mathematical attributes: ones and tens, comparison) but struggles to perform the pinch gesture (subject technological attributes: fine motor skills), and the intervals do not change (artifact technological attribute: gesture recognition). The child continues trying (subject personal attribute: persistence) and an animated demonstration of the pinching gesture appears (artifact structural attribute: scaffolding).
2.4. Attribute Modification
Attributes do not remain static, and attribute alignment affects attribute modification [
34,
35]. Alignment of content attributes (e.g., mathematical attributes) and technological attributes varies. For example, estimating magnitude on a number line to 1000 may be developmentally appropriate for an eight-year-old child (i.e., relatively aligned mathematical attributes), but is likely to be developmentally inappropriate for a six-year-old child who is still working with number lines to 10 (i.e., misaligned mathematical attributes) [
50]. Subjects and artifacts affect attribute alignment by modifying attributes. Modifying attributes involves either changing attributes being applied (e.g., subject improves comparison skills) or applying different attributes (e.g., subject uses a new gesture; artifact changes tasks from comparing integers to comparing decimals). Attribute modification is proactive or reactive [
34,
35]. Reactive attribute modification occurs when an artifact modifies artifact attributes, resulting in the subject applying and modifying subject attributes. When the attributes sufficiently align, the subject successfully completes the task. In response, the artifact modifies artifact attributes by presenting tasks involving a different combination of attributes (e.g., removes scaffolding; presents slightly different mathematics content). The subject responds by continuing the cycle, applying and modifying subject attributes. Proactive attribute modification occurs when artifacts modify artifact attributes, subjects modify subject attributes, and subjects also modify artifact attributes. In the context of interacting with an app, proactive attribute modification does not require programming new attributes of the app; rather, it involves purposefully causing the app to apply different attributes. For example, a child who struggles to complete a task may proactively choose a task that requires a different combination of mathematical attributes. However, few apps offer extensive user control over individual app attributes [
18].
One can view attribute alignment and modification through the lens of ACAT, applied to an extension of the aforementioned activity involving Motion Math: Zoom. The child may complete a level by accurately completing tasks involving integers from 0 to 100 by intervals of one and ten (aligned mathematical attributes), rarely requiring changing intervals by pinching. The app then presents a level featuring tasks involving intervals integers from 0 to 1000 by intervals of one, ten, and one hundred (modified artifact mathematical attributes), and pinching to change intervals is often required (modified artifact attributes). At first, the child attempts mathematically accurate actions (aligned mathematical attributes) but struggles to pinch effectively (misaligned technological attributes). Over time, the child hones the gesture (modifying subject technological attributes aligns technological attributes). The child completes the level and the app presents another level with slightly different mathematics content (reactive attribute modification). Eventually, the child reaches a level featuring tasks involving whole numbers and decimals from 0 to 5 by intervals of one hundredth, one tenth, and one whole. The child can perform the required gestures (aligned technological attributes) but struggles to correctly complete tasks due to being unfamiliar with hundredths (misaligned mathematical attributes). Upon failing to advance to the next level, the child may allow the app to repeat the level (reactive attempts to modify subject attributes) or return to the menu and choose a level featuring decimals to tenths (subject proactively modifies object mathematical attributes). Attribute modification occurs throughout responsive, interactive activity between subject and object, mediated by an artifact. Therefore, this study investigated patterns of attribute modification during activity that occurred as children interacted with mathematics apps to inform research, practice, and design of educational technology.
3. Materials and Methods
Researchers used iterative exploratory qualitative methods to conduct this study, building on a prior research study. The lead researcher designed and conducted the initial exploratory study, which led to emergent themes, including attribute modification [
34]. For this study, the two researchers conducted a focused, deeper analysis of the data, specifically examining attribute modification. The addition of a second researcher integrated multiple perspectives into this analysis, both distinguishing it from the results of the initial exploratory study and providing triangulation to strengthen validity [
51]. However, as the study is qualitative and exploratory [
52], the primary focus is on trustworthiness through transparency and consistency of methods, analyses, results, and discussion, as well as their alignment with the theoretical framework [
53]. As is standard for exploratory work, the researchers acknowledge that additional studies are required to address delimitations of sampling, setting, and other features of the present study [
52]. Similar to other studies focusing on children’s interactions with virtual manipulative touchscreen tablet apps [
11], pre-study pilot activities included choosing the apps, creating interview and observation protocols, and refining data collection techniques [
34]. The research question that guided this study was: what patterns of proactive and reactive attribute modification occur when children interact with mathematics virtual manipulative touchscreen tablet apps?
3.1. Setting and Participants
The study occurred in interview rooms on the campus of a public university in the U.S. Participants were 10 fifth-grade children: six male and four female, five 10 years old and five 11 years old. Methodologists recommend samples large enough to achieve data saturation without hindering in-depth analysis [
54], with ten participants considered appropriate [
55,
56]. To recruit participants, the lead researcher worked with local elementary schools to distribute fliers. The study accepted all qualified children (i.e., enrolled in fifth grade, no previous experience with the chosen apps) whose parents consented to allow participation until reaching the target sample size. As in other studies of children’s interactions with apps [
11], the lab setting was chosen due to the availability of resources (e.g., recording devices linked to secure server, adjoining one-way window observation room with sound feed for parents).
3.2. Materials
The piloting process involved selecting apps based on specific criteria (e.g., developmentally appropriate mathematics content) and seeking feedback from children who interacted with the initial group of apps [
34]. Piloting resulted in the choice of two mathematics virtual manipulative touchscreen tablet apps (henceforth, “apps”): Motion Math: Zoom and DragonBox Algebra 12+.
3.2.1. Motion Math: Zoom
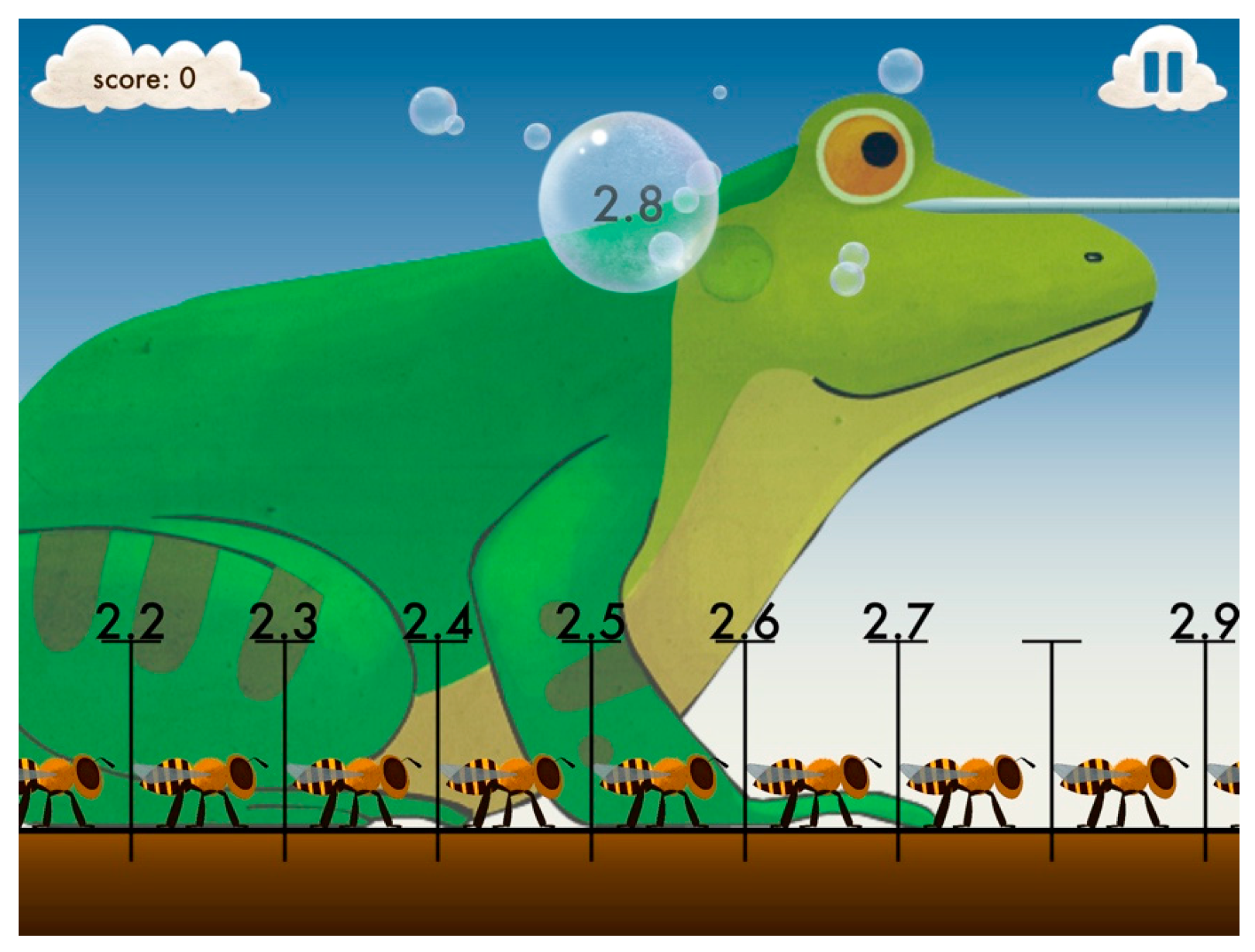
Motion Math: Zoom features content related to magnitude, number comparisons, place value, and estimation on the number line, including decimals to the thousandths place, integers to 10,000, and positive and negative numbers (see
Figure 2). To find and input an answer, one must swipe or drag left or right to change position on the number line and tap to pop bubbles in the intended location. At times, one must “pinch” horizontally by bringing two fingers apart or together to zoom, which alters the intervals between visible numbers (e.g., ones, tens, hundreds, etc.). Each level consists of a series of tasks, such as navigating the number line to place 35 when the number line initially shows 60–100 with intervals of ten (i.e., 60, 70, 80, 90, 100). After one completes Level 1 (introduction with demonstration) Motion Math: Zoom permits access to several levels (2, 6, 9, 12, and 15) of the 24 levels from the menu. Successful completion of certain levels unlocks additional opportunities to skip levels via the menu. One can also activate or deactivate the “needle” timer, which pops the bubble and ends the level if one has not quickly placed the number. The default needle setting is inactive, but after one quickly completes Level 6, the app suggests skipping levels. If accepted, the app presents Level 15 and activates the needle. This is the only situation in which the app automatically activates the needle. In this study, all ten participants attempted levels involving positive integers to 1000, and nine participants attempted levels involving positive integers to 10,000. All ten participants also attempted at least one level involving thousandths. However, only four participants attempted more than seven different levels.
3.2.2. DragonBox Algebra 12+
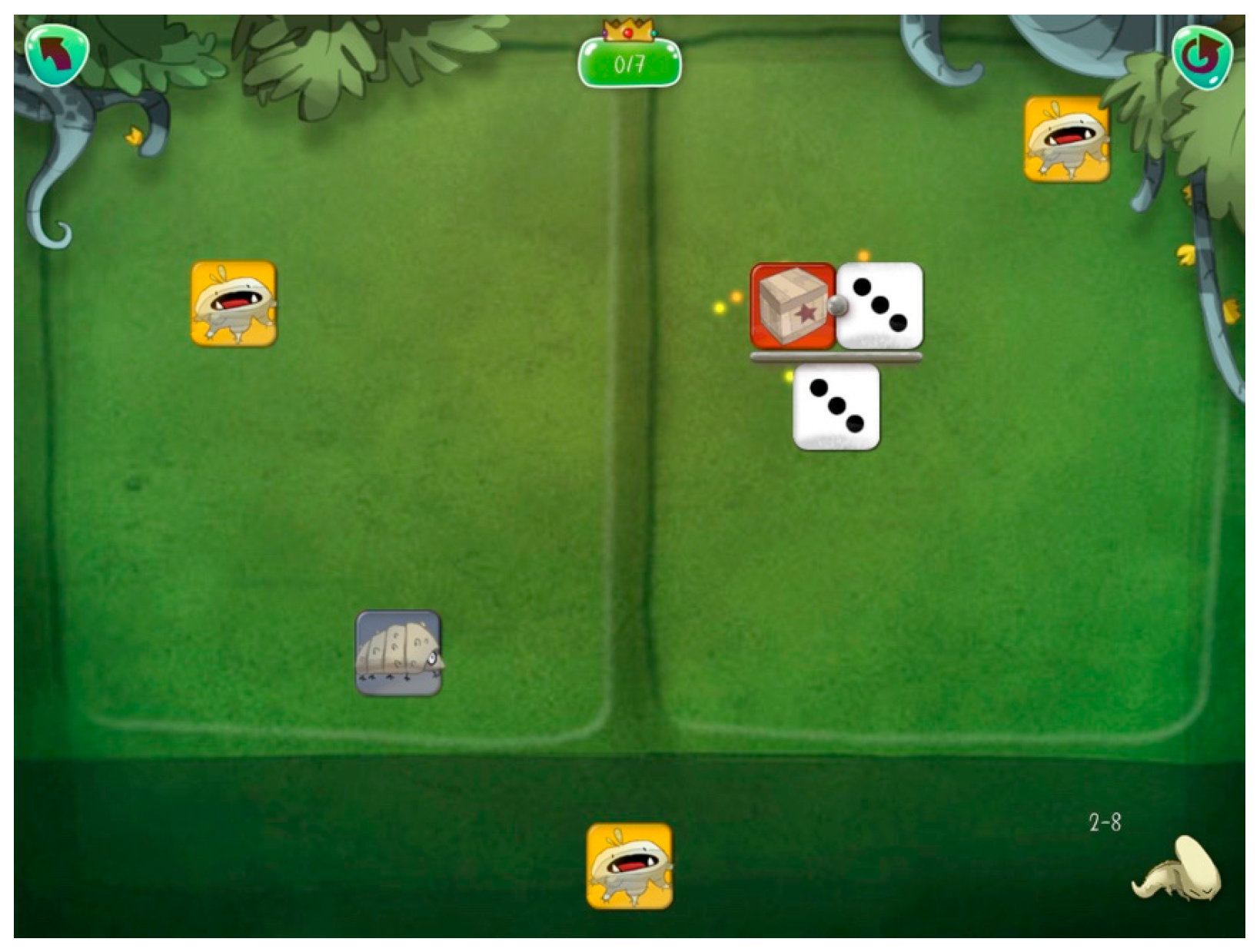
DragonBox Algebra 12+ includes content related to additive and multiplicative properties, operations, solving expressions and equations, negative and positive values, and fractions. The app consists of ten 20-level chapters wherein one completes levels in each chapter to grow a dragon. To complete a level, one must solve an equation or expression (see
Figure 3), isolating the “dragon box” or X. The app includes demonstration levels to introduce new content (“new powers”) before integrating the content into subsequent levels. Each level consists of one task with several steps required for completion, such as applying the additive inverse property and the additive identity property. Depending on the level, this can involve using combinations of values from outside the equation space (e.g., x + y = b + c: add −y to both sides), within one side of the equation (e.g., x + y + −y = b + c: add y + −y), and across sides of the equation (e.g., x + y = b + c: subtract y from both sides). One employs single-touch drag or tap gestures to interact with tiles to perform the steps to necessary to complete each level. The app presents levels in sequential order, but one may return to previously completed levels through the menus outside a level. Menu options within a level allow for watching an animation of the solution to the level, restarting a level, or undoing a move. In this study, all ten participants encountered additive identity, inverse, and equality properties, and nine participants encountered multiplicative inverse and identity properties. Two participants progressed to using the additive inverse property across the equation space, with one also progressing to using the multiplicative inverse across the equation space.
3.3. Study Procedures
Each child participated in one individual task-based interview conducted by a researcher, akin to other investigations of children’s interactions with apps [
11]. During each semistructured task-based interview (cf. [
57]), the lead researcher provided environments in which to solve problems (apps) that presented tasks in an organized manner (i.e., levels), but the researcher did not assist in task completion. During piloting, this structure was chosen over prompted think-aloud protocols (cf. [
58]), which produced few informative utterances while distracting participants from physically interacting with the apps. The semistructured task-based interview structure afforded separate periods focusing on physical interactions and reflection. The lead researcher had prior experience teaching elementary school and conducting individual task-based interviews, but had not met any of the children prior to participation.
The semistructured interview (see
Figure 4) began with an introduction to outline the procedures and answer the participant’s questions. Next, the participant interacted with the first app for up to 30 min. The researcher avoided interrupting the interactions and the participant could choose to end the interaction at any time. After the app interaction time, the researcher asked follow-up questions pertaining to interactions with the first app (e.g., How did you figure out…?; How did you use what you already knew?; What did you learn?; What could make the app better?). The process was repeated for the second app. All questions were semistructured, allowing flexibility to focus on key, often emergent themes while accounting for participants’ responses [
59]. After the participant completed both interaction-question sections, the researcher asked brief, semistructured summative questions (e.g., Which app did you like better? Why?; What mathematics did you notice in these apps?; What helped you complete the tasks? How did it help?). To control for possible effects of the interview sequence, five participants started with Motion Math: Zoom and five participants started with Dragon Box Algebra 12+. However, analyses revealed no noticeable effects of interview sequence.
3.4. Data Sources and Instruments
Video recordings and observation field notes served as data sources for this study. The recordings provided audiovisual records of the activity and participants’ responses to questions, as in other research concerning activity involving children and apps [
60]. Two devices, a computer camera immediately adjacent to the iPad and a wall-mounted camera, both focused on the interaction space (see
Figure 5), recorded each session. The interviewer followed an observation protocol to take observation field notes that complemented video data. Thus, the researchers could examine data from multiple sources to address the research questions [
61]. To preserve anonymity, the lead researcher assigned each participant a unique code to label all relevant data. The lead researcher checked the videos to insure participants’ faces and names were not present.
3.5. Analysis
This study involved two phases of analyses. As part of a larger exploratory study, the lead researcher conducted eight iterative, interrelated stages of analytic memoing, eclectic coding, and analysis during and after data collection [
34]. Analytic memoing is effective for recording information and interpretations concerning the data and the analysis process, especially for creating codeable textual data that accompanies visual data [
56]. Eclectic coding involves applying multiple coding methods and recoding based on interpretations of the initial coding [
62] and is appropriate for iterative data analyses. The first analysis phase resulted in codes, categories, themes, and an integrated conceptual framework [
34]. The second phase of analysis, conducted for this study, consisted of a deeper investigation focused solely on the emergent theme of attribute modification. This analysis involved both researchers returning to the videos to generate and code analytic memos centered on attribute modification. The provisional coding categories of proactive and reactive attribute modification emerged in the exploratory study, but the researchers identified specific subcategories of interaction patterns during this analysis. As in other qualitative studies [
63], researchers sought consensus through discussion and comparison to ensure clear and reliable coding, rather than quantifying a reliability measure.
4. Results
Results indicated that reactive and proactive attribute modification occurred throughout the interactions. This section presents three categories of evidence of patterns related to attribute modification: reactive attribute modification, proactive attribute modification, and unperceived attributes and opportunities for proactive attribute modification. Within each section, results appear by specific pattern. The categorization is descriptive, rather than prescriptive; therefore, the researchers did not quantify combinations of attributes, degrees of attribute changes, or number of attempts required for success, etc. for membership in a category or subcategory. The categories describe activity, not children; across their task-based interview, each participant could exhibit any combination of these patterns.
4.1. Reactive Attribute Modification
Reactive attribute modification occurred when participants attempted to align attributes by modifying subject attributes or combinations of attributes applied in response to the app modifying its artifact attributes. Two categories of reactive modification patterns emerged: (a) linear progression, and (b) repeated repetition. Each category of reactive modification could involve mathematical and technological attributes.
4.1.1. Linear Progression
Linear progression patterns occurred when participants sufficiently modified subject attributes to progress through a sequence of levels in the order suggested by the app, often intended to be of increasing difficulty. This involved either applying versions of the same attribute or applying different attributes. Participants could linearly progress through levels by applying versions of the same attribute. All participants did this at some time during interactions with at least one of the apps. For example, while interacting with DragonBox Algebra 12+, every participant sufficiently modified and applied subject attributes to progress from Level 1:03 to Level 1:08 without restarting a level or using the Solution feature. These tasks required applying the newly introduced additive inverse property (i.e., aligning mathematical attributes) in different equations. Sometimes, participants modified subject attributes by changing which attributes they applied, such as during Level 1:05, when Participant 10 tried to isolate the dragon box using the multiplicative inverse property, attempting to move variables from one side of the equation space to the other instead of using the additive inverse property to simplify the equation. However, the app did not yet permit using the multiplicative inverse property, and Participant 10 soon correctly applied the additive inverse property to complete the task (i.e., modified subject mathematical attributes to apply required property, aligning subject and artifact mathematical attributes). Other participants (2, 3, 4, 9) consistently correctly applied additive inverse property and did not struggle during these tasks (i.e., interactions showed aligned subject and artifact mathematical attributes). During interactions with Motion Math: Zoom, participants often progressed linearly by reactively modifying subject attributes and applying them on subsequent tasks and levels. Six participants (1, 3, 6, 7, 9, 10) sequentially completed Levels 2–5 without repeating a level. Every task in these levels required comparing positive integers, progressing from comparing within 0–40 by ones (Level 2) to comparing within 0–1000 by ones, tens, or hundreds (Level 5), and these participants modified and applied their subject mathematical attributes accordingly.
Participants also linearly progressed through tasks using reactive attribute modification by applying markedly different combinations of user attributes from one task to the next. For example, to complete Levels 1:01–1:02 in Dragon Box Algebra 12+, participants were only required to use the tap input gesture (i.e., combination of technological attributes). However, beginning on Level 1:03, the app required the drag input gesture for some tasks. All participants reacted to this change in artifact technological attributes by sufficiently modifying and applying relevant subject technological attributes (i.e., using the tap input or drag input gesture as necessary) to progress through the tasks. All tasks in Motion Math: Zoom required comparing rational numbers, but only Levels 9–11, 17, and 21–24 included tasks that required comparing negative numbers. All participants modified and applied subject mathematical attributes related to comparison of rational numbers (e.g., comparison and magnitude of integers), but only Participants 4, 5, and 6 encountered tasks wherein they could modify and apply subject mathematical attributes specific to comparison of negative numbers (e.g., comparison and magnitude of negative numbers). Participants could thus reactively modify subject attributes by applying versions of the same attribute or applying different attributes in a linear progression.
4.1.2. Repeated Repetition
Repeated repetition patterns occurred when a participant struggled to appropriately modify subject attributes, either becoming stuck on a single level or becoming stuck on multiple levels that required applying the same attribute. The former involved insufficiently modifying subject attributes to complete a single level, while the latter involved cycles of modifying subject attributes enough to advance to the next level only to struggle to apply the modified attributes enough to succeed. Participants became stuck on a single level when they insufficiently modified subject attributes to progress yet repeatedly attempted the same level when prompted by the app. Every participant replayed Level 15 of Motion Math: Zoom (decimals to hundredths, range of 0–2) multiple times in succession: three participants (4, 5, 8) made 3–5 consecutive attempts, three participants (1, 6, 7) made 11–18 consecutive attempts, three participants (2, 9, 10) made 24–27 consecutive attempts, and one participant (3) made 44 consecutive attempts. Although many of these attempts were brief, six participants spent more than half of their Motion Math: Zoom interaction time attempting Level 15. During these interactions, some participants only insufficiently modified one type of subject attribute. For example, Participant 9 efficiently applied input gestures required for number line navigation, but repeatedly chose inappropriate intervals to travel along the number line on the individual tasks (e.g., traveling from 1.52 to 1.06 using only hundredths instead of tenths then hundredths). Thus, for these tasks, Participant 9 sufficiently modified subject technological attributes to align them with artifact technological attributes, but did not successfully modify subject mathematical attributes enough to align them with artifact mathematical attributes. During the follow-up interview, Participant 9 admitted to trying to memorize the task sequence within Level 15, which remained nearly identical, rather than focusing on the mathematics. Other participants struggled to sufficiently modify both subject mathematical and technological attributes. For example, Participant 2 repeatedly chose inappropriate ranges to zoom in on the number line (e.g., zooming to hundredths at 0.70–0.80 when finding 1.79 from 0.50) while struggling to perform the pinching gesture required to zoom.
Participants became stuck throughout a series of related tasks when they struggled to modify and apply the same attributes across these tasks. While interacting with Motion Math: Zoom, three participants completed Level 15 and began Level 16 (decimals to hundredths within 0–10). Despite the similar attributes involved, all three participants struggled to complete the new tasks, and none completed the level. While interacting with DragonBox Algebra 12+, eight of the nine participants who reached Level 2:11, which involved the multiplicative inverse property with external variables (e.g., yx = 3 + 2: choose from tiles featuring y or z), insufficiently modified and applied the subject mathematical attributes required for sustained success. Often, participants attempted to use an incorrect property. For example, Participant 6 repeatedly attempted to use additive properties instead of multiplicative properties (e.g., yx = 3 + 2: adding tile y instead of dividing by tile y). Through Levels 2:12–2:14, Participant 6 would make this error, repeat the level until correcting the error, then advance to the next level, only to repeat the same error. Explaining the same set of levels, Participant 3 explained, “sometimes I tried a pattern and it worked, but I tried it on the next level and it didn’t work.” Thus, participants could become stuck on a particular level or throughout a series of related levels when they struggled to reactively modify and apply subject attributes. Participants reactively modified subject attributes throughout these interactions, leading to linear progression or repeated repetition.
4.2. Proactive Attribute Modification
Proactive attribute modification occurred when participants attempted to affect attribute alignment by modifying artifact attributes. Two categories of proactive modification patterns occurred, as participants sought either equilibrium or disequilibrium. Equilibrium was a high degree of attribute alignment, whereas disequilibrium was a low degree of attribute alignment. In this context, proactive modification involved changing mathematical and structural attributes of the apps, as these apps did not permit modification of only artifact technological attributes.
4.2.1. Seeking Equilibrium
Most proactive attribute modification involved the subject modifying artifact attributes to seek equilibrium (i.e., increased attribute alignment). Participants modified artifact attributes in an attempt to allow them to build connected subject attributes or strengthen the same combination of attributes. Five participants proactively modified artifact mathematical attributes by returning to or selecting a level featuring artifact mathematical attributes more aligned with their subject mathematical attributes to build subject mathematical attributes related to the more difficult level. However, no participants did this during interactions with both apps. During interactions with DragonBox Algebra 12+, when Participants 2 and 10 struggled to complete level 2:13, featuring multiple properties including application of multiplicative inverse by introducing variables from outside the equation space, they returned to level 2:11, which demonstrated this form of the multiplicative inverse property in isolation. Both participants eventually successfully completed Level 2:13. Participant 2 explained this decision, saying “my parents tell me if something gets too hard stop on that and then go back and you’ll get better ideas.” While interacting with Motion Math: Zoom, Participants 4, 5, and 6 chose to play a previous level when faced with a level they could not effectively complete, eventually working toward more advanced levels. For example, after repeatedly struggling to complete Level 15 (decimals to hundredths within 0–2) and failing to complete Level 16 (decimals to hundredths within 0–10), Participant 6 returned to Level 12 (decimals to tenths within 0–3) as part of eventually attempting Level 21 (mixed review including decimals to thousandths). When asked about this decision, Participant 6 said, “If a level seemed too hard I would try another level and see if I got better at that, and I would come back to it when I felt like I could do it.”
Participants could proactively modify artifact attributes as part of strengthening the same combination of subject attributes. During interactions with DragonBox Algebra 12+, six participants (1, 2, 6, 7, 8, 9) modified artifact structural attributes, using the Solution feature as a scaffold to demonstrate how to complete the task. However, some participants failed to immediately replicate the solution, such as when Participant 7 watched the Solution multiple times across a series of attempts to complete Level 1:14. Only Participant 1 proactively modified artifact mathematical attributes to strengthen the same combination of user attributes, choosing to repeat Levels 1:15 and 2:09 after inefficiently completing each. However, Participant 1 claimed, “I play so I can get one or two stars” (i.e., reward feedback) and did not reference learning or mathematical content. While interacting with Motion Math: Zoom, no participants chose to strengthen the same combination of subject attributes by repeating a level when the app directly offered an opportunity to advance to the next level. Only Participant 8 modified artifact structural attributes while interacting with Motion Math: Zoom, deactivating the needle timer after struggling to complete Level 15. Nonetheless, Participant 8 continued to struggle to hone pinching gestures required for zooming (i.e., modify subject technological attributes) and identify the range in which the target number was located (i.e., modify subject mathematical attributes).
4.2.2. Seeking Disequilibrium
Some proactive attribute modification involved the subject modifying artifact attributes to achieve disequilibrium (i.e., decreased attribute alignment). This was not possible during interactions with DragonBox Algebra 12+, which presented levels in sequence and did not permit skipping levels not yet completed (e.g., attempting Level 2:03 before completing 2:02). However, Motion Math: Zoom permitted menu-based access to several levels out of sequence and directly offered participants a chance to skip ahead from Level 6, without specifying that this would both present Level 15 and activate the needle timer. Only Participant 5 refused this offer, having already begun proactively returning to the menu to choose a level to “make it to challenges.” Participants 4 and 8 did not receive this offer, having already proactively sought disequilibrium by choosing Level 15. Participant 6 also sought disequilibrium, unlocking and skipping to Level 18 and later Level 21. Only Participant 8 sought disequilibrium by activating the needle timer (i.e., modifying artifact structural attribute).
4.2.3. Seeking Equilibrium and Disequilibrium
Some participants switched between seeking equilibrium and disequilibrium during interactions with Motion Math: Zoom. Participants 4, 5, and 6 initially sought disequilibrium and proactively modified artifact mathematical attributes by skipping to advanced levels. However, all three participants reached a point where they could no longer successfully complete tasks and sought equilibrium by proactively modifying artifact mathematical attributes as part of returning to earlier levels that featured less difficult tasks (i.e., more aligned mathematical attributes). Participant 5 explained this, saying “I tried to go to the hardest [level overall] but when I played the hardest [level I reached] it wouldn’t let me go up levels so I went back and I tried to [play] as many levels as I could.” Participant 8 proactively modified artifact attributes while balancing equilibrium and disequilibrium. After completing Level 1, Participant 8 immediately sought disequilibrium, skipping to Level 15, which involved relatively challenging mathematical tasks and required frequent zooming (i.e., proactively modified artifact mathematical and technological attributes). Despite inefficiently completing Level 15 with the needle timer inactive, Participant 8 activated the needle timer (i.e., proactively modified artifact structural attribute) and struggled to complete the level. Participant 8 then deactivated the needle timer (i.e., proactively modified artifact structural attribute) for a final attempt at Level 15. Therefore, results indicated that participants proactively modified artifact attributes to seek equilibrium or disequilibrium, and that some participants proactively modified artifact attributes for both purposes.
4.3. Unperceived Attributes and Opportunities for Proactive Attribute Modification
Another common pattern was that participants often did not perceive certain attributes or opportunities for proactive attribute modification.
4.3.1. Unperceived Attributes
Many participants did not perceive certain attributes involved in the interactions. While interacting with Motion Math: Zoom, participants often attempted to complete Level 3 without zooming using the pinching gesture (technological attributes), which the app had not permitted during Level 2. Although zooming was not required, it would have been a more efficient way to complete the tasks. Additionally, many participants did not perceive mathematical attributes relevant to interactions with DragonBox Algebra 12+. Participant 8 remarked, “there was absolutely no math in there… I don’t know why you gave this game to me, it’s not a math game. I thought this was a study on math games.” Most participants described the app as a game focused on matching or problem solving. Participants 2, 4, and 10 mentioned fractions but did not elaborate, and Participant 3 first claimed that there was no mathematics involved but later admitted that some tasks “reminded me of the identity property a little bit.”
4.3.2. Unperceived Opportunities for Proactive Attribute Modification
At times, unperceived attributes contributed to missed opportunities for proactive attribute modification. Both apps included opportunities for participants to proactively modify artifact mathematical and structural attributes, but modification of artifact technological attributes was only possible indirectly (e.g., in Motion Math Zoom, returning to a level that did not permit zooming also presented different mathematical content). Participants’ comments regarding interactions with Motion Math: Zoom indicated unperceived opportunities for proactive modification of both artifact mathematical and structural attributes. For example, Participant 2 wanted to “choose what [math] it would have you do,” which one could do via the menu. Similarly, when asked about not changing levels despite repeated unsuccessful attempts to complete Level 15, Participant 1 responded, “Because I couldn’t. You have to complete a level to continue.” In these cases, participants did not recognize the menu access button that appeared between attempts to complete a level. Other comments revealed unperceived opportunities to modify artifact structural attributes. When asked what made tasks challenging, Participant 6 indicated, “the time kept going faster to find the number,” and asked for “a longer period of time to find the number.” Participant 2 also attributed the increased difficulty of levels to the needle timer, asserting that it would have been possible to finish harder levels without the needle. Although some participants returned to the menu, only Participant 8 recognized how to control the needle function, stating, “It said that the needle was off and I clicked on it and it said the needle was on.”
Participants could proactively modify artifact attributes while interacting with DragonBox Algebra 12+ by returning to the menu to select a previously completed level (modifying artifact mathematical attributes) or accessing the Solution feature to demonstrate how to complete a level (modifying artifact structural attribute: scaffolding). Only Participants 2 and 10 returned to the menu to choose a different level, suggesting that the other participants may not have perceived the opportunity to proactively modify artifact mathematical attributes. Some participants’ suggestions for improving the app indicated they did not perceive the Solution feature, as Participant 10 proposed “hav[ing] it show how to do something if you can’t get it,” and Participant 3 requested the addition of “hints or clues to help.” Others recognized attributes that signified this feature, such as Participant 1 who noted that, “all light bulbs do that. A light bulb over your head gives you an idea.” Participants’ comments indicated a mixed awareness of opportunities to proactively modify artifact attributes.
5. Discussion
The results have implications for those involved in designing, teaching with, and researching educational technology, particularly those involving mathematics. Reactive attribute modification was common, such as when participants attempted levels in the order presented by the app. Proactive modification also occurred, such as when participants chose levels to attempt, exerting some control over the mathematics they encountered. However, in some situations, participants did not perceive certain attributes or proactive attribute modification opportunities, such as when they requested ways to choose the mathematics content involved in the tasks. Reactive attribute modification contributed to varying patterns of progress through tasks, while participants engaged in proactive attribute modification to seek equilibrium or disequilibrium. Importantly, this study was not an evaluation of app quality, a measurement of mathematical fluency, or an exact replication of in-class app use; rather, the intent of the study was to examine children’s independent interactions with the apps in the context of using technology to support children’s learning.
5.1. Design
The results imply that designers of educational technology should consider its attributes, the ways it modifies these attributes, and the opportunities for users to become aware of and modify these attributes. Some designers attempt to create research-based, developmentally appropriate technology tools [
6,
18,
26], which implies efforts to align artifact attributes with potential subject attributes. These efforts can also involve the upper right triangle of ACAT, artifact–object-rules, which accounts for the influence of the “rules” of mathematics education and technology design [
18], in relation to the subject. In particular, developers can purposefully include developmentally appropriate, flexible attributes that support independent learning, as the artifact-centric activity does not always occur with experts present.
Designers could use attribute modification and related patterns to consider tasks and task sequence. It is important that the artifact offers a variety of appropriate tasks with sufficiently different combinations of attributes in order to maximize usefulness. Repetition of nearly identical prompt sequences in Motion Math: Zoom led some participants to focus on the repetition, rather than the mathematics, to eventually complete tasks. These participants later struggled on similar tasks, suggesting that this may not have been an ideal strategy. Designers could also consider artifact modification of attributes when sequencing tasks. For example, Motion Math: Zoom included levels in a reasonably developmentally appropriate sequence, but offered users a chance to skip ahead combined with added time constraints, without returning to the menu. Despite being at the older end of the target age group for the app, most participants who accepted this offer encountered repeated repetition, becoming stuck on the tasks while relying on reactive attribute modification for an extended period of time. Although many of these participants remained engaged and claimed to enjoy interacting with the app, unrecognized alternative interactions might have been more mathematically productive. As in other research [
12], participants did not appear to reflect on their strategies, often continuing to take the same approach.
Thus, designers may consider creating artifacts so that users are aware of attributes and opportunities to proactively modify attributes. The repeated repetition that occurred in this study when participants became stuck on a task or stuck on a series of related tasks implies that what may appear to be developmentally appropriate subject matter and interaction techniques may be less effective without appropriate scaffolding or when children are unaware of the potential for proactive attribute modification. For example, while interacting with Motion Math: Zoom, few participants attended to the symbol that allowed them to return to the menu to proactively choose mathematics content. Of those that returned to the menu, only one attended to the labeled image that signified the opportunity to proactively (de)activate the needle timer. However, some participants did recognize symbols, such as the light bulb that activated the Solution video in DragonBox Algebra 12+. This aligns with research indicating that people do not always perceive potential uses of objects, but that labels may help people recognize these uses [
31]. However, labels must be familiar and not easily ignored, with explanations provided via easily accessible instructions when target audiences can read.
Many participants admitted that they did not perceive any of the mathematics involved in DragonBox Algebra 12+, similar to the lack of reflection during interactions with technology identified in other research [
12]. To make these connections explicit, developers could include attributes such as labels that identify the properties as children apply them. Making such attributes optional and controlled by the user [
18] would allow children or teachers to implement them as developmentally appropriate. For example, initial independent interactions may occur without labels to encourage exploration, but during follow-up discussions, teachers may activate labels to help highlight the mathematics present. Teachers might also activate labels for children who appear to understand the mathematics but struggle to recall the vocabulary. Combining these implications, it may be beneficial for the app to provide intentionally designed, flexible attributes to facilitate independent learning, especially because experts are not always involved during interactions with apps. Therefore, it may be productive for those who develop educational technology to consider attributes, attribute modification and relevant patterns, and perception of attributes and attribute modification during the design process.
5.2. Teaching
The results also have implications for teaching using educational technology. In this study, participants made varying degrees of progress through the apps due to the changing degree of alignment of their (subject) attributes in relation to the app (artifact) attributes. In order to maximize the potential benefits of educational technology, teachers must effectively facilitate its use [
2,
3]. When evaluating technology for use in the classroom, teachers should consider the attributes of both the technology and their students, as well as how these attributes may change during the interactions. Importantly, teachers should play an active role in these classroom-based interactions, which would involve the lower left triangle of ACAT (subject-artifact-group), accounting for context and supporting instrumental generation via instrumental orchestration. This may include offering appropriate external scaffolding [
32], supporting awareness of potential proactive attribute modification, and encouraging children to reflect on the interactions as a regular part of their mathematics learning experiences [
12]. As no attribute modification pattern was always productive or always unproductive, teachers might instead encourage a balance of equilibrium and disequilibrium.
Technology such as the mathematics virtual manipulative touchscreen tablet apps involved in this study can support teachers but cannot replace them. Teachers must make intentional, informed decisions to encourage effective use of technology [
2,
3]. This may involve recognizing how and when to offer scaffolding beyond what the technology presents [
32], such as to support attribute modification and productive changes in mathematical practices. For example, repeated repetition may indicate that a child is unproductively struggling to align attributes and the task, in which case the teacher may suggest an alternative approach to completing the task, such as using two hands to zoom instead of one hand or using a different property as a first step. In these situations, the teacher could facilitate proactive attribute modification by suggesting the child attempt a different task that may build toward the challenging task.
Teachers can also encourage appropriate proactive attribute modification before children interact with technology. This may be specific, such as by drawing children’s attention to particular features of the technology (e.g., menu, instructions), or general, such as by reminding children they can find appropriate tasks while interacting with the technology (i.e., seek equilibrium and disequilibrium). However, both proactive and reactive attribute modification could lead to interactions that were relatively productive (e.g., building connected attributes, linear progress) and unproductive (e.g., unnecessary increase in difficulty, repeated repetition). It may be beneficial for teachers to frame children’s awareness of attribute modification in terms of seeking equilibrium and disequilibrium, flexibly modifying attributes by context to alter the degree of difficulty, rather than favoring a particular approach at all times. Aligning with other research [
12], participants in this study did not spontaneously reflect on their interactions, often repeating the same approach regardless of its success or mathematical implications. Participants were often unaware of the mathematics involved in their interactions and the potential to proactively modify attributes. Even when children were aware of the mathematics content, they often focused on ways to beat the game (e.g., memorizing prompt sequences) without considering ways to modify mathematical attributes. Therefore, teachers should encourage reflection and discussion about the activity, including the mathematics and mathematical learning involved, such as strategies and reasoning used to choose and complete tasks. Thus, teachers play a critical role in classroom implementation of educational technology, such as by offering appropriate scaffolding, fostering recognition of potential for proactive attribute modification, and supporting reflection on the interactions.
5.3. Research
The results imply that attribute modification types and seeking equilibrium and disequilibrium may be important themes for research involving interactions with educational technology. As all subjects and artifacts have attributes, many of which may change during interactions, one can use attribute modification to describe these changes. In the context of ACAT, these attributes inform the activity that contributes to and provides evidence of learning. Indeed, these results shed additional light on research that includes attributes as the base of a conceptual framework describing interactions with technology, which was originally set within embodied cognition [
34,
35]. This implies that attributes and attribute modification may be relevant in multiple theoretical contexts, and it may be productive to consider the rest of the framework in a similar fashion. Furthermore, the specific types of attribute modification, proactive and reactive, may be useful for categorizing interactions with technology based on the degree of control a person exercises. Researchers may also investigate relationships among this and other attribute classification systems (e.g., [
36,
37,
38]) in order to determine appropriate applications and inform the evolution of scholarship involving attributes.
An important emergent finding is that participants used proactive attribute modification to seek equilibrium and disequilibrium. Participants proactively modified attributes in the same category (e.g., mathematical content) to make tasks easier or more difficult (e.g., choosing levels in Motion Math: Zoom), and some participants did both. This implies that some children will look for tasks they believe to be appropriate if presented with both tasks they perceive to be inappropriate and a recognized opportunity to choose alternatives. Even when participants did not perceive opportunities for proactive attribute modification, some still expressed the desire for a way to seek equilibrium or disequilibrium (e.g., Participant 2 wanted to “choose what [math] it would have you do”). Future research could examine combinations of attributes (e.g., content knowledge, scaffolding) that contribute to proactive and reactive attribute modification, seeking equilibrium and disequilibrium, and associated outcomes. This research built on an exploratory qualitative study featuring ten individual students each using mathematics two apps for one session. To account for the inherent limitations of such research, subsequent investigations of attributes and attribute modification patterns could involve mixed methods, micro-longitudinal designs, and larger samples. These studies could also involve different contexts (e.g., classroom), technologies (e.g., computers), and content (e.g., biology), and support for reflection.
6. Conclusions
As educational technology becomes ubiquitous, understanding children’s interactions with technology is critical to informing practice, design, and research efforts. These results indicate that attribute modification patterns were present as children interacted with the mathematics virtual manipulative touchscreen tablet apps. Reactive attribute modification was common. When children proactively modified attributes, they sought a mixture of equilibrium and disequilibrium. However, children often did not perceive opportunities for proactive attribute modification. The results imply that designers, teachers, and researchers who are involved with educational technology should recognize that attributes and attribute modification are integral to technology-mediated activity. While it is important to apply research-based design principles to technology development, the teacher’s role in facilitating student learning remains paramount. Designers may primarily focus on artifact attributes while teachers may primarily focus on subject attributes, but during technology-mediated activity, the two relate to one another as part of learning mathematics. Therefore, designers, researchers, and teachers should account for both sets of attributes, as well as attribute modification, when considering educational technology. In order to make progress in this critical area of education, research, design, and implementation of educational technology should continue to move forward in ways that are accessible and applicable to stakeholders across the spectrum.