Examining Pinterest as a Curriculum Resource for Negative Integers: An Initial Investigation

1. Introduction

Over the last decade, social media has become a component of the lives of nearly two-thirds of American adults [1]. This is an almost ten-fold increase since 2005. It is particularly popular with adults aged 18–29 years with 90% reporting to use it. Although social media sites were designed for purposes not necessarily germane to education, some have started to become tools for teachers. In particular, research has shown that the website Pinterest has become a popular resource for teachers at all levels [2,3,4,5,6]. In a survey of mathematics and English language arts teachers, 87% of elementary and 62% of secondary teachers reported that they consulted Pinterest when planning lessons [2]. Moreover, these teachers consulted Pinterest more often than websites designed specifically for mathematics instruction such as corestandards.org, illuminations.nctm.org, and engageny.org. Overall, the only site more popular than Pinterest was Google.

Just what is Pinterest and why is it popular with teachers? In contrast to social networking sites, which focus on individuals interacting and exchanging information with each other, Pinterest is a kind of social bookmarking site. Users create, organize, and share content by creating visual bookmarks called pins. These visual bookmarks link to various online resources including webpages, pictures, and videos. Once a pin is created, it can be discovered by other users via keyword searches, saved to a collection of similar pins called a board, liked, or commented on. The act of saving a pin to a board is known as a repin. Users typically design Pinterest boards around a central theme (e.g., mathematical topic). This makes the boards a space for organizing online content as well as a means for providing other users with easy access to a collection of teaching ideas.

Performing a keyword search on Pinterest yields a collection of visual bookmarks, which appear as rectangular icons (Figure 1). As a user scrolls down the page, more bookmarks are loaded. This creates a continuous feed of content that the user can navigate. Hovering over a bookmark reveals a URL at the bottom of the image that can be clicked on to navigate to the source. Likewise, the name of the author of a pin can be clicked on to open up their profile page. Clicking anywhere else on a bookmark loads a secondary page showing a larger version of the bookmark, comments from other users, and related pins.

The visual layout of the Pinterest feed is designed to allow the user to easily browse through many pins quickly. However, the feed itself provides little information for evaluation of a particular pin. As shown in Figure 1, within a feed, each bookmark contains basic information about a pin including an image from the linked content, a title, the name of the pin creator, and a number indicating repin activity. Apart from these details, no other information is provided within the feed.

Understanding the content of Pinterest is a critical issue in mathematics education. Given that mathematics teachers are already using Pinterest in their practice [2], there is a need for our community to provide guidance to inform this decision-making process. Initial educational research concerning Pinterest has been focused on understanding how teachers are using the website [3,4,5,6]. These studies can provide information on how individuals incorporate features of Pinterest into their practice. Missing, however, is an understanding of the mathematical content that the teachers are actually viewing when they use the site. To take initial steps in understanding Pinterest as a curriculum resource for mathematics, we conducted a research project focused on available negative integer resources.

Framing Our Work

Within this article, we adopt the lens of connectivism, which builds on principles from theories concerning networks, chaos, self-organization, and complexity. Drawing from this lens, we view learning as “a process that occurs within nebulous environments of shifting core elements—not entirely under the control of the individual” [7] (paragraph 21). We view Pinterest, which is a space formed by networks of linked pins, as this kind of nebulous environment. Users have the ability to explore pins, but cannot modify the pins of others. At the same time, changes by individual users result in an overall state of flux for the network of pins. Thus, the core elements of Pinterest are continuously being transformed.

Learning within a changing environment such as Pinterest, requires a focus on careful decision-making. As noted by Siemens [7], decision-making is a key component of the connectivism lens:

Connectivism is driven by the understanding that decisions are based on rapidly altering foundations. New information is continually being acquired. The ability to draw distinctions between important and unimportant information is vital. The ability to recognize when new information alters the landscape based on decisions made yesterday is also critical [7] (paragraph 22).

As we have described, using Pinterest is primarily an activity of sorting through visual bookmarks. Making good decisions within this space requires quickly discerning information from pins and recognizing how it relates to one’s current understanding. Users seeking to understand the corpus of resources available for a given topic are left with the task of browsing through their feed, which, as we have described, provides only a few details about a pin including a picture, description, author, and the number of repins. Of these details, the number of repins is the only consistently presented numerical information.

Our choice to investigate negative integer resources available on Pinterest is intentional and based on knowledge of the difficulties associated with teaching and learning about integers, which have been shown to be notoriously challenging for all [8,9,10,11]. Specific challenges with integers include a focus on procedures [12], difficulty with subtraction [13,14], and language issues [11,15]. Although research has shown that young children are capable of reasoning with integers [16,17,18,19], there are many examples of adults struggling with the content. Piaget [9] pointed to the difficulty of integer operations for secondary and university students. Likewise, Bofferding and Richardson [12] illustrated that preservice teachers often focus on procedures when solving integer addition and subtraction problems. Recent research has also pointed to the difficulties that secondary students have connecting integers and contexts [11]. Drawing on a historical lens, mathematicians in the 1700s and 1800s modeled integer addition and subtraction on a number line, but struggled to do the same for integer multiplication and division [8].

Part of the challenge with integers is rooted in the difficulty of physically representing negative integers [20]. For example, although we may talk about two objects or 2 feet in width, the same cannot be said for −2. Consequently, the negativity of −2 needs to be attributed to an object, such as one physical chip representing −1, negatives on a temperature scale, or even conceptualizing borrowing 2 dollars as −2. The challenge of the physical embodiment of negative integers [21] causes educators and researchers to draw on various models with integers (e.g., [22,23,24]). We acknowledge that there are various interpretations of the word model [25], and align the definition in this paper with Vig, Murray, and Star [26], who also reported on the use of models with integers. To this end, we use the term mathematical model (i.e., model) to refer to “material, visual sketches, paradigmatic situations, schemes, diagrams, and even symbols” that help students manage, document, communicate, or interpret mathematical ideas and phenomena [27] (p. 13). Much of the research with integers supports the use of the number line model [10,28] and chip model [29], though some researchers have also described models such as elevators [13,22,24]. Research examining textbooks and curricula in the domain of integer operations [30] has shown the use of number lines, chip models, and contexts as models for dealing with integer operations. Likewise, traditionally-printed curricula (e.g., Lappan CMP) supports number lines and chip models [31] with integer operations. Importantly, research has also highlighted that all models for integer operations have affordances and breaking points [26].

A further obstacle in teaching about integers is that although curricula and tasks exist that support conceptual understandings of integers (e.g., [28,32,33]), it is a challenge to support teachers in developing the ability to discern between materials that are conceptually focused versus those that are procedurally focused. This is particularly the case for integer subtraction, where different number sentences support different types of reasoning [13]. Integer subtraction is difficult because the “rules” for whole numbers no longer hold for integers—adding does not always make bigger, subtracting does not always make smaller, and the commutative property does not hold for problems such as 2–3 and 3–2 [12,13,14]. Furthermore, subtraction is complicated by the number sentence type (e.g., −2 − −5 compared to −5 − −2 is more challenging) [21]. Additionally, language presents challenges when working with integers. For example, identifying whether money referenced in a contextualized problem with integers is viewed from the perspective of the lender or borrower of the money [11]. Similarly, it is challenging for students to coordinate what the words “more” or “less” mean with integers [15].

Taken together, the challenges related to teaching and learning about negative integers make it likely that teachers may feel underprepared to teach the content and seek resources outside of the classroom for assistance in planning. In this search for resources, many may turn to Pinterest as a curriculum resource for pedagogical and content information. With this group of teachers in mind, we conducted a research investigation focused on understanding the scope and characteristics of available negative integer content on Pinterest. Our study was guided by the following research questions:

• What are the characteristics of pins related to negative integers?
• What association, if any, exists between the number of repins and the presence of errors in linked content (e.g., models, language, worked examples)?

2. Materials and Methods

During January, 2016, we gathered a database of pins for analysis. Our sampling method was purposeful and intended to build a database containing classroom resources that teachers (both preservice and in-service) might use. We established three criteria for pin inclusion: (a) relevance to teaching about negative integers; (b) link to free content; and (c) at least 50 repins. The reason for the first criteria is self-explanatory. We formed the second criteria based on the assumption that preference would be given to free materials over those that cost money. The threshold of 50 repins was selected based on an assumption that any pin having at least 50 repins would be regarded as having some popularity and therefore seen as more valuable when browsing. This excluded pins that focused on other topics (e.g., negative exponents, graphing on the coordinate plane), were designed to sell a product (e.g., t-shirt, math app, poster), linked directly to a pay website (e.g., teacherspayteachers.com, teachersnotebook.com), and those that had broken links.

Pins were identified using keyword searches for the terms negative integers, integers negative, and negative integer activities. We used web browser extensions to simplify the process of loading multiple pages of pins for a particular set of keywords and sorting these pins by the number of repins. We then worked through this list using the information provided by the visual bookmarks and included pins that met all three criteria. Additionally, as it was possible for the same pin to be identified by different sets of keywords, new pins were checked against the existing database to ensure there were no duplicates. Overall, we identified 176 pins for analysis.

Table 1. Number of pins identified by keywords.

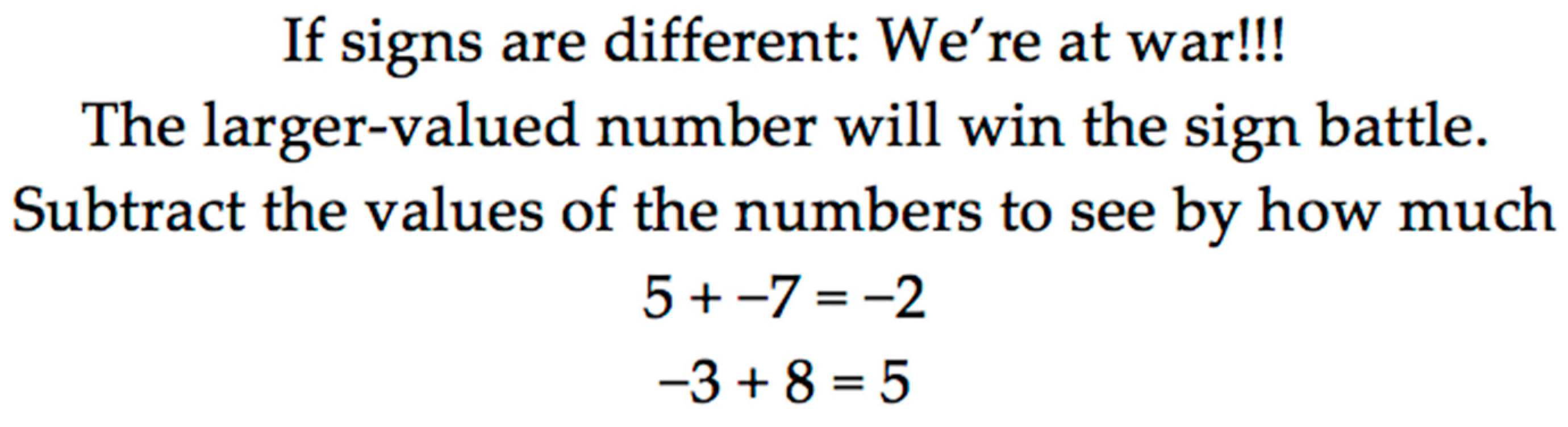
Keywords	Number of Pins Identified
negative integer	126 (66%)
integers negative	36 (19%)
negative integer activities	14 (7%)

summarizes the number of pins that were identified by each set of keywords.

After assembling the database, we analyzed pins to identify general characteristics and understand the data set as a whole. Our methodological process was a content analysis [34]. Rather than beginning with a predefined set of characteristics to analyze, we developed coding categories using an inductive process [35]. We began by examining pins from the dataset to identify characteristics in pin content that were common. As potential characteristics for comparison were identified, we checked them against other pins. This process was iterative and exhaustive. The final coding scheme focused on a set of characteristics that were easily identifiable across all pins. It included the mathematical operations used, the presence of negative numbers, the use of real-world context, the url of the source, and the presence of a mathematical model. Additionally, we identified if there were errors in mathematical language, notation, or discussion. A binary coding scheme was used for all characteristics (0 = characteristic is absent from pin, 1 = characteristic is present). Coding was primarily done by the first author with check coding by the second author to ensure consistent use of the coding scheme.

3. Results

3.1. General Characteristics

Table 2. Summary of general characteristics of pins.

Characteristics of Pin	Percent
Includes negative integers	77%
Operations
Addition	82%
Subtraction	70%
Multiplication	29%
Division	27%
Includes a model	55%
References game	32%
Includes links to paysites	22%
Use of real-world context	15%

provides a summary of the general characteristics of pins in the dataset. As shown, one of the first observations we made was that only 77% of pins we identified actually dealt with negative integers. This is despite the fact that all of the pins were identified using keyword searches that included the words negative and integers. The other 23% of pins typically dealt with whole number operations but did not include or discuss negative integers.

With regard to operations, the majority of pins dealt with either addition (82%) or subtraction (70%). Less than one-third of the pins had content with multiplication (29%) or division (27%). Roughly half of the pins (55%) included a model of some kind. Less than one-third of the pins (32%) referenced a game with integers and only 15% of pins incorporated the use of a real-world context. Additionally, although we intentionally excluded pins that linked directly to paysites, we found that content in 22% of the pins still included direct links to these websites (e.g., a blog post with links to a teachers-pay-teacher page). Pins drew from 84 different websites, the most popular of which was blogspot.com (34%). The second most popular source was an image hosting site (8%). Almost completely missing from the dataset were traditional online resources such as those provided by textbook publishers or professional organizations.

3.2. Errors within Pin Content

Our intention in identifying errors in mathematical language, notation, or discussion was to gain a rough measure of the mathematical correctness of the pins within the dataset. Overall, we found that 31% of the pins contained some kind of error. Although errors were varied, the most common was a confounding of order and magnitude when explaining the addition of integers. In what follows, we discuss a few representative pins containing this error.

Pin ID 9 presents one example of the error of confounding order and magnitude. At the time of analysis, the pin had 588 repins. Pin content was drawn from a personal blog, focused only on the addition of integers, referenced the chip model for integer addition, and made explicit reference to using a game to teach integers. Although much of the discussion within the content is mathematically correct, the excerpt in Figure 2, which is centered on rules for adding integers, contains an error:

Within the pin discussion, two suggested phrases to use in teaching the addition of integers are presented. The first of these phrases contains the error of confounding order and magnitude. The author suggests saying “If the signs are DIFFERENT, find the DIFFERENCE! taking the sign of the bigger number.” Problematic in this suggestion is the use of the phrase “bigger number”. For example, consider the number sentence −5 + 2 = ?. The first part of the “signs are different” rule suggests finding the difference of 5 and 2, which is 3. The second part of the rule states “taking the sign of the bigger number,” but it is not clear what “bigger number” means. The conventional interpretation of bigger is related to order (i.e., given two numbers, the bigger number is the one that is plotted farthest to the right on a number line). Following this definition of bigger, 2 is bigger than −5 and the sign of the difference should be positive. However, this does not yield the correct answer. Therefore, the rule requires interpreting bigger as meaning magnitude (i.e., the distance a number is from zero). In this case, since the magnitude of −5 is greater than the magnitude of 2 (i.e., |−5| > |2|), the sign of the difference must be negative. Also problematic is the fact that the rule will work with a conventional interpretation of bigger in situations such as −2 + 5 where the positive number has a larger magnitude than the negative number.

Pin ID 61 (Figure 3) presents another example of this error. This pin, which had 75 repins at the time of analysis, linked directly to an image with no additional text.

As shown, the image contains rules for adding integers and includes the sentence “when adding two integers with different signs subtract and take the sign of the higher number.” Again, the standard mathematical interpretation of the word “higher” is related to order. However, the worked examples show the word as being understood as magnitude.

A third example of this error can be found in Pin ID 83. The pin, which had 1141 repins at the time of analysis, linked to a personal blog. Pin content focused on foldables for a variety of topics including integer addition and subtraction. No mathematical model was used or referenced in discussion. Figure 4 shows instructions that were included with the foldables focusing on addition of integers.

The instructions presented in Figure 4 are problematic for a number of reasons. For example, the meaning of “larger-valued number” is unclear. Based on the examples, it appears to be referencing magnitude. Additionally, the phrase “win the sign battle” has no clear meaning. Nor do the instructions to “subtract the values of the numbers to see by how much” provide guidance on the actual procedure that should be followed. Taken together, these issues present a number of opportunities to misunderstand addition of integers.

As noted earlier, a repin is one of the features that a user has access to on Pinterest as he or she browses. Unique about this number is the fact that it can be used to compare different pins while viewing the feed. Consequently, users might view the size of the number as a proxy for any number of characteristics of a pin including whether or not the pin is free from mathematical errors. To investigate if there is an association between the number of repins and the presence of an error in pin content, we conducted a point-biserial correlation using the statistical software package R. The point-biserial correlation measures the strength of association between a continuous variable and dichotomous variable. Results showed a weak negative correlation r_PB (156) = −0.2, p = 0.01.

4. Discussion

Although the study reported here is only an initial investigation, the results suggest several implications concerning the use of Pinterest as a curriculum resource for negative integers. Drawing on connectivism, two guiding principles related to learning are that (a) a diversity of ideas is central for developing knowledge of a topic and (b) acquiring accurate and up-to-date knowledge is the intent of learning. The results from this work, however, suggest that the Pinterest curriculum for negative integers does not meet either of these principles fully.

Related to a diversity of ideas, results show that the Pinterest curriculum is shallow. Pins related to negative integers tend to concern a narrow range of content focused on integer addition and subtraction with little coverage of multiplication or division. Within pin content, models are present roughly 50% of the time. This absence, which suggests that mathematical models are not necessary when teaching or learning about negative integers, is in opposition to findings from mathematics education research showing that the challenges associated with negative integers warrants providing students (and teachers) with methods of enacting the operations [22,23,24]. Similarly, the near absence of real-world context suggests that problems and activities involving real-life situations are not of value. However, real-world contexts are foundational knowledge for reasoning about negative integers [11]. Overall, the results show that the curriculum of Pinterest related to negative integers lacks the depth found in the curriculum of textbooks [30,31].

Connecting to accuracy, the fact that roughly one-third of pins had mathematical errors should give anyone pause for concern when using this resource. Although this finding may seem moot to more experienced practitioners who have come to view online content as needing more review in general, we caution that many seeking assistance with integer instruction may lack the necessary background knowledge to conduct a careful review. For these users, subtle errors in language may be lost.

Furthermore, the results show that the number of repins is not of practical relevance when assessing whether or not a pin contains a mathematical error. Yet the fact remains that the number of repins is clearly presented to the user when browsing Pinterest and can easily be interpreted as a useful metric for evaluating many aspects of a pin including its perceived mathematical quality. Again, for a teacher unfamiliar with negative integers, questions about the particular content of a pin may well be overridden by the assumption that the number of repins is an indicator of mathematical correctness and pin quality.

Additionally, the wide range of online sources that the Pinterest pins draw from (the most popular being blogspot) raises concerns related to the accuracy of mathematical content. As noted, few pins drew from traditional mathematics education focused websites such as the one maintained by the National Council of Teachers of Mathematics. What sets traditional resources apart is that they undergo a process of peer-review in their creation and publication. Other online content (e.g., personal blogs) does not undergo the same review. Although we acknowledge there is an active mathematics education community engaged in reading and interacting via blogs, we believe it is naïve to assume that this interaction can accomplish the same scrutiny of resources as more traditional routes.

Finally, the finding that the popularity of a pin provides no practical information for evaluating pin content is in opposition to the accepted social norm that associates value with popularity. For example, users see both trending topics and viral videos as valuable because of the fact that they are popular. However, this value is not necessarily related to the quality of their content. Moreover, the popularity of these resources also makes them valuable to other groups (e.g., businesses, marketers) because of the potential to monetize the resource in some way. Thus, there is motivation for some groups to seek out ways to increase the popularity of pins for monetary gain.

4.1. Future Directions

Given the increasing popularity of Pinterest, we believe there are a number of directions that future research should consider. Related to this work, more in-depth analysis of the pin content is needed to understand the conceptual models [36] promoted, different affordances and hindrances of model use [26], and depth of content focus. Likewise, research is needed understanding the embedded mathematics of resources. As noted, our identification of errors was intended to provide a general assessment of the presence of inaccuracies rather than a fine-grained analysis. The process of error identification left us considering how one might conduct a more robust assessment of the mathematical correctness of pin content that could account for different degrees of error. For example, when assessing the correctness of content, should errors identified from language issues carry more of less weight than errors born from mathematical missteps? Pondering the feasibility of answering this and similar questions has left us considering whether there might be an underlying construct, which we might call mathematical integrity, which could allow for more meaningful comparison between pins.

More broadly, there is a need for additional research to understand the mathematical resources Pinterest provides in comparison to other educational materials. For example, do pins mirror traditional resources or offer new approaches? To what extent do pins reflect current trends and recommendations in mathematics education? How are the models of integers present within pin content similar to or different from those promoted in traditional resources? To what extent is there focus on procedures?

Additionally, research is needed examining repins change over and digging more deeply into what characteristics, if any, the number of repins might indicate. However, we caution that the number of repins may be arbitrarily inflated since Pinterest provides users with the ability to promote pins. Targeting an audience and paying to promote a pin allows someone to guarantee that more users see the pin within their feed. Likewise, organizations with large numbers of followers might share specific pins and encourage repinning for advertisement or promotion of a product. Thus, we conjecture that repins may be closely associated with these kind of monetization actions, however, more research is needed to investigate the validity of this conjecture.

4.2. Limitations

We believe that the results from this study are best understood as a snapshot of Pinterest at a point in time. As such, the results are useful for gaining bearings and guidance in navigating the terrain of Pinterest, but they should not be used as a sole source of information to understand the entire landscape. There are many reasons that we suggest this interpretation. First, unlike traditional resources (e.g., textbooks), which are designed, produced, and occasionally updated, Pinterest is a resource in a state of change. New content is added on a daily basis, links become obsolete as resources change, and the popularity of a particular pin can change quickly due to exposure. Moreover, the website as a whole is still being improved.

Second, our research was focused on the mathematical topic of negative integers, which was specifically chosen because of the challenges it presents for both teaching and learning. We did not consider other mathematical topics in our analysis. Therefore, although these results can inform similar investigations, generalization beyond negative integers is not appropriate.

Third, as noted in the discussion, our use of a dichotomous coding scheme to identify errors excluded the possibility of more nuanced levels or degrees of error. A more fine-grained analysis of errors may yield a stronger correlation between repins and errors.

Finally, as we noted previously, our intention in this investigation was to gain a general understanding of the available mathematical content on Pinterest related to negative integers. This objective influenced the decisions made throughout the study including the bounds set on pin identification and the methods followed for content analysis. It is possible that the pins excluded from our coding may have other common characteristics not captured with our coding scheme.

5. Final Thoughts

The growth of social media has begun to change the face of curricula as teachers find and use freely available resources as supplements in their planning [2,3,4,5,6]. As social media becomes more integrated into the teaching profession, there is a pressing need for our field to see the way that technology is being drawn into the learning process and enabling individuals access to nebulous environments. Within these environments, the decisions about information presented are of critical importance. Although experienced educators may be able to easily avoid obstacles in using Pinterest, these pitfalls may trap inexperienced teachers. In particular, individuals with weak knowledge of content or pedagogy related to negative integers may turn to Pinterest as a resource. Unfortunately, these are the very individuals that may lack the knowledge needed to separate helpful resources from those that are inaccurate.

The growth of these resources also offers new opportunities for mathematics educators to connect with practicing teachers. In particular, as noted, Pinterest boards are often designed around a theme. Thus, there are opportunities for leaders within our field and professional organizations to become more active in the Pinterest space by linking to more traditional resources that are freely available and building boards to provide users with direction in selecting quality resources. However, this kind of engagement requires a continued commitment, which may present obstacles. The ease of finding resources should not supersede the need to locate quality materials. Yet, as the web has grown, access to resources has greatly outpaced analysis. We believe it is critical that the mathematics education community become more engaged within Pinterest and embrace the potential of the site for improving classroom resources and bridging the divide between research and practice.