1. The Inextricable Relationships among Curriculum, Instruction, and Formative Assessment
There is no acceptable purpose for educational assessment other than to improve student learning. This may be done indirectly, as in the case of year-end summative assessment where the results can be used for accountability purposes, or to support decisions by policy makers. However, another form of assessment, formative assessment, is designed to directly improve student learning. While there is growing agreement that formative assessment should be an equal component with curriculum and instruction in a learning triangle [
1], the empirical evidence of the efficacy of formative assessment is lacking. More research regarding proper use of formative assessment is needed [
2,
3].
Just as we need the compound sodium chloride (salt) in our diets, although separately ingesting the constituent elements would be deadly, students need a learning process in which assessment, curriculum, and instruction are seamlessly integrated [
1]. Otherwise, there will be unintended consequences that are deleterious to learning. Despite decades of articles and professional development programs on formative assessment, integrating formative assessment into the learning process remains challenging. In this paper, we ask whether the use of learning map systems (we use the somewhat awkward phrase learning map system because the use of learning map
® as a noun is trademarked) might address this issue and improve the efficacy of formative assessment in support of student learning. We do this from a theoretical and logical basis grounded in the existing research literature. We also describe how a learning map system can supplement traditional approaches to curriculum and act as an organizing structure to provide the coherence necessary to address some of the obstacles teachers face in their implementation of the learning triangle.
The learning map structure can be particularly helpful in mathematics instruction. Learning mathematics requires students to make sense of concepts and connect them in meaningful ways to computational procedures, different mathematical representations, and other concepts [
4,
5]. Understanding of mathematical ideas is characterized by complex networks of knowledge; this structure reflects conscious organizations of related facts and processes [
6,
7,
8,
9,
10,
11,
12].
To help students achieve this understanding of significant mathematics concepts, the National Council of Teachers of Mathematics (NCTM) encourages educators to create classroom environments that cultivate inquiry, discourse, and collaboration [
4]. NCTM recommends that students and teachers explore mathematical ideas through effective instructional tasks and activities that offer students opportunities to acquire, demonstrate, apply, and evaluate their knowledge [
4]. Similarly, teachers should take every opportunity to observe, listen, and respond to students so that instructors can intervene where and however necessary to redirect student learning through effective feedback [
4].
Consistent with these recommendations, frameworks for formative assessment employ common priorities that can be viewed as sequential steps, or as part of a cyclic process [
13,
14,
15,
16]:
Establish clear aims or learning goals, along with success criteria that the learner understands;
Implement activities directed at the learning goals;
Elicit and interpret evidence of learning;
Provide feedback that responds to the learner’s needs;
Use assessment outcomes to guide instructional decisions about next steps.
These priorities demonstrate that teachers must possess and rely on substantial specialized content and pedagogical knowledge to implement effective instructional tasks and activities [
4,
17]. Both NCTM and the Conference Board for the Mathematical Sciences emphasize the importance of teachers developing the different types of content and pedagogical knowledge previously identified by Schulman [
18] and Ball, Thames and Phelps [
19], and reorganized by NCTM [
4]. Teachers also need information about how students learn particular mathematics concepts and skills, yet this information may not be obvious to a novice or a teacher who depends heavily on provided curricular resources. Without adequate preparation or experience, teachers may be challenged to design effective instruction, elicit evidence of learning, or provide the feedback students need to improve their understanding. In this paper, we describe how a learning map system can enhance teachers’ knowledge about how students learn mathematics and can support teachers’ ability to determine learning goals, implement rich instructional tasks, pose worthwhile questions, and respond to their students.
2. Without an Organizing Structure, Formative Assessment Is Prone to Failure
Although formative assessment has long been touted as a powerful part of instruction [
20], in their 2011 meta-analysis, Kingston and Nash showed an effect size of only 0.20 [
3]. This was surprising given John Hattie’s 2009 compendium of educational effect sizes, in which he found that the use of feedback had one of the largest effect sizes of any educational intervention [
21], and given that formative assessment is intended to include rich feedback.
Perhaps this inconsistency can be explained by Hattie and Timperley’s 2007 paper in which they used many previous studies to develop a model of effective use of feedback [
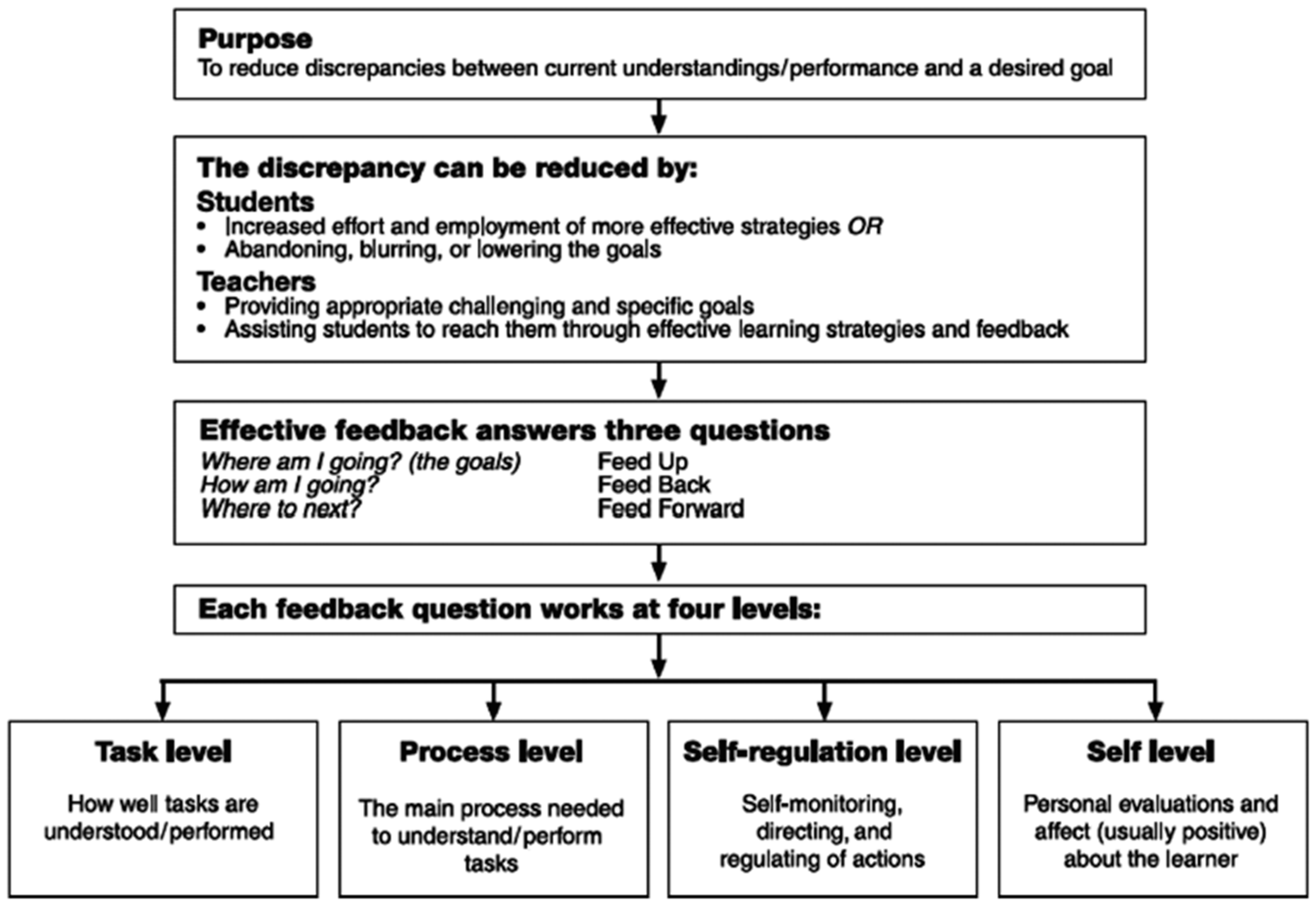
22]. Their model, shown in
Figure 1, posits how both teachers and students can use feedback regarding student performance and that, for each audience, effective feedback must answer three questions: (1) Where am I going? (the goals); (2) How am I going? and (3) Where to next? It appears prescient that several years before the use of learning map systems as a basis of assessment, Hattie and Timperley phrased their questions consistent with the map metaphor.
It appears the discrepancy between the results of Kingston and Nash and Hattie and Timperley can be explained by the fact that, while formative assessment should be a process that helps answer Hattie and Timperley’s three questions, publishers promote mere collections of test items as formative tools. We argue that without additional, well-structured support, the use of test items to implement formative assessment, at best, provides student with some information about their correct and incorrect responses but, at worst, focuses students on their current proficiency status without stimulating ongoing learning. Calling an assessment formative without embedding it in a structure that answers these three questions is an impoverished attempt to provide teachers and students with the evidence they need to determine next steps in the learning process. In contrast, Black asserts that classroom dialogue and discussion are critical activities wherein students become invested in their learning [
23]. Despite the limited availability of direct examples of the nature of effective dialogue, Heritage and Heritage include vignettes to document and illustrate this assessment practice [
24].
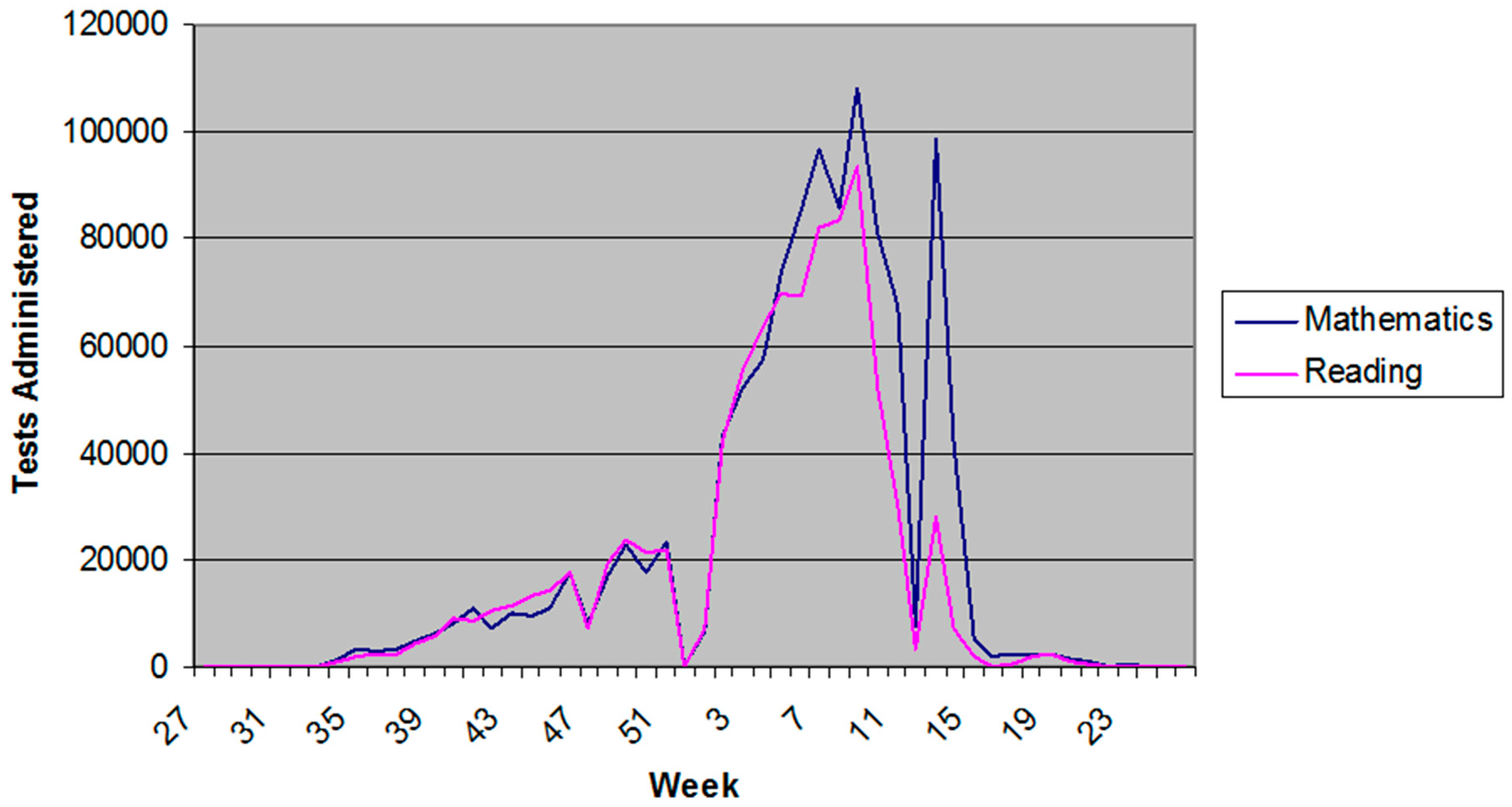
Even short, focused tests intended to be used as part of a formative process are not immune.
Figure 2 shows the usage patterns in 2007 of the Kansas formative tools, being short, focused computer-administered tests (about ten items each) that were intended to be used as part of a formative assessment process. Such a process would be expected to have steady usage throughout the instructional school year because formative assessment is equally useful throughout instruction. However, the pattern does not demonstrate an even level of use, as seen in
Figure 2. Usage slowly rose between August and December, and then dramatically increased about six weeks before the start of summative assessment. This pattern is consistent with using these tools as practice tests.
3. Some Background on Learning Map Systems
In recent years, attention and use of organized learning models—learning progressions, learning trajectories, and learning map systems—have been increasing. Several major multi-state testing programs in the United States have used organized learning models as part of the creation of their test specifications. One of these, aptly named the Dynamic Learning Maps
® (DLM
®) alternate assessment, is designed with learning map systems as its central feature. DLM provides instructionally embedded and year-end learning maps–based assessment in English language arts and mathematics for students with significant cognitive disabilities in grade 3 through high school. It is also currently developing a learning map system in science. The use of learning map systems as part of the DLM assessment was reported by Kingston, Karvonen, Bechard, and Erickson [
25]. The development of the DLM learning map system is described in detail in pages 24–36 of the DLM technical manual [
26]. In general, a four-step process was used:
Identification and representation of learning targets;
Identification and representation of additional supporting skills;
Linking the DLM Maps to content standards (essential elements);
Development and connections among nodes and building alternative pathways.
These steps were supported by review of research syntheses about student learning and review by more than 100 educators.
Figure 3 shows a snapshot in time of the University of Kansas mathematics learning map system. It contains 2554 nodes (aspects of mathematical knowledge) and 5605 connections among those skills.
Obviously, the detail in
Figure 3 is unreadable. It is shown only to provide evidence of the size and interconnectedness of the underlying mathematical concepts. Even
Figure 4, which only includes the mathematics nodes intended to be taught in grade 7, appears overwhelming. Viewing the map at this level provides an appreciation for the breadth and complexity of the material taught at a single grade level, but this view is not instructionally useful.
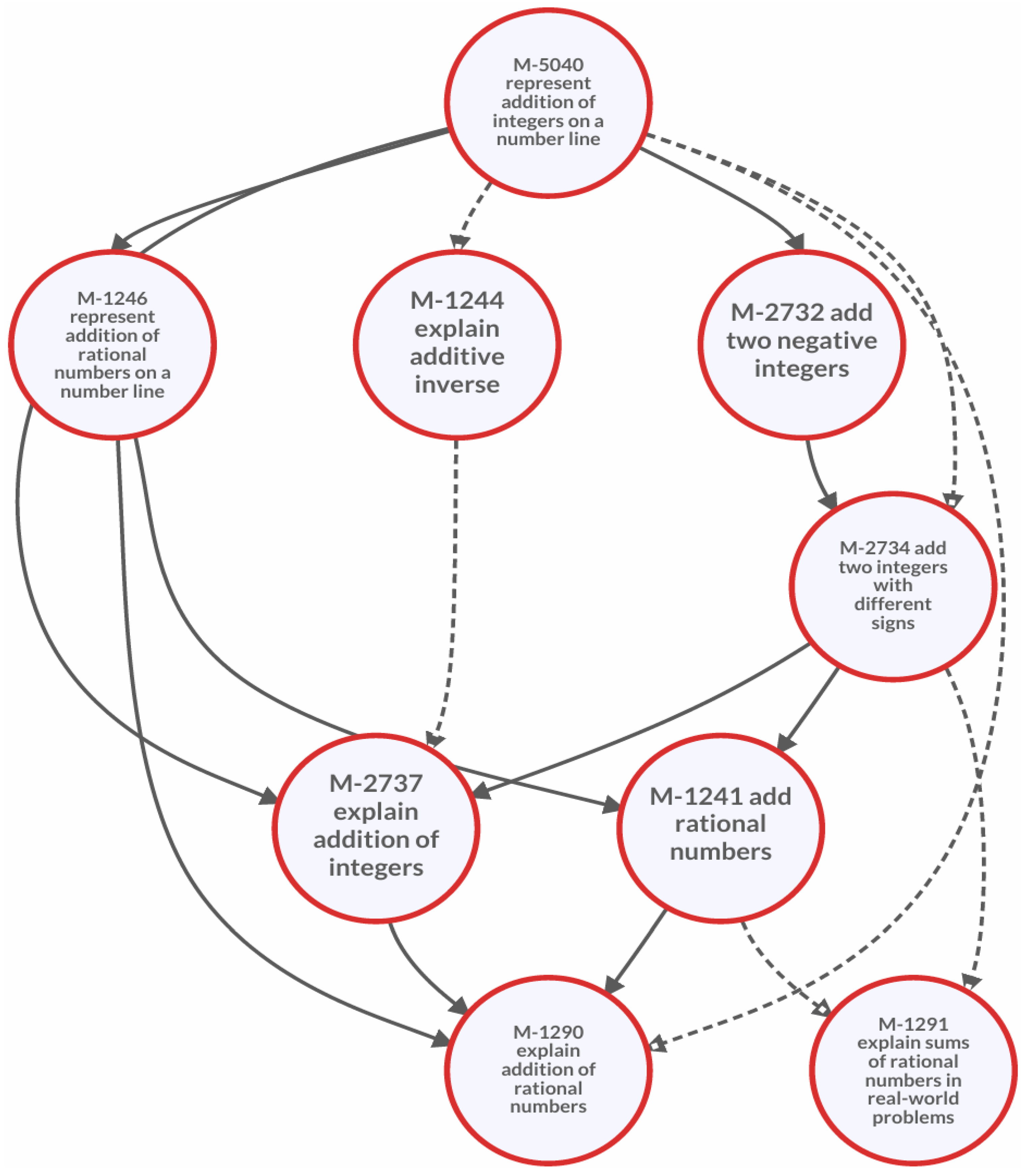
Figure 5 shows the neighborhood with nine nodes and 16 connections that relate to the addition of rational numbers. This view would be useful for preparing a lesson because it provides information about critical relationships among concepts and skills that can inform teachers’ choices of instructional tasks and purposeful questions. The solid lines indicate direct pathways, and the dashed lines indicate intervening nodes that are not shown. In the electronic version of the map, clicking on a dashed line displays those intervening nodes.
An additional advantage of learning map systems is that maps support a more powerful approach to feedback than has been traditionally used, because they enable consistency in language and interrelationship among all elements of the learning triangle. For example, during training in the most recent learning maps project, teachers wanted to walk around their classrooms with an image of the map section related to the day’s lesson and write students’ names by the nodes the educator believed represented each student’s understanding. Teachers saw the map as a tool they could viably use during instruction.
For enhanced feedback to students and parents, nodes in the map can be organized into common learning progressions for each educational target.
Figure 6 shows a portion of a DLM alternate assessment score report. Rather than trying to summarize student performance in a single score, or even a set of subscores, this report provides concrete representations of what a child can complete, what a child is currently learning, and what the child’s long-term targets are.
4. Learning Map Systems as an Organizing Structure for Formative Assessment
According to NCTM, effective mathematics instruction requires educators to deeply understand the content they teach and to appreciate how students construct mathematical knowledge [
4]. NCTM’s eight mathematics teaching practices build on previous work by Shulman [
18] and Ball et al. [
19] and are outlined under the teaching and learning principle, which describes how teachers must draw on their knowledge of content and pedagogy to provide effective instruction. The eight teaching practices [
4] are shown below.
Establish mathematics goals to focus learning;
Implement tasks that promote reasoning and problem solving;
Use and connect mathematical representations;
Facilitate meaningful mathematical discourse;
Pose purposeful questions;
Build procedural fluency from conceptual understanding;
Support productive struggle in learning mathematics;
Elicit and use evidence of student thinking.
Practices numbered 1, 2, 4, 5, and 8 each address one or more aspects of the formative assessment process, and can be informed and strengthened by access to learning map systems. Sztajn, Confrey, Wilson, and Edgington linked learning trajectories to four well-documented teaching models [
27]: mathematics knowledge for teaching [
19]; task analysis [
28]; orchestrating productive discourse [
29]; and formative assessment [
30]. Sztajn et al. reinterpreted the components of each model in terms of learning trajectory–based instruction, thereby promoting learning trajectories as a unifying structure for professional learning and instruction [
27]. Similarly, we propose that learning map systems can organize curriculum, instruction, and assessment into a coherent learning structure that supports students and teachers, by focusing on how students learn particular mathematics concepts and skills, and by informing teachers’ instructional decisions.
While learning map systems are new to the field, researchers have investigated how teachers can use similar models, (i.e., learning progressions, which tend to have significantly fewer nodes and are arranged linearly), as instructional resources [
31,
32,
33,
34]. These studies have determined that teachers have difficulty using learning progressions with assessment data to productively inform instructional decisions; specifically, teachers struggle to consider evidence of student thinking in terms of the characteristics of the different levels of understanding described in a learning progression. In the studies, teachers judged student learning in terms of whether students had either attained or not attained a specified level in a learning progression. This “gets it/does not get it” perspective did not adequately support teachers or students in determining effective next steps in the learning process. Teachers needed more information that tied specific teaching strategies or exemplary instructional practices to levels in the learning progression at hand. We argue that for teachers to make informed instructional decisions, they need additional support to coordinate theoretical information about how students learn (provided in a learning map system) with information they observe or collect about their actual students’ progress.
The ELM project is an extension of the work of the Dynamic Learning Maps Alternate Assessment, in which the map was extended to cover elementary and secondary school learning for all students. This project positions learning map systems at the center of a coordinated suite of materials that enhance teacher understanding of how students learn particular content, while also providing the necessary scaffolds for implementing effective instruction and formative assessment. Additionally, the materials enable teachers to instruct and assess in ways that are simultaneously consistent with the learning theory depicted in the learning map system, and reflective of recommended instructional practices. We believe that this organization of resources around a learning map system provides the tools needed to overcome teachers’ documented difficulties in using learning progressions and assessment data to inform their instructional decisions, and to improve the achievement of struggling students [
31,
33,
34].
As we developed our coordinated model, we investigated how teachers can use and prefer to use learning map systems to study the content they teach, plan instruction, and interpret student work products [
35]. Findings from these studies agreed with the conclusions of Furtak, Morrison, and Kroog [
34], who suggest that, although organized learning models provide teachers valuable insights to how students learn, teachers need additional scaffolds to carry out instruction and assessment activities that cultivate the learning and development described in the learning models. One teacher shared this reflection about her use of a learning map system to plan instruction focused on multiplying fractions:
Before we saw the learning map, we taught students the standard algorithm and thought that was enough. After considering the learning map and improving our own understanding of how area models represented what was really happening when we multiplied fractions, we changed our instruction. We used the area model earlier in our teaching and found that our students were then better able to understand the standard algorithm, either arriving at it on their own or through guided conversations. We also noted how our struggling students in particular appeared to hang on to their understanding better than when we focused on the procedure instead of the concepts.
Teachers want instructional materials aligned to a learning map systems that includes sufficient supporting materials which describe essential prerequisites and important conceptual connections [
35]. They want lesson plans, discussion questions, and relevant tasks that support personalized class-level instruction. Materials should explicitly point out multiple pathways when they exist, allowing for variations in student learning and instructional approaches. Learning map systems for particular standards or collections of standards should explicitly locate students’ different skill levels in relation to the learning goal. The maps should also show the various pathways from a student’s current skill level to the learning goal. Whereas learning map systems particularly benefit less experienced teachers by helping them understand sequences of learning, experienced teachers can profit from learning map systems that show the connections among nodes, which can suggest updated instructional approaches that were not previously obvious. Learning map systems, associated professional learning opportunities, and formative assessment materials, have the potential to provide teachers with the instructional supports they need to guide students of all ability levels along the path towards standard mastery.
The learning map system alone is limited in its ability to impact teaching; it is intended to be integrated into (or perhaps form the foundation of) the learning triangle. To this end, we have used learning map systems as an organizing structure and have embedded them with specific, relevant materials and tools specifically designed to help teachers and students tie evidence of student thinking directly to where students are in their learning. This connection provides the basis for actionable feedback [
20]. The embedded materials engage teachers and students in classroom activities that foster the conditions for (1) developing understanding consistent with the learning theories embedded in the learning map system; (2) engaging in rich discourse that exposes student thinking and provides opportunities for effective feedback; and (3) generating evidence of student learning through performance tasks and object measures of learning that are linked to the learning map system
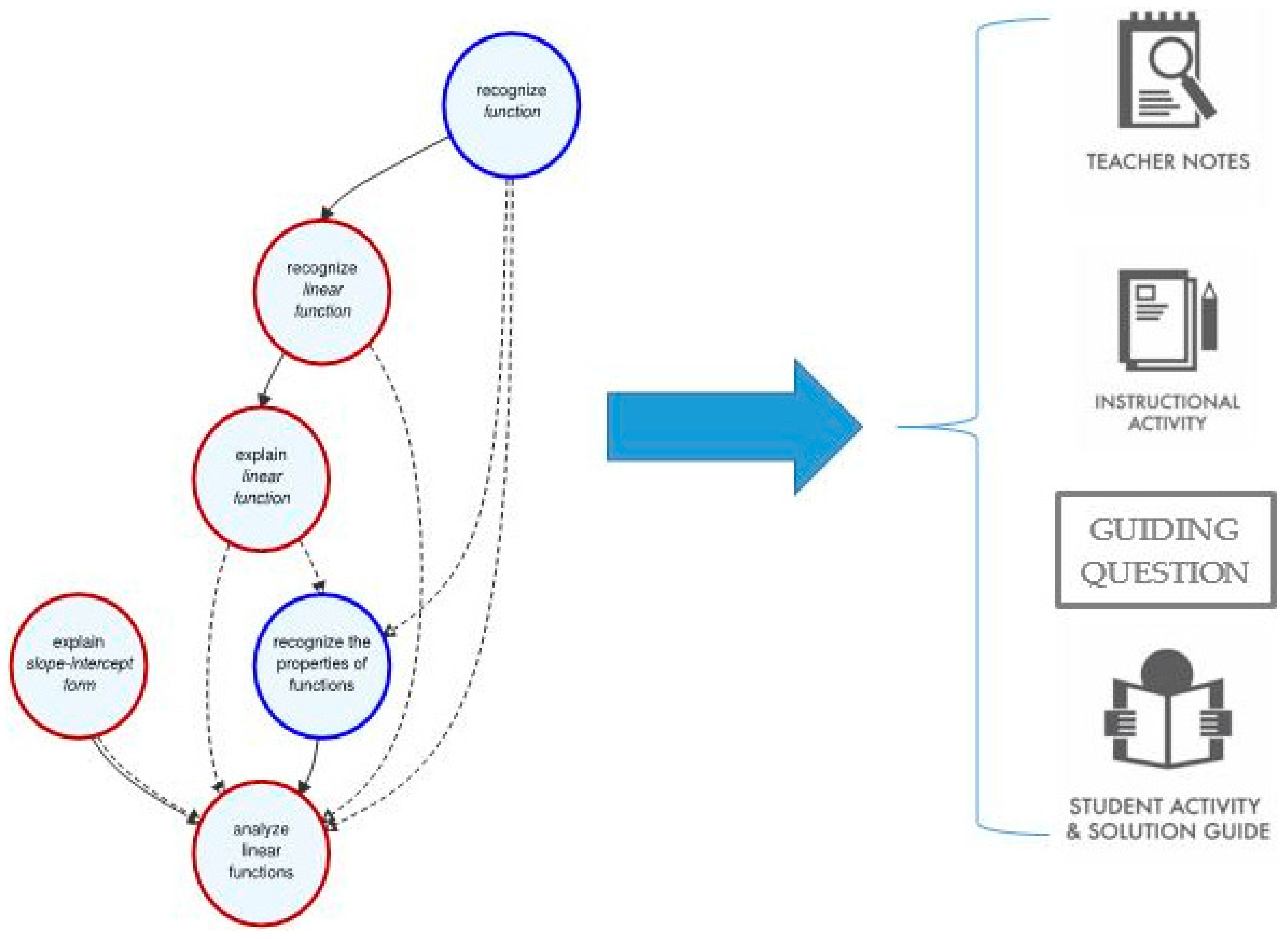
Figure 7 presents some of the elements of the informed instruction system. Teacher notes, instructional activities, guiding questions, and student activities are all associated with nodes or neighborhoods of nodes in the map.
Teacher notes briefly explain the research that informed the map’s structure and summarize scholarly recommendations for instruction. In our work with practicing teachers, we learned that our sample of educators wanted to know what researchers had determined about how students learn material most effectively and that teachers benefited from these explanations. To imitate these highly productive discussions with small groups of teachers, we created teacher notes documents and videos for map sections associated with particular academic standards.
In response to teachers’ pleas for high quality lesson ideas, we created instructional activities that correspond with the map’s structure and the research-based instructional approaches. These activities are designed for class-level instruction and include guiding questions that target the nodes in each learning map section. Two types of guiding questions help teachers engage students in discussion about the mathematics at hand: questions that uncover student thinking and questions that elicit evidence of student progress. The activities are detailed enough to be used by novice teachers but include opportunities and suggestions for variation that accommodate adaptations by more experienced teachers.
To help teachers practice authentic formative assessment, student activities provide mathematics tasks for students to work independently or in small groups. The accompanying solution guide provides correct responses along with example incorrect responses, based on common misconceptions and errors. For each incorrect response, the solution guide suggests which node in the learning map system the student may need to clarify. Thus, the instruction and assessment tools maintain direct connections to the nodes in the learning map system, grounding all features of the learning experience in the centrally positioned learning map system.
As our title suggests, we argue that instruction and formative assessment are inextricably linked. In this section, we describe how our informed instruction system inherently supports teachers in practicing formative assessment.
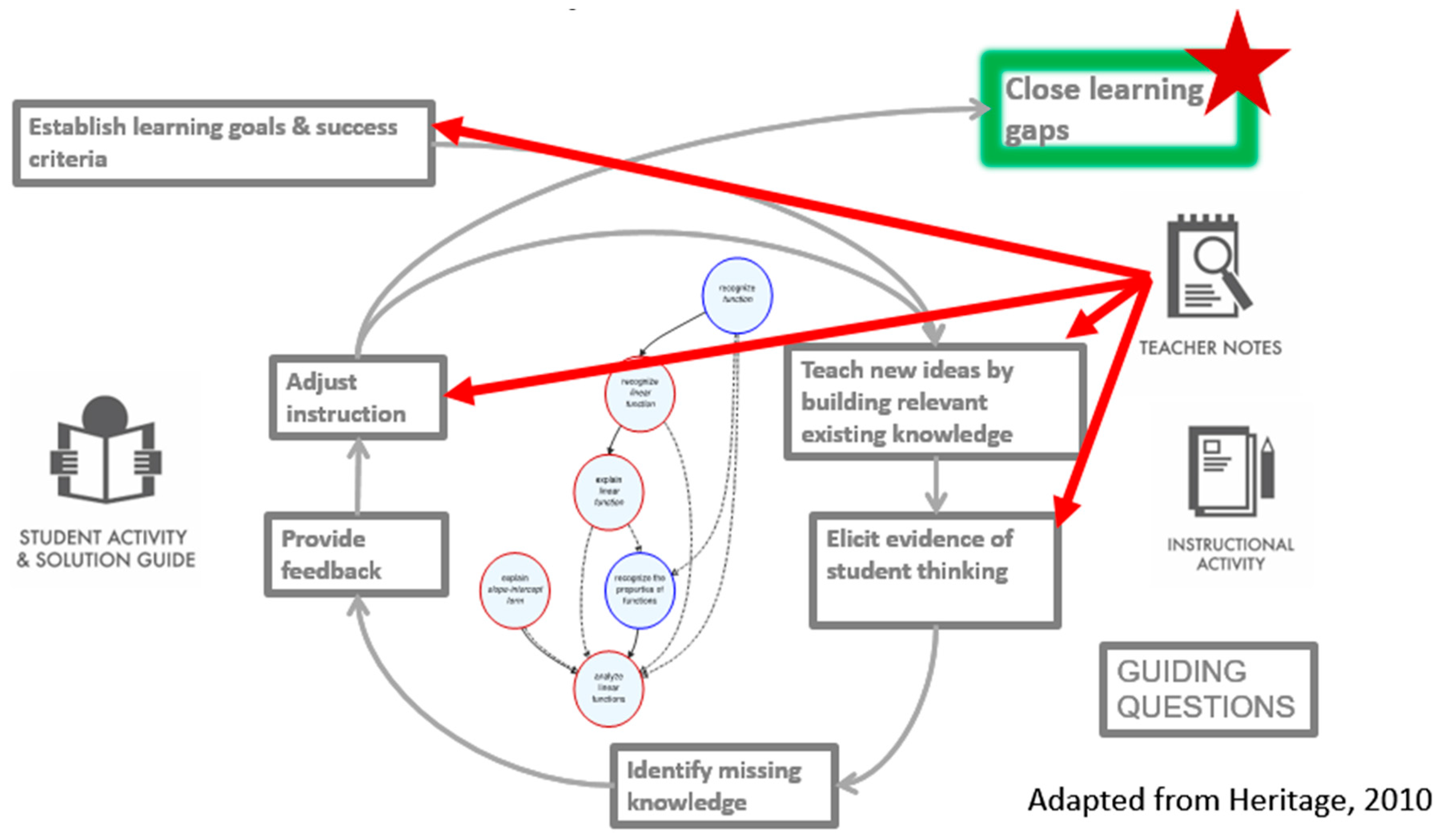
Figure 8 illustrates how we have embedded our informed instruction system in an adapted version of Heritage’s model of formative assessment, which looks to close learning gaps in six steps [
14]:
Establish learning goals and success criteria;
Teach new ideas by building relevant existing knowledge;
Elicit evidence of student thinking;
Identify missing knowledge;
Provide feedback;
Adjust instruction.
Our coherent suite of instructional tools addresses each of these six steps.
Table 1 shows the correspondence of our learning maps–based instructional materials to the steps in the informed instruction system.
5. Summary and Next Steps
In this article, we have posited that effective learning requires instruction that incorporates formative assessment to organize lessons, gather evidence of student learning, and use of that evidence to adjust instruction. Furthermore, we have suggested that assessment detached from curriculum and instruction is not useful for student learning and can even be detrimental. Other current research projects such as FaSMEd, (Improving Progress for Lower Achievers through Formative Assessment in Science and Mathematics Education), have used comparable evidence to come to similar conclusions regarding the desirability of technology supports for implementing formative assessment [
36].
We proposed learning map systems as an organizing structure for formative assessment and described aspects of a project that provides teaching tools and professional development to facilitate educators’ everyday integration of formative assessment within their instruction. In this project, learning map systems organize and connect curriculum, instruction, and formative assessment and are accompanied by focused professional development resources. A small group of teachers have just begun to use these materials and to provide formative feedback on the map, instructional tools, and technology that houses and delivers the materials. The cadre will increase in size over the next two years, as will the amount of material available to teachers for use in grades 2–8.
In two years, a summative evaluation of the efficacy of this approach will be performed using a sample of about 400 teachers and their students. Although the current project aims to evaluate the effectiveness of these teachers’ instruction on their students’ grade-level proficiency in mathematics and English language arts, the project also includes some measures to gauge the gains teachers experience in their professional and pedagogical knowledge. This information from and about teachers will inform future research focused on learning map systems, including their use as tools for professional development. As the first direct consumers of learning maps information, teachers can help guide future investigations into how learning map systems can be used more directly with learners. In an age of multi-media representations, we believe learning map systems have great potential as tools that provide visual and dynamic means for interacting with content and that can be used directly with learners of all ages.