Abstract
In 2022, the Programme for International Student Assessment (PISA) assessed the creative thinking skills of 15-year-old students, measuring their ability to generate creative ideas and improve others’ ideas. The present study used a correlational design to explore the relationship between creative thinking test scores and the frequency of participation in school activities. Surprisingly, the results show that countries with higher participation in school activities obtained worse results in the global PISA test for creative thinking and scientific problem-solving. Even after adjusting for PISA performance in 2018 and 2022, the increase in school activities did not improve low creativity scores. PISA identified this result as counterintuitive but analyzed it at the student level. However, we examined the phenomenon at the country level, which allows us to suggest another explanation. These findings indicate that such activities may need to be more enriching, focusing more on developing divergent rather than convergent skills. The complexity and cognitive load teachers require to design and carry out highly creative activities may explain these results. This study proposes reconsidering the pedagogical implementation of these activities and incorporating generative artificial intelligence as a fundamental tool to enhance creative development in the educational environment.
1. Introduction
Education aims to provide students with the opportunities to develop the skills required to participate in society actively. Emerging technologies and the need to tackle complex, unprecedented problems will shape future labor markets, creating new sectors and roles that do not yet exist. In this context, it is essential to design educational approaches that foster the development of key competencies, such as critical thinking, collaboration, effective communication, and creative thinking (Araya, 2023; Kafai et al., 2024).
1.1. Creative Thinking
Although many studies have explored this concept and offered various definitions (Alabbasi et al., 2022; Gerver et al., 2023; Samaniego et al., 2024), PISA 2022 describes it as the ability to engage effectively in creating, evaluating, and improving ideas, leading to innovative and effective solutions for both problem-solving and decision-making. This competency, grounded in theoretical knowledge and practical experience, equips individuals to achieve better outcomes, especially in situations with limitations and challenges (OECD, 2024d). As global organizations and societies face emerging challenges, the need for innovation and knowledge generation becomes increasingly critical (OECD, 2010b). This highlights the importance of innovation and creative thinking as essential collective efforts to drive progress and ensure continuous adaptation in a constantly changing world. Additionally, this competency is vital in academic and professional settings and individuals’ personal and social development (OECD, 2014). This is particularly relevant in a world where the rapid pace of technological and social change demands flexibility and innovative thinking and where various domains of creative thinking, such as science, art, and technology, require specific approaches to foster innovation (Amabile, 2018).
1.1.1. Domains of Creative Thinking
The literature primarily describes two approaches regarding creative domains: domain generality and domain specificity. Domain generality suggests that creative skills are transferable across different areas of knowledge; in other words, a creative person can apply their creativity in any field. This view was supported by the first generation of creative thinking tests, such as Torrance’s (1959), which assumed that creative performance in one domain could be transferred to another. In contrast, domain specificity argues that the skills and traits necessary to be creative are specific to each area of knowledge (Baer, 2016). From this perspective, a person may be creative in a particular field, such as the sciences, but not necessarily in another, like the arts. Recent studies support this view, suggesting that creativity depends on domain-specific knowledge and skills (Holinger et al., 2024). Similarly, some models of creativity attempt to integrate both approaches, proposing that while certain aspects of creativity may be general, others are domain-specific (Baer & Kaufman, 2005).
Based on a self-report study of 2318 university students, Kaufman (2012) identified five domains of creative thinking that should be measured. These domains are Personal/Everyday, Academic, Interpretative (which includes writing and music), Mechanical/Scientific, and Artistic. The Personal/Everyday domain refers to creativity applied in daily life and personal problem-solving. The Academic domain encompasses creativity in educational and research contexts. The Interpretative domain covers creative activities related to expression through writing and music. The Mechanical/Scientific domain involves creativity in invention, engineering, and the exact sciences. Finally, the Artistic domain focuses on the visual and plastic arts. This classification provides a comprehensive framework for assessing and fostering creativity across different areas of life and knowledge.
1.1.2. Measuring Creative Thinking
Since the early studies in the 1960s (Guilford, 1967; Torrance, 1968) through to more recent research, the measurement of creativity or creative thinking has generally relied on divergent thinking tests (Holinger et al., 2024). These tests evaluate individuals’ ability to generate multiple solutions to a problem, reflecting their creative potential. However, measurement approaches in studies vary considerably, leading to inconsistent results (Reiter-Palmon et al., 2019). The way participant responses are scored is particularly relevant, as this is where studies tend to differ (Acar et al., 2024). Traditionally, responses are evaluated based on ideational fluency, which measures the total number of ideas generated by an individual in a given period, ideational flexibility, which assesses the ability to think across different categories and perspectives, demonstrating an individual’s capacity to approach a problem from multiple angles, and originality, which measures the novelty and uniqueness of ideas (Said-Metwaly et al., 2018).
In this context, creative thinking has primarily been evaluated through the Torrance Tests of Creative Thinking (TTCT), which have proven to be a reliable and valid tool for measuring creativity in students across various educational levels (Kim, 2006).
To contribute to the development of creativity and creative thinking, Craft et al. (2001) suggested the existence of two different types of creativity: Big “C” Creativity and little “c” creativity. Big “C” Creativity refers to exceptional and groundbreaking creativity, often associated with brilliant individuals who make significant and lasting contributions to their fields, such as Albert Einstein or Leonardo da Vinci. In contrast, little “c” creativity refers to everyday creativity that anyone can exercise daily, such as finding an ingenious solution to a household problem or designing an original classroom activity. They argue that we should foster little “c” creativity in the educational context. This perspective emphasizes the importance of recognizing and cultivating the creative potential of all students, not just those with exceptional talents, thus promoting an environment where everyday creativity is valued and developed in daily school life.
Later, Kaufman and Beghetto (2009), following the guidelines proposed by Craft et al. (2001), expanded on the idea of creativity by proposing a continuum of four levels: (i) Mini-c: Closely linked to learning, mini-c creativity manifests whenever someone tries a new task. While the outcomes at this level may not be innovative to the world, they are new and meaningful to the individual. (ii) Little-c: This reflects the development of creative skills that, with proper feedback, may become valuable to others. This level extends personal growth into creative products that can be appreciated in everyday contexts. (iii) Pro-c: This involves creativity exercised in a professional realm, supported by years of practice and deliberate training. Not everyone at this level makes a living from their creative activity, but many aspire to do so. (iv) Big-c: This represents creativity that leaves a lasting mark on history. This level evaluates a person’s career and contributions, comparing them to those of other great innovators.
This model allows for a more nuanced understanding of creativity, recognizing that it can manifest in various ways and at different levels throughout a person’s life. This approach can significantly contribute to students’ holistic development, preparing them to face the challenges of today’s world with innovative thinking.
1.1.3. Creative Thinking in the Educational Context
Creative thinking is considered a transversal skill in nearly all curricula of OECD member countries (Care et al., 2018). According to Cignetti and Rabella (2023), 60% of jurisdictions participating in PISA 2022 include references to creative thinking in most subjects within primary education curricula (>75% of subjects), while 34% do so in some subjects (between 25% and 75%). However, only 24% of jurisdictions have systematic guidelines or evaluations that describe this competency and how it is taught.
The integration of creative thinking is most prominent in disciplines such as the visual arts (93%) and performing arts (92%) in primary education, extending to technology and literature in secondary education (88% and 86%, respectively). In contrast, it is less frequently referenced in subjects like physical education, history, and citizenship, where the percentages are considerably lower (60%, 59%, and 56%, respectively) (OECD, 2024d).
While various studies have identified positive and significant effects associated with implementing programs, training, and interventions that foster creativity in schools (Muñoz Silva et al., 2021; Rodrigues & Chagas-Ferreira, 2023), its integration faces several essential obstacles. An overcrowded curriculum, a lack of assessment focus on creativity, and insufficient teacher training and resources are the main challenges to incorporating creative thinking into education (Cignetti & Rabella, 2023; OECD, 2020a).
There are also notable gaps in the literature regarding the systematic adoption and integration of creative thinking models in educational systems and the potential consequences of effectively developing students’ creative skills (Saeed & Ramdane, 2022). Empirical evidence that clearly and robustly links the implementation of specific creative thinking approaches with tangible improvements in students’ innovative competencies remains scarce (Forte-Celaya et al., 2021).
In this context, the creative problem-solving model is the most widely used approach for developing these skills, as it combines the practice of divergent and convergent thinking in a cyclical process (Foster & Schleicher, 2022).
In the social domain, creative thinking enables students to address problems from a broad perspective, considering not only technical aspects but also the emotional and social needs of those affected. This approach relies on students’ ability to empathize, recognize patterns, evaluate specific needs, and generate ideas with emotional significance (Amabile, 2018).
In the scientific domain, creative thinking manifests in activities such as formulating new ideas that contribute to scientific knowledge, designing experiments to test hypotheses, developing inventions to address specific problems, and innovatively implementing engineering projects (Hernández-Ramos et al., 2021). Developing creative thinking in scientific contexts requires balancing originality and validity. Although creativity is essential, it must be supported by a basic understanding of scientific principles to ensure the relevance of the proposed solutions (Martínez et al., 2021).
1.2. PISA Test and Creative Thinking
The PISA test by the Organisation for Economic Co-operation and Development (OECD) assesses how education systems prepare students to apply their knowledge and skills in tasks relevant to their present and future lives. It is administered every three years to 15-year-old students and focuses on reading, mathematics, and the natural sciences. Since 2012, PISA has incorporated the assessment of innovative domains, evaluating areas considered essential for determining whether students are ready to face emerging problems in the present and the near future. These areas include creative problem-solving (OECD, 2014), collaborative problem-solving (OECD, 2017), and global competence (OECD, 2020b).
In the 2012 PISA test, guidelines were established to measure the cognitive processes involved in creative problem-solving based on four aspects: (i) Exploring and understanding: Examining and understanding the problem situation. This includes observing and interacting with the situation, seeking relevant information, and recognizing limitations or obstacles. (ii) Representing and formulating: This entails using various means, such as tables, graphs, symbols, or words, to represent aspects of the problem situation. It also involves formulating hypotheses about relevant factors and their relationships, thereby constructing a coherent mental representation of the problem. (iii) Planning and executing: This focuses on designing and implementing a plan or strategy to solve the problem. This includes clarifying the overall goal, setting sub-goals, and taking steps to reach the solution. iv) Monitoring and reflecting: This involves tracking progress toward the problem’s solution, responding to feedback, and reflecting on the solution achieved, the information provided, and the strategy adopted (OECD, 2014).
In the 2022 PISA test, a creative thinking assessment was included. This evaluation was designed to focus on tasks that promote creativity, minimizing the influence of innate talent and highlighting the malleable capacity of individuals to demonstrate creative thinking. This type of creativity is applicable in both artistic contexts and in the resolution of social or scientific problems. The PISA assessment addressed convergent cognitive processes, which involve identifying and refining ideas, and divergent processes, which focus on generating creative ideas (Cropley, 2006). In this framework, “creativity” specifically covers creative thinking, creative problem-solving, and innovation. On the other hand, entrepreneurship, critical thinking, and collaboration are expressly excluded from the scope of this definition.
For measurement purposes, the assessment evaluated a model based on three key aspects: (i) Generating diverse ideas: This aspect refers to the student’s ability to think flexibly, producing ideas significantly different from one another. (ii) Generating creative ideas: Creative ideas are both novel and valuable. In the context of PISA, while 15-year-olds are not expected to generate unique ideas, originality remains a crucial criterion. (iii) Evaluating and improving ideas: This process involves students’ ability to identify limitations in their initial ideas and improve their originality.
Additionally, the questions were organized into four specific domains: Written Expression, Visual Expression, Social Problem Solving, and Scientific Problem Solving. (i) Written Expression: This domain evaluates students’ ability to communicate ideas and thoughts coherently and effectively through writing. Creativity is assessed in the structure, language use, and originality of presenting ideas. (ii) Visual Expression: This domain measures the ability to convey concepts and emotions visually. It evaluates creativity using visual elements such as color, shape, design, and composition to communicate innovative messages. (iii) Social Problem Solving: This domain focuses on students’ ability to address and resolve societal issues. Creativity is assessed by identifying problems, developing novel solutions, and implementing strategies that promote social well-being. (iv) Scientific Problem Solving: This domain assesses the ability to apply creative thinking to solve scientific challenges. It includes the ability to formulate hypotheses, design experiments, interpret data, and propose innovative solutions to complex scientific problems.
For scoring, the PISA assessment provides average scores by country and OECD-associated economy and individual scores in each specific domain (see Table S1).
In this application, the PISA assessment collected information on students’ participation in various classes and school activities, measured through self-reports. These activities were selected to encompass a broad range of experiences that could contribute to developing creative thinking. The activities included are as follows:
- Art classes/activities (e.g., painting, drawing).
- Music classes/activities (e.g., choir, band).
- Computer programming classes/activities.
- Creative writing classes/activities.
- Science club.
- Drama/theatre class/activities.
- Debate club.
- Publications (e.g., newspapers, yearbooks, literary magazines).
As is customary, the PISA assessment also collected detailed information on students’ various daily and contextual activities (OECD, 2024b, 2024d). This included economic aspects, allowing for an analysis of how socioeconomic conditions influence academic performance. Gender-related data were also gathered, providing a more comprehensive understanding of the potential disparities and barriers faced by students of different genders. Furthermore, specific data on family environment, access to educational resources, attitudes toward learning, and other student-specific characteristics were collected, offering a deeper understanding of the factors that affect learning and creativity in different contexts. This comprehensive approach enables the identification of patterns and trends that can inform more inclusive and effective educational policies.
Linking Pedagogies to Progress: Creative Thinking in PISA and Economic Growth
PISA scores are a good indicator of the future quality of the workforce in each country, and it has been demonstrated that workforce quality is a decisive factor in determining nations’ long-term growth rates (OECD, 2010a). Economists have focused on why some countries grow faster than others. In this line, large-scale international studies (ILSAs) have proven to be critical tools for measuring the cognitive skills essential for economic growth, showing that countries with limited knowledge capital need help in improving productivity and experience slower and less inclusive growth. This relationship between cognitive skills and economic development is evident in developing nations and advanced economies, highlighting the importance of development goals promoting universal minimum skills acquisition. Research has established a direct and causal connection between improving the skills of the population and faster economic growth, underscoring that strengthening human capital is a decisive factor in long-term economic progress (Hanushek & Woessmann, 2022).
Researchers at the Brookings Institution have been monitoring the global expansion of skills like creative thinking for several years (Taylor et al., 2020). In 2018, they conducted a study covering 152 countries, revealing the extent to which educational curricula evolve toward a greater focus on developing creative thinking. This shift reflects a significant transformation in global educational priorities, highlighting creativity as one of the most mentioned skills in national policy documents in more than 60 countries.
A complementary study, based on the Center for Curriculum Redesign’s classification, evaluated 22 educational jurisdictions, including both countries and states. Of these, 21 explicitly mention the importance of developing creativity and critical thinking in their curricula. However, the analysis reveals a key finding: while these skills are present in the educational agenda of many jurisdictions, there still needs to be more specific guidelines on how to implement them pedagogically and, particularly, how to assess them effectively (Care et al., 2018).
Among the regions that have made significant progress in integrating creative and critical thinking into their education systems, Singapore, Finland, Hong Kong, and Australia stand out. These cases represent successful examples of how these skills are effectively implemented in curricula, serving as a reference for other regions seeking to advance in this direction (Lucas, 2022).
Based on the questionnaires for teachers and school principals applied in PISA 2022, it is clear that most teachers believe that creativity is a developable skill, that it is possible to be creative in any subject, and that there are multiple ways to express it. These beliefs are common among teachers from socioeconomically disadvantaged backgrounds and the most privileged (OECD, 2024e).
Although creativity development is formally included in many initial teacher training programs across numerous countries, the report highlights a persistent gap in understanding and implementing creative pedagogies, especially in regions such as Latin America. For instance, in countries such as the Dominican Republic, Panama, Colombia, and Costa Rica, teachers place significant importance on fostering creativity in their students and employ strategies that students perceive as creative in the classroom. However, overall creativity scores in these countries still need to improve. While there is a pedagogical intention to encourage creativity, the lack of specific training and resources to implement effective practices can limit the impact of these efforts.
This claim is supported by Figure 1, which presents a Creative Thinking Pedagogy Index based on the perspectives of school principals and students. The figure highlights countries such as the Philippines, the Dominican Republic, Albania, and Uzbekistan, which achieve notably high scores on both indices. However, these countries rank among the lowest results in the PISA creative thinking assessment (for the ranking details, see Table S1).
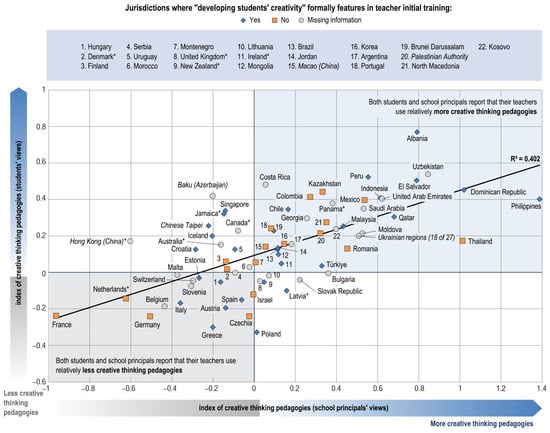
Figure 1.
Opinions of students and school principals on teachers’ use of pedagogies that foster creative thinking (OECD, 2024c). * Caution is required when interpreting estimates because one or more PISA sampling standards were not met.
This discrepancy suggests that, although there is a widespread perception of a greater emphasis on fostering creativity, more is needed to translate into better performance in creative thinking. This gap could indicate limitations in the effectiveness of the pedagogical practices implemented to develop creative skills. In other words, while teachers and principals may adopt strategies that promote creativity, these only sometimes yield the expected outcomes, possibly due to insufficient training, inadequate resources, or inconsistent application of such practices.
The PISA report also highlights that students from socioeconomically disadvantaged schools are more actively engaged in school activities than their predominantly higher socioeconomic background peers. This observation suggests that in less advantaged contexts, students may view school participation as a meaningful form of engagement or a pathway to overcome the external limitations associated with their environment.
On the other hand, PISA hypothesizes that students from more privileged backgrounds tend to prioritize traditional academic subjects such as reading, mathematics, and science, viewing them as essential for transitioning to higher education and securing well-paid jobs. This emphasis may explain why students from higher socioeconomic backgrounds often achieve better results in PISA assessments in these areas. However, this prioritization could limit their engagement in extracurricular activities and learning strategies that foster non-traditional skills, such as creativity.
This study is particularly significant as it focuses on analyzing the relationship between students’ participation in various school activities and the average scores achieved by countries in the 2022 PISA Creative Thinking assessment.
2. Research Questions
RQ1. Is there a significant relationship between participation in school activities and the scores obtained on the Creative Thinking test in the 2022 PISA assessment?
RQ2. How does participation in science clubs and programming-related activities influence the score obtained in the scientific problem-solving domain assessed in the Creative Thinking test of the 2022 PISA assessment?
RQ3. How are the scores obtained in the Creative Thinking test of the 2022 PISA assessment related to the scores in reading, mathematics, and science from the 2018 and 2022 PISA assessments?
3. Materials and Methods
3.1. Sample Selection
Approximately 690,000 students from 81 countries and economies participated in PISA 2022, representing a significant effort to understand and compare educational systems globally. The students assessed are between 15 years and 3 months and 16 years and 2 months of age at the time of testing, having completed at least six years of formal schooling. This standardized age range, applied uniformly in all participating countries and all assessment cycles, ensures a reliable basis for international comparisons. In this implementation, 64 countries and economies implemented the creative thinking cognitive test, and 74 countries and economies implemented the creative thinking questionnaire items (OECD, 2023).
For this study, we used data obtained from four primary sources. These include scores from the 2018 and 2022 PISA assessments, the 2022 PISA Creative Thinking test results, and the detailed characterization of the students who participated in the latter assessment.
The specific inputs are as follows: (i) Mean performance in creative thinking across countries and economies (64 records). (ii) Snapshot of performance across ideation processes and context domains, referring to the scores obtained in each of the four domains assessed in the test (64 records). (iii) Percentage of students reporting that they are participating in creative classes/activities (art, music, computer programming, creative writing, science club, drama or theatre, debate club, and publications) in their school at least once a week (74 records) (OECD, 2024b). (iv) PISA 2018 (78 records) and 2022 (80 records) results (OECD, 2020b, 2024d).
We excluded records where one or more sampling standards were missing or those flagged with caution due to specific circumstances. Additionally, we retained only records that contained all the fields related to the inputs i, ii, iii, and iv mentioned above. This inclusion criterion was essential to ensure the integrity and comparability of the data used in this study.
This methodological approach allows for an internationally precise and comprehensive evaluation of creative thinking, providing valuable data to understand the competencies and activities that foster creative development among students.
3.2. Study Design
This study adopts a quantitative approach using the data mentioned in the previous section. It focuses on analyzing the potential correlation between the scores in the Creative Thinking assessment, the overall PISA 2018 and 2022 scores, and students’ participation in school activities. The study’s structure allows for a comparative evaluation among the different participating countries and economies, providing a broad and detailed view of the variables that might influence creative thinking on a global scale.
3.3. Data Analysis
We analyzed the collected data using a combination of descriptive and inferential analyses. We employed statistical techniques such as linear regression and principal component analysis to identify patterns and significant relationships among the variables.
For the data analysis, we used the SPSS statistical software v.25, supplemented with advanced analysis tools in R. These programs enabled a thorough and detailed data analysis, ensuring the results’ accuracy and reliability.
4. Results
Following the inclusion criteria detailed in Section 2, we excluded records from the following countries due to differences in sampling standards: Australia, Canada, Denmark, Hong Kong, Ireland, Jamaica, Latvia, the Netherlands, New Zealand, Panama, and the United Kingdom. Consequently, the sample used in this study included 54 OECD countries and associated economies that met the established inclusion criteria. In this way, the final sample represented 84% of the countries and economies that participated in the creative thinking test. The complete list of countries and economies included in this study is in Table S1.
4.1. Relationship Between Participation in School Activities and Scores on the Creative Thinking Test in the 2022 PISA Assessment (RQ1)
Based on the analysis of the percentage of students’ weekly participation in school activities, as described in Section 1.2, and their creative thinking scores, we obtained the Pearson correlation for the sample (Table 1).

Table 1.
Pearson correlation between creative thinking scores and participation in school activities.
We then conducted a principal component analysis (PCA) on the school activities to identify underlying patterns and group activities with similar characteristics. This approach provides a deeper understanding of the relationships among the various activities and their joint contribution to students’ creative thinking development. To ensure the suitability of the data for factor analysis, we applied the Kaiser–Meyer–Olkin (KMO) test, which yielded a value of 0.787, indicating an acceptable level of adequacy for PCA. Additionally, we performed Bartlett’s test of sphericity, which was statistically significant (p < 0.05), suggesting that the data are appropriate for factorization (Table S2).
The PCA reveals two factors with eigenvalues greater than one among the eight potential factors. These two factors, used as categorical variables, explain 68.2% and 19.3% of the total variance, respectively, with a cumulative percentage of 87.6%. Although a third factor presents an eigenvalue lower than 1, it contributes an additional 5.4% to the explained variance, bringing the total to 93% (Table 2). Therefore, including this third factor is justified to provide a more comprehensive explanation of the total variance.

Table 2.
Total variance.
We employed an orthogonal Varimax rotation to facilitate the interpretation of the principal components. This rotation technique maximizes the variance of the resulting factors, allowing for a more precise and distinct understanding of the groupings of school activities.
The interpretation of the rotated data associates Component 1 with activities related to writing, science clubs, theater, debate, and school publications. These activities are grouped due to their focus on verbal communication and critical thinking skills. On the other hand, Component 2 includes art and music activities, which are more related to artistic expression. Computer programming activities, meanwhile, are assigned to Component 3. This separation is consistent with the variance values obtained, where the first two components explain most of the total variance (Table 3).

Table 3.
Rotated component matrix (rotation method: Varimax with Kaiser normalization).
Based on the new variables derived from the PCA, we conducted a new correlation analysis between the creative thinking score and these variables (Table S3).
Based on the factor analysis, generating new variables using the identified principal components is valid. This approach simplifies and summarizes the original information into representative variables, thus facilitating their analysis and interpretation. To calculate the new variables, Variable 1 (Var 1) is obtained by taking the simple average of the school activities constituting Component 1, which include creative writing, science clubs, theater, debate, and school publications. Variable 2 (Var 2) is calculated as the simple average of the school activities constituting Component 2, which include art and music activities. By averaging the activities that make up each principal component, we create a composite measure that more coherently reflects the collective influence of these activities on students’ creativity (Table 4).

Table 4.
Pearson correlation between creative thinking score and the new variables calculated through simple averaging.
We generated scatter plots to graphically represent the relationship between the score obtained in the creative thinking test and the generated variables. These plots include the regression line equation and the R-squared (R2) value, which quantifies the strength and direction of the relationship between the variables (Figure 2 and Figure 3).
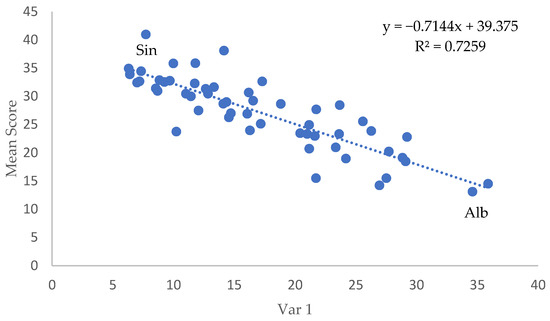
Figure 2.
Relationship between Var 1 and creative thinking score. For reference, we highlight the highest score in the sample (Singapore, Sin) and the lowest score in the sample (Albania, Alb).
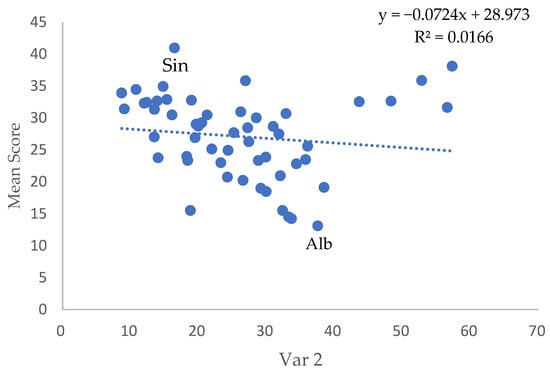
Figure 3.
Relationship between Var 2 and creative thinking score. Similarly, we highlight the highest score in the sample (Singapore, Sin) and the lowest score in the sample (Albania, Alb).
Finally, based on the newly generated variables and the variable for computer programming, we created a regression model to explain the score obtained on the creative thinking test. This model allows us to analyze how school activities influence students’ creative performance and is expressed as:
where Y is the response variable (creative thinking score). The explanatory variables are X1, X2, and X3 (Var 1, Var 2, and programming, respectively). β0, β1, β2, and β3 are the model parameters.
Y = β0 + β1X1 + β2X2 + β3X3 +ε
In the model summary (Table 5), two models are presented. Model 1 includes only Var 1 as a predictor, showing a correlation coefficient (R) of 0.852 and an adjusted R-squared of 0.721, indicating that 72.1% of the variability in the creative thinking score can be explained by Var 1. Model 2 adds Var 2 as a second predictor variable. This model shows a slight improvement in fit, with a correlation coefficient (R) of 0.881 and an adjusted R-squared of 0.768, indicating that 76.8% of the variability in the creative thinking score is jointly explained by Var 1 and Var 2.

Table 5.
Regression model summary predicting creative thinking test scores.
Table 6 shows the resulting coefficients from the linear regression analysis, presenting two models that include Var 1 and Var 2 as independent variables. In Model 1, only Var 1 is included as the independent variable. The standardized coefficient (Beta) for Var 1 is −0.852, indicating a strong negative influence of Var 1 on the creative thinking test score. The t-value is −11.736, and the significance level is 0.000, indicating that this result is highly significant. The equation for this model is expressed as follows:
Mean Score = 39.375 − 0.714 Var 1

Table 6.
Regression coefficients for the predictor model of the creative thinking test score.
In Model 2, Var 1 and Var 2 are included as independent variables. The standardized coefficient (Beta) for Var 1 increases to −0.949, suggesting an even more substantial negative influence of Var 1 when Var 2 is included in the model. The standardized coefficient (Beta) for Var 2 is 0.245, indicating a moderate positive relationship between Var 2 and the creative thinking test score. Both coefficients are significant, with t-values of −13.180 for Var 1 and 3.409 for Var 2 and significance levels of 0.000 and 0.001, respectively. The equation for this model is expressed as:
Mean Score = 37.161 − 0.796 Var 1 + 0.138 Var 2
Notably, the programming variable has been excluded in both models due to its lack of statistical significance. In Model 1, the significance level for programming is 0.604; in Model 2, it is 0.448. Both are well above the accepted threshold.
Additionally, we calculated the Pearson correlation to analyze the relationship between Var 1 and Var 2 with the different domains of the creative thinking test (Table 7).

Table 7.
Pearson correlation between the domains of the creative thinking test and the variables Var 1 and 2.
We also developed regression models linking these domains with the previously mentioned variables. These models aim to identify potential predictive relationships to understand better how certain factors impact student performance in each assessed domain. Table S4 provides an overview of the linear regression models applied to the different domains of the creative thinking test. Tables S5–S8 present the regression coefficients resulting from the linear regression analysis for each model applied to the various domains of the Creative Thinking test. An important observation consistent across all models is that the variable related to participation in programming activities remains insignificant once again.
4.2. Relationship Between Participation in Science Clubs and Programming Activities/Classes and Scores in the Scientific Problem-Solving Domain of the 2022 PISA Creative Thinking Test (RQ2)
We calculated the Pearson correlation to identify how these specific activities contribute to the scientific problem-solving domain. The results are displayed in Table 8.

Table 8.
Pearson correlation between the scientific problem-solving domain and the frequency of participation in science clubs and programming activities.
Similarly, we created scatter plots to visually represent the relationship between these activities and the scientific problem-solving domain (Figure 4 and Figure 5).
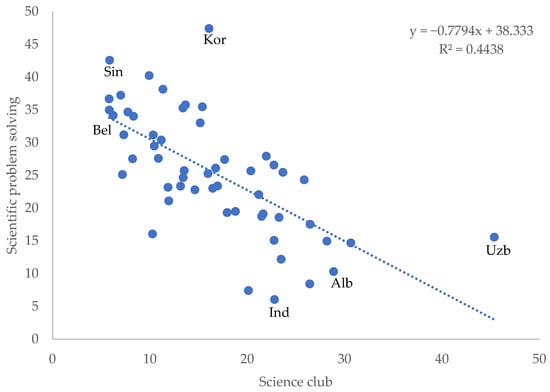
Figure 4.
Relationship between frequency of participation in science clubs and the score in the scientific problem-solving domain. The highest score (Korea, Kor) and the lowest score in the domain (Indonesia, Ind) are indicated for reference. The highest score (Uzbekistan, Uzb) and lowest score (Belgium, Bel) for participation in science clubs, and the highest score (Singapore, Sin) and lowest score (Albania, Alb) in the creative thinking test are also noted.
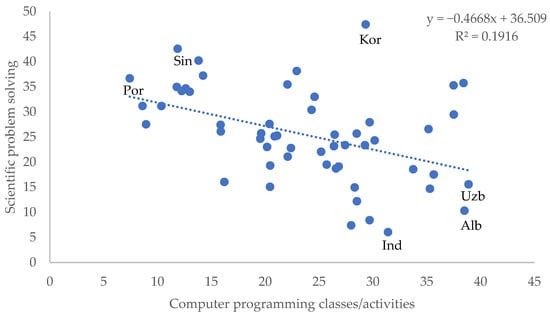
Figure 5.
Relationship between frequency of participation in programming activities and the score in the scientific problem-solving domain. The highest score (Korea, Kor) and the lowest score in the domain (Indonesia, Ind) are indicated for reference. The highest score (Uzbekistan, Uzb) and lowest score (Portugal, Por) for participation in programming activities, and the highest score (Singapore, Sin) and lowest score (Albania, Alb) in the creative thinking test are also noted.
4.3. Relationship Between Scores Obtained in the 2022 PISA Creative Thinking Test and Scores in Reading, Mathematics, and Science in the 2018 and 2022 PISA Assessments (RQ3)
Table 9 presents a summary of the linear regression models where the dependent variable is the score on the creative thinking test. In this case, we included the 2018 PISA mathematics, science, and reading scores as independent variables, the frequency of participation in science clubs and programming activities, and the Var 1 and 2 variables.

Table 9.
Regression model summary predicting the creative thinking test score.
Model 1 includes only the reading ability variable as a predictor, showing a correlation coefficient (R) of 0.912 and an adjusted R-squared of 0.829, indicating that the reading assessment score can explain 82.9% of the variability in the creativity score. Model 2 adds Var 1 as a second predictor variable. This model shows a slight improvement in fit, with a correlation coefficient (R) of 0.929 and an adjusted R-squared of 0.857, indicating that 85.7% of the variability in the creativity score is explained by both variables together.
Table S9 presents the coefficients for both models and highlights the variables that were not included due to a lack of statistical significance. In both models, the inclusion of the 2018 PISA mathematics and science scores did not reveal a significant relationship with creativity performance, and along with the other variables, they were excluded to optimize the model’s accuracy.
To contrast these results, we applied the same procedure, but this time incorporating the variables related to the scores in reading, mathematics, and science from the 2022 PISA assessment. The results of the resulting regression model are detailed in Table 10.

Table 10.
Summary of the regression model predicting the creative thinking test score.
Similar to the previous analysis, Model 1 includes only the reading ability variable as a predictor. This model shows a correlation coefficient (R) of 0.941 and an adjusted R-squared of 0.883, suggesting that 88.3% of the variability in the creativity score can be explained by performance in the 2022 reading assessment. On the other hand, Model 2 introduces programming as a second predictor variable. With the inclusion of this variable, the model shows a correlation coefficient (R) of 0.950 and an adjusted R-squared of 0.898. This indicates that both variables jointly explain 89.8% of the variability in the creativity score.
Table S10 presents the coefficients for both regression models, highlighting the variables not included in the final analysis due to their lack of statistical significance. As with the PISA 2018 analysis, in both models for the 2022 PISA assessment, the inclusion of mathematics and science test scores did not show a statistically significant relationship with creativity performance.
We replicated the analysis procedure, focusing on the specific domain of scientific problem-solving. By applying the model in this new context, we sought to identify how skills related to scientific problem-solving are associated with students’ academic performance in areas such as mathematics, science, and reading.
Table 11 presents the results of the linear regression analysis, where the dependent variable is the score obtained in the scientific problem-solving domain. In this case, we included as independent variables the PISA 2018 scores in mathematics, science, and reading, as well as the frequency of participation in science clubs and programming activities, along with Var 1 and 2.

Table 11.
Summary of the regression model predicting the score in the scientific problem-solving domain (PISA 2018).
The model summary includes only the reading test score as a predictor, showing a correlation coefficient (R) of 0.870 and an adjusted R-squared of 0.751, suggesting that the reading score can explain 75.1% of the variability in the scientific problem-solving Score.
Table S11 presents the coefficient of the model, which indicates that the reading ability score positively and significantly impacts the creativity score. On the other hand, the table also reflects the variables not included in the model due to their lack of statistical significance. Although initially considered possible predictors, these variables did not significantly correlate with creativity performance and were excluded to optimize the model’s accuracy.
Using the variables associated with PISA 2022 and the scientific problem-solving domain, we generated a new regression model incorporating only the reading test variable, as shown in Table 12. Since the variables corresponding to the mathematics and science test scores did not reach statistical significance in this analysis, they were again excluded from the model to optimize accuracy. The coefficients corresponding to this model are presented in Table S12.

Table 12.
Summary of the regression model predicting the score in the scientific problem-solving domain (PISA 2022).
5. Discussion
5.1. Relationship Between School Activities and Creative Thinking Test Scores (RQ1)
The correlations in Table 1 indicate a negative correlation between Creative Thinking scores and activities related to art (−0.154) and music (−0.094). However, in both cases, these correlations are not statistically significant (p > 0.05), meaning there is insufficient evidence to suggest a real relationship between participation in these activities and creative thinking scores. The lack of significance could be due to various factors; for example, art and music classes and activities in the study context may need to be explicitly designed to foster creative thinking. According to Donahue and Stuart (2024), the effectiveness of arts education in developing creative skills depends on the pedagogical approach and curriculum implemented. Additionally, access to and the quality of participation in artistic and musical activities may vary significantly among students, which could affect the observed correlation.
In contrast, significant negative correlations were observed for other school activities: computer programming classes (−0.578), creative writing activities (−0.700), science club (−0.810), theater/drama activities (−0.802), debate club (−0.841), and publications (−0.868). All these correlations are statistically significant (p < 0.001), indicating a strong negative relationship between participation in these activities and creative thinking scores.
The high statistical significance of these negative correlations suggests that greater participation in these activities is consistently associated with lower creative thinking scores. This is graphically illustrated in the case of Albania, as shown in Figure 2. This finding is particularly counterintuitive, as one might expect that participation in these activities, especially those that foster communication and critical thinking skills, would correlate positively with creative thinking (Asquith et al., 2024; Azaryahu et al., 2024; Irawan et al., 2024).
This could be explained from various perspectives, such as that participation in a science club that primarily focuses on memorization and repetition of knowledge may not develop creative thinking skills to the same extent as a project-based and problem-solving approach (Aguilera & Perales-Palacios, 2020). This is supported by Roth et al. (2022), who argue that the environment and teaching method are crucial for creativity development. Furthermore, academic workload and stress could be relevant factors in explaining these results. The pressure to achieve high grades and the associated stress may inhibit students’ ability to think creatively. According to Byron et al. (2010), academic stress limits students’ capacity to engage in divergent thinking processes, which are essential for creativity. These results align with the variables generated from the PCA (Table 4), where although both variables show negative correlations, only Var 1, associated with verbal, communication, and critical thinking skills, is statistically significant.
Similarly, analyzing the regression model and its coefficients in Table 5 and Table 6 confirms that Var 1 exerts the most significant influence on creative thinking scores. However, this influence manifests negatively, suggesting that increased school activities associated with Var 1 could be related to decreased creative thinking scores. On the other hand, Var 2 also shows an impact on creative thinking scores, but in a positive direction. Although its effect is significant, it is considerably smaller compared to the impact of Var 1. This may indicate that while participation in school art activities contributes positively, its ability to predict changes in creative thinking scores is more limited. The variable related to programming does not have a significant impact in this context, as it was excluded from both regression models.
Based on the above, the methodology used to assess creative thinking may only capture some aspects of the creative skills developed through these activities. Therefore, analyzing the domains presented in the PISA Creative Thinking test is valid.
From the results presented in Table 7, we observe that participation in activities related to communication and critical thinking, represented by Var 1, shows a strong negative correlation with all the domains evaluated in the creative thinking test. This finding is consistent with the results of the regression models presented in Tables S4–S8, which reinforce the idea that these activities not only do not favor performance on the test but may have a significantly negative impact.
On the other hand, in the second model of each studied domain, Var 2 contributes positively to improving performance in the domain. This result suggests that Var 2 plays a relevant role in explaining the variability in scores, providing a beneficial effect for students. However, it is essential to note that while Var 2 helps raise test performance, its influence is not strong enough to counteract the negative impact of Var 1 fully.
In this sense, Var 2 acts as a compensatory factor that mitigates, but does not eliminate, the unfavorable effect that Var 1 has on performance in the different domains evaluated. This indicates that while both predictors are relevant, their interaction is not entirely balanced, and the negative effect of Var 1 still carries significant weight in the final results.
Similarly, while programming skills are valuable in the current technological context, their impact on creativity and critical thinking is limited or indirect, as measured in this test. This finding suggests that educational approaches should consider a more holistic integration of programming skills, ensuring that they are taught as technical competencies and linked to the development of broader cognitive skills (Avello et al., 2020; Chevalier et al., 2020).
5.2. Science Clubs and Programming Activities in Scientific Problem Solving (RQ2)
From the data presented in Table 8, we found a negative and significant correlation (p < 0.001) for both participation in science clubs (−0.666) and participation in programming-related activities (−0.438) with the scientific problem-solving domain. This finding is consistent with the previously observed pattern in the overall creative thinking test score. As students become more involved in science clubs or programming classes, their performance in the scientific problem-solving domain decreases. Examples of this can be observed in the cases of Indonesia, Albania, and Uzbekistan, as reported in Figure 4 and Figure 5, which show the relationship between science clubs and programming-related activities, respectively.
This result is unexpected, especially in the case of science clubs. One might assume that participation in these activities correlates positively with scientific problem-solving, as both focus on developing analytical and critical thinking skills. However, the negative correlation suggests that the nature of these activities may need to align with the specific skills evaluated in the creative thinking test.
According to Bi et al. (2020), creative thinking in science relies on four specific processes, each exhibiting varying levels of effectiveness. Interventions focused on problem-solving and collaborative learning emerge as the most promising approaches for fostering scientific creativity, while scientific reasoning and conceptual construction provide more targeted and complementary contributions.
The findings from PISA 2022, which highlight the limited connection between scientific problem-solving and science clubs, could be attributed to an unbalanced school approach. This imbalance may favor conceptual construction—emphasizing the accumulation of scientific knowledge—over applying such knowledge to solve problems. As a result, the educational focus may inadvertently prioritize expanding theoretical understanding at the expense of developing the practical problem-solving skills essential for cultivating creativity in science (Sidek et al., 2020).
Regarding activities related to computer programming, the specialized literature is clear: more than merely presenting pre-established codes for students to copy and compile is required to develop their programming skills fully (Avello et al., 2020; Islas Torres et al., 2019; Romeike, 2007). While this approach may be a basic introduction to programming languages, it does not foster the critical thinking or logical reasoning necessary to tackle complex problems, such as scientific problems.
Creativity in computer programming requires problem scenarios where students design effective solutions based on the logic of an algorithm and its subsequent coding. This approach necessitates a pedagogical shift toward active methodologies that promote computational thinking and creativity. Instead of repetitive and mechanical tasks, students should engage with scenarios that simulate real-world problems, where they can identify variables, formulate hypotheses, design algorithms, and test their solutions through iterative processes, fostering technical competence and developing transversal skills such as problem-solving and critical analysis (Martínez et al., 2021).
In this context, the results reported in PISA 2022 may highlight inadequate pedagogical practices related to programming activities. Often centered on structured and predictable exercises, these practices limit students’ opportunities to develop more profound and transferable programming skills.
Both science clubs and computer programming would deviate considerably from what is proposed in scientific problem solving as presented in the PISA test. Scientific problem-solving focuses on generating multiple original ideas or solutions to open problems without a predefined correct answer and values the diversity and plausibility of the proposed ideas (OECD, 2024d). Therefore, it is becoming increasingly necessary to rethink educational approaches and adopt pedagogical strategies combining knowledge acquisition and practical and technical learning with creative thinking (Pont-Niclòs et al., 2024).
5.3. Relationship Between Creative Thinking and Performance in PISA 2018 and 2022 (RQ3)
The analysis of the regression models for PISA 2018 and 2022, presented in Table 9 and Table 10, provides a deep insight into the factors influencing students’ creative thinking development, revealing significant similarities and differences between both data sets.
The reading test score emerged as the strongest and most consistent predictor of creative thinking in both assessments. This suggests that reading comprehension skills are fundamental to the development of creativity. In agreement with Segundo et al. (2020), reading allows students to explore different perspectives, ideas, and narratives and is closely related to their ability to think creatively and generate innovative solutions.
In this context, Sulistiyarini et al. (2022) highlight that activities related to developing reading skills contribute to creativity, particularly in originality, fluency, and flexibility. This finding suggests that reading enhances textual comprehension and serves as a catalyst for generating novel ideas and approaching problems from diverse perspectives. The consistency of this observation in the data reported by PISA in 2018 and 2022 underscores the importance of integrating intentional reading practices into school curricula. These practices should go beyond mere text decoding, promoting activities that stimulate critical thinking, imagination, and the ability to connect ideas. For example, strategies such as active reading, creating narratives based on texts, and interpretative analysis can be practical tools for fostering creativity in the classroom (Choirunisa et al., 2024; Ivanova, 2023; Widiana et al., 2023). Globally, PISA data reveal that approximately 25% of the top-performing students in creative thinking also achieve superior results in reading. This correlation underscores the close relationship between these two competencies, suggesting that the ability to comprehend and process written information is a key factor in developing creative thinking (OECD, 2024a).
Moreover, in both 2018 and 2022, variables related to PISA 2022 scores in mathematics and science and school activities linked to programming and science clubs were statistically insignificant in predicting performance in creative thinking. This finding suggests that these disciplines, while essential for overall academic development and contributing to analytical and conceptual skills, do not directly influence creative thinking as measured in PISA 2022. This result is particularly notable given that mathematics was the central focus of PISA 2022. Based on the test design, approximately 86% of students who participated in the creative thinking assessment also completed an additional hour of mathematics items. The remaining 14% were evenly split between reading (approximately 7%) and science (approximately 7%) during the second hour of testing (OECD, 2024d). This indicates that despite the dominant presence of mathematics in the assessment framework, its impact on creative thinking performance was not significant. This finding highlights the need to explore the potential disconnect between specific skills cultivated in mathematics and science and the competencies required for creative thinking tasks.
In PISA 2018 (Table S9), Var 1 emerged as a significant and negative predictor of creative thinking in Model 2. This suggests that certain aspects of Var 1 may inhibit creativity, especially when considered alongside the reading score. This result may reflect a more rigid pedagogical or curricular approach that limits students’ creative expression. On the other hand, in the PISA 2022 data, Var 1 was not included as a significant variable, which may indicate changes in educational practices or the test structure between 2018 and 2022.
In PISA 2022 (Table S10), programming was included as a significant negative predictor in Model 2, suggesting that focusing on programming skills may be related to decreased creative thinking. This contrasts with the 2018 results, where programming was not a significant predictor. The difference in results between the two years could be linked to changes in how programming skills are taught or how students balance programming with other activities that foster creativity.
Similarly, analyzing the PISA 2018 and 2022 assessments about the scientific problem-solving domain (Tables S11 and S12, respectively) revealed consistent results. Reading scores emerged as a strong predictor of performance in both years in this domain. This finding underscores the significant role that reading proficiency plays in measuring comprehension and analytical capacity.
The robustness of reading as a predictor suggests that the skills involved in understanding and interpreting text—such as extracting key information, identifying relationships between ideas, and synthesizing knowledge—are closely aligned with the cognitive processes required for effective scientific problem-solving.
Moreover, this result highlights the interdisciplinary nature of problem-solving in science, where the ability to interpret written instructions, hypotheses, or experimental results is essential (Pont-Niclòs et al., 2024). It also points to the importance of integrating literacy-focused strategies into science education. For instance, encouraging students to critically analyze scientific texts, interpret research findings, and articulate their reasoning in writing could further strengthen their problem-solving abilities (Aguilera & Perales-Palacios, 2020).
These findings reinforce that reading literacy is a foundational skill for academic success and a cross-cutting competency that supports performance across multiple domains (Lafontaine & Schillings, 2015; Lopes et al., 2022).
6. The Synergy of Creative Thinking and Artificial Intelligence: Implications for Future Learning
Advances in language models like Generative Pre-trained Transformers (GPTs) have enabled these models to participate in creative processes traditionally considered exclusive to humans, such as writing, composing music, and creating art. This phenomenon raises fundamental questions about the nature of creativity and the relationship between humans and these models in creative processes.
To date, AI has demonstrated its ability to generate novel and plausible content in everyday creativity contexts (“mini-c” and “little-c”). However, to achieve higher levels of creativity, such as “big-C” or genius creativity, a deeper understanding of culture, intrinsic motivation, and the capacity for innovation is required—traits that remain essentially human. In this sense, we believe the true potential of generative AI lies in “co-creativity”, a hybrid intelligence approach where human and AI capabilities can complement each other, expanding the boundaries of creativity. Rather than replacing human creativity, AI can amplify it, opening new possibilities in various fields, particularly in education.
Traditional school curricula could benefit from integrating generative artificial intelligence (GenAI) tools into subjects and activities assessed in international frameworks such as PISA. These technologies can enhance the educational experience by addressing convergent and divergent processes related to ideation, fostering more profound and creative learning outcomes.
In this context, tools like ChatGPT position themselves as versatile GPTs capable of contributing to various school activities assessed by PISA. For instance, in areas related to reading and writing, this technology can assist students in generating ideas for stories, developing characters, and suggesting plots or scenarios, thereby enhancing their creative expression (Lys, 2024; Wahid et al., 2023). Furthermore, in artistic disciplines, ChatGPT can analyze photographs of artworks and provide recommendations on composition, color, or style, helping students refine and improve their artistic skills (Chiu, 2023).
A critical factor in maximizing the impact of these tools in education is the formulation of effective prompts. The quality of prompts directly influences the AI’s ability to optimize cognitive processes, both convergent (focused on finding specific solutions) and divergent (centered on generating multiple ideas and perspectives), associated with creative thinking. Various educational institutions have developed manuals and guidelines to craft effective prompts in response to this need. These strategies enhance interactions with GenAI tools and promote generating innovative ideas or optimizing concepts from new perspectives (Chen et al., 2024; Federiakin et al., 2024; Holmes & Miao, 2023; Lee et al., 2024).
From a teaching perspective, fostering creative thinking in the classroom requires a pedagogical approach beyond memorization and repetition of established procedures. As Nobel laureate in physics Richard Feynman (1985) observed in his experience interviewing students in Brazil, students can memorize concepts without truly understanding them. This traditional approach, although common, limits students’ ability to explore and inquire deeply. However, the challenge of implementing a teaching model that promotes creativity and exploration is significant, as it demands of teachers greater subject mastery and advanced management skills (Hernández-Ramos et al., 2023a).
In this vein, Cuban (2013) points out that significantly changing classroom routines requires a considerable investment of time, energy, and skills from the teacher. The metaphor of the teacher as a juggler is especially relevant in this context: a traditional teacher-centered class is comparable to a juggler with one ball, where the control of time, content, and interactions is manageable. However, when introducing a more student-centered teaching approach, which encourages exploration and group work, the teacher becomes a juggler with multiple balls of different sizes and weights, adding overwhelming complexity. This approach, though enriching for the teaching–learning process, creates a considerable cognitive load for the teacher. Emotional management also becomes essential in this dynamic environment, as teachers must manage multiple interactions and unexpected situations in real time. As Labaree (2010) notes, adopting a student-centered role involves considerable emotional management on the part of the teacher, adding a layer of challenge to their work.
In this context, AI emerges as a potentially transformative tool to support teachers in creating more creative learning environments (Hernández-Ramos et al., 2023b; Ravi et al., 2023). Language models (LLMs) can assist teachers in lesson preparation in real time, helping monitor students’ progress, providing timely feedback, and assessing complex work that could not be evaluated using predefined rubrics.
For example, platforms like ConectaIdeas (Araya & Diaz, 2020) have opted to implement quickly graded exercises, such as multiple-choice questions, combined with a limited number of open-ended questions reviewed through peer evaluation. This strategy balances the teacher’s cognitive load but limits the possibility of including more open-ended activities that foster creative thinking.
As explored in recent research, incorporating AI in these processes allows teachers to focus on more complex activities without being overwhelmed by their cognitive load (Feldon, 2007). Machine learning (ML) and LLM-based tools can assist in grading open-ended questions, freeing up time and energy for teachers to focus on guiding students toward more profound and creative learning (Urrutia & Araya, 2024).
Finally, AI can act as constant support during class sessions, enabling teachers to more efficiently manage creative activities, foster teamwork, and provide feedback tailored to students’ individual needs (Tapia-Mandiola & Araya, 2024). This technological support has the potential to significantly alleviate teachers’ cognitive load and facilitate the implementation of pedagogical strategies that may foster creative thinking and promote more meaningful learning experiences in the classroom.
7. Limitations of This Study
This study analyzes creative thinking as defined within the PISA 2022 framework. While this approach provides a structured and systematic perspective, it may only partially capture the multidimensional nature of creativity. PISA’s assessment concentrates on specific domains, such as written expression, visual expression, and the resolution of social and scientific problems, potentially excluding other significant forms of creativity, such as interpersonal creativity, artistic innovation, or unconventional cultural expressions.
Furthermore, creativity is deeply influenced by cultural and educational contexts, which can vary significantly across regions and countries. The PISA framework, designed to ensure international comparability, may not adequately reflect these cultural particularities. Consequently, the study’s findings may not be fully generalizable to educational systems whose practices, values, and pedagogical approaches differ significantly from the standards prioritized in the PISA assessment.
The purpose of this study does not include a detailed exploration of pedagogical practices, the identification of successful strategies, or the design of concrete recommendations for implementation. Instead, this study aims to provide an overview of the potential limitations of current school activities regarding their impact on creative thinking, leaving open the need for future research to delve into the analysis of effective pedagogies and their applications in diverse cultural and educational settings.
8. Conclusions
The results obtained in this study provide a complex and nuanced understanding of how the frequency of participation in school activities impacts the development of creative thinking, as measured by the PISA 2022 test. While some activities, particularly those linked to communication skills and critical thinking (Var 1), show a significant negative correlation with creative thinking, others, such as artistic activities (Var 2) and programming, do not present a statistically significant correlation.
This finding suggests that, although school activities are fundamental in student development, their impact on creativity might be more oriented toward developing specific and convergent skills rather than directly fostering divergent and creative thinking. This highlights the need to re-evaluate and potentially redesign how these activities are implemented and taught within the educational context.
On the other hand, the PISA 2018 and 2022 results reveal that student creativity, as measured by PISA across its four domains, is strongly influenced by their reading skills, with the score in this area standing out as a significant and positive predictor of performance on the creative thinking test. Additionally, although creativity differs from non-creative cognitive knowledge and skills, the analyses show that even when adjusting for performance on PISA tests, the increased number of activities in science clubs, programming, writing, and arts does not reverse the poorer results in creativity. This suggests that while these activities are valuable, they are not enriching enough to develop creativity effectively.
A possible explanation lies in the absence of an effective creative pedagogy, particularly in developing countries, where educational activities focus on a traditional instruction-based approach. In these contexts, students often follow structured directions, which limits their engagement in creative thinking processes. Furthermore, designing and implementing activities that genuinely foster creativity for an entire class represents a significant challenge for teachers, as it imposes a greater cognitive load and complexity in generating teaching dynamics that stimulate innovative thinking. Planning such activities requires advanced pedagogical skills, time, and resources, often needing more developed educational settings.
In this context, more holistically and evenly integrating technical and cognitive skills into the school curriculum is essential to fostering student creativity.
From the school, it is essential to implement concrete actions that foster the development of creative thinking as a transversal skill. Reading is a key tool because it can be easily integrated into the curriculum and linked to other school activities. For instance, problem-based scenarios could involve students analyzing texts to identify challenges and propose solutions, or collaborative dynamics could encourage discussion and the generation of original ideas through shared reading experiences. These practices strengthen reading comprehension and stimulate divergent and critical thinking.
Additionally, the integration of technical aspects can be improved through creative approaches. For example, students could design simple applications or prototypes using basic algorithms and everyday materials. This approach links practical skills with ideation processes, fostering creativity in programming and problem-solving. Combining theoretical and practical activities creates a dynamic environment where students can apply their knowledge innovatively and meaningfully.
In this context, GenAI is a complementary tool with immense potential. Through AI-based tools, students can refine their initial proposals, receive real-time feedback, or generate new inputs to optimize their final products.
On the other hand, generative AI can also help teachers create more innovative and personalized activities, facilitating a learning environment that promotes creativity more effectively.
This technological support is key to alleviating teachers’ cognitive load, thereby facilitating the implementation of pedagogical strategies that promote creative thinking and more meaningful learning in the classroom.
Finally, we foresee the need for future research to examine why school activities in countries with different socioeconomic levels fail to influence the development of creative thinking significantly. Additionally, we highlight the importance of investigating the role of gender in this development, considering both cognitive and contextual factors. These studies will be key to designing more inclusive and effective educational strategies that foster student creativity.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/educsci15020133/s1, Table S1. The database used in this study was structured according to the scores obtained. Table S2. KMO and Bartlett’s test. Table S3. Pearson correlation between creative thinking score and the variables reported by the PCA. Table S4. Summary of the regression models predicting the creative thinking test domains. Table S5. Regression coefficients for the scientific problem-solving domain score predictor model. Table S6. Regression coefficients for the predictor model of the social problem-solving domain score. Table S7. Regression coefficients for the written expression domain score predictor model. Table S8. Regression coefficients for the visual expression domain score predictor model. Table S9. Regression coefficients for the creative thinking test score predictor model. Table S10. Regression coefficients for the creative thinking test score predictor model. Table S11. Regression coefficients for the predictor model of the score in the scientific problem-solving domain. Table S12. Regression coefficients for the predictor model of the score in the scientific problem-solving domain. Figure S1. Relationship between PISA creative thinking test scores and students’ identification of pedagogies that promote creative thinking.
Author Contributions
Conceptualization, R.A.; methodology, J.H.-R. and R.A.; formal analysis, J.H.-R. and R.A.; writing of the first draft of the manuscript, J.H.-R.; writing—revising and editing of the manuscript, R.A.; supervision, R.A.; project administration, R.A.; funding acquisition, R.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was founded by ANID/PIA/Basal Funds for Centers of Excellence FB0003/Support 2024 AFB240004.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article or Supplementary Materials.
Acknowledgments
Support from ANID/PIA/Basal Funds for Centers of Excellence FB0003/Support 2024 AFB240004 is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Acar, S., Lee, L. E., & Scherer, R. (2024). A reliability generalization of the torrance tests of creative thinking-figural. European Journal of Psychological Assessment, 40(5), 396–411. [Google Scholar] [CrossRef]
- Aguilera, D., & Perales-Palacios, F. J. (2020). What effects do didactic interventions have on students’ attitudes towards science? A meta-analysis. Research in Science Education, 50(2), 573–597. [Google Scholar] [CrossRef]
- Alabbasi, A. M. A., Paek, S. H., Kim, D., & Cramond, B. (2022). What do educators need to know about the torrance tests of creative thinking: A comprehensive review. Frontiers in Psychology, 13, 1000385. [Google Scholar] [CrossRef]
- Amabile, T. M. (2018). Creativity in context: Update to the social psychology of creativity. Routledge. [Google Scholar] [CrossRef]
- Araya, R. (2023). What and how to teach mathematics for the future? The Mathematician Educator, 4(2), 84–108. Available online: https://ame.org.sg/2023/09/06/tme2023-vol-4-no-2-pp-84-108/ (accessed on 1 October 2024).
- Araya, R., & Diaz, K. (2020). Implementing government elementary math exercises online: Positive effects found in RCT under social turmoil in Chile. Education Sciences, 10(9), 244. [Google Scholar] [CrossRef]
- Asquith, S. L., Wang, X., Quintana, D. S., & Abraham, A. (2024). Predictors of change in creative thinking abilities in young people: A longitudinal study. The Journal of Creative Behavior, 58(2), 262–278. [Google Scholar] [CrossRef]
- Avello, R., Lavonen, J., & Zapata-Ros, M. (2020). Coding and educational robotics and their relationship with computational and creative thinking. A compressive review. Revista de Educación a Distancia (RED), 20(63), 1–21. [Google Scholar] [CrossRef]
- Azaryahu, L., Broza, O., Cohen, S., Hershkovitz, S., & Adi-Japha, E. (2024). Development of creative thinking via fractions and rhythm. Thinking Skills and Creativity, 52, 101514. [Google Scholar] [CrossRef]
- Baer, J. (2016). Domain specificity of creativity. Academic Press. [Google Scholar] [CrossRef]
- Baer, J., & Kaufman, J. C. (2005). Bridging generality and specificity: The amusement park theoretical (APT) model of creativity. Roeper Review, 27(3), 158–163. [Google Scholar] [CrossRef]
- Bi, H., Mi, S., Lu, S., & Hu, X. (2020). Meta-analysis of interventions and their effectiveness in students’ scientific creativity. Thinking Skills and Creativity, 38, 100750. [Google Scholar] [CrossRef]
- Byron, K., Khazanchi, S., & Nazarian, D. (2010). The Relationship between stressors and creativity: A meta-analysis examining competing theoretical models. Journal of Applied Psychology, 95(1), 201–212. [Google Scholar] [CrossRef]
- Care, E., Kim, H., Vista, A., & Anderson, K. (2018). Education system alignment for 21st century skills: Focus on assessment. Center for Universal Education at The Brookings Institution. [Google Scholar]
- Chen, E., Wang, D., Xu, L., Cao, C., Fang, X., & Lin, J. (2024). A systematic review on prompt engineering in large language models for K-12 STEM education. arXiv, arXiv:2410.11123. [Google Scholar]
- Chevalier, M., Giang, C., Piatti, A., & Mondada, F. (2020). Fostering computational thinking through educational robotics: A model for creative computational problem solving. International Journal of STEM Education, 7(1), 39. [Google Scholar] [CrossRef]
- Chiu, T. K. F. (2023). The impact of generative AI (GenAI) on practices, policies and research direction in education: A case of ChatGPT and midjourney. Interactive Learning Environments, 32(10), 6187–6203. [Google Scholar] [CrossRef]
- Choirunisa, N., Biruni, I. B., Ruslina, E., Fahruli, M. T. A., Jasman, M. W., Karomika, D., Abdillah, R. R., Hardyanto, Y. S. P., Wulanningsih, U. A., Rahmana, A. Y., & Sofyan, M. A. (2024). Reading questioning answering (RQA) for the empowerment of students’ creative thinking skills. In AIP conference proceedings. AIP Publishing. [Google Scholar]
- Cignetti, M., & Rabella, M. F. (2023). How are education systems integrating creative thinking in schools? In PISA in Focus, 122. OECD Publishing. [Google Scholar]
- Craft, A., Jeffrey, B., & Leibling, M. (2001). Creativity in education. A&C Black. [Google Scholar]
- Cropley, A. (2006). In praise of convergent thinking. Creativity Research Journal, 18(3), 391–404. [Google Scholar] [CrossRef]
- Cuban, L. (2013). Inside the black box of classroom practice: Change without reform in American education. Harvard Education Press. [Google Scholar]
- Donahue, D., & Stuart, J. (2024). Artful teaching: Integrating the arts for understanding across the curriculum K-8. Teachers College Press. [Google Scholar]
- Federiakin, D., Molerov, D., Zlatkin-Troitschanskaia, O., & Maur, A. (2024). Prompt engineering as a new 21st century skill. Frontiers in Education, 9, 1366434. [Google Scholar] [CrossRef]
- Feldon, D. F. (2007). Cognitive Load and Classroom Teaching: The Double-Edged Sword of Automaticity. Educational Psychologist, 42(3), 123–137. [Google Scholar] [CrossRef]
- Feynman, R. P. (1985). “Surely you’re joking, Mr. Feynman!”: Adventures of a curious character. WW Norton & Company. [Google Scholar]
- Forte-Celaya, J., Ibarra, L., & Glasserman-Morales, L. D. (2021). Analysis of creative thinking skills development under active learning strategies. Education Sciences, 11(10), 621. [Google Scholar] [CrossRef]
- Foster, N., & Schleicher, A. (2022). Assessing creative skills. Creative Education, 13(1), 1–29. [Google Scholar] [CrossRef]
- Gerver, C. R., Griffin, J. W., Dennis, N. A., & Beaty, R. E. (2023). Memory and creativity: A meta-analytic examination of the relationship between memory systems and creative cognition. Psychonomic Bulletin and Review, 30(6), 2116–2154. [Google Scholar] [CrossRef]
- Guilford, J. P. (1967). The nature of human intelligence. McGraw-Hill. [Google Scholar]
- Hanushek, E. A., & Woessmann, L. (2022). The Political Economy of ILSAs in Education: The Role of Knowledge Capital in Economic Growth. In T. Nilsen, A. Stancel-Piątak, & J.-E. Gustafsson (Eds.), International handbook of comparative large-scale studies in education: Perspectives, methods and findings (pp. 27–53). Springer International Publishing. [Google Scholar] [CrossRef]
- Hernández-Ramos, J., Cáceres-Jensen, L., & Rodríguez-Becerra, J. (2023a). Educational computational chemistry for in-service chemistry teachers: A data mining approach to e-learning environment redesign. Education Sciences, 13(8), 796. [Google Scholar] [CrossRef]
- Hernández-Ramos, J., Pernaa, J., Cáceres-Jensen, L., & Rodríguez-Becerra, J. (2021). The effects of using socio-scientific issues and technology in problem-based learning: A systematic review. Education Sciences, 11(10), 640. [Google Scholar] [CrossRef]
- Hernández-Ramos, J., Rodríguez-Becerra, J., Cáceres-Jensen, L., & Aksela, M. (2023b). Constructing a novel E-learning course, educational computational chemistry through instructional design approach in the TPASK framework. Education Sciences, 13(7), 648. [Google Scholar] [CrossRef]
- Holinger, M., Boldt, G. T., & Kaufman, J. C. (2024). Recent trends in creativity research: An analysis of keywords in four prominent creativity journals. Creativity Research Journal. [Google Scholar] [CrossRef]
- Holmes, W., & Miao, F. (2023). Guidance for generative AI in education and research. UNESCO Publishing. [Google Scholar]
- Irawan, F., Maghfiroh, H., Zubaidah, S., & Sulisetijono, S. (2024). The correlation between science literacy skills and scientific explanation on creative thinking skills through Remap-STAD learning model. AIP Conference Proceedings, 3106(1), 070020. [Google Scholar] [CrossRef]
- Islas Torres, C., Carranza Alcántar, M. d. R., Pérez Poch, A., & Salán Ballesteros, N. (2019). Study on creativity related to the ability of university programmers. Revista Electrónica de Investigación Educativa, 21. [Google Scholar] [CrossRef]
- Ivanova, N. (2023). Mastery of reading strategies, through which students’ creative thinking is developed. Bulgarski Ezik I Literatura-Bulgarian Language and Literature, 65(6), 102–109. [Google Scholar] [CrossRef]
- Kafai, Y. B., Proctor, C., Cai, S., Castro, F., Delaney, V., DesPortes, K., Hoadley, C., Lee, V. R., Long, D., & Magerko, B. (2024, June 10–14). What does it mean to be literate in the time of AI? Different perspectives on learning and teaching AI literacies in K-12 education. Proceedings of the 18th International Conference of the Learning Sciences-ICLS 2024 (pp. 1856–1862), Buffalo, NY, USA. [Google Scholar]
- Kaufman, J. C. (2012). Counting the muses: Development of the kaufman domains of creativity scale (K-DOCS). Psychology of Aesthetics, Creativity, and the Arts, 6(4), 298–308. [Google Scholar] [CrossRef]
- Kaufman, J. C., & Beghetto, R. A. (2009). Beyond big and little: The four c model of creativity. Review of General Psychology, 13(1), 1–12. [Google Scholar] [CrossRef]
- Kim, K. H. (2006). Can we trust creativity tests? A review of the torrance tests of creative thinking (TTCT). Creativity Research Journal, 18(1), 3–14. [Google Scholar] [CrossRef]
- Labaree, D. F. (2010). Someone has to fail the zero-sum game of public schooling. Harvard University Press. [Google Scholar] [CrossRef]
- Lafontaine, D., & Schillings, P. (2015). Evaluating reading-literacy in international surveys: Challenges and perspectives. Revue Francaise De Linguistique Appliquee, 20(2), 9–20. [Google Scholar] [CrossRef]
- Lee, U., Han, A., Lee, J., Lee, E., Kim, J., Kim, H., & Lim, C. (2024). Prompt Aloud!: Incorporating image-generative AI into STEAM class with learning analytics using prompt data. Education and Information Technologies, 29(8), 9575–9605. [Google Scholar] [CrossRef]
- Lopes, J., Oliveira, C., & Costa, P. (2022). School and student determinants of reading performance: A multilevel analysis with Portuguese students. Revista de Psicodidáctica, 27(1), 29–37. [Google Scholar] [CrossRef]
- Lucas, B. (2022). Creative thinking in schools across the world. The Global Institute of Creative Thinking. [Google Scholar]
- Lys, F. (2024). Creating stories: Generative artificial intelligence tools as writing tutors. In AI in language teaching, learning, and assessment (pp. 222–243). IGI Global. [Google Scholar] [CrossRef]
- Martínez, O. I. H., Fernández-Samacá, L., & Cárdenas, L. F. S. (2021). Trends and opportunities by fostering creativity in science and engineering: A systematic review. European Journal of Engineering Education, 46(6), 1117–1140. [Google Scholar] [CrossRef]
- Muñoz Silva, F. D., Luna Guevara, J. R., & López Regalado, O. (2021). Creative thinking in the educational context. Revista Científica de la UCSA, 8, 39–50. [Google Scholar] [CrossRef]
- OECD. (2010a). The high cost of low educational performance. OECD. [Google Scholar] [CrossRef]
- OECD. (2010b). The OECD innovation strategy. OECD. [Google Scholar] [CrossRef]
- OECD. (2014). PISA 2012 results: Creative problem solving (Vol. V). OECD. [Google Scholar] [CrossRef]
- OECD. (2017). PISA 2015 results (Vol. V). OECD. [Google Scholar] [CrossRef]
- OECD. (2020a). Curriculum overload: A way forward. OECD. [Google Scholar] [CrossRef]
- OECD. (2020b). PISA 2018 results (Vol. VI). OECD. [Google Scholar] [CrossRef]
- OECD. (2023). PISA 2022 assessment and analytical framework. OECD. [Google Scholar] [CrossRef]
- OECD. (2024a). PISA 2022 database, table III.A8.1. OECD. Available online: https://stat.link/o12ktl (accessed on 22 September 2024).
- OECD. (2024b). PISA 2022 database, tables III.2.1, III.4.2 and III.6.1. OECD. Available online: https://stat.link/wk20gv (accessed on 22 September 2024).
- OECD. (2024c). PISA 2022 database, tables III.B1.6.1 and III.B1.6.67. OECD. Available online: https://stat.link/da2q5i (accessed on 22 September 2024).
- OECD. (2024d). PISA 2022 results (Vol. III). OECD. [Google Scholar] [CrossRef]
- OECD. (2024e). School environment and creative thinking. OECD. [Google Scholar] [CrossRef]
- Pont-Niclòs, I., Martín-Ezpeleta, A., & Echegoyen-Sanz, Y. (2024). Scientific creativity in secondary students and its relationship with STEM-related attitudes, engagement and work intentions. Frontiers in Education, 9, 1382541. [Google Scholar] [CrossRef]
- Ravi, P., Broski, A., Stump, G., Abelson, H., Klopfer, E., & Breazeal, C. (2023, November 13–15). Understanding teacher perspectives and experiences after deployment of AI literacy curriculum in middle-school classrooms. 16th Annual International Conference of Education, Research and Innovation, Seville, Spain. [Google Scholar]
- Reiter-Palmon, R., Forthmann, B., & Barbot, B. (2019). Scoring divergent thinking tests: A review and systematic framework. Psychology of Aesthetics Creativity and the Arts, 13(2), 144–152. [Google Scholar] [CrossRef]
- Rodrigues, M. S. B., & Chagas-Ferreira, J. F. (2023). Programs to stimulate creativity in schools: A systematic review. Linhas Críticas, 29, e47206. [Google Scholar] [CrossRef]
- Romeike, R. (2007, June 27–29). Three drivers for creativity in computer science education. Proceedings of Informatics, Mathematics and ICT: A ‘Golden Triangle’, Boston, MA, USA. [Google Scholar]
- Roth, T., Conradty, C., & Bogner, F. X. (2022). Testing creativity and personality to explore creative potentials in the science classroom. Research in science education, 52(4), 1293–1312. [Google Scholar] [CrossRef]
- Saeed, B. A., & Ramdane, T. (2022). The effect of implementation of a creative thinking model on the development of creative thinking skills in high school students: A systematic review. Review of Education, 10(3), e3379. [Google Scholar] [CrossRef]
- Said-Metwaly, S., Fernández-Castilla, B., Kyndt, E., & Van den Noortgate, W. (2018). The factor structure of the figural torrance tests of creative thinking: A meta-confirmatory factor analysis. Creativity Research Journal, 30(4), 352–360. Available online: https://www.tandfonline.com/doi/abs/10.1080/10400419.2018.1530534 (accessed on 22 September 2024).
- Samaniego, M., Usca, N., Salguero, J., & Quevedo, W. (2024). Creative thinking in art and design education: A systematic review. Education Sciences, 14(2), 192. [Google Scholar] [CrossRef]
- Segundo, R. I., López, V., Daza, M. T., & Phillips-Silver, J. (2020). Promoting children’s creative thinking through reading and writing in a cooperative learning classroom. Thinking Skills and Creativity, 36, 100663. [Google Scholar] [CrossRef]
- Sidek, R., Halim, L., Buang, N. A., & Arsad, N. M. (2020). fostering scientific creativity in teaching and learning science in schools: A systematic review. Jurnal Penelitian dan Pembelajaran Ipa, 6(1), 13–35. [Google Scholar] [CrossRef]
- Sulistiyarini, A., Sukarno, & Triyanto. (2022). Pre-lesson reading activities on creative thinking skills: Implementation, impact, and constraints. Pegem Egitim ve Ogretim Dergisi, 12(4), 89–101. [Google Scholar] [CrossRef]
- Tapia-Mandiola, S., & Araya, R. (2024). From play to understanding: Large language models in logic and spatial reasoning coloring activities for children. AI, 5(4), 1870–1892. [Google Scholar] [CrossRef]
- Taylor, R., Fadel, C., Kim, H., & Care, E. (2020). Competencies for the 21st century: Jurisdictional progress. Brookings Institution. Available online: https://www.brookings.edu/wp-content/uploads/2020/10/Competencies-for-the-21st-century-jurisdictional-progress-FINAL-1.pdf (accessed on 1 October 2024).
- Torrance, E. P. (1959). Current research on the nature of creative talent. Journal of Counseling Psychology, 6(4), 309–316. [Google Scholar] [CrossRef]
- Torrance, E. P. (1968). A longitudinal examination of the fourth grade slump in creativity. Gifted Child Quarterly, 12(4), 195–199. [Google Scholar] [CrossRef]
- Urrutia, F., & Araya, R. (2024). Who’s the best detective? large language models vs. traditional machine learning in detecting incoherent fourth grade math answers. Journal of Educational Computing Research, 61(8), 187–218. [Google Scholar] [CrossRef]
- Wahid, R., Mero, J., & Ritala, P. (2023). Editorial: Written by ChatGPT, illustrated by midjourney: Generative AI for content marketing. Asia Pacific Journal of Marketing and Logistics, 35(8), 1813–1822. [Google Scholar] [CrossRef]
- Widiana, I. W., Triyono, S., Sudirtha, I. G., Adijaya, M. A., & Wulandari, I. (2023). Bloom’s revised taxonomy-oriented learning activity to improve reading interest and creative thinking skills. Cogent Education, 10(2), 2221482. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).