Challenges in Science, Technology, Engineering, Arts, and Mathematics Education in Cape Verde: A Study of a Mathematics Teacher Training Project

Abstract

This study investigates strategies to empower Cape Verdean mathematics teachers in adopting Science, Technology, Engineering, Arts, and Mathematics (STEAM) methodologies, focusing on mathematics education. Using an interactive, reflective continuous professional development (CPD) model—including teaching simulations, classroom practice, and structured reflection—qualitative research was conducted via thematic analysis of published data over two project-training cycles. In the first cycle, 27 teachers participated, with 24 later acting as trainers in the second cycle, which involved 44 non-higher education teachers. The project, a collaboration between institutions in Cape Verde, Portugal, and Austria, was guided by Rogers’ Diffusion of Innovations theory and the Technological Pedagogical Content Knowledge (TPACK) framework. GeoGebra software was employed to support STEAM adoption. Results indicate significant advancements in teachers’ technological and pedagogical skills, leading to improved student engagement and understanding. However, challenges remain, especially in integrating STEAM across disciplines due to limited resources and a lack of systemic CPD. The study concludes that sustained support is essential for fully embedding STEAM in Cape Verde’s education system.

1. Introduction

The global push towards Science, Technology, Engineering, Arts, and Mathematics (STEAM) education has sparked numerous initiatives aimed at preparing students for the complex, interdisciplinary challenges of the 21st century. STEAM education emphasises the integration of these subjects, promoting problem-solving, creativity, and critical thinking through innovative teaching methods. However, successfully implementing STEAM education in under-resourced contexts poses significant challenges, particularly in developing countries like Cape Verde, where limited access to technology and professional development opportunities hinders the adoption of such innovative approaches. This study investigates the potential of a structured continuous professional development (CPD) programme to equip Cape Verdean mathematics teachers with the skills to integrate STEAM methodologies, focusing specifically on the use of GeoGebra 5.0, a dynamic mathematics software programme.

In Portugal, continuous teacher training is a critical component of the education system, aimed at supporting professional development and maintaining high educational standards. This system features several key elements, such as its role in career advancement, the establishment of Professional Development Centres (CFAEs), the implementation of a National Qualification System (SAF), and the oversight provided by national Pedagogical and Scientific Councils. It also includes participation in educational projects, networks, and the provision of in-service training credits. Additionally, there is substantial engagement in European and international collaborations, in line with the strategic framework for European cooperation in education and training (European Commission and Directorate-General for Education, Youth, Sport and Culture, 2021).

In contrast, African nations with Portuguese as an official language (PALOP), while having distinct educational systems, share similarities due to historical and linguistic connections Fehn (2019). These include foundational teacher education, the creation of pedagogical institutes, a focus on language instruction, and the provision of in-service training programmes to enhance pedagogical skills. However, unlike Portugal, these programmes in PALOP countries are typically project-based, and are not systematically integrated into the broader educational framework, nor are they tied to career progression (Julião, 2020).

Cape Verde, one such PALOP country, lacks specific legislation governing CPD for teachers. The Basic Law of the Education System, first enacted in 2010 (Cape Verde Republic, 2010) and reaffirmed in 2018 (Cape Verde Republic, 2018), asserts that CPD is both a right and a duty for educators, with the aim of improving teaching quality through ongoing skill acquisition. This process is generally initiated by training institutions, teachers, and their representative bodies (Cape Verde Republic, 2018, Article 67, p. 20).

This persistent issue has posed challenges for the project “Strengthening the Training of Mathematics Teachers in Portuguese-speaking Countries in a STEAM & GeoGebra Framework,” supported by the Calouste Gulbenkian Foundation and co-financed by the Organization of Ibero-American States (OEI). This initiative, developed in collaboration with the University of Cape Verde (Uni-CV), the Ministry of Education of Cape Verde (MECV), and the Portuguese State, highlights the need for specific legislation to institutionalise CPD. Silveira (2015) advocates for accreditation and validation processes to formalise such training.

Since 2016, the GeoGebra Institute at Uni-CV, in partnership with the GeoGebra Institute of Portugal and with initial support from the OEI, has been implementing training initiatives designed to enhance mathematics teaching in Cape Verde. These initiatives incorporate a research component into teaching practice, contributing to the professional and personal development of mathematics teachers. The first intervention cycle, from 2016 to 2017, introduced the GeoGebra Trainer Training Project at Uni-CV. The second cycle, which ran from 2020 to 2022, expanded the scope to include STEAM education under the “Strengthening the Training of Mathematics Teachers in Portuguese-speaking Countries in a STEAM & GeoGebra Framework” project. Data from both projects are used to assess how these training processes can empower teachers to integrate STEAM principles, particularly in mathematics, into their teaching practices.

Assuming a reflective CPD model, grounded in the principles of action research, this study emphasises the five progressive levels of TPACK, as outlined by (Niess et al., 2009, p. 9). This model, which draws upon Diffusion of Innovations theory (Rogers, 1962), promotes a critical and reflective approach to integrating technologies—especially GeoGebra—into educational contexts. The ultimate aim is to enable teachers to master these tools within a multidisciplinary STEAM framework, seeking to create conditions for quality mathematics teacher training, as mentioned in the UNESCO report “Mathematics for action: Supporting science-based decision-making” (UNESCO, 2022).

The key objectives of this study are to analyse the perceptions of GeoGebra in supporting STEAM education, to assess the professional development of Cape Verdean teachers through a reflective CPD model, and to identify the systemic challenges that hinder the full integration of STEAM practices in resource-constrained educational settings. Specifically, the study addresses the following research questions: How do participants perceive the integration of GeoGebra as enhancing their technological and pedagogical competencies in the context of STEAM education? What challenges and opportunities arise from implementing STEAM methodologies in Cape Verde’s schools? And what support systems are necessary to sustain the integration of STEAM principles in the long term?

2. Framework

The framework of this study integrates well-established theories and models that explain the adoption and diffusion of innovations within educational contexts, particularly focusing on the role of technology in STEAM education and teacher training. These theoretical foundations address key research questions, including how innovative teaching practices in mathematics can be effectively adopted and diffused among Cape Verdean teachers, and what the critical factors are for integrating technology into mathematics education in Cape Verde. By examining the Diffusion of Innovations theory, the evolution from Shulman’s model to the TPACK framework, and the specific context of STEAM education and teacher training in Africa, this section provides the necessary groundwork for understanding the challenges and opportunities that Cape Verde faces. Additionally, the role of technology, particularly tools like GeoGebra, is explored to highlight effective strategies for professional development.

2.1. Diffusion of Innovations Theory

Rogers’ Diffusion of Innovations theory has been widely applied across various disciplines, including education. For instance, in Czech primary schools, the theory was employed to assess teachers’ attitudes towards ICT implementation, revealing a high occurrence of Innovators (Cirus & Simonova, 2020). The model has also been extensively used in studies of technology diffusion and adoption (Sahin, 2006). Within the context of STEAM education, which promotes interdisciplinary methods and innovative approaches, the theory is particularly relevant for understanding how innovative teaching practices can be adopted and diffused among educators (Li et al., 2018).

Rogers’ innovation-decision process in education outlines the progression from initial exposure to an innovation to its adoption and evaluation. It begins with the knowledge stage, where individuals or organisations become aware of an innovation and understand its functionality, such as teachers learning about new teaching methods or technologies. This is followed by the persuasion stage, where attitudes—positive or negative—are formed based on perceived benefits or drawbacks. In the decision stage, individuals choose to adopt or reject the innovation, exemplified by educators deciding whether to implement new approaches. The implementation stage involves the active use of the innovation, such as integrating new methods into classroom practice. Finally, the confirmation stage entails evaluating its effectiveness, with the possibility of either reinforcing the decision to adopt or reconsidering it based on ongoing experiences (Chen, 2024).

Rogers’ theory identifies key characteristics of innovations that influence their adoption in education, including relative advantage, compatibility, complexity, trialability, and observability. Relative advantage reflects the perceived superiority of an innovation over existing practices, with factors like economic benefits and convenience accelerating adoption. Compatibility relates to how well an innovation aligns with educators’ values, experiences, and needs, with greater alignment promoting faster uptake. Simpler innovations with lower complexity are adopted more readily, while trialability allows educators to experiment on a small scale, reducing uncertainty. Observability, or the visibility of an innovation’s outcomes, also enhances adoption. For instance, a study on Smart ID technology adoption in Estonia highlighted ease of use and convenience as critical factors, underscoring the importance of these characteristics in shaping educators’ decisions (Sai, 2018).

Rogers’ framework identifies five categories of adopters—Innovators, Early Adopters, Early Majority, Late Majority, and Laggards—which describe how individuals within a social system accept a new idea or technology. Individuals classified as Innovators are highly enthusiastic and willing to take risks, playing a key role in initiating the diffusion of innovations. Early Adopters are influential within their communities, embracing change and encouraging broader adoption. The Early Majority follows, marking a significant increase in adoption rates, while the Late Majority adopts more cautiously, showing gradual acceptance as innovations gain widespread recognition. Laggards, the most resistant, adhere to tradition and adopt innovations only when necessary, creating challenges for achieving universal adoption (Chen, 2024). The stages of innovation diffusion, from initial awareness to full adoption, help frame the challenges and strategies for promoting STEAM teaching in Cape Verde.

2.2. From Shulman Model to TPACK

Shulman (1986) introduced the concept of Pedagogical Content Knowledge (PCK), arguing that teachers must possess more than a mere understanding of their subject matter; they must also know how to teach it effectively. Shulman distinguished between Subject Matter Knowledge (SMK) and PCK. SMK involves understanding the structure of a subject and identifying core and non-core topics, while PCK encompasses methods for representing the subject in a way that makes it understandable to learners. It also includes an understanding of the challenges learners may face with specific topics (Shulman, 1986, p. 9). Building on Shulman’s work, Loewenberg Ball et al. (2008) refined these knowledge domains specifically for mathematics teaching, developing the Mathematical Knowledge for Teaching (MKT) framework. This framework includes three subdomains of content knowledge (CK) (common content knowledge, specialised content knowledge, and horizontal content knowledge) and three subdomains of Pedagogical Content Knowledge (knowledge of content and students, knowledge of content and teaching, and knowledge of content and curriculum). This model underscores the significance of articulating both content and pedagogical knowledge in teacher preparation programs. Further expanding on Shulman’s concept, several researchers Carrillo-Yañez et al. (2018); Dreher et al. (2018) developed frameworks describing the integration of content knowledge, pedagogical knowledge, and technology. This led to the development of the TPACK framework Koehler et al. (2013), which identifies three critical areas for teaching practice: pedagogical, content, and technological knowledge. Observing these aspects in initial teacher training helps identify the obstacles in developing and implementing strategies for effective teaching.

The emphasis on TPACK in this study is particularly significant in resource-limited settings like Cape Verde, where teachers often face constraints in access to technology and lack systematic training.

This study assumes TPACK, as a conceptual framework that highlights the integration of teachers’ knowledge in three domains: content, pedagogy, and technology. It encompasses subject-specific content knowledge, pedagogical expertise in teaching methods, and technological proficiency in tools that enhance instructional practices. This framework stresses the dynamic interactions between these components, enabling teachers to use technology not only to communicate and engage students but also to facilitate deeper understanding and real-world applications of concepts (Irwanto, 2021).

2.3. STEAM and Teacher Training in Africa

STEAM education can be understood as an approach to teach science through a multidisciplinary integration of Science, Technology, Engineering, Arts, and Mathematics, making learning more meaningful and engaging. The application of the STEAM approach has been shown to make students more active learners, improving their affective, psychomotor, and cognitive abilities (Maghfiroh et al., 2023). Research on continuous teacher training highlights global trends, such as the influence of globalisation, digital technologies, and demographic changes, all of which impact teacher training and lifelong learning (Cascio, 2019). For instance, Salmerón Aroca et al. (2023) emphasised the need for lifelong learning for teachers, focusing on both initial and CPD. In the context of African teacher training, several studies have emphasised the importance of sustainable and effective professional development programs. Fareao (2013) highlights the need for CPD in Nigeria, while Breda et al. (2023) discusses the need for sustainable in-service teacher training systems in Kenya, Malawi, and Zambia. Additionally, Ono and Ferreira (2010) propose using the Japanese lesson study model as an alternative form of professional development in South Africa, particularly for improving mathematics and science learning. In Cape Verde, however, scientific studies addressing STEAM Education are scarce. The integration of mathematics as a tool for knowledge production within science contexts only began with the project “Strengthening the Training of Mathematics Teachers in Portuguese-speaking Countries in a STEAM & GeoGebra Framework” (Silveira, 2015).

In this study, STEAM education is understood as an integrative approach that facilitates teaching across Science, Technology, Engineering, Arts, and Mathematics, tailored to the specific needs and priorities of schools in Cape Verde. Depending on the educational or administrative priorities set by school leaders, teachers may be assigned to teach mathematics or other subjects. Although mathematics is often a central focus due to its importance in problem-solving, STEAM encourages teachers to draw connections between all disciplines, creating flexible and holistic learning experiences. The National Council of Teachers of Mathematics underscores the significance of engaging students with both intra-mathematical and extra-mathematical problems, promoting the use of technology, collaboration, and diverse problem-solving strategies (National Council of Teachers of Mathematics, 2014). These principles align with the STEAM approach, which aims to cultivate creativity, critical thinking, and real-world relevance.

2.4. Technology in Mathematics Education

The integration of technology in mathematics education is a fundamental aspect of modern pedagogy. The National Council of Teachers of Mathematics (NCTM) highlights technology as essential for teaching and learning mathematics, asserting that it influences the content taught and enhances students’ understanding (National Council of Teachers of Mathematics, 2000, p. 24). Additionally, NCTM emphasises that an effective mathematics program must integrate technology and mathematical tools to help students learn mathematical concepts, reason mathematically, and communicate their ideas clearly (National Council of Teachers of Mathematics, 2014, p. 78). Research shows that multimedia technology can positively impact student performance and attitudes in mathematics (GebreYohannes et al., 2016). A variety of ICT tools—including dynamic geometry software, computing, programming tools, and e-learning platforms—have been shown to enhance teaching and learning (Nathan, 2010; Ng et al. 2019). Tools such as graphing calculators and software like GeoGebra have become integral to contemporary mathematics education (Phillips, 2010).

Technology in Training Mathematics Teachers

Improving technology training for mathematics teachers has been the focus of numerous studies. For example, Kamau (2014) identifies the need to enhance technology training for secondary school teachers in Kenya, where a lack of training and incentives limits the adoption of new technologies. Quek et al. (2012) underscore the importance of spreading innovation in mathematical problem-solving, while Daher et al. (2018) successfully applied the Innovation Diffusion Model to integrate ICT into in-service teacher training. In South Africa, the integration of technology in mathematics classrooms has often been procedural rather than transformative. Data projectors are the most widely used tools, but the overall pedagogical shift towards innovative technology use remains limited (Marien Alet Graham & Kapp, 2021). Some studies suggest that pre-service teachers use technology more for their own learning than for teaching, due to limited resources in schools (Bansilal, 2015). Therefore, professional development programs that emphasise pedagogical shifts and provide specialised mathematics software are essential (Bansilal, 2015; Kamau, 2014). GeoGebra, in particular, has been widely used in teacher training. Research demonstrates that teachers are willing to adopt GeoGebra, with positive outcomes in problem-solving and active learning environments (Bu et al., 2013; Mwingirwa et al., 2015; Waluyo, 2016; Yanti et al., 2020). In Cape Verde, the first GeoGebra initiative began in 2015 with Praia’s mathematics teachers (Silveira, 2015), and further training programs have since been developed to expand its use across the archipelago (Dos Santos & Silveira, 2021; Dos Santos et al., 2022).

2.5. The Case of Cape Verde

In Cape Verde, technology in mathematics education was first introduced through the Mundu Novu program in 2014. While this initiative aimed to modernise educational practices through technology, it faced challenges related to infrastructure, technical and pedagogical support, and access to resources ([NOSI] Núcleo Operacional para a Sociedade de Informação, 2009). However, the program did succeed in incorporating digital technologies into the curriculum and training teachers to use these tools effectively. In 2019, the curriculum review for basic education in Cape Verde followed international trends, incorporating recommendations from NCTM for using GeoGebra in secondary mathematics teaching to create more dynamic learning environments (Direção Nacional de Educação, 2019; National Council of Teachers of Mathematics, 2000, 2014). Various studies, including doctoral and master’s theses, have shown the potential of GeoGebra to enhance mathematics education in Cape Verde (Monteiro, 2023; Moreira, 2021; Neves, 2019; Silveira, 2015). While challenges remain, such as limited access to technology and infrastructure, the integration of frameworks like TPACK and tools like GeoGebra offers significant opportunities for improving both teacher training and student learning in Cape Verde.

3. Methods

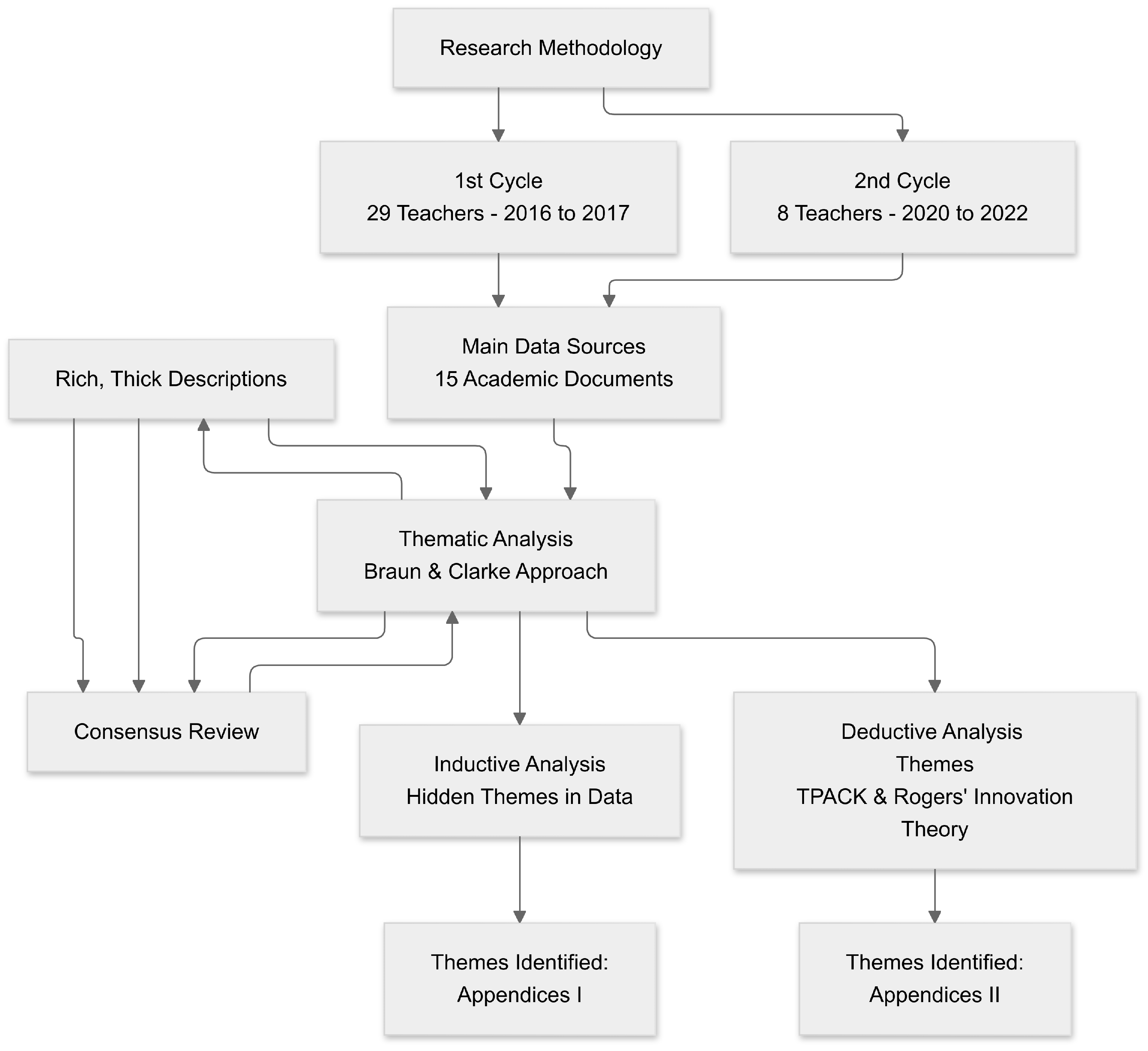
This section outlines the methodology adopted in this research, focusing on the participants, objectives, strategies, and procedures used to explore and enhance STEAM education through mathematics in Cape Verde. The study was centred on a teacher training programme aimed at empowering educators to incorporate GeoGebra into STEAM activities, particularly in mathematics classes.

3.1. Participants

The study involved a convenience sample of two distinct participant groups from two intervention cycles. In the first cycle (2016–2017), 27 mathematics educators with varied teaching experience from the Cape Verdean islands of Santiago and São Vicente were selected. The second cycle (2020–2022) involved 49 new mathematics teachers from the same islands, though this study only considers the published work of 8 participants. Although the National Education Office (DNE) initially listed 140 teachers, and the project-training team attend 100; for the second cycle, only 49 completed the training, with 8 contributing to published findings.

Participants were selected based on their willingness to engage in the continuous professional development (CPD) programme and availability for both face-to-face and online sessions. This convenience sampling approach relied on participants who agreed to participate in the training project. Additionally, 300 students across primary, secondary, and higher education levels were indirectly involved in the study, participating in teaching experiments conducted by the trained teachers.

The teachers who participated in the first project-training cycle with a total of 29 participants (11 female, 18 male), published articles in an international journal and obtained certification as GeoGebra trainers represent a diverse group in terms of professional experience and, academic background and qualification levels. This group is composed of teachers who are predominantly older, ranging from 35 to 61 years old, average 47.2, reflecting a more experienced group, ranging from 5 to 31 years of teaching and average 14.6. The majority of the teachers have more than a decade of experience, with some having a career spanning almost three decades. There are even PhDs in the areas of Multimedia in Education, Mathematical Education and Physics-Mathematics, which reinforces the level of specialisation of the group. It should be noted that the teachers who agreed to integrate training into the first cycle of intervention completed all phases of the training process initially planned, namely the publication of the results through the production of an article, blindly and peer-reviewed in a journal of free access and in Portuguese.

In the second cycle of project training, the teachers who participated and published articles in an international magazine, with a total of 8 participants (4 female, 4 male), representing a heterogeneous group in terms of academic training, with age ranging from 28 to 40 years old and an average of 32.6, teaching experience ranging from 5 to 17 years and an average of 12.1, showing that participants include both teachers who are at the beginning of their career or at the mid-career level, as well as those with a more established trajectory, although they share certain common characteristics that reinforce the profile of a specialised faculty committed to technological education. The academic training of teachers predominantly focuses on Mathematics, although there is a case of specialisation in Management Informatics. This diversity of experience is an enriching element, as it allows an exchange of knowledge and practices between teachers with different perspectives and experiences in the area of education.

In the second cycle of intervention, the dissemination and initial selection of the training program proved to be complex. Since the project was intended to extend to more teachers and a greater extension to the country’s island territory, national and local education authorities intervened in the process, which caused many constraints. The training groups initially expected 100 participants, and many had difficulty accessing the places where the training would take place, so the training team needed to reorganise the groups, with 48 teachers actually starting the training. Of those who started training, 40 completed all phases with the exception of publishing the results in the form of an article, and only 8 completed all phases of the initially planned training program, i.e., they published the results of their work in a free access newspaper, in Portuguese language, and reviewed blindly by peers. It should also be noted that, during this process, the constraints of the COVID-19 pandemic were felt in an aggravated way in Cape Verde.

3.2. Data Collection and Analysis

Thematic analysis was chosen as the primary methodology for its effectiveness in identifying, analysing, and reporting patterns within qualitative data. Two types of thematic analysis were conducted. First, an inductive thematic analysis, driven by the data, identified hidden themes in qualitative data without a predefined structure. Second, a deductive thematic analysis was conducted according to Braun and Clarke’s approach (Braun & Clarke, 2021), which supports theory-driven analysis. Both approaches followed key steps: familiarisation with the data, initial coding, theme identification, theme review, theme definition, and final report production (Braun & Clarke, 2006). The researchers read the initial texts produced by participants in the study, in two groups, corresponding to the first and second cycles, repeatedly to become familiar with the content and identify initial patterns related to technology use in education (see Figure 1).

A qualitative thematic analysis was conducted to examine the integration of technology in mathematics and STEAM education in Cape Verde, based on content from 15 academic published documents (

Table 1. Published results in the first and second cycles of the planned intervention and number of participants involved.

Type of Publication	Education Level	Mathematics Topic	Connections	Participants		Ref.	Code.
				Teachers	Students
1st Cycle
Article	Basic (8th year)	Geometry	Hands craft, Art & Technologies	1	21	Silveira (2018)	Doc 1A
	Secondary (9th year)	Geometry	Technologies	9	2	Furtado and Martins Andrade (2018)	Doc 1B
	Secondary and University	Geometry & Algebra	Physic & Technologies	2	n-d.	Furtado and Mendes Gonçalves (2018)	Doc 1C
	University	Geometry & Algebra	Economy & Technologies	3	9	Sousa et al. (2018)	Doc 1D
				13	22
Experience Report	Secondary (10th year)	Geometry	Technologies	2	18	Rocha and Pires Rocha (2018)	Doc 1E
	Secondary (10th year)	Algebra: Functions	Technologies	3	10	Da Cruz et al. (2018)	Doc 1F
	Secondary (12th year)	Algebra: Functions	Technologies	1	11	da Costa (2018)	Doc 1G
	Secondary (12th year)	Algebra: Trigonometry	Technologies	3	10	Sousa de Brito et al. (2018)	Doc 1H
	University	Algebra: Sequences. Reasoning	Technologies	1	14	Gomes Furtado (2018)	Doc 1I
	Secondary (9th year)	Geometry	Technologies	1	32	Vaz (2018)	Doc 1J
	Basic (6th year)	Geometry	Technologies	4	10	Almeida Ganeto et al. (2018)	Doc 1K
	University	Calculus	Technologies	1	6	Fortes Cruz (2019)	Doc 1L
				16	111
2nd Cycle
Article	Secondary (10th year)	Algebra & Functions	Technologies	2	14	Monteiro and Silva (2023)	Doc 2A
	Secondary (12th year)	Algebra & Trigonometry	Technologies	2	18	Pereira and Vaz (2022)	Doc 2B
	Secondary (10th year)	Geometry & Algebra	Technologies	4	21	I. Moreira et al. (2023)	Doc 2C
				8	53
			Total	35 *	186

Notes: Documents are referred to as Doc XY, where X is a number that identifies the project cycle and Y is the letter that identifies the document. Teachers = participants in this study. Students = students taught by participants. * In first cycle, two participants contribute in two articles.

), which represent the outcomes of training for 37 teachers; 29 in the first cycle and 8 in the second. It should be noted that to compare the two cycles achievements the research option was to contemplate the analysis of participants that complete all the phases of the process initially defined, publishing the experiences in a journal. The documents published during the two cycles of the study were coded. This process enabled the identification of patterns and themes that emerged from participants’ engagement with STEAM-related activities.

Table 2. Percentage of coded fragments by categories identified in inductive and deductive thematic analysis by cycle and in both cycles.

	Inductive thematic analysis categories
Cycles	Technology as a Pedagogical Tool	Impact on Student Engagement	Enhanced Problem-Solving Skills	Student-Centred Learning	Student Autonomy and Creativity	Collaborative Learning	Pedagogical Innovation	Teacher Professional Development	Challenges and Implementation Barriers
1st	9.8%	8.3%	7.5%	8.3%	6.8%	6.8%	8.3%	8.3%	9.0%
2nd	12.0%	12.0%	6.0%	6.0%	10.0%	8.0%	6.0%	6.0%	8.0%
Both	10.4%	9.3%	7.1%	7.7%	7.7%	7.1%	7.7%	7.7%	8.7%
	Deductive thematic analysis categories
Cycles	View of STEAM Education	Relationship between Professional Development and STEAM	Relevance of TPACK and Rogers’ Innovation Diffusion Theory
1st	9.8%	9.8%	7.5%
2nd	10.0%	8.0%	8.0%
Both	9.8%	9.3%	7.7%

Note: Total of fragments the text coded in all documents was 183, 133 in 12 documents of first cycle and 50 in 3 documents of second cycle.

presents the percentage of coded fragments assigned to each thematic category, while

Table 3. Distribution of coded texts by frequency on documents.

Number of Codes in Documents (n)	Frequencies (f)	nf	%
8	1	8	4.37%
9	0	0	0.00%
10	2	20	10.93%
11	5	55	30.05%
12	3	36	19.67%
13	0	0	0.00%
14	1	14	7.65%
15	0	0	0.00%
16	1	16	8.74%
17	2	34	26.00%
Total		183	100%

Note: statistical measures of f: minimum 8; maximum 17; mode and median. equal to 11; average of codes by document 11.86; standard deviation 2.38.

displays the distribution of these codes across the documents. The data presented in Table 2 and Table 3 have been anonymised and aggregated to ensure the confidentiality of participants. No identifying information has been included, and all analyses adhere to the ethical guidelines established for this study.

Participants were tasked with creating a report that included a theoretical and methodological framework for a task designed to foster intra- or extra-mathematical connections using technology. The report was to describe the implementation of this task in a classroom setting, include an analysis of students’ outputs in light of guiding principles, and reflect on the experience. Finally, participants were required to adjust their reports to align with the editorial standards of a peer-reviewed journal to ensure dissemination.

The analysis of the reports adhered to a rubric with three levels: Level 1 demonstrated the integration of technology to support mathematical concept development and establish connections; Level 2 highlighted the ability to create and disseminate innovative GeoGebra materials; and Level 3 showcased innovative practices, practitioner research, and peer support capabilities. Reports were categorised based on their adherence to the journal’s editorial criteria: articles included theoretical and methodological discussions supported by result analyses, while experience reports focused on classroom implementations and practical reflections, concluding with considerations that promote GeoGebra’s use in teaching.

Trainers and researchers ensured that final training reports highlighted the most relevant aspects of the training phase for classroom implementation. The final training reports aimed to reflect on the entire training process and, at the same time, provide practical guidance for other teachers to adapt similar experiences, with flexibility in format and terminology. Preparing the final training reports was an ongoing process throughout the training academic year. To widely disseminate the practices, the results were published in an open access magazine in Portuguese, where the participants adhered to the structure required by the magazine, with this work corresponding to the last phase of the designed training process, having verified that while in the first cycle, all participants were available to carry out this last phase, the same did not happen in the second cycle. The articles were authored by the participants and not the researchers. It should also be noted that the training and research team encouraged all participants to begin this final phase; however, the training evaluation process required differentiated certification at three levels, the last two involving the publication of articles.

As previously mentioned, the research aimed to explore themes related to the use of GeoGebra as a teaching tool, professional development’s role, and the relevance of TPACK and Rogers’ Innovation Diffusion Theory in technology adoption.

Inductive and deductive thematic analyses were applied to these 15 articles, include studies on mathematics education, teacher professional development, and technology integration in STEAM learning. These documents provided qualitative data that enabled an in-depth exploration of the experiences, challenges, and successes in implementing STEAM education and adopting technology.

The thematic analysis categories outline the integration and impact of technology, particularly GeoGebra, in mathematics and STEAM education. Technology as a pedagogical tool highlights how tools like GeoGebra enable dynamic, visual, and interactive learning, making abstract concepts accessible. Impact on student engagement and learning captures the increased motivation and active participation fostered by such tools. Enhanced problem-solving skills reflects how exploratory tasks using technology help students connect prior knowledge, test hypotheses, and refine understanding through immediate feedback. Student-centred learning describes the shift to student-driven knowledge construction, with teachers acting as facilitators, while student autonomy and creativity emphasises opportunities for learners to innovate and personalise problem-solving. Collaborative learning focuses on group knowledge-building through peer interaction, deepening understanding via shared reasoning. Pedagogical innovation signals the shift from traditional methods to dynamic, technology-enhanced teaching. Teacher professional development underscores the necessity of ongoing training to equip educators for effective technology integration. Challenges and implementation barriers address obstacles like limited resources, infrastructure, and resistance to change. The view of STEAM education explores how technology fosters interdisciplinary learning, blending arts with STEM to enhance creativity and problem-solving. Professional development and STEAM highlights training to enable educators to integrate interdisciplinary and technological approaches effectively. TPACK and Rogers’ Innovation Diffusion Theory provide frameworks for technology integration, with TPACK emphasising the fusion of content, pedagogy, and technology, while Rogers’ model explains the stages of technology adoption and strategies for addressing barriers.

During the inductive analysis, relevant sections were coded based on recurring topics, such as GeoGebra use, professional development’s role, technology adoption challenges, and theoretical references to TPACK and Rogers’ Innovation Theory. The codes were grouped into broader themes: (i) Technology as a Pedagogical Tool; (ii) Impact on Student Engagement and Learning; (iii) Enhanced Problem-Solving Skills; (iv) Student-Centred Learning; (v) Student Autonomy and Creativity; (vi) Collaborative Learning; (vii) Pedagogical Innovation; (viii) Teacher Professional Development; and (ix) Challenges and Implementation Barriers. Themes were reviewed for consistency across documents, with refinements for clarity and coherence. Each theme was defined, with specific examples, such as “Teacher Professional Development”, reflecting how CPD programmes enable effective technology integration in teaching practices. A thematic analysis table (see

Table A1. Inductive thematic analyses of first and second cycle with evidence.

Themes	Examples Quotes
(i) Technology as pedagogical Tool	“GeoGebra revealed itself to be a stimulating environment for the meaningful learning of geometric content, encouraging students and teachers to dynamically construct, visualise, and manipulate geometric objects.” (Doc 1A)
	“The dynamic software GeoGebra was instrumental in helping students grasp complex geometric transformations that are difficult to visualise through traditional methods.” (Doc 1A)
	“The use of GeoGebra enables students to understand mathematical concepts through interactive visualisations, which was previously difficult through traditional means.” (Doc 1B)
	“Teachers must recognise the importance of integrating technologies like GeoGebra as essential tools in the learning process to provide students with new and innovative ways to engage with content.” (Doc 1F)
	“GeoGebra transformed the teaching-learning process into a dynamic and interactive experience.” (Doc 2A)
	“The technology shifted the role of the teacher from a knowledge provider to a learning facilitator.” (Doc 2A)
	“Using GeoGebra allowed students to interact with mathematical concepts visually.” (Doc 2B)
	“GeoGebra software was applied to provide a visual learning experience.” (Doc 2B)
	“The Pythagorean theorem, when demonstrated with GeoGebra, became more accessible for students to explore visually.” (Doc 2C)
	“GeoGebra Classroom enabled students to experiment with abstract ideas in real time, enhancing learning.” (Doc 2C)
(ii) Impact on Student Engagement and Learning	“The introduction of dynamic software like GeoGebra encouraged students to actively engage in lessons, transforming their approach to problem-solving in geometry.” (Doc 1A)
	“The enthusiasm in the classroom was palpable, as students who had never used computers in math lessons before were eager to explore the tools offered by GeoGebra.” (Doc 1B)
	“Students showed a marked improvement in participation and enthusiasm when technology was incorporated into lessons, particularly in constructing and experimenting with geometric figures.” (Doc 1E)
	“The majority of students agreed that the use of computers, specifically GeoGebra, had a positive effect on their learning, enhancing their understanding of mathematical concepts.” (Doc 1L)
	“Students were curious, asking more questions and actively participating in lessons.” (Doc 2A)
	“The use of technology, particularly dynamic software, made learning more engaging and relevant to students.” (Doc 2A)
	“The visual and interactive nature of the tool increased student motivation.” (Doc 2B)
	“Students felt more engaged in lessons when they could manipulate the visual content in GeoGebra.” (Doc 2B)
	“Student participation significantly increased when using GeoGebra.” (Doc 2C)
	“Through the interactive platform, learners were more involved in constructing their knowledge.” (Doc 2C)
(iii) Enhanced Problem-Solving Skills	“By working through problem-based activities using GeoGebra, students were able to make connections between newly acquired knowledge and their previous experiences.” (Doc 1C)
	“Continuous teacher training was crucial in enabling educators to integrate GeoGebra effectively into their lessons, allowing for a richer learning experience for students.” (Doc 1D)
	“The use of dynamic software facilitated problem-solving by allowing students to test hypotheses and adjust their understanding based on visual feedback from the software.” (Doc 1G)
	“The exploratory nature of the tasks, supported by GeoGebra, fostered students’ problem-solving abilities.” (Doc 2A)
	“The dynamic manipulation of objects within GeoGebra facilitated deeper problem-solving.” (Doc 2B)
	“Solving mathematical problems became more intuitive when students used GeoGebra to visualise relationships.” (Doc 2C)
(iv) Student-Centred Learning	“In this new learning paradigm, the teacher transitions from the sole knowledge holder to a facilitator, encouraging students to develop their understanding autonomously.” (Doc 1A)
	“Through interactive learning environments, students take ownership of their learning process, building knowledge through exploration rather than passively receiving information.” (Doc 1D)
	“By allowing students to experiment with geometric constructions, GeoGebra encouraged them to discover properties and relationships independently, fostering a deeper understanding.” (Doc 1E)
	“GeoGebra fostered an environment where students took responsibility for their learning by engaging with the technology.” (Doc 2A)
	“Students worked independently on tasks while receiving timely feedback through the platform.” (Doc 2B)
	“Students’ autonomy in learning was encouraged, with the teacher acting as a guide.” (Doc 2C)
(v) Student Autonomy and Creativity	“Students demonstrated their creativity in constructing and manipulating geometric figures using GeoGebra, developing a more personalised approach to problem-solving.” (Doc 1B)
	“The autonomy granted to students in using dynamic tools allows them to test various solutions, fostering both creative and critical thinking.” (Doc 1C)
	“The platform allowed students to experiment and create their own methods, fostering creativity.” (Doc 2A)
	“Learners explored multiple solutions to the same problem using different GeoGebra features.” (Doc 2B)
	“GeoGebra enabled students to test their ideas, promoting creativity in solving complex tasks.” (Doc 2C)
(vi) Collaborative Learning	“Students collaborated effectively in groups, constructing graphical representations and discussing their findings collectively, which deepened their understanding of the content.” (Doc 1A)
	“The collaborative nature of the tasks performed on GeoGebra allowed students to work in pairs, thereby reinforcing the value of peer-to-peer learning.“ (Doc 1L)
	“The collaborative nature of the tasks allowed students to discuss their reasoning, solve problems together, and reach a common understanding, significantly reducing individual errors.” (Doc 1I)
	“Students collaborated in real-time using GeoGebra, sharing ideas and solving problems together.” (Doc 2A)
	“Students worked in groups, interacting with the platform and solving tasks collaboratively.” (Doc 2B)
	“The GeoGebra Classroom encouraged teamwork, with each member contributing their solutions to shared problems.” (Doc 2C)
(vii) Pedagogical Innovation	“The use of GeoGebra and other educational technologies marks a shift towards pedagogical innovation, empowering teachers to adopt new teaching methodologies that enhance learning.” (Doc 1D)
	“Pedagogical practices were transformed through the integration of technology, allowing for the creation of dynamic, interactive learning environments.” (Doc 1F)
	“The integration of GeoGebra into the classroom represented a significant pedagogical shift, promoting interactive and student-centred learning.” (Doc 2A)
	“The introduction of digital tools like GeoGebra brought a more innovative approach to teaching mathematics.” (Doc 2B)
	“GeoGebra helped shift teaching methods, allowing for real-time feedback and dynamic exploration of concepts.” (Doc 2C)
(viii) Teacher Professional Development	“Professional development programmes focused on dynamic software provided teachers with the necessary skills to incorporate these innovations into their classrooms.” (Doc 1A)
	“The success of integrating technology in education heavily relies on continuous professional development, ensuring that teachers are equipped to utilise these tools effectively.” (Doc 1F)
	“Teachers learned to effectively use technology, moving from traditional pedagogical models to a technology-integrated approach.” (Doc 2A)
	“Professional development ensured that teachers could implement technology in a way that enhanced student learning.” (Doc 2B)
	“The training helped teachers adopt new digital tools, improving their ability to guide students in a technology-enriched classroom.” (Doc 2C)
(ix) Challenges and Implementation Barriers	“Challenges such as insufficient infrastructure and resistance to change amongst educators pose significant barriers to the widespread adoption of educational technologies.” (Doc 1C)
	“The lack of adequate computer resources in many schools limited the potential of implementing GeoGebra across all classes.” (Doc 1G)
	“The introduction of new technologies in schools is hindered by teachers’ lack of familiarity and confidence with these tools, compounded by limited access to technical resources.” (Doc 1L)
	“The key challenge was providing classrooms with adequate technological infrastructure to support the full adoption of GeoGebra.” (Doc 2A)
	“While the software was beneficial, limitations in technology access and classroom infrastructure presented barriers to full implementation.” (Doc 2B)
	“Implementation was challenged by inadequate access to computers and inconsistent internet connectivity.” (Doc 2C)

in Appendix A) presents themes with supporting quotes.

The deductive thematics analysis was guided by TPACK and Rogers’ Innovation Diffusion Theory. The TPACK model was employed to understand the integration of technology, pedagogy, and content knowledge, while Rogers’ framework explained how educational innovations, like GeoGebra, are adopted. The TPACK analysis explored how CPD addressed technology integration into pedagogy and content knowledge, balancing these domains to enhance STEAM teaching. In Rogers’ theory, the innovation-decision process (knowledge, persuasion, decision, implementation, confirmation) and innovation characteristics (relative advantage, compatibility, complexity, trialability, observability) informed teachers’ adoption of new technologies. For deductive thematic analysis, three themes were central: (x) STEAM Education; (xi) Relationships between Professional Development and STEAM; and (xii) Relevance of TPACK and Rogers’ Innovation Diffusion Theory (see

Table A2. Deductive thematic analyses of first and second cycle with evidence.

Themes	Example Evidences
(x) View of STEAM Education	Integrating the arts into STEM subjects through technological tools creates a more holistic educational experience, promoting interdisciplinary learning and creative problem-solving. (Doc 1E) STEAM education, supported by technology, helps students focus on creative thinking by automating routine processes, thus enhancing cognitive engagement in more complex tasks. (Doc 1G)
	The adoption of STEAM, integrating technology into education, aligns with global demands for interdisciplinary skills development. (Doc 2A) STEAM education fosters interdisciplinary learning, preparing students for complex problem-solving across disciplines. (Doc 2B) Using technology like GeoGebra in STEAM encourages students to connect mathematical concepts with real-world applications. (Doc 2C)
(xi) Professional Development and STEAM	Professional development is key to ensuring that teachers are capable of integrating STEAM principles into their teaching, particularly through the use of innovative technologies. (Doc 1A) STEAM education necessitates a continuous learning process for educators, requiring them to stay abreast of new technologies and teaching methodologies. (Doc 1F)
	Teacher training in STEAM education provided a framework for integrating GeoGebra into classrooms, improving interdisciplinary teaching. (Doc 2A) Professional development programmes focused on equipping teachers with the skills necessary to apply STEAM frameworks using technology. (Doc 2B) STEAM education, supported by professional development, allowed teachers to guide students through interdisciplinary problem-solving. (Doc 2C)
(xii) TPACK Model and Rogers Innovation Diffusion Theory to Teacher Training in STEAM	The TPACK model underscores the importance of combining content knowledge, pedagogical knowledge, and technological expertise in order to effectively teach in a STEAM context. (Doc 1E) Rogers Innovation Diffusion Theory provides a framework for understanding the stages of technology adoption by teachers, helping to identify where support is needed to reduce uncertainty. (Doc 1F)
	The TPACK model enabled teachers to effectively combine technology, pedagogy, and content, creating a cohesive learning experience. (Doc 2A) Rogers diffusion model helps explain the adoption of GeoGebra, especially through its observability and trialability in classroom settings. (Doc 2B) Teachers gradually adopted GeoGebra, starting with small trials before moving to full-scale implementation, as Rogers’ theory suggests. (Doc 2C)

, in Appendix B).

While field notes and direct observations provided contextual insights, the primary data source was the reports written by participants, as these formed the basis of the published findings. To ensure credibility, the researchers used data triangulation, examining multiple documents namely all of the research notes than include research journals and direct observation carried out in the training sessions and or teaching experiences, to cross-check emergent themes; rich, thick descriptions, detailing themes with direct quotes; and consensus review, verifying that identified themes were accurately represented in the data. The categorisation process was conducted in three stages: initially, two researchers who had been directly involved in the training analysed the documents alongside their field notes and observations. Subsequently, two external researchers, with no directly involvement in the training sessions, independently reviewed the initial categorisation. Finally, all four researchers reached a consensus to finalise the categorisation.

4. Project Training

4.1. Objective and Strategies of the Project Training

The main objective of this study is to assess the potential for developing STEAM activities in Cape Verdean schools, specifically through mathematics classes enhanced by the use of GeoGebra. To achieve this, participants engaged in a comprehensive training program that involved both trainer training and teacher training. The training methodology was informed by the Lesson Study approach, a collaborative professional development model that originated in Japan. Lesson study encourages teacher collaboration and reflective practice, focusing on student learning through research-based lessons Murata (2011). The project closely mirrored this approach, with participants engaging in similar tasks during both intervention cycles.

The training program incorporated Rogers’ Diffusion of Innovations theory and the TPACK model. Given the diverse backgrounds of the trainees, the initial workshops focused on developing technological and mathematical skills (see TCK in Figure 1). This was follows: by pedagogical training that involved lesson plan adaptation and creation, see TPCK in Figure 1. In the final stage, participants implemented these activities in their classrooms, analysed their experiences, and shared their insights through teaching meetings or publications (see TPACK in Figure 2).

4.2. First Cycle of Intervention

The first intervention cycle, conducted between 2016 and 2017, focused on training teachers to use GeoGebra across various school levels. This cycle included two face-to-face sessions on Santiago Island, totalling 16 h, and a final 10 h seminar on São Vicente Island, where participants presented their work, and were involved 29 teachers in training. Additionally, five synchronous online sessions (totalling 10 h) and five asynchronous online sessions (totalling 10 h) were held monthly. The training was divided into five modules, detailed in

Table 4. Training modules of the course implemented in the first cycle of the research project.

Modules	Objectives
Module 1 GeoGebra: an introduction to its use in teaching and learning Mathematics.	Manipulate the dynamic geometry interface, providing teachers with the opportunity to perform simple applications of GeoGebra for teaching elementary mathematical topics. Participants should acquire basic skills to use GeoGebra Tube as a repository for their work.
Module 2 Applications of GeoGebra in teaching and learning of 2D Geometry.	Use the graphical interfaces of GeoGebra for algebraic manipulation and working with functions. Participants should be able to utilise intercommunication between GeoGebra windows to study algebraic and calculus-related problems.
Module 3 GeoGebra in the teaching and learning of functions and modelling.	Manipulate and explore two-dimensional geometry applications in GeoGebra, including constructing geometric demonstrations with a ruler and compass, and creating different geometric loci. Discuss the use of GeoGebra for developing hypothetical-deductive reasoning.
Module 4 Three-dimensional Geometry GeoGebra applications in modelling.	Easily manipulate the graphical interfaces of GeoGebra for three-dimensional objects, utilising intercommunication between different GeoGebra windows to study problems related to truncations of solids and modelling.
Module 5 Creating tasks with GeoGebra for mathematical education.	Discuss various educational perspectives related to mathematics tasks and their implications for creating tasks involving GeoGebra. Participants are expected to create tasks using GeoGebra, discussing associated methodologies and theoretical frameworks. Based on student productions, participants will analyse them considering the assumptions guiding their implementation

, which covered GeoGebra’s use in teaching, 2D and 3D geometry, algebraic manipulation, and mathematical modelling. The face-to-face sessions provided hands-on training, while the online sessions allowed for ongoing support and reflection. The training sessions not only equipped teachers with technological skills, but also promoted reflective teaching practices. Two of the synchronous online sessions focused on developing mathematical models and creating interdisciplinary classroom activities.

Participants were tasked with creating lesson plans, experimenting in classrooms, and reflecting on their practice. These experiences culminated in presentations at the final seminar and the production of articles for possible publication. The teaching experiments allowed participants to integrate GeoGebra into their mathematics classes, promoting collaborative learning and reflecting on their teaching practices. These experiences was later in published articles, as mentioned in Table 1.

4.3. Second Cycle of Intervention

The second intervention cycle, conducted between 2020 and 2022, aimed to expand participation and develop STEAM activities more broadly. This phase included both training for trainers and continuous teacher training. Participants from the first cycle were invited to mentor new trainees, and 24 of them accepted the challenge.

In the second cycle, around 100 new teachers from Santiago and São Vicente participated, organised into 20 classes. These groups included teachers from nine school groups on the island of Santiago, as well as two non-group schools in São Vicente. Only 44 teachers completed all phases of the training project, implementing tasks in their mathematics classes, as well as preparing the application report and orally communicating their results in the final seminar. However, only 8 of the 44 teachers who completed training in this second cycle of intervention published their results.

The primary objectives of the second cycle were to improve mathematics education through GeoGebra, integrate GeoGebra into STEAM activities, and develop innovative teaching practices. Training sessions involved five face-to-face workshops (totalling 56 h) and four online sessions (totalling 24 h); see the details in

Table 5. Organisation and agenda for teacher training in the second cycle of the research project.

n°	Type	Duration (h)	Agenda
1	Face-to-face	8 (4 + 4)	· Introduction to GeoGebra and its associated platforms
2	Face-to-face	12 (4 + 4 + 4)	· Planning and building tasks to implement in different contexts.
3	Online Synchronous	2	· Ongoing analysis of diagnostics and familiarisation tasks that teachers carried out with students.
4	Online Asynchronous	10	· Reporting of obtained results. · Sharing of partial results on the GeoGebra Groups platform. · Selecting or designing materials to be used in class.
5	Face-to-face	12 (4 + 4 + 4)	· Reflection on issues related to Teaching Experiences. · Planning and building tasks to implement in Teaching Experiences.
6	Online Synchronous	2	· Ongoing analysis of Teaching Experiences carried out with students. · Sharing of results on GeoGebra Groups.
7	Online Asynchronous	10	· Reporting of obtained results. · Preparation of written work. · Sharing of results on GeoGebra Groups.
8	Face-to-face	12 (4 + 4 + 4)	· Reflection and discussion about the Teaching Experiences · Planning and building tasks to implement in Teaching Experiences.
9	Face-to-face	12 (4 + 4 + 4)	· Assistance with finalising presentations or written works for publication. · Final seminar, with presentation of results by the participants.
	Total	80 h

.

Specific documents were prepared for training sessions, including topics such as constructivism, problem-based learning, and STEAM education. This documents take attention for the role of tasks (Da Ponte, 2020), the use of effective classroom orchestration (Stein et al., 2008), and the importance of the hypothetical learning trajectory to the experiences in classrooms (Simon et al., 2018). The second cycle also included specific tasks for developing STEAM activities with GeoGebra. Trainers prepared activities such as analysing geometric patterns, modelling shells with 3D geometry, and designing typical Cape Verdean vases using GeoGebra. These tasks aimed to encourage trainees to integrate GeoGebra into STEAM activities and reflect on how technology can enhance learning.

In this second cycle, the intervention model based on Rogers’ Diffusion of Innovations theory Rogers (1962) and the TPACK framework, for effective integration of a specific technology in mathematics teaching and learning presented by Niess et al. (2009, p. 9), continued to guide the project. Trainers were encouraged to adapt their teaching methods to integrate GeoGebra and STEAM activities into their classrooms, creating a dynamic and innovative learning environment. All of the participants present their results orally in the final seminar and produce reports; however, only 8 participants published articles with their results, as mentioned in Table 1.

5. Results

This section presents the key findings from the two cycles of intervention aimed at training Cape Verdean teachers in STEAM education using GeoGebra, only considering the thematic analysis, inductive and deductive, of the participants published results (Table 1). The results are presented to address the study’s objectives of understanding the perceived effectiveness of GeoGebra integration and the competencies acquired by teachers. These findings, derived from teacher publications, highlight perceived advancements in pedagogical strategies, technological proficiency, and their alignment with the STEAM framework. Given that the results are based on participants’ self-reports, these findings should be interpreted as reflective of their perceptions of the training’s impact, rather than as definitive measures of competency acquisition. The impact on teacher competency, student learning, and the overall integration of GeoGebra in mathematics education is discussed, alongside the challenges and successes encountered during the project. The categorisation of reports into articles and experience reports provided a nuanced understanding of participant engagement. Articles offered insights into theoretical and methodological perspectives, while experience reports illuminated practical classroom applications and challenges.

The thematic analysis identified two types of categories: emergent (inductive) and a priori (deductive). Emergent categories were derived directly from participants’ narratives in the articles, representing themes such as “Student Autonomy and Creativity” or “Collaborative Learning”. For example, the category “Technology as a Pedagogical Tool” included assertions that allow us to identify the integration of technology to visualise abstract concepts dynamically. In the inductive thematic analysis, the categories were defined through recurring patterns in the data, with examples quotes provided in Appendix A.

Conversely, a priori categories were defined based on established theoretical models in deductive analysis, specifically the TPACK framework and Rogers’ Diffusion of Innovations Theory. For instance, “Relative Advantage” was defined as the perceived benefits of technologies over traditional methods; for example, in Doc2C, “GeoGebra Classroom enabled students to experiment with abstract ideas in real time, enhancing learning” was stated, which is emerging evidence that teachers gradually adopted GeoGebra, starting with small trials before moving to full-scale implementation, as Rogers’ theory suggests; see Appendix B. The findings reveal key insights into the prevalence of thematic categories identified during the two cycles of the study. As shown in Table 2, concerning to inductive thematic analysis, the theme “Technology as a Pedagogical Tool” accounted for 10.4% of all coded fragments, reflecting its central role in the integration of STEAM practices. Similarly, themes such as “Impact on Student Engagement” (9.3%) and “Challenges and Implementation Barriers” (8.7%) were consistently identified across the data, underscoring their significance in the participants’ experiences. In addition, concerning to deductive thematic analysis, the theme “View of STEAM Education” accounted for 9.8% of all coded fragments, reflecting perception of participants about STEAM Education in documents (Table 2).

The distribution of coded texts across documents is presented in Table 3. The mode and median of 11 codes per document indicate an even spread of thematic representation, with the average number of codes being 11.86 per document. The standard deviation of 2.38 demonstrates a relatively consistent coding process across all documents, enhancing the reliability of the findings. These statistical measures illustrate that the identified themes were not disproportionately concentrated but were distributed across the data set.

5.1. Inductive Thematic Analysis

The inductive thematic analysis of the results, from both intervention cycles, is organised around key themes that highlight the transformative role of technology in education. Each theme provides a deeper understanding of how GeoGebra, as a pedagogical tool, influenced teaching practices, student engagement, and learning outcomes. The analysis explores the shifts towards student-centred learning, enhanced problem-solving, and greater autonomy, while also addressing the challenges that arose in implementing technology effectively. The exemplar quotes addressing our findings are in Table A1 (see Appendix A).

Significant insights were revealed by the inductive thematic analysis into how technology has transformed classroom practices, with GeoGebra emerging as a central tool. Through an inductive approach, nine key themes were identified, highlighting shifts in pedagogy, student engagement, and the challenges faced during implementation. These themes include: Technology as a Pedagogical Tool, which examines the integration of digital tools like GeoGebra into teaching; Impact on Student Engagement and Learning, focusing on how technology enhances motivation and active participation; and Enhanced Problem-Solving Skills, which explores how interactive tools foster critical thinking.

Additionally, the themes of Student-Centred Learning and Student Autonomy and Creativity underscore the shift from traditional, teacher-led instruction to more exploratory, independent learning environments. The theme of Collaborative Learning highlights how technology facilitates teamwork and peer interaction, while Pedagogical Innovation emphasises the broader move towards inquiry-based and technology-driven teaching strategies. Meanwhile, Teacher Professional Development focuses on the importance of continuous training for effective technology integration. Finally, the theme of Challenges and Implementation Barriers addresses persistent infrastructural and readiness issues that limit the full adoption of technological tools. These themes provide a comprehensive view of the role technology plays in reshaping educational practices, while identifying both the benefits and challenges experienced across the two cycles of intervention.

Now, we will be present the results for each theme to provide view of both the successes and limitations observed during the interventions.

5.1.1. Technology as a Pedagogical Tool

Technology, particularly GeoGebra, is identified as a critical pedagogical tool, with the majority of analysed documents reporting that its use transformed traditional learning environments into interactive, learner-centred spaces. These findings align with the TPACK model’s emphasis on integrating content, pedagogy, and technology to create meaningful learning experiences. In the first cycle, GeoGebra transforms traditional learning environments into interactive, learner-centred spaces, helping students visualise abstract concepts (Doc 1L). This integration of technology into pedagogy is in line with the TPACK framework, which emphasises the synergy between technology, pedagogy, and content knowledge. In the second cycle, this role is further reinforced, as GeoGebra not only facilitates interactive engagement, but also shifts teaching towards a more student-centred approach, turning teachers into “guides on the side”, rather than the primary source of instruction (Doc 2A, Doc 2B). This shift reflects the transformative potential of technology in reshaping pedagogical practices.

5.1.2. Impact on Student Engagement and Learning

In both cycles, technology is shown to enhance student engagement significantly. In the first cycle, the interactive nature of GeoGebra enables students to engage more fully with geometric concepts by allowing them to manipulate and experiment with figures, which leads to greater involvement compared to passive learning (Doc 1L). This aligns with Rogers’ theory of innovation, particularly the attribute of relative advantage, where the clear benefits of digital tools over traditional methods become evident. In the second cycle, this engagement deepens, with students showing increased motivation and curiosity. As noted in Doc 2A and Doc 2C, the visual and interactive aspects of GeoGebra help students better grasp complex mathematical concepts, contributing to a sense of ownership and active participation in their learning.

5.1.3. Enhanced Problem-Solving Skills

Enhanced problem-solving abilities were a consistent theme, with the majority of analysed documents reporting that GeoGebra enabled students to manipulate variables and test hypotheses interactively. For example, in one described classroom activity where students used GeoGebra to experiment with geometric constructions, leading to a deeper understanding of relationships between angles and shapes. Such activities align with Rogers’ “Trialability” characteristic, illustrating how interactive experimentation fosters student engagement and skill development.

In the first cycle, GeoGebra encourages students to apply theoretical knowledge to practical problems, promoting critical thinking through real-time feedback and solution revision (Doc 1L). This aligns with Rogers’ attribute of trialability, where the opportunity to experiment with solutions increases the likelihood of successful adoption of the technology. By the second cycle, the impact on problem-solving becomes more apparent. As highlighted in Doc 2B, students use GeoGebra to manipulate variables and visualise complex mathematical relationships, which enhances their ability to approach problems in a hands-on, dynamic manner. The real-world applicability of these problem-solving skills is a key outcome observed in this cycle.

5.1.4. Student-Centred Learning

GeoGebra’s role in fostering student-centred learning is a prominent theme across both cycles. In the first cycle, the software is noted for shifting the focus away from teacher-led instruction towards a more student-driven approach, where learners actively construct their own understanding (Doc 1B). This reflects the TPACK model’s emphasis on the interaction between pedagogy and technology. By the second cycle, the theme evolves further, with classrooms becoming more exploratory spaces where students independently engage with the material. Teachers act as facilitators, stepping in only when necessary to guide students’ autonomous learning (Doc 2A). This shift underscores the role of technology in transforming the learning environment into one that encourages independent knowledge construction.

5.1.5. Student Autonomy and Creativity

The themes of student autonomy and creativity are evident in both cycles, with GeoGebra playing a central role in fostering these qualities. In the first cycle, students use the software to explore solutions independently, demonstrating a high level of autonomy in their learning (Doc 1B). This aligns with Rogers’ attribute of compatibility, as the technology supports students’ desire for self-directed learning. By the second cycle, creativity becomes more pronounced, with students not only taking ownership of their learning but also experimenting with different approaches to solving mathematical problems (Doc 2A, Doc 2C). GeoGebra encourages students to think creatively and develop personal strategies, leading to deeper cognitive engagement and innovative problem-solving.

5.1.6. Collaborative Learning

Collaborative learning is another recurring theme, with its importance growing from the first to the second cycle. In the first cycle, GeoGebra facilitates collaboration by allowing students to work together on digital platforms to solve problems and share ideas (Doc 1B). This social aspect of learning is enhanced in the second cycle, where the collaborative capabilities of GeoGebra Classroom enable students to engage in real-time teamwork (Doc 2B). Students not only construct solutions together but also improve their communication and critical thinking skills, making collaboration a key outcome of the technology-enhanced learning environment.

5.1.7. Pedagogical Innovation

The use of technology, especially GeoGebra, is consistently linked to pedagogical innovation in both cycles. In the first cycle, the software supports the shift towards a more inquiry-based, interactive educational model, where students are encouraged to generate and test hypotheses (Doc 1B). This move towards more dynamic and engaging learning experiences is further reinforced in the second cycle, where teachers use GeoGebra to provide real-time feedback, creating a more immersive and responsive learning environment (Doc 2C). The use of technology thus represents a significant shift from traditional teaching methods towards a more innovative, learner-centred approach.

5.1.8. Teacher Professional Development

Teacher professional development emerges as a crucial factor in the successful integration of technology. In the first cycle, the need for continuous professional development is highlighted, with training sessions focusing on equipping teachers with the technical and pedagogical skills necessary to maximise the impact of digital tools like GeoGebra (Doc 1B). This theme is further developed in the second cycle, where proper training is identified as essential for teachers to fully integrate GeoGebra into their lessons (Doc 2A, Doc 2C). Without adequate professional development, the potential of these technologies cannot be fully realised, underscoring the importance of ongoing teacher training.

5.1.9. Challenges and Implementation Barriers

Despite the clear advantages of using technology in the classroom, both cycles identify significant challenges to its implementation. In the first cycle, barriers such as inadequate infrastructure and teacher readiness are cited as obstacles to the effective use of GeoGebra (Doc 1B). These challenges persist into the second cycle, where the lack of access to adequate technology and internet connectivity remains a major issue (Doc 2A, Doc 2C). These limitations hinder the full realisation of the benefits that technology like GeoGebra can offer, highlighting the need for better resources and support to overcome these barriers.

5.2. Deductive Thematic Analysis

The deductive thematic analysis conducted over two cycles of interventions in a STEAM education project reveals key insights into the evolution of understanding, teacher preparedness, and the practical application of technology in education. Across both cycles, the focus remained on critical themes, including the view of STEAM education, the relationship between professional development and STEAM, and the relevance of the TPACK model and Rogers’ Innovation Diffusion Theory; see Table A2 (see Appendix B).

5.2.1. View of STEAM Education

Across both cycles, the concept of STEAM education emerges as a forward-thinking educational paradigm that seeks to integrate traditional academic subjects with technology, fostering an interdisciplinary approach to learning. In the first cycle, STEAM education is portrayed as emphasising the blending of creative and technical disciplines, with technology serving as a conduit for innovation and interdisciplinary thinking. This perspective underscores the “relative advantage” technology brings to the STEAM context, particularly in enhancing learning processes and nurturing 21st-century skills like critical thinking and problem-solving.

In the second cycle, this view of STEAM education continues to evolve, with a stronger emphasis on practical problem-solving through technology. The document reveals that tools like GeoGebra help bridge the gap between theoretical knowledge and real-world applications, making abstract concepts more tangible for students. This shift in focus, from the more theoretical advantage of technology to its practical implementation, reflects the maturing understanding of how technology can be used not only as an enhancement but as a bridge between different domains within the STEAM framework.

5.2.2. Relationship Between Professional Development and STEAM Education

The role of professional development is recognised as pivotal in both cycles, but the emphasis shifts slightly from one cycle to the next. In the first cycle, professional development is acknowledged as essential to helping teachers navigate the rapidly evolving technological landscape, particularly as they integrate technology into their lessons. The analysis highlights how ongoing training is necessary to ensure teachers remain equipped to maximise the potential of STEAM initiatives. Without this training, there is a risk that teachers may struggle to keep pace with technological advancements, thus limiting the full impact of STEAM education.

In the second cycle, this theme is revisited with an added layer of complexity. Professional development is now seen not only as a means of familiarising teachers with new technologies like GeoGebra, but also as a crucial element in helping them apply interdisciplinary approaches to teaching. Teachers were trained in methods that align with STEAM’s holistic framework, suggesting that professional development went beyond technical skills to foster deeper pedagogical shifts. This reflects a deeper integration of professional growth into the broader goals of STEAM education, as teachers move towards creating enriched, technology-enhanced learning environments that benefit students in multiple disciplines.

5.2.3. Relevance of the TPACK Model and Rogers’ Innovation Diffusion Theory

The relevance of the Technological Pedagogical Content Knowledge (TPACK) model and Rogers’ Innovation Diffusion Theory is consistently highlighted across both cycles, though the analysis shows a maturation of understanding and application.

TPACK Model

In the first cycle, the TPACK model is presented as a comprehensive framework that combines technological, pedagogical, and content knowledge to support the effective integration of technology in teaching. Each knowledge area—technological, pedagogical, and content—plays a crucial role in preparing teachers to use tools like GeoGebra in ways that enhance both teaching methods and learning outcomes. The documents emphasise that teachers need to not only understand how to operate these tools, but also know how to integrate them into inquiry-based and student-centred pedagogical strategies.

In the second cycle, this model is revisited with further practical implications. Here, the TPACK framework is described as essential for developing cohesive STEAM learning experiences. Teachers are not only using GeoGebra, but are doing so in a way that blends their knowledge of mathematics (content) with interactive strategies (pedagogy) and digital tools (technology). This represents a deeper and more nuanced application of TPACK, where the balance between these domains creates more interactive and engaging learning environments. The second cycle analysis indicates that the TPACK model is now seen not only as a guide for integrating technology, but also as a mechanism for fostering interdisciplinary learning. By applying the TPACK framework within the structured CPD model, the study effectively tracked and measured the growth of teachers’ technological, pedagogical, and content competencies. This analysis, guided by thematic analysis of teacher reports, directly addresses the research objective of assessing professional development outcomes and answers the research question concerning the challenges and opportunities in integrating STEAM. The results highlight specific areas where further support and professional development are needed to overcome systemic challenges and fully integrate STEAM principles into Cape Verdean classrooms.

Rogers’ Innovation Diffusion Theory

The study situates Cape Verdean teachers along the adoption curve proposed by Rogers, identifying Innovators and Early Adopters as the teachers who engaged most effectively with the training, and Late Majority or Laggards as those who struggled to fully integrate STEAM into their classrooms. This theoretical lens enables a clearer understanding of the systemic barriers and personal hesitations teachers face when implementing STEAM education in under-resourced settings.

In the first cycle, Rogers’ Innovation Diffusion Theory is used to frame how teachers adopt new technologies like GeoGebra, progressing through stages of knowledge, persuasion, decision, implementation, and confirmation. The analysis of the first cycle illustrates how professional development plays a critical role in the “knowledge” stage, while other stages, such as “persuasion” and “trialability”, reflect the importance of teachers witnessing the relative advantage of the technology for encouraging its adoption.

By the second cycle, the application of Rogers’ theory becomes more practical, particularly in the attributes of “trialability” and “observability”. Teachers begin with small-scale trials of GeoGebra, gradually expanding its use as they observe positive outcomes in their classrooms. The documents from the second cycle also highlight the entire innovation-decision process, confirming that as teachers move through these stages, they solidify their use of technology like GeoGebra in their pedagogical practices. The increasing confidence in using technology, seen in the confirmation stage, marks the culmination of the gradual and supported integration process.

Across both intervention cycles, the reports indicated a predominance of Innovators and Early Adopters, who demonstrated enthusiasm and effectiveness in integrating STEAM methodologies using GeoGebra. In contrast, some groups exhibited characteristics of the Early Majority or Late Majority, reflecting more cautious or gradual adoption. These observations highlight the need for differentiated support to address the varying levels of engagement and integration challenges faced by different groups.

6. Discussion

This study explores how GeoGebra, a dynamic digital tool, influences mathematics teachers in Cape Verde in adopting STEAM education approaches. Cape Verde, striving to cultivate 21st-century skills amid socio-economic development, emphasises strengthening STEAM competencies. Our research investigates teacher competency enhancement, student engagement, and systemic barriers within the Cape Verdean context. Using the TPACK framework (Koehler et al., 2013) and Rogers’ Diffusion of Innovations Theory (Rogers, 1962), the findings provide essential insights into how GeoGebra can support STEAM education in resource-limited settings like Cape Verde. These findings align with Rogers’ innovation-decision process, particularly highlighting the stages of persuasion and implementation, as participants experimented with GeoGebra and observed its potential to transform pedagogy. The relative advantage of GeoGebra, perceived through its ability to simplify complex concepts, emerged as a key factor in its adoption.

The quantitative insights derived from the thematic analysis provide a nuanced understanding of the dimensions influencing the integration of STEAM education into professional development contexts. For instance, the prominence of the theme “Challenges and Implementation Barriers” (8.7%, Table 2) aligns with prior research on the difficulties of adopting innovative practices in educational settings. This finding highlights the need for targeted interventions to address these challenges, particularly through sustained teacher professional development. Furthermore, the relatively high frequency of the theme “Impact on Student Engagement” (9.3%) suggests that STEAM education fosters meaningful student-teacher interactions, reinforcing its pedagogical value. The distribution of codes across documents, as depicted in Table 3, illustrates the participants’ varied yet balanced engagement with these themes, reflecting a comprehensive exploration of the research focus.

The findings highlight the potential of GeoGebra to address challenges in STEAM education, particularly in resource-constrained settings. For instance, the reported improvements in student engagement and autonomy align with global studies demonstrating the effectiveness of dynamic tools in promoting inquiry-based learning (Daher et al., 2018). However, the self-reported nature of the data necessitates caution in generalising these results, as perceptions may not fully capture the depth of acquired competencies. Future studies should complement self-reported perceptions with classroom observations or student performance data to provide a more comprehensive understanding of the impact of STEAM training.

This section reflects on the research objectives, emphasising the potential and challenges of integrating STEAM education via GeoGebra in Cape Verdean mathematics classrooms. Key theoretical lenses, including TPACK, Rogers’ Diffusion of Innovations, and continuous professional development (CPD), shape the analysis.

The study highlights GeoGebra’s transformative potential as a pedagogical tool, aligning with TPACK’s integration of technology, pedagogy, and content knowledge (Koehler et al., 2013). In a setting where educational resources are limited, GeoGebra offers a low-cost, accessible approach to enriching mathematics instruction. The platform helps demystify abstract mathematical concepts by providing interactive, visual representations, making learning more tangible for students and promoting a shift toward learner-centred instruction. This shift contrasts with Cape Verde’s historically teacher-led approaches (Shulman, 1986), and fosters a student-centred learning environment where teachers adopt more facilitative roles, aligning with Cape Verde’s broader educational reforms focused on critical thinking and problem-solving skills (de Educação, 2017; Direção Nacional de Educação, 2019; Fortes & Monteiro, 2021).

GeoGebra proved essential in creating visually engaging and interactive learning experiences that increased student participation. TPACK underscores the effective alignment of content knowledge (CK) and technological knowledge (TK) when integrating digital tools, which was evident in teachers’ deployment of GeoGebra to facilitate collaborative, inquiry-based problem-solving (Koehler et al., 2013). GeoGebra enabled students to explore mathematical concepts independently and engage in meaningful peer discussions (Vygotsky, 1980). However, while it effectively supported mathematics learning, there was limited interdisciplinary application, signalling a need for more professional development on connecting mathematical learning with broader STEAM subjects, such as engineering and the arts. This finding suggests that GeoGebra’s potential for comprehensive STEAM integration requires further support for interdisciplinary teaching skills.

GeoGebra’s impact on student engagement and motivation is substantial in the Cape Verdean STEAM context. As Cape Verde views STEAM initiatives as essential for socio-economic advancement, GeoGebra’s introduction created a notable increase in student enthusiasm. By facilitating active exploration of mathematical concepts, GeoGebra encouraged a shift toward inquiry-based learning aligned with the STEAM framework (Koehler et al., 2013). This increased engagement reflects Rogers’ concept of “relative advantage” (Rogers, 1962), as both students and teachers observed GeoGebra’s benefits in promoting hands-on learning over traditional methods. Additionally, Vygotsky’s social constructivism theory Vygotsky (1980) supports this shift, as students worked collaboratively, which deepened their understanding and retention of mathematical concepts.

These findings resonate with the broader literature on technology integration in mathematics education. For instance, Kamau (2014) emphasises the need for sustained professional development to overcome adoption barriers, which is evident in the challenges reported by Cape Verdean teachers. Similarly, studies on in-service training in Africa highlight how resource constraints, such as limited access to technology and infrastructure, impact the adoption of innovative tools (Banda, 2014). These parallels suggest that the barriers identified in Cape Verde are not unique but reflect broader systemic issues in similar educational contexts.

This success in boosting student engagement answers a core research question on improving learning outcomes. In Cape Verde’s limited-access educational environment, GeoGebra’s role is transformative, suggesting that even a single, well-integrated tool can foster a significant pedagogical shift. This finding highlights GeoGebra’s potential to aid students in developing critical skills required for Cape Verde’s job market, and aligns with the broader STEAM objectives. This study highlights the importance of analysing trainee teachers’ perceptions to understand the potential of GeoGebra and STEAM methodologies in professional development. While the findings offer valuable insights into perceived technological and pedagogical benefits, the reliance on self-reported data underscores the need for further research, integrating direct measures of student outcomes and competency development.

GeoGebra played a significant role in fostering critical thinking and problem-solving skills, aligning with Cape Verde’s STEAM-focused goals to prepare students for complex real-world challenges. Across intervention cycles, GeoGebra enabled students to experiment with mathematical variables and independently develop problem-solving strategies, fostering self-efficacy and adaptability. This aligns with Rogers’ Diffusion of Innovations’ “trialability” concept (Rogers, 1962), where students see problem-solving as an interactive, explorative process. This independent learning approach addresses research questions on student outcomes, underscoring GeoGebra’s role in preparing students with the critical and transferable skills central to STEAM education.

Cape Verdean teachers face specific challenges in adopting digital tools, with limited access to professional development opportunities posing a significant hurdle. Both the TPACK framework (Koehler et al., 2013) and Rogers’ model (Rogers, 1962) emphasise the importance of support at initial learning and implementation stages for effective technology integration. In early cycles, teachers focused on learning GeoGebra’s technical aspects, progressing to interdisciplinary STEAM integration in later cycles. This evolution underscores the need for targeted, continuous professional development that addresses technical skills and pedagogical shifts for effective GeoGebra use in Cape Verde’s mathematics curriculum. Findings reveal that long-term professional development is essential for technology integration, highlighting its role in supporting Cape Verde’s STEAM education goals. Continuous professional support for teachers is critical to building their skills and confidence, contributing to the broader success of digital tools like GeoGebra.

Reflective practice emerged as a key component, enabling teachers to integrate GeoGebra meaningfully through ongoing cycles of action research. This method allowed teachers to collaboratively evaluate and refine their strategies, a model supported by findings from other African educational contexts (Banda, 2014; Ono & Ferreira, 2010). However, the impact of reflective CPD varied among participants, particularly those new to the project in subsequent cycles. This finding suggests the importance of structured, long-term support to maximise CPD benefits for sustainable pedagogical changes in Cape Verdean classrooms.

Despite GeoGebra’s advantages, infrastructural barriers hinder its full adoption, with limited internet access and technical support challenging consistent use. Rogers’ “complexity” concept (Rogers, 1962) is relevant here, as inadequate technology access impedes GeoGebra’s implementation. Moreover, limited administrative support for CPD initiatives presented difficulties, with many teachers lacking the resources to integrate GeoGebra across varying classroom environments effectively. This gap reflects the need for a comprehensive policy framework addressing digital infrastructure and professional development. Without structural support, realising GeoGebra’s potential for STEAM integration will remain challenging.

Cape Verde’s linguistic context, where Cape Verdean Creole predominates despite Portuguese as the official instructional language, poses additional challenges. GeoGebra facilitated a more collaborative environment where students could use Creole more freely, increasing accessibility and engagement. Integrating language considerations into CPD can potentially enhance GeoGebra’s impact by accommodating linguistic diversity in Cape Verdean classrooms, an area warranting further study.

Limitations and Implications for Future Research

Finally, this study is subject to several limitations that must be acknowledged. First, the use of a convenience sample and the analytical choices made may impact the generalizability of the results. These results are based on a subset of data collected during a training initiative that aims to integrate technology into mathematics education and promote STEAM approaches in a context characterised by limited technological resources. While these findings are not intended to be universally applicable, the study seeks to explore the results achieved by participants who completed the structured training process.

An important limitation is the reliance on self-reported data, which introduces potential subjectivity. Teachers may have overestimated their abilities or the effectiveness of integrating GeoGebra into their classrooms. Although triangulation was employed, involving direct observation during the training process as well as supervision of self-reported episodes, future research should incorporate other types of data such as participant interviews. Additionally, analysing student outcomes can provide a more comprehensive understanding of results.

Another limitation is the narrow focus on interdisciplinary applications of STEAM, particularly in the context of mathematics. Future professional development initiatives should consider broader strategies for integrating STEAM disciplines in order to support a more global approach.

7. Conclusions and Final Remarks

This study is a part of a research project aimed to enhance mathematics education in Cape Verde by integrating STEAM practices through the use of GeoGebra in mathematics classrooms. Through two cycles of interventions, significant progress was made in equipping teachers with the skills and knowledge required to use technology as a teaching tool, while simultaneously fostering an environment that supports creative and interdisciplinary learning. The study analyse part of the results of this research project, corresponding to the participants that conclude the training and produce articles published were they share their results.

The inductive thematic analysis of the two cycles underscores the transformative impact of technology on teaching and learning. GeoGebra, in particular, plays a pivotal role in enhancing student engagement, promoting problem-solving, and fostering autonomy and creativity. However, the persistent challenges related to infrastructure and teacher readiness highlight the need for continued investment in both professional development and technological resources. The project illustrates a clear progression towards more innovative and student-centred learning environments, though the full potential of these technological tools can only be realised by addressing the barriers that remain. The study, through the deductive thematic analysis conducted, also demonstrates GeoGebra’s potential to transform STEAM education in Cape Verde, enabling a shift towards interactive, student-centred learning that aligns with the nation’s educational goals. This study, grounded in the TPACK framework and Rogers’ Diffusion of Innovations Theory, shows how digital tools can bridge traditional learning methods with STEAM objectives. However, we must bear in mind that these results correspond to the vision of the participants who published the results of their work. It should be noted, that while in the first cycle of intervention all participants published the results obtained, in the second cycle only 8 of the 44 teachers in training published their results, despite all participants in the second cycle of intervention having presented their results in oral communications and training reports prepared. In this sense, future research should consider the perspective of participants who did not feel engaged in publishing their results.

Also, the project allows strengthening teachers’ technological and mathematical competencies. The GeoGebra-based training provided participants with valuable tools to engage students more actively in mathematics lessons, enhancing both their understanding and interest in the subject. Teachers were able to incorporate GeoGebra’s interactive features into their teaching practices, which contributed to a more dynamic classroom environment. The adoption of Rogers’ Diffusion of Innovations theory and the TPACK framework also demonstrated the importance of integrating content, pedagogy, and technology in teacher training. This combination fostered a reflective approach to teaching, encouraging educators to critically examine their practices and continuously refine their teaching methods. However, the study also revealed that while GeoGebra and other technologies were effectively used to enhance mathematics instruction, the broader adoption of STEAM practices—encompassing Science, Technology, Engineering, Arts, and Mathematics—was more limited. Teachers primarily focused on mathematics and technology, often neglecting the interdisciplinary potential of STEAM education, as was noted in other research. This suggests the need for more focused training on how to integrate non-mathematical disciplines into STEAM activities.

7.1. Addressing Challenges

Several challenges were identified during the project and in the analysis of the documents produced by teacher participants, the most prominent being the limited access to technological resources in schools. Without adequate infrastructure, it was difficult for some teachers to fully implement the training and integrate GeoGebra into their classrooms. This disparity highlights the need for greater investment in educational technology and infrastructure in Cape Verdean schools. Another significant challenge was the lack of an institutionalised framework for CPD. In Cape Verde, CPD is not systematically integrated into the education system or tied to career progression, which limits its potential impact. The absence of a formal CPD structure means that teachers are less likely to receive ongoing support for professional growth, making it harder to sustain innovative teaching practices over time. Moreover, the linguistic environment in Cape Verde posed unique challenges. The use of Portuguese as the language of instruction, despite many students speaking Cape Verdean Creole as their first language, sometimes hindered classroom communication. Interestingly, the use of technology, such as GeoGebra, enabled students to communicate more freely in their native Creole, fostering a more inclusive learning experience. This highlights the potential for technology to bridge linguistic gaps in education.

7.2. Recommendations for Future Work

To fully realise the potential of STEAM education in Cape Verde, several key actions should be taken. First, there is a need for greater investment in technological infrastructure, ensuring that all schools are equipped with the necessary tools to support digital learning. Expanding access to computers, software, and reliable internet will allow more teachers to integrate technology into their classrooms effectively. Second, institutionalising CPD is crucial. A formal CPD framework would provide teachers with the ongoing support and training needed to continually improve their teaching practices. Such a system could also link professional development to career progression, incentivising teachers to engage more fully in training opportunities. Third, future training programs should focus more explicitly on the interdisciplinary nature of STEAM education. Teachers need support in designing lessons that integrate science, engineering, and the arts with mathematics, thereby fostering more holistic and creative learning experiences for students. Finally, more attention should be given to the linguistic context of Cape Verde. While Portuguese is the official language of instruction, the integration of tools like GeoGebra offers opportunities to make learning more accessible for students who primarily speak Creole. Future projects should explore how technology can be used to create a more inclusive, bilingual educational environment.

7.3. Closing Thoughts

The two cycles of this project have shown that Cape Verdean teachers are both capable and eager to adopt new technologies and pedagogical approaches. However, the full potential of STEAM education has yet to be realised. By addressing the infrastructural, institutional, and pedagogical challenges highlighted in this study, future initiatives can build on the successes of this project and help transform the education system in Cape Verde into one that fully embraces the possibilities of STEAM learning. The use of GeoGebra has proven to be an tool for fostering technological literacy and improving mathematics education. With sustained support and further development of interdisciplinary teaching approaches, Cape Verdean teachers can continue to advance STEAM education, ultimately preparing students for the demands of a rapidly evolving global landscape.