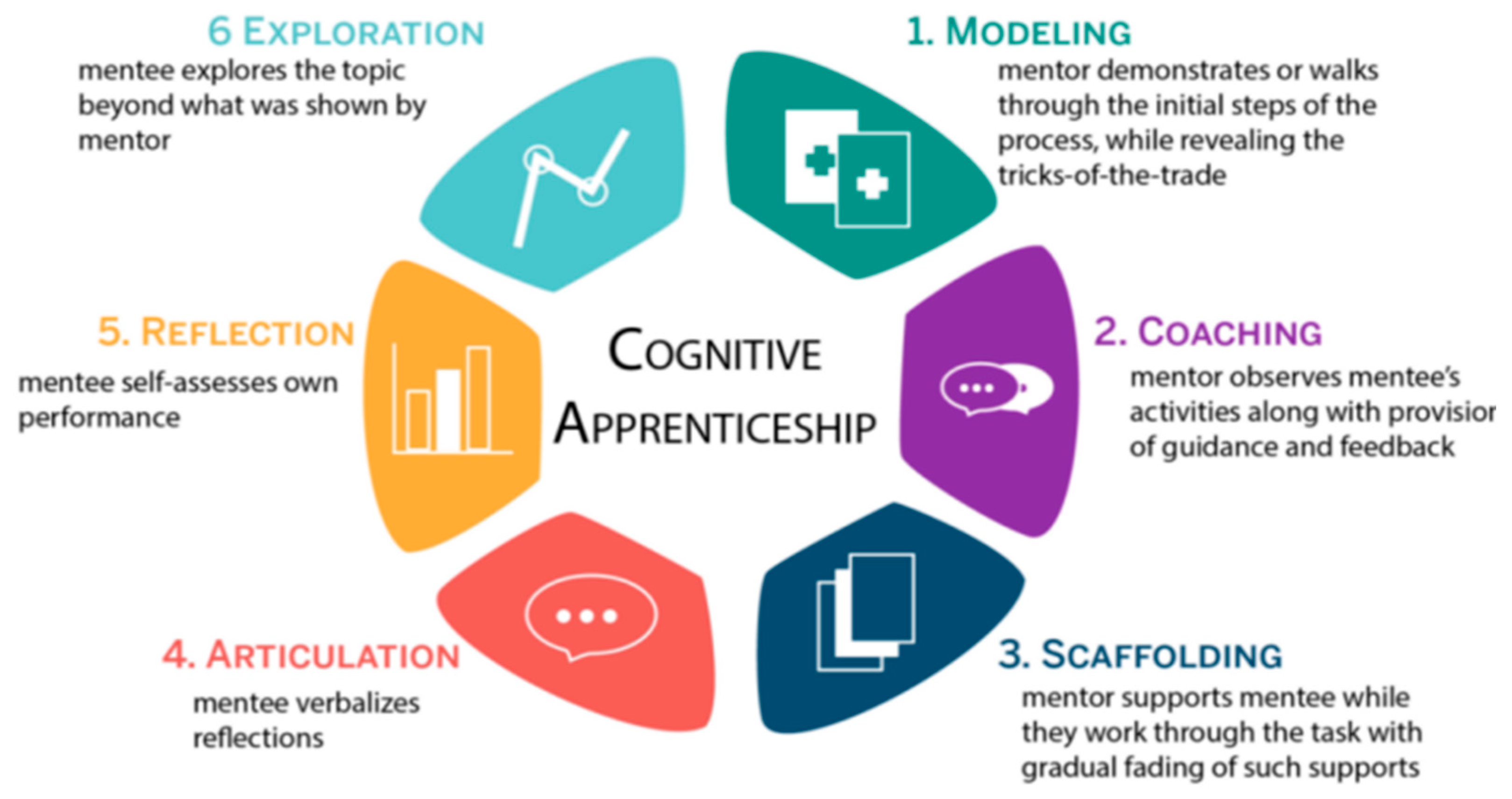
2.1. Research Design
This study employed a quasi-experimental design appropriate for educational research. This design allowed for a comparison between the groups exposed to different teaching strategies. This study included a randomized sample of 150 9th-grade students from an international baccalaureate (IB) high school in China, renowned for its all-encompassing and thorough education, which includes a varied and applicable IB mathematics curriculum (International Baccalaureate Organization [
22]. An IB high school was selected due to its rigorous academic standards and emphasis on comprehensive, inquiry-based learning [
26]. The IB mathematics curriculum provides a robust framework for assessing the effectiveness of different instructional strategies [
27]. Additionally, the IB program’s focus on critical thinking, problem-solving, and real-world application of knowledge ensures that the students are engaged in a high level of academic rigor [
28], making it an ideal environment to evaluate the impact of the cognitive apprenticeship model (CAM) and the stratified cognitive apprenticeship model teaching module (SCTM)
Of the 150 students selected to participate in this study, these students were divided into 6 classes, with each class consisting of 25 students. Two classes were randomly allocated to Treatment Group 1 (CAM group), two classes to Treatment Group 2 (the SCTM group), and the remaining two classes were assigned to the conventional teaching (CI) group. The unit of analysis for this study was therefore the class, rather than individual students, allowing for a comparison between the instructional strategies at the class level.
The control group consisted of two classes, Class A and Class B, with 25 students each, and each was taught using traditional Chinese methods focusing on teaching, practice, and memorization. Treatment Group 1 (CAM group) also comprised two randomly assigned classes, Class C and Class D, each with 25 students, where a single teacher implemented the CAM strategy to assess its effectiveness compared to traditional methods. Both the CAM and CI groups were randomly assigned to ensure that the two classes within each group had similar predicted performance levels based on pre-test scores.
In Treatment Group 2 (SCTM group), students were divided based on their pre-test scores into Class E (high-performance class) and Class F (low-performance class), each with 25 students. The SCTM approach was applied, with differentiated learning objectives tailored for each subgroup to evaluate the model’s impact on diverse student needs.
It is important to note that different teachers were assigned to each instructional method to avoid any teacher effect. Specifically, one teacher was assigned to teach both classes in the CI group, another teacher was assigned to teach both classes in the CAM group, and a third teacher was assigned to teach both classes in the SCTM group. This ensured consistency within each instructional method, and a total of three teachers were involved in the study. To maintain the integrity of each method, classroom observations were conducted to ensure teachers adhered to their designated instructional methods. This protocol, detailed in
Table 1, systematically documented aspects such as the use of stratified teaching and CAM strategies, group collaboration, feedback, and task differentiation. The classroom observation form captured critical elements like content delivery, student interactions, and feedback effectiveness, verifying the implementation of stratified teaching methods.
It was justified that at the initial stage, each group (CI, SCTM, and CAM) had an equal number of lower and higher-performing students, with approximately 50 students in each group. Therefore, these three groups were balanced in terms of lower and higher-performing students. Additionally, a pretest was used as a covariate to control for bias due to differences in student abilities across these three groups.
Both teachers rigorously applied the CAM and SCTM approaches as trained. It was essential that all students were provided the same learning opportunities, such as solving the same problems and answering the same questions, to ensure that only the instructional approach varied. The control group and CAM group did not have lower and upper-level classes. This division was unique to the SCTM group to evaluate differentiated instruction based on pre-test performance. The pre-test was implemented after dividing the students into control and treatment groups.
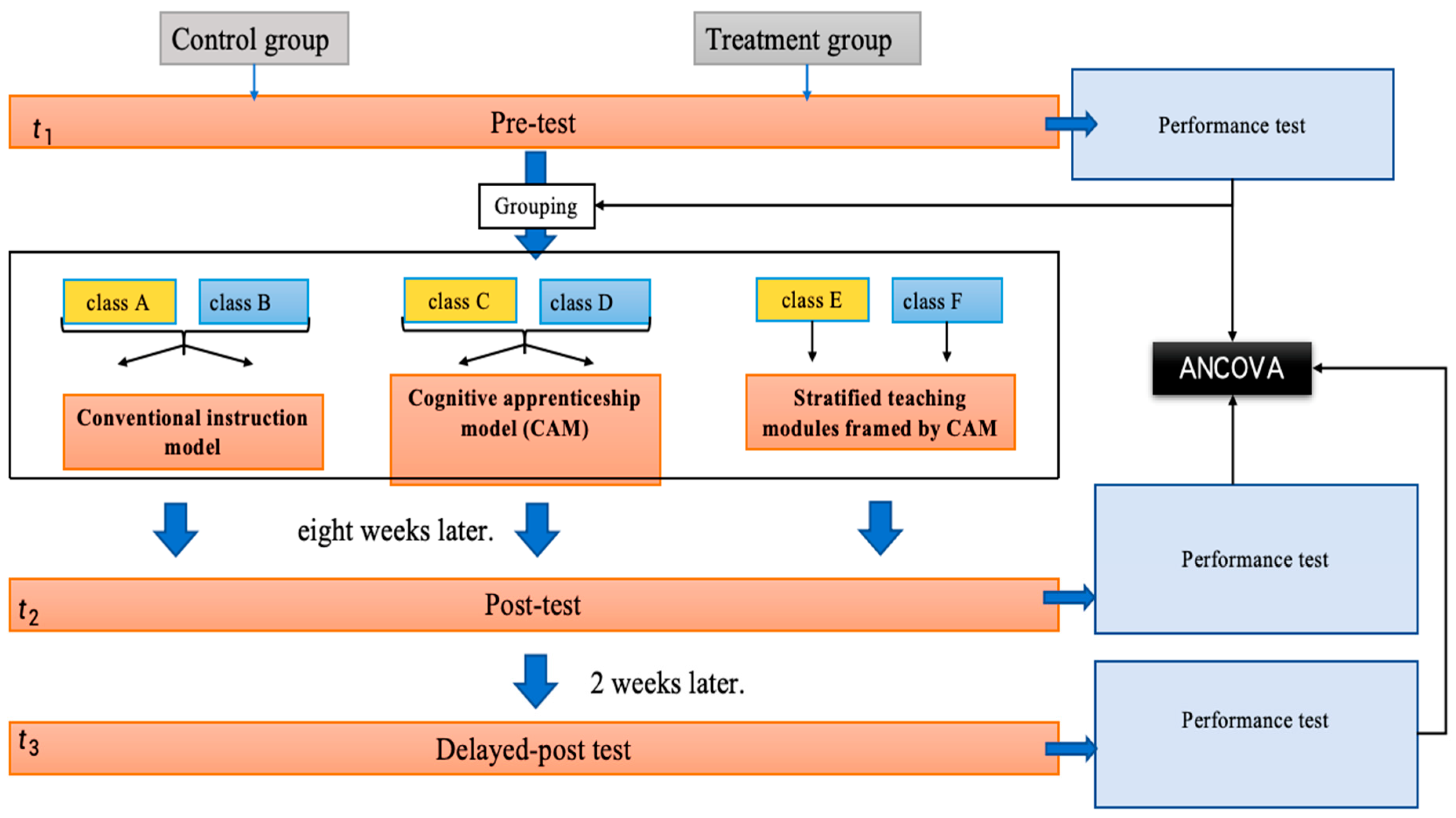
As shown in
Figure 3, the quasi-experimental design used in this study, including the pre-test, post-test, and delayed post-test stages, along with the grouping of students and the different instructional methods (CI, CAM, SCTM) applied.
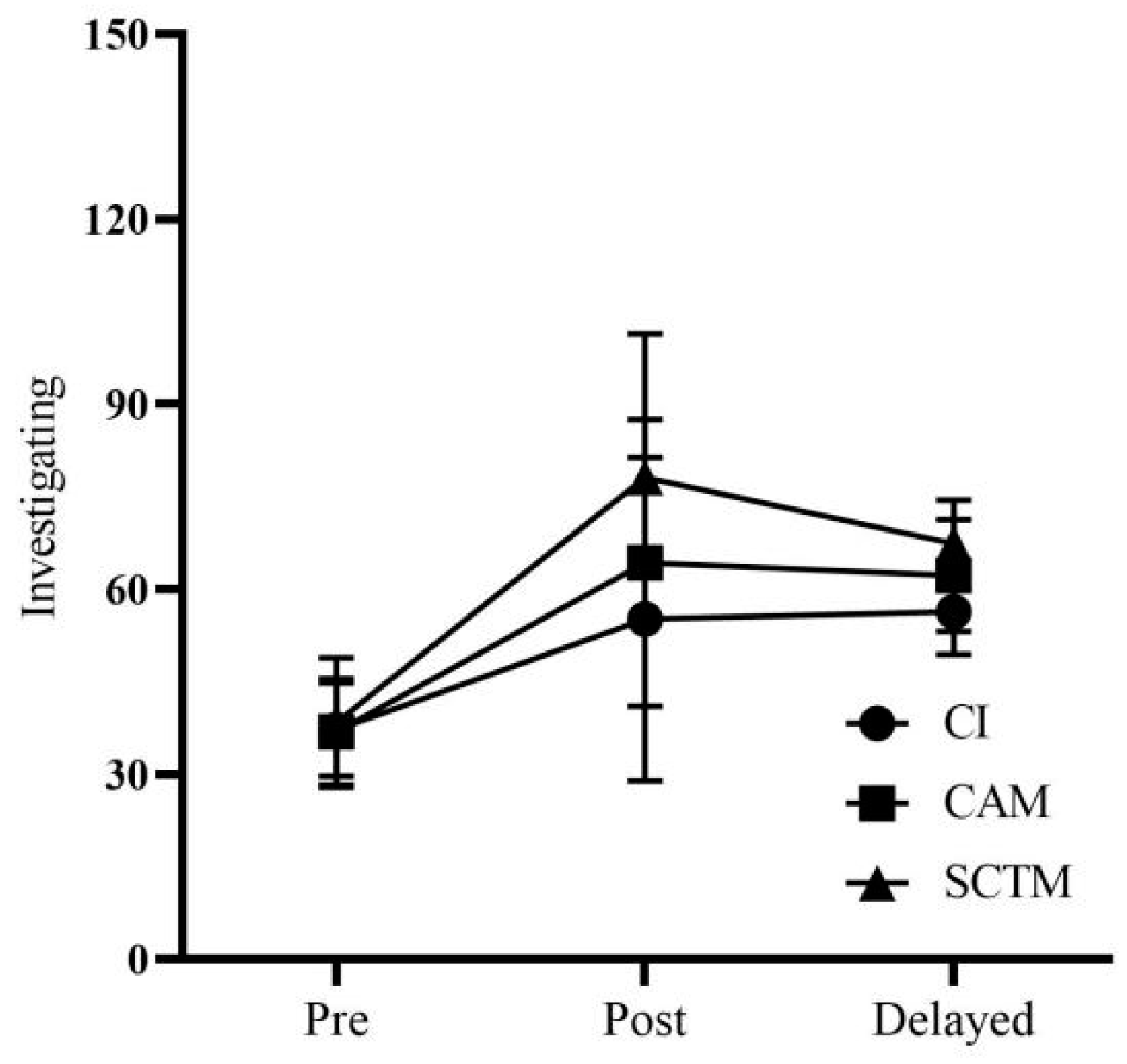
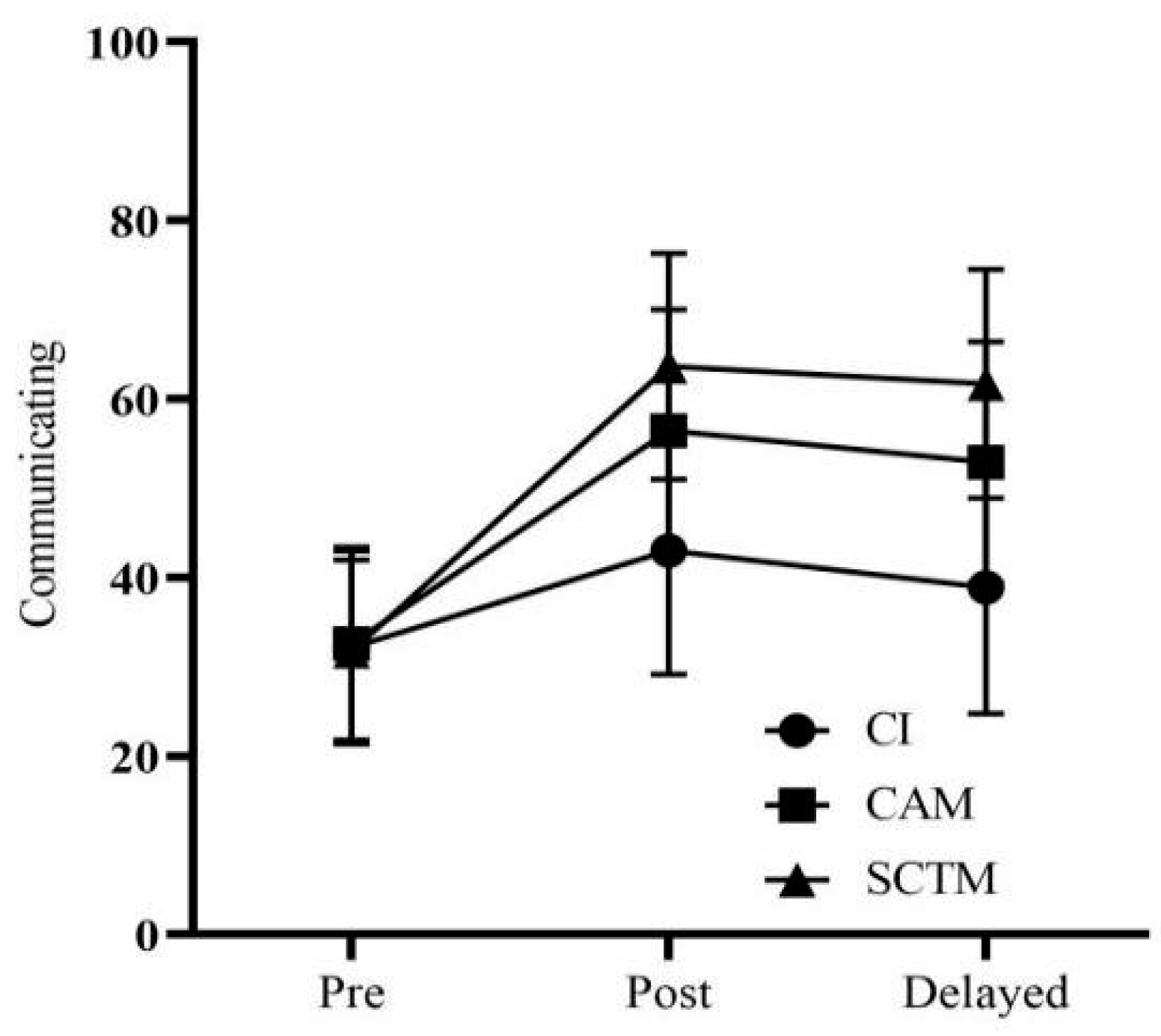
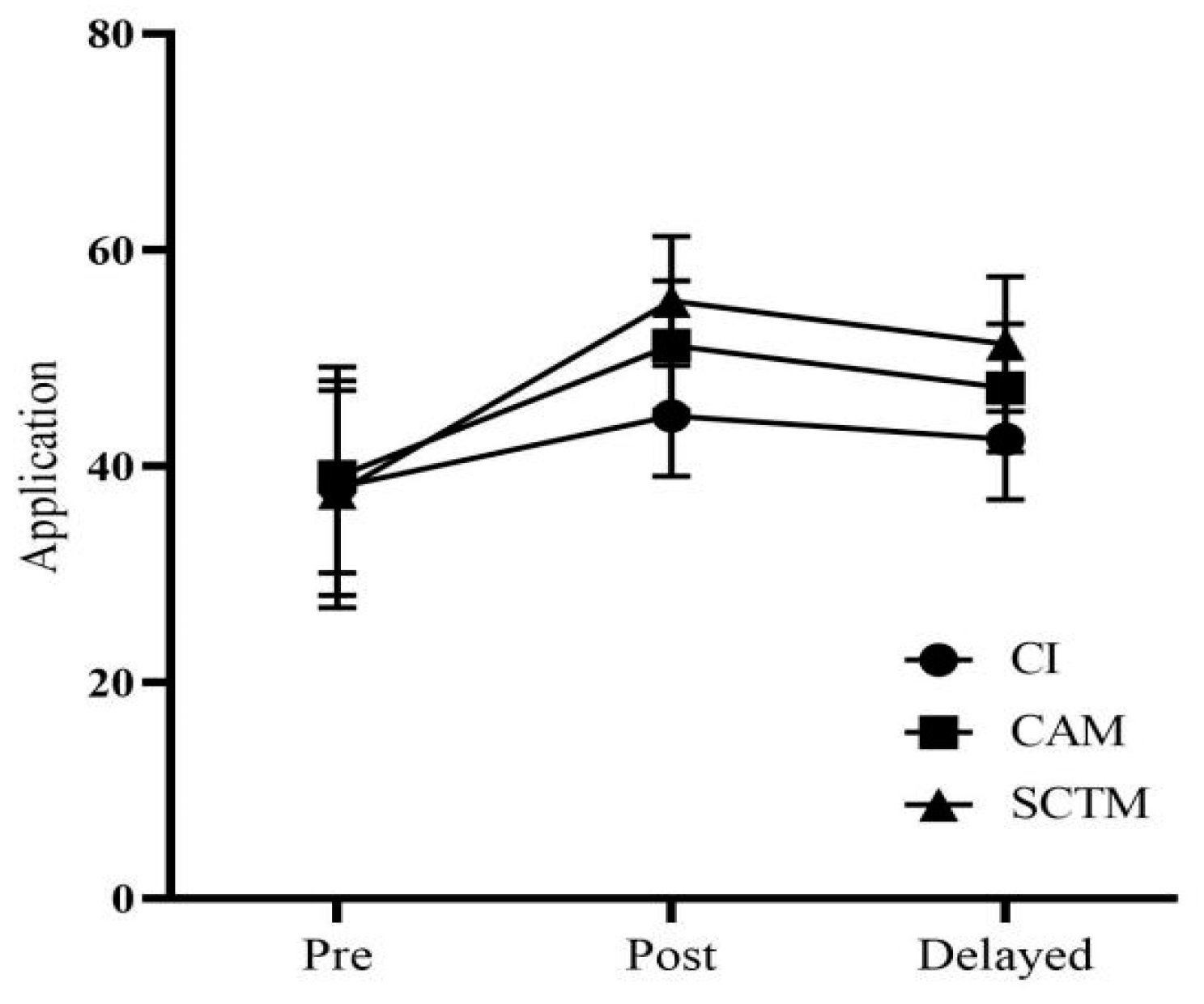
An 11-week mathematics teaching experiment was conducted in this study, consisting of an 8-week teaching experiment, followed by a 2-week gap, and then a 1-week delayed post-test period. Before the experiment began, the students took a pre-test (t = t1) to determine their scores on the four dimensions of learning ability: knowing and understanding, investigating patterns, communication, and application.
Following eight weeks of instruction, the middle year program (MYP) post-test (t = t
2) was administered to the three groups of students, and scores were obtained across the four dimensions of learning ability. Two weeks later, the MYP-delayed post-test (t = t
3) was administered to all three groups of students. Scores on the four dimensions of learning ability were recorded for each group. Although a two-week gap between the post-test and the delayed post-test might seem short, previous research has demonstrated the effectiveness of such intervals in assessing retention and understanding [
29,
30,
31]. The chosen interval allows for a practical balance between assessing immediate retention and minimizing external factors that might influence long-term memory.
Cronbach’s alpha measures internal consistency reliability, with values ranging from 0 to 1; higher values indicate higher reliability [
32]. As shown in
Table 2, Cronbach’s alpha coefficients for all three variables were relatively high, with values of 0.910, 0.897, and 0.900 for the pre-, post-, and delayed post-tests, respectively. This indicated that the items within each set of variables were highly consistent, suggesting that the measures were reliable and internally consistent. Overall, these results provide evidence that the measures used in this study are reliable and consistent, thus increasing confidence in the validity of the findings.
The initial versions of the three test papers (pre-, post-, and delayed post-tests) were selected from a school question bank. The examiners were IB teachers who reviewed all tests. Before the study, the students were selected to complete the tests, which allowed us to investigate their reliability. To revise the project, item analysis was conducted to determine the difficulty and discrimination of the items.
2.2. Research Procedures
The research process began with a pilot study conducted at a high school, involving 100 9th-grade students. The students were divided into a control group using traditional teaching methods and an experimental group using the new stratified cognitive apprenticeship model teaching module (SCTM). The pilot study helped refine the research methods and ensured the validity and reliability of the data.
The formal study involved 150 students, divided into three groups: CI, CAM, and SCTM. The data collection procedure lasted 11 weeks. Initially, a pre-test was administered, followed by an eight-week teaching experiment, and concluded with a post-test and a delayed post-test after two weeks to measure immediate and long-term learning outcomes.
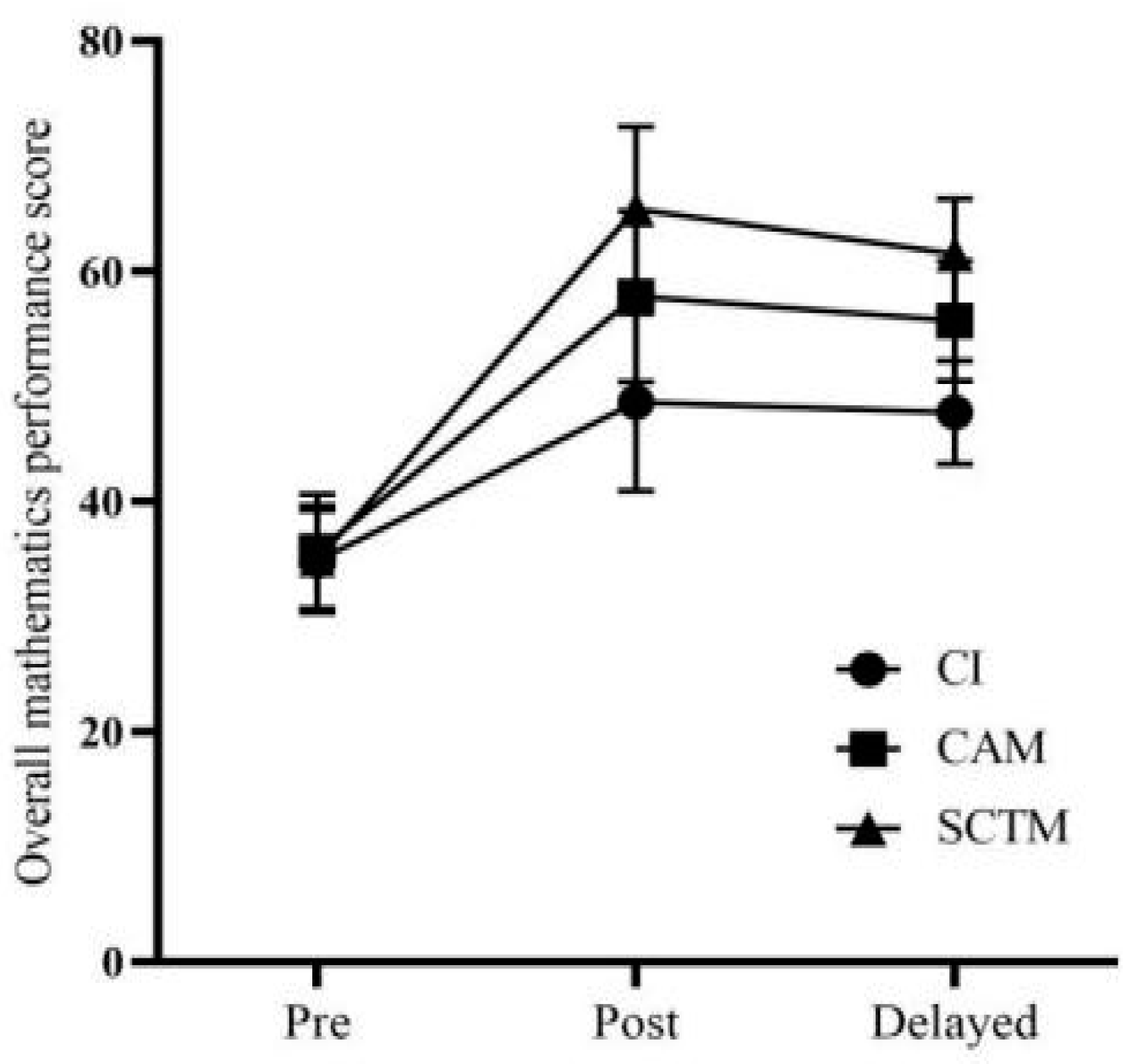
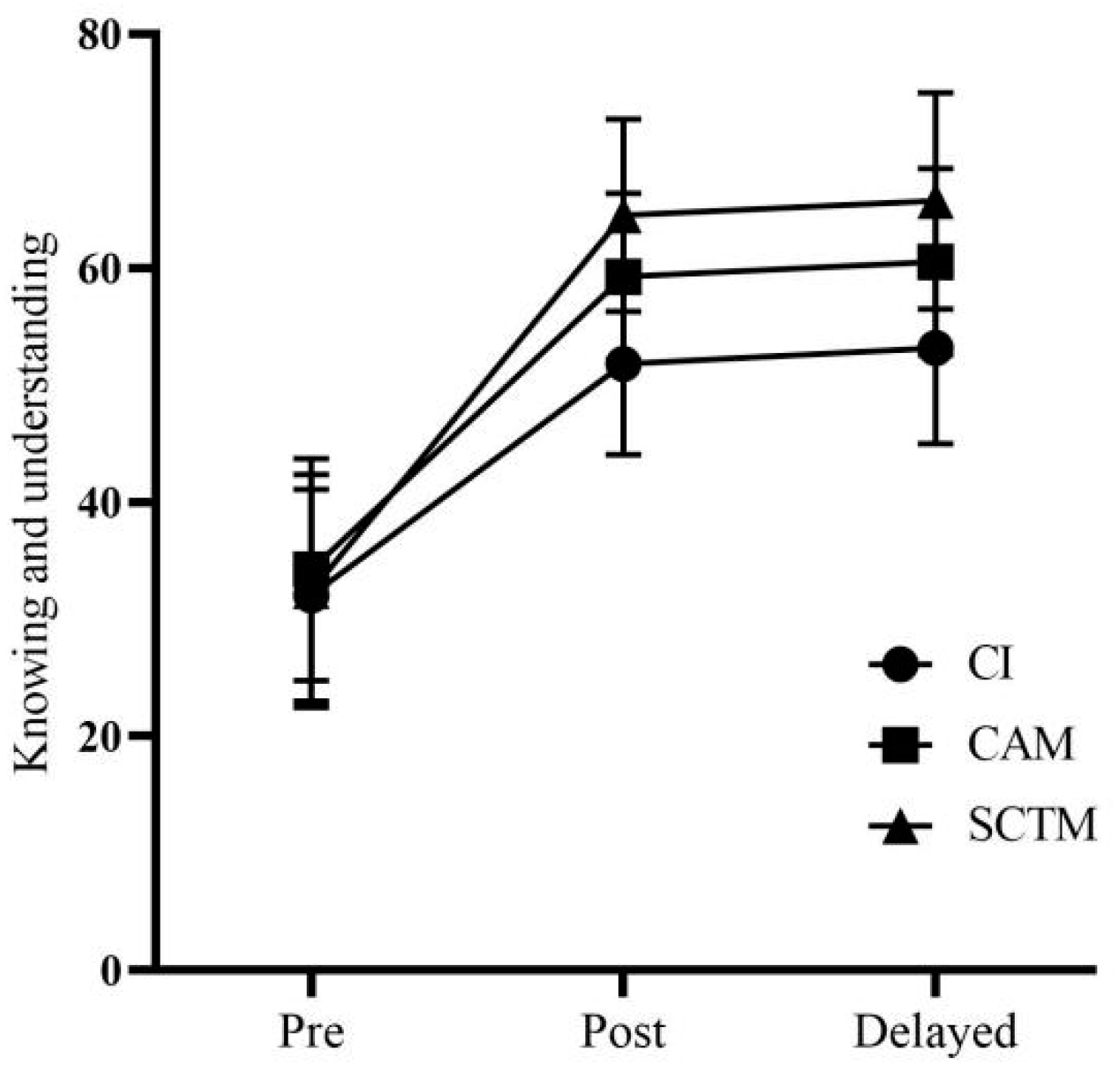
An analysis of covariance (ANCOVA) was employed to control for pre-test differences and assess the effectiveness of the interventions on the post-test and delayed post-test scores. This approach allowed for comparing the adjusted means of mathematics performance across the three instructional strategies, distinguishing between their short-term effectiveness and long-term impact.
To understand both the immediate and long-term impacts of the instructional strategies, two types of tests were used: post-tests to measure immediate learning outcomes and delayed post-tests to assess the retention of knowledge over time. This dual approach helps in distinguishing between the short-term effectiveness and the lasting impact of the interventions on students’ mathematics performance.