Next Article in Journal
The Interplay of Self-Regulated Learning, Cognitive Load, and Performance in Learner-Controlled Environments
Previous Article in Journal
Im/Mobilities during the COVID-19 Pandemic: Perspectives from International Graduate Students Studying in the Southern United States
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Education Sciences
Volume 14
Issue 8
10.3390/educsci14080859
education-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Context and Development of Teachers’ Collective Reflections on Student Data

by
Sam Prough
1,*,
Amber Webster
2 and
Lynsey K. Gibbons
2
1
Department of Mathematical Sciences, Ball State University, Muncie, IN 47304, USA
2
College of Education and Human Development, University of Delaware, Newark, DE 19716, USA
*
Author to whom correspondence should be addressed.
Educ. Sci. 2024, 14(8), 859; https://doi.org/10.3390/educsci14080859
Submission received: 9 May 2024 / Revised: 24 July 2024 / Accepted: 27 July 2024 / Published: 8 August 2024
(This article belongs to the Section Teacher Education)
Browse Figures
Versions Notes

Abstract

:
In the United States, teachers are often expected to use student assessment data to inform their instructional decisions. This study explores how teachers’ collective reflections on students’ mathematical thinking are influenced by the specific contexts of their classroom, school, and current events like the COVID-19 pandemic. The study uses audio recordings of a group of elementary teachers’ reflections on student thinking through Cognitive Interview Reports. The results highlight how teachers’ reflections on student data are heavily influenced by the shifting contexts of what is important in the world of teaching due to the COVID-19 pandemic. This ultimately shaped what the teachers were able to pay attention to in student data and what they identified as possible in their future practice.

1. Introduction

To make a meaningful impact on students’ learning that addresses their specific needs, scholars suggest that mathematics teachers use assessment data to inform their instructional decisions [1] and adapt their instruction to respond to students’ current understanding [2]. Teaching in these ways is complex. Teachers need sets of supports, including developing their own knowledge to make sense of students’ thinking and consider how to respond next in their teaching [3,4].
When teachers are provided with tools to interpret students’ thinking, they can benefit from having time to reflect on what they find in collaboration with colleagues [5]. There has been a push in the United States to use tools and resources to make sense of how students respond to a mathematics task (referred to in the United States as “student data”) and thus interpret students’ understanding [6]. Research on teachers’ reflections about student data often considers how teachers interpret it and make decisions [7,8] as well as how teachers’ school context [9] and broader societal context [10] can impact those interpretations. Thus, studying how teachers interpret students’ mathematical learning and how their present socially constructed context with particular meaning ascribed to certain actions (i.e., figured worlds) [11] influence those interpretations is important.
In this paper, we share an analysis that examined how a group of elementary teachers in the United States collectively reflected on reports of their students’ mathematical thinking. We created reports called “Cognitive Interview Reports” at the beginning of the 2021–2022 school year after returning to in-person schooling following disrupted learning from the COVID-19 pandemic. Mathematics education researchers crafted these reports to capture students’ strategies in solving various mathematical tasks related to numbers and operations in order to provide teachers with this information, which went beyond what was typically captured in the assessments from their curriculum. The teachers were trying to understand their new students’ current understandings, given the disruption in schooling the prior year due to the COVID-19 pandemic, and make sense of teaching mathematics within new contextual constraints because of the pandemic. Thus, our aim for this study was to understand who and what influenced teachers’ reflections of student thinking based on the larger changes to teaching returning from the virtual teaching of the pandemic. We see the use of figured worlds as a necessary framework for examining teacher interpretations of student data that have the potential to provide new insights into how teachers made sense of students’ mathematical thinking within their current school and classroom context. The questions that guided our study were: How do teachers collectively interpret student thinking through Cognitive Interview Reports? How do the settings within which they work influence their interpretations? We hypothesize that the new-figured world of teaching as a result of the COVID-19 pandemic has shaped how teachers think about their classrooms and students, thus shaping their reflections on student thinking.

2. Interpreting Student Thinking

Understanding student thinking is a key component of developing teacher learning as it can direct teachers to pay attention to that thinking in their practice and inform their future instruction. Rooney and Boud (2019) refer to this process as “informed decision making” [12] (p. 441). Attention to student sensemaking to better support teacher decision-making goes back decades to the model of Cognitively Guided Instruction [13,14]. We thus view the Cognitive Interview Reports as a prompt that allows teachers to center their interpretations on student ideas and strategies.
More recent research is focused on how teachers make sense of student thinking by considering teachers’ in-the-moment reflections of the classroom [3] as well as how teachers interpret assessments to inform future instruction [7,9]. Reflection has also been incorporated into professional learning [15]. “Noticing” is one popular construct within professional learning for understanding how teachers attend to the different features of teaching and learning by making sense of student thinking in reflection [16,17]. Other scholars have shown how providing teachers with opportunities for reflection allows for better learning and space to develop better instructional practice [18]. While this paper focuses on teachers’ interpretations of students’ mathematical thinking, other content areas have also shown interest in making sense of teacher reflections about student thinking [19].
Additionally, we focus our attention more specifically on teachers’ interpretation of student data. Since the implementation of the No Child Left Behind (NCLB) Act in the United States, schools in the country have directed significant time and value to school and instructional improvement through the analysis of data, such as test scores [1]. We are particularly interested in how teachers use and interpret data differently from the era of NCLB, given the continued federal mandates for standardized testing and the rise in one-to-one computers for students in both elementary and secondary classrooms. Such access to technology and educational platforms provides even more extensive data about students’ mathematical thinking that could be collected. Our study uses a version of the student work as the artifact of data through a Cognitive Interview Report intended to better direct teachers to focus on student strategy use.
Given that teachers benefit from considering how to adapt instruction when they collaboratively reflect on student thinking with one another [20,21], we want to apply this approach to teachers’ reflections on student data specifically. Because research across the globe has shown the importance of teacher collaboration for their teaching development [22,23,24], we wanted to understand how teachers interacted with one another about what they noticed in the Cognitive Interview Reports and how they worked together to make sense of students’ thinking [25]. We were curious about how they heard and engaged with perspectives from their colleagues, some of which may be different from their own [26]. Thus, we analyzed what teachers chose to discuss in their reflections and how they took up the reflections and questions of their colleagues. As they collectively examined the Cognitive Interview Reports, they considered the implications of their current context in interpreting student thinking as well as deciding possible responses.

Interpreting Student Thinking in Figured Worlds

Teachers’ surrounding context influences their interpretations of student thinking. Thus, we find figured worlds [11] a useful construct for understanding what immediate features of a teacher’s environment influence their ability to reflect on students’ mathematical thinking as it attends to the meaning given to the different actors, actions, and artifacts in a given environment. A figured world describes “a socially and culturally constructed realm of interpretation in which particular characters and actors are recognized, significance is assigned to certain acts, and particular outcomes are valued over others” [11] (p. 62).
In the figured world of schooling, interpreting student thinking does not happen in a vacuum; it is framed by several experiences and contexts in which teachers work [27,28]. For example, Shabtay and Heyd-Metzuyanim (2018) found that teachers operating from different figured worlds of schooling interpreted the same classroom event differently [28]. What strategies and tools teachers value in students’ mathematical thinking are built from the figured world of schooling that ascribes legitimacy and meaning to particular actors, actions, and artifacts. Figure 1 shows what features of the figured world of schooling (different actors, actions, and artifacts) have been described as central across the literature [27,29,30,31]. In other words, these are the features of events and materials within schooling that hold significance for how teachers engage in the work of teaching. The socially and culturally constructed interpretations frame experiences for a group of teachers as they collectively make sense of student thinking. In our analysis, we wanted to examine what actors, actions, and artifacts are granted attention and legitimacy in teachers’ collective reflections of students’ mathematical thinking when examining the reports. We believe that teachers’ specific contexts shape their figured worlds and will influence the details of their reflections on the Cognitive Interview Reports.
Although schooling itself is its own figured world [29], we argue that nuances exist with what makes up the figured world of a given school, shaped by time, policies, and people. A recent and significant impact on the figured world of schooling is the COVID-19 pandemic, which introduced an increased use of computer-based programs for students’ in- and out-of-class work due to remote and hybrid learning [32,33]. This changed which actors, actions, and artifacts had meaning in the school of the study participants.

3. Materials and Methods

We conducted a qualitative analysis of teachers’ reflections on student thinking in a mathematical assessment. This was performed by analyzing the transcribed audio recordings of each grade-level team’s conversation about the assessment through an inductive coding process. To better make sense of the teachers’ reflections, we describe the context of Rivers that prompted these assessments, the details of the assessment given to students, and further information on the teachers’ reflections on the assessment below. Given our interest in how teachers reflect on students’ mathematical thinking given their particular figured world, our findings focus on the analysis of these teachers’ reflections.
This study is situated within a more extensive project between university teacher educators and Rivers Elementary School to support classroom discussions. Rivers is a public school situated in the Northeastern United States with 17 teachers, kindergarten through 5th grade, and 372 enrolled students. At the time of the study, the teachers’ prior teaching experience ranged from 4 to 29 years in general elementary education. At the beginning of our partnership in 2021, students had just returned to classrooms after a year-and-a-half of remote learning. School leaders and teachers grappled with how to teach students in the best way while maintaining safety precautions. As a result, the district adopted a computer-based mathematics curriculum for Rivers to use from the start of their remote learning centered on a program’s pre-recorded videos and virtual assignments. Although students returned to in-person learning, district leaders elected to have teachers at Rivers and other schools in the district continue using the mathematics curriculum that had been adopted for virtual learning; this meant that for a good portion of mathematics instruction, students would complete virtual lessons alone on laptops with headphones.

3.1. Unpacking and Understanding Students’ Mathematical Thinking

Upon returning to in-person schooling, teachers were uncertain of the impact of the disrupted learning environment on students’ opportunities to learn mathematics. To build rapport with educators and get to know students at the beginning of a larger school-university partnership, we offered to assist the teachers and school leaders in learning about students’ current mathematical thinking. Thus, several university teacher educators, including the authors, conducted cognitive interviews with every student who was present within the three weeks that the interviews were given (spanning September and October). A total of 334 students (90% of students at Rivers) participated in the interviews.
The cognitive interviews used were originally developed by Kazemi and colleagues, though some of the contexts were modified slightly (see [34,35]). Kazemi and colleagues (2016) explain that cognitive interview assessments, unlike typical assessments, provide opportunities for educators to attend to the intricacies of students’ strategy use [34]. The assessments consisted of 3–5 tasks for each student, with some modification in the number values based on the student’s grade level according to the state mathematics standards [36]. Kindergarten students were given counting, join result unknown, and multiplication tasks. First grade students were given a relational thinking task in addition to the same tasks as kindergarten. Students between second and fifth grade completed a join change unknown, multiplication, fair sharing, relational thinking, and division tasks. As students solved their tasks, the teacher educator would ask questions to understand the student’s thought processes and strategies as they worked. As students described their strategies, the teacher educator recorded their responses directly on a student’s paper, near their representations. An example of how we attended to students’ solution strategies for the join result unknown and join change unknown tasks is presented in Table 1.

3.1.1. Cognitive Interview Reports

After completing the cognitive interviews, the teacher education team coded each task to identify the child’s strategy and whether they came to the correct answer (e.g., see possible solutions strategies in Table 1). We saw an opportunity to extend cognitive interviews into a simple easy-to-read summary that could act as a tool to center teachers’ reflections on students’ mathematical thinking. Several studies point to the importance of improving teachers’ attention to students’ mathematical thinking through the use of different tools or support structures [4,5,37]. Once all the cognitive assessment items were coded for each student and each task, Kendra Lomax (Kendra Lomax helped co-develop this assessment approach (see [31,32]) with the first and third authors included in the process to refine the reports) and two of the authors created a Cognitive Interview Report for each classroom teacher. The reports consisted of an account of the strategies, observations from student work, and recommendations. Each teacher received a copy of their classroom’s Cognitive Interview Report as well as the opportunity to reflect on its contents in grade-level meetings. An example of the main components of a report is provided in Figure 2 for grade 2. Analysis of teachers’ conversations about the reports highlights how teachers’ collective sensemaking about student thinking unfolds in the context of their environment.
The data in the report showed the frequency of strategies that students used and the accuracy of their answers for each task, as well as a detailed narrative of how subsets of students engaged with the problem beyond showing correctness as in more typical assessments. The Cognitive Interview Reports also contained recommendations for how to support the group of students toward more elegant and sophisticated ways of reasoning, which included suggestions for instructional activities teachers could engage in with students. Finally, the Cognitive Interview Reports described what percentage of students used the various strategies to solve each task, the percentage of students that used a valid strategy (i.e., a strategy that could obtain a correct solution), and if the valid strategies resulted in a correct response. The report template was set up such that information from the student cognitive interviews could be entered and automatically generated as data elements of the report. Such display generation means that in the future, teachers will be able to create aspects of the Cognitive Interview Reports themselves after conducting cognitive interviews.

3.1.2. Debriefing Conversations about the Cognitive Interviews

Teachers in grade-level teams who taught first through fifth grade (the kindergarten team was unable to meet with the facilitator to have a synchronous conversation due to time constraints and elected to view the reports on their own) met with the first author to discuss the reports during a weekly grade-level teacher workgroup meeting. During these conversations, teachers had the opportunity to collectively view the reports alongside their students’ work and reflect on their students’ mathematical thinking. The facilitator (first author) asked teachers what stood out about their students’ strategies, often redirecting teachers to focus on strategies used instead of correctness. For example, the facilitator asked, “What are some things you are noticing?”, “What do these noticings make you think about in relation to what happens in class?”, or (when a constraint or challenge is identified) “How can we support students in [challenge teachers identified]?”.
The first-, second-, and fourth-grade teachers were willing to have the conversation recorded, which was then transcribed. We first met with the fourth-grade team and then adjusted our facilitation protocol for the first- and second-grade teams to encourage more conversations among teachers. As such, the analysis described below focuses on the conversations of the first-grade teachers (Leah, Delilah, and Lucy) and the second-grade teachers (Allison, Madison, and Evelyn) (all teacher names are pseudonyms).

3.2. Data Analysis

Because we were interested in understanding how teachers collectively interpret students’ mathematical thinking, we analyzed the transcripts of their debrief conversations to see how they built upon one another’s reflections. The first and second authors engaged in inductive coding, looking for common themes. The inductive process followed tenets of grounded theory to ask sensitizing, practical, and guiding questions of the transcripts [38]. Sensitizing questions included inquiry into what the teachers said and meant. Practical questions related to what topics repeatedly emerged in the teacher’s reflections to warrant a theme. Guiding questions included considering the themes’ purpose and what they might represent about the teachers’ debrief. The general themes that arose were focused on the context of the classrooms, school, and district and its relation to student thinking and were organized into how the teachers saw them as general noticings, constraints, or possibilities in teaching (see Table 2). These contexts were later unpacked into the actors, actions, and artifacts that held meaning for the teachers within their figured worlds. After independent coding and identifying themes, the two researchers compared coding, collapsed themes where appropriate, and reached a consensus across the final common themes.

4. Results

In order to understand how teachers reflect on student data and the influence of their professional setting, we considered which aspects of the Cognitive Interview Report and student work the teachers focused on during their reflection meetings. We look at how aspects of the teachers’ reflections build up (as teachers agree and refine the interpretations of their colleagues) and what actors, actions, and artifacts they identified as important in their teaching context. In the following sections, we describe the elements with meaning for the teachers’ current figured world, especially as it differs from what the literature has described as the figured world of schooling prior to 2020 (see Figure 1). Next, we identify the common constraints and opportunities the teachers described in their reflections, as well as how their interpretations from these reports build on each other’s ideas. Then, we highlight how their interpretations are situated in their figured world of teaching. We share these details for both the first- and second-grade teams in order to highlight the commonalities as a larger shared-figured world of their school context. The differences in the grade level teams’ reflections help illuminate the more particular features of their grade level team’s figured worlds.
Figure 3 shows what features of participants’ figured world during the COVID-19 pandemic may have meaning for teaching mathematics. The examples in Figure 3 are built from our conversations with teachers and initial analysis of the Cognitive Interview Report reflections. New actions that hold meaning are watching virtual mathematics lessons through screens and new classroom artifacts, including the desks’ orientation, spread out evenly across the room. Even though most instruction had returned to being in-person, many teachers from our partner school were expected to closely follow a scripted and computer-based curriculum where the majority of students’ mathematical learning was completed individually through a computer screen. We began to see how this learning through screens shaped what and how teachers were able to interpret students’ learning [39]. As another example, the classroom configuration (i.e., spread-out desks) was a new artifact due to COVID-19 policies. While the goal was to prevent the spread of germs, the policy impacted what was and was not possible for group instruction. At other times, or even in other spaces, an artifact such as the arrangement of desks may not hold the same meaning in mathematics instruction [11]. The nuance in who or what has meaning in a teacher’s figured world makes it essential to see how that figured world influences how teachers interpret students’ mathematical thinking.

4.1. First-Grade Teachers’ Collective Reflections

The first-grade teachers began their reflections on the reports by pointing out particular features about student correctness and capability attached to evidence of strategy use or looking more closely at individual student work. The majority of reflections expressed by the first-grade teachers in looking at the reports focused on the constraints of the classroom (30 out of 55 teacher reflections). Some of the most common concerns when considering how to support or interpret student mathematical thinking were related to the curriculum and technology (i.e., the online-based program, where students complete activities asynchronously on computers with headphones). Together, these noticings and described constraints meant themes in teachers’ reflections about what students were able to comprehend about problem-solving, given the limited nature of the curriculum and, consequently, what students could or could not do as a result.
We share an excerpt from the first-grade teachers’ debrief that highlights the major themes that came up during their conversation: a focus on student comprehension and assumptions of what students can and cannot do. The remainder of the section details how the teachers’ reflections built on one another’s statements to show the development in their interpretations of students’ mathematical thinking.
The teachers looked at the Cognitive Interview Reports and student work to focus on the students’ strategies and solutions for solving the multiplication task, which asked, “There were three tables. 5 children were sitting at each table. How many children were there altogether?”:
Leah: Interesting. How they don’t really have–we’ve been working on it a lot, kind of drawing a picture of what is happening in the story, if they don’t even really even know where to start. {But} they’re recognizing the numbers, they saw the five and the three. But they’re not getting three tables {and} what that really means, kind of not paying attention to maybe all those details or not really sure how to draw that out.
Lucy: I think they’re also just overgeneralizing. They’re so used to us just adding or just subtracting. They just assume all the problems are going to do that.
Facilitator: I wondered about the visualization…I wondered about that phrase, whether kids were familiar with that phrase sitting at every table.
Leah: These guys and our kindergarten guys haven’t really seen anybody more than two sitting at a table. It’s not like we’re sitting at tables like normal for these past two years. You know what I mean?
Delilah: But they should, because we did tons of work with subitizing. They should be able to picture a five on a dice. When you say there’s five kids at that table…
Lucy: With five frames they always did.
Delilah: Yeah. They should be able to {imagine} that amount and say, oh yeah, five and five, and there’s a five…They should have had that skill down pat. Because we do that fluency with them constantly.
Leah, Lucy, and Delilah consider why students solved the task in the way they did, considering what approach they have used before (e.g., generalizing) and what they have discussed in class (e.g., subitizing). Their reflections focus on noticing features of student capability and the impact of classroom spacing of chairs (i.e., artifacts with new meaning in this figured world) for student comprehension. After Leah’s attention to what students can and cannot do in direct modeling of the task, Lucy interprets why so many students used an invalid strategy of adding the two quantities—that represented the number of groups and quantities in each group—instead of considering how the two quantities related to one another and using a strategy to figure out the total number of children. Lucy’s comments reflect how she interprets students’ comprehension of the task, which further clarifies Leah’s interpretation of students not paying attention to details to identify how students think to respond to all tasks similarly. In this way, Leah and Lucy are adding specificity to their reflections about student strategies for this multiplication task by interpreting why students solved the task in the ways that they did.
After the facilitator asked about what students were familiar with in the context of the task, the teachers discussed what students should be mathematically capable of, both in the context of the task and the types of activities they did in class. Regarding assumptions about what students can or cannot do, Delilah followed up shortly after Lucy’s interpretation about overgeneralizing the task to consider what students should be able to do to figure out the task. Delilah’s comments leveraged her experience from the previous school year teaching kindergarten to support children in subitizing quantities, suggesting that what they had learned should support them in solving such a problem.
Delilah’s comments demonstrate how the teachers’ reflections built on one another, beginning with Leah’s comment that students did not know how to comprehend the word problem, followed by Lucy’s interpretation about why students may have struggled to solve the task, and finally Delilah’s connection to the mathematical ideas that students learned the year prior that could have supported students to visualize the quantities correctly. This moment shows how teachers relate students’ current comprehension and assumption of what they can or cannot do to the relevant contexts students have experienced with groupings and related classroom activities.

Situating Interpretations into Figured Worlds

Teachers’ interpretations of students’ mathematical thinking are influenced by the experiences and contexts in which teachers work [27]. The significance ascribed to particular teaching actions and resources is built from the figured worlds of teaching [11]. With the students returning to in-person learning, the team spoke about the challenges of supporting a group of students that did not have the experiences of in-person kindergarten and what actions would be important to prepare them to learn first-grade content as well as acclimate them to what it means to be in school. Concerns regarding expectations for time spent on a computer-based mathematics curriculum in the mathematics block were particularly salient. Teachers felt this time did not allow for deeper engagement with the content. Teachers tried implementing the computer-based curriculum and commented that it did not offer details about how students obtained an answer.
The first-grade team discussed the challenges of their curriculum and the time spent attending to student thinking. The curriculum is an artifact of their figured world that shapes how they interpret student thinking in the report, as they relate what students were able to comprehend as a result of common activities in the curriculum lessons. Regarding time, the first-grade team talked about how little time there is to work with students to build understanding when they are expected to get through a certain number of mathematics lessons in the computer-based program each week. As Delilah phrased it, “it’s a challenge to fit things in when there’s things that you have to do instead [of] the things you need to do.” The district leaders mandating the curriculum use became important actors in the first-grade team’s figured world as it influenced what actions (or responses) they had for addressing students’ mathematical and social needs, which are often constrained by timing.

4.2. Second-Grade Teachers’ Collective Reflections

Similar to the first-grade team, the second-grade teachers also began their reflections on the reports by pointing out particular features of student capability with evidence from students’ strategy use. Their remaining reflections were fairly evenly split between describing the constraints of the classroom (14 out of 40 teacher reflections) and proposing possibilities to attend to student mathematical thinking (19 out of 40 teacher reflections). The most common concerns when considering how to interpret or respond to student thinking are related to student capability, the limitations of the digital curriculum, and managing the logistics of the classroom given the new pandemic protocols. However, the team also frequently interposed comments about challenges with particular tools or teaching strategies they might try to better address them in support of students’ mathematical learning.
Given the focus of the second-grade team on student capability and thinking about appropriate responses, we share an excerpt from their debrief that highlights these themes and how they built off of one another’s statements. The teachers looked at the students’ strategies and their solutions for solving the join change unknown task presented to students as follows: “Jayden had 38 stickers. His friend gave him some more stickers. Now Jayden has 81 stickers. How many stickers did his friend give him?”:
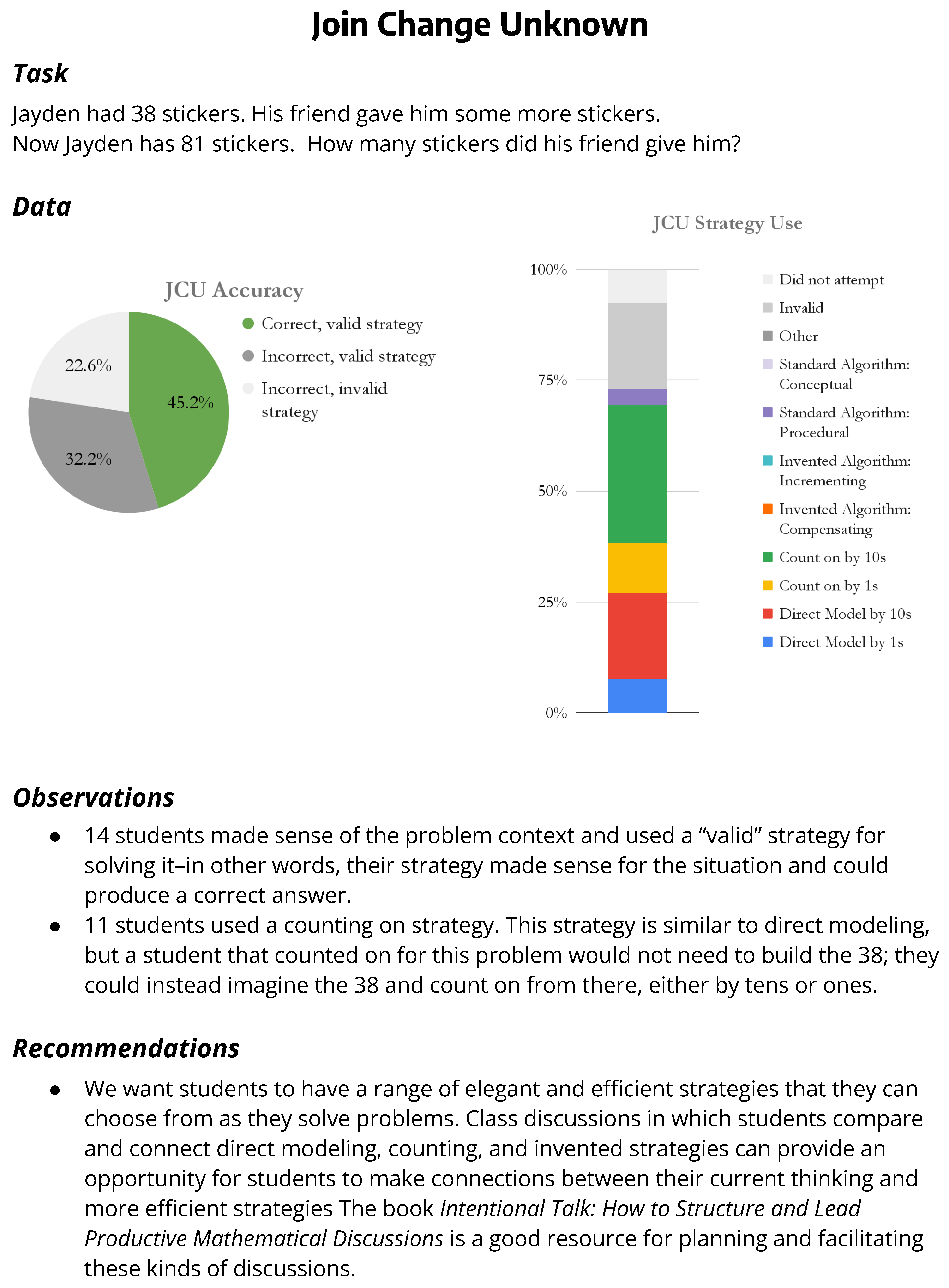
Evelyn: If we see the word ‘altogether’ is this addition or subtraction, and it’s just like jump starting them selecting their strategy before they start.
Madison: Yeah, yeah. Because I think I’ve noticed too, even last year, my kids have always had issues of like when there’s a missing part. If it is 38 plus blank equals {81}, finding that missing part. It’s almost like if it’s not in order 32 plus 15 equals…or subtraction order, my guys get confused by that. Of what to do with it having that missing part.
Evelyn: They don’t like it when they get the sum first in the question. That’s the end goal.
Madison: Yeah. That way. Right. It’ll say, 72 equals 32 plus what. It’s just if the signs are mixed up or a part is missing it throws them off… Because on the assessment, they have to end up doing that at the end of the module. But I probably need to practice that more.
Allison: Or just go back to those number bonds with part-part-whole, where we have the whole {and} we have the part. How do we solve it?
Evelyn: They’re so used to doing repetitive, rote, 40 problems in a row that are the exact same kind of problem. But they’re not really thinking about it, it’s just–
Allison: Yeah. Like a repetition thing.
Evelyn: Yeah. But they’re not really thinking about “what is the author asking you to solve here?”
Allison: Yeah. I also know that they like to rush.
Madison: Yes.
Evelyn: Yeah, yeah.
Allison: They think everything’s a race.
Evelyn: They do. And I find that a lot of the computer programs that we have, it’s like they get that instant gratification when they move on. It’s like a video game, moving on to the next level.
After the teachers examined what students did about this task, they attributed students’ confusion about what to do with the quantities (add or subtract) to how the structure of the join-change-unknown task type is challenging to students. Their reflections focus on the constraints of what students are able to do based on the limitations of the frequent technology use (i.e., an artifact of the figured world), leading to suggestions of possibilities for change. Madison interpreted why several students chose to add 38 and 81 together in the task as confusion of the structure, with a missing part that was not the result, where students did not comprehend what they needed to do with the quantities in the task. Evelyn clarified Madison’s statement about how students are more comfortable with the result-unknown structures. Allison connected to a representation, namely number bonds, that teachers indicated make the parts and whole of number relationships clear, in this case, 38, 43, and 81. When the teachers ascribed meaning to why students did not comprehend the task structure (interpreting), they agreed with each other on what they had seen before in practice problems, as well as the nature of solving problems in a rush, with statements of agreement. Their reflections normalized what challenges students in comprehending the problem while refining their argument. All three teachers contributed to the discussion of student comprehension across the tasks, considering the role of students’ understanding in their ability to solve the problems in the ways that they did.
The excerpt also demonstrates the common trend of the second-grade team’s debriefs in order to consider possible activities or tools to support students’ learning. For example, Madison followed up on how students might be confused about different problem structures with a statement about needing to practice those problems more. Allison’s comments immediately following proposed an interpretation of where students comprehend such problem structure (number bonds) and how returning to that structure in an activity may help Madison’s students comprehend future similar problems. The comments from the teachers built off of Madison’s original comments about student comprehension but deepened it to consider a more detailed interpretation and a possible response. As a team, the second-grade teachers were interested in creating access to mathematics through understanding the problem itself, engaging in varied problem types, or the use of tools and manipulatives that would allow students to deepen their mathematical understanding.

Situating Interpretations into Figured Worlds

Evelyn, Allison, and Madison discussed their interpretations of student thinking and their possible responses within the context of their current setting. Two of the challenges the team reiterated were the use of the computer-based mathematics curriculum (i.e., an artifact of the figured world) and the limitations on what they could do with the safety protocols of COVID-19 (i.e., logistics or action of the figured world). On the challenges of the computer-based curriculum, Evelyn described how the students felt about receiving instant gratification. The other teachers agreed with Evelyn that students saw the computer-based mathematics curriculum as a race or a game instead of an opportunity to grapple with mathematical thinking. Another challenge the team highlighted was the logistics of using common mathematics manipulatives when COVID-19 protocols meant they needed to be careful of who used what supplies. Their concern centered on having these resources available to students in a way that would best support students and follow the new safety guidelines. These constraints presented the most pressing relevance as they impacted how students approached mathematics and what the teachers struggled to do to develop student understanding.
The team’s comments about the challenges of attending deeply to student thinking were often followed by what resources or tools (i.e., artifacts) might help them address such challenges. For example, when Evelyn and Madison talked about the challenges of not sharing manipulatives due to COVID protocols, Allison offered up what she does to give students their own sets of materials. Evelyn connected to Allison’s suggestion that a resource station could have individual material sets but be manageable when used by only a small group. What was salient in their discussions of what was possible was the use of tools and strategies to support student conceptualization and understanding of tasks. What these teachers saw as possible changes to their practice in the given context of expected curriculum use speaks to how the shifts in the figured worlds have influenced the meaning behind common tools and activities used in the classroom.

5. Discussion

Teachers better adapt their instruction to meet their students’ needs when they have opportunities to closely examine students’ mathematical thinking alongside their colleagues [2,5]. In this study, we wanted to understand how teachers used the Cognitive Interview Reports—designed to focus their attention on students’ mathematical thinking and strategy use—to collectively make sense of students’ thinking and consider implications for future practice within their new figured world of teaching. We found that written reports functioned as a tool for teachers to support their group reflections on students’ mathematical thinking; however, their reflections were influenced by the elements of their figured world [31]. The context for the first- and second-grade teams reflects what actors (e.g., students and teachers), actions (e.g., common mathematical strategies used), and artifacts (e.g., counting videos and hundreds charts) were ultimately granted legitimacy in the figured worlds of their teaching. Their contextualized interpretations related to and built off the ideas of their colleagues as they worked to add detail to similar noticings and collectively constructed possible reasons for why students solved a task in the ways they did.

5.1. Collective Interpretations as Collective Sensemaking

When considering how teachers collectively interpreted student thinking, we found that the Cognitive Interview Reports provided the teachers with a space to deepen their interpretations as they built upon their colleagues’ comments and suggested responses. Teachers’ reflections became more complex as they considered what students did and their interpretations of why they did it. For example, consider the first-grade team’s collective building on how students may or may not be able to interpret word problems, where each teacher contributes to a more nuanced picture of student thinking. Student data and curated reports have been framed as tools that can deepen teachers’ understanding of student thinking [1]. However, researchers rarely consider teachers’ collective reflections on student data (see [9], for an exception). In their reflections on the first and second-grade teams, the teachers demonstrated specific and detailed interpretations of student thinking that evolved through the interactions they had with one another. Their collective reflections unfolded in a way that allowed them to build on each other’s thinking by adding detail, helping each other interpret why students may have solved tasks with particular strategies and considering possible teaching responses together. The reports provided opportunities for teachers to engage in collective sensemaking as they interacted and iteratively referred to the same ideas or questions [25].

5.2. Teachers’ Figured Worlds—Challenges with Computer-Based Curriculum

Upon consideration of how the settings within which the teachers’ work influenced their interpretations of student work, we found that the context of their figured worlds, particularly about their computer-based mathematics curriculum, contributed to their reflections. The use of the curriculum shaped the expected actions of instruction (student independent use of computers), the actors who influenced the use of this curriculum (the top-down expectations of district leaders), and the artifacts needed to implement the curriculum (the use of headphones and spread-out desks). Studies discuss the role context plays in what and how teachers interpret student thinking [11,31,40]. The adaptations in the figured world of schooling created tensions for the teachers in being able to interpret students’ mathematical thinking, similar to what other studies have characterized as tensions experienced in shifting figured worlds [41]. In this analysis, the district leaders were the actors who ascribed meaning to the teachers, with expectations of what they could and could not do in their teaching. This may have influenced teachers’ responses in their noticing. The action of selecting tasks and problems becomes meaningful in this context as both groups of teachers consider what they can ask based on students’ comprehension (or lack thereof), given the students’ focus on speed over understanding to solve problems in the computer-based curriculum. Finally, a meaningful artifact for both teacher groups was the computers and the computer-based curriculum itself, where teachers’ interpretations of what students could comprehend or not were based on what types of problems they were familiar with solving.
The teachers’ attention to what students tried to comprehend about mathematics was situated within what actors, actions, and artifacts were given meaning in their environment [11]. For the teachers at Rivers Elementary, the role of technology and the impact of the pandemic has impacted how they attend to and respond to their students’ mathematical thinking. Thus, what was ascribed meaning in this environment was not just about what counted as teaching and learning but what district leaders counted as ‘good’ teaching and ‘good’ students [29]. As such, teachers’ interpretations of student thinking when looking at the reports were informed by what was expected of them to promote ‘good’ teaching and ‘good’ students, lamenting the challenges of maintaining the pacing of the online modules for students and responding to student comprehension needs with the current structures of the physical classroom.
Many other schools also returned to in-person instruction during the COVID-19 pandemic but approached it differently than Rivers Elementary. While these other schools, for example, might have computer-based programs, they may have different expectations and values associated with them that could inform their noticing about students’ mathematical thinking. Thus, there are implications from this analysis point on the importance of considering teachers’ figured worlds when addressing what they notice within their practice.

5.3. Limitations

While we provide an interpretation of teachers’ collective interpretations of student thinking, other possible explanations exist for the teachers’ reflections. We present a case where the teachers used reports of students’ thinking gathered from cognitive interviews as a tool to frame their reflections, building off of each other’s ideas by attending to particular student strategies, interpreting why they used those strategies, and considering possible responses. It is also possible that this method of engaging with student thinking is typical for the teachers but they have merely limited time to do so. Additionally, we worked with the data of the two smaller groups of teachers for a fine-grained analysis of their interactions with the Cognitive Interview Reports. We can show how these sets of teachers collectively make sense within these conversations but cannot generalize how other teachers, particularly those with different contexts and constraints, may collectively make sense of student thinking through similar reports.

6. Conclusions

Future research could extend the use of reports of students’ mathematical thinking to different teacher settings as a way to understand how different figured worlds shape teacher reflections of students’ thinking. Such research would help answer questions about what is most salient in teachers’ interpretations of student thinking across contexts and how different contexts shape teachers’ collective reflection practices. Furthermore, this research would help us understand what teachers feel is possible given their constraints and opportunities within their figured worlds.
This analysis of teachers’ reflections on their figured worlds has theoretical and practical implications. Theoretically, it contributes to our understanding of how the context in which teachers work, or their figured worlds, impacts/influences what they attend to when examining student thinking and considering how to respond in immediate future instruction. Also, we found that through teachers’ collective sensemaking [25], their reflections considered specific details about student ideas, building off of one another’s interpretations of why students used the strategies they did. Engaging in collective sensemaking allowed teachers to co-construct meanings of students’ mathematical thinking and dream up how to prepare instruction that is responsive to those noticings. Practically, the analysis has implications for instructional leaders who work alongside teachers to develop their instructional practices. First, instructional leaders need to work to understand the context in which teachers work, e.g., what teachers are held accountable for, what support they receive, curricular resources, etc. [42]. Second, there are richer opportunities for teachers to make sense of student thinking collectively, allowing teachers to build on one another’s interpretations, which can lead to the potential for deeper sensemaking about students’ current understandings and how to respond. Thus, instructional leaders should create structures and adopt tools that support teachers in working alongside each other, considering the changing landscape of schooling and the newly figured worlds of teaching.

Author Contributions

Conceptualization, S.P. and L.K.G.; methodology, S.P. and A.W.; formal analysis, S.P. and A.W.; data curation, L.K.G.; writing—original draft preparation, S.P. and A.W.; writing—review and editing, S.P.; supervision, L.K.G.; funding acquisition, L.K.G. All authors have read and agreed to the published version of the manuscript.

Funding

This work was done with the support of grant 220020522 from the James S. McDonnell Foundation. All opinions expressed are those of the authors and do not necessarily represent the views of the Foundation.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board of the University of Delaware (IRBNet ID# 1797521-1 on 29 September 2021).

Informed Consent Statement

Informed consent was obtained from all participants involved in the study.

Data Availability Statement

The data presented in this article are not readily available due to participant privacy.

Acknowledgments

The cases we present in this article are based on work conducted in collaboration with the authors and our partner classroom teachers. We are grateful for the people who supported the cognitive interview collection process: Charles Hohensee, Christy Metzger, and Sarah Ryan. We would also like to thank James Hiebert, Kendra Lomax, Latrice Marianno, Robyn Pinilla, and Anne Garrison Wilhelm for their reviews and feedback on the earlier drafts of this article.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Diamond, J.B.; Cooper, K. The uses of testing data in urban elementary schools: Some lessons from Chicago. Teach. Coll. Rec. 2007, 109, 241–263. [Google Scholar] [CrossRef]
  2. Carpenter, T.P.; Fennema, E.; Franke, M.L.; Levi, L.; Empson, S.B. Children’s Mathematics: Cognitively Guided Instruction, 2nd ed.; Heinemann: Portsmouth, NH, USA, 2015. [Google Scholar]
  3. Kooloos, C.; Oolbekkink-Marchand, H.; van Boven, S.; Kaenders, R.; Heckman, G. Building on student mathematical thinking in whole-class discourse: Exploring teachers’ in-the-moment decision-making, interpretation, and underlying conceptions. J. Math. Teach. Educ. 2022, 25, 453–477. [Google Scholar] [CrossRef]
  4. Sherin, M.G.; Han, S.Y. Teacher learning in the context of a video club. Teach. Teach. Educ. 2004, 20, 163–183. [Google Scholar] [CrossRef]
  5. Kazemi, E.; Franke, M.L. Teacher learning in mathematics: Using student work to promote collective inquiry. J. Math. Teach. Educ. 2004, 7, 203–235. [Google Scholar] [CrossRef]
  6. Garner, B.; Horn, I. Using standardized-test data as a starting point for inquiry: A case of thoughtful compliance. In Cases of Teachers’ Data Use; Barns, N., Fives, H., Eds.; Routledge: Abingdon, UK, 2018; pp. 96–111. Available online: https://www.taylorfrancis.com/chapters/edit/10.4324/9781315165370-7/ (accessed on 1 May 2024).
  7. Oláh, L.N.; Lawrence, N.R.; Riggan, M. Learning to Learn from Benchmark Assessment Data: How Teachers Analyze Results. Peabody J. Educ. 2010, 85, 226–245. Available online: http://www.jstor.org/stable/20720821 (accessed on 2 April 2024). [CrossRef]
  8. Vanlommel, K.; Schildkamp, K. How Do Teachers Make Sense of Data in the Context of High-Stakes Decision Making? Am. Educ. Res. J. 2019, 56, 792–821. Available online: http://www.jstor.org/stable/45237708 (accessed on 2 April 2024). [CrossRef]
  9. Horn, I.S.; Kane, B.D.; Wilson, J. Making sense of student performance data: Data use logics and mathematics teachers’ learning opportunities. Am. Educ. Res. J. 2015, 52, 208–242. Available online: https://www.jstor.org/stable/24546753 (accessed on 2 April 2024). [CrossRef]
  10. Ehrenfeld, N. Framing an ecological perspective on teacher professional development. Educ. Res. 2022, 51, 489–495. [Google Scholar] [CrossRef]
  11. Holland, D.; Lachiotte WJr Skinner, D.; Cain, C. Figured Worlds. Identity and Agency in Cultural Worlds; Harvard University Press: Cambridge, MA, USA, 2001; pp. 49–65. [Google Scholar]
  12. Rooney, D.; Boud, D. Toward a Pedagogy for Professional Noticing: Learning through Observation. Vocat. Learn. 2019, 12, 441–457. [Google Scholar] [CrossRef]
  13. Carpenter, T.P.; Fennema, E.; Franke, M.L. Cognitively Guided Instruction: A Knowledge Base for Reform in Primary Mathematics Instruction. Elem. Sch. J. 1996, 97, 3–20. Available online: http://www.jstor.org/stable/1001789 (accessed on 12 January 2022). [CrossRef]
  14. Fennema, E.; Carpenter, T.P.; Franke, M.L.; Levi, L.; Jacobs, V.R.; Empson, S.B. A Longitudinal Study of Learning to Use Children’s Thinking in Mathematics Instruction. J. Res. Math. Educ. 1996, 27, 403–434. Available online: http://www.jstor.org/stable/749875 (accessed on 5 January 2022). [CrossRef]
  15. Matos, J.F.; Power, A.; Sztajn, P.; Ejersbø, L.; Hovermill, J. The Professional Education and Development of Teachers of Mathematics. In Mathematics Teachers’ Professional Development: Processes of Learning in and from Practice; Springer: Boston, MA, USA, 2009; pp. 167–183. [Google Scholar]
  16. Jacobs, V.R.; Lamb, L.L.C.; Philipp, R.A. Professional Noticing of Children’s Mathematical Thinking. J. Res. Math. Educ. 2010, 41, 169–202. Available online: http://www.jstor.org/stable/20720130 (accessed on 16 March 2022). [CrossRef]
  17. van Es, E.A.; Sherin, M.G. Expanding on prior conceptualizations of teacher noticing. ZDM 2021, 53, 17–27. [Google Scholar] [CrossRef]
  18. Mansfield, J. The Search for Pedagogical Equilibrium. Developing a Professional Knowledge of Teacher Practice; Routledge: Abingdon, UK, 2019; pp. 9–24. [Google Scholar]
  19. Rosebery, A.S.; Warren, B.; Tucker-Raymond, E. Developing interpretive power in science teaching. J. Res. Sci. Teach. 2016, 53, 1571–1600. Available online: https://onlinelibrary.wiley.com/doi/10.1002/tea.21267 (accessed on 22 November 2022). [CrossRef]
  20. Cobb, P.; Zhao, Q.; Dean, C. Conducting design experiments to support teachers’ learning: A reflection from the field. J. Learn. Sci. 2009, 18, 165–199. [Google Scholar] [CrossRef]
  21. Goh, T.L.; Hannon, J.C.; Webster, C.A.; Podlog, L. Classroom teachers’ experiences implementing a movement integration program: Barriers, facilitators, and continuance. Teach. Teach. Educ. 2017, 66, 88–95. Available online: https://www.sciencedirect.com/science/article/pii/S0742051X17305929 (accessed on 16 December 2021). [CrossRef]
  22. Adamson, B.; Walker, E. Messy collaboration: Learning from a lesson study. Teach. Teach. Educ. 2011, 27, 29–36. [Google Scholar] [CrossRef]
  23. Kuusisaari, H. Teachers’ collaborative learning—Development of teaching in group discussions. Teach. Teach. 2013, 19, 50–62. [Google Scholar] [CrossRef]
  24. Rolando, L.G.R.; Salvador, D.F.; Silva Souza, A.H.; Luz, M.R.M.P. Learning with their peers: Using a virtual learning community to improve an in-service biology teacher education program in Brazil. Teach. Teach. Educ. 2014, 44, 44–55. [Google Scholar] [CrossRef]
  25. Coburn, C.E. Collective sensemaking about reading: How teachers mediate reading policy in their professional communities. Educ. Eval. Policy Anal. 2001, 23, 145–170. Available online: http://journals.sagepub.com/doi/10.3102/01623737023002145 (accessed on 17 May 2022). [CrossRef]
  26. Kelly, P. What is teacher learning? A socio-cultural perspective. Oxf. Rev. Educ. 2006, 32, 505–519. [Google Scholar] [CrossRef]
  27. Hatt, B. Smartness as a Cultural Practice in Schools. Am. Educ. Res. J. 2012, 49, 438–460. [Google Scholar] [CrossRef]
  28. Shabtay, G.; Heyd-Metzuyanim, E. Examining teachers’ discourse on students’ struggle through figured worlds. In Proceedings of the 42nd Conference of the International Group for the Psychology of Mathematics Education, Umeå, Sweden, 3–8 July 2018; pp. 155–162. [Google Scholar]
  29. Gomez, M.L. Examining Discourses of an Aspiring Teacher of Color in the Figured World of Schooling. Teach. Educ. Q. 2014, 41, 35–58. Available online: http://www.jstor.org/stable/teaceducquar.41.1.45 (accessed on 7 May 2024).
  30. Esmonde, I.; Langer-Osuna, J.M. Power in numbers: Student participation in mathematical discussions in heterogeneous spaces. J. Res. Math. Educ. 2013, 44, 288–315. [Google Scholar] [CrossRef]
  31. Wager, A.A.; Foote, M.Q. Locating praxis for equity in mathematics: Lessons from and for professional development. J. Teach. Educ. 2012, 64, 22–34. Available online: http://jte.sagepub.com/content/64/1/22 (accessed on 15 February 2019). [CrossRef]
  32. Cone, L. The platform classroom: Troubling student configurations in a Danish primary school. Learn. Media Technol. 2021, 29, 52–64. [Google Scholar] [CrossRef]
  33. Kerssens, N.; van Dijck, J. Governed by Edtech? Valuing pedagogical autonomy in a platform society. Harv. Educ. Rev. 2022, 92, 284–303. [Google Scholar] [CrossRef]
  34. Kazemi, E.; Gibbons, L.K.; Lomax, K.; Franke, M.L. Listening to and learning from student thinking. Teach. Child. Math. 2016, 23, 182–190. [Google Scholar]
  35. Learning from Children: Learning from Our Most Powerful Teachers: Children and One Another. Available online: https://learningfromchildren.org (accessed on 1 February 2022).
  36. National Governors Association Center for Best Practices & Council of Chief State School Officers. Common Core State Standards for Mathematics; NCTM: Washington, DC, USA, 2010. [Google Scholar]
  37. Benedict-Chambers, A.; Aram, R. Tools for teacher noticing: Helping preservice teachers notice and analyze student thinking and scientific practice use. J. Sci. Teach. Educ. 2017, 28, 294–318. [Google Scholar] [CrossRef]
  38. Corbin, J.; Strauss, A. Strategies for qualitative data analysis. In Basics of Qualitative Research: Techniques and Procedures for Developing Grounded Theory, 3rd ed.; SAGE Publications, Inc.: Thousand Oaks, CA, USA, 2008; pp. 65–86. [Google Scholar] [CrossRef]
  39. Kavanagh, S.S.; Bernhard, T.; Gibbons, L.K. ‘Someone else in the universe is trying to teach you’: Teachers’ experiences with platformized instruction. Learn. Media Technol. 2024, 1–17. [Google Scholar] [CrossRef]
  40. Knapp, N.F.; Peterson, P.L. Teachers’ Interpretations of “CGI” after Four Years: Meanings and Practices. J. Res. Math. Educ. 1995, 26, 40–65. Available online: http://www.jstor.org/stable/749227 (accessed on 4 January 2022).
  41. Rainio, A.P. Developing the classroom as a “figured world”. J. Educ. Chang. 2008, 9, 357–364. [Google Scholar] [CrossRef]
  42. Gibbons, L.; Wilhelm, A.; Marianno, L.; Pinilla, R. Responsive research and professional learning: Coming to know adults and children in a new partnership. In Proceedings of the 44th Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Nashville, TN, USA, 18 November 2022. [Google Scholar]
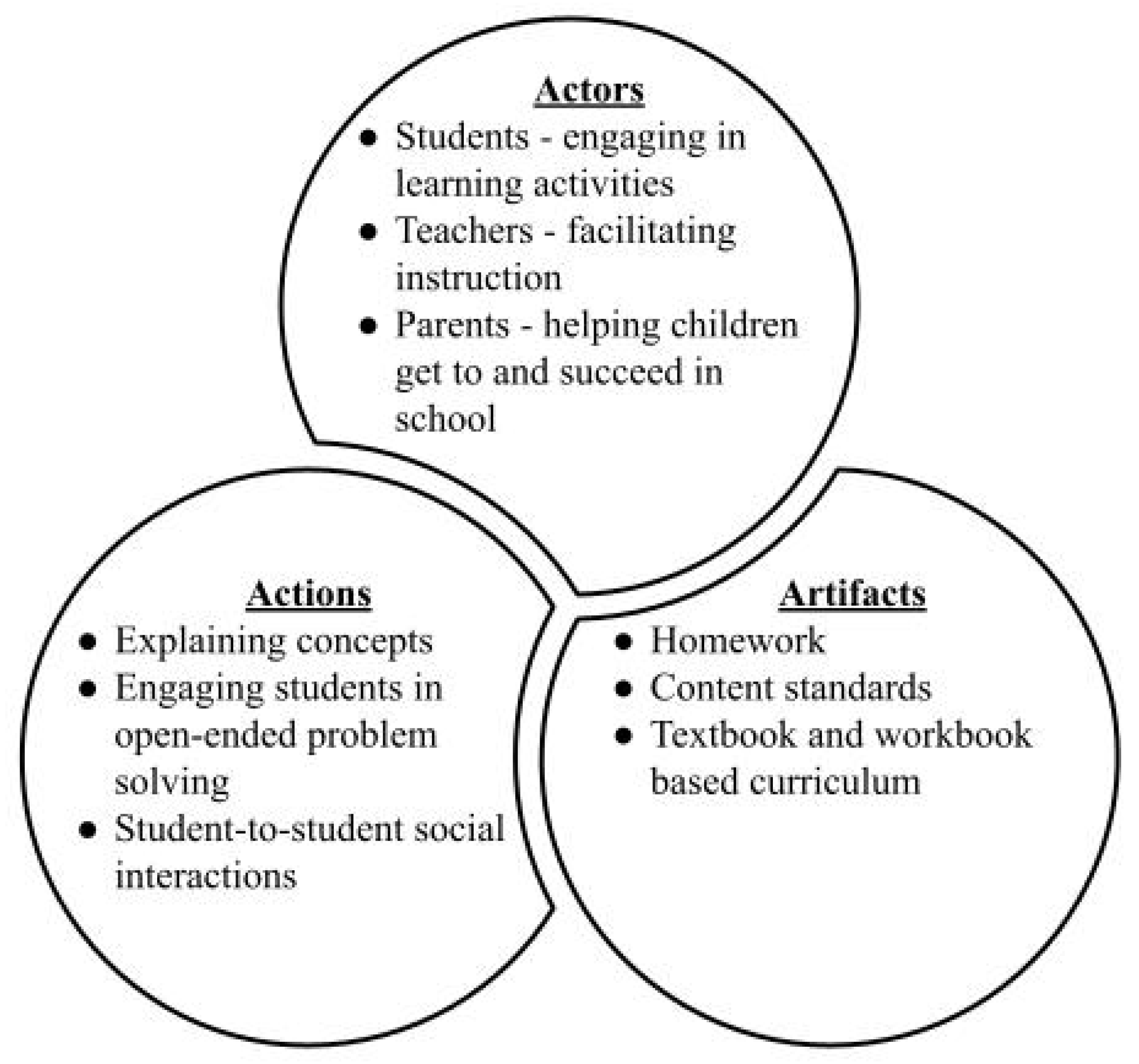
Education 14 00859 g001
Figure 1. Actors, actions, and artifacts relevant to the figured world of schooling.
Figure 1. Actors, actions, and artifacts relevant to the figured world of schooling.
Education 14 00859 g001
Education 14 00859 g002
Figure 2. Sample Cognitive Interview Report.
Figure 2. Sample Cognitive Interview Report.
Education 14 00859 g002
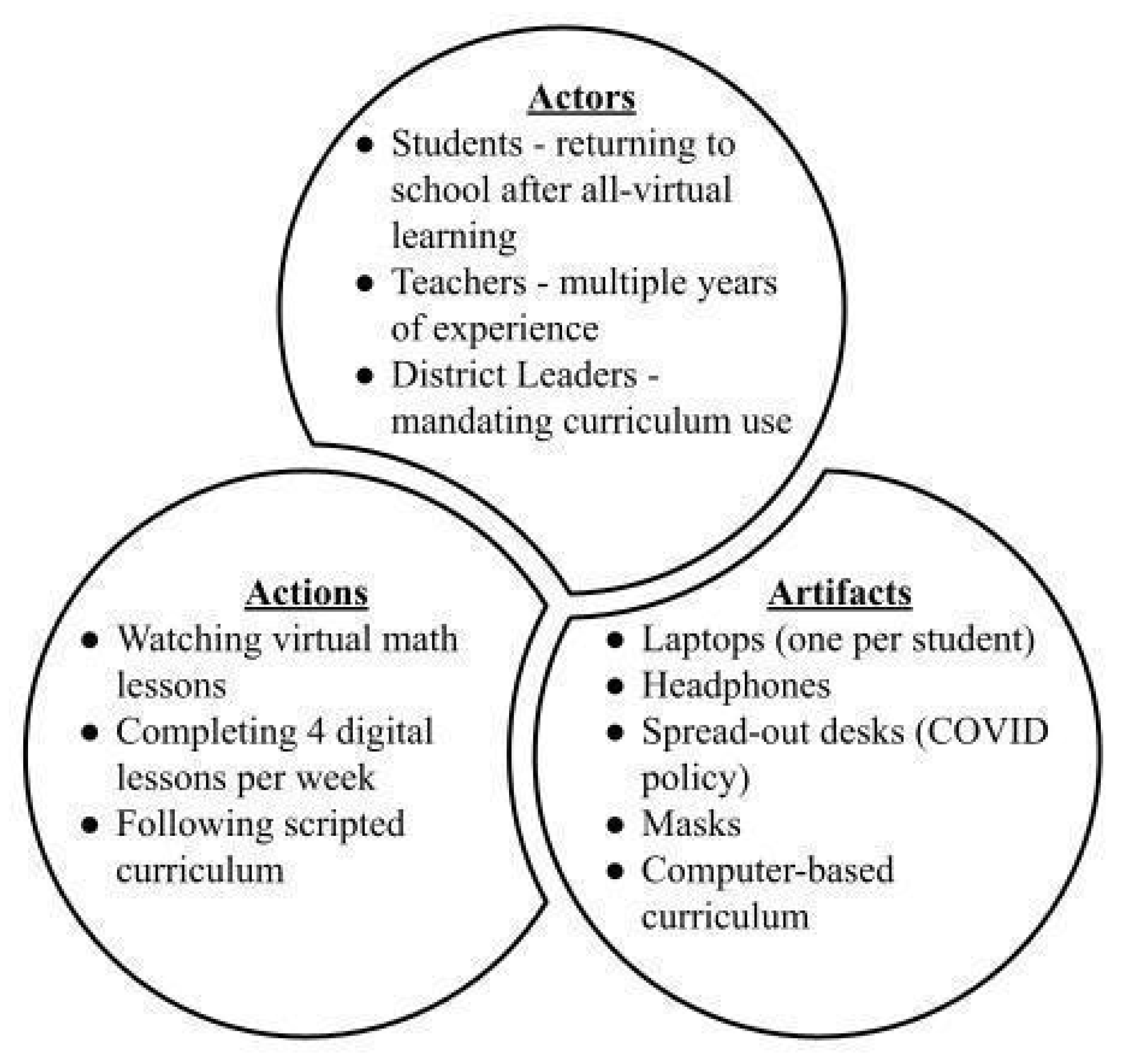
Education 14 00859 g003
Figure 3. Actors, actions, and artifacts relevant to the participants’ figured world.
Figure 3. Actors, actions, and artifacts relevant to the participants’ figured world.
Education 14 00859 g003
Table 1. Sample tasks given in cognitive interviews.
Table 1. Sample tasks given in cognitive interviews.
Type of TaskTaskPossible Solution Strategies
Join Result Unknown (K,1)Keisha had 6 seashells. Her friend gave her 7 seashells. How many seashells does she have in all?Did not attempt
Invalid
Direct Model
Counting On
Derived fact
Recall
Join Change Unknown (2–5)Jayden had 38 a stickers. His friend gave him some more stickers. Now Jayden has 81 a stickers. How many stickers did his friend give him?Did not attempt
Invalid
Direct Model by 1 s
Direct Model by 10 s
Count on by 1 s
Count on by 10 s
Invented Algorithm: Compensating
Invented Algorithm: Incremental
Only Used Standard Algorithm
Other
a Quantities were changed for each grade level (grade 2: 38, 81; grades 3–5: 38, 111).
Table 2. Themes and descriptions.
Table 2. Themes and descriptions.
CategoryThemesDescriptionFigured World Element
NoticingCorrectnessFocused on what percentage of students answered the problems accuratelyAction
Student CapabilityIdentifying what students can and cannot do yet based on strategies used in the reportsAction
ConstraintStudent CapabilityPerceptions of what students can and cannot do, not attached to findings in the reportsAction
TechnologyHow students’ use of technology impacts how they engage and respond to learningArtifact
CurriculumUse of structured materials for teaching in how teachers must instructArtifact
TimeTime needed to teach and learn mathematics materialAction
Logistics/ManagementManaging the materials and space for student use to support mathematical learningAction
Top-down ExpectationsExpectations pertaining to daily procedures and operations of the classroom set by administrationActor
PandemicClassroom structures, routines, and strategies developed as a response to the pandemicAction
PossibilityTools and StrategiesAdditional instruments and techniques used to support student thinking to make sense of problemsArtifacts
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Prough, S.; Webster, A.; Gibbons, L.K. The Context and Development of Teachers’ Collective Reflections on Student Data. Educ. Sci. 2024, 14, 859. https://doi.org/10.3390/educsci14080859

AMA Style

Prough S, Webster A, Gibbons LK. The Context and Development of Teachers’ Collective Reflections on Student Data. Education Sciences. 2024; 14(8):859. https://doi.org/10.3390/educsci14080859

Chicago/Turabian Style

Prough, Sam, Amber Webster, and Lynsey K. Gibbons. 2024. "The Context and Development of Teachers’ Collective Reflections on Student Data" Education Sciences 14, no. 8: 859. https://doi.org/10.3390/educsci14080859

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop