A Content Analysis of the Algebra Strand of Six Commercially Available U.S. High School Textbook Series
Abstract
1. Introduction
The modern point of view … especially in the reform curricula has sort of taken the position [that] the world has changed a lot …. And so they’ve accordingly transformed the way they think of introducing algebra. So for a function, classically [it] was given by a formula, y = f (x), and then you’d try to graph it, etc. And now, a function is given by a collection of data points … you want to look for some pattern in them. So it’s a kind of an homage, a bending in the direction of analysis of data and trying to fit data …. So, it leads to very different curricular trajectories and various different things that get foregrounded and backgrounded …. If you think of algebra as sort of situated on a big landscape or a big mountain … there’s sort of different trails around the territory but they’re not highly connected with each other. And in particular, the set of skills and knowledge that they cultivate by the time kids leave high school are very different, depending on which of these approaches you take …. The curriculum people sort of took the liberty to redefine algebra. Basically in terms of curriculum, they’re actually talking about a different subject, to some extent, that doesn’t merge with classical algebra until probably post high school …. So instead of clarifying the language, and explain what the two things are that people are engaged in, they’re using the same name and doing a kind of colonial war about which one has the rightful claim to the territory …. It’s not at all clear that there’s a well-established consensus about which kind of treatment is most appropriate for all students.
- What algebra content, including the breadth, sequence, and depth of topics covered, do students have opportunities to learn?
- What sets of behaviors are expected of students as they engage with the content?
- To what extent are problems set in real-world contexts, and to what extent are tools (technology and manipulatives) required to solve problems?
1.1. Centrality of Algebra in the School Curriculum
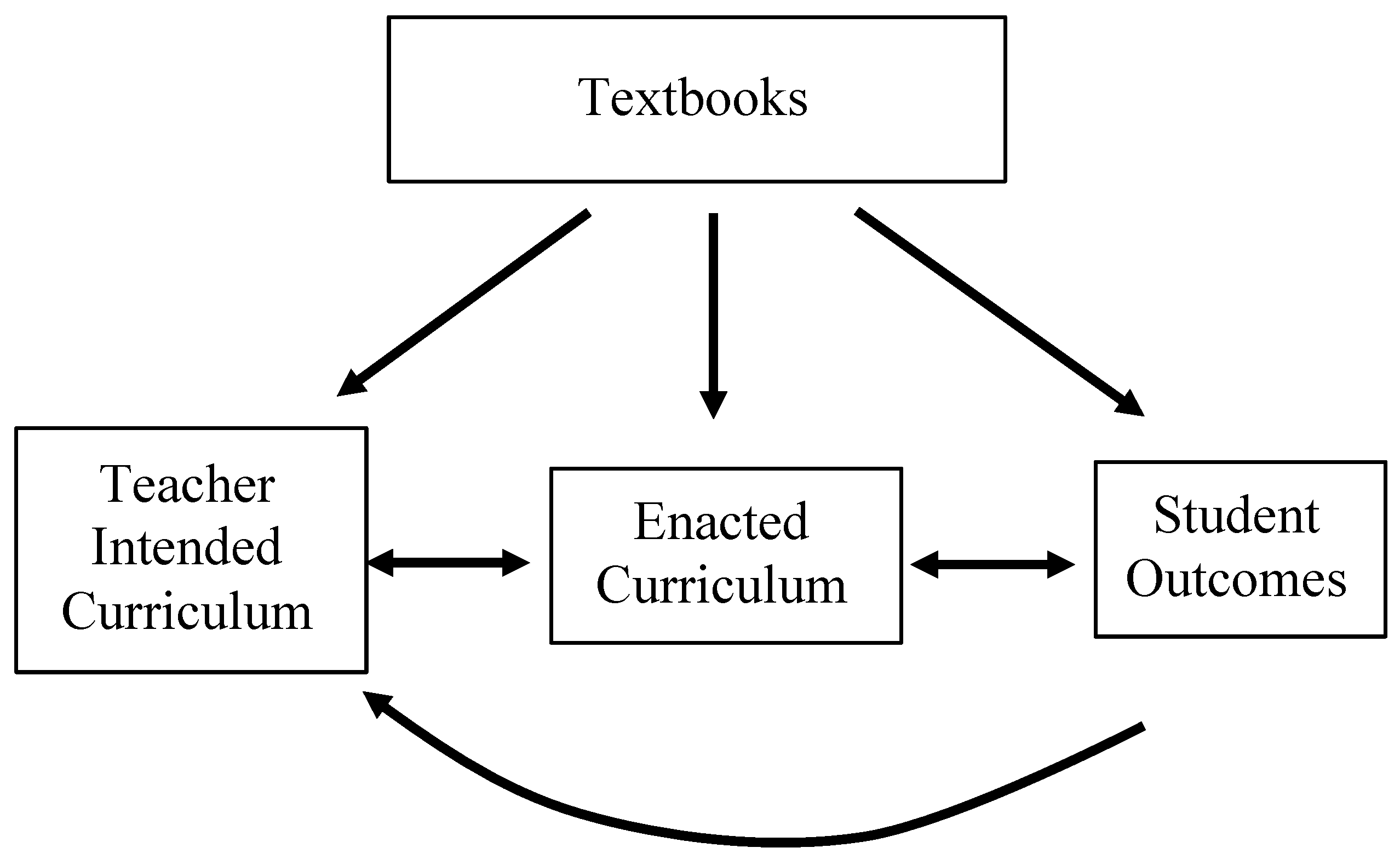
1.2. Textbooks as Dominant Forces in the School Mathematics Curriculum
1.3. Analyses of the Algebra Strand in High School Textbooks
2. Materials and Methods
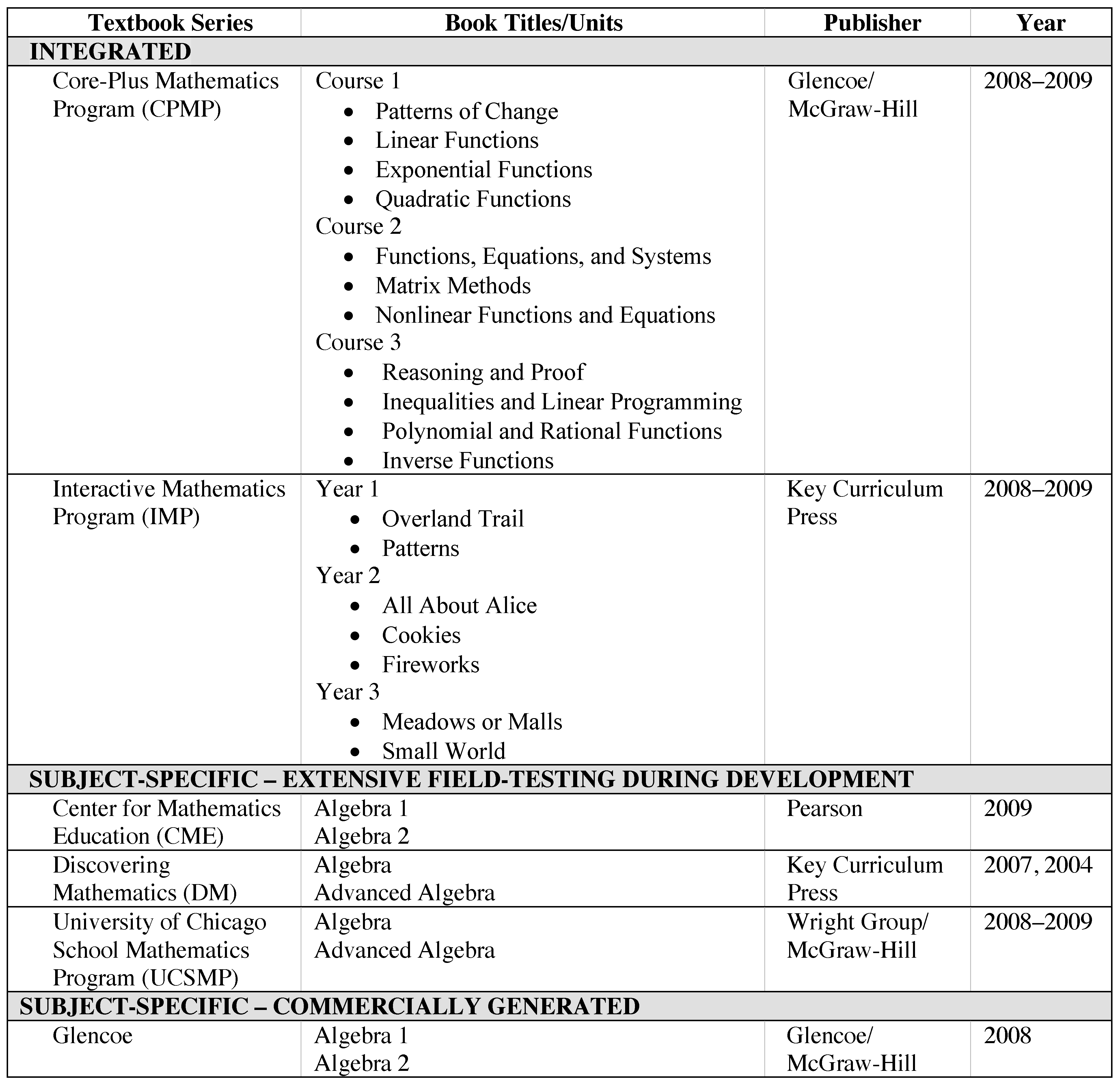
2.1. Textbooks and Unit of Analysis
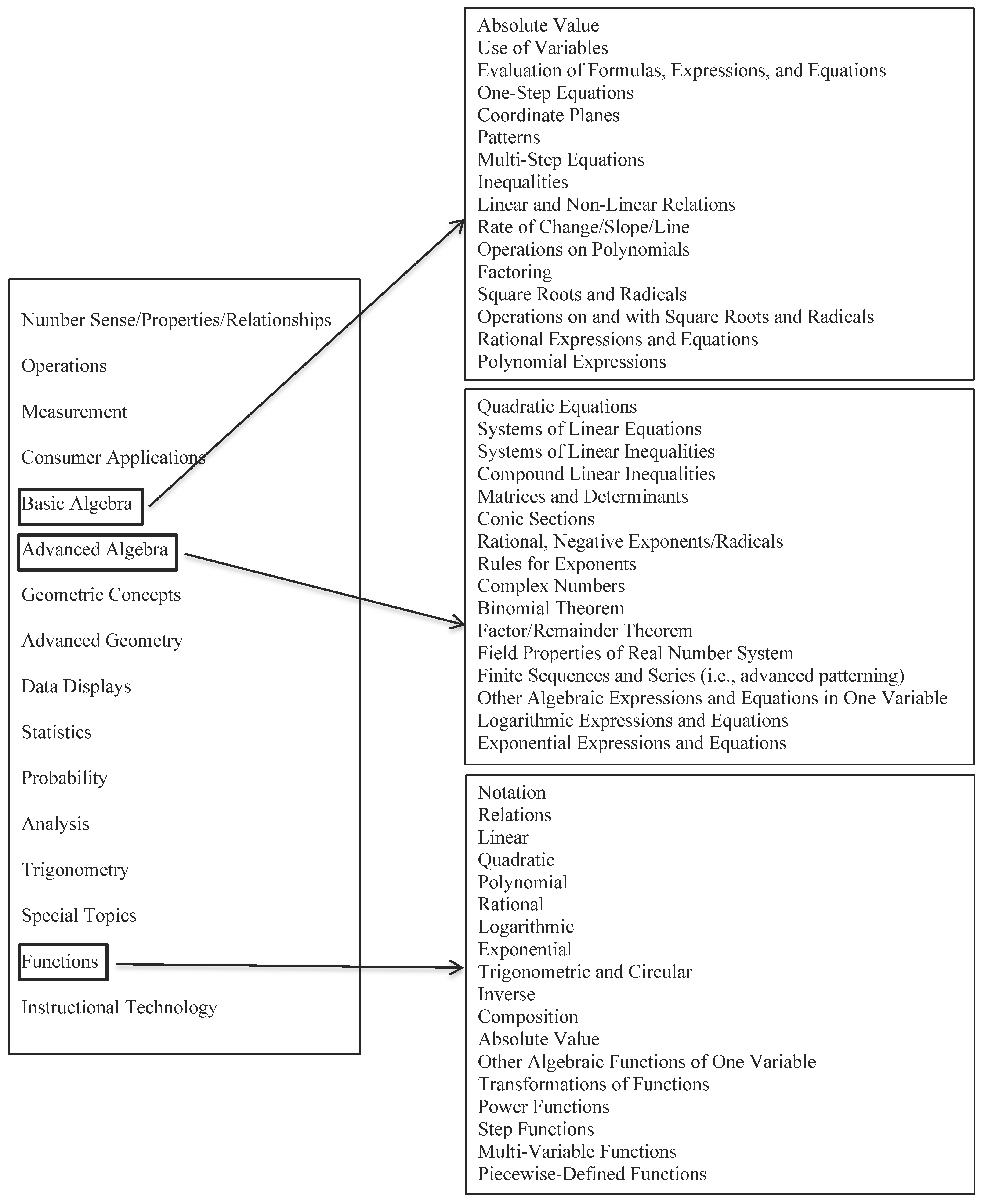
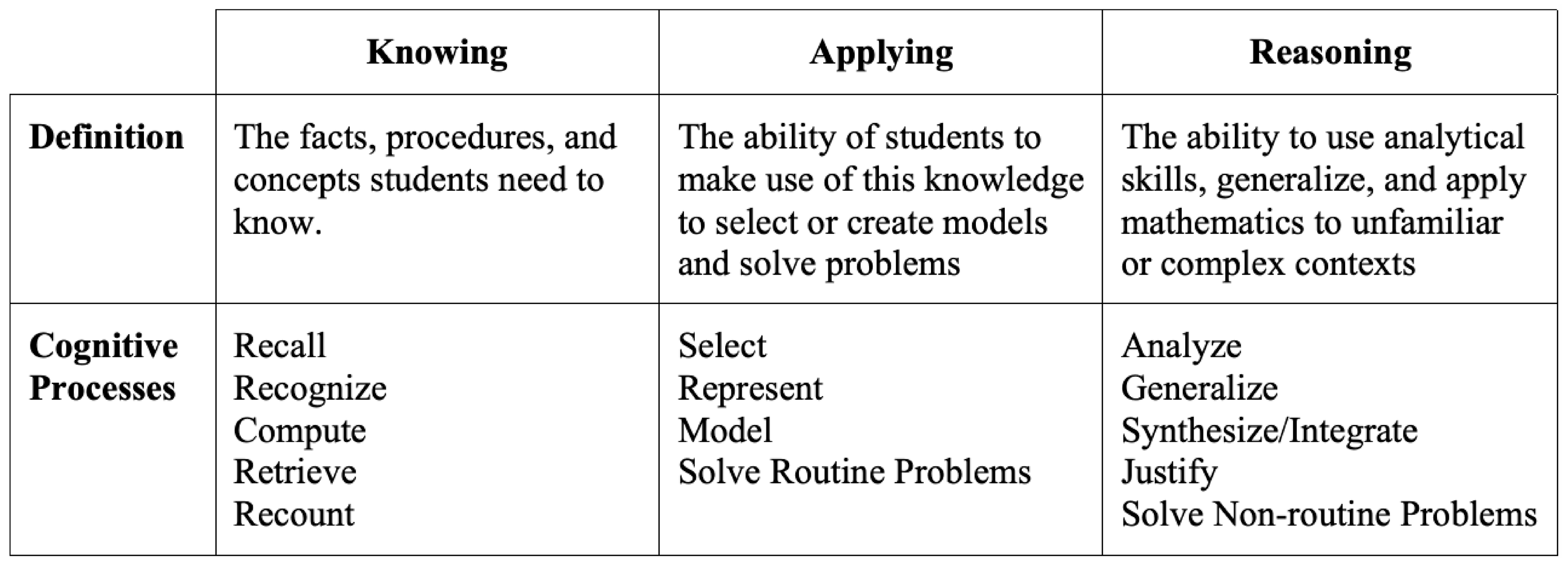
2.2. Analytic Frameworks
2.3. Coding Procedure
3. Results
3.1. Findings from the Content Analysis
3.1.1. Number of Items Coded and Emphasis on Algebra, Advanced Algebra, and Functions
3.1.2. Most Frequently Used Content Codes
3.1.3. Density, Distribution, and Sequencing of Content
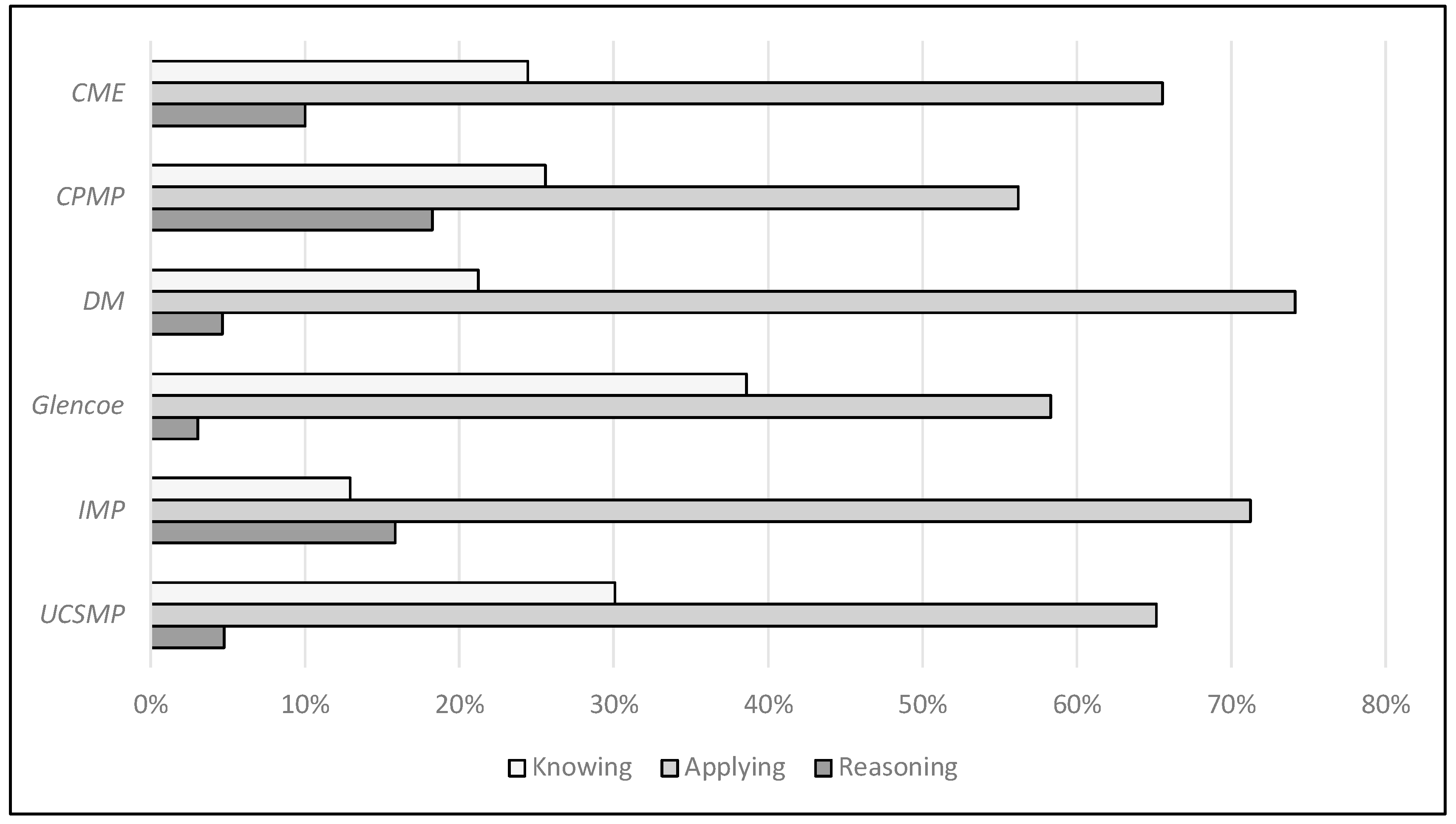
3.2. Findings from the Cognitive Behavior Analysis
3.3. Other Findings
4. Feedback from Textbook Series Authors
4.1. Textbook Series Authors’ Views on the Coding Taxonomies
[I] did the best [I] could under the constraints of the allowable categories, but I have serious concerns about the categories themselves …. I found the categories quite unsatisfactory for describing the design of [my textbook] (or any curriculum, for that matter) … so many of the problems [that I coded in my textbook] are aimed at helping students develop the habit of abstracting a process from repeated numerical calculations. So, while a suite of problems may all look like computations, they are actually building to a punchline.
Given the tool used, K-12 Math Taxonomy, the codes applied were as accurate as they could be. However, this tool seems too simple and limiting …. For example, One-Step Equations (solving one-step linear equations OR setting up and solving one-step equations) are coded as if these two types of tasks are at the same level of complexity. Most students can solve questions like 5x − 3 = 7. Students can do the naked algebra. What they can’t do is generate this simple type of equation from a situation. Solving an equation is not the same as setting up and solving the equation. If that were true, most students wouldn’t dread the so-called word problems in a traditional algebra textbook. Another concern is that the codes and the domains can not and do not reflect the complexity of the task. For example [at this point the author provides a specific example from her/his textbook] this is the correct coding but this particular problem takes hours to solve and requires sophisticated ways of organizing the data, none of which you can pick up from a code and a domain. I realize … the categories of cognitive processes are supposed to help differentiate between knowing, applying, and reasoning with algebra. However, these two sets of tools can only give a glimpse of what the authors’ goals and purposes are for students [sic] understanding and learning of algebra.
One thorny issue here is that ostensibly routine curricular content can be taught richly in a way that fosters cognitive complexity and deep understanding, and, on the other hand, ostensibly rich curricular content can be taught in a way that routinizes it and makes it cognitively shallow. For example, we have had well-meaning teachers break down the [problems] into small-step worksheets so that they are easier for students (and teachers) but this then short circuits the thinking process and detracts from the deep-understanding goals. This can make the coding problematic …. Related to this is the issue of how much scaffolding is provided, how it’s provided, and when. This is an adjustment that is made on the fly by good teachers in the classroom, but is very difficult to craft when writing a textbook. And it can make the coding problematic …. [In our textbook we] state the problem in a more open-ended way in the stem, then provide “hints”, which are given as parts a-d of the problem. There are typically notes in the Teachers Edition that point out the options of less or more scaffolding. Of course, the students and teachers almost always go straight for the hints, parts a-d. However, if students did the problem in the less-scaffolded way, then the cognitive code becomes R, rather than K and A.
4.2. Textbook Series Authors’ Views on the Methodology
It is very difficult to take an integrated curriculum where algebra is learned, developed, and used as a language over four years and compare it to a traditional algebra book. You would have to look at every problem in every unit [in an integrated program] over all four years to see all the ways algebra is learned and used.
I can understand the concept of NOT coding the worked examples in the text, but in each lesson of [my textbook] you will often find open-ended questions that are there to at least prompt some thinking, and at best open a class discussion …. These questions can pop up anywhere including in the “solution” to a worked example.
The inclusion of examples from the narrative of a lesson as coding items is a good idea. It is more reflective of the intent of [my] textbook, since the … author assumes a student would read the lesson at some point.
It might be interesting to triangulate results from coding the student text, the teacher edition, and the provided assessment resources. What sort of content and cognitive behaviors are emphasized in the teacher edition? In the quizzes and tests, and other assessment resources? How do the expectations in the student edition, teacher edition, and assessments compare?
What make[s] one text different from another is the developed progression of thought as much as the topics covered and depth of each. So content and cognitive behavior I would say are complete and fairly accurate. But a good text also must put these pieces in an order that makes sense to students so that ideas accumulate to reinforce one-another and connect between. How can this be measured or judged?
I don’t think this process will capture the essence of the book’s content and cognitive behaviors of students as they engage with the content… The way you tackle a problem in [my textbook], [students are] taught to not take everything at face value. You need to understand why pi is pi, or why this formula is this formula, or why we are solving this problem this way. I’m not sure coding textbooks can capture this level of difference between textbooks. It is hard to capture how students are asked to create their own problems and discover relationships and generalizations.
Coding a textbook cannot reflect the essence of the book’s content. How does one capture essence by coding? Any coding process is simply a compilation of check marks or instances of the inclusion of a content topic. Essence is much more encompassing than a quantity of check marks.
4.3. Advice and Other Comments from Textbook Series Authors
I think that there are very different beliefs about what algebra is, what is important for students to know and be able to do in algebra, what learning is, and what the purpose of school is. If you think the learning of algebra is primarily to pass on a certain body of mathematical knowledge, you develop a certain type of textbook. If you believe that students should learn to think and reason mathematically, and use algebra where appropriate, you develop a different type of textbook.
5. Discussion
5.1. Limitations of This Study
- “So while a suite of problems may all look like computations, they are actually building to a punchline;” and
- “What make[s] one text different from another is the developed progression of thought as much as the topics covered and depth of each … a good text also must put these pieces in an order that makes sense to students so that ideas accumulate to reinforce one-another and connect between.”
5.2. Constructing Mosaics: Ideas for Further Investigations
5.3. Curricular Choices and Opportunity to Learn
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
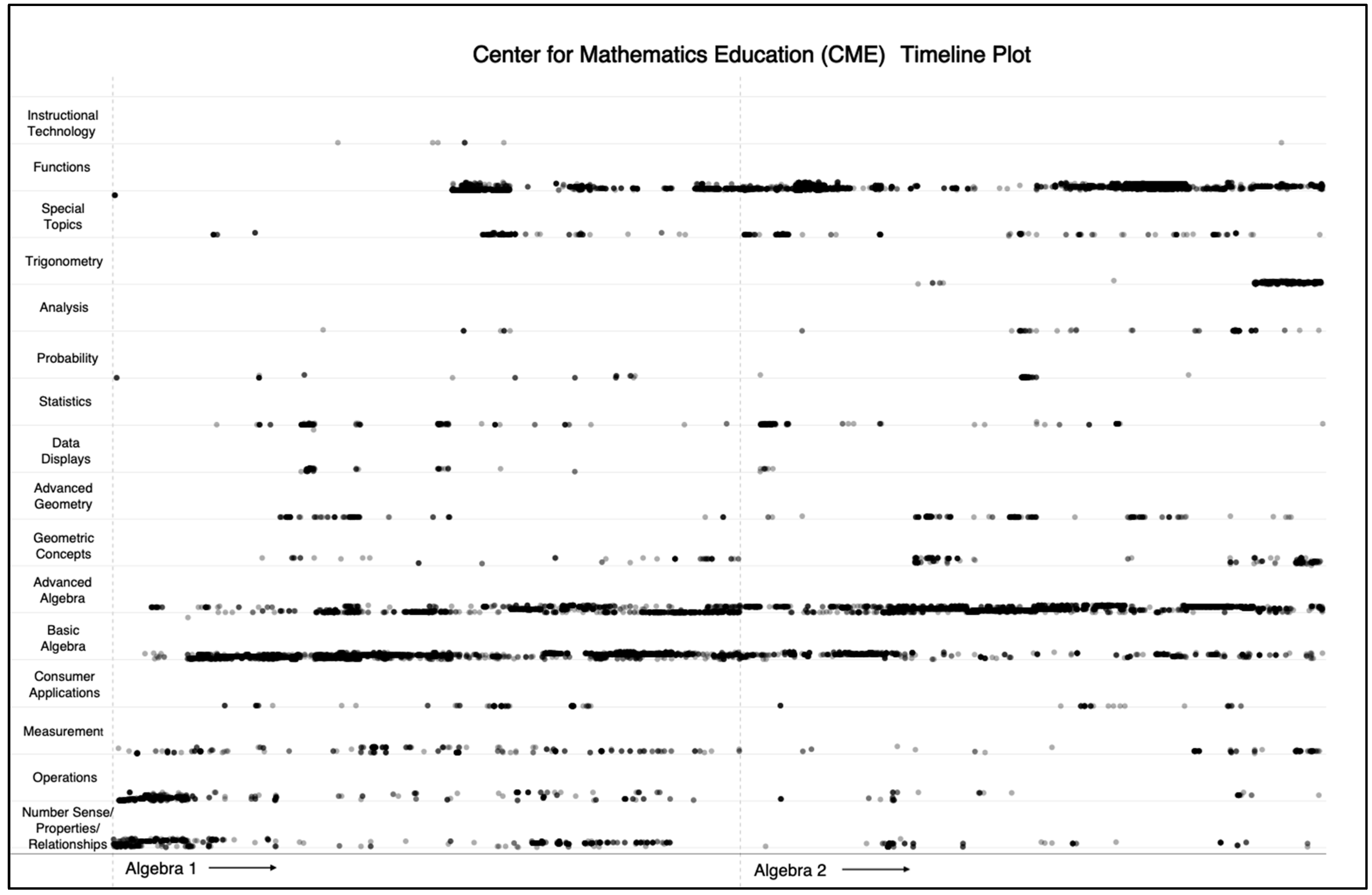


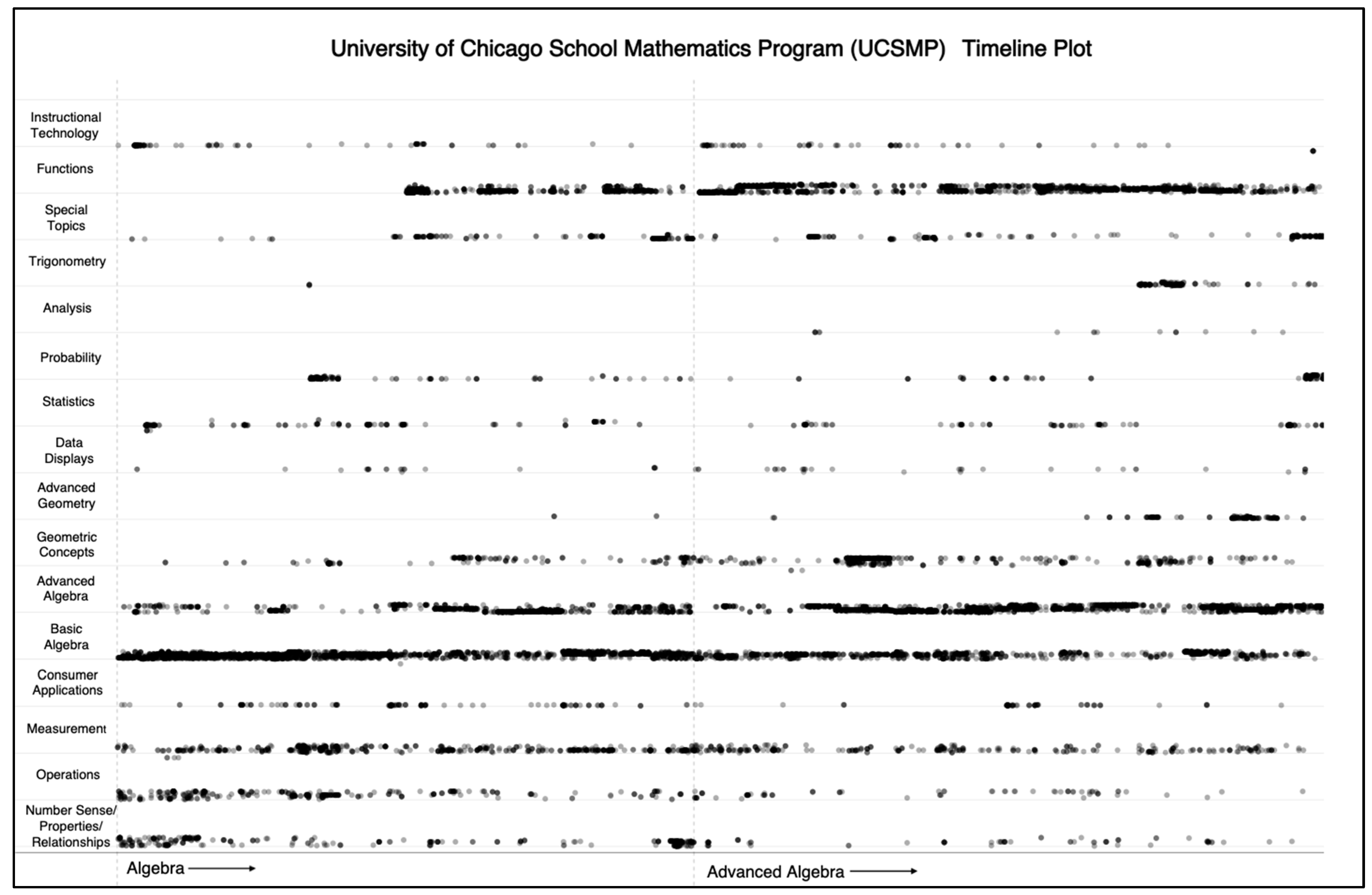
Appendix B
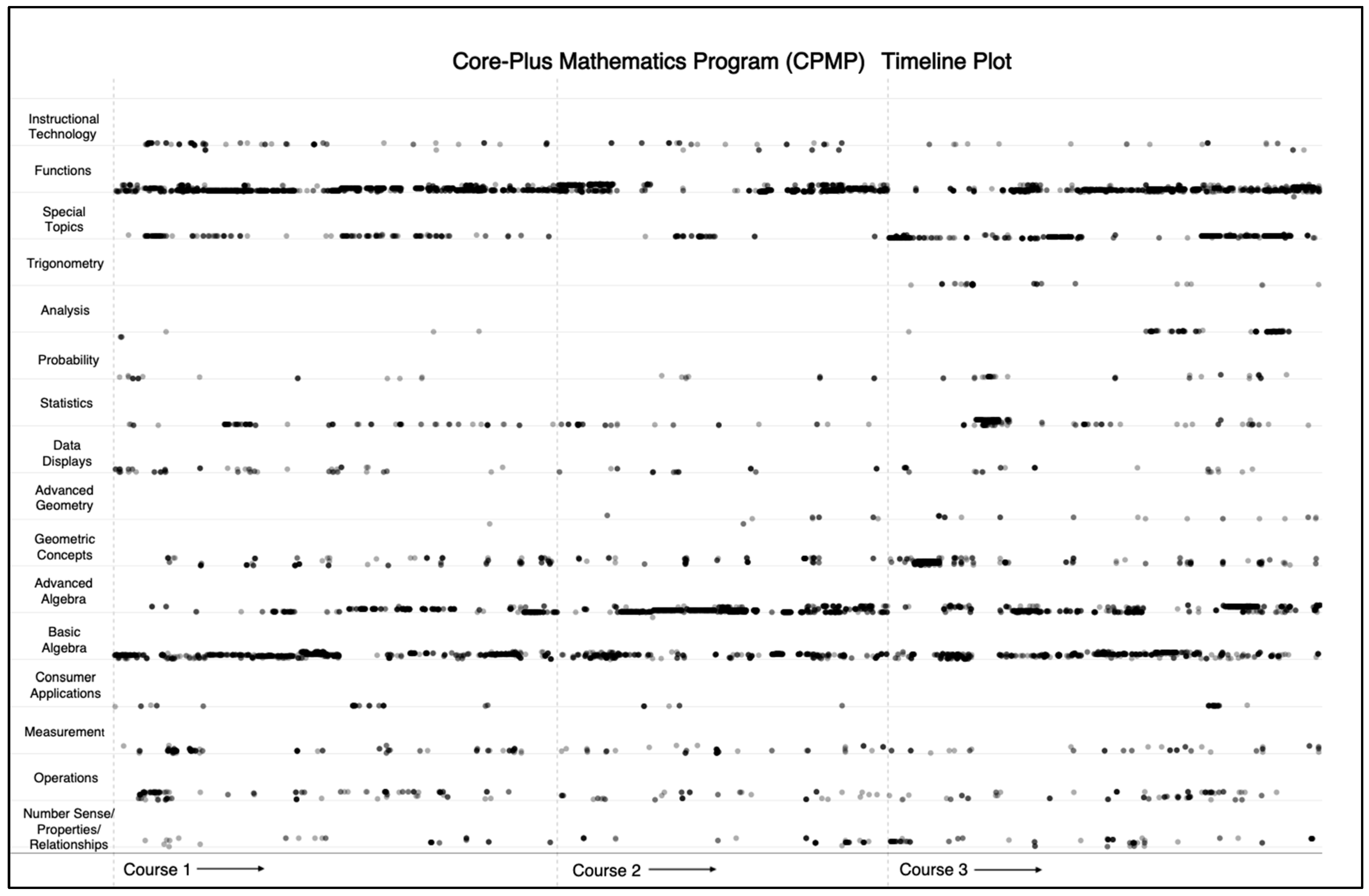
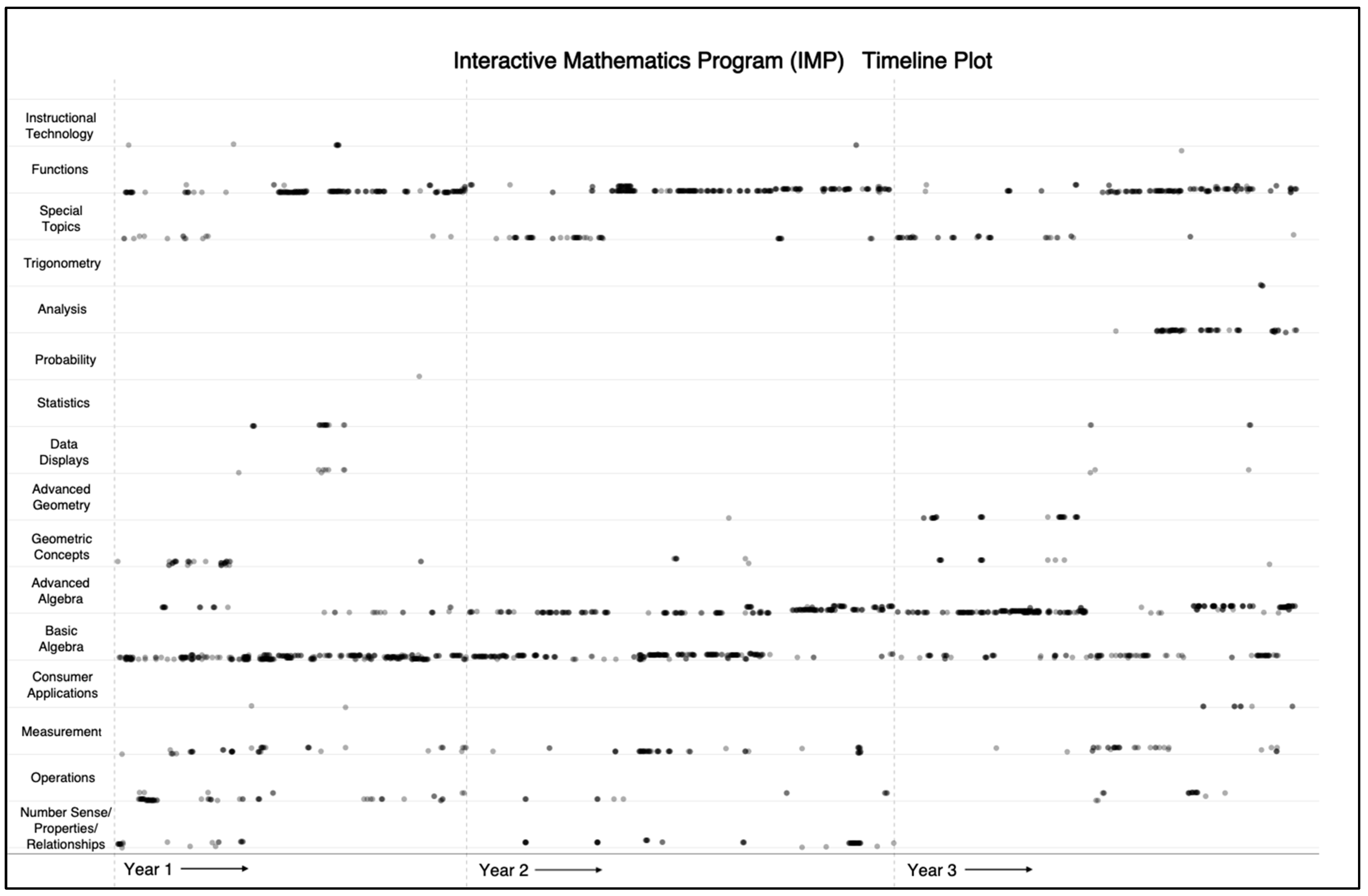
References
- Kendal, M.; Stacey, K. Algebra: A world of difference. In The Future of the Teaching and Learning of Algebra: The 12th ICMI Study; Stacey, K., Chick, H., Kendal, M., Eds.; Springer: Dordrecht, The Netherlands, 2004; pp. 329–346. [Google Scholar] [CrossRef]
- Yerushalmy, M.; Chazan, D. Flux in school algebra: Curricular change, graphing technology, and research on student learning and teacher knowledge. In Handbook of International Research in Mathematics Education; English, L., Ed.; Lawrence Erlbaum: Mahwah, NJ, USA, 2002; pp. 725–755. [Google Scholar]
- Kieran, C. Learning and teaching of algebra at the middle school through college levels: Building meaning for symbols and their manipulation. In Second Handbook of Research on Mathematics Teaching and Learning; Lester, F.K., Jr., Ed.; Information Age Publishing: Charlotte, NC, USA, 2007; pp. 707–762. [Google Scholar]
- Bass, H.; (University of Michigan, Ann Arbor, MI, USA). Personal communication, 2008.
- Begle, E.G. Some lessons learned by SMSG. Math. Teacher 1973, 66, 207–214. [Google Scholar] [CrossRef]
- Floden, R.E. The measurement of opportunity to learn. In Methodological Advances in Cross-National Surveys of Educational Achievement; Porter, A.C., Gamoran, A., Eds.; National Academies Press: Washington, DC, USA, 2002; pp. 231–236. [Google Scholar]
- Robitaille, D.F.; Travers, K.J. International studies of achievement in mathematics. In Handbook of Research on Mathematics Teaching and Learning; Grouws, D.A., Ed.; National Council of Teachers of Mathematics: Reston, VA, USA, 1992; pp. 687–709. [Google Scholar]
- Schmidt, W.H.; McKnight, C.C.; Raizen, S.A. A Splintered Vision: An Investigation of U.S. Science and Mathematics Education; Kluwer: New York, NY, USA, 1997. [Google Scholar] [CrossRef]
- Thompson, D.R.; Senk, S.L.; Johnson, G.J. Opportunities to learn reasoning and proof in high school mathematics textbooks. J. Res. Math. Educ. 2012, 43, 253–295. [Google Scholar] [CrossRef]
- Usiskin, Z. We need another revolution in secondary school mathematics. In The Secondary School Mathematics Curriculum: 1985 Yearbook of the National Council of Teachers of Mathematics; Hirsch, C.R., Zweng, M.J., Eds.; National Council of Teachers of Mathematics: Reston, VA, USA, 1985; pp. 1–21. [Google Scholar]
- Valverde, G.A.; Bianchi, L.J.; Wolfe, R.G.; Schmidt, W.H.; Houang, R.T. According to the Book: Using TIMSS to Investigate the Translation of Policy Into Practice Through the World of Textbooks; Kluwer: New York, NY, USA, 2002. [Google Scholar] [CrossRef]
- National Governors Association Center for Best Practices & Council of Chief State School Officers [NGA & CCSSO]. Common Core State Standards for Mathematics; NGA & CCSSO: Washington, DC, USA, 2010. [Google Scholar]
- Gamoran, A.; Hannigan, E.C. Algebra for everyone? Benefits of college-preparatory mathematics for students with diverse abilities in early secondary school. Educ. Eval. Policy Anal. 2000, 22, 241–254. [Google Scholar] [CrossRef]
- Moses, R.P.; Cobb, C.E., Jr. Radical Equations: Math Literacy and Civil Rights; Beacon Press: Boston, MA, USA, 2001. [Google Scholar]
- Katz, V.J. (Ed.) Algebra: Gateway to a Technological Future; Mathematical Association of America: Washington, DC, USA, 2007. [Google Scholar]
- Committee on Prospering in the Global Economy of the 21st Century. Rising Above the Gathering Storm: Energizing and Employing America for a Brighter Economic Future; National Academies Press: Washington, DC, USA, 2007. [Google Scholar] [CrossRef]
- RAND Mathematics Study Panel. Mathematical Proficiency for All Students: Toward a Strategic Research and Development Program in Mathematics Education; RAND: Santa Monica, CA, USA, 2003. [Google Scholar] [CrossRef]
- Fan, L.; Kaeley, G. The influence of textbooks on teaching strategies: An empirical study. Mid-W. Educ. Res. 2000, 13, 2–9. [Google Scholar]
- Huntley, M.A.; Suurtamm, C.; Thompson, D.R. Transcending boundaries: What have we learned? In International Perspectives on Mathematics Curriculum; Thompson, D.R., Huntley, M.A., Suurtamm, C., Eds.; Information Age Publishing: Charlotte, NC, USA, 2018; pp. 227–237. [Google Scholar]
- Grouws, D.A.; Smith, M.S.; Sztajn, P. The preparation and teaching practices of United States mathematics teachers: Grades 4 and 8. In Results and Interpretations of the 1990–2000 Mathematics Assessments of the National Assessment of Educational Progress; Kloosterman, P., Lester, F.K., Jr., Eds.; National Council of Teachers of Mathematics: Reston, VA, USA, 2004; pp. 221–267. [Google Scholar]
- Banilower, E.R.; Smith, P.S.; Malzahn, K.A.; Plumley, C.L.; Gordon, E.M.; Hayes, M.L. Report of the 2018 NSSME+; Horizon Research: Chapel Hill, NC, USA, 2018. [Google Scholar]
- Remillard, J.T.; Heck, D.J. Conceptualizing the curriculum enactment process in mathematics education. ZDM—Int. J. Mathe. Educ. 2014, 46, 705–718. [Google Scholar] [CrossRef]
- McKnight, C.C.; Crosswhite, F.J.; Dossey, J.A.; Kifer, E.; Swafford, J.O.; Travers, K.J.; Cooney, T.J. The Underachieving Curriculum: Assessing U.S. School Mathematics from an International Perspective; Stipes: Champaign, IL, USA, 1987. [Google Scholar]
- Schmidt, W.H.; McKnight, C.C.; Houang, R.T.; Wang, H.; Wiley, D.E.; Cogan, L.S.; Wolfe, R.G. Why Schools Matter: A Cross-National Comparison of Curriculum and Learning; Jossey-Bass: San Francisco, CA, USA, 2001. [Google Scholar]
- Baker, D.; Knipe, H.; Collins, J.; Leon, J.; Cummings, E.; Blair, C.; Gamson, D. One hundred years of elementary school mathematics in the United States: A content analysis and cognitive assessment of textbooks from 1900 to 2000. J. Res. Math. Educ. 2010, 41, 383–423. [Google Scholar] [CrossRef]
- Ball, D.L.; Feiman-Nemser, S. Using textbooks and teacher’s guides: A dilemma for beginning teachers and teacher educators. Curr. Inquiry 1988, 18, 401–423. [Google Scholar] [CrossRef]
- National Research Council [NRC]. On Evaluating Curricular Effectiveness: Judging the Quality of K-12 Mathematics Evaluations; National Academies Press: Washington, DC, USA, 2004. [CrossRef]
- Reys, B.J.; Reys, R.E.; Chávez, O. Why mathematics textbooks matter. Educ. Leadership 2004, 61, 61–66. [Google Scholar]
- Senk, S.L.; Thompson, D.R. (Eds.) Standards-Based School Mathematics Curricula: What are They? What do Students Learn? Erlbaum: Mahwah, NJ, USA, 2003. [Google Scholar] [CrossRef]
- Weiss, I.R.; Knapp, M.S.; Hollweg, K.S.; Burrill, G. Investigating the Influence of Standards: A Framework for Research in Mathematics, Science, and Technology Education; National Academies Press: Washington, DC, USA, 2002. [Google Scholar] [CrossRef]
- Woodward, A.; Elliott, D.L. Textbook use and teacher professionalism. In Textbooks and Schooling in the United States: Eighty-Ninth Yearbook of the National Society for the Study of Education, Part I; Elliott, D.L., Woodward, A., Eds.; University of Chicago Press: Chicago, IL, USA, 1990; pp. 178–193. [Google Scholar] [CrossRef]
- Fan, L. Textbook research as scientific research: Towards a common ground on issues and methods of research on mathematics textbooks. ZDM—Int. J. Mathe. Educ. 2013, 45, 765–777. [Google Scholar] [CrossRef]
- Sherman, M.F.; Walkington, C.; Howell, E. Comparison of symbol-precedence view in investigative and conventional textbooks used in algebra courses. J. Res. Math. Educ. 2016, 47, 134–146. [Google Scholar] [CrossRef]
- Nathan, M.J.; Long, S.D.; Alibali, M.W. The symbol precedence view of mathematical development: A corpus analysis of the rhetorical structure of textbooks. Disc. Proc. 2002, 33, 1–21. [Google Scholar] [CrossRef]
- Chávez, O.; Grouws, D.; Tarr, J.; Ross, D.; McNaught, M. Mathematics Curriculum Implementation and Linear Functions in Secondary Mathematics: Results from the Comparing Options in Secondary Mathematics Project [Paper Presentation]. In Proceedings of the American Educational Research Association Annual Meeting, San Diego, CA, USA,, 13–17 April 2009. [Google Scholar]
- Chávez, O.; Papick, I.; Ross, D.; Grouws, D. The Essential Role of Curricular Analyses in Comparative Studies of Mathematics Achievement: Developing “Fair” Tests [Paper Presentation]. In Proceedings of the American Educational Research Association Annual Meeting, Denver, CO, USA, 30 April–4 May 2010. [Google Scholar]
- American Association for the Advancement of Science [AAAS]. Algebra Textbooks: A Standards-Based Evaluation; American Association for the Advancement of Science: Washington, DC, USA, 1999. [Google Scholar]
- Rivers, J. Contextual Analysis of Problems in Algebra I Textbooks [Paper Presentation]. In Proceedings of the American Educational Research Association Annual Meeting, Boston, MA, USA, 16–20 April 1990. [Google Scholar]
- National Council of Teachers of Mathematics. Curriculum and Evaluation Standards for School Mathematics; National Council of Teachers of Mathematics: Reston, VA, USA, 1989. [Google Scholar]
- Brown, J.; Schiller, K.; Roey, S.; Perkins, R.; Schmidt, W.; Houang, R. Algebra 1 and Geometry Curricula: Results from the 2005 High School Transcript Mathematics Curriculum Study (Report No. NCES 2013-451); U.S. Department of Education: Washington, DC, USA, 2013.
- Adams, L.; (Univ. of WA, Seattle, WA, USA); Tung, K.K.; (Univ. of WA, Seattle, WA, USA); Warfield, V.M.; (Univ. of WA, Seattle, WA, USA); Knaub, K.; (Univ. of WA, Seattle, WA, USA); Mudavanhu, B.; (Univ. of WA, Seattle, WA, USA); Yong, D.; (Univ. of WA, Seattle, WA, USA). Middle School Mathematics Comparisons for Singapore Mathematics, Connected Mathematics Program, and Mathematics in Context (Including Comparisons with the NCTM Principles and Standards 2000), Report to the U.S. National Science Foundation [Unpublished Manuscript]. 2000.
- Senk, S.L.; Thompson, D.R.; Johnson, G.J. Reasoning and Proof in High School Textbooks From the USA [Paper Presentation]. In Proceedings of the International Congress on Mathematics Education, Monterey, Mexico, 6–13 July 2008. [Google Scholar]
- Huntley, M.A.; Terrell, M.S.; Fonger, N.L. Lessons learned in creating mosaics to portray the algebra strand of U.S. high-school textbooks. In Lessons Learned From Research on Mathematics Curriculum; Thompson, D.R., Huntley, M.A., Suurtamm, C., Eds.; Information Age Publishing: Charlotte, NC, USA, 2024; in press. [Google Scholar]
- Hirsch, C.R.; Fey, J.T.; Hart, E.W.; Schoen, H.L.; Watkins, A.E. Core-Plus Mathematics Program Courses 1–3, 2nd ed.; [Teacher Texts]; Glencoe/McGraw-Hill: New York, NY, USA, 2009. [Google Scholar]
- Fendel, D.; Resek, D.; Alper, L.; Fraser, S. Interactive Mathematics Program Year 1, 2nd ed.; [Teacher Texts]; Key Curriculum Press: Emeryville, CA, USA, 2009. [Google Scholar]
- Fendel, D.; Resek, D.; Alper, L.; Fraser, S. Interactive Mathematics Program Year 2, 2nd ed.; [Teacher Texts]; Key Curriculum Press: Emeryville, CA, USA, 2010. [Google Scholar]
- Fendel, D.; Resek, D.; Alper, L.; Fraser, S. Interactive Mathematics Program Year 3, 2nd ed.; [Teacher Texts]; Key Curriculum Press: Emeryville, CA, USA, 2011. [Google Scholar]
- Benson, J.; Cuoco, A.; D’Amato, N.A.; Erman, D.; Baccaglini-Frank, A.; Golay, A.; Gorman, J.; Harvey, B.; Harvey, W.; Hill, C.J.; et al. Center for Mathematics Education Project Algebra 1; [Teacher Text]; Pearson: Boston, MA, USA, 2009. [Google Scholar]
- Cuoco, A.; Baccaglini-Frank, A.; Benson, J.; D’Amato, N.A.; Erman, D.; Harvey, B.; Harvey, W.; Kerins, B.; Kilday, D.; Matsuura, R.; et al. Center for Mathematics Education Project Algebra 2; [Teacher Text]; Pearson: Boston, MA, USA, 2009. [Google Scholar]
- Murdock, J.; Kamischke, E.; Kamischke, E. Discovering Algebra: An Investigative Approach, 2nd ed.; [Teacher Text]; Key Curriculum Press: Emeryville, CA, USA, 2007. [Google Scholar]
- Murdock, J.; Kamischke, E.; Kamischke, E. Discovering Advanced Algebra: An Investigative Approach, 2nd ed.; [Teacher Text]; Key Curriculum Press: Emeryville, CA, USA, 2010. [Google Scholar]
- Brown, S.A.; Breunlin, R.J.; Wiltjer, M.H.; Degner, K.M.; Eddins, S.K.; Edwards, M.T.; Metcalf, N.A.; Jakucyn, N.; Usiskin, Z. University of Chicago School Mathematics Project Algebra, 3rd ed.; [Teacher Text]; Wright Group/McGraw-Hill: Chicago, IL, USA, 2008. [Google Scholar]
- Flanders, J.; Lassak, M.; Sech, J.; Eggerding, M.; Karafiol, P.J.; McMullin, L.; Weisman, N.; Usiskin, Z. University of Chicago School Mathematics Project Advanced Algebra, 3rd ed.; [Teacher Text]; Wright Group/McGraw-Hill: Chicago, IL, USA, 2010. [Google Scholar]
- Holliday, B.; Luchin, B.; Marks, D.; Day, R.; Cuevas, G.J.; Carter, J.A.; Casey, R.M.; Hayek, L.M. Algebra 1; [Teacher Text]; Glencoe/McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Holliday, B.; Luchin, B.; Marks, D.; Day, R.; Cuevas, G.J.; Carter, J.A.; Casey, R.M.; Hayek, L.M. Algebra 2; [Teacher Text]; Glencoe/McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Garden, R.A.; Lie, S.; Robitaille, D.F.; Angell, C.; Martin, M.O.; Mullis, I.V.S.; Foy, P.; Arora, A. TIMSS Advanced 2008 Assessment Frameworks; TIMSS & PIRLS International Study Center: Chestnut Hill, MA, USA, 2006. [Google Scholar]
- Wisconsin Center for Education Research [WCER]. SEC K–12 Mathematics Taxonomy; WCER: Madison, WI, USA, 2007. [Google Scholar]
- Wolfram Research, Inc. Mathematica (Version 8), [Computer software]; Wolfram Research, Inc.: Champaign, IL, USA, 2010.
- Wolfram Research, Inc. Mathematica (Version 9), [Computer software]; Wolfram Research, Inc.: Champaign, IL, USA, 2012.
- ter Braak, C.J.F.; Smilauer, P. Canoco (Version 5.0), [Computer software]; Microcomputer Power: Ithaca, NY, USA, 2012.
- Porter, A.C. Curriculum assessment. In Handbook of Complementary Methods in Education Research; Green, J.L., Camilli, G., Elmore, P.B., Eds.; Lawrence Erlbaum: Mahwah, NJ, USA, 2006; pp. 141–159. [Google Scholar]
- Cuoco, A. The case of the CME project. In Perspectives on the Design and Development of School Mathematics Curricula; Hirsch, C.R., Ed.; National Council of Teachers of Mathematics: Reston, VA, USA, 2007; pp. 119–127. [Google Scholar]
- Huntley, M.A.; Rasmussen, C.L.; Villarubi, R.S.; Sangtong, J.; Fey, J.T. Effects of Standards-based mathematics education: A study of the Core-Plus Mathematics Project algebra and functions strand. J. Res. Math. Educ. 2000, 31, 328–361. [Google Scholar] [CrossRef]



| Items Coded in the Algebra Strand | ||||
|---|---|---|---|---|
| Textbook Series | Number of Items Coded | Algebra % (n) | Advanced Algebra % (n) | Functions (n) |
| CME | 12,752 | |||
| CPMP | 7546 | (2037) | (2098) | (3584) |
| DM | 10,446 | (2726) | ||
| GLENCOE | 17,020 | (7012) | (3625) | |
| IMP | 1735 | (680) | (566) | (593) |
| UCSMP | 13,675 | (4855) | (4376) | (3692) |
| Real-World Context | Calculator or Computer | Manipulatives | |
|---|---|---|---|
| CME | 10.3 | 10.3 | 0.1 |
| CPMP | 44.9 | 22.2 | 0.3 |
| DM | 43.8 | 33.4 | 1.3 |
| Glencoe | 22.9 | 13.5 | 0.9 |
| IMP | 54.3 | 13.3 | 1.8 |
| UCSMP | 28.3 | 19.9 | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huntley, M.A.; Terrell, M.S.; Fonger, N.L. A Content Analysis of the Algebra Strand of Six Commercially Available U.S. High School Textbook Series. Educ. Sci. 2024, 14, 845. https://doi.org/10.3390/educsci14080845
Huntley MA, Terrell MS, Fonger NL. A Content Analysis of the Algebra Strand of Six Commercially Available U.S. High School Textbook Series. Education Sciences. 2024; 14(8):845. https://doi.org/10.3390/educsci14080845
Chicago/Turabian StyleHuntley, Mary Ann, Maria S. Terrell, and Nicole L. Fonger. 2024. "A Content Analysis of the Algebra Strand of Six Commercially Available U.S. High School Textbook Series" Education Sciences 14, no. 8: 845. https://doi.org/10.3390/educsci14080845
APA StyleHuntley, M. A., Terrell, M. S., & Fonger, N. L. (2024). A Content Analysis of the Algebra Strand of Six Commercially Available U.S. High School Textbook Series. Education Sciences, 14(8), 845. https://doi.org/10.3390/educsci14080845








