Abstract
Our study employs multi-level agent-based modeling and computational techniques to explore education as a complex system. With an underlying focus that education should be underpinned by a scientific understanding of student learning, we created computational models that simulated learning dynamics in classrooms, integrating both quantitative and qualitative insights. Through these models, we conducted experiments aligned with real classroom data to address key questions, such as “How can we effectively support the academic progress of underperforming students, who are disproportionately from low socio-economic status (SES) backgrounds, to close their multi-year achievement gap in mathematics?” Our study analyzes various instructional approaches for mathematical learning, and our findings highlight the potential effectiveness of Productive Failure as an instructional approach. Considerations of the broader applicability of computational methods in advancing educational research are also provided.
1. Conceptual Rationale and Aims
In our study, we embarked on an exploratory journey to illuminate the dynamics of education through the lens of a multi-level agent-based model (ML-ABM) created within the NetLogo language and environment [1]. This research is driven by a recognition of the complex, dynamic, multifaceted nature of classroom learning, which can best be understood through sophisticated computational techniques that can simulate the nuanced interplay between student cognition, collaborative learning endeavors, and the broader socio-economic contexts in which education unfolds. Our approach aligns with advocacy for embedding computational methods within educational research, aiming to bridge the gap between theoretical models and practical classroom applications [2,3]. Through this, our study aims to contribute to a deeper and more comprehensive understanding of educational dynamics, offering potential insights for enhancing learning outcomes in diverse educational settings.
The justification for employing computational methods in our study is twofold. Firstly, these methods allow for the simulation and analysis of complex educational phenomena that are difficult to observe and measure in traditional research settings. An example of this might include the simulation and analysis of multiple perspectives, complex collaborations, and interactions across multiple actors in a school environment, such as those between pre-service teachers and in-service teachers [4]. By creating detailed models that can represent the dynamics of classroom learning, researchers can manipulate variables in ways that would be difficult in real-life contexts, providing valuable insights into the mechanisms driving educational outcomes [5]. Secondly, computational models can serve as a powerful tool for predicting real-world system behavior and the consequences of changes, such as the effects of educational interventions before their implementation in actual classrooms [6]. This predictive capacity enhances the efficiency and effectiveness of educational research by guiding the development of more targeted interventions. Also, it supports evidence-based decision making in educational policy and practice. We propose the use of computational models as a complement to existing research methods. By exploring and integrating computational methods, our study contributes to developing a more rigorous, nuanced understanding of educational processes, facilitating the translation of theoretical insights into actionable strategies for improving student learning.
Central to our investigation are the following two innovative concepts: “Productive Failure” [7] and “Multi-Mediator Modeling” (MMM) [8]. The former challenges traditional instructional methodologies by engaging students in complex problem solving before formal instruction, while the latter integrates agent-based modeling (ABM) and Systems Dynamics to offer a comprehensive view of educational phenomena across multiple dimensions. This combination of methodologies allows us to explore intricate processes that underlie learning outcomes, with a focus in this article on enhancing the academic trajectory of low-performing students.
By detailing our model’s assumptions, parameter configurations, and the processes by which it has been empirically validated, we aim to provide a transparent and replicable framework that not only simulates real-world educational dynamics but also invites further scholarly inquiry and empirical testing. Through our consideration of the model’s limitations and a comparative analysis with existing educational theories and frameworks, we seek to underscore our model’s unique contributions as well as highlight areas for potential integration and improvement. Ultimately, our objective is to foster a collaborative research environment where models such as ours serve as a foundation for ongoing dialogue, refinement, and innovation in understanding educational dynamics.
The practical implications of our work extend beyond the academic realm, offering educators, policymakers, and fellow researchers valuable insights into effective, equitable educational strategies and interventions. Moreover, we chart a course for future research, pinpointing specific areas where computational methods can further enrich our understanding of educational systems and contribute to the ongoing effort to bridge educational disparities. Ultimately, our study advocates for a paradigmatic shift towards a more integrated and computationally informed perspective in educational research, one that not only embraces the complexity of learning environments but also strives to ensure educational equity and excellence for all students [9,10].
2. Literature Review
The integration of computational science techniques is particularly relevant in the context of mathematics education among low-performing student populations. Research indicates a significant socio-economic status (SES)-related performance gap in mathematics achievement, underscoring the need for targeted interventions [11]. Furthermore, the relationship between executive function (EF)—key cognitive processes for goal-directed behavior—and math problem-solving skills suggests that addressing cognitive development is as crucial as mitigating socio-economic challenges [12]. Computational models may serve as a powerful tool in this context, allowing researchers to simulate various instructional strategies and learning environments to uncover potential effective practices for enhancing both cognitive skills and mathematical understanding. This multifaceted approach, informed by computational science, promises to deliver holistic strategies that address intertwined cognitive and socio-economic challenges, paving the way for a comprehensive improvement in educational outcomes for both low SES and broader student populations.
Jacobson, Levin, and Kapur [2] advocated for the incorporation of computational science techniques—traditionally applied in physical, biological, and social domains—into educational research. This integration is posited as a complement to conventional quantitative and qualitative methods, offering a novel lens through which to view and analyze the complexities of educational systems. Among the methodologies discussed, agent-based modeling (ABM) and Systems Dynamics stood out as particularly promising. ABM, as explained by Wilensky and Rand [13], adopts a “bottom-up” approach, simulating individual agent behaviors to understand collective system dynamics. Systems Dynamics, outlined by [14], contrasts this by offering a “top-down” perspective, using equation-based models to explore system interactions over time. Together, these methodologies provide a rich analytical toolkit, enabling researchers to capture both micro-level behaviors and macro-level trends within educational settings.
Our study adopts the Multi-Mediator Modeling (MMM) framework of Levin and Datnow [8], which integrates elements from both ABM and Systems Dynamics. Using the MMM approach, we developed a model that spans the following three critical domains: the effectiveness of pedagogical strategies, the impact of SES on mathematics achievement, and the interplay between EF and math problem-solving skills. By merging MMM with ABM and Systems Dynamics, we aim to offer a multidimensional analysis that captures the intricate dynamics of educational environments. This approach not only illuminates the individual behaviors of learners and teachers but can also shed light on the overarching policies and practices shaping educational outcomes.
Addressing educational disparities in mathematics for students from low socio-economic status (SES) backgrounds is critically important, and one effective strategy is the adoption of the ‘Funds of Knowledge’ approach. This pedagogical framework, as outlined by Moll, Amanti, Neff, & Gonzalez [15], champions the recognition and integration of the rich and diverse knowledge that students acquire from their family, culture, and community experiences directly into the classroom environment. A body of research, including a meta-analysis by Lawson, Hook, and Farah [16], highlights the presence of SES disparities in EF, pointing to the need for inclusive and responsive teaching methods. Hammond [17] further underscores this by detailing how culturally responsive teaching practices are instrumental in supporting neurological development and fostering cognitive engagement among students. By embedding learning experiences that resonate with students’ lived realities, educators not only enhance engagement but also deepen students’ understanding of mathematical concepts. The practical application of the Funds of Knowledge approach in mathematical education, as demonstrated by Civil [18] and Moll et al. [15], significantly increases the relevance and efficacy of teaching, bridging the gap between academic content and the student’s own experiences.
Productive Failure, a concept introduced by Kapur [7], advocates for the educational power of grappling with challenges before receiving Direct Instruction. This method, which initiates learning by engaging students in difficult problem-solving tasks, serves to deepen understanding by leveraging the cognitive struggles inherent in such challenges. It is particularly effective in mathematics education across diverse student demographics, enhancing not just academic achievement but also leading to greater conceptual understanding and students’ ability to transfer to novel problems [19]. This approach also has the potential to synergize with culturally responsive pedagogy by valuing and weaving students’ cultural and experiential backgrounds—what is known as their Funds of Knowledge—into the fabric of their educational experience, thereby making learning more relevant and engaging. Kapur and Bielaczyc [10] underscored the potential of Productive Failure to transform learning environments into spaces that bridge the divide between students’ home and school lives, encouraging the application of existing knowledge in new and challenging contexts. This not only respects and activates students’ backgrounds but also positions them to navigate and persist through complex problems, fostering an educational climate that is ripe for exploration. Such a model not only contrasts with the commonly used Direct Instruction approach but also offers a holistic, inclusive framework that empowers students by acknowledging and utilizing their unique perspectives and experiences.
In a contrasting approach to Productive Failure, Direct Instruction focuses on designing instructions with logically flawless communication, predicting its comprehension by the learner, observing the actual learning outcomes, and tailoring subsequent instruction based on behavioral analysis if the initial outcomes indicate learning difficulties [20]. This method supports the cognitive load theory proposed by Sweller [21], which argues that reducing unnecessary cognitive load can enhance learning by allowing the working memory to focus on the relevant information [22]. Direct Instruction minimizes confusion and misunderstanding by providing clear, immediate guidance, thereby managing cognitive load and facilitating the efficient acquisition of specific skills and knowledge [21,23]. While highly effective for imparting specific skills and knowledge, Direct Instruction may not foster as strong connections between personal experiences and the curriculum as Productive Failure. Rosenshine’s principles of instruction emphasize the importance of clarity, systematic presentation, and guided practice in improving student learning outcomes [23], marking a clear departure from the exploratory, student-centered methodology of Productive Failure. Reflecting Sweller’s cognitive load theory, this juxtaposition suggests that instructional strategies should be tailored to the learner’s stage of expertise, with Direct Instruction being particularly beneficial for novices [22]. Research consistently shows that Productive Failure not only significantly surpasses direct or explicit pedagogical methods in developing deeper conceptual understanding and transferable problem-solving skills but also yields comparable results in procedural knowledge to approaches that prioritize Instruction followed by Problem Solving [24].
3. Method
Our research aimed to address the following research question: “How can we effectively support the academic progress of underperforming students, who are disproportionately from low socio-economic status (SES) backgrounds, to close their multi-year achievement gap in mathematics?”. To attempt to address this research question, we developed a Math Learning Model (see Appendix A for a link to the model). This model enabled us to manipulate independent variable settings and run computational experiments. These experiments were informed by a meta-analytic review by Sinha and Kapur [25], with our initial focus on the potential impact of a Learning Activities independent variable on student learning.
The Math Learning Model developed for this project utilizes the agent-based modeling tool NetLogo [1]. This model represents educational challenges as complex systems [2], with nodes (circles) symbolizing agents or elements and links (lines) denoting their interactions. The model consists of the following three levels: a classroom level representing Learning Activities and Math Results; a cognitive level with nodes for students’ Prior Math Knowledge (conceptual structures) and Low EF and High EF processes; and a cultural level depicting students’ socio-economic status (SES). Green lines represent positive interactions, while red lines depict negative interactions. The more active a node is, the more active another node will be that is connected to it by a positive link, and the less active a node will be that is connected to it by a negative link. The activity values for all the nodes in the network are updated as the model runs.
In the computational experiments, independent variable settings were adjusted using sliders for each node, as shown in the upper right-hand table in Figure 1. With each step, the sizes and numerical states of nodes representing dependent variables changed. Figure 1 displays the initial settings for independent variables, like the low SES level, low Prior Math Knowledge, Low Math Knowledge, and no Learning Activities. Our model also supports the ML-ABM through LevelSpace, which is a NetLogo extension to support the modeling of cross-level interactions, the coupling of heterogeneous models, and the efficient resource use of simulations through the (dynamic) adaptation of levels of detail [26].
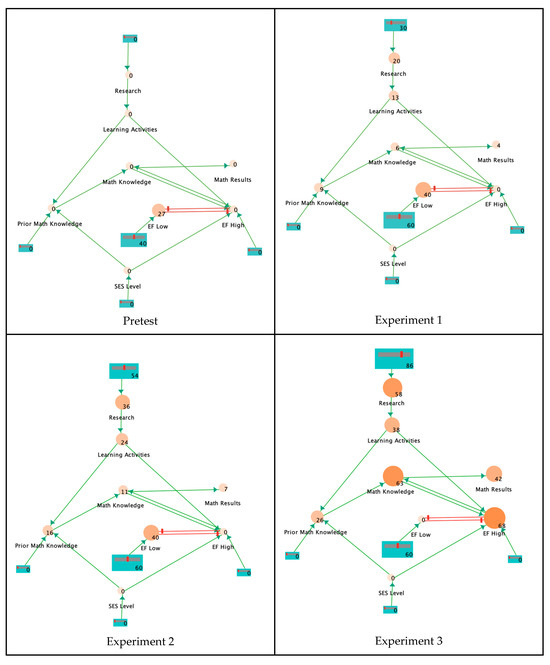
Figure 1.
Math Learning Model Experiment Link/Node States. Screenshots of the Math Learning Model link/node states for the Pretest and each experiment.
The study conducted four computational experiments, all starting from the initial Pretest state and only varying the independent variable of Learning Activities. These changes were informed by data from the meta-analytic review by Sinha and Kapur [25]. Activation values were assigned to the Learning Activities node based on their findings. Sliders attached to the nodes enabled the initial manipulation of the activation values of each node. When running the model, interactions in the system were represented by node sizes and their corresponding values. These nodes would either stay the same size or increase or decrease in size. Requiring the visibility of these changes was an underlying reason for selecting circle shapes as nodes. Node sizes categorized as “small” indicated “0” activation (no instruction). An activation value of “0.2” corresponded to “I-PS” (Instruction followed by Problem Solving), and Hedge’s g effect size of 0.20 was equivalent to one year of instruction. A value of “0.36” represented the “PS-I” (Problem Solving followed by Instruction) with Hedge’s g effect size of 0.36, equivalent to 2.8 years of instruction. Lastly, “0.58” denoted the “PF” (Productive Failure) with Hedge’s g effect size of 0.58, equivalent to 3.9 years of instruction.
Nodes in the model were also connected with one of two types of arrows representing different types of influences between nodes. Green arrows depicted a positive influence from one node to another, while red arrows depicted a negative or suppressing influence. To help reflect real-world dynamics, connections between nodes were also influenced by a globally set attenuation figure. This adjusted the strength of the influence that one node exerts on another, which in our model is attenuated by 0.67. This means any effect, whether from an excite or inhibit link, is multiplied by 0.67 when transferred from one node to another.
4. Results
The results of our computational experiments aimed to highlight potential pedagogical interventions aimed to improve student learning. The computational experiments are shown in the screenshots of the Math Learning Model link/node states for the Pretest and each experiment in Figure 1. Table 1 shows the settings for independent variables and the results for the Math Results and High EF dependent variables.

Table 1.
Independent variable settings and dependent variable results for three computational experiments.
Both numerical values and the dimensions of the Math Knowledge, Math Results, and High EF nodes in Figure 1 show minimal changes between the Pretest phase and Experiments 1 and 2 for the I-PS and PS-I Learning Activities. However, Experiment 3, involving the PF Learning Activity, displayed a significant surge in numeric values associated with these dependent variables, reflected in the expanded size of each corresponding node.
5. Discussion
The preliminary outcomes from the initial version of the Math Learning Model align with empirical evidence from Sinha and Kapur [25], particularly highlighting higher Math Results for the Problem Solving followed by Instruction (PS-I) sequence over the Instruction followed by Problem Solving (I-PS) approach. This finding is consistent with the research conducted by Sinha and Kapur [25], which demonstrated the superior learning outcomes achieved through the PS-I sequence. According to Sinha and Kapur [25], starting the learning process with problem-solving activities before introducing formal instruction significantly boosts student engagement, motivation, and, ultimately, the effectiveness of learning. This method employs active learning principles, ensuring that students are actively engaged in the learning process, which facilitates deeper cognitive processing. Freeman et al. [27], in their comprehensive study on active learning, affirmed that such strategies, by promoting active participation, significantly improve students’ understanding and retention of information. By stimulating curiosity and providing context, the initial problem solving in the sequence prepares students for the targeted instruction that follows, addressing the gaps in their understanding identified during the problem-solving phase. The alignment of the Math Learning Model with the empirical findings of Sinha and Kapur [25], alongside the principles of active learning and cognitive load management, underscores the importance of incorporating evidence-based practices in educational strategies. This not only substantiates the theoretical underpinnings of the model but also offers practical insights for improving math education through optimized instructional sequencing.
One of the findings from running the Math Learning Model was the correlation between low executive function (EF) and reduced mathematical achievement for both the Instruction followed by Problem Solving (I-PS) and Problem Solving prior to Instruction (PS-I) interventions. These results also align with research on the importance of the relationship between EF and general problem solving, suggesting that “to successfully solve life’s complex problems, one must be able to identify the problem and set a goal for its solution, generate alternative ideas, utilize prospective memory for predicting consequences based on past experience, and shift from solutions that are not effective to ones that are. One must also be able to inhibit automatic responses and take the time to think of more effective ones” [28]. This alignment of model results and EF research provides a preliminary demonstration of the model’s validity.
In relation to this, an unexpected result in Experiment 3 found that the Productive Failure learning treatment not only led to a substantial increase in Math Results but also exhibited a non-linear rise in executive function. While this increase in EF might be a model artifact (a possibility to explore in further research), research does indicate a connection between EF components such as cognitive flexibility, working memory, and patterning performance, where patterns are identified within a sequence of ordered units [29], and cognitive flexibility and mathematic performance [30]. Considering the general lack of published research on assisting students in learning or developing High EF skills, future investigations could explore whether a highly effective math learning approach like PF could potentially enhance students’ EF skills, potentially negating the need for specialized EF-focused training. This is particularly salient, as research suggests that while training in specific EF components may result in significant, medium-sized near-transfer effects, there is no evidence to suggest far-transfer effects [12]. However, research in PF has shown significant results on across domain far transfer problem solving [31].
6. Limitations
As this article discusses a preliminary study, several limitations are important to consider. First, the generalizability of computational models to various educational contexts may be limited, which is a challenge noted by Blikstein and Wilensky [32] regarding agent-based models’ applicability across different learning environments. Second, the inherent simplifications required for computational modeling may not fully encapsulate the complexity of human behavior and interpersonal classroom dynamics, which is an issue Epstein [33] discusses in the context of social simulation models. This could impact the model’s predictive accuracy and the relevance of its insights to real-world educational practices. Furthermore, the reliance on existing datasets and the literature to parameterize the models introduces potential biases, which is a critical concern raised by O’Neil [34], pointing to the broader issue of data-driven models perpetuating inequalities. Additionally, by focusing predominantly on outcomes such as mathematics achievement and executive function, important aspects like emotional and social intelligence, motivation, and resilience—which significantly influence educational outcomes—are potentially sidelined, as Durlak et al. [35] emphasized the crucial role of social and emotional learning factors. Lastly, Fullan [36] highlights the practical challenges of translating research findings into actionable educational strategies, underlining the gaps in teacher training and policy adaptations that are necessary for implementing innovative instructional approaches.
However, despite these limitations, we argue that computational models offer a valuable framework for hypothesis testing and theory development in educational research. By simulating complex dynamic phenomena that are otherwise difficult to observe or experiment with directly, these models can illuminate patterns and potential interventions that might not be apparent through traditional research methods. This bridging of theoretical and empirical insights enriches our understanding of educational dynamics and guides practical innovations in teaching and learning strategies. Sengupta and Farris [37] underscore this point by demonstrating how educational simulations, as a specific application of computational modeling, can effectively engage students in learning about complex systems, providing a robust tool for exploring and understanding intricate scientific phenomena. These considerations suggest the need for future research to incorporate a wider range of data sources, explore additional outcome variables, and develop more sophisticated models that can accurately reflect the complexities of educational environments to validate the applicability and efficacy of computational methods in educational research.
7. Conclusions
In this article, we discuss how computational modeling may be used to study educational complex systems. In particular, we developed the Math Learning Model, which is a Multi-Mediator Model (MMM) [8] with the following three levels: a classroom level representing Learning Activities and Math Results; a cognitive level for students’ Prior Math Knowledge and for Low EF and High EF processes, and a cultural level for students’ socio-economic status (SES). The settings for the model parameters were based on effect size data from the meta-analysis study of Sinha and Kapur [25], with the results of the computational experiments largely consistent with their empirical data.
More generally, our innovative MMM approach allowed computational investigations of the multi-level interactions between individual-level determinants, such as cognition and motivation, and broader social influences, such as social and economic factors, which would be difficult to study in real-world classroom settings. The utility of the MMM approach for computational modeling extends beyond mere analysis; it can serve as a tool in the formulation of research questions, such as those based on observed interactions, the prediction of educational outcomes, and the design of experiments that span the diverse domains of educational research.
We believe that the fusion of computational science techniques with culturally informed pedagogical practices represents a new direction in educational research—one that complements currently used quantitative and qualitative methods. By integrating these approaches, we aim to expand the tools of educational research to richly investigate critical issues. These issues include improving educational equity and excellence and identifying educational activities that can ensure all learners have the opportunity to achieve their fullest potential. This interdisciplinary approach not only facilitates a deeper understanding of the complex dynamics within educational settings [2,13], but also ensures that these insights are grounded in the real-world experiences and cultural contexts of students [38].
Future research is necessary to further explore and refine these methodologies and to explore how computational approaches combined with quantitative and qualitative research on cognitive and socio-cultural factors might advance the field of educational research. Furthermore, we hope this research can stimulate further interest in the broader educational research community to investigate the use of computational modeling as we collectively strive to advance our understanding of complex educational systems and shape the future of learning through innovative, evidence-based practices, with the ultimate goal of reducing educational inequalities and enhancing academic success across diverse student populations.
Author Contributions
Conceptualization, methodology, validation, formal analysis, investigation, resources, data curation, writing—original draft preparation, writing—review and editing, project administration, J.V., M.J.J., J.A.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The Math Learning Model is available under the ‘Computational Educational Research’ section on this website: http://mmm.ucsd.edu/mmm.html, (accessed on 6 April 2024).
References
- Wilensky, U. NetLogo; Center for Connected Learning and Computer-Based Modeling, Northwestern University: Evanston, IL, USA, 1999; Available online: http://ccl.northwestern.edu/netlogo/ (accessed on 1 February 2024).
- Jacobson, M.J.; Levin, J.A.; Kapur, M. Education as a complex system: Conceptual and methodological implications. Educ. Res. 2019, 48, 112–119. [Google Scholar] [CrossRef]
- Williamson, B.; Potter, J.; Eynon, R. New research problems and agendas in learning, media and technology: The editors’ wishlist. Learn. Media Technol. 2019, 44, 87–91. [Google Scholar] [CrossRef]
- Willegems, V.; Consuegra, E.; Struyven, K.; Engels, N. Teachers and pre-service teachers as partners in collaborative teacher research: A systematic literature review. Teach. Teach. Educ. 2017, 64, 230–245. [Google Scholar] [CrossRef]
- Sengupta, P.; Wilensky, U. Learning Electricity with NIELS: Thinking with Electrons and Thinking in Levels. Technol. Knowl. Learn. 2009, 14, 21. [Google Scholar] [CrossRef]
- Poile, C.; Safayeni, F. Using Computational Modeling for Building Theory: A Double Edged Sword. J. Artif. Soc. Soc. Simul. 2016, 19, 1. [Google Scholar] [CrossRef]
- Kapur, M. Productive Failure. Cogn. Instr. 2008, 26, 379–424. [Google Scholar] [CrossRef]
- Levin, J.A.; Datnow, A. The principal role in data-driven decision making: Using case study data to develop multi-mediator models of educational reform. Sch. Eff. Sch. Improv. 2012, 23, 179–201. [Google Scholar] [CrossRef]
- Jacobson, M.J. Complexity Conceptual Perspectives for Research About Educational Complex Systems. J. Exp. Educ. 2020, 88, 375–381. [Google Scholar] [CrossRef]
- Kapur, M.; Bielaczyc, K. Designing for Productive Failure. J. Learn. Sci. 2012, 21, 45–83. [Google Scholar] [CrossRef]
- Australian Department of Education. Students from Low Socio-Economic Areas. 2022. Available online: https://www.education.gov.au/australian-curriculum/national-stem-education-resources-toolkit/i-want-know-about-stem-education/which-school-students-need-stem-education/students-low-socio-economic-areas (accessed on 1 February 2024).
- Kassai, R.; Futo, J.; Demetrovics, Z.; Takacs, Z.K. A meta-analysis of the experimental evidence on the near- and far-transfer effects among children’s executive function skills. Psychol. Bull. 2019, 145, 165–188. [Google Scholar] [CrossRef]
- Wilensky, U.; Rand, W. An Introduction to Agent-Based Modeling: Modeling Natural, Social, and Engineered Complex Systems with NetLogo; The MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Smith, P. Systems Thinking and Systems Dynamics; Emerald Group Publishing: Bradford, UK, 2007. [Google Scholar]
- Moll, L.C.; Amanti, C.; Neff, D.; Gonzalez, N. Funds of knowledge for teaching: Using a qualitative approach to connect homes and classrooms. Theory Into Pract. 1992, 31, 132–141. [Google Scholar] [CrossRef]
- Lawson, G.M.; Hook, C.J.; Farah, M.J. A meta-analysis of the relationship between socioeconomic status and executive function performance among children. Dev. Sci. 2018, 21, e12529. [Google Scholar] [CrossRef]
- Hammond, Z. Culturally Responsive Teaching and the Brain: Promoting Authentic Engagement and Rigor among Culturally and Linguistically Diverse Students; Corwin: Thousand Oaks, CA, USA, 2015. [Google Scholar]
- Civil, M. Culture and mathematics: A community approach. J. Math. Cult. 2002, 1, 2–44. [Google Scholar] [CrossRef]
- Kapur, M. Productive Failure in Learning Math. Cogn. Sci. 2014, 38, 1008–1022. [Google Scholar] [CrossRef]
- Engelmann, S.; Carnine, D. Theory of Instruction: Principles and Applications; Irvington Publishers: New York, NY, USA, 1982. [Google Scholar]
- Sweller, J. Cognitive load during problem solving: Effects on learning. Cogn. Sci. 1988, 12, 257–285. [Google Scholar] [CrossRef]
- Sweller, J.; Ayres, P.; Kalyuga, S. Cognitive Load Theory: Explorations in the Learning Sciences, Instructional Systems and Performance Technologies; Springer: New York, NY, USA, 2011. [Google Scholar]
- Rosenshine, B. Principles of instruction: Research-based strategies that all teachers should know. Am. Educ. 2012, 36, 12–19. [Google Scholar]
- Jacobson, M.J.; Vulic, J.; Levin, J.A. Nexus for STEM problem solving and transfer research: Instruction first or Productive Failure first? In Ways of Thinking in STEM-based Problem Solving: Teaching and Learning in a New Era; English, L.D., Lehmann, T., Eds.; Routledge: London, UK, 2024. [Google Scholar]
- Sinha, T.; Kapur, M. When problem solving followed by instruction works: Evidence for Productive Failure. Rev. Educ. Res. 2021, 91, 761–798. [Google Scholar] [CrossRef]
- Morvan, G. Multi-level agent-based modeling—A literature survey. arXiv 2013, arXiv:1205.0561. [Google Scholar] [CrossRef]
- Freeman, S.; Eddy, S.L.; McDonough, M.; Smith, M.K.; Okoroafor, N.; Jordt, H.; Wenderoth, M.P. Active learning increases student performance in science, engineering, and mathematics. Proc. Natl. Acad. Sci. USA 2014, 111, 8410–8415. [Google Scholar] [CrossRef]
- Aberson, B. Building executive functioning in children through problem solving. In Handbook of Executive Functioning; Goldstein, S., Naglieri, J.A., Eds.; Springer Science + Business Media: New York, NY, USA, 2014; pp. 509–521. [Google Scholar] [CrossRef]
- Bock, A.M.; Cartwright, K.B.; McKnight, P.E.; Patterson, A.B.; Shriver, A.G.; Leaf, B.M.; Mohtasham, M.K.; Vennergrund, K.C.; Pasnak, R. Patterning, Reading, and Executive Functions. Front. Psychol. 2018, 9, 1802. [Google Scholar] [CrossRef]
- de Santana, A.N.; Roazzi, A.; Nobre, A.P.M.C. The relationship between cognitive flexibility and mathematical performance in children: A meta-analysis. Trends Neurosci. Educ. 2022, 28, 100179. [Google Scholar] [CrossRef] [PubMed]
- Jacobson, M.J.; Goldwater, M.; Markauskaite, L.; Lai, P.K.; Kapur, M.; Roberts, G.; Hilton, C. Schema abstraction with productive failure and analogical comparison: Learning designs for far across domain transfer. Learn. Instr. 2020, 65, 101222. [Google Scholar] [CrossRef]
- Blikstein, P.; Wilensky, U. An atom is known by the company it keeps: A constructionist learning environment for materials science using agent-based modeling. Int. J. Comput. Math. Learn. 2009, 14, 81–119. [Google Scholar] [CrossRef]
- Epstein, J.M. Why model? J. Artif. Soc. Soc. Simul. 2008, 11, 12. Available online: http://jasss.soc.surrey.ac.uk/11/4/12.html (accessed on 6 April 2024).
- O’Neil, C. Weapons of Math Destruction: How Big Data Increases Inequality and Threatens Democracy; Crown Publishing: New York, NY, USA, 2016. [Google Scholar]
- Durlak, J.A.; Weissberg, R.P.; Dymnicki, A.B.; Taylor, R.D.; Schellinger, K.B. The impact of enhancing students’ social and emotional learning: A meta-analysis of school-based universal interventions. Child Dev. 2011, 82, 405–432. [Google Scholar] [CrossRef]
- Fullan, M. The New Meaning of Educational Change, 4th ed.; Teachers College Press: New York, NY, USA, 2007. [Google Scholar]
- Sengupta, P.; Farris, A. Learning kinematics in elementary grades using agent-based computational modeling: A visual programming-based approach. In Proceedings of the IDC ‘12: The 11th International Conference on Interaction Design and Children, Bremen, Germany, 12–15 June 2012; ACM International Conference Proceeding Series. pp. 78–87. [Google Scholar] [CrossRef]
- Gonzalez, N.; Moll, L.C.; Amanti, C. Funds of Knowledge: Theorizing Practices in Households, Communities, and Classrooms; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 2005. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).