On Reading Mathematical Texts, Question-Asking and Cognitive Load
Abstract
1. Introduction
2. Theoretical Background
3. The Study
3.1. The Research Goal and Derived Research Questions
- How do PMTs perceive the effect of question-asking while reading historic mathematical texts on their cognitive load?
- What are the differences between high- and low-achiever PMTs’ perceptions regarding the effect of question-asking while reading historic mathematical texts on their cognitive load?
3.2. The Study Participants
3.3. The Learning Environment
3.4. Research Method
3.5. Research Instruments
3.5.1. The Tool for Collecting Quantitative Data
3.5.2. Instruments for Collecting Qualitative Data
- (i)
- Think-aloud protocols. The real-time reporting [13] was obtained using think-aloud protocols, an approach for collecting data whereby people are asked to verbalize and document (whether in writing or audio/video recording) their thought processes as they manage a specific task [24,25]. Employing this tool, the experimental group members were asked to audio record the questions they asked, the answers they gave, and their thoughts while engaging with the mathematical texts at the same three points in time mentioned in Section 3.5.1. These recordings were transformed by the researchers into written protocols. It should be noted that, reviewing 94 studies (involving almost 3500 participants), Fox, Ericsson, and Best [26] found no reliable differences in cognitive performance with or without the employment of the think-aloud technique.
- (ii)
- Justifications of the self-esteem index of cognitive load. The retrospective reporting [13] was part of the self-esteem CL index questionnaire, where the PMTs were asked to justify their rankings. For this purpose, they were asked to recall relevant episodes that occurred while coping with the texts.
- (iii)
- Group interview. The group interview is intended to gather information from several individuals simultaneously. In educational settings, the group interview is beneficial for gaining insights into students’ reactions to certain aspects of a course [27]. Four times throughout the academic year (twice in each semester), we conducted a group interview intended to elicit the PMTs’ thinking about issues related to their engagement with the texts. The interviews were recorded and transcribed.
3.6. Data Analysis
3.7. Ethical Issues
4. Results
4.1. Empirical Results Obtained from the Self-Esteem Index of the Cognitive Load Questionnaire
4.1.1. General Empirical Results
4.1.2. General Results Related to High and Low Achievers
4.1.3. Examination of Differences between Groups
4.2. Qualitative Data Obtained from the Think-Aloud Protocols
4.2.1. Think-Aloud Protocol No. 1—Egyptian Multiplication
- 1:
- The Egyptian multiplication looks unclear.
- 2:
- I read it several times and can’t figure out why they multiplied the numbers by 2.
- 3:
- I keep thinking about why they did not use the method we use today, and I must admit, this distracts my mind, and obviously, I can’t answer it.
- 4:
- O.K., so before giving up, it seems the right time to start asking questions.
- 5:
- I noticed that in the two examples you presented, the multiplicand was an odd number, while the multiplier was an even number.
- 6:
- Since I can’t figure out the underlying rationale, the question I ask is whether I can repeat the process with the other three combinations of multiplying natural numbers—even-odd, odd-odd, even-even.
- 7:
- While checking these combinations, I feel I am acting automatically, just reproducing the method steps without understanding why I am doing that.
- 8:
- Now I just want to make sure the products are correct.
- 9:
- Yes. The calculator verifies it.
- 10:
- O.K. These 4 examples convinced me that the Egyptian method is valid for any multiplication of two natural numbers.
- 11:
- The next obvious question is why? How can I justify the method? To be honest, I have no idea where to start.
- 12:
- So, I’ll just keep asking questions about the validity of the method as regards additional types of numbers.
- 13:
- For example, fractions. Perhaps this will help me to figure out the rationale.
- 14:
- I know from the introduction section that the Egyptians dealt with unit fractions, so I’ll try to reproduce the method for multiplying …. hmmm… I’m stuck with the .
- 15:
- Obviously, I am missing something.
- 16:
- I don’t get to the bottom of the rationale of the method.
- 17:
- I merely replicate procedures.
- 18:
- Just for the protocol—I have no more questions to ask to help me get into the rationale of the method.
- 19:
- I feel like reaching the end of the road. So, let me think of another direction.
- 20:
- What is the connection between this method and the method we learned at school?... I don’t know what to say, because I don’t find any connection.
- 21:
- Perhaps I should rephrase my question and ask—is there a connection between the methods at all? If there is any connection, I can’t see it.
- 22:
- So, at this point, I give up and choose to present the questions I asked at the class meeting, to get feedback that will help me to proceed.
4.2.2. Think-Aloud Protocol No. 2—Babylonian Method for Solving a Set of Two Equations
- 1:
- After reading the Babylonian method of solving two equations with two unknown variables, I must say that I was fascinated.
- 2:
- The method is so different from the way we learned in math lessons.
- 3:
- We learned to solve the equations using an algebraic method, while the Babylonians used geometric considerations.
- 4:
- In the algebraic method, one option is to isolate one of the variables from one of the two equations and substitute it in the second equation to get an equation with one unknown variable and then solve it using the quadratic roots formula.
- 5:
- The Babylonian method uses geometry, and I have to recall my geometry knowledge regarding the area and perimeter of squares and rectangles.
- 6:
- O.K., Now to asking questions. First, does it work with other numbers? For example: a + b = 16 and a·b = 90… hmmm… [checking]. Something is not working here.
- 7:
- what happened here? Why doesn’t the method work for these numbers? I got a negative difference (64–90). You can’t create a square with a negative area!
- 8:
- Let me check it using the algebraic method.
- 9:
- O.K., I got a quadratic equation with no real roots. This is why the numbers are not good.
- 10:
- They, I mean, the writers of the historical text, forgot to mention that the multiplication of the two numbers must be smaller than the area of the square.
- 11:
- But why does it have to be smaller?
- 12:
- I have no idea. I think I leave the problem for a while to refresh my mind.
- 13:
- [a day after] The problem kept bothering me and I think I have a breakthrough.
- 14:
- I remember that we learned that of all rectangles with a given perimeter, the square has the maximum area.
- 15:
- Hence, the area of the rectangle in the second equation must be smaller than the area of the square whose side equals 16/2. So now it’s OK.
- 16:
- My next question is- does the method works for any rational numbers?
- 17:
- I am skipping the checking of the case that one, the first equation, is a natural number and the other, the second equation, is not, and get to the case that both numbers are not natural numbers.
- 18:
- I am now checking the case of a + b = 15.7 and a·b = 58.3.
- 19:
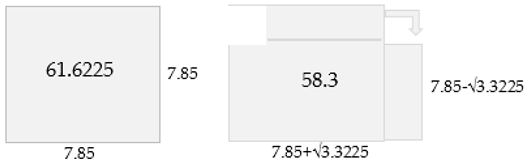
- O.K. The a = b = 15.7/2 = 7.85 is the side of a square with which to start.
- 20:
- So, to get the area of 58.3, I have to remove a square whose area is 61.6225 − 58.3 = 3.3225. Hence the side of this square is √3.3225.
- 21:
- Now I need to put the left rectangle, as you can see in the next draw, to the side of the square and get a rectangle.
- 22:
- The rectangle’s sides are: 7.85 + √3.3225 and 7.85 − √3.3225, and the area of this rectangle is 58.3.
- 23:
- Wow! It works!
- 24:
- Now, how can I prove the general case?
- 25:
- Will the algebra help to get the proof? Let’s see.
- 26:
- What now? How can I connect the above expression to the Babylonian method?
- 27:
- I have no clue.
- 28:
- I feel I’m stuck!
- 29:
- This is frustrating since I like the Babylonian method, but I can’t show why it always works.
4.2.3. Think-Aloud Protocol No. 3—Vedic Method for Squaring Two-Digit Numbers
- 1:
- In our school mathematics, we did not learn a particular method for squaring a given number.
- 2:
- So, it is interesting to learn about the Vedic method for finding such a number.
- 3:
- Let’s try other numbers to see if it also works for them.
- 4:
- 5:
- O.K. I’ll check the result with the calculator… It works! Now I’ll try to generalize it.
- 6:
- 7:
- What now? How is it connected to the Vedic method?
- 8:
- Maybe I have to write it differently?
- 9:
- I’ll now return to one of the examples from the text and try to write it differently:
- 10:
- 11:
- So, what in this expression might imply about the Vedic method?
- 12:
- Hmmm…. I’ll try to write it like this:
- 13:
- O.K. what do we have here? 10 (the number + the unit number) + the square of the unit number.
- 14:
- Does it look clear now? Hmmm… Of course! I got it!
- 15:
- Now I can try to generalize it.
- 16:
- I have to replace the tens and unit digits with a and b, in accordance.
- 17:
- 18:
- 19:
- Wow! They are genius!
- 20:
- It would be interesting to see if I can adapt it for 3-digit numbers.
5. Discussion and Conclusions
5.1. PMTs’ Perceptions Regarding the Effect of Question-Asking While Reading Historic Mathematical Texts on Their Cognitive Load and Differences between High and Low Acheivers
5.2. Insights Gained from the Think-Aloud Protocols
“The questions I had to ask prevented me from giving up right after the first reading of the texts. Since I was unfamiliar with this technique [QA], I started with questions that helped me repeat the algorithms without necessarily understanding them. Then it occurred to me that I have to cope with different questions that will lead to a breakthrough in my attempts to make sense of the algorithms”.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bohn-Gettler, C.M.; Kendeou, P. The interplay of reader goals, working memory, and text structure during reading. Contemp. Educ. Psychol. 2014, 39, 206–219. [Google Scholar] [CrossRef] [PubMed]
- Österholm, M. Characterizing reading comprehension of mathematical texts. Educ. Stud. Math. 2006, 63, 325–346. [Google Scholar] [CrossRef]
- Österholm, M.; Bergqvist, E. What is so special about mathematical texts? Analyses of common claims in research literature and of properties of textbooks. ZDM-Math. Educ. 2013, 45, 751–763. [Google Scholar] [CrossRef]
- Berger, M. Reading mathematics text: A study of two empirical readings. Int. J. Sci. Math. Educ. 2019, 17, 385–404. [Google Scholar] [CrossRef]
- Lepik, M.; Grevholm, B.; Viholainen, A. Using textbooks in the mathematics classroom–the teachers’ view. Nord. Stud. Math. Educ. 2015, 20, 129–156. [Google Scholar]
- Carmo, M. (Ed.) END 2020—International Conference on Education and New Developments; World Institute for Advanced Research and Science: Zagreb, Croatia, 2020. [Google Scholar]
- Clark, R.C.; Nguyen, F.; Sweller, J. Efficiency in Learning: Evidence-Based Guidelines to Manage Cognitive Load; Pfeiffer: Zurich, Switzerland, 2005; ISBN 9-780-78797-728-3. [Google Scholar]
- Sweller, J. Cognitive load during problem solving: Effects on learning. Cogn. Sci. 1988, 12, 257–285. [Google Scholar] [CrossRef]
- Sweller, J. Cognitive Load Theory. In Psychology of Learning and Motivation; Academic Press: Cambridge, MA, USA, 2011; Volume 55, pp. 37–76. [Google Scholar] [CrossRef]
- Lin, J.J.H.; Lin, S.S. Cognitive load for configuration comprehension in computer-supported geometry problem solving: An eye movement perspective. Int. J. Sci. Math. Educ. 2014, 12, 605–627. [Google Scholar] [CrossRef]
- Shriki, A.; Lavy, I. Engagement in Vedic mathematics as a means for strengthening self-efficacy of low achievers. In Proceedings of the EDULEARN18 Conference, 10th Annual International Conference on Education and New Learning Technologies, Palma de Mallorca, Spain, 2–4 July 2018. [Google Scholar]
- Wong, K.Y. Use of student mathematics questioning to promote active learning and metacognition. In Proceedings of the 12th International Congress on Mathematical Education (ICME-12), Seoul, Republic of Korea, 8–15 July 2012; Cho, S.J., Ed.; Springer International Publishing: Cham, Switzerland; pp. 1086–1100. [Google Scholar]
- Paas, F.G.W.C.; Tuovinen, J.E.; Tabbers, H.; Van Gerven, P.W. Cognitive load measurement as a means to advance cognitive load theory. Educ. Psychol. 2003, 38, 63–71. [Google Scholar] [CrossRef]
- Paas, F.G.W.C.; Van Merriënboer, J.G.; Adam, J. Measurement of cognitive load in instructional research. Percept. Mot. Ski. 1994, 79, 419–430. [Google Scholar] [CrossRef]
- Sweller, J.; Van Merriënboer, J.J.G.; Paas, F.G.W.C. Cognitive architecture and instructional design. Educ. Psychol. Rev. 1998, 10, 251–296. [Google Scholar] [CrossRef]
- Orru, G.; Longo, L. The Evolution of Cognitive Load Theory and the Measurement of its Intrinsic, Extraneous and Germane Loads: A Review. In International Symposium on Human Mental Workload: Models and Applications; Springer: Cham, Switzerland, 2018; pp. 23–48. [Google Scholar] [CrossRef]
- Sweller, J. Measuring cognitive load. Perspect. Med. Educ. 2018, 7, 1–2. [Google Scholar] [CrossRef]
- Johnson, R.B.; Christensen, L. Educational Research: Quantitative, Qualitative, and Mixed Approaches, 5th ed.; SAGE Publications Inc.: Thousand Oaks, CA, USA, 2014; ISBN 9-781-45224-440-2. [Google Scholar]
- Mihalca, L.; Salden, R.J.; Corbalan, G.; Paas, F.; Miclea, M. Effectiveness of cognitive-load based adaptive instruction in genetics education. Comput. Hum. Behav. 2011, 27, 82–88. [Google Scholar] [CrossRef]
- Maciejewski, M.L. Quasi-experimental design. Biostat. Epidemiol. 2020, 4, 38–47. [Google Scholar] [CrossRef]
- Gopalan, M.; Rosinger, K.; Ahn, J.B. Use of quasi-experimental research designs in education research: Growth, promise, and challenges. Rev. Res. Educ. 2020, 44, 218–243. [Google Scholar] [CrossRef]
- Shadis, W.R.; Cook, T.D.; Campbell, D.T. Experimental and Quasi-Experimental Designs for Generalized Causal Inference; Houghton Mifflin Company: Boston, MA, USA, 2002; Available online: https://www.alnap.org/system/files/content/resource/files/main/147.pdf (accessed on 6 May 2023).
- Corder, G.W.; Foreman, D.I. Nonparametric Statistics for Non-Statisticians: A Step-by-Step Approach; Wiley: Hoboken, NJ, USA, 2009; ISBN 9-781-11816-588-1. [Google Scholar]
- Van Someren, M.W.; Barnard, Y.F.; Sandberg, J.A.C. The Think Aloud Method: A Practical Approach to Modeling Cognitive; Academic Press: London, UK, 1994; ISBN 0-127-142-270-3. [Google Scholar]
- Ortlieb, E.; Norris, M. Using the think-aloud strategy to bolster reading comprehension of science concepts. Curr. Issues Educ. 2012, 15, 1–10. [Google Scholar]
- Fox, M.C.; Ericsson, K.A.; Best, R. Do procedures for verbal reporting of thinking have to be reactive?: A meta-analysis and recommendations for best reporting methods. Psychol. Bull. 2011, 137, 316–344. [Google Scholar] [CrossRef]
- Edmiston, V. The group interview. J. Educ. Res. 2014, 37, 593–601. [Google Scholar] [CrossRef]
- Creswell, J.W. Educational Research: Planning, Conducting, and Evaluating Quantitative and Qualitative Research, 4th ed.; Pearson: Boston, MA, USA, 2012; ISBN 9-780-13136-739-5. [Google Scholar] [CrossRef]
- Healy, M.; Perry, C. Comprehensive criteria to judge the validity and reliability of qualitative research within the realism paradigm. Qual. Mark. Res. Int. J. 2000, 3, 118–126. [Google Scholar] [CrossRef]
- Haapalainen, E.; Kim, S.; Forlizzi, J.F.; Dey, A.K. Psycho-physiological measures for assessing cognitive load. In Proceedings of the 12th ACM International Conference on Ubiquitous Computing, Copenhagen, Denmark, 26–29 September 2010; pp. 301–310. [Google Scholar] [CrossRef]
- Galy, E.; Cariou, M.; Mélan, C. What is the relationship between mental workload factors and cognitive load types? Int. J. Psychophysiol. 2012, 83, 269–275. [Google Scholar] [CrossRef]
- Sweller, J. Cognitive load theory, learning difficulty, and instructional design. Learn. Instr. 1994, 4, 295–312. [Google Scholar] [CrossRef]
- Boutyline, A.; Soter, L.K. Cultural schemas: What they are, how to find them, and what to do once you’ve caught one. Am. Sociol. Rev. 1988, 86, 728–758. [Google Scholar] [CrossRef]
- Movshovitz-Hadar, N. Stimulating presentation of theorems followed by responsive proofs. Learn. Math. 1988, 8, 12–30. [Google Scholar]
- Malek, A.; Movshovitz-Hadar, N. The effect of using transparent pseudo-proofs in linear algebra. Res. Math. Educ. 2011, 13, 33–58. [Google Scholar] [CrossRef]
- Neumann, K.L.; Kopcha, T.J. The use of schema theory in learning, design, and technology. TechTrends 2018, 62, 429–431. [Google Scholar] [CrossRef]
- Van Kesteren, M.T.R.; Meeter, M. How to optimize knowledge construction in the brain. NPJ Sci. Learn. 2020, 5, 5. [Google Scholar] [CrossRef] [PubMed]

| Variable Name | Variable | Items | Cronbach’s Alpha |
|---|---|---|---|
| ECL_text 1 | Text 1 | a–f | 0.906 |
| ICL_text 1 | Text 1 | g–j | 0.858 |
| ECL_text 2 | Text 2 | a–f | 0.891 |
| ICL_text 2 | Text 2 | g–j | 0.862 |
| ECL_text 3 | Text 3 | a–f | 0.916 |
| ICL_text 3 | Text 3 | g–j | 0.874 |
| Data Source | Data Type | Analysis Methods |
|---|---|---|
| Self-esteem index of cognitive load questionnaire | Quantitative | Friedman test [23] |
| Qualitative | Coding (open, axial, selective) [28] | |
| Transcripts of think-aloud protocols | Qualitative | |
| Transcripts of group interviews | Qualitative |
| Control Group | Experimental Group | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HA (N = 6) | LA (N = 14) | Total (N = 20) | HA (N = 6) | LA (N = 14) | Total (N = 20) | ||||||||
| M | SD | M | SD | M | SD | M | SD | M | SD | M | SD | ||
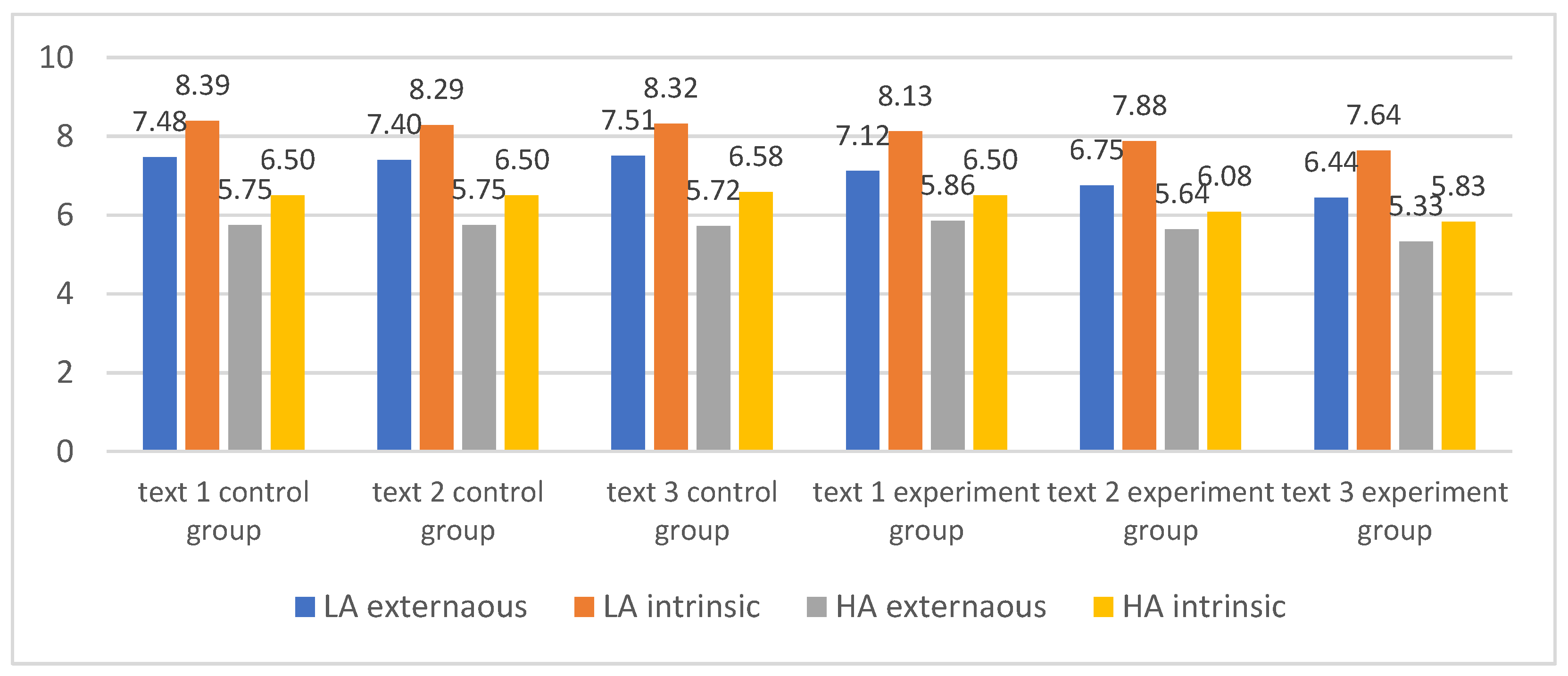
| Extraneous | Text 1 | 5.75 | 0.57 | 7.48 | 0.36 | 6.96 | 0.91 | 5.86 | 0.31 | 7.12 | 0.35 | 6.74 | 0.68 |
| Text 2 | 5.75 | 0.50 | 7.40 | 0.40 | 6.91 | 0.88 | 5.64 | 0.19 | 6.75 | 0.32 | 6.42 | 0.59 | |
| Text 3 | 5.72 | 0.53 | 7.51 | 0.47 | 6.98 | 0.96 | 5.33 | 0.21 | 6.44 | 0.28 | 6.11 | 0.58 | |
| χ2 (df = 2) | 0.50 | 3.26 | 2.68 | 9.36 | 19.09 | 27.61 | |||||||
| p | 0.779 | 0.196 | 0.262 | 0.009 | <0.001 | <0.001 | |||||||
| Intrinsic | Text 1 | 6.50 | 0.27 | 8.39 | 0.32 | 7.82 | 0.94 | 6.50 | 0.22 | 8.13 | 0.40 | 7.64 | 0.84 |
| Text 2 | 6.50 | 0.39 | 8.29 | 0.34 | 7.75 | 0.91 | 6.08 | 0.30 | 7.88 | 0.34 | 7.34 | 0.90 | |
| Text 3 | 6.58 | 0.34 | 8.32 | 0.32 | 7.80 | 0.88 | 5.83 | 0.34 | 7.64 | 0.29 | 7.10 | 0.90 | |
| χ2 (df = 2) | 1.14 | 4.17 | 1.64 | 8.82 | 12.53 | 20.87 | |||||||
| p | 0.565 | 0.124 | 0.441 | 0.012 | 0.002 | <0.001 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lavy, I.; Shriki, A. On Reading Mathematical Texts, Question-Asking and Cognitive Load. Educ. Sci. 2023, 13, 678. https://doi.org/10.3390/educsci13070678
Lavy I, Shriki A. On Reading Mathematical Texts, Question-Asking and Cognitive Load. Education Sciences. 2023; 13(7):678. https://doi.org/10.3390/educsci13070678
Chicago/Turabian StyleLavy, Ilana, and Atara Shriki. 2023. "On Reading Mathematical Texts, Question-Asking and Cognitive Load" Education Sciences 13, no. 7: 678. https://doi.org/10.3390/educsci13070678
APA StyleLavy, I., & Shriki, A. (2023). On Reading Mathematical Texts, Question-Asking and Cognitive Load. Education Sciences, 13(7), 678. https://doi.org/10.3390/educsci13070678