Abstract
This article reports on physics teaching in upper-secondary school with a focus on communication and relations made between mathematics, theoretical models in physics, and reality. Video data from four physics classrooms in three different teaching contexts, i.e., lessons, problem solving, and lab work, have been analysed by combining two theoretical frameworks: the Ternary Framework and Joint Action Theory in Didactics. Four physics teachers were selected from among a range of teachers who had responded to a web-based questionnaire, representing different teacher profiles from the questionnaire. The results indicate that the teacher profiles, including information on curriculum emphasis and views of mathematics, physics, and physics teaching, were good predictors for communication in the classrooms. The teacher profiles were found to influence teaching and the communication more than the teaching contexts. The benefits of formally correct mathematical treatment during physics teaching are discussed based on the results.
1. Introduction and Background
Physics teaching is subject to ongoing discussions concerning aims and learning goals, relation to modern society, and the role of mathematics [1,2,3,4]. The purpose is to develop ways of teaching that would allow more students to find physics and mathematics interesting and meaningful. In this study, we continue to seek the role of mathematics in physics teaching. There are possibilities for students to develop their understanding of mathematics not only during mathematics teaching but also when they encounter mathematics in other subjects. The subject of physics has a special position in this regard. Mathematics is often used during physics lessons, giving students opportunities to practice and develop their understanding of both mathematics and physics, and this has been studied from a physics education research perspective [5,6,7,8,9,10,11,12]. A recent example is the study by Pols et al. [13] concerning upper secondary school students’ empirical work in physics, where the students managed to collect and represent data, but not analyse them. The students struggled to discern pivotal features of graphs and had difficulties interpreting data in order to draw conclusions. Therefore, in the present work, we differentiate the terms technical and structural with respect to the use of mathematics in physics teaching. Technical indicates that mathematics is viewed as a calculation tool with an instrumental use of mathematics as a consequence [4,14,15]. The structural use of mathematics indicates that mathematics is used as a reasoning instrument with an emphasis on interpretations or consequences and logical reasoning [4,14,15].
Researchers in mathematics education have also been interested in mathematical competence, problem solving, and modelling in physics [9,16,17] and, generally, in what it means to possess mathematical competencies in recent years [18]. We view mathematical competencies in accordance with the perspectives formulated by Niss and Jensen [19] and Niss and Højgaard [18], which focus on engagement in the mathematical activities and processes that will be applied in physics teaching. According to Niss and Højgaard, mathematical competence is defined as ‘someone’s insightful readiness to act appropriately in response to all kinds of mathematical challenges pertaining to given situations’ [18] (p. 12).
The needs for further research on physics teaching are diverse. Several authors have also substantiated that physics teaching presents different curriculum emphases. The general picture presented in the literature is that relationships between teachers’ views, curriculum emphases, classroom practices, problems, and possible student shortcomings are of utmost importance and need further study [2,10,20,21,22]. This is corroborated by Zhao et al. [12], who recently reported that instructors provide different opportunities for the sensemaking of equations when covering the same science content during biology and mathematics lessons. They discuss this in terms of pre-established sensemaking patterns that teachers adhere to.
Based on the above, we want to further investigate how mathematics is used in communication between teachers with different teaching profiles and their students in physics classrooms. The classroom study presented herein is part of a project on the role of mathematics in upper-secondary physics teaching that also included a web-based questionnaire administered to upper-secondary school physics teachers in Sweden [20]. In this article, we report the results of a video study of four different classrooms. The involved teachers’ views on the aims, characteristics, and challenges related to physics teaching and their teaching habits, specifically concerning their attitudes toward physics and mathematics, have been identified through the web-based questionnaire [20,23].
2. Theoretical Framework
The joint action theory in didactics (JATD) is used to capture processes of teaching and learning in a learning game [24]. The joint goal for the teacher and student concerned is for the student to learn something. The paradigm focuses on individuals’ (1) joint attention (JAT), i.e., shared attention toward the same object in the joint action [25,26]; (2) joint affordance (JAF), i.e., recognition of the same affordances in the same joint action [27]; and (3) common ground (CG), i.e., shared preconceptions and conceptions that enable communication between individuals in the joint action [28]. The theory of didactic situations [29] is adopted in JATD as a cornerstone of the analytical process alongside didactic contracts and milieus [24]. A didactic contract consists of the (often implicit) agreements between students and teachers in their joint actions. A breach of the contract may be a situation in which a teacher refers to situations or phenomena outside of the students’ experiences or introduces a mathematical formula that is new to the students. The didactic milieu is the environment for learning, i.e., the joint activity in a broad sense. The didactic milieu may, in itself, give students feedback on their actions [24]. For example, if a student is working in a computer environment involving functions and derivatives and the student thinks that all functions and derivatives cross the x-axis at the same points, the milieu with visual attributes gives the student feedback stressing that there is a need to adjust such a conviction. In this regard, Sensevy et al. [30] discuss a contract–milieu dialectic, as the contract refers to what is brought into the game and the milieu refers to knowledge development through the didactic game. Hence, the contract and the milieu in a situation can be considered complementary entities since new knowledge builds on prior experience and what is already known [30]. There are possible elements of resistance in didactic milieus that challenge students’ conceptions and give them opportunities for learning. Tiberghien et al. [31] studied the evolution of knowledge in a physics classroom within the joint action theory of didactics. In their case, the evolution of knowledge was studied in terms of epistemic certainty and uncertainty as an active way of handling knowledge in order to form new knowledge as opposed to beliefs about knowledge.
Furthermore, this project uses a semantic view focusing on theoretical models in physics [5,32,33,34], where theoretical models are viewed as forming families or classes linking theories with experiments and practices and where the focus is on the explanatory power of the theoretical models. Hence, to be able to analyse the content, i.e., the knowledge at stake, common ground, and affordance of the joint actions, a theoretical model designed to identify different foci in classroom communication, as depicted in Figure 1, was used [5]. The ternary framework allows for the identification of relations made between the three entities, namely, Reality (R)/Reality School (RS), Theoretical models (TM), and Mathematics (M), hence enabling the analysis of common ground and affordances in terms of connections made between these three entities.
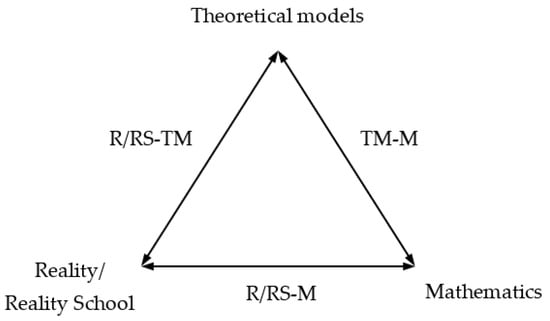
Figure 1.
The analytical framework for modelling the relationship between Reality/Reality School–Theoretical models–Mathematics in physics teaching. It has been adapted from [35].
Reality refers to objects or phenomena (or observations thereof) in the real world. Reality has broad connotations comprising, for example, well-known objects, phenomena, and events that students have experienced in their everyday lives and the phenomena observed (either directly or by using measuring equipment) in physics teaching during demonstrations and lab work. We distinguish Reality (R) from Reality School (RS) [6,35]. Reality comprises well-known objects, phenomena, and events that students have experienced in their everyday lives. Reality School represents a form of ‘reduced reality’ often encountered in physics teaching, where factors influencing a real-world phenomenon are either conceived of as constant or disregarded, e.g., a frictionless movement. It also encompasses phenomena only observed during demonstrations and lab work, sometimes by using complex measuring equipment. Furthermore, R and RS have been used with an internal structure distinguishing between recalled (R1/RS1) or systematically described (R2/RS2) realities following the description provided by Triantafillou et al. [36], which was based on the work of Bliss et al. [37].
The term Theoretical models refers to theoretical models in physics and concepts related to them, whether mathematically or qualitatively formulated. We distinguish between an Instrumental approach (TM1) and a Relational approach to theoretical models (TM2) in a manner aligned with what Skemp [38] introduced for mathematics [6,21,35]. An Instrumental approach means that constituents of the theoretical model (concepts and representations) are used or mentioned without relation to the involved theoretical model or phenomenon. A Relational approach is characterised by connected concepts and representations present in a discussion, hence allowing the students to engage in meaning making on a systemic level.
Mathematics refers to mathematical competencies and the performance of mathematical activities and processes as described by Niss and Højgaard [18]. Moreover, we distinguish technical use of mathematics (M1), indicating that mathematics is viewed as a ‘calculation tool’ [4,14,15] from a structural use of mathematics (M2), meaning that mathematics is used as a ‘reasoning instrument’ with an emphasis on interpretations or consequences, from logical reasoning [4,14,15]. So, by employing the previously published ternary framework [6,35], the instituted contract and the generated didactic milieu can be analysed in terms of joint attention, common ground, and joint affordance. Thus, we seek to empirically test the intertwinement of the two frameworks in our analysis. Therefore, joint attention refers to mutual focus toward R/RS and M, common ground refers to a shared understanding of involved theoretical models (TM) and mathematics (M), and joint affordance emerges when the participants of the didactic game share affordances of the situation or phenomenon through a mutual common ground in terms of theoretical models and mathematics. This is a view related to the notion of disciplinary affordance, i.e., ‘the inherent potential of a given representation to provide access to disciplinary knowledge’ [3].
Aim and Research Questions
The aim of this article is to further explore the role of mathematics in physics teaching and learning in upper-secondary school by investigating the utterances and actions of teachers and students during physics lessons. The research questions are as follows:
- How can the intertwined theoretical frameworks Reality/Reality School–theoretical models–Mathematics and JATD be used to analyse communication in physics classrooms?
- How is mathematics used during communication between teachers and students in relation to reality and theoretical models
- by teachers with differing views of physics teaching;
- in different kinds of instructional situations (lectures, lab work, and problem-solving situations)?
3. Methods
Four physics teachers with different views on physics, mathematics, and physics teaching were, based on the analysis of a web-based questionnaire sent to upper-secondary school physics teachers in Sweden [20], selected for qualitative analysis of their teaching practices.
3.1. The Questionnaire
The web-based questionnaire [20] is briefly described in this section to render the selection of teachers transparent. Furthermore, resulting constructs from the analysis [20] are used in the analysis presented in this article. The questionnaire covers teachers’
- Curriculum emphases;
- Views of the nature of physics and mathematics;
- Physics-teaching strategies and the role of mathematics.
Part A of the survey (39 items) was based on an adaptation of the three ‘curriculum emphases’ developed by van Driel, Bulte, and Verloop [39], which, in turn, were based on the seven curriculum emphases developed by Roberts [40,41,42]. The three curriculum emphases were adapted such that they also encompassed biology and physics by de Putter-Smits et al. [43]. The curriculum emphases used in the survey given to physics teachers were as follows: (1) Fundamental physics (FP), combining ‘solid foundation’ and ‘correct explanations’ [42], where fundamental theories and concepts are introduced as a basis for further studies; (2) Physics, technology, and society (PTS), merging ‘science/technology/decisions’ and ‘everyday applications’ [42], i.e., capturing interrelationships between applications of science and technology with students’ everyday lives and decision making; and (3) Knowledge development in physics (KDP), combining ‘scientific skill development’, ‘structure of science’, and ‘personal explanation’ [42], i.e., project-oriented work focusing on scientific processes.
Part B of the questionnaire (46 items) concerned physics teachers’ views about the nature of mathematics, with statements from Grigutsch and Törner [44], and the nature of science, with statements from Chen [45]. Part C of the questionnaire (54 items) concerned physics teachers’ views on teaching strategies, shortcomings, and the role of mathematics in physics teaching and it was based on TIMSS Advanced [46] and other published instruments [47,48]. Competences, concepts, and areas of mathematics relevant to physics were addressed [20].
Factor analyses of the responses to the questionnaire were conducted [20]. The teachers’ views about aims and goals were analysed through the three curriculum emphases: FP, KDP, and PTS. Their views of classroom strategies were categorised according to the scales teacher centred or student centred, and their perceived shortcomings and problems in physics teaching led to the use of the following scales: mathematics, curriculum overload, views of mathematics and physics, qualitative understanding, and practical issues. Teachers that highly agreed with FP tended to view ‘mathematics’ and ‘views on mathematics and physics’ as problems in physics teaching. These teachers agreed to a greater degree with items implying teacher-centred teaching strategies. However, teachers that highly agreed with PTS indicated that ‘views of mathematics and physics’ and ‘practical issues’ were the most problematic areas with regard to teaching physics. These teachers agreed to a greater extent with items implying student-centred teaching strategies. Teachers that highly agreed with KDP indicated that the main problems in physics teaching are too much content and too little time and student-related qualitative understanding. These teachers also agreed to a greater extent with items implying student-centred teaching strategies. Hence, there was a tentative correlation between held curriculum emphasis and views on teaching processes [20].
The three scales used to analyse views of physics in part B of the questionnaire were called paradigm and social impact (including views of theory-laden measurements and social impacts on development), value-free observations (including views of objective measurements and cumulative development), and invented theories (concerning views of whether theories are invented or discovered). The descriptive factors of views of mathematics were adopted from the work of Grigutsch and Törner [44], i.e., formal, schema, process, and application. The formal aspect is characterised by strictness and logic at various levels, e.g., in the use of language and symbols, reasoning, and deduction. The schema aspect focuses on mathematics as a complete set of knowledge that can be recalled and used when applying rules and definitions. The process aspect concerns the dynamicity of mathematics, i.e., the terms, ideas, and relations between them. Discovery and understanding are key components. Lastly, the application aspect is about the practical use of mathematics in applications or real life, whether personal or societal.
3.2. The Teachers and Courses
Four teachers from three different schools in different municipalities were observed in their physics classrooms. They all taught at ‘The Natural Science programme’ at upper secondary school, wherein they all taught mathematics as well. Upper-secondary physics in Sweden is outlined by a national curriculum [49] stipulating ‘The Natural Science programme’, which is a three-year programme that includes physics in three courses (Physics 1, 2, and 3). The description of physics in the national curriculum encompasses the role of mathematics and is formulated in a goal-oriented sense, leaving itself open for interpretation by schools and teachers. Regarding mathematical methods, the curriculum states that in Physics 1, teaching should cover the core content, ‘Identifying and studying problems using reasoning from physics and mathematical modelling covering linear equations, power and exponential equations, functions and graphs, and trigonometry and vectors’ [49]. The core content for Physics 2 has a similar formulation (but with slightly different mathematical concepts): ‘linear and non-linear functions, equations and graphs, and derivatives and vectors’ [49]. Teachers 1, 2, and 3 were studied when teaching the Physics 1 course. while Teacher 4 was studied when teaching Physics 2. The selected physics lessons were chosen so that three types of instructional situations, i.e., lectures, problem solving, and laboratory work, would be included in the analysis to enable comparisons of different physics-teaching settings. The four teachers included were selected based on their responses to the questionnaire described in the introduction of this article and in [20,23]. Table 1 and Table 2 display the categorisation of responses from the visited teachers.

Table 1.
Results from the questionnaire [20]. Preferred curricular emphases and problems in physics teaching.

Table 2.
Results from the questionnaire [23]. Views of mathematics and physics.
Teachers with dissimilar profiles, as depicted in Table 1 and Table 2, were selected from among a group of volunteers out of the 379 respondents. The aim was to compare the different responses to their actual performance in the classrooms. In total, 8 lessons were video- and audio-recorded with several cameras and microphones. One camera was trained on the teacher and whiteboard, one camera was trained on the class, and small cameras and audio recorders were employed for each of the student groups.
All ethical considerations adhered to recommendations by the Swedish Research Council [50], including with regard to informing the participants about their voluntary participation, explaining that they had the right to cancel their participation if they wished, and giving both the participants and schools pseudonyms in the data when the study was reported. Specific attention was applied to obtaining informed consent from participating teachers and students.
3.3. Analysis
The video and audio recordings from all sessions were transcribed in full, and episodes of potential importance were selected and discussed by the researchers. An episode constitutes an interaction between the teacher and one or several students concerning a question, task, or comment relevant to physics, mathematics, or both topics. Communications about other topics were not regarded as episodes and were hence discarded. The final set of episodes was jointly defined by the researchers. Categorisation was conducted according to the two frameworks as presented in the theory section. It was initially conducted by one of the authors and then discussed by all the authors. A portion of the data was categorised by two or three of the authors independently to ensure high validity and reliability in the analysis. The episodes were categorised using categories from both frameworks (TM, R/RS, and M as well as CG, JAT, JAF, and Contract and Milieu; see Table 3).

Table 3.
Categories from the theoretical framework used in the analysis, which were exemplified by episodes.
The lengths of the episodes vary, and short ones tend to belong to fewer categories than the longer ones. There was still a problem with respect to determining when one episode ended and another began when communication was carried out between several persons. Therefore, we have not taken a quantitative approach to the analysis but have employed a qualitative focus on the trends in the four teachers’ classrooms. Episodes of special interest from the teachers’ sessions were selected, which are presented in the results section, to provide a sense of the types of communication taking place in the different classrooms. The categorised episodes were compared to the classifications of the teachers from the questionnaire [20], as depicted in Table 1 and Table 2. The aim was to find relations between the categorisation of the episodes and the teacher profiles from the questionnaire.
4. Results
The results section is structured based on the research questions, and selected episodes from the four classrooms and the three different teaching contexts, namely, lectures, problem solving, and lab work, are presented below. The episodes are categorised based on the ternary framework (Theoretical models, Reality/Reality School, and Mathematics) and the JATD framework (Common ground, Joint attention, Joint affordance, and Contract and Milieu).
4.1. The Intertwined Theoretical Frameworks
The selected episodes below highlight different aspects of the analysis conducted using the two intertwined theoretical frameworks. The power of intertwining the two frameworks for the analysis of classroom communication is shown in example episodes. One of these episodes is E1.2, when a metaphor related to the relational use of the theoretical model (TM2) instilled common ground (CG) with resulting joint affordance (JAF) about the movement of charges/electrons in a circuit, which, in turn, led to the students’ structural use of mathematics (M2) in relating resistance to the formula I = U/R. Furthermore, episode E3.1 is an example of the structural use of mathematics related to the real world, aiding the process of establishing joint affordance. Teacher 1 explicitly connected known reality (R1) in the problem to the theoretical model (TM) and mathematics (M2), which led to the establishment of joint affordance (JAF). Hence, intertwining the two theoretical frameworks, i.e., the ternary Reality–Theoretical–Mathematics models and Joint Action Theory of Didactics (JATD), has been found to be effective for the analysis of classroom communication in the cases investigated. The ternary framework provides a means of realising possible reasons for successful outcomes and the establishment of joint affordance (JAF) in the ‘teaching-learning game’. Our analysis, as exemplified by the episodes, has shown that the analysis of the ‘teaching-learning game’ in the milieu influenced by joint attention, common ground, and joint affordance can be further elucidated by the addition of the ternary framework. The categorisation derived from the ternary framework adds to the description and understanding of successful teaching–learning games, where, for instance, cases of the structural use of mathematics (M2) or systematic reference to reality (R2) led to joint affordance (JAF) and fruitful communication.
4.2. Use of Mathematics
The results from the analysis related to research question 2 concerning the links made between the three entities of the ternary framework (Figure 1) during communication in the classroom are presented here in two steps, starting with the analysis related to the teacher profiles (cf., Table 1 and Table 2), followed by that related to content and specific use of mathematics.
4.2.1. Teachers with Differing Views of Physics Teaching
Teacher 1 had a profile with a KDP emphasis, was teacher-centred, and viewed a crowded curriculum, but not mathematics and practical issues, as a problem (cf., Table 1 and Table 2). Teacher 1’s views of mathematics were categorised as Process rather than Formal, and physics from the perspective Paradigm and social impact, contributing a view that theoretical models in physics are invented by researchers. Teacher 1 dominated their lecture and adhered to the intended curriculum with a well-defined didactical milieu. There were several questions and comments from the students during the lecture, but the process remained teacher-centred, with questions posed to the students. The problem-solving session was about problems from a book chapter and reflected the teacher profile. The lab session was distinguished by several discussions of the role of graphs linked to the fitting of polynomial functions to measured and plotted data points. The KDP emphasis of Teacher 1 concurs with Paradigm and social impact, including a view that theoretical models in physics are invented by researchers but related to empirical research, which is exemplified by episode E1.4. The teaching was teacher-centred as it was driven by the teacher who established the milieu by referring to continuants of the contract concerning both mathematics (M) and theoretical models (TM) and aspects of reality (mostly RS). The categorisation of a process view of mathematics in the sense of Grigutsch and Törner [44] from the analysis of the questionnaire indicates a dynamic view where mathematical concepts and their relations are important for the discovery and understanding of the physical processes. This view that fits well with KDP and is exemplified by episodes E1.1 and E1.3.
Teacher 2′s profile, depicted in Table 1 and Table 2, indicates a KDP emphasis and a mix of teacher- and student-centred teaching. Teacher 2 viewed a crowded curriculum, but not mathematics, as a problem. The analysis of responses to the survey conveys a view of mathematics as a Process rather than an Application and presents a view of physics from the perspective we call Value-free observations, including a view that theoretical models in physics are discovered by researchers. The lecture was teacher-driven, wherein Teacher 2 frequently asked questions for the students to reflect on and answer individually, or discuss in pairs, and then in dialogue with the teacher, thereby developing their answers and sharing their thoughts with the rest of the class. This is in accordance with the mixed teaching style ascribed to Teacher 2 shown in Table 1. During the lecture, the teacher’s views on physics, physics theories, and research were made clear, which concurs with the teacher’s profile KDP with Value-free observations and Discovered physics theories (see Table 1 and Table 2). Similarly, problem solving and the lab session were teacher-driven, with the teacher asking questions and encouraging the students to share their reasoning and experiences (cf., E2.1). Hence, Teacher 2 strived to involve all the students, inviting them to reason and share their thoughts, thereby creating opportunities for joint attention (JAT) and joint affordance (JAF) with common ground (CG). Moreover, Teacher 2 conscientiously separated reality school (RS) and theoretical models (TM) in asking the students to first ‘describe’ and then ‘explain’ what they see, and the link between RS and TM thus becomes explicit.
Teacher 3 indicated a PTS emphasis (cf., Table 1 and Table 2), with a mix of teacher- and student-centred teaching, viewing a crowded curriculum and mathematics as problems but not qualitative understanding and practical issues. Teacher 3 viewed mathematics as Formal rather than being a Schema and physics from the perspective Paradigm and social impact; however, they contributed a view that theoretical models in physics are discovered by researchers. Teacher 3 was the dominating actor in the classroom but invited students to participate in discussions. There was a strong focus on formulae, which corresponds to the categorisation of Formal rather than Schema. Episode E3.1 is an example of the structural use of mathematics related to the real world, aiding the process of establishing joint affordance. The teacher often repeated statements concerning mathematical treatment in an attempt to ease the students’ way through the content of the lecture. This corresponds to the categorisation of experienced teaching problems in terms of a crowded curriculum and mathematics from Table 1. Examples of such views from a teaching session on energy transfer and phases of water are given, especially with respect to linear regression and the process of fitting data points to a linear function (cf., E3.2).
Teacher 4′s profile is a mix of KDP and PTS emphases and student-centred teaching. Teacher 4 regarded individuals’ views of physics and mathematics as a problem but not mathematics per se or practical issues. The teacher viewed mathematics as Formal rather than from a Schema perspective and physics from a mixed perspective, contributing a view that theoretical models in physics are invented by researchers. Teacher 4 dominated the lecture but actively invited students into the discussion. The teacher asked the students many questions. The episodes regarding Teacher 4 (E4.1, E4.2, E4.3, and E4.4) are in concordance with the classification of this teacher’s answers to the questionnaire. Teacher 4 was eager to activate the students’ knowledge development (as indicated in lecture episode E4.1). Teacher 4 viewed mathematics formally rather than as a schema in the sense of Grigutsch and Törner [44], and there was a high rate of common ground (CG) and joint affordance (JAF) in the corresponding classroom communication, as in episode E4.4, when formal mathematics was structurally (M2) used when a student asked a question pertaining to a model (TM2). The explanation was successful, and joint affordance (JAF) accomplished. There were, however, aspects in their teaching that suggested a non-formal approach to mathematics, especially in terms of handling negative signs. Teacher 4′s adherence to the Physics, Technology, and Society (PTS) type of emphasis was shown when, e.g., the teacher linked theoretical models (TM2) to examples the students were likely to understand from reality (R). There were many examples from reality in the lessons. The teacher’s adherence to the Knowledge Development in Physics (KDP) emphasis is expressed in episode E4.4, where a theoretical model (TM2) was developed and used in a mathematical explanation (M2).
4.2.2. Mathematics and Practices in Physics Teaching
Example episodes categorised according to the intertwined frameworks are presented below. The examples initially focus on mathematics per se and then on theoretical models and scientific processes. The categorisation is presented with the category acronyms presented in parentheses (TM, R/RS, M, CG, JAT, JAF, and Contract and Milieu). Hyphens (-) indicate that the category is missing in the episode. Lecture episode E1.1 exemplifies how constituents of the contract (theoretical models from mechanics) are fused with the milieu (electrostatics), and Teacher 1′s process-oriented view of mathematics is denoted by the interchanging of lower and upper case of q, which risks losing joint affordance (JAF) towards the end of the episode.

Lecture episode E1.2 is an example of a student questioning the tradition connected to the custom in physics to discuss vectors in terms of scalars, taking the direction of the vector for granted. JAF seems to be lost temporarily due to confusion concerning this use of notation and nomenclature. The less conscientious use of mathematical formalism and nomenclature in this case seems to obstruct the continuity of joint affordance (JAF) in this episode (E1.2).

During problem solving (in episode E2.1), Teacher 2 provided a rationale behind prefixes and powers of 10. In this case, Teacher 2 did not take negative coefficients into consideration (‘if you have made the 10 power larger, you should make the number in front smaller’), considering the absolute value of the coefficient and the “number in front”. In this episode, Teacher 2 did not attempt to make the students reason conceptionally in a mathematical context (M2), instead recommending the use of calculators to check their answers. This is consistent with Teacher 2′s view of mathematics as a process (see Table 2).

The problem-solving episode E1.3 concurs with Teacher 1′s profile including a process view of mathematics, which is shown here in the treatment of the negative sign. The excerpt also brings to light the physics custom regarding negative signs being omitted and negative numbers treated with implicit absolute value signs, which were recurring results in the analysis of all four teachers.

Teacher 4 engaged in a somewhat ad hoc treatment of the negative sign in Lenz’s law as depicted in lecture episodes E4.1-2 and in problem-solving episode E4.3. The informal treatment of the negative sign in this case was justified by referring to the inherent difficulty of the time derivative, and the contract was discernible when the teacher paused.

The problem-solving session with Teacher 4 was devoted to the content of the lecture and included many references to applications and reality. The relaxed attitude to mathematical stringency seems to lead to problems for Teacher 4′s students and to the questioning of the contract (with episode E4.3 containing a contract breach), indicating that the students were not comfortable with the more lenient use of formalism.

4.2.3. Theoretical Model, Scientific Processes, and Mathematics
We have seen that scientific processes become visible in teaching and learning when students are free to formulate formulae in their own ways, e.g., as in Teacher 4′s classroom, where a student was deriving a formula from relations between variables. The milieu enabled the students’ scientific development, and the contract was visible, which was also the case when the students indicated breaches (e.g., E4.3 above). Teacher 1 emphasised the limitations of the model in episode E1.4, which concurs with Teacher 1′s KDP profile with Paradigm and social impact (see Table 1 and Table 2). The structural use of mathematics in this episode aids the learning game and leads to joint affordance (JAF).

Lecture episode E1.2 in Teacher 1′s classroom (see earlier transcript) brings to light a discussion of electron movement in a conductor that is characterised by JAF in that it connects to contract. However, it seems that the metaphor used previously leads the students to assume a more ordered movement than is the case (cf., [51] on pitfalls in using metaphors in science teaching). Another example of the overinterpretation of models used was found in Teacher 3′s lecture preceding a lab. Teacher 3 projected a diagram (see Figure 2) on the whiteboard and asked the students to discuss the information they could infer from the diagram.
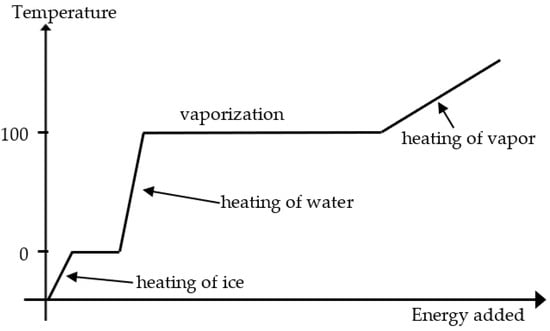
Figure 2.
Diagram of the different phases of water illustrated by the teacher.
After Teacher 3 had listened to the students’ discussions, the teacher held a joint discussion and asked the students to explain their conclusions related to the figure (Figure 2).
Episode E3.1 exemplifies how Teacher 3 connected reality (R1) to a theoretical model (TM1) and used mathematics structurally (M2), leading to the establishment of joint affordance (JAF) concerning the heating of water and ice, respectively, even though the discussion is categorised as an instrumental use of theoretical models (TM1).

The lab-work episode E1.6 started with highlighting Teacher 1′s profile concerning KDP emphasis and view of physics as an empirical science. In this episode (E1.6), a student realised that the plotted dataset did not fit a linear function (contract). The student seemed to struggle to incorporate the observation with an anticipation of a linear relationship and a constant resistance. The measured points could not be represented by a linear function and was indicated that the student and teacher lacked common ground (CG) for the established milieu. However, Teacher 1 helped the student through the structural use of mathematics in discussing whether it has to be a linear relationship, and joint affordance (JAF) was established.

During lab work (cf., episode E3.2), the students were instructed by Teacher 3 to use their graphing calculators to ‘draw your measured points’ and ‘draw added energy [Q] as a function of the temperature difference ΔT’. This formulation did not appear to be based on common ground (CG), and no link was made to theoretical models (TM), which seemed to confuse the students and hinder joint affordance (JAF). Hence, the students discussed the formulation ‘Draw … as a function of …’ and their conceptions of the function concept, especially with respect to what variables should represent x and y on their calculators. This seemed to be a breach of contract since the notion to put their values in lists on their calculators and use the ‘stat-plot’ feature to plot values were not part of the contract and there was no common ground concerning linear regression and the ‘fitting of data points’ through linear regression.

Teacher 3 often told the students that their measured ‘points’ (ΔT, Q) lie on a straight line and that they should calculate the line’s equation using linear regression (episode E3.2). There seemed to be no common ground regarding the use of a theoretical model here, and joint affordance was not reached. Teacher 3 did not explicitly discuss the theoretical model; it remained implicit. Concepts related to a linear function were mentioned, but there seems to be no common ground in connection to the measured points. The students did not question this description of the measured points or why they should use linear regression if the points lie on a straight line. This is an example of Teacher 3’s tendency to interpret data values based on a theoretical model and use mathematical concepts from the model in situations that do not correspond to the concepts. At one point, Teacher 3 gathered students from two groups and explained how they should perform linear regression after they had put a series of values for Q and ΔT in lists in their calculators and made plots on their calculators. In this case, the students focused on the teacher’s handling of the calculator and how to perform the calculations. They did not ask any questions or comment on Teacher 3’s description of linear regression.
In episode E4.4, Teacher 4 used formal mathematics structurally (M2) when a student asked a question pertaining to a model (TM2). The explanation was successful and joint affordance (JAF) was accomplished despite the different modes assumed by the teacher and student.

5. Discussion
We have seen through the presented episodes that intertwining the two theoretical frameworks, i.e., the ternary model of Reality–Theoretical models–Mathematics [5] and the joint action theory in didactics [24], is effective for analysis of classroom communication in the investigated cases. Sensevy et al. [30] indicate the importance of specifying the type of knowledge students are expected to understand within the structures of the ‘teaching-learning game’. The ternary framework has provided a means of analysing data specifying modes of communication as well as detailed treatments of concepts occurring in physics classrooms with a focus on mathematical competencies as defined by Niss and Højgaard [18]. The combination of the two frameworks provides opportunities to realise possible reasons for successful outcomes and the establishment of joint affordances (JAFs) concerning, for example, how teachers communicate mathematics related to the utilised physics models and the expectations from the students they mediate in their teaching. One teacher used silence to mark that student participation was expected in the discussion, expecting the students to know enough to be able to contribute knowledgeably. Furthermore, we have seen a clear relationship between the structural use of mathematics [4,5,6] and the relational use of theoretical models [35] concerning the establishment of joint affordance in teaching. Hence, we can conclude that the use of the ternary framework can aid the analysis of the teaching and learning game as described and analysed using JATD [30]. The analysis and corresponding results presented herein provide a richer picture of physics teaching, thus responding to Belo et al.’s [2] suggestion for researchers to study rationales for teachers’ actions in teaching, but they are also in line with the results presented in earlier work [2,10,12,20,21,22].
The second research question concerns how different teachers in different contexts use mathematical concepts and reasoning during communication with their students in relation to reality and theoretical models. The results show that the processes were mainly influenced by the teachers and their profiles. The dominating factor influencing the established communication was the teacher and not the context, i.e., lectures, lab work, and problem-solving activities. Earlier work has reported on differences in views of mathematics in classrooms [10,11,12,22]; however, in this study, we extend these reports since we can relate to more comprehensive teacher profiles based on the preceding questionnaire [20]. This was particularly clear in the case of Teacher 2, who, in all contexts and in line with the profile presented in Table 1 and Table 2, pointed out the difference between reality and theoretical models by explicitly asking the students to first observe and describe a phenomenon before introducing a theoretical explanatory model to develop an explanation. Teacher 2 and Teacher 4 both clarified the links between reality and theoretical models and wanted students to be active in the classrooms. This is in line with the results from the questionnaire [20], which showed that Teacher 2 had a mixed teaching approach while Teacher 4 had a student-centred approach (Table 1). Teacher 1 had a teacher-centred teaching approach, which was evident from their teaching. Even though the students were involved and responsive, the teacher engaged in fewer diversions compared to the other teachers. Teacher 3, who had a mixed teaching approach, started in reality but was quick to present reality through models. This teacher posed questions to the students, involving them in the teaching while leading the communication.
The hypothesis that teachers’ views of physics teaching, as indicated by the analytical results of the preceding web-based survey [20,23], constitute a good predictor for communication and the established learning games in the classrooms was verified in this study. The herein-established importance of teacher profiles corroborates with the results from, for example, Zhao et al. [12] work on the sensemaking patterns used by the teachers in their study.
The teachers communicated mathematics with weak mathematical stringency in all four classrooms, thereby influencing the processes of deciphering the notations used in communication as Sensevy et al. [30] described. Teacher 1 treated vectors as scalars and was not very conscientious about the use of lower- and uppercase lettering for convenience in the context at hand. Teacher 4 simplified the use of the negative sign to tend to the difficulties in dealing with the new area of time derivatives (E4.1-3). Teacher 2 regularly excluded negative numbers in calculations (e.g., E2.1). All the teachers had a relaxed approach when using absolute value notations and negative signs. There were also tendencies to avoid conceptual reasoning, as in the case of Teacher 2 regarding prefixes (E2.1) or Teacher 3 concerning the concept of function (E3.2). Teacher 3’s mathematically incorrect treatment of linear regression and related concepts probably kept the students from grasping the relationship between the measured experimental values (measuring points) and the corresponding graph with respect to linear regression. Clarity from the teacher is particularly important in such contexts, as upper secondary school students are known to struggle with interpreting empirical data through graphs [13]. The didactic contract includes an agreement on the meaning of the notations used [30]. In the cases where the teachers investigated in this study used notations or concepts ambiguously or even wrongly, the didactic contracts were broken. In addition, when mathematics was dealt with technically, it seemed difficult to support students’ relational understanding of a theoretical model in physics. This kind of contract breach was pointed out by the student in Teacher 4′s classroom in episode E4.3.
The part of the study reported here was conducted within a qualitative paradigm that naturally limits the ability to generalise the results. The analysis entailed subjective categorisation by the three researchers. To obtain a reliable and valid result, the researchers analysed part of the data together, as depicted in the analysis section. The time spent collecting data was brief compared to the time the teachers spent teaching; hence, the results are images of the studied occasions. This is part of the research design, and the results give proof of the existence rather than evidence of trends in the teachers’ practices.
6. Conclusions and Implications
We conclude that the ternary model of Reality–Theoretical models–Mathematics [5] and the joint action theory in didactics [24] together provide a powerful analytical tool for analysis of physics teaching. Furthermore, our results support and deepen the collected knowledge about the importance of teachers in accordance with earlier results from both science and mathematics education research on the use of mathematics in physics teaching [8,9,11,15]. Teachers’ lack of mathematical stringency may have negative effects on students’ communication habits and mathematics and physics education. Further studies of such effects would be useful for both research and practice. We also agree with the view presented in [52] with respect to seeing the need to compare teachers’ mathematical stringency between mathematics and physics classrooms, which is something we have started to follow up [53] on and intend to study further in future work. Using the presented analytic framework can help teachers and teacher educators develop physics teaching methods and lead to the improvement of students’ essential skills in mathematics and physics, thus opening pathways for further studies in STEM areas. The discovery of ways to help students develop essential skills in mathematics during their science studies at this level has recently been proposed as important factor for durable education leading to STEM degrees and careers [7]. We support this idea and see a need for further research investigating the possible correlations between teacher profiles, physics teaching, and students’ knowledge in physics and choices concerning STEM degrees and careers.
Author Contributions
Conceptualisation, A.R., K.J. and Ö.H.; Data curation, A.R., K.J. and Ö.H.; Formal analysis, A.R., K.J. and Ö.H.; Funding acquisition, A.R., K.J. and Ö.H.; Investigation, A.R., K.J. and Ö.H.; Methodology, A.R., K.J. and Ö.H.; Project administration, A.R.; Resources, A.R.; Writing, A.R., K.J. and Ö.H.; Writing—review and editing, A.R., K.J. and Ö.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Swedish Research Council (721-2008-484).
Institutional Review Board Statement
Ethical considerations for this research adhere to the recommendations stipulated by the Swedish Research Council and meet the ethics requirements of our institution.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Angell, C.; Lie, S.; Rohatgi, A. TIMSS Advanced 2008: Fall i fysikk-kompetanse i Norge og Sverige. Nord. Stud. Sci. Educ. 2011, 7, 17–31. [Google Scholar] [CrossRef]
- Belo, N.A.; van Driel, J.H.; van Veen, K.; Verloop, N. Beyond the dichotomy of teacher-versus student-focused education: A survey study on physics teachers’ beliefs about the goals and pedagogy of physics education. Teach. Teach. Educ. 2014, 39, 89–101. [Google Scholar] [CrossRef]
- Fredlund, T.; Airey, J.; Linder, C. Exploring the role of physics representations: An illustrative example from students sharing knowledge about refraction. Eur. J. Phys. 2012, 33, 657. [Google Scholar] [CrossRef]
- Karam, R. Framing the structural role of mathematics in physics lectures: A case study on electromagnetism. Phys. Rev. ST Phys. Educ. Res. 2014, 10, 010119. [Google Scholar] [CrossRef]
- Hansson, L.; Hansson, Ö.; Juter, K.; Redfors, A. Reality—Theoretical Models—Mathematics: A ternary perspective on physics lessons in upper-secondary school. Sci. Educ. 2015, 24, 615–644. [Google Scholar] [CrossRef]
- Redfors, A.; Hansson, L.; Hansson, Ö.; Juter, K. A framework to explore the role of mathematics during physics lessons in upper-secondary school. In Insights from Research in Science Teaching and Learning. Book of Selected Papers from the ESERA 2013 Conference; Contributions from Science Education Research; Papadouris, N., Hadjigeorgiou, A., Constantinou, C.P., Eds.; Springer: Dordrecht, The Netherlands, 2016; Volume 2, pp. 139–151. [Google Scholar]
- Cohen, R.; Kelly, A.M. Mathematics as a factor in community college STEM performance, persistence, and degree attainment. J. Res. Sci. Teach. 2020, 57, 279–307. [Google Scholar] [CrossRef]
- Meli, K.; Zacharos, K.; Koliopoulos, D. The integration of mathematics in physics problem solving: A case study of Greek upper secondary school students. Can. J. Sci. Math. Technol. Educ. 2016, 16, 48–63. [Google Scholar] [CrossRef]
- Michelsen, C. Mathematical modeling is also physics—Interdisciplinary teaching between mathematics and physics in Danish upper secondary education. Phys. Educ. 2015, 50, 489–494. [Google Scholar] [CrossRef]
- Redish, E.F. Using math in physics: Overview. Phys. Teach. 2021, 59, 314–318. [Google Scholar] [CrossRef]
- Turşucu, S.; Spandaw, J.; Flipse, S.; de Vries, M.J. Teachers’ beliefs about improving transfer of algebraic skills from mathematics into physics in senior pre-university education. Int. J. Sci. Educ. 2017, 39, 587–604. [Google Scholar] [CrossRef]
- Zhao, F.F.; Chau, L.; Schuchardt, A. Blended and more: Instructors organize sensemaking opportunities for mathematical equations in different ways when teaching the same scientific phenomenon. Int. J. STEM Educ. 2021, 8, 26. [Google Scholar] [CrossRef]
- Pols, C.F.J.; Dekkers, P.J.J.M.; de Vries, M.J. What do they know? Investigating students’ ability to analyse experimental data in secondary physics education. Int. J. Sci. Educ. 2021, 24, 274–297. [Google Scholar] [CrossRef]
- Pietrocola, M. Mathematics as structural language of physical thought. In Connecting Research in Physics Education with Teacher Education; Vicentini, M., Sassi, E., Eds.; International Commission on Physics Education: Trieste, Italy, 2008; Volume 2. [Google Scholar]
- Uhden, O.; Karam, R.; Pietrocola, M.; Pospiech, G. Modelling Mathematical Reasoning in Physics Education. Sci. Educ. 2012, 21, 485–506. [Google Scholar] [CrossRef]
- Højgaard Jensen, J.; Niss, M.; Jankvist, U.T. Problem solving in the borderland between mathematics and physics. Int. J. Math. Educ. Sci. Technol. 2017, 48, 1–15. [Google Scholar] [CrossRef]
- Niss, M. What is physics problem-solving competency? The views of Arnold Sommerfeld and Enrico Fermi. Sci. Educ. 2018, 27, 357–369. [Google Scholar] [CrossRef]
- Niss, M.; Højgaard, T. Mathematical competencies revisited. Educ. Stud. Math. 2019, 102, 9–28. [Google Scholar] [CrossRef]
- Niss, M.; Jensen, T.H. Kompetencer og Matematiklæring—Ideer og Inspiration til Udvikling af Matematikundervisning i Danmark [Competencies and Mathematical Learning—Ideas and Inspiration for the Development of Mathematics Teaching and Learning in Denmark]; The Ministry of Education: Copenhagen, Denmark, 2002. [Google Scholar]
- Hansson, L.; Hansson, Ö.; Juter, K.; Redfors, A. Curriculum Emphases, Mathematics and Teaching Practices—Swedish Upper-Secondary Physics Teachers’ views. Int. J. Sci. Math. Educ. 2021, 19, 499–515. [Google Scholar] [CrossRef]
- Johansson, A.; Andersson, S.; Salminen-Karlsson, M.; Elmgren, M. “Shut up and calculate”: The available discursive positions in quantum physics courses. Cult. Stud. Sci. Educ. 2018, 13, 205–226. [Google Scholar] [CrossRef]
- Şengören, S.K.; Çoban, A.; Büyükdede, M. Physics teacher candidates’ awareness of idealizations used in mathematical models. Eur. J. Phys. 2020, 42, 015705. [Google Scholar] [CrossRef]
- Hansson, L.; LISMA, Kristianstad University, Kristianstad, Sweden; Hansson, Ö.; LISMA, Kristianstad University, Kristianstad, Sweden; Juter, K.; LISMA, Kristianstad University, Kristianstad, Sweden; Redfors, A.; LISMA, Kristianstad University, Kristianstad, Sweden. Physics Teachers’ views on Nature of Science and Mathematics in Relation to Teaching at Upper-Secondary school. Unpublished work. 2023. [Google Scholar]
- Sensevy, G. About the joint action theory in didactics. Z. Erzieh. 2012, 15, 503–516. [Google Scholar] [CrossRef]
- Bruner, J. Early social interaction and language acquisition. In Studies in Mother-Infant Interaction; Schaffer, H.R., Ed.; Academic Press: Cambridge, MA, USA, 1977; pp. 271–289. [Google Scholar]
- Eilan, N.; Hoert, C.; Teresa, M.; Johannes, R. Joint Attention: Communication and Other Minds; Clarendon Press: Oxford, UK, 2005. [Google Scholar]
- Gibson, J.J. The Ecological Approach to Visual Perception; Lawrence Erlbaum: Hilsdale, NJ, USA, 1979. [Google Scholar]
- Clark, H. Using Language; Cambridge University Press: Cambridge, NY, USA, 1996. [Google Scholar]
- Brousseau, G. The Theory of Didactic Situations in Mathematics; Kluwer: Dordrecht, The Netherlands, 1997. [Google Scholar]
- Sensevy, G.; Gruson, B.; Forest, D. On the Nature of the Semiotic Structure of the Didactic Action: The Joint Action Theory in Didactics Within a Comparative Approach. Interchange 2015, 46, 387–412. [Google Scholar] [CrossRef]
- Tiberghien, A.; Cross, D.; Sensevy, G. The evolution of classroom physics knowledge in relation to certainty and uncertainty. J. Res. Sci. Teach. 2014, 51, 930–961. [Google Scholar] [CrossRef]
- Adúriz-Bravo, A. A ‘Semantic’ View of Scientific Models for Science Education. Sci. Educ. 2012, 22, 1593–1611. [Google Scholar] [CrossRef]
- Giere, R.N. Understanding Scientific Reasoning, 4th ed.; Harcourt Brace College Publishers: Cambridge, MA, USA, 1997. [Google Scholar]
- Koponen, I.T. Models and modelling in physics education: A critical re-analysis of philosophical underpinnings and suggestions for revisions. Sci. Educ. 2007, 16, 751–773. [Google Scholar] [CrossRef]
- Hansson, L.; Hansson, Ö.; Juter, K.; Redfors, A. A case study of the role of mathematics in physics textbooks and in associated lessons. In Mathematics in Physics Education; Pospiech, G., Michelini, M., Eylon, B., Eds.; Springer: Dordrecht, The Netherlands, 2019; pp. 293–316. [Google Scholar]
- Triantafillou, C.; Spiliotopoulou, V.; Potari, D. The Nature of Argumentation in School Mathematics and Physics Texts: The Case of Periodicity. Int. J. Sci. Math. Educ. 2016, 14, 681–699. [Google Scholar] [CrossRef]
- Bliss, J.; Monk, M.; Ogborn, J. Qualitative Data Analysis for Educational Research; Croom Helm: Dundee, UK, 1983. [Google Scholar]
- Skemp, R. Instrumental understanding and relational understanding. Math. Teach. 1976, 77, 20–26. [Google Scholar]
- van Driel, J.H.; Bulte, A.M.; Verloop, N. Using the curriculum emphasis concept to investigate teachers’ curricular beliefs in the context of educational reform. J. Curric. Stud. 2008, 40, 107–122. [Google Scholar] [CrossRef]
- Roberts, D.A. Developing the concept of ‘curriculum emphases’ in science education. Sci. Educ. 1982, 66, 243–260. [Google Scholar] [CrossRef]
- Roberts, D.A. What counts as science education? In Development and Dilemmas in Science Education; Fensham, P.J., Ed.; Falmer Press: London, UK, 1988; pp. 27–54. [Google Scholar]
- Roberts, D.A. Junior high school science transformed: Analysing a science curriculum policy change. Int. J. Sci. Educ. 1995, 17, 493–504. [Google Scholar] [CrossRef]
- de Putter-Smits, L.G.A.; Taconis, R.; Jochems, W.M.G. Mapping context-based learning environments: The construction of an instrument. Learn. Environ. Res. 2013, 16, 437–462. [Google Scholar] [CrossRef]
- Grigutsch, S.; Törner, G. World views of mathematics held by university teachers of mathematics science. In Schriftenreihe des Fachbereichs Matematik; Reprint 420; Gerhard Mercator University: Duisburg, Germany, 1998. [Google Scholar]
- Chen, S. Development of an instrument to assess views on nature of science and attitudes toward teaching science. Sci. Educ. 2006, 90, 803–819. [Google Scholar] [CrossRef]
- IEA. TIMSS Advanced 2015. Trends in International Mathematics and Science Study. Teacher Questionnaire Physics; IEA: Paris, France, 2014. [Google Scholar]
- Buabeng, I. Teaching and Learning of Physics in New Zealand High Schools. Ph.D. Thesis, University of Canterbury, School of Educational Studies and Leadership, St. Petersburg, FL, USA, 2015. [Google Scholar]
- Angell, C.; Guttersrud, Ø.; Henriksen, E.K.; Isnes, A. Physics: Frightful, But Fun Pupils’ and Teachers’ Views of Physics and Physics Teaching. Sci. Educ. 2004, 88, 683–706. [Google Scholar] [CrossRef]
- Swedish National Agency for Education. Upper Secondary School 2011—Revised 2018; Fritzes: Stockholm, Sweden, 2018. [Google Scholar]
- Swedish Research Council. Good Research Practice; Swedish Research Council: Stockholm, Sweden, 2016. [Google Scholar]
- Duit, R. On the role of analogies and metaphors in learning science. Sci. Educ. 1991, 75, 649–672. [Google Scholar] [CrossRef]
- Veith, J.M.; Bitzenbauser, P.; Girnat, B. Exploring learning difficulties in abstract algebra: The case of group theory. Educ. Sci. 2022, 12, 516. [Google Scholar] [CrossRef]
- Juter, K.; Hansson, Ö.; Redfors, A. Actions in the learning environment: Analyzing physics and mathematics lessons in the case of ODE. In Proceedings of the 14th International Congress on Mathematical Education, ICME-14, Shanghai, China, 12–19 July 2020. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).