Abstract
In this article, we analyze the basis of a proposal that allows teaching the notions of reflection, refraction, interference and diffraction from a unified perspective, using Fermat’s variational principle, recovered by Richard Feynman in his formulation of the paths sum for quantum mechanics. This allows reconsidering the notions of geometrical and physical optics, using the probabilistic and unified model of quantum mechanics by means of mathematical notions that are accessible to high school students.
Keywords:
light; quantum; interference; teaching; secondary school; Feynman; Fermat; probability; paths 1. The School Study of Light
Light, and the phenomena in which it intervenes, have always had and still have a universal interest because they are inherently linked to the history of humanity. The purpose of studying these phenomena is present both in formal education institutions, from the first levels of the educational system to high school, and in informal education institutions such as science museums or planetariums [1,2,3,4,5,6,7,8,9,10,11]. In this sense, we can consider that light is a conceptual field involving various sciences, such as physics, astrophysics, chemistry, nuclear medicine, etc.
However, for diverse reasons, the curriculum, school organization, and teaching successively divide knowledge, first into areas and disciplines, which may or may not be supported by scientific, technological, or professional communities of reference that validate this knowledge. Thus, the curriculum refers to physics, chemistry, astronomy, language, natural sciences, social sciences, earth sciences, biology, health sciences, mathematics, art, etc., to then, within each one of them, atomize knowledge into “topics” that comprise the program of those school disciplines. In almost all of the aforementioned areas, phenomena related to the behavior of light arise, which, in the best of cases, are studied in an atomized way, without an interdisciplinary or intra-disciplinary relationship.
Likewise, closer examination of the segmentation of the world that is carried out for educational purposes, the phenomena related to light are proposed within what is called optics, which is defined as a branch of physics that studies light. The school study of light is basically developed from two models: that of geometric optics, which adopts the notion of light ray as the rectilinear trajectory of “material particles” coming from luminous bodies. In this mechanistic and corpuscular model, we could inscribe some representatives of classical Greece and Newton himself, Descartes and Snell, who provided an account of the phenomena of reflection, refraction, and the decomposition of light, as well as the detailed study of various types of lenses. The so-called Law of Refraction was first discovered by Ibn Sahl in the 10th century, who used it to resolve the shapes of anaclastic lenses (which focus light with geometric aberrations). It was rediscovered in the 16th century and revealed again in the 17th century by Snell. In French-speaking countries, Snell’s law is known as the “second law of contraction” or “Descartes’ law”).
On the other hand, in 1690, Huygens (1629–1695) proposed a wave model for light and deduced the laws of reflection and refraction. Light waves were understood as longitudinal, and his model required the existence of a mechanical medium, which was called ether, disputing his ideas with Newton. In the 19th century, Young discovered the phenomena of interference and diffraction of light, which are explained with the wave model, but not with the ray model. In addition, he assumed that they were three-dimensional transverse waves. For his part, Faraday established an interplay between electromagnetism and light by noting that the direction of polarization of a light ray can be altered by the action of a strong magnetic field and suggested that light could have an electromagnetic nature. James Clerk Maxwell (1831–1879) in turn, extensively developed the wave model and demonstrated that light waves, such as radio waves, X-rays, etc., are electromagnetic waves, and they do not need any material medium to propagate.
Subsequently to these events, at the beginning of the 20th century, more specifically in 1905, Einstein received the Nobel Prize for explaining the photoelectric effect, proposing the quantization of energy and the “strange” event that when light falls on the cathode in a vacuum tube, it manages to “pull” electrons that generate a current, the intensity of which depends on the frequency of the incident light. From these facts, new phenomena and debates linked to the interactions between “matter” and “radiation” began. Einstein presented a solution by means of the most famous formula in the world, which also appears in one of his 1905 papers: the paper proposing the Special Theory of Relativity, which he would generalize in 1915 by formulating General Relativity. However, the news and facts requiring explanation did not end there. The photoelectric effect, the quantization of energy applied to the study of the atom and atomic spectra, to black body radiation and to radioactive phenomena that revealed the emergence of new particles, opened the way to new controversies linked to phenomena of the field that today we know as “Quantum Mechanics”, where facts involving light arise.
As a general rule, the knowledge developed since the mid-19th century, including wave mechanics, special relativity, and quantum mechanics, is not commonly taught in schools as an integrated subject. Furthermore, it is worth noting that there is a significant variation in how this topic is approached in different countries, particularly in Latin America [12,13,14,15]. Thus, students study atomized parts of optics and electromagnetism without even dabbling in the wave model, nor in the phenomena of interference and diffraction, even when their study is prescribed in the curriculum. However, the curricular inclusion of relativistic phenomena and quantum models is more the exception than the rule.
Let us mention that it is not our aim to provide a comprehensive historical account of the development of optics in this paper, and therefore, many of its major contributors are not included. Rather, we have focused on the key figures that we consider to be pillars for the conceptual framework we propose, specifically Fermat and Feynman. By doing so, we aim to offer a more focused discussion of the theoretical underpinnings of our work.
In high school, reflection and refraction are typically taught through the lens of geometric optics, but not through the framework of wave optics or quantum mechanics. We believe that this limited approach can be a disadvantage when it comes to understanding these phenomena across different scales and experimental contexts, which can prevent students from fully exploring their potential. It is particularly noteworthy that the quantum context is almost entirely neglected in the teaching of these concepts, which further limits students’ understanding and exploration of the phenomena.
In this paper, we try to answer the following questions:
- o Can waveless wave optics be taught in high school?
- o How can geometrical, wave and quantum optics be taught together in secondary school?
2. Fermat’s Principle
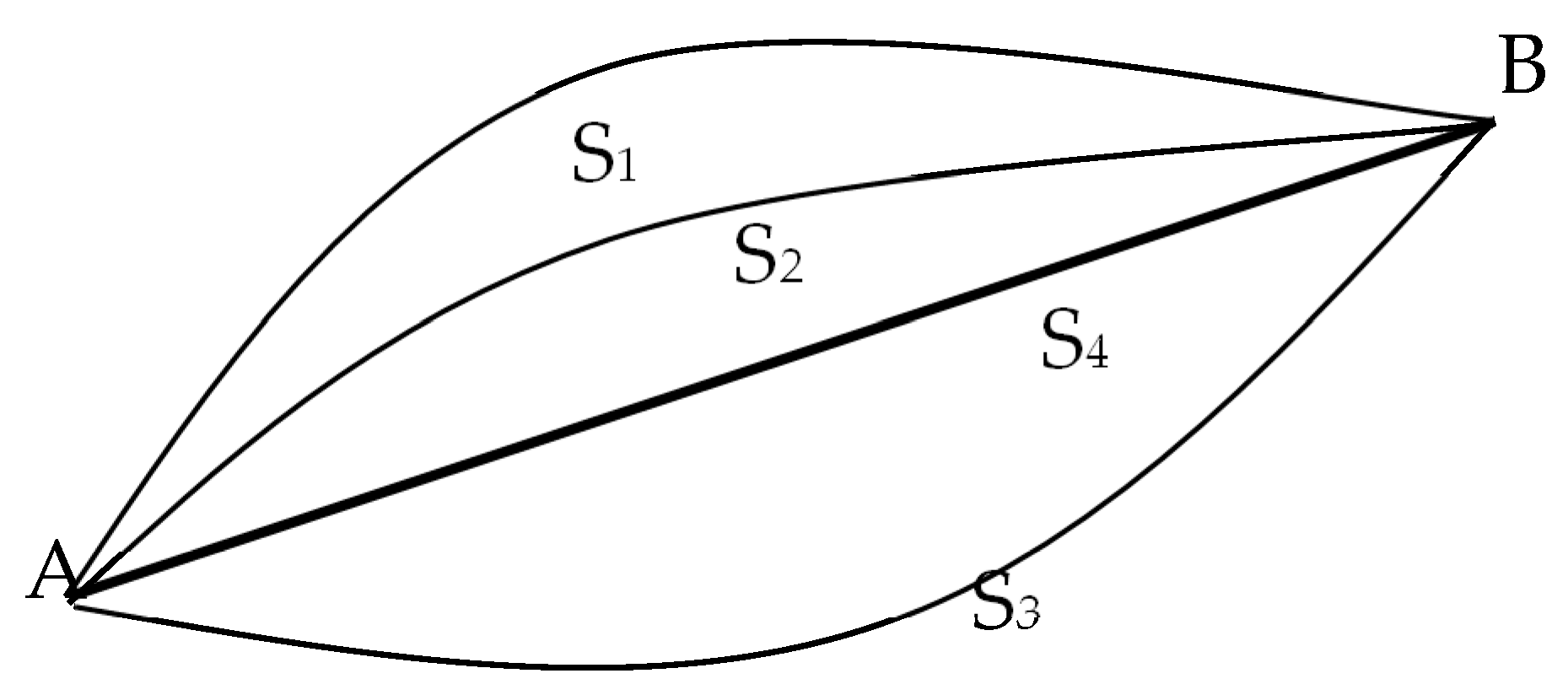
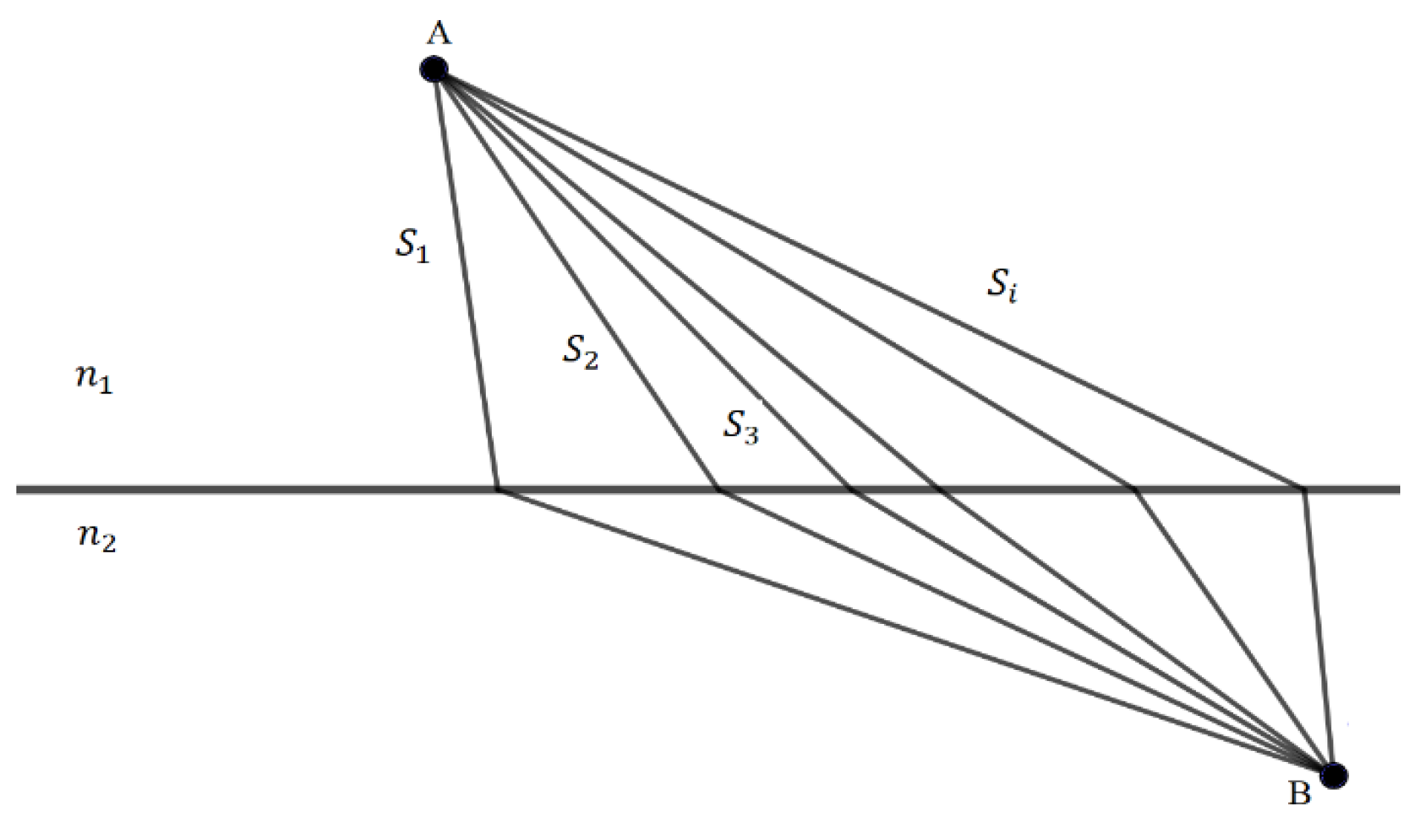
Fermat (1601–1665) made a central contribution in his time, which, as we try to show in this work, has acquired a greater dimension today. In 1650, he enunciated a fundamental principle for light rays, which is still valid today. This expresses that of all the paths that light can follow to go from one point to another as illustrated in Figure 1; it always “chooses” the one that corresponds to the shortest time. Fermat’s is a variational principle, which is very relevant from a physical and didactic point of view, because in this second case, it makes possible the quantum treatment of light that we have been trying to introduce in secondary education for several years. Variational principles express mathematically the fact that a natural phenomenon seems to occur in the most optimal way possible.
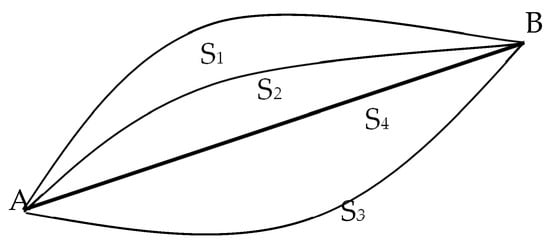
Figure 1.
Representation of Fermat’s Principle. The path of least time is S4.
As we know, the refraction index associated with a given medium is defined by:
where c the speed of light in the vacuum and v the speed of light in that medium. Traveling time can be expressed as
where s is the distance traveled by light in the medium. Thus, in a homogeneous medium, the minimum time corresponds to rectilinear propagation (the shortest path). However, if the medium changes, minimizing time implies traveling “as much as possible” in the medium with the highest speed, that is, with the lowest n. This is the reason why the path of light is “broken” when passing from one medium to another in refraction. We will look at this and other aspects in more detail in the next section.
3. Reflection
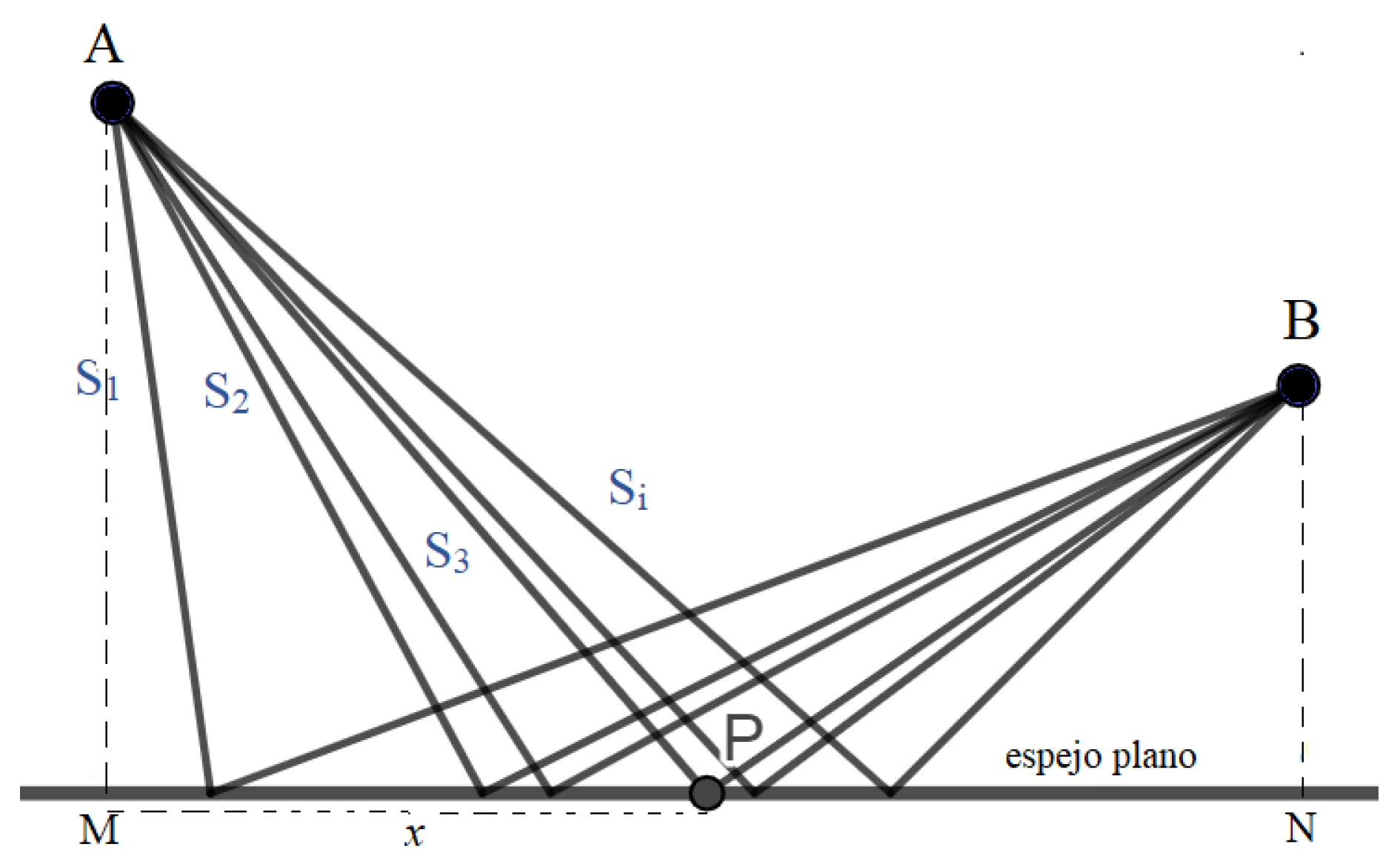
In addition to the experimental evidence that exists for the laws of reflection and refraction, these laws can be obtained relatively easily using Fermat’s principle. Take, for example, a beam of light that propagates from point A to point B, reflecting on a flat mirror as showed in Figure 2.
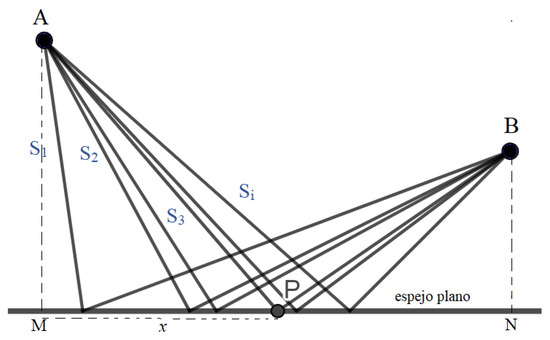
Figure 2.
Possible paths of a beam of light reflected from a plane mirror. The incident rays on P correspond to the path of least time.
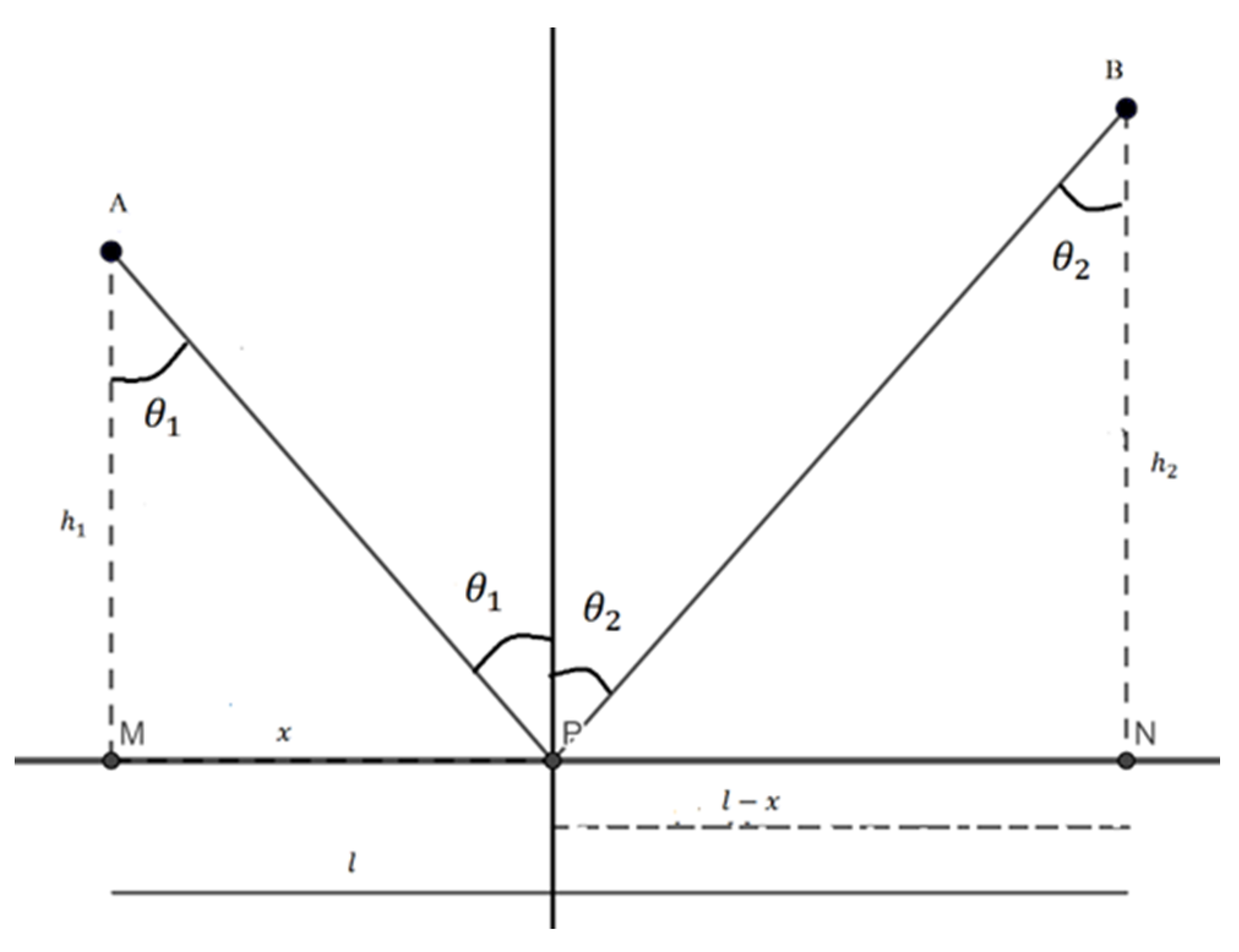
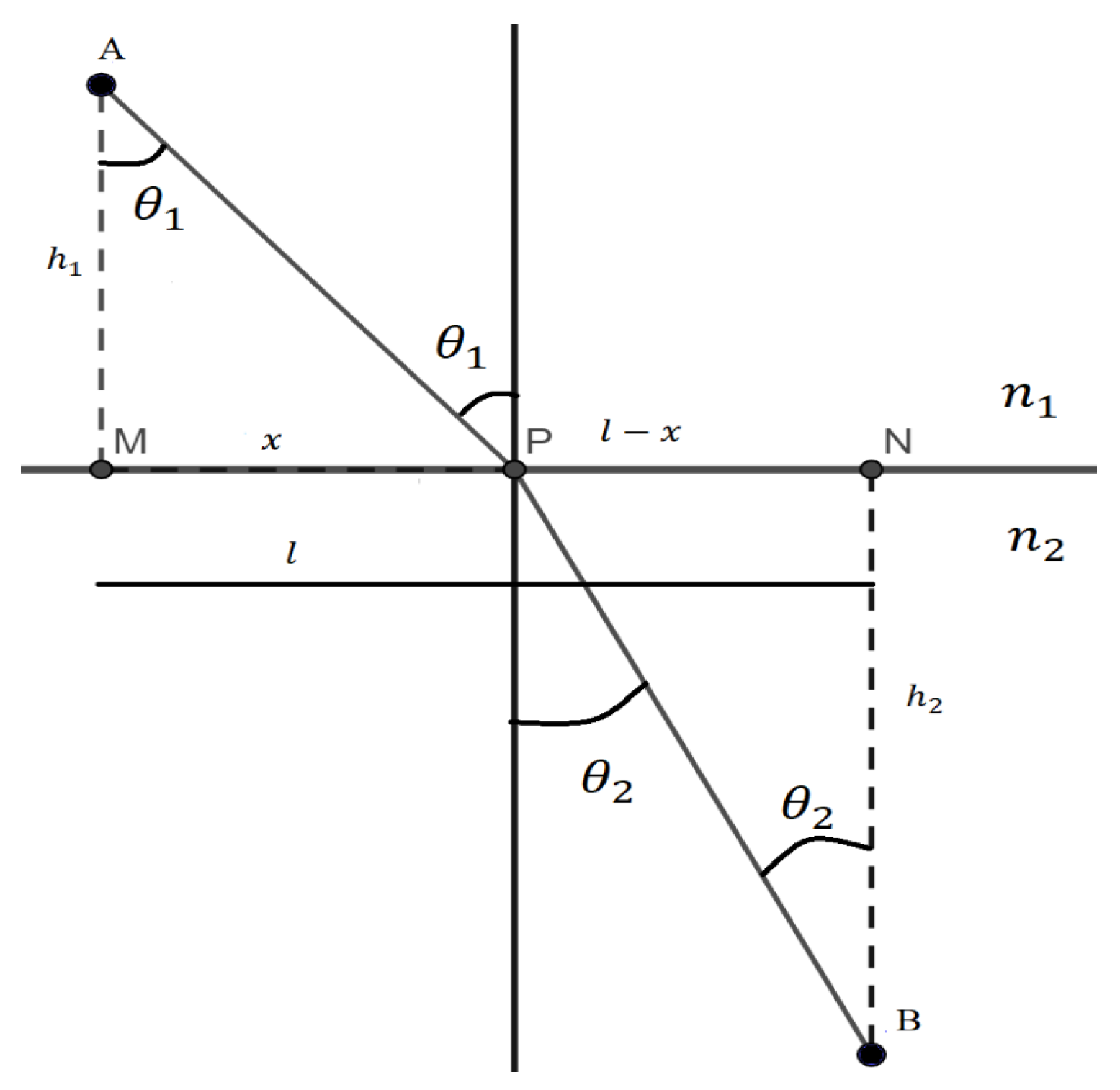
Obviously, we can imagine infinite trajectories for the beam of light and it is clear that these depend on the point of the mirror in which that beam is reflected. The position of point P is the one that corresponds to the real, least time, trajectory. In Figure 3, points M, N represent the intersection of the orthogonal projections of points A and B on the plane mirror and x the distance from P to point M. Thus, it can be written:
then
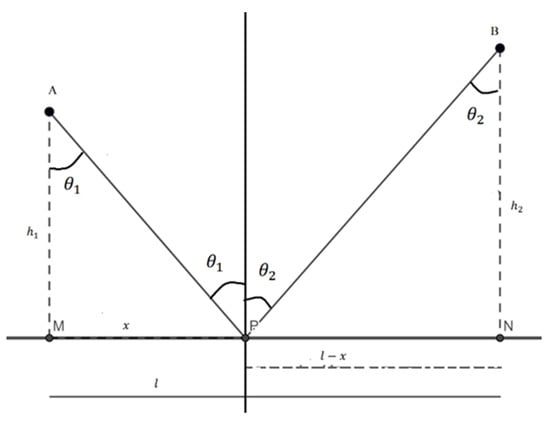
Figure 3.
Calculation of the minimum time path.
Then, the length of the path of the light beam will be:
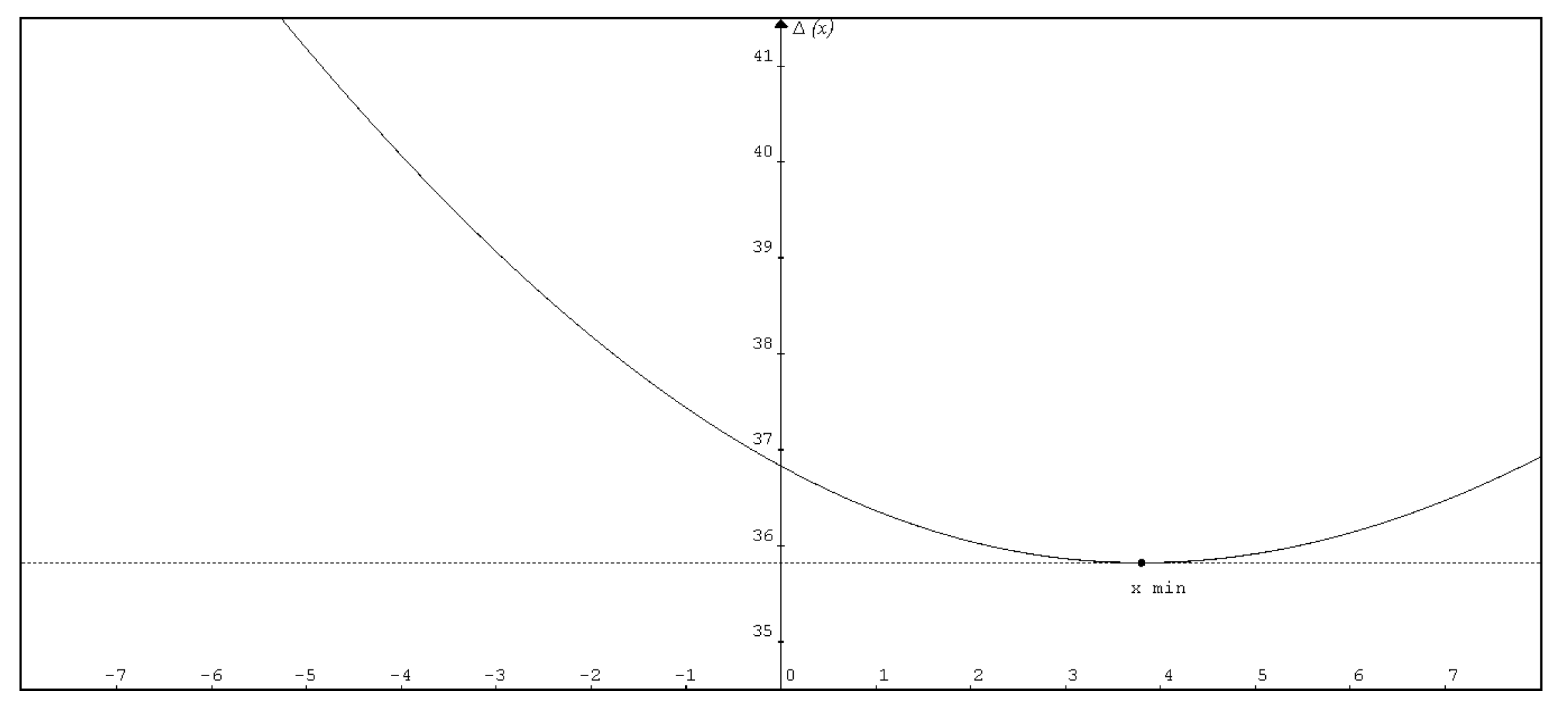
while the time it takes light to travel the distance s, which is represented in Figure 4, will be:
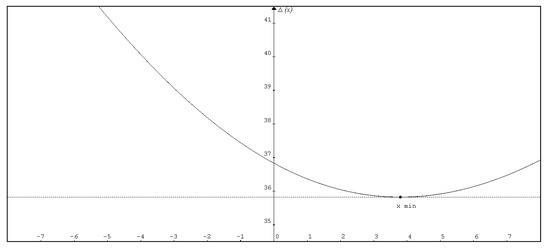
Figure 4.
Graphical representation of the time used by different paths depending on the abscissa of the point of incidence (see Figure 2).
Note that x is the variable that indicates the different paths. Applying Fermat’s Principle, the derivative of the time with respect to x is calculated and set equal to zero:
from which results
That is, for the time to be minimal, the angles of incidence and reflection must be equal when the reflection of light occurs. Note that the test of the first zero derivative at a point is a necessary condition for a relative minimum, but not a sufficient one. For it to be a relative minimum, the second derivative must be positive in that point. We do not elaborate further here (or in what follows) on this because it is standard, but the reflection point can be shown to be an absolute minimum in this case.
4. Refraction
Similarly, the Snell–Descartes law for refraction can be obtained using Fermat’s Principle. Let us consider, for example, the case of a light beam that propagates from point A located in a medium of refractive index n1 to a point B located in a medium of refractive index n2 as indicated in Figure 5.
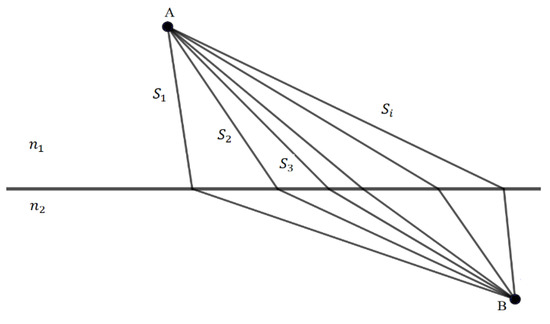
Figure 5.
Possible paths of a refracted light beam when passing from one medium to another, connecting points A and B.
In this case, we can also imagine infinite trajectories that differ by the position of the point P on the interface. Next, we consider one of the possible paths s that light can follow, as shown in Figure 6. The length will be:
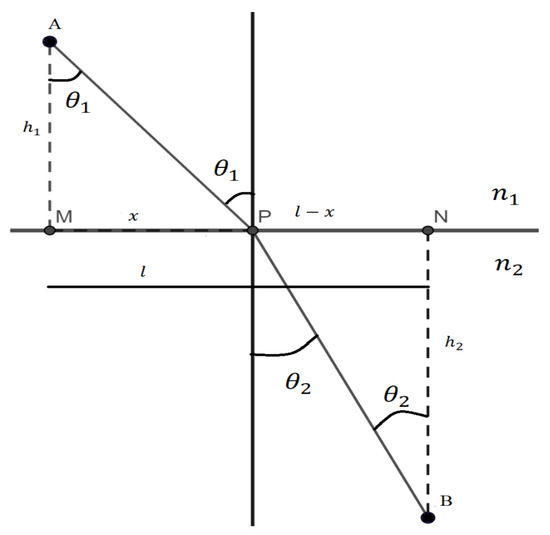
Figure 6.
Calculation of the minimum time path.
While the time it takes for light to travel s will be
Applying Fermat’s Principle, the time derivative is calculated and set equal to zero:
from which it results
This formula, called Snell’s Law, must be fulfilled for the least time path in the light refraction.
Another important consequence of Fermat’s principle is the principle of reversibility. This principle establishes that if s is the trajectory which, according to Fermat’s principle, a beam of light that propagates from A to B follows, then s in the opposite direction is followed when going from B to A.
5. Curved Mirrors and Reflection
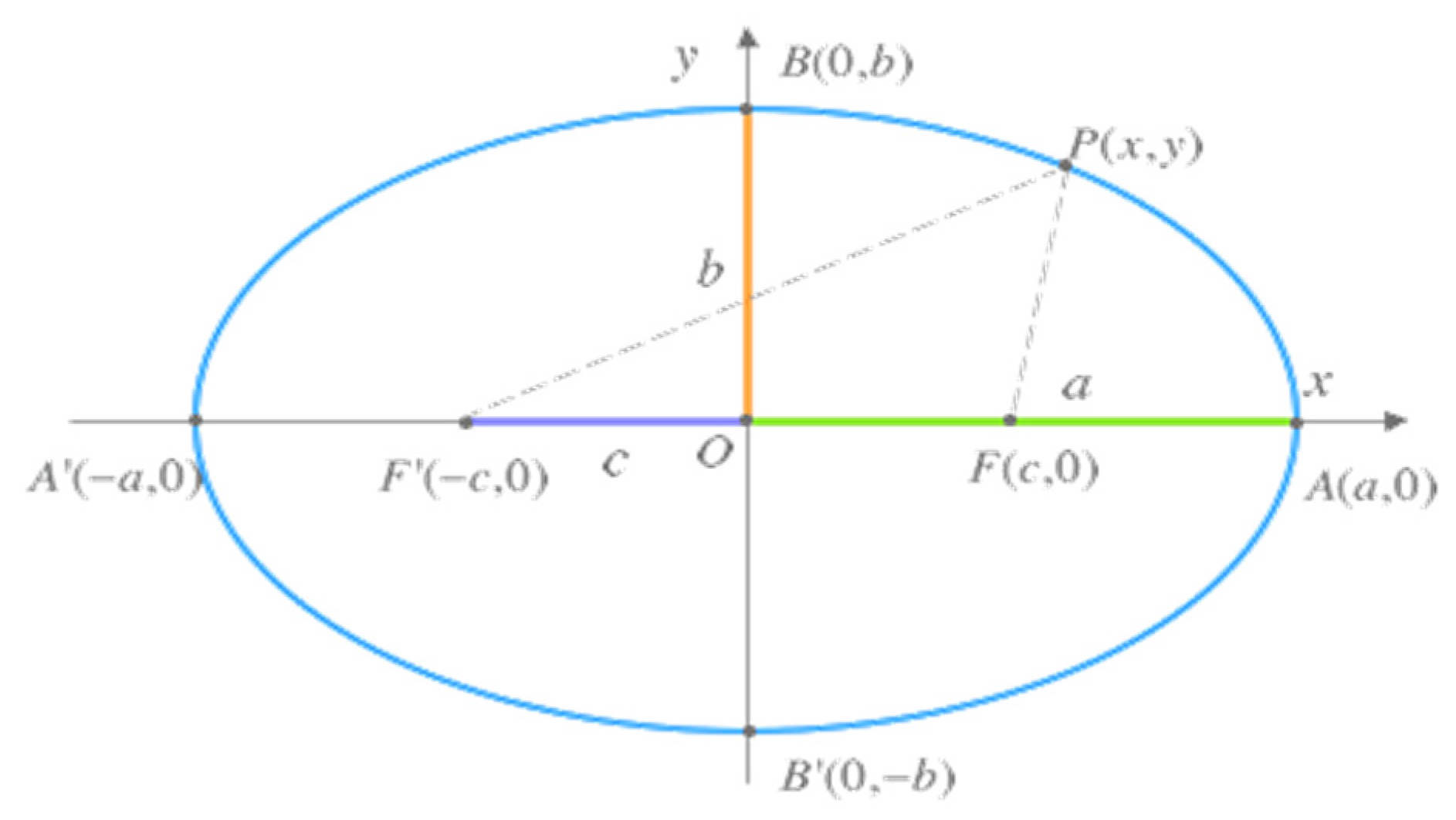
What happens when light reflects off an elliptical, parabolic, or hyperbolic surface? Let us consider for example the case of the ellipse, represented in Figure 7. As we know, the ellipse is defined by the set of all points P in a plane, such that the sum of the distances d from P to two fixed “foci” points F and F′ on the plane is constant. If the coordinates of the foci are F = (c,0) and F′ = (−c,0), every point P that belongs to the ellipse satisfies that d(P,F) + d(P,F′) = k, where k is a constant greater than zero.
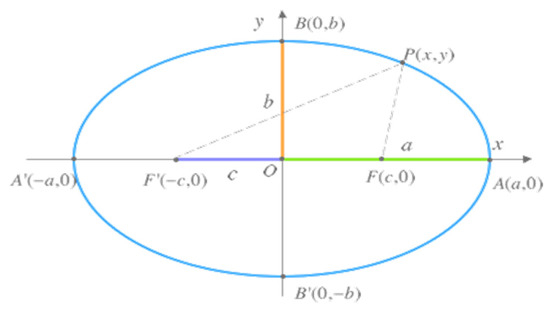
Figure 7.
Basic diagram of the ellipse with the principal elements, focus, and major and minor semiaxis.
If in particular the point A that belongs to the ellipse is taken, it is established that k = 2a. Then any point P on the ellipse satisfies the equation:
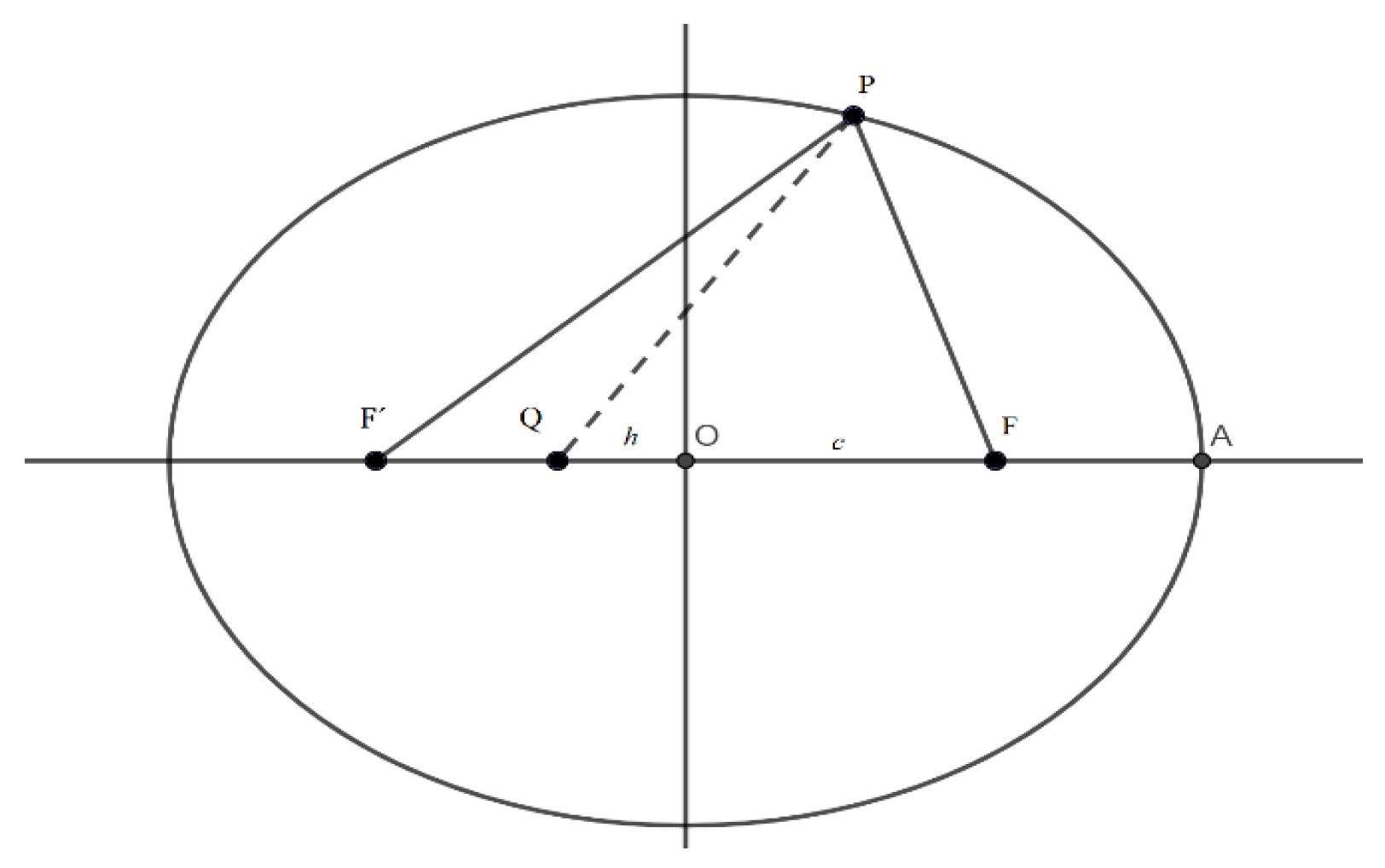
Now suppose that a ray of light had come out of one of the sources and had been reflected in P arriving at Q as showed in Figure 8.
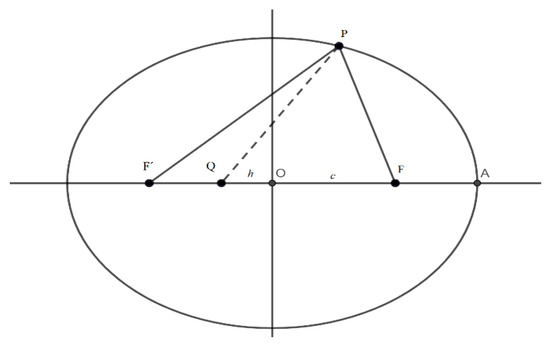
Figure 8.
Diagram for the application of Fermat’s principle of the minimum time for reflection on an elliptical surface.
Then the time that light takes for that path is
where v is the speed of light in the medium. Its derivative with respect to x is
The derivative is zero when h = −c. The application of Fermat’s principle indicates that of all the possible paths that light could take (the ray that starts from one focus, is reflected in the ellipse and passes through the other focus), is the path of least time.
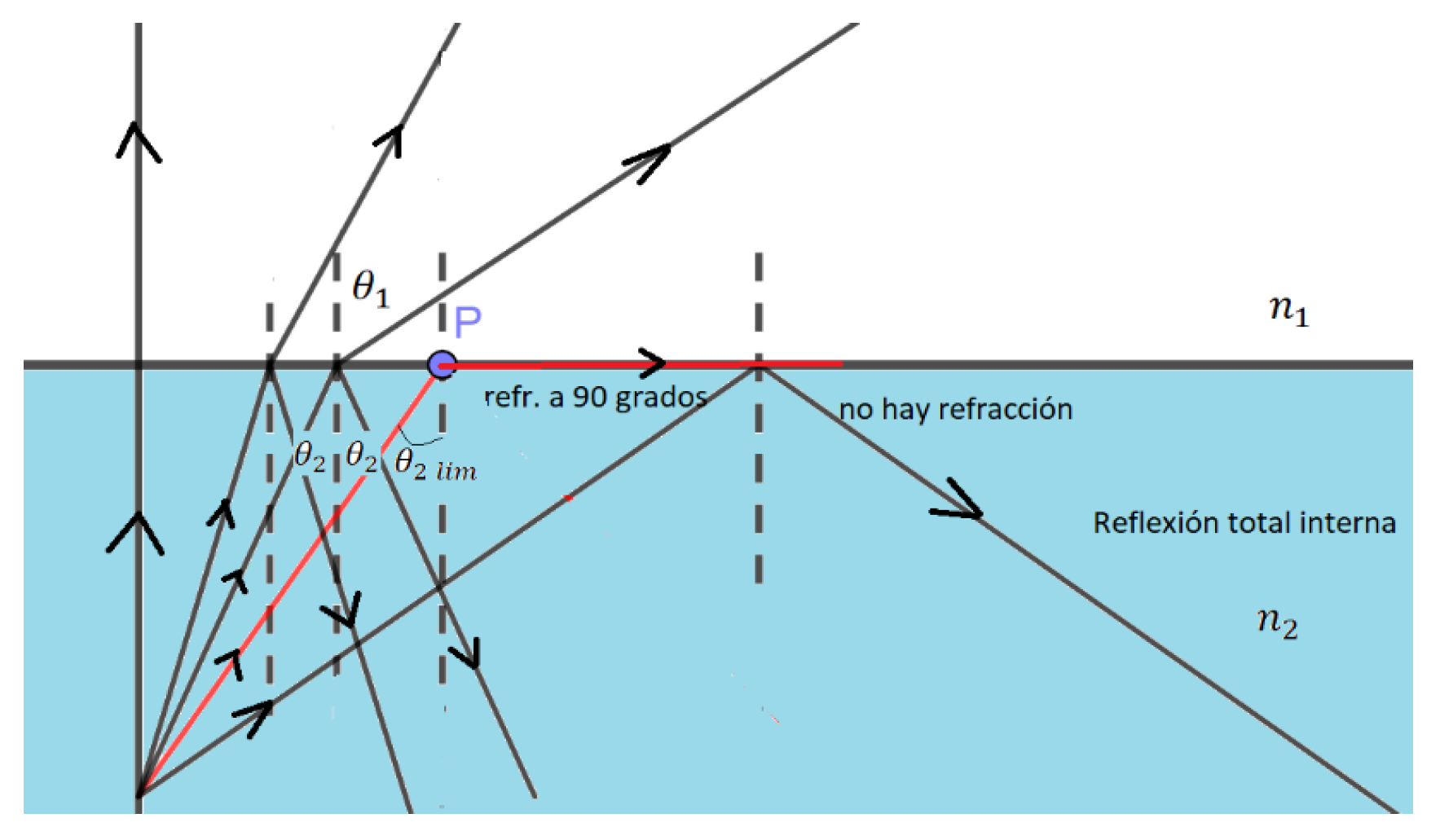
6. Total Internal Reflection
Apart from the classical applications to lenses (which are not covered here), an interesting application of Snell’s law occurs when there are two media with refractive indices n1, n2, where n2 > n1 and the light source is located in the medium with the highest index of refraction (here, the incidence is in medium 2, in contrast to the previous section). In this case, according to Snell’s law: , the angle of refraction is always greater than the angle of incidence .
As can be seen in Figure 9, the limiting case occurs when the refracted ray is parallel to the interface between both media (indicated in red). The limiting incidence angle (for which ), is fulfilled according to Snell’s law:
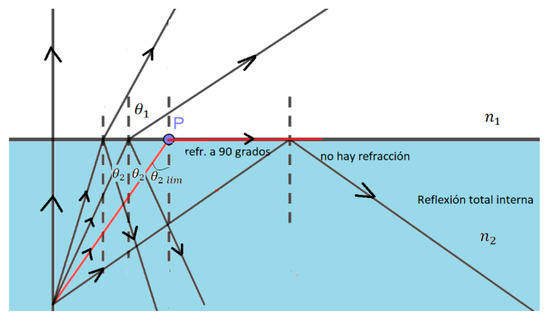
Figure 9.
Scheme of total internal reflection and critical angle.
In other words, the limiting incidence angle depends on the relationship between the refractive indices of the two media. It follows that for angles of incidence greater than , the should assume values greater than one, this being mathematically impossible. From a physical point of view, this is interpreted considering that if the light rays hit with angles greater than , there will be no refraction. Experimentally it can be seen that in this case there is only reflection and no refraction, so the interface works as a perfect mirror. This phenomenon is called total internal reflection and is used in the propagation of light in optical fibers, where information loss due to refraction is avoided.
7. Quantum Mechanics and the Feynman Approach Applied to Light Phenomena
Quantum mechanics and the theory of relativity are the most important revolutions in physics of the first quarter of the twentieth century. Although the latter is probably better known, quantum mechanics has had a much greater impact on subsequent technological development. After almost a century, the concepts of quantum mechanics continue to defy common sense, which is based on the macroscopic world, on a human scale. In particular, the wave–particle duality has been the basis of the difficulties involved in conceptualizing the notion of a quantum system. The central question within the framework of this work is to introduce the basic ideas of a complex subject such as quantum physics in an accessible way for high school students, and to explain light phenomena with a unified framework.
Feynman’s Multiple Paths approach is an alternative for studying the behavior of electrons and electromagnetic radiation that allows us to address the concept of probability, the principle of superposition and correspondence, and offers the possibility of understanding the fundamental and universal nature of the laws of quantum mechanics. Its potential, from a didactic point of view, consists in the use of a vector geometric framework to calculate probabilities, which is applied to a simple case of emission and detection of light or a free electron. Then, the results can be applied to more complex cases, such as diffraction and interference, for example in the Double Slit Experience (DSE).
Our proposal for teaching quantum mechanics is based on the path integral technique, which we will call here the sum of all alternatives (SAA) developed by R. Feynman in 1949, making use of the previous ideas of Paul Dirac. Such a formulation is equivalent to the traditional approach to quantum mechanics, the canonical Hamiltonian formalism, previously developed by Schrödinger, Heisenberg, and Dirac in 1925–1926. There are several proposals for teaching quantum mechanics based on the SAA approach and the use of computational tools, such as that of [16,17,18,19,20,21,22,23]. In general, these proposals focus on the behavior of light and the electron, using computer simulations.
Here, we propose to expose the main ideas of the method, eliminating the mathematical formalism. It is worth mentioning that our group has implemented and analyzed didactic sequences based on Feynman’s approach for quantum mechanics oriented to high school, both for the behavior of electrons and light [24,25,26,27,28,29,30]. It is important to recall that these works were not based on the wave–particle duality. In addition, these didactic investigations used the theoretical framework of the Theory of Conceptual Fields (TCC) [31], as well as the notions of didactic transposition and teaching by inquiry [32]. While our work focuses on the transpositive aspects of teaching optics using this approach, it is important to note that analysis of conceptualization will require classroom implementation. As such, we plan to explore this aspect further in future research involving actual classroom settings.
Research on the presentation of quantum concepts related to light in school books [12,14,15,33] shows that little importance is given to the various scientific models that explain light phenomena, since they do not explain their basic principles or assumptions in either geometric optics or wave optics. A limited number of bibliographical sources make reference to the quantum characteristics of light, or do so in a way that is both physically and didactically questionable. For instance, some texts use the photoelectric effect as a means to introduce the quantization of light, and in doing so unequivocally link the notion of photon to this experiment, while referring to “the components of light” in a way that suggest the photon to be a tiny corpuscle. Furthermore, educational materials tend to prioritize the wave–particle duality, a topic that often leads students into a discourse that seems absurd, since the idea of wave and particle does not represent anything more divergent than these two concepts.
This article adopts a semantic and pragmatic perspective on scientific models, according to [34,35]. Within this conceptual framework, science is not concerned with ontological truth, but instead uses models as tools in order to represent the world and gain significant knowledge about it.
7.1. The Feynman Approach
We start with some concepts related to quantum mechanics and its validation in general.
Events: In Quantum Mechanics we consider events. For instance, in the reflection of light from a flat surface, an event may be that light emitted at A is reflected in the mirror at point P (Figure 2).
Probabilities: Quantum Mechanics does not predict the certainty, but rather the probability of an event. In the above example, it is possible to predict the probability that the light emitted at A will be reflected at point P in the mirror.
Theory–experiment comparison: the predictions of the theory are compared with the experiment in the following way: if P(e) is the probability predicted by the theory for the occurrence of an event e, Ne is the number of times the event occurs in the experiment and N is the total number of recorded events, then P(e) tends to Ne/N, as N grows. In the example of Figure 2, e can be the light detection event at a point P on the surface, then Ne is the observed number of times light is detected at that point and N is the total number of detections (on the entire surface).
Note the crucial difference between the quantum model and the Fermat model. In the latter, there is only “one” case: the one of least time. However, in the quantum model, there are many alternatives and probabilities for each of them.
After analyzing how to compare theory and experiment, the rules of Quantum Mechanics to calculate P(e) are considered. To simplify, we will restrict to the case of light in a vacuum, although all the concepts are easily generalizable to other situations.
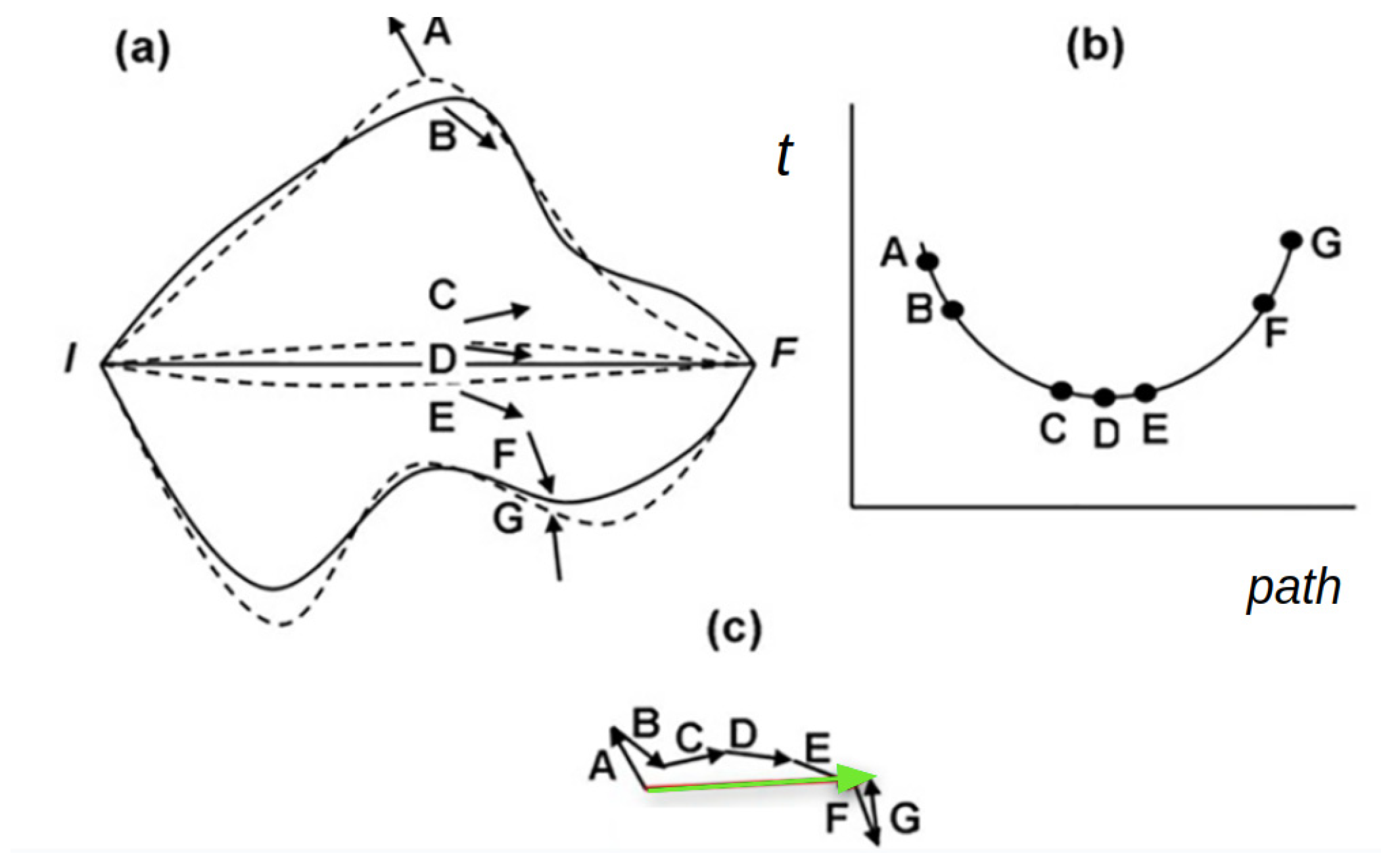
Consider a particular event e which is the detection of light at a point on a screen F having been emitted from I. For this general situation, Feynman defines a method which is adapted here to a language that involves no more than vector addition.
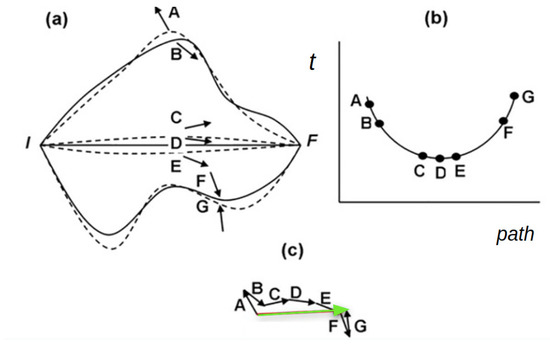 Figure 10. Alternative paths connecting I with F (a). The shortest path (D) and its surroundings, represented by C and E, have approximately the same length (b) and are the ones that contribute the most to the sum, indicated by green in (c). The square module of the green sum vector is proportional to the probability of going from I to F.
Figure 10. Alternative paths connecting I with F (a). The shortest path (D) and its surroundings, represented by C and E, have approximately the same length (b) and are the ones that contribute the most to the sum, indicated by green in (c). The square module of the green sum vector is proportional to the probability of going from I to F.- A vector for each path. To each possible path that connects I with F we associate a vector. The module (length) of this vector does not depend on the path, it is always the same, and it is assigned module 1.
- The angle θ that the vector associated with a given path forms with the x-axis is proportional to the time t it would take light to travel that path. The proportionality constant between the angle and the time is the “classical” light frequency ω:
Note that from the point of view presented by the model, ω is a constant that simply takes different values for each “type” of light. In other words, it will adopt different values depending on whether it is “red”, “green”, etc. Although frequency is a concept associated with the classical wave model of light, this association is deliberately omitted, since we intend to present a purely quantum model that extends Fermat’s point of view to multiple alternatives.
For a homogeneous medium, the time spent by light is proportional to the distance traveled: d = vt, where v is the speed of light in that medium. This is practical and allows the analysis both in terms of times and distances (as we did with the Fermat principle).
- Sum of the contributions of all paths (principle of superposition). The vectors associated with all the possible paths connecting I with F are added. This gives the resulting vector, as shown in green in Figure 10c.
- Probability calculation. The square module of the resulting vector is proportional to the probability of the event considered. This raises the problem of adding “infinite” vectors. Next, we will see how to approximately calculate this sum. To this end, let us consider again the Figure 10a. The path (D) that is in the center is the shortest, that is, a straight line. Around it, there are also very close paths (C,E) that have approximately the same length as the straight line. Since the direction of the vector associated with a given path is proportional to the length of that path, the vector associated with the straight line and its surroundings will have approximately the same direction. It is observed that around the shortest path (D) the length changes are such that the associated vectors maintain approximately the same direction. This is due to the properties of the minimum (variations to the first order are 0). In contrast, paths further away, such as A, B, F and G in the figure, have completely arbitrary lengths, so their associated vectors point in arbitrary, unrelated directions. Figure 10b schematically shows this behavior.
If one could sum “all” the possible paths to calculate the probability of detecting light in F having been emitted in I, it would be observed that the contributions of the paths far from the shortest would tend to cancel each other (statistically). The final result would be that only the contribution of the shortest path and those of its closest environment contribute to the final sum (green arrow in Figure 10c), and therefore, to the probability. In this sense, it is possible to conclude that the most probable path to go from I to F is the line that joins them, which is the one predicted by the Fermat model. Assuming the point of view of the rules for the addition of paths for light from Quantum Mechanics previously exposed, next we return to analyze the experiments of the first part.
7.2. The Law of Reflection: The Shortest Path Is the Most Probable
Let us analyze the reflection of light, according to the laws of Quantum Mechanics. Light detection events are considered as shown below.
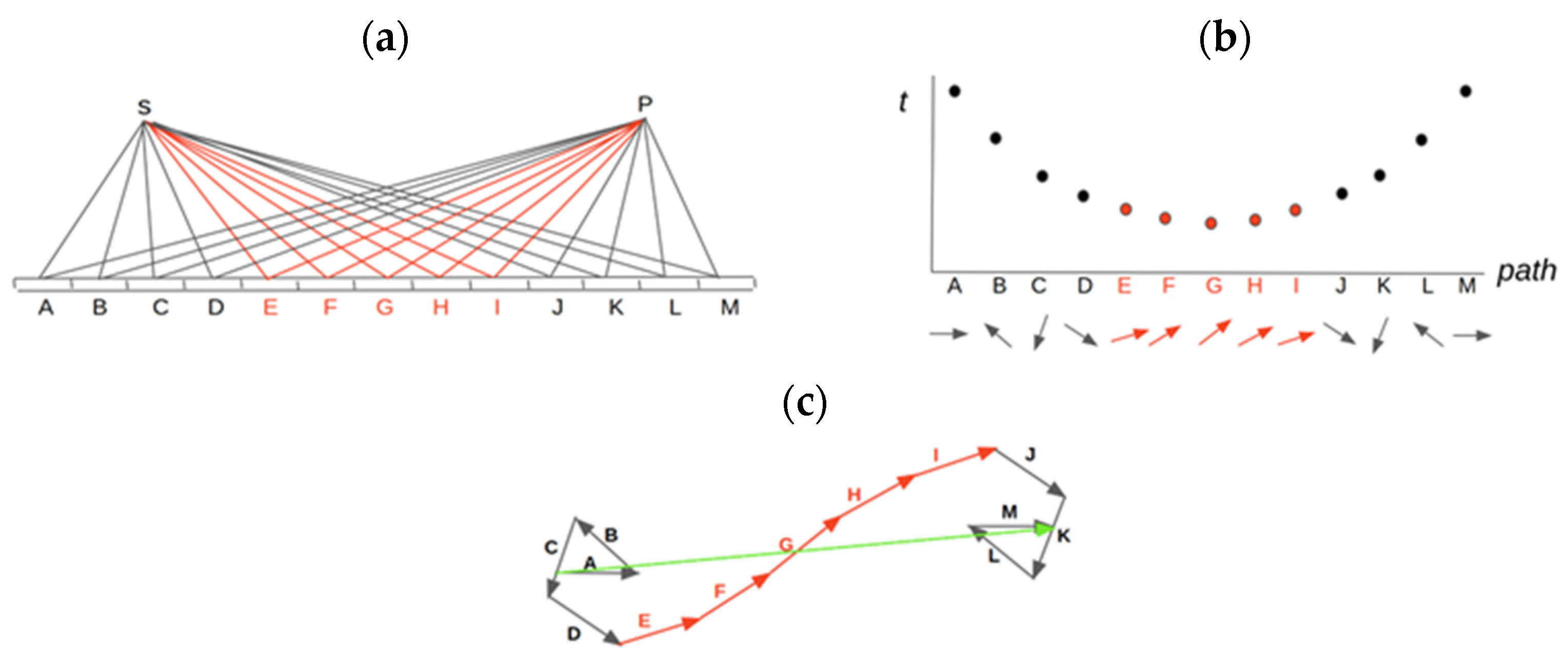
Some possible paths are selected to calculate the probability of detecting light at P that is emitted at S and reflected in the mirror, as shown in Figure 11a. As we have seen, around the shortest path G (classical reflexion) the length changes are such that the associated vectors maintain approximately the same direction. However, around the paths away from G, the variations are longer (Figure 11b). When performing the sum, the vectors corresponding to the paths that are far from the shortest path and with the shortest time for light cancel out and do not contribute to the sum, while the minimum classical path and its surroundings have associated vectors of similar length, and then they contribute to the sum (Figure 11c).
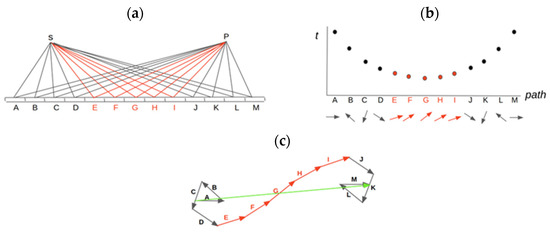
Figure 11.
Possible paths connecting the light detection point P with the emission point S, reflecting in the mirror (a). The shortest (least time) path is G. The vectors that contribute the most to the sum correspond to the paths closest to the shortest path and are indicated in red (b). The square module of the resulting vector (indicated in green) is proportional to the probability of detecting light at P that was emitted at S and reflected in the mirror (c).
Consequently, from the quantum point of view, all events are possible, although the event in which the angle of incidence and reflection are equal, which is the shortest path, is the most probable and is the one that is most easily detected. If a very careful experiment were carried out, light would be detected at other points that do not satisfy the reflection law. That is, the classical reflection law that was formulated experimentally with a macroscopic model is an “approximate” law.
7.3. Refraction from the Quantum Model
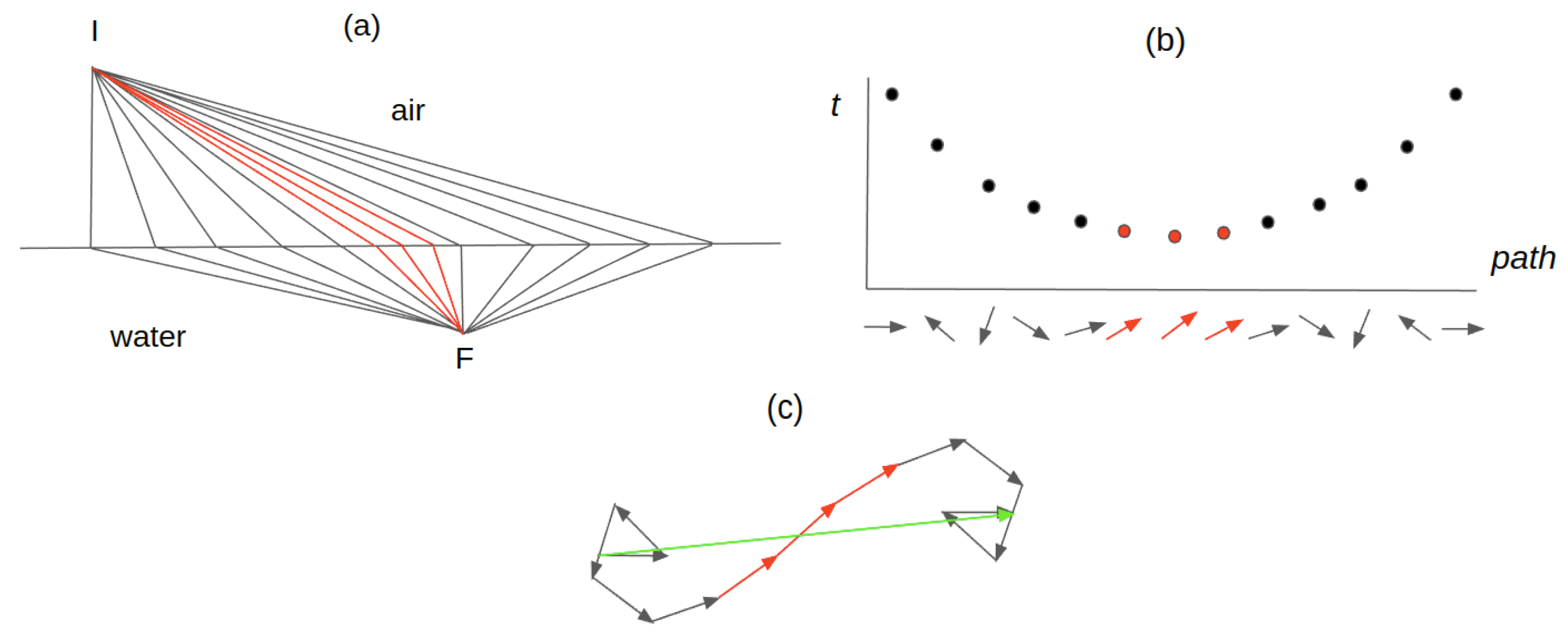
As we have already analyzed from Fermat’s Principle, if light travels from one medium to another, its trajectory changes. Here, the angle of incidence and the angle of the refracted beam are different. Using the Quantum Mechanics model, the probabilities of an event where the angle of incidence differs from the refracted one are analyzed. Using the Feynman method, light detection events are considered as shown in Figure 12a. Among the possible paths that light could follow to go from I to F, we seek to calculate the probability of detecting light in F having started from I, for which it is necessary to analyze the contribution to the sum of each path. As before, around the minimum time path, which in this case will not be the shortest because there is a change of medium, the time variations are such that the associated vectors maintain approximately the same direction (Figure 12b). Around paths away from the least-time path, the changes are greater. As before, when performing the sum, the paths far from the shortest time path for light cancel and do not contribute to the sum, while the shortest time path and its surrounding paths are the ones that contribute the most (Figure 12c).
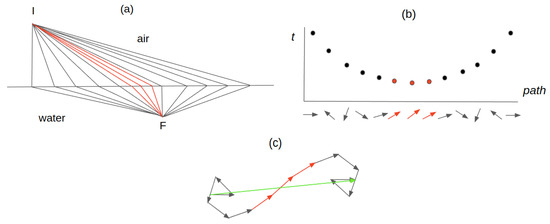
Figure 12.
(a) Possible pathways connecting the light detection point F with the exit point I, having passed from air to water. (b) There is a shortest path. (c) Vectors that contribute to the sum are those that correspond to the paths close to the path of least time.
Therefore, from the quantum point of view, all events are possible, although the path in which light takes the shortest time is the most likely. If an extremely careful experiment were carried out, we could detect light at other points that do not “comply” with the phenomenon of refraction.
8. The Double Slit Experience from Feynman’s Approach
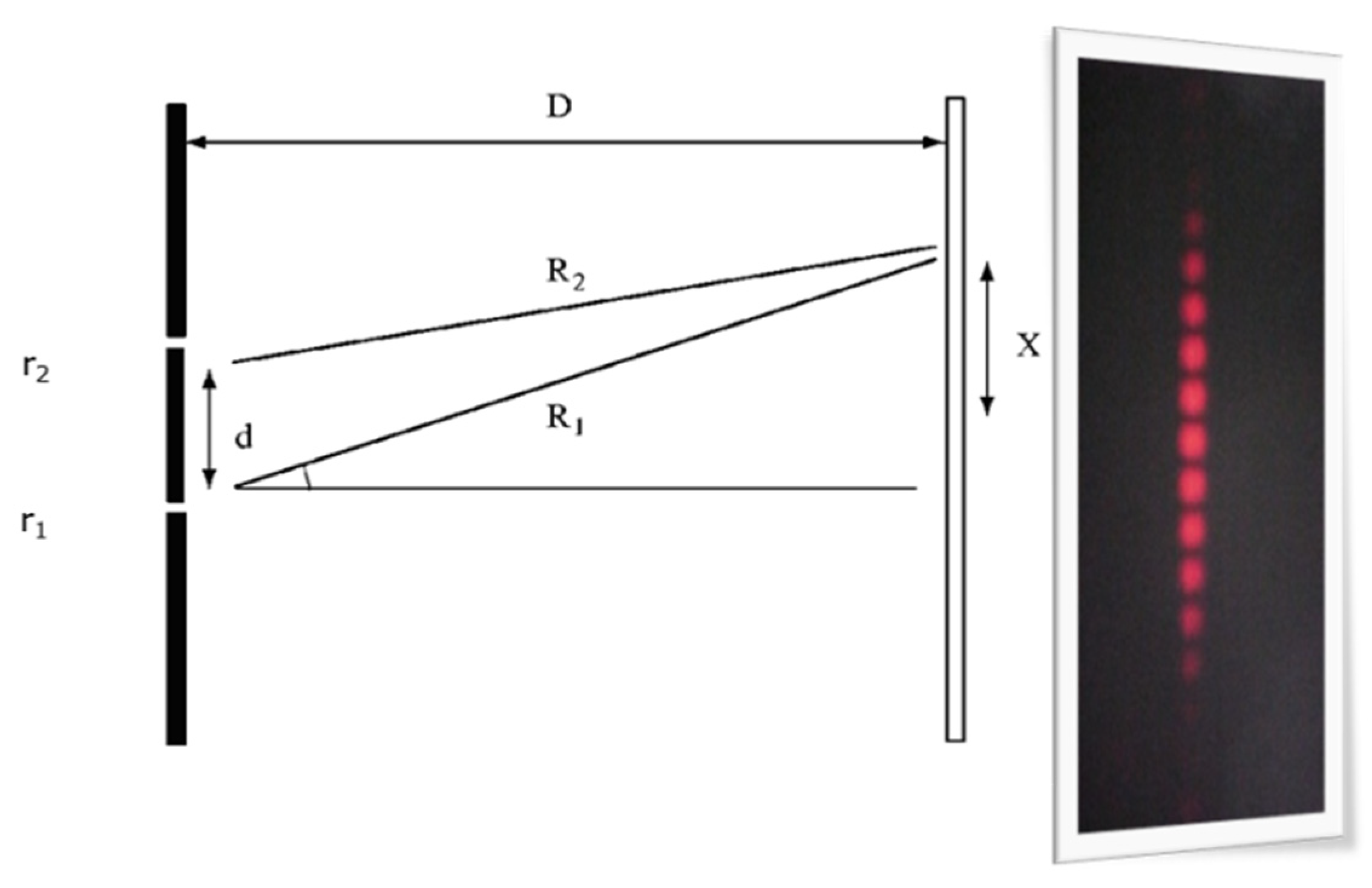
In this section, we analyze the double slit experiment from the point of view of path addition of quantum mechanics. The double slit experiment can be carried out simply in the laboratory. Figure 13 schematizes this experiment. Light from a laser (not shown in the figure) incised from the left on a screen with two very thin slits, separated by a distance d. This gives rise to a pattern of alternating stripes on a detection screen located at a distance D ≫ d, indicated schematically to the right of Figure 13.
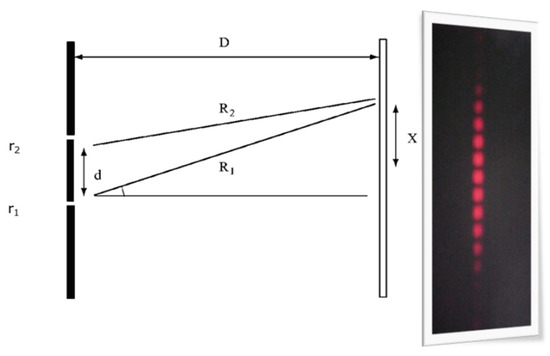
Figure 13.
Scheme of the double slit experiment, indicating the two main paths R_(1,2) that are used in the path addition method of Quantum Mechanics, and the corresponding experimental result (see text for further details).
The pattern of alternate stripes does not admit a description in terms of rays, that is, Fermat’s principle does not account for the phenomenon. The “classical” description of this behavior is (as we know) in wave terms, considering light as an electromagnetic wave and applying wave superposition.
This is a standard textbook procedure, which we do not follow here, because it involves an extensive entry into Maxwell’s electromagnetism, which we avoid in this work. However, briefly and accepting an underlying wave model, we can say that places on the detection screen where the waves arrive in phase “interfere” constructively, whereas those where waves arrive in out of phase cancel each other out. This gives rise to the pattern observed on the screen, which is distributed as a continuum of intensities that alternates between maxima and minima.
Figure 14 shows images of pattern formation on the detection screen, in increasing times, from left to right. The first thing to notice is that the pattern is not continuous, but rather that light is detected on the screen as discrete events (dots). At first, as can be observed in the panels on the left, the detection events do not show a definite pattern; they appear to be randomly distributed. However, as the exposure time increases and more events are detected, a regularity begins to emerge (middle panel of Figure 14). The more events are detected, the more the pattern of alternating fringes is defined (right panel of Figure 14). In the limit of a long exposure time, this granularity is “lost” and merges into a continuum, which is what we observe in Figure 13.

Figure 14.
Experimental sequence of images showing the detection screen in increasing times in the double-slit experiment, carried out with very low intensity light. The initially scattered dots in the left panels represent individual light detection events that appear random. However, as the exposure time progresses, the images show a granular distribution of alternating fringes of maximums and minimums, as shown in the panels on the right.
Figure 13 and Figure 14 show two aspects of the interference phenomenon. Figure 13 shows it in a “classical” context where there is no granularity and the classical electromagnetism framework appropriately describes the intensity distribution on the screen. On the other hand, Figure 14 shows the “detail” of the pattern formation with very low intensity light, which allows us to follow the formation process. In this context, the “quantum” discrete character of the detection events is central and the pattern formation exhibits a statistical character.
Here, as mentioned above, we avoid the description of the interference in terms of classical electromagnetism and will directly describe the phenomenon from the quantum point of view. This has several advantages. On the one hand, it describes the phenomenon at all scales, that is, Figure 13 and Figure 14 as extreme cases. On the other hand, the idea of Fermat paths is taken up again through the generalization of Feynman path sums. Finally, it avoids the incursion into classical electromagnetism, which also only accounts for the “classical” part of the phenomenon.
To apply Feynman’s method to interference, consider Figure 13 to calculate the probability of detection at a given point on the screen. Note that the quantum approach incorporates the discreteness of the detection events shown in the formation of the pattern in Figure 14. Unlike the classical model, which considers the intensity distribution, the quantum model describes a probability distribution. Both concepts are “proportional”, although it should be clarified that they belong to different models.
Let us start by calculating the sum of the vectors associated with all the paths that go from the source to a point on the screen.
There are two direct paths connecting the source to a given point x on the screen, as shown in Figure 13. One is the one that goes from the source and passes through the bottom slit, and the other is the one that goes through the top slit. There are multiple possible alternatives; for example, going through one of the slits and taking a completely arbitrary path until reaching the screen. However, according to the previous analysis, we know that the shortest path and its surroundings are the most important. Then, only the contributions of the two main paths are taken (even neglecting the neighborhood of each one) to calculate the probability. Note the difference in the application of the technique with respect to previous cases of quantum reflection for example. Although always (except in the center) one direct path is shorter than the other, depending on x, the two main paths are needed here to capture the interference from the quantum point of view.
Furthermore, this is a concrete example of quantum superposition. Now, let us analyze the conditions in which a maximum is found at a point on the screen. According to the quantum mechanics rules, the vectors associated with the two main paths that go from each slit to that point should point in the same direction. One case where this will happen is at the center of the screen, since the distances of the slits to the center of the screen are equal and then their associated vectors have the same angle, so their sum, and therefore, the probability, is maximal. That is to say, that the theory predicts a maximum in the center of the screen and this is observed experimentally. However, there are also other maxima, for example when in the difference of paths, the vector gives an integer number of cycles. The same strategy can be followed to detect the minima on the screen. Any resemblance to the classical mathematics of interference is not coincidental. However, here we are dealing with the purely quantum model.
To obtain the expression of the probability as a function of the distance to the screen (not only maxima and minima), we proceed as follows. We consider the two-unit vectors associated with the two main paths (R1 and R2 in Figure 13), whose angles are proportional to the time that light takes in each case. Then, we add both vectors and calculate the square module of the sum vector.
For the first slit the associated vector V1 is:
in which , that is, we can express the angle as a function of time or distance by changing the constant of proportionality from ω to k = ω/v, where v is the speed of light in the medium. Similarly, the main contribution for the other slit is:
Therefore, the resulting vector is:
whose square module is proportional to the Probability P(x) of detecting light at a point x on the screen (Figure 13). By performing this calculation (which is omitted because it only involves trigonometric algebra) we obtain:
where the proportionality constant is irrelevant here. The previous formula can be expressed in terms of distances by using
We can additionally express the difference in paths R1 − R2 as a function of the separation between the slits d and the distance between the screen and the wall D. Considering that D ≫ d, we compare similar triangles in Figure 13, that:
Then, replacing this expression in P(x) we finally obtain:
Strictly speaking, this expression does not represent a probability because it is not normalizable; that is, the sum of all the probabilities of detecting light in any part of the screen is not 1, but diverges. It is interpreted as a probability that “oscillates” between 0 and a relative maximum value of probability of finding light. It is not a punctual probability either, but a probability density; that is, it gives the probability of detecting light between x and x + dx, although here we continue talking about probability, leaving technicalities aside.
This is the expression for the probability of detecting light at a distance x from the center of the screen, which is derived from quantum mechanics, and allows us to predict not only the maxima and minima, but all intermediate values of probability.
This formula also allows us to analyze the dependence of the probability on the color of the light, which was initially fixed; that is, increase or decrease the value of k, leaving the other parameters (d and D) constant. Another possibility would be to fix the color and carry out the experiment varying the separation of the slits, and analyze the dependence of the probability with this separation. As can be seen, working with the parameters of the expression can be very enriching, not only for the quantum mechanical aspect related with probability, but also because it allows us to check the limits of validity of wave optics.
Finally, it is important to note that this formula describes a wave phenomenon, such as the distribution of maxima and minima on the screen, without the need to discuss any underlying wave mechanism.
9. Didactic Considerations for Teaching Optics Based on Fermat’s Principle and Its Quantum Generalization
In this section, we present the general framework of our didactic proposal for teaching optics based on Fermat’s principle and its quantum generalization by Feynman. We address key aspects for its implementation in the classroom and contextualize it in terms of our previous research. The purpose of this didactic proposal is to teach high school students in the last or penultimate year of their studies fundamental concepts about light from the unified framework of quantum mechanics, using the path integral technique proposed by Richard Feynman.
In previous investigations using this approach, we developed a didactic sequence to teach the quantum behavior of matter, focusing on the electron as a quantum system, the probabilistic function, and the quantum-classical transition. This proposal was successfully implemented in two courses of the last year of high school in Argentina [24,25,26,27,28,29,30] and in four courses of high school in Colombia, with 118 students aged 16 to 17 [13].
To teach the behavior of light using Feynman’s Path Integrals approach, we use elementary mathematical concepts, such as vectors and vector sums, through a sequence of situations related to the behavior of light. A first didactic sequence was designed, implemented, and evaluated to teach the quantum behavior of light, considering simple experiments involving reflection, refraction, and the double-slit experiment. This sequence was implemented in four courses (83 students) in the Argentina high school [36] in the subject of Physics, which is taught for three hours per week. The sequence has an approximate duration of eight weeks.
Based on our previous investigations, this paper revisits the physical foundations and key concepts that are essential to teaching optics in a broad context in secondary school. These notions cover both traditional optical aspects and the phenomena of interference and diffraction, without delving into classical wave optics. We accomplish this through the application of Feynman’s approach, which generalizes Fermat’s Principle of least time. Building on our previous work, we propose to extend and generalize our didactic sequence to include the treatment of Fermat’s principle in addition to experiences of reflection, refraction, and total internal reflection.
To avoid mathematical formalism, we utilize existing simulations of the experiments and others specifically designed using GeoGebra. These simulations allow us to analyze the mathematical expressions of the time it takes light to travel a certain path and the minimum time required when applying Fermat’s principle to the aforementioned experiments. This approach enables us to effectively teach these fundamental concepts without the need for extensive mathematical knowledge, making it accessible to secondary school students.
This didactic sequence comprises four phases, each consisting of different situations. Phase 1 (situations 1–4), starts with a situation about light reflection, which is studied by conducting an experiment with a laser pointer and a mirror. Here, by applying Fermat’s principle, the Snell–Descartes law is derived. In situation 2, the behavior of light when passing from air to a liquid is studied with a laser pointer, a container of liquid, and a protractor. Fermat’s principle is applied to obtain the law of refraction. To complement both experiences, free simulation software will be used, namely https://phet.colorado.edu/sims/html/bending-light/latest/bending-light_all.html?locale=es and http://www.sc.ehu.es/sbweb/fisica3/ondas/fermat/fermat.html (accessed on 1 May 2023). Situation 3 proposes carrying out an experiment with a laser pointer, a metal plate with two thin slits spaced d = 10−3 m apart, and projecting the light onto a wall located at a distance of D = 1 m from the slits. This produces a visible image similar to that presented in Figure 13, allowing students to identify “places” or “zones” on the screen where there is light and zones of darkness,” demonstrating that the light is not distributed uniformly on either the screen or the two regions corresponding to the slits. Finally, in situation 4, the results of the experiment are analyzed based on a set of images showing the discrete arrival of light, as depicted in Figure 14.
Phase 2 of the sequence (situations 5–6) addresses the quantum model of light and the use of the technique of summing all alternative paths. After analyzing the behavior of light in Phase 1, it is necessary to propose a set of principles or laws that describe all the experiments from a unified conceptual framework. In this phase, we present the formulation of the laws of quantum mechanics for light, using Feynman’s path integral technique, referred to in the sequence as the “Sum Alternative Paths” (SAP) [28]. We adapted the original technique, which involved advanced mathematical methods, to make it suitable for classroom use, using essential mathematical concepts, such as vectors, angles, and geometric vector addition, that students already possess. Situation 5 briefly introduces the students to the fundamental concepts of this theory, such as events and probability, and describes the steps of the probability amplitude calculation method that will be used to describe from a quantum point of view the four experiments presented. It also includes a simulation designed by our team that allows students to visualize the connection between the selected paths and the angle of the associated vector. Situation 6 enables the calculation of the probability amplitude from the graphical addition of vectors. It presents a set of results obtained from the previous simulation, and challenges the students to perform the geometric addition of vectors in GeoGebra.
Students can conclude that vectors associated with paths far from the path of least time cancel each other out and do not contribute to the sum, and hence, to the probability. Only paths close to the path of least time contribute to the sum. Therefore, only the path of least time and those in its vicinity should be considered when calculating the probability of the event considered.
Phase 3 of the sequence (situations 7–9) groups together situations where the SAP technique is applied to the experiments conducted in phase 1. In Situation 7, the technique is employed in reflection through a simulation conducted using GeoGebra. Students can select various alternative paths that connect the starting point of light and the endpoint, and observe the angles of the vectors associated with each of them. Situations 8 and 9 apply the SAP technique to refraction and total internal reflection, respectively.
Finally, phase 4 of the sequence (situations 10–11) involves applying the SAP technique to the double-slit experiment. In Situation 10, probability is calculated according to the experiment’s variables. Situation 11 interprets the results of the double-slit experiment on the screen from the quantum theory perspective. Students establish the correspondence between the probability maxima and minima graphically represented in Situation 10, and the results of the double-slit experiment that show individual detections.
Assessment in a sequence of this nature arises from the activity that students carry out in each stage. We have discussed the advantages of this sequence in the conclusions of this work.
In summary, this proposal introduces new simulations in GeoGebra and other simulation tools, which expand on our previous implementations [36]. In this way, we strengthen our vision of a broad-spectrum optics education based on the principle of least time and its generalization in quantum mechanics.
10. Discussion and Final Considerations
In the preceding sections, we have analyzed certain aspects of light in a unified and non-traditional framework, which adapts and contextualizes Feynman’s Path Integrals approach with the aim, in this case, of applying it to the explanation of phenomena of light. This approach has the following main advantages:
Avoids the confusing development of the photon concept that is presented in most textbooks. In this sense, we advocate not imposing quantum concepts and principles on students and developing an explanatory mechanism that addresses the fundamental aspects of Quantum Mechanics, such as the probabilistic description and the notion of event, probability and superposition, using elementary mathematical notions, since at this level there are not many physical or mathematical concepts available.
The technique is applied to monochromatic light of any kind, particularly lasers, which are easily accessible to students. We emphasize that the mathematical level used is based on elementary operations with vectors (addition and module) and that the probabilistic aspect of Quantum Mechanics is emphasized.
Despite the complex mathematical level that its technical implementation implies, the understanding of the main idea and the results of applying the technique of considering Alternative Paths can be visualized through the use of calculation simulation computer tools especially designed for it. In particular, these tools replace the analytical framework with the geometric one, using basic operations with vectors. The geometric context would allow students to visualize the addition process and reaffirm the idea that it is the phase of the vector and not the module that varies from one path to another.
Special care is taken to refer only to properties of light, avoiding asking the usual question in school books, “what is light?”, since as we pointed out before, in physics and in sciences, this type of essentialist questions makes no sense. In other words, it is explicitly assumed that physics seeks to build models to account for the observed phenomena and predict new ones, generating more knowledge.
Finally, we emphasize that this way of linking the knowledge of school physics provided by the approach proposed here connects two aspects that habitual teaching presents in a very distant and separate way, when it does so. We refer to Fermat’s Principle of least time and to Feynman’s quantum electrodynamics in its formulation of path integrals.
In traditional teaching, geometric optics begins adopting a ray model. Usually, a unifying variational principle, such as Fermat’s least time, is not presented, but rather the laws of rectilinear propagation, reflection and refraction are stated directly. In contrast, when Fermat’s principle is mentioned, it is done to support the idea of the rectilinear propagation of light, without applying it to the physical phenomena of reflection and refraction.
Occasionally, certain aspects of the wave model are introduced to account for phenomena such as interference and diffraction, which cannot be described with the geometric model. However, taking this step properly requires dealing with the classical electromagnetism. Light, from this point of view, is an emergent of the interaction between electric and magnetic fields described by the set of five Maxwell equations. It is well known that in order to approach this phenomenology, mastery of mathematical techniques for solving differential equations and notions of analytic and vector geometry are required, which are not available at the secondary level or in the first years of university.
Even in the case of having notions of classical electromagnetism, conceptually it is still halfway there, because classical electromagnetism cannot account for the phenomenon of “granularity” that is observed in the formation of the interference pattern in the experiment of the double slit shown in Figure 14, nor of the underlying statistical character. This is one among many examples of quantum behavior that are not approachable from the classical electromagnetism model.
The next step, then, is to embark on the study of quantum mechanics. From the traditional (canonical) point of view, it begins with the quantum treatment of “matter” at a non-relativistic level with the Schrödinger equation. The quantum approach to light is considered an “advanced” quantum mechanics topic. For this, and always in the canonical formalism, the electromagnetic field is “quantized”, from which the “enigmatic” photon emerges. An even more complete treatment calls for incorporating relativistic aspects, which finally leads to quantum electrodynamics, or QED. Finally, this theory can account for the “granularity” of the formation of the interference pattern of Figure 14 and much more.
Consequently, from this perspective it would seem impossible, in the school time available, to be able to find a framework that allows, at least qualitatively, to address such a variety of phenomena: from rectilinear propagation following the principle of least time, to the granularity or discreteness of quantum phenomena.
The adaptation of Feynman’s framework of path integrals, with the entire chain of delicately designed didactic transformations, which were initiated by Feynman himself and continue to this day [25,26,27,29,30,37,38], seem the most satisfactory way to communicate these aspects of light apparently so far away.
Unlinking the interference to the wave phenomena of classical electromagnetism is a prescription that we assume in terms of the didactic proposal. In no way it implies that we should stop studying electromagnetism in high school. Our approach takes a quantum point of view from the beginning, based on the idea of least time and its generalization to Feynman multiple paths. In this way it is possible to “overlook” the classical wave optics and describe the interference phenomena from a general point of view.
This framework and its associated didactic proposals connect two worlds, two eras, two visions, and the genius of Fermat and Feynman in a unified model. As we have tried to show through the examples, this framework makes it possible to approach directly, without sophistication, without excesses of language and with a mathematics accessible at the secondary and elementary university level, the vast range of phenomena that are involved in the functioning of a magnifying glass, fiber optics and lasers.
Author Contributions
Conceptualization, M.R.O. and M.F.A.; methodology, M.R.O. and M.F.A.; investigation, M.R.O. and M.F.A.; writing—original draft preparation, M.R.O. and M.F.A.; writing—review and editing, M.R.O. and M.F.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by CONICET.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kaltakci-Gurel, D.; Eryilmaz, A.; McDermott, L.C. Development and application of a four-tier test to assess pre-service physics teachers’ misconceptions about geometrical optics. Res. Sci. Technol. Educ. 2017, 35, 238–260. [Google Scholar] [CrossRef]
- Métioui, A.; Trudel, L. The model of the rectilinear propagation of light and the study of the variation of the size of a shadow. US-China Educ. Rev. 2012, 2, 173–186. [Google Scholar]
- Guesne, E. Light. In Children’s Ideas in Science; Driver, R., Guesne, E., Tiberghien, A., Eds.; Open University Press: Philadelphia, PA, USA, 1985; pp. 10–32. [Google Scholar]
- Chen, J.-Y.; Chang, H.-P.; Guo, C.-J. The development of a diagnostic instrument to investigate students’ alternative concep-tions of reflection and refraction of light. Chin. J. Sci. Educ. 2004, 12, 311–340. [Google Scholar]
- Galili, I.; Bendall, S.; Goldberg, F. The effects of prior knowledge on understanding image formation. J. Res. Sci. Teach. 1993, 30, 271–301. [Google Scholar] [CrossRef]
- Carpentieri, M.A.; Fano, G.; Jurinovich, S.; Domenici, V. Introduction to Light Properties and Basic Principles of Spectroscopy at the High-School Level: A Pilot Study. Educ. Sci. 2023, 13, 316. [Google Scholar] [CrossRef]
- Zhao, L.; He, W.; Liu, X.; Tai, K.H.; Hong, J.C. Exploring the effects on fifth graders’ concept achievement and scientific epistemological beliefs: Applying the prediction-observation-explanation inquiry-based learning model in science education. J. Balt. Sci. Educ. 2021, 20, 664–676. [Google Scholar] [CrossRef]
- Aydin, S. Remediation of misconceptions about geometric optics using conceptual change texts. J. Educ. Res. Behav. Sci. 2012, 1, 1–12. [Google Scholar]
- Fyttas, G.; Komis, V.; Ravanis, K. Ninth grade students’ mental representations of the refraction of light: Didactic implications. Revis. Mexic. Fisica E 2013, 59, 133–139. [Google Scholar]
- Ravanis, K.; Boilevin, J.-M. A comparative approach to the representation of light for five- eight- and ten-year-old children: Educational perspectives. J. Balt. Sci. Educ. 2009, 8, 182–190. [Google Scholar]
- Ravanis, K.; Christidou, V.; Hatzinikita, V. Enhancing conceptual change in preschool children’s representations of light: A socio-cognitive approach. Res. Sci. Educ. 2013, 43, 2257–2276. [Google Scholar] [CrossRef]
- González, E.M.; Muñoz Burbano, Z.E.; Solbes, J. La enseñanza de la física cuántica: Una comparativa de tres países. Góndola Enseñanza Y Aprendiz. Las Cienc. 2020, 15, 239–250. [Google Scholar] [CrossRef]
- Alvarado Puentes, K.A. Enseñanza y Aprendizaje de Aspectos Fundamentales de Física Cuántica en la Escuela Secundaria Colombiana a Partir Del Enfoque de Feynman. Ph.D. Thesis, Universidad Nacional del Centro de la Provincia de Buenos Aires, Buenos Aires, Argentina, 2020. [Google Scholar] [CrossRef]
- Lobato, L.; Greca, I. Análise da inserção de conteúdos de Teoria Quântica nos currículos de Física do ensino médio. Ciência Educ. Bauru 2005, 11, 119–132. [Google Scholar] [CrossRef][Green Version]
- Perales Palacios, J. Enseñanza de la óptica. Rev. Alambique 1994, 1, 133–138. [Google Scholar]
- Dowrick, N.J. Feynman’s sum–over–histories in elementary quantum mechanics. Eur. J. Phys. 1997, 18, 75–78. [Google Scholar] [CrossRef]
- Arlego, M. Los fundamentos de la mecánica cuántica en la escuela secundaria utilizando el concepto de integral de camino. Rev. Electrónica Investig. Educ. Cienc. 2008, 3, 59–66. [Google Scholar] [CrossRef]
- Taylor, E.; Stamatis Vokos, J.; O’Meara, M.; Thornber, N. Teaching Feynman’s Sum Over Paths. Quantum Theory. Comput. Phys. 1998, 12, 190–199. [Google Scholar] [CrossRef]
- Ogborn, J.; Hanc, J.; Taylor, E. A First Introduction to Quantum Behavior. In Proceedings of the GIREP Conference 2006, Modelling in Physics and Physics Education, Amsterdam, The Netherlands, 20–25 August 2006; AMSTEL Institute: Amsterdam, The Netherlands, 2006; p. 213. [Google Scholar]
- Hanc, J.; Tuleja, S. The Feynman quantum mechanics with the help of Java applets and physlets in Slovakia. In Proceedings of the 10th Workshop on Multimedia in Physics Teaching and Learning, Cairns, Australia, 8–10 October 2008; Freie Universität: Berlin, Germany, 2005. [Google Scholar]
- Malgieri, M.; Onorato, P.; De Ambrosis, A. Teaching quantum physics by the sum over paths approach and GeoGebra simulations. Eur. J. Phys. 2014, 35, 055024. [Google Scholar] [CrossRef]
- Malgieri, M.; Onorato, P.; De Ambrosis, A. What is Light? From Optics to Quantum Physics Through the Sum over Paths Approach. In Proceedings of the Teaching/Learning Physics Integrating Research into Practice GIREP–MPTL 2014 Conference Proceedings, Palermo, Italy, 7–12 July 2015; UNIPA: Palermo, Italy, 2015; pp. 639–646. [Google Scholar]
- Malgieri, M.; Onorato, P.; De Ambrosis, A. Test on the effectiveness of the sum over paths approach in favoring the construction of an integrated knowledge of quantum physics in high school. Phys. Rev. Phys. Educ. Res. 2017, 13, 01010113. [Google Scholar]
- Fanaro, M.; Otero, M.R.; Arlego, M.J.F. Teaching the foundations of quantum mechanics in secondary school: A proposed conceptual structure. Investig. Ensino Ciências 2009, 14, 37–64. [Google Scholar]
- Fanaro, M.; Arlego, M.; Otero, M.R. A Didactic Proposed for Teaching the Concepts of Electrons and Light in Secondary School Using Feynman’s Path Sum Method. Eur. J. Phys. Educ. 2012, 3, 1–11. [Google Scholar]
- Fanaro, M.; Otero, M.R.; Arlego, M. A proposal to teach the light at secondary school from the Feynman method. Probl. Educ. 21st Century 2012, 47, 27–39. [Google Scholar] [CrossRef]
- Fanaro, M.; Otero, M.R.; Arlego, M. Teaching Basic Quantum Mechanics in Secondary School Using Concepts of Feynman’s Path Integrals Method. Phys. Teach. 2012, 50, 156–158. [Google Scholar] [CrossRef]
- Fanaro, M.; Otero, M.R.; Arlego, M. The double slit experience with light from the point of view of Feynman’s sum of multiple paths. Rev. Bras. Ensino Fís. 2014, 36, 2308. [Google Scholar] [CrossRef]
- Otero, M.R.; Fanaro, M.A. Emotions, Feelings and Conceptualizations in Physics Didactic. In Science Education Research in South and Latin America; El-Hani, C.H., Fleury Mortimer, E., Pietroccola, M., Otero, M.R., Eds.; Science Publisher (Brill): Leiden, The Netherlands, 2020; pp. 113–156. [Google Scholar]
- Fanaro, M.A.; Arlego, M.; Otero, M.R.; Elgue, M. Students’ Interpretations of Quantum Mechanics Concepts from Feynman’s Sum of all Paths Applied to Light. Int. J. Phys. Chem. Educ. 2018, 10, 41–47. [Google Scholar]
- Vergnaud, G. La théorie des champs conceptuels. Rech. Didact. Mathématiques 1990, 10, 133–170. [Google Scholar]
- Chevallard, Y. Vers Une Didactique de la Codisciplinaire. Notes Sur Une Nouvelle Epistémologie Scolaire. 2004. Available online: http://yves.chevallard.free.fr/ (accessed on 1 May 2023).
- Elgue, M.; Fanaro, M.A.; Otero, M.R.; Arlego, M. Tratamiento de la naturaleza de la luz en los libros de Texto: Un análisis crítico. In Actas en el I Congreso Internacional de Enseñanza de las Ciencias y la Matemática (I CIECyM) y II Encuentro nacional en Enseñanza de las Ciencias (II ENEM); UNICEN: Tandil, Argentina, 2011; pp. 643–656. [Google Scholar]
- Giere, R.N. Science Without Laws; University of Chicago Press: Chicago, IL, USA, 1999. [Google Scholar]
- Giere, R.N. How Models Are Used to Represented Reality. Philos. Sci. 2004, 71, 742–752. [Google Scholar] [CrossRef]
- Elgue, M. Enseñanza y Aprendizaje de Aspectos Fundamentales de Física Cuántica en la Escuela Secundaria a Partir del Estudio de la luz. Ph.D. Thesis, Universidad Nacional del Centro de la Provincia de Buenos Aires, Buenos Aires, Argentina, 2015. [Google Scholar]
- Fanaro, M.; Arlego, M.; Otero, M.R. El método de caminos múltiples de Feynman para enseñar los conceptos fundamentales de la Mecánica Quántica en la escuela secundaria. Cad. Catarin. Ensino Física 2007, 22, 233–260. [Google Scholar]
- Fanaro, M.A.; Arlego, M.; Otero, M.R. The double slit experience with light from Feynman´s Sum of Multiple Paths viewpoint. Rev. Bras. Ensino Física. 2014, 35, 1–7. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).