Learning Difficulties with the Concept of Function in Maths: A Literature Review
Abstract
1. Introduction
2. Materials and Methods
2.1. Search and Literature Analysis
- (1)
- The study referred to the mathematical concept of function. We discarded works focused on functions with other meanings, such as role in economics or code in programming. Moreover, works that contained the word «function» in the title or abstract but were not related to the topic of the study were also discarded.
- (2)
- Only studies that refer to learning difficulties and misconceptions about the concept of function were considered. It is important to remark that we did not consider in our study other types of studies related to the concept of function, such as those based on interventions to improve the understanding of the concept, or those based on how the learning of functions evolves in students.
2.2. Characterization of the Selected Studies
3. Results
3.1. Literature Review
- «threshold concept» and «function», 3856 papers;
- «learning progression» and «function concept», 140 papers;
- «mathematics education» and «function concept», 533 papers;
- «learning difficulties» and «function concept», 885 papers;
- «misconception» and «function concept», 329 papers.
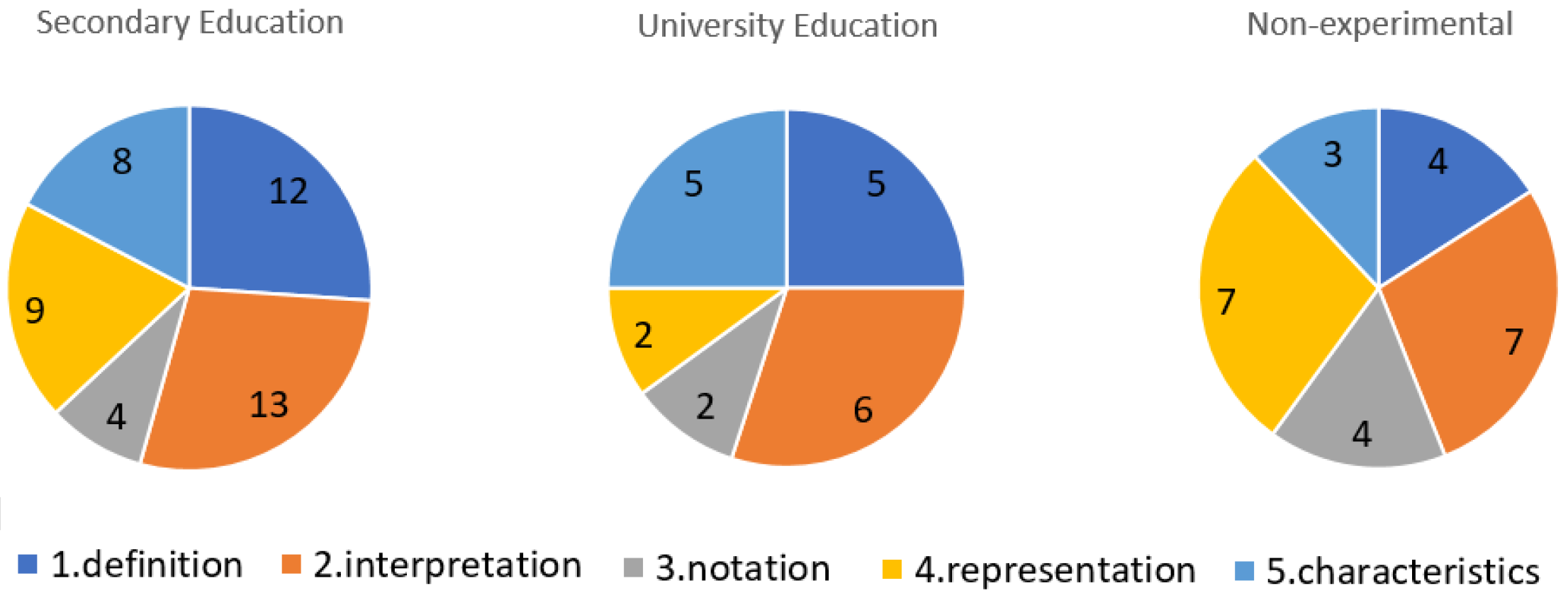
3.2. Learning Difficulties and Misconceptions in the Concept of Function
3.2.1. Definition (D1)
3.2.2. Interpretation or Meaning (M2 and D2)
3.2.3. Notation and Expression (D3)
3.2.4. Graphic Representation (M4 and D4)
3.2.5. Management and Characteristics (M5 and D5)
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Meyer, J.H.F.; Land, R. Threshold concepts and troublesome knowledge (2): Epistemological considerations and a conceptual framework for teaching and learning. High. Educ. 2005, 49, 373–388. [Google Scholar] [CrossRef]
- Pettersson, K. Algoritmiska, Intuitiva och Formella Aspekter av Matematiken i Dynamiskt Samspel: En Studie av hur Studenter Nyttjar Sina Begreppsuppfattningar Inom Matematisk Analys; Chalmers Tekniska Hogskola: Gothenburg, Sweden, 2008. [Google Scholar]
- Lima, P.D.S.N.; das Almas Silva, L.; Félix, I.M.; de Oliveira Brandão, L. Difficulties in basic concepts of mathematics in higher education: A systematic review. In Proceedings of the 2019 IEEE Frontiers in Education Conference (FIE), Covington, KY, USA, 16–19 October 2019; pp. 1–7. [Google Scholar]
- Thomas, M.O.; Freitas Druck, I.D.; Huillet, D.; Ju, M.K.; Nardi, E.; Rasmussen, C.; Xie, J. Key mathematical concepts in the transition from secondary school to university. In Proceedings of the 12th International Congress on Mathematical Education, Seoul, Republic of Korea, 8–15 July 2012; Springer: Cham, Switzerland, 2015; pp. 265–284. [Google Scholar]
- Bergeron, J.C.; Herscovics, N. Levels in the understanding of the function concept. Proc. Conf. Funct. 1982, 1, 39–46. [Google Scholar]
- Janvier, C. Translation processes in mathematics education. In Problems of Representation in the Teaching and Learning of Mathematics; Janvier, C., Ed.; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1978; pp. 27–31. [Google Scholar]
- Herscovics, N.; Van Barnveld, G.; Krabbendam, H. Problems related to the understanding of functions. Conference on junctions 1982 Enschede, The Netherlands Foundation for Curriculum Development 67-84 Report 1.
- Even, R. Subject matter knowledge for teaching and the case of functions. Educ. Stud. Math. 1990, 21, 521–544. [Google Scholar] [CrossRef]
- Vinner, S. Concept definition, concept image and the notion of function. Int. J. Math. Educ. Sci. Technol. 1983, 14, 293–305. [Google Scholar] [CrossRef]
- Dubinsky, E.; Harel, G. The concept of function. In Aspects of Epistemology and Pedagogy; Mathematical Association of America (MMA): Washington, DC, USA, 1992. [Google Scholar]
- Abdullah, S.A.S. Comprehending the concept of functions. Procedia-Soc. Behav. Sci. 2010, 8, 281–287. [Google Scholar] [CrossRef]
- Akkoç, H.; Tall, D. The function concept: Comprehension and complication. Proc. Br. Soc. Res. Learn. Math. 2003, 23, 1–6. [Google Scholar]
- Bardini, C.; Pierce, R.; Vincent, J.; King, D. Undergraduate Mathematics Students’ Understanding of the Concept of Function. Indones. Math. Soc. J. Math. Educ. 2014, 5, 85–107. [Google Scholar] [CrossRef]
- Borke, M. Student Teachers’ Knowledge of Students’ Difficulties with the Concept of Function. LUMAT Int. J. Math Sci. Technol. Educ. 2021, 9, 670–695. [Google Scholar] [CrossRef]
- Cansiz, S.; Küçük, B.; Isleyen, T. Identifying the secondary school students’ misconceptions about functions. Procedia-Soc. Behav. Sci. 2011, 15, 3837–3842. [Google Scholar] [CrossRef]
- Carlson, M.; Oehrtman, M. Key aspects of knowing and learning the concept of function. Math. Assoc. Am. Res. Sampl. 2005, 9. [Google Scholar]
- Clement, L.L. Connecting research to teaching: What do students really know about functions? Math. Teach. 2001, 94, 745–748. [Google Scholar] [CrossRef]
- Dogan-Dunlap, H. Reasoning with metaphors and constructing an understanding of the mathematical function concept. In Proceedings of the 31st Conference of the International Group for the Psychology of Mathematics Education, Seoul, Republic of Korea, 8–13 July 2007; Volume 2, pp. 209–216. [Google Scholar]
- Dreyfus, T.; Eisenberg, T. Intuitive functional concepts: A baseline study on intuitions. J. Res. Math. Educ. 1982, 13, 360–380. [Google Scholar] [CrossRef]
- Dubinsky, E.; Wilson, R.T. High school students’ understanding of the function concept. J. Math. Behav. 2013, 32, 83–101. [Google Scholar] [CrossRef]
- Eames, C.L.; Graf, E.A.; van Rijn, P.W.; Budzban, G.; Voepel, T. The finite-to-finite strand of a learning progression for the concept of function: A research synthesis and cognitive analysis. J. Math. Behav. 2021, 62, 100864. [Google Scholar] [CrossRef]
- Evangelidou, A.; Spyrou, P.; Elia, I.; Gagatsis, A. University Students’ Conceptions of Function; International Group for the Psychology of Mathematics Education: Karlsruhe, Germany, 2004. [Google Scholar]
- Font Moll, V.; Acevedo Nanclares, J.I. Fenómenos relacionados con el uso de metáforas en el discurso del profesor: El caso de las gráficas de funciones. Enseñanza Las Cienc. Rev. Investig. Exp. Didácticas 2003, 21, 405–481. [Google Scholar] [CrossRef]
- Hatisaru, V.; Erbas, A.K. Mathematical knowledge for teaching the function concept and student learning outcomes. Int. J. Sci. Math. Educ. 2017, 15, 703–722. [Google Scholar] [CrossRef]
- Hitt, F. Difficulties in the articulation of different representations linked to the concept of function. J. Math. Behav. 1998, 17, 123–134. [Google Scholar] [CrossRef]
- Leinhardt, G.; Zaslavsky, O.; Stein, M.K. Functions, graphs, and graphing: Tasks, learning, and teaching. Rev. Educ. Res. 1990, 60, 1–64. [Google Scholar] [CrossRef]
- Markovits, Z.; Eylon, B.S.; Bruckheimer, M. Functions today and yesterday. Learn. Math. 1986, 6, 18–28. [Google Scholar]
- Martínez-Planell, R.; Trigueros Gaisman, M. Students’ ideas on functions of two variables: Domain, range, and representations. In Proceedings of the 31st annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Georgia State University, Atlanta, Georgia, 23–26 September 2009; Volume 5, pp. 73–80. [Google Scholar]
- O’Shea, A.; Breen, S.; Jaworski, B. The development of a function concept inventory. Int. J. Res. Undergrad. Math. Educ. 2016, 2, 279–296. [Google Scholar] [CrossRef]
- Panaoura, A.; Michael-Chrysanthou, P.; Philippou, A. Teaching the concept of function: Definition and problem solving. In Ninth Congress of the European Society for Research in Mathematics Education CERME; Charles University in Prague, Faculty of Education and ERME: Prague, Czech Republic, 2015; Volume 9, pp. 440–445. [Google Scholar]
- Parhizgar, Z.; Dehbashi, A.; Liljedahl, P.; Alamolhodaei, H. Exploring students’ misconceptions of the function concept through problem-posing tasks and their views thereon. Int. J. Math. Educ. Sci. Technol. 2021, 53, 3261–3285. [Google Scholar] [CrossRef]
- Pettersson, K.; Stadler, E.; Tambour, T. Transformation of students’ discourse on the threshold concept of function. In Eighth Congress of European Research in Mathematics Education CERME; Middle East Technical University and ERME: Manavgat/Side, Turkey, 2013; Volume 8, pp. 2406–2415. [Google Scholar]
- Pettersson, K. The Threshold Concept of a Function–A Case Study of a Student’s Development of Her Understanding; Eighth Swedish Mathematics Education Research Seminar: Umeå, Sweden, 2012. [Google Scholar]
- Sajka, M. A secondary school student’s understanding of the concept of function—A case study. Educ. Stud. Math. 2003, 53, 229–254. [Google Scholar] [CrossRef]
- Sierpinska, A. On understanding the notion of function. Concept Funct. Asp. Epistemol. Pedagog. 1992, 25, 23–58. [Google Scholar]
- Tall, D.; Bakar, M. Students’ mental prototypes for functions and graphs. Int. J. Math. Educ. Sci. Technol. 1992, 23, 39–50. [Google Scholar] [CrossRef]
- Thomas, H. The concept of function. In Children’s Mathematical Concepts: Six Piagetian Studies in Mathematical Education; Rosskopf, M., Ed.; Teachers College Press: New York, NY, USA, 1975; pp. 145–172. [Google Scholar]
- Thompson, P.W. Students, functions, and the undergraduate curriculum. In Research in Collegiate Mathematics Education; Dubinsky, E., Schoenfeld, A.H., Kaput, J.J., Eds.; American Mathematical Society: Providence, RI, USA, 1994; pp. 21–44. [Google Scholar]
- Vinner, S.; Dreyfus, T. Images and definitions for the concept of function. J. Res. Math. Educ. 1989, 20, 356–366. [Google Scholar] [CrossRef]
- Walde, G.S. Difficulties of concept of function: The case of general secondary school students of Ethiopia. Int. J. Sci. Eng. Res. 2017, 8, 1–10. [Google Scholar] [CrossRef]
- Widada, W.; Herawati, A.; Fata, R.; Nurhasanah, S.; Yanty, E.P.; Suharno, A.S. Students’ understanding of the concept of function and mapping. J. Phys. Conf. Ser. 2020, 1657, 012072. [Google Scholar]
- Yusof, Y.M.; Othman, M.F.B.; Mahmood, A. Making Students’ Thinking Explicit: Learning What They Know about Functions. In Proceedings of the 2014 International Conference on Teaching and Learning in Computing and Engineering, Kuching, Malaysia, 11–13 April 2014; pp. 256–261. [Google Scholar]
- Thompson, P.W.; Carlson, M.P. Variation, covariation, and functions: Foundational ways of thinking mathematically. In Compendium for Research in Mathematics Education; Cai, J., Ed.; National Council of Teachers of Mathematics: Reston, VA, USA, 2017; pp. 421–456. [Google Scholar]
- Doorman, M.; Drijvers, P.; Gravemeijer, K.; Boon, P.; Reed, H. Tool use and the development of the function concept: From repeated calculations to functional thinking. Int. J. Sci. Math. Educ. 2012, 10, 1243–1267. [Google Scholar] [CrossRef]
- Kleiner, I. Evolution of the function concept: A brief survey. Coll. Math. J. 1989, 20, 282–300. [Google Scholar] [CrossRef]
- Veith, J.M.; Bitzenbauer, P.; Girnat, B. Exploring Learning Difficulties in Abstract Algebra: The Case of Group Theory. Educ. Sci. 2022, 12, 516. [Google Scholar] [CrossRef]
- Cuesta Borges, A. El Proceso de Aprendizaje de los Conceptos de Función y Extremo en Estudiantes de Economía: Análisis de Una Innovación Didáctica. Ph.D. Thesis, Universitat Autònoma de Barcelona, Barcelona, Spain, 2007. [Google Scholar]
- Veith, J.M.; Bitzenbauer, P.; Girnat, B. Assessing Learners’ Conceptual Understanding of Introductory Group Theory Using the CI2GT: Development and Analysis of a Concept Inventory. Educ. Sci. 2022, 12, 376. [Google Scholar] [CrossRef]
| Author | Family name of the author, two authors, or the first in a list of authors, followed by the year of publication |
| Sample size | Number of participants in the study. In the case of being a theoretical study without experimentation, the acronym NE is used |
| Educational level | Secondary education (SE) or university education (UE) |
| Topic | Learning issues studied related to the concept of function (1: definition; 2: interpretation or meaning; 3: notation; 4: representation; 5: management and characteristics) |
| Results and conclusions | Main results and conclusions classified with respect to learning difficulties and misconceptions |
| Reference | Sample Size | Educational Level | Topic | |
|---|---|---|---|---|
| [11] | Abdullah, 2010 | 4 | SE | 1, 2, 3 |
| [12] | Akkoç y Tall, 2003 | 9 | SE | 1, 2 |
| [13] | Bardini et al., 2014 | 383 | UE | 1, 2, 5 |
| [14] | Borke, 2021 | NE | NE | 2 |
| [15] | Cansiz et al., 2011 | 61 | SE | 2, 4, 5 |
| [16] | Carlson y Oehrtman, 2005 | NE | NE | 1, 2, 3, 4, 5 |
| [17] | Clement, 2001 | 60 | SE | 2, 4 |
| [18] | Dogan, 2007 | 2 | SE | 1, 2 |
| [19] | Dreyfus y Eisenberg, 1992 | 443 | SE | 1, 2, 4 |
| [20] | Dubinsky y Wilson, 2013 | 15 | SE | 1, 3, 4, 5 |
| [21] | Eames et al., 2021 | 680 | SE | 1, 2, 4 |
| [22] | Evangelidou et al., 2014 | 164 | UE | 4 |
| [8] | Even, 1990 | NE | NE | 2 |
| [23] | Font et al., 2003 | NE | NE | 2 |
| [24] | Hatisaru y Erbas, 2017 | 56 | SE | 5 |
| [25] | Hitt, 1998 | 30 | SE | 4 |
| [26] | Leinhardt et al., 1990 | NE | NE | 1, 2, 3, 4 |
| [27] | Markovits et al., 1986 | NE | NE | 4 |
| [28] | Martinez Planell et al., 2009 | 9 | SE | 1, 2 |
| [29] | O’Shea et al., 2016 | 117 | UE | 1, 2, 3, 4, 5 |
| [30] | Panaoura et al., 2015 | 756 | SE | 1, 4, 5 |
| [31] | Parhizgar et al., 2021 | 74 | SE | 1, 4, 5 |
| [32] | Petterson et al., 2013 | 4 | UE | 1, 2, 5 |
| [33] | Petterson, 2012 | 4 | UE | 1, 2, 5 |
| [34] | Sajka, 2003 | 1 | SE | 1, 2, 3 |
| [35] | Sierpinska, 1992 | NE | NE | 1, 2, 3, 4, 5 |
| [36] | Tall y Bakar, 1992 | 28 | SE | 2, 5 |
| [37] | Thomas, 1975 | 50 | SE | 1, 2 |
| [38] | Thompson, 1994 | NE | NE | 1, 2, 3, 4, 5 |
| [39] | Vinner y Dreyfus, 1989 | 271 | SE | 2, 5 |
| [40] | Walde, 2017 | 352 | SE | 1, 2, 3, 4, 5 |
| [41] | Widada et al., 2020 | 1 | UE | 1, 2, 3, 4, 5 |
| [42] | Yusof et al., 2014 | 52 | UE | 2 |
M2. With the interpretation or meaning:
|
M4. With the graphic representation:
|
M5. With the management and characteristics:
|
D1. With the definition:
|
D2. With the interpretation or meaning:
|
D3. With the notation and expression:
|
D4. With the graphic representation:
|
D5. With the management and characteristics:
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trujillo, M.; Atarés, L.; Canet, M.J.; Pérez-Pascual, M.A. Learning Difficulties with the Concept of Function in Maths: A Literature Review. Educ. Sci. 2023, 13, 495. https://doi.org/10.3390/educsci13050495
Trujillo M, Atarés L, Canet MJ, Pérez-Pascual MA. Learning Difficulties with the Concept of Function in Maths: A Literature Review. Education Sciences. 2023; 13(5):495. https://doi.org/10.3390/educsci13050495
Chicago/Turabian StyleTrujillo, Macarena, Lorena Atarés, María José Canet, and María Asunción Pérez-Pascual. 2023. "Learning Difficulties with the Concept of Function in Maths: A Literature Review" Education Sciences 13, no. 5: 495. https://doi.org/10.3390/educsci13050495
APA StyleTrujillo, M., Atarés, L., Canet, M. J., & Pérez-Pascual, M. A. (2023). Learning Difficulties with the Concept of Function in Maths: A Literature Review. Education Sciences, 13(5), 495. https://doi.org/10.3390/educsci13050495





