Transdisciplinary STEM: Examples of Student Thinking within Nonformal Learning Experiences

Abstract

Calls for more integrated approaches to STEM have reached every sector of education, including formal and nonformal spaces, from early childhood to tertiary levels. The goal of STEM education as an integrated effort shifts beyond acquiring knowledge in any one or combination of STEM disciplines and, instead, focuses on designing solutions to complex, contextual problems that transcend disciplinary boundaries. To realize this goal, we first need to understand what transdisciplinary STEM might actually look and sound like in action, particularly in regard to the nature of student thinking. This paper addresses that need by investigating student reasoning during nonformal STEM-focused learning experiences. We chose four learning episodes, all involving elementary students working on engineering design tasks, to highlight the various ways transdisciplinary thinking might arise or not. In our analysis, we highlight factors that may have supported or hindered the integration of mathematical, scientific, technological, and engineering ways of thinking. For example, the nature of the task, materials provided, and level of adult support influenced the nature of student reasoning. Based on our findings, we provide suggestions for how to promote transdisciplinary thinking in both formal and nonformal spaces.

1. Introduction

Calls for more integrated approaches to STEM have reached every sector of education, including formal, nonformal, and informal learning settings, and spanning the pre-K to university spectrum [1]. As articulated by Kennedy and Odell [2], “STEM education has evolved into a meta-discipline, an integrated effort that removes the traditional barriers between these subjects, and instead focuses on innovation and the applied process of designing solutions to complex contextual problems using current tools and technologies” (p. 246). Advocates argue that solving current and yet-to-be-defined societal problems requires STEM knowledge, skills, and practices that transcend disciplinary boundaries [3].

Alongside this shift, there has been a substantial expansion in engineering education—especially at the elementary level. Such efforts are aimed not only at academic preparation, but also on broadening participation in STEM through interest and identity development [4,5]. Engineering design offers unique opportunities for learners to draw on mathematical and scientific principles and engage in evidence-based reasoning that spans the STEM disciplines [6,7]. Equally compelling, engineering design tasks that are personally meaningful or locally relevant can spark curiosity, build interest, or provide motivation to pursue future STEM learning opportunities or careers [8].

Despite the promise of STEM integration, we see several dilemmas that need to be addressed in order to capitalize on the learning potential of integrated STEM experiences. Most prominent are the reported difficulties in achieving transdisciplinary STEM—touted as the most advanced level of STEM integration—in school settings [9,10]. Second, a broad overview of the STEM education research highlights the contrasting, though complementary, goals for STEM integration across formal and nonformal settings. Whereas studies in school settings often focus on academic impacts and authentic integration of disciplinary knowledge and practices from mathematics, science, and engineering, the research on nonformal STEM education tends to target affective outcomes, such as interest, engagement, or career aspiration [11,12]. Perhaps for this reason, transdisciplinary STEM education as a conceptual framing is relatively nonexistent in scholarship situated in nonformal or informal learning environments. Thus, it is difficult to compare student experiences across formal and nonformal programs and activities, leading to an incomplete picture of contextual or situational influences on student thinking. Finally, regardless of the setting, there is little research on exactly what transdisciplinary STEM education looks like—not from a curricular standpoint but, rather, at the student activity level. In other words, we lack research demonstrating how students think when engaged in transdisciplinary STEM.

To move the field forward we see a need to better define transdisciplinary STEM in terms of student thinking and, in that attempt, work toward bridging the gap between formal and non-formal educational settings. In our scholarship, we distinguish formal, nonformal, and informal learning environments as described by Eshach [13]. A formal learning setting is often highly structured and sequential, teacher-led, and compulsory for students (e.g., school). Learning is also evaluated. A nonformal learning setting is structured and nonsequential, teacher-guided, voluntary, and does not prioritize assessment of learning (e.g., museum). An informal learning environment is unstructured, spontaneous, and learner-centered. Informal learning can occur anywhere, such as when children observe an unknown insect, such as a citrus stink bug, in their backyard [14].

In this paper, we address dilemmas surrounding transdisciplinary thinking and the apparent research disconnect between formal and informal settings outlined above by exploring two inter-related research questions:

• What is the nature of student thinking during engineering-focused STEM activities in nonformal settings?
• To what extent do students integrate concepts and ways of reasoning from multiple disciplines while engaging in these STEM activities?

Our analysis sets the stage for discussion of the possibilities for and challenges to promoting transdisciplinary thinking within and outside of school.

2. Literature Review and Theoretical Underpinnings

2.1. Perspectives on Transdisciplinary STEM Education

This study addresses a gap in the literature by empirically describing the nature of student thinking in transdisciplinary STEM settings. Definitions of integrated STEM range from the simple combination of two or more STEM disciplines within an authentic context to an approach in which disciplinary boundaries are suspended in the quest to answer questions greater than any one discipline [15,16]. Within this latter interpretation, referred to as transdisciplinary, the focus is on the problem to be solved. In their efforts to create novel solutions to authentic problems, learners go “beyond the discipline” to draw on prior knowledge or acquire new knowledge from multiple disciplines [17,18]. Because of its connection to problem-based learning and focus on solving complex, real-world problems, transdisciplinary STEM is considered both the most advanced and the most difficult level of integration to achieve in classrooms [10].

The term “transdisciplinary” is rarely, if ever, part of the conversation among educators working in nonformal settings, perhaps because the knowledge and skills needed to solve problems outside of school are rarely confined to specific academic boundaries. However, while the term itself is not evoked, nonformal educational spaces might provide the best environment for transdisciplinary thinking to emerge [12]. Although there is some intentionality in curriculum design, nonformal educators are not bound to content standards or specific disciplinary learning targets. Educators in nonformal spaces are also more likely to perceive a sense of urgency and importance for project-based STEM learning, and report having more freedom and resources to enact STEM activities for youth [19]. Within nonformal spaces, concepts and practices from various disciplines are often supportive or generative of each other. Learning experiences in nonformal environments promote fluid transitions from one type of disciplinary reasoning to another, with learners themselves unaware of making distinctions among STEM ideas.

Within nonformal STEM education, research and design is seldom focused primarily on imparting specific knowledge and skills from any singular discipline [11]. Instead, experiences are intended to spark interest and motivation to continue pursuing STEM learning opportunities or careers [11,12]. In addition to providing a setting for solving problems that are personally or socially relevant [20], we argue that non-formal environments foster a more relaxed space for learners to explore problems that are personally and socially relevant. However, the perception that nonformal STEM is all about fun highlights a potential divide in researching impacts of STEM education across settings. As Allen and Peterman [11] articulate, within nonformal STEM learning environments, student interest, enthusiasm, and engagement are visible, but it is less clear what or if students are learning. In contrast, while student learning might be evident within school settings, questions arise as to whether student engagement in STEM will be sustained. By investigating the nature of student thinking in nonformal STEM environments, we fill a current void in the literature related to our understanding of students’ transdisciplinary thinking in this increasingly common learning context.

2.2. Engineering as a STEM Integrator

Given the convergences between engineering practices and scientific inquiry [21,22], it is not surprising that engineering design arises as the context for many integrated STEM lessons—both in and outside of school. These convergences include an emphasis on learning by doing, uncertainty as a starting point, and the use of evidence to reason about alternative theories, causes, and solutions [6,22]. The learning episodes analyzed in this study focused on engineering practices as a basis for transdisciplinary learning contexts.

Engineering design provides a context for students to apply knowledge and skills from the STEM disciplines as they move from problem to solution [23,24,25]. The centrality of engineering design is one of seven key characteristics in Roehrig et al.’s [24] framework for integrated STEM. Additional characteristics include a focus on real-world problems, both context and content integration, and opportunities to develop and enact STEM practices and 21st century skills (e.g., critical thinking, communication, and collaboration). The selection of a real-world problem that generates interest and motivates all learners and also has potential to elicit knowledge and skills from multiple STEM disciplines is critical [26,27]. Researchers calling for STEM integration through engineering design also insist that the connections among disciplines should be made explicit to learners [15,25]. However, there is limited evidence on the precise nature of student thinking in these contexts [28].

The argument for making disciplinary content explicit is based on inherent challenges when using engineering as a context for STEM integration. Specifically, there is evidence that students do not always draw on disciplinary knowledge in integrated contexts and, thus, need support to elicit the relevant scientific or mathematical ideas in an engineering or technological design context [1,29]. Use of authentic mathematics has been singled out as particularly difficult to achieve, as mathematics integration is often limited to simplistic calculations (e.g., cost analysis) [25,30,31]. However, with explicit scaffolding and opportunities for learners to reflect on how their engineering designs are informed by mathematics and science principles, these meaningful connections can occur [32,33,34].

2.3. Connections to Experiential Learning

Kolb’s [35] theory of experiential learning positions life experiences as a central and necessary component of learning. As such, it has influenced decades of research on learning in diverse fields such as nursing [36], law [37], and nonformal and informal education [38,39]. Experiential learning is defined as “the process whereby knowledge is created through the transformation of experience” [40] (p. 49), where the emphasis is on learning as a process of adaptation rather than acquisition of an independent entity.

As illustrated in Figure 1, experiential learning occurs within a recursive cycle that includes opportunities to experience (CE—concrete experiences), reflect (RO—reflective observation), think (AC—abstract conceptualization), and act (AE—active experimentation). Concrete experiences are described as in-the-moment, uncontrived experiences, wherein learners assume full or collaborative responsibility for the learning process and are engaged socially, intellectually, and physically. Experiential learning necessarily involves risk as it incorporates novel, challenging experiences that involve unpredictability and experimentation.

To provide further clarity on the nature of concrete experiences, T.H. Morris [41] conducted a systematic review of how the theory of experiential learning has been used in studies across a range of settings, including museums, fieldwork, and service learning. This review revealed five themes that have implications for all four components (CE, RO, AC, and AE): learners are involved, active participants; knowledge is situated in place and time; learners are exposed to novel experiences that involve risk; learning demands inquiry into specific real-world problems; and critical reflection acts as a mediator of meaningful learning. Based on this review, Morris offered a revision to Kolb’s [35] model wherein experiential learning consists of “contextually rich concrete experience, critical reflective observation, contextual-specific abstract conceptualization, and pragmatic active experimentation.”

Within the theory of experiential learning, learning environments can be characterized by the extent to which they are oriented toward one or more of four learning modes [39]. These four modes, affective, perceptual, symbolic, and behavioral, refer to the overall climate of the learning environment and reflect the targeted skill or outcome that defines the learning task. Opportunities for deep learning are enhanced when all four learning modes are present. In an affectively rich learning environment, learners are engaging in the actions of a professional in the field—acting, doing, and speaking like mathematicians or scientists, for example. The information discussed is current and thinking is emergent. The primary goal of perceptually complex learning environments is understanding to be able to identify relationships among concepts, define problems, or research a solution. Reflection and exploration are encouraged, and the emphasis is on process rather than definitive solutions. In contrast, symbolically complex environments involve abstract problems for which there is typically one right answer or best solution. Learners are often required to recall specific rules or concepts and the nature and flow of activity is usually predetermined by a teacher or other expert. Finally, the behaviorally complex learning environment emphasizes applying knowledge or skills to a practical or real-world problem. The focus is on completing the task, with the learner left to make decisions about their behavior, what to do next or how to proceed, in relation to the overall problem to be solved. Success is measured with respect to agreed-upon criteria (e.g., how well something worked, cost, and aesthetics).

These modes, coupled with definitions of concrete experiences, are helpful in thinking about the affordances and constraints of the various settings in which STEM learning may occur, including those in this study. Several connections can be drawn between key tenets of experiential learning and expectations for transdisciplinary STEM education, most notably, the centrality of the problem(s) to be solved and the focus on situated, active experimentation. Thus, we revisit these descriptions later in the discussion when we consider the role of nonformal STEM education and how to support transdisciplinary thinking in school settings.

In sum, transdisciplinary STEM learning rises above specific content goals to encompass emergent thinking and action as learners pursue solutions to ill-structured problems that require a range of knowledge and skills. This vision seems well aligned to characteristics of out-of-school learning environments [12]. There may be multiple reasons for this, including the differing goals for STEM education espoused by nonformal educators and classroom teachers [19], or the simple fact that physically getting out of the classroom is more conducive to active experimentation. In this paper, we use examples from our data to illustrate the nature of transdisciplinary thinking in nonformal learning environments. By doing so, we set the stage for exploring factors that encourage or discourage transdisciplinary STEM learning in formal and nonformal settings. Our exploration of transdisciplinary, engineering-based contexts that are grounded in experiential learning sheds much needed light on the precise ways students think in these increasingly common learning situations.

3. Methods

This qualitative study is part of a larger project investigating the nature of student thinking in integrated STEM contexts. The full corpus of data includes video of more than 20 STEM experiences in both formal and nonformal settings spanning grades pre-K to 12 [42,43]. To address our research questions, we focus here on four learning episodes, all of which occurred in nonformal settings. These four episodes highlight the transdisciplinary nature of student thinking in nonformal STEM environments, therefore, addressing a gap in our current scholarship base regarding what transdisciplinary STEM education looks like at the student activity level.

3.1. Data Collection

We centered our analysis of student thinking on the presence and nature of the claims made by students during the learning experience. Drawing on Toulmin [44] and McNeill and Krajcik [45], we define a claim as the beginning of an argumentation process in which a position is taken. The claim can then be supported by evidence and reasoning. We hypothesize that the nature of the claims, evidence, and reasoning exhibited by students throughout a learning experience can reveal a variety of aspects related to their thinking. Argumentation (e.g., creating evidence-based explanations in science or engineering or constructing viable arguments in mathematics) is recognized as a key practice across the STEM disciplines for both knowledge generation and communication. However, differences in the type of evidence and forms of reasoning considered acceptable within each discipline highlight critical distinctions in their epistemological nature.

Our data set for this study consists of four videotaped learning experiences. While the learning context for each episode was a nonformal setting, there were several differences among them, which we detail in

Table 1. Description of learning episodes.

Learning Episode	Task Description	Setting	Participants	Duration
Programing Dash	Design a path and then program a robot to follow a path created by another group.	School-based makerspace; teacher-created task	5th grade; 3 boys and 1 girl	22 min
Roller Coaster Wall	Use foam pipe insulators to build a “roller coaster” affixed to a wall.	School gymnasium, part of after school program led by local science museum	Three 2nd grade students	32 min
Rain Gauge	Work through a design kit for building a rain gauge with LED lights	At home, family activity weekend “rainy day” activity; researcher-developed kit	5th grade girl (working with her mother)	36 min
Catapult	Create a catapult that will launch a cotton ball into a basket.	School-based makerspace; teacher-created task	5th grade, 2 boys and 1 girl	20 min

below. Prior to collecting any data, ethical approval was obtained from author B’s local institutional review board. Parent/caregiver consent and student assent were obtained as well. Pseudonyms are used to identify participants. In each case, students voluntarily participated in the STEM experiences. With the exception of the rain gauge, these activities occurred in school spaces as part of after school or weekend STEM enrichment.

The first learning experience, programing Dash, took place in a school-based makerspace. Students volunteered to engage in three days of STEM-focused activities developed by their teacher, Mrs. B. The activity occurred in two parts and lasted approximately 22 min. In Part 1, students were provided the following directions by Mrs. B: “Using a roll of tape, create a path from one side of the room to the other. This path should be one that Dash can travel on.” In Part 2, students were to use the app, Blockly [46], to program Dash to traverse the taped path constructed by another group. Students were provided with an iPad, a tape measure, and a pencil to complete this phase of the activity. Our analysis focused on four 4th grade students—Alex, Ryan, Fawn, and Peter—and the video recording of Fawn, who wore a GoPro camera on her chest.

The second learning experience, building a roller coaster wall, occurred in a 12-week STEM-enriched after-school program for elementary-aged students developed and led by a local science museum. For two days of each week, two museum educators implemented the various activities, while three after-school employees typically worked alongside the students during the activities. For this activity, students were given different lengths of Styrofoam pipe insulation halves and were tasked with affixing the noodles to a wall to transport a marble from the beginning to the end of the “roller coaster” without using their hands. Our analysis focused on three 2nd grade students—Gary, Steve, and Lake. We analyzed the 32 min video of Gary, who wore a GoPro camera on his chest.

The third learning experience, constructing an LED rain gauge, was part of a larger study in which local families with at least one child aged 8–12 engaged with engineering kits in their home environments. The kits were developed by author B in collaboration with other members of a research team. In this kit, families were given the following engineering task:

Several cities across the U.S. are experiencing their wettest year to date. The National Weather Service is asking for your help in measuring and reporting the amount of rainfall in your city. Using the provided material, build a rain gauge to measure the amount of liquid precipitation over a set period of time.

This activity required families to create a simple circuit so that LED lights would light up when a certain amount of rainfall had accumulated (e.g., 1 cm = green light, 2 cm = blue light). The kit provided all the necessary materials, including a child-centered and a facilitator-centered guide, and supported the development of a rain gauge prototype through an engineering design process—research, plan, create, test, improve, and communicate. In addition, each family was provided with a tablet to record their interactions with one another. We analyzed a 36 min video from a mother–daughter dyad. Sara was a fifth-grade student at the time of the study.

The fourth learning experience, building a catapult, was part of the three-day STEM-focused activities within the school-based makerspace described above. For this activity, Mrs. B tasked the students with constructing a catapult that would shoot a cotton ball into a student-created basket. Students were constrained by the materials. They were provided with 10 popsicle sticks, 1 sheet of paper, 1 plastic cup, 3 inches of tape, 1 pencil, and a pair of scissors. Students were given approximately 20 min to complete this activity. We analyzed a video from a stand-alone camera of one group of 5th grade students—Evelyn, Byron, and Walker.

3.2. Data Analysis

Initial video analysis of the learning experiences consisted of the identification of claim sequences, which may consist of a single comment or action or a set of comments and actions that collectively comprise a single claim. For each learning experience, two of the authors independently identified claim sequences and provided a summary or transcription of what students said or did during the exchange. The pair of authors then met to resolve any differences and refine the claim transcriptions. In some instances, new claim sequences were identified.

3.2.1. Claim, Evidence, Reasoning Coding

Once the claim sequences were identified for a particular learning experience, the same two authors independently coded the nature of the claims, evidence, and reasoning, utilizing a CER framework. We developed the CER coding framework based on argumentation literature across the STEM disciplines and multiple cycles of collaborative video viewing and discussion (see [42] for details). As stated above, distinctions among argumentation structures provide a unique window into the ways in which student thinking connects to one or more of the STEM disciplines. Thus, the CER coding framework provided a useful tool for addressing our research questions. The nature of the claim was categorized along several dimensions, such as whether it was explicitly stated, represented a novel idea or offered a challenge or different perspectives, or was communicated using formal vocabulary versus informal language or gesture. Each claim was also given one or more disciplinary codes to indicate whether it was grounded in science, technology, engineering, mathematics, or some combination. Evidence codes included facts or prior experiences learners drew on to support their claims as well as more immediate evidence, such as that coming from a test, observation, or physical manipulation of some part of the environment. Codes for reasoning included general characteristics (e.g., explicit or inferred, experiential or abstract, based on personal or external authority, drawing on experiential or abstract principles) as well as discipline-specific types of reasoning, such as spatial or quantitative (mathematics), cause-effect, analogic (science), constraint or materials-based (engineering), or algorithmic (technology). As with the claim, reasoning was also given an overall disciplinary code. Although this code generally mirrored those applied to the claim (i.e., when the claim was coded as science, the reasoning was also science), there were some exceptions and, thus, we felt it important to keep these codes separate.

3.2.2. Identifying Transdisciplinary Thinking

After coding each learning experience, we turned our attention to identifying and characterizing episodes of transdisciplinary thinking. We had many conversations about the grain size of transdisciplinary thinking—does it exist within a single sequence or is it more of a holistic way of thinking that spans the entire learning experience? Without a clear answer to this question, we utilized differing sources of evidence to identify the examples we present below. First, we considered individual claim sequences and denoted all those that were coded as containing two or more discipline codes for either the claim or the reasoning. The total number of such claims is represented as “multidisciplinary” in

Table 2. Summary of select CER codes from learning episodes.

	Program Dash (36 Claims)		Roller Coaster Wall (29 Claims)		Rain Gauge (60 Claims)		Catapult (45 Claims)
Multidisciplinary	19	53%	9	31%	20	33%	1	2%
Science	0		8		25		1
Mathematics	23		1		13		0
Engineering	23		29		43		45
Technology	17		0		0		0
Fact	0		5		23		3
Prior experience	2		1		6		1
Observation/manipulation	30		26		36		36
Test	11		13		23		18
Cause–effect reasoning	3		14		18		14
Spatial reasoning	22		12		16		11
Quantitative reasoning	2		0		6		0
Constraints-based	6		1		0		2
Materials-based	5		10		31		16

. Next, we looked at the total number of claims coded for each discipline (i.e., how many engineering, math, science, or technology claims or general reasoning codes). From this perspective, a learning experience that contained a more even mix of disciplinary codes would be indicative of transdisciplinary thinking. Finally, we considered a middle ground approach, wherein we went line by line down the coded spreadsheet looking for shifts in disciplinary codes from one claim sequence or one chunk of activity to the next.

4. Illustrations of Transdisciplinary Thinking

The four learning episodes illustrate the range of ways that transdisciplinary thinking may occur (or not) during STEM learning experiences. As described above, all the learning episodes occurred in nonformal settings with tasks designed by a variety of education providers for use with elementary grade students. See Table 1 for summary descriptions. The tasks differ in content and objective, from programing a robot to building a catapult, but all afforded an immediate means of testing for success.

4.1. Learning Experience 1—Programing Dash

The goal of this task was to program a robot to follow the tape path another group had created on the floor (see Figure 2). As shown in Table 2, there was a relatively even distribution of math, engineering, and technology evidenced in student claim making. Given the emphasis on programing, the prevalence of technology (present in 17 of the 36 claims—far more than in any other learning episode) is not surprising. However, engineering and mathematical thinking occurred at an even higher rate, with each present in 64% of claim sequences.

From the start, roles were quickly assigned or assumed, with two male students (Ryan and Alex) immediately jumping in to measure and/or estimate each segment of the path. This involved determining the length of a straight section or estimating the angle of a turn. During students’ initial work, engineering reasoning primarily surfaced with respect to materials and task constraints (e.g., time and limited mobility of Dash). The following three excerpts illustrate the nature of these brief claim sequences.

Alex: (using a tape measure to measure the first strip of tape) So 79.

Ryan: You can’t code 79 though, so 80.

Ryan: So it’s a 90-degree turn.

Alex: That’s about a 90-degree turn, that’s easy to do.

Ryan: So 19 or 20-ish.

Alex: 19 to 20.

In these interactions, student reasoning and decision making regarding measurement precision was grounded in technology, engineering, and mathematics. For example, Dash could only be programed to move forward in increments of 10 cm (e.g., “You can’t code 79 though, so 80.”) and, when constructing the original path, students were told “Dash can’t do narrow angles.” Throughout the learning episode students considered these engineering and technology constraints on the robot’s mobility and on the level of precision that was necessary or even possible in the Blocky program. Mathematically, while students attempted to measure length with some degree of precision, they consistently relied on estimation and an intuitive sense of angle measure to determine the number of degrees Dash needed to turn at each juncture.

Later in the activity, after shouting out several different measurements, the students revised their work plan and employed the engineering practice of test, revise, and retest.

Ryan: So do you want to, after every two (measurements) we test?

Others: Yeah, let’s test it.

Ryan: Every two we test.

Alex: Yeah, let’s test the first one. (group finally tests the 80 cm they originally programed.)

The testing cycle allowed the students to revise the program in the moment—supporting further integration of math, technology, and engineering thinking. For example, the following exchange occurred after testing the first command:

Ryan: (after repositioning Dash and re-running the program) That’s a little too far.

Alex (and others): Do 78.

(Dash runs again)

Alex: Try 70.

(Dash runs and stops at end of line)

Other: Perfect.

Alex: Yeah, 70 is good.

In the above exchange, students used spatial reasoning to refine their estimated measurements through the engineering design cycle of testing and recoding.

As illustrated in the following two claim sequences, this integration of mathematics, technology, and engineering ways of thinking was common across the activity:

(After Dash runs through the first few commands.)

Other: Put in 10 cm.

Alex: No, we can’t do 10 cm because 10 cm would make it go here.

Ryan: No, like 10 cm that way. (points)

Alex: Oh, 10 cm that way. (moves Dash that way)

Ryan: You need to put it on a slight angle though.

Ryan: Yeah, 20. Make that 20. … You have to make it a left 90-degree turn.

Alex: A left 90-degree turn? Ok.

Ryan: Now turn left 45 degrees.

Alex: 45?

Ryan: Yeah.

Alex: (while entering the code) Why don’t we do like 30 degrees to test, then we move to 45?

After testing the initial steps of the program (engineering design thinking), students discussed changes to the program (technology) based on testing Dash’s movement coupled with their understanding of length and angle measurements (mathematics).

As demonstrated in this final excerpt and throughout the activity, students felt at ease putting ideas on the table, relying on personal authority when doing so. Several aspects of the learning environment afforded this freedom. The only adult interventions throughout the entire episode were reminders about how much time students had left to complete the task. The task directions themselves were minimal, providing an end goal through an ill-structured design task—program the robot to follow the tape path—rather than prescribing a method and/or assigning student roles or specific tasks. In addition, the students all seemed to have had prior experience with the robot and the coding program being used, with Ryan quickly declaring himself “really good at coding.”

In sum, mathematics and engineering principles and practices were threaded seamlessly within students’ reasoning around how to create the proper sequence within the Blocky program (technology) to successfully complete the task. Mathematically, students used tools (tape measure) and spatial reasoning to inform the programing decisions. This work was situated within engineering design thinking, particularly the application of the test, revise, and retest cycle leading to a final solution. The engineering design cycle played an even more prominent role in the learning episode we present next.

4.2. Learning Experience 2—Building a Roller Coaster Wall

In this task, students constructed a roller coaster out of assorted lengths of grooved Styrofoam tubes and tape. The roller coaster was to be attached to the wall and students were to design the path for a small metal ball to follow (see Figure 3). While the primary thinking involved was clearly within engineering, with all 29 claim sequences coded as such, there were several instances of science and a solo instance of mathematics also evident in student claims. Engineering claims primarily focused on the overall design of the roller coaster and redesign after failed tests, which often also included reasoning around materials. Science principles surfaced in students’ informal language and reasoning about the amount of power, energy, and speed being generated by steeper drops.

In the following interaction, five minutes into the activity, Gary and Steve share intuitive ideas about potential and kinetic energy:

Gary: Now we need to go up.

Steve: No, we can’t do it or else it won’t go.

Gary: We need to just make it straight.

Steve: That would make it straight down like a roller coaster.

Gary: And then up just a little bit… Because I imagine it has a lot of energy in this.

Both Gary and Steve use informal language and rely on their prior experiences with roller coasters to reason about whether the metal ball would have enough energy to go back up. In this way, scientific principles are naturally embedded in the students’ reasoning about engineering design.

Ten minutes later, after a failed test, we again hear Gary thinking through some of the scientific principles underlying the design:

Gary: Look. It’s going so fast… It’s going so fast that it doesn’t… It’s going so fast that it doesn’t have time to go up and at like right here (pointed), it flings up and just hits that and then ricochets back. Watch. It’s going faster (inaudible) and then it ricochets off…

(continuing) Look. This is where it’s getting stuck. Right here… Maybe if we make it go lower. (lowers one end of the last noodle) Like that.

Our analysis revealed that transdisciplinary thinking was less prevalent in the roller coaster wall than in the Dash episode. However, Gary’s self-talk in these two excerpts illustrates the interaction between engineering and scientific principles and practices as well as the cause–effect and spatial reasoning that were common across the nine multidisciplinary claims. As was the case throughout the roller coaster learning episode, the scientific ideas were expressed informally and, in this instance, it is not exactly clear what connections Gary is making between “going too fast” and the metal ball needing “time to go up.” However, these intuitive understandings of science and design thinking are central to Gary’s reasoning process.

This episode also reveals a high level of agency and authority assumed by Gary and the other students. The students had freedom to make conjectures and seemed comfortable offering new ideas. Students seldom used academic vocabulary or formal language and instead spoke with confidence from their own understanding of scientific concepts. In the discussion, we revisit the role of personal authority and its potential role in promoting transdisciplinary thinking. Interestingly, claims made in the rain gauge learning episode, which we describe next, were also primarily based on personal authority, despite the fact that the student was working one on one with a parent.

4.3. Learning Experience 3—Constructing an LED Rain Gauge

The task objective for this activity was to construct a rain gauge with LED indicator lights that would signify when the rainfall total reached the decided upon increments (see Figure 4). Similar to programing Dash, this activity also elicited fluid transitions across disciplinary content in the students’ thinking. Within the 60 identified claim sequences, 25 were coded as science, 13 mathematics, and 43 engineering, with approximately one third of the claim sequences coded as multiple disciplines (Table 2). The natural influx of mathematics and science principles into the engineering design thinking occurred in two distinct parts of the task.

Mathematics principles of measurement and volume were central to the first part of the task, in which Sara had to decide what increments to use to measure rainfall and mark the plastic cup that would gather the water accordingly. Upon reading the task instructions, Sara drew on her own experiences and understanding of measurement to immediately challenge the directive to create markings of equal height.

Sara: But it’s a cup.

Parent: You want to measure volume huh?

Sara: Yeah, because if it’s a cup, the volume will change through it (moving her hand up and down to indicate the cup’s shape), so it wouldn’t really be accurate if you measured it in cm.

Following her own suggestion, Sara then worked to decide on a reasonable unit of volume. After putting 1.2 mL of water into the cup and noting that it was “just a drop,” Sara suggested they try 5 mL. This sparked a back-and-forth exchange wherein Sara drew on spatial reasoning and estimation to decide whether 15 or 30 mL increments would be best. Sara eventually decided on 30 mL and provided this justification: “Well actually, I just realized if we do 30 mL, it’s eventually going to space out, so it will probably work if we just measure it carefully.”

After marking the water level for a series of 30 mL increments, the parent intervened with a wondering about the height-to-volume relationship.

Parent: I’m curious how this might correlate with our measurements on the ruler. Just more of a curiosity really.

Sara: Yeah because if it actually… shows a pattern (grabs ruler). But you can see the first one was bigger than the second one and the second one was way bigger than the third (pointing to the lines on the side of the cup).

Sara: (after placing a ruler vertically alongside the cup) It’s because it’s spacing out so it’s carrying more volume. So see right now, it’s barely going up by the 15, and 30 is only going to be a little…

Parent: Why do you think that is?

Sara: Like I said, it’s spacing out a little, see these two are the same.

Parent: So the cup gets wider as it goes up.

Sara: Yeah, so it’s going to get smaller and smaller and smaller (see Figure 5).

Parent: So if you wanted to measure something and have more visual height, what would you want to do for your cup?

Sara: I would want to make it like… a tube (gesturing a long, narrow cylinder).

Parent: More narrow?

Sara: Yeah, more narrow.

Throughout this interaction, evidence for transdisciplinary thinking can be seen and heard in the way Sara naturally integrated mathematical reasoning in service of the first sub-goal of the design task. Specifically, Sara was drawing on measurement principles and concepts of volume to reason relationally about how the width of the cup effects the height when constant volume increments of water are added. Critical decisions about the engineering design (i.e., what increments would be “best” and when to stop marking) were based on Sara‘s mathematical understanding of this functional relationship between volume of liquid and the visual height. Alongside this mathematical reasoning, Sara brought in pragmatic reasoning about what volumes were possible with the measuring tools at hand (kitchen measuring spoons) and what would be the most readable, as well as her everyday experiential knowledge of how much rain was typical in her area. By voicing her “curiosity” about the height measurement, and later posing a direct question about what shape of cup would create a greater visual height per volume, the parent played a key role in making some of Sara’s reasoning explicit. We see these interjections as important opportunities to promote reflective observation.

After marking the cup, Sara turned her attention to the second part of the task, attaching the LED lights and completing the circuitry for the rain gauge. To accomplish this, Sara drew on her understanding of science principles related to electricity and conduction to guide her construction decisions. For example, after first establishing which wires were positive and which were negatively charged, Sara completed mini circuits to test each of the LED lights before attaching them into the rain gauge device. As illustrated in the following excerpts, scientific principles were also naturally intertwined with Sara’s reasoning about why or if the device would work.

Sara: But water is connected to electricity. Water is a… conductor. So, it should work… Does it still work I wonder with the glue?

Parent: We can test it and see.

Sara: If not we might have to find some other way (to attach the LED lights).

In this sequence of claims, engineering and science-based reasoning are inextricably linked. Sara first asserted that, because water conducts electricity, the rainwater would, in effect, complete the circuit and, hence, the LED lights should come on. Sara further reasoned that the glue they were using to attach the LED lights to the plastic cup also needed to be a conductor. In both instances, scientific evidence, in the form of facts about conductors and electric circuits, was used in conjunction with materials-based reasoning (considering specific properties of the glue) to support design choices.

Over 50% of the claims were coded as materials-based reasoning, which we defined as referencing a specific property or inherent feature of a material as the basis for a claim. We provide one final excerpt to illustrate what this sounded like and illustrate how it often marked an interdisciplinary way of thinking that combined engineering and science. This interaction occurred during the final construction steps, after all the LED lights were attached, and the various wires needed to be connected and secured.

Parent: How would you like to secure this? You have a couple of materials available.

Sara: We could just glue that part down. Just this side, cause I don’t think the other side needs it and that way its (the glue) not touching the wires either.

Sara: Wait is electric tape a conductor?

Parent: I don’t think so, that’s why it’s electric tape because you can wrap it around your wire and it won’t conduct. That’s a good question though.

Here, Sara is actively considering scientific principles, i.e., the conductive properties of glue and tape, to make engineering design decisions (how to physically secure the rain gauge components). Her mother confirms that tape is not a conductor and reinforces the good thinking behind Sara’s question.

In summary, Sara drew heavily on mathematics to create a reasonable scale for measuring the rainfall totals during the first phase of construction. Relying on her own understanding of volume, Sara challenged the original directions (which asked the students to simply mark off equal height intervals) to account for the cup’s shape and reason accordingly about the height-to-volume relationship. In this second part of the activity, completing the circuitry and attaching the LED lights to the cup, an understanding of scientific principles related to conductors, insulators, and the flow of electric current was helpful. These scientific principles were inextricably linked to engineering-based reasoning around the materials and overall construction of the rain gauge.

4.4. Learning Experience 4—Building a Catapult

We share the catapult task as a “non-example” of transdisciplinary thinking not to dismiss the students’ activity and learning but, rather, to generate discussion around the potential limitations in our analysis and raise questions about the implicit vs. explicit nature of transdisciplinary thinking. The goal of this task was to create a catapult from the given materials (plastic cup, construction paper, tape, straw, rubber band, and tongue depressors) that would launch a cotton ball into a basket that students were also to create from the materials (see Figure 6).

In contrast to the above learning experiences, our analysis did not reveal much in the way of transdisciplinary thinking. As shown in Table 2, the activity resided purely in the engineering realm, with only one claim sequence also coded as science. The predominant form of reasoning in support of claims was spatial, cause–effect, and/or directly connected to the materials that were provided. The excerpts below are indicative of this reasoning pattern.

Byron: It keeps on like going to the left. We should like add more tape to the base.

Walker: Yeah, that’s the thing. It keeps turning at the bottom. (adds tape)

Byron: Yeah, so it keeps turning at the bottom.

Evelyn: Or we could use this to…

Walker: No, we just need the tape.

and later:

Byron: It’s going like too far down, so it’s hitting the ground. It keeps going too far down.

Walker: We need to keep it farther back. We have to have it at a slant so it doesn’t go down. (continues to add tape to front of the base)

Even though the entire workings of a catapult are based on science principles (e.g., laws of physics governing projectile motion, potential, and kinetic energy), students never drew on those principles—at least in an explicit way. This is not to say that students were not drawing on their intuitive sense of trajectory or laws of motion, perhaps grounded in their own everyday experiences. Students relied on trial and error, spatial reasoning, and estimation to build, test, and revise their catapult device.

5. Discussion

The goal of this paper was to explore the range of ways students engage in transdisciplinary thinking when working on STEM-focused tasks in nonformal settings. Our analysis of four learning episodes revealed a mix of student reasoning that spanned disciplinary boundaries. We begin the discussion with a review of results demonstrating the varied degrees of integration evidenced in student thinking, responding to research question 2. We then expand on the role of personal authority as a critical theme that emerged in our analysis of the nature of student thinking across all four episodes. Finally, we discuss the affordances and constraints of nonformal settings and provide recommendations for educators in both formal and nonformal settings.

5.1. Integrated Nature of Student Thinking

The degree of integration evident in student thinking varied significantly, with over 50% of claims in programing Dash coded as two or more disciplines, a third coded as more than one discipline in both the rain gauge and roller coaster wall, and only 2% in catapult. While each setting was unique, several contextual factors and task features were shared across the learning episodes. For example, in all cases, elementary grade students were working on engineering design tasks in nonformal settings. Three of the four episodes occurred in the school as part of after-school programing, with tasks designed by a teacher (Dash and catapult) or by local museum educators (roller coaster wall). In contrast, the rain gauge task was designed by an outside researcher as a stand-alone activity for families to work through at home.

In Dash, there was a relatively even balance of technology-, engineering-, and mathematically-based reasoning. The overarching task goal, program Dash to follow a given path, was grounded in engineering and technology. To accomplish this goal, students relied on mathematical knowledge and skills, including an understanding of units of measure for both length and angle. Students also had to reconcile principled understandings of precision and accuracy with the measurement and coding tools at hand. The rain gauge activity also elicited disciplinary claims and reasoning that were relatively balanced across the whole of the learning episode. While the overarching task—build an LED rain gauge—was primarily an engineering task, the two phases of construction required differing knowledge from other fields. Specifically, the first phase elicited mathematical content understandings, while scientific principles of electricity were important to the second phase of the engineering design. Similar to the rain gauge, approximately 30% of claims made during the roller coaster learning episode included more than one disciplinary code. However, in this case, the integration took on a single form, with one student drawing on informal language and understandings of science principles related to energy, power, and speed to reason about the engineering design. In stark contrast, students working to build a catapult did not utilize the underlying science principles (e.g., potential energy and projectile motion) to guide the original design or make adjustments.

Indicative of active experimentation (a pillar of experiential learning), evidence used to support claims across all learning episodes came primarily from tests and in-the-moment observations or manipulation of the physical materials. This correlated with the cause–effect, spatial, and materials-based reasoning that dominated all but programing Dash. These specific ways of reasoning, aligned with science, mathematics, and engineering practices, respectively, were seamlessly integrated and used in service of solving the design problem at hand.

5.2. Role of Personal Authority

Across all learning episodes, over 97% of claim sequences were coded as personal authority. The nature of the tasks and of the overall learning environment promoted student agency and autonomy. The ultimate goal for each of the tasks was determined by others and relatively straight-forward: “create a ____ that will do the following…” However, the pathway to achieve the goal was left to students, allowing them freedom to explore alternative ideas, design, test, and redesign. In some instances (e.g., rain gauge) the students were afforded opportunities to change the parameters of the task. The simplistic nature of the task statements was also supportive in terms of removing barriers due to lack of knowledge of a specific mathematics or science concept or procedure. This low-floor entry allowed students to access the task with minimal support and, with the exception of the rain gauge episode, we saw little interference from adults in the room. Apart from a few reminders of the time remaining or clarification of other constraints (as noted in catapult), students were left to their own devices to determine what to do next and worked in groups without adult intervention.

The few references to external authority most often occurred after a direct intervention by a teacher/facilitator. For example, during the catapult learning episode, the teacher/facilitator intervened to clarify the difference between a catapult and a slingshot and later focused students’ attention on the fact that the catapult needed to be attached to the table. Armed with these constraints, now accepted as facts, the students immediately shifted their design. In the rain gauge, the parent played a key role in making the underlying mathematics and science principles inherent in the task explicit. Rather than provide answers, however, the parent posed purposeful questions that promoted active reflection and allowed Sara to assert her personal authority.

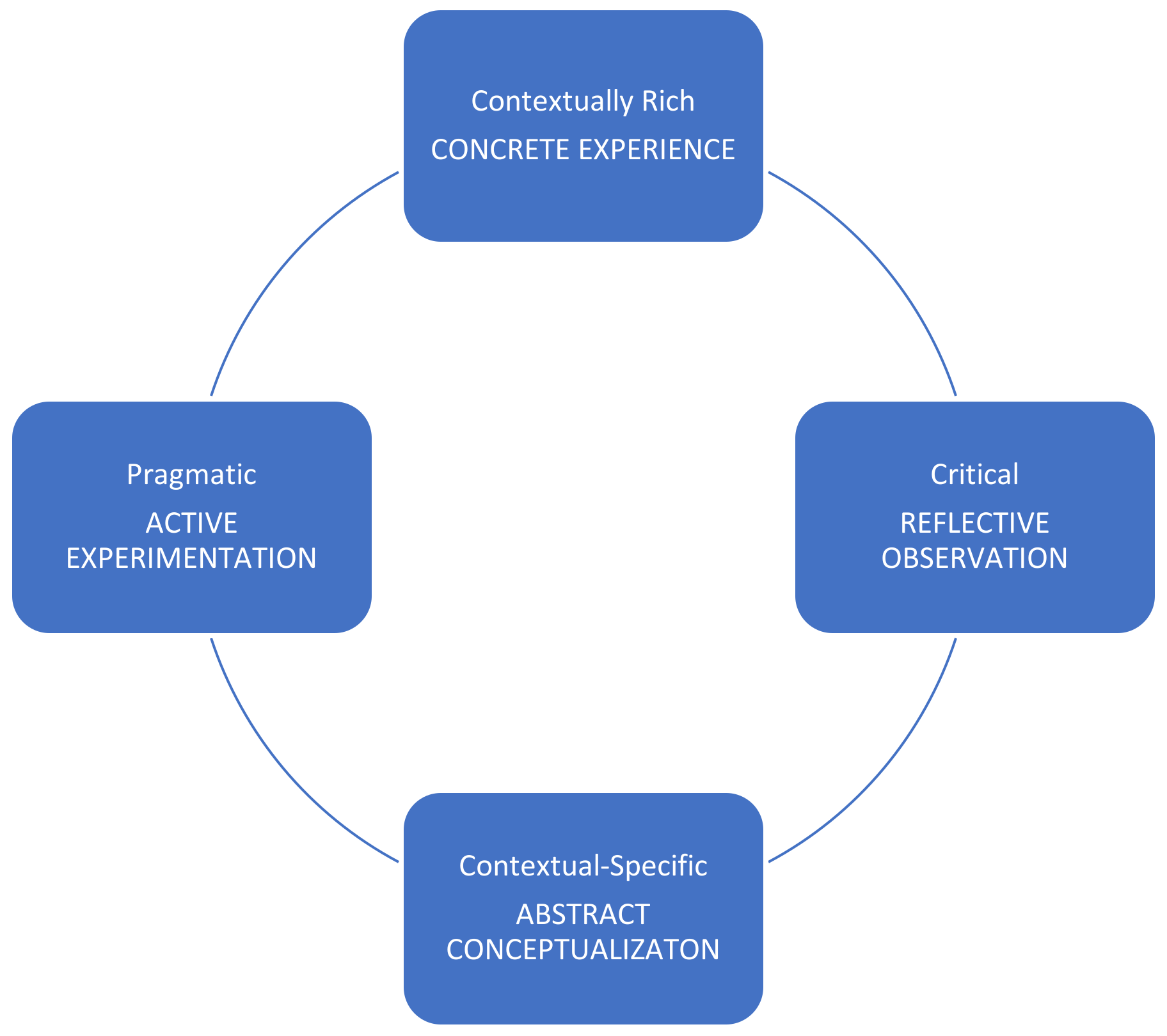
Promoting student agency through the pursuit of solutions that are personally meaningful has significant connections to experiential learning and our conceptualization of transdisciplinary thinking. Active experimentation demands that learners take responsibility and act pragmatically to find solutions [41]. In the process, learners need to respond to unforeseen challenges and unpredictability by being creative and willing to take risks. From a transdisciplinary perspective, students’ agentic activity has the potential to expand students’ school understandings of STEM content in ways that are more authentically aligned with epistemic practices within and across the STEM disciplines [10,30].

5.3. Promoting Transdisciplinary Thinking in Nonformal and Formal STEM Learning Environments

The characteristics of experiential learning, and the four modes of learning, provide a useful frame to consider the benefits of situating STEM learning in nonformal settings. Similar to formal school experiences, there is structure and intentionality involved in planning nonformal STEM activities [13]. However, attendance is voluntary and there is no formal assessment or evaluation of the learning that occurs. Further, students are often able to utilize task criteria to make their own judgments regarding success. For these reasons, we argue that nonformal STEM environments are generally oriented toward affective and behavioral modes of learning [39]. This is especially true when the activity is focused on engineering design, as was the case in the four learning episodes analyzed in this study.

The nonformal space was conducive to physical movement and the hands-on-materials promoted a sense of freedom and experimentation. Task goals and constraints were communicated verbally, with the exception of the rain gauge, where Sara was guided by the directions provided with the researcher-developed kit. Again, with the exception of the rain gauge, the adults in the room had little direct influence on how students engaged in the tasks. These features worked in combination to open up more transdisciplinary thinking. However, as revealed in our analysis, student reasoning in these nonformal settings was rarely grounded in mathematics and science principles, at least not at an explicit level. Thus, we see value in attending more intentionally to task implementation within nonformal education settings. This might involve creating facilitation guides that outline a range of approaches students might take depending on content knowledge understandings. Armed with anticipated approaches, facilitators might be better positioned to ask open questions and support connections to mathematics and science principles they see emerging in student activity. We also suggest nonformal educators embed opportunities for students to slow down and reflect on their process and observations. Encouraging students to draw on prior knowledge or generalize from their observations and tests can support connections across all four stages of the learning cycle (experiencing, reflecting, thinking, and acting) [40].

We provide these facilitation suggestions with a note of caution that this might actually create barriers to transdisciplinary learning or influence student thinking in less than helpful ways. Given the value of personal authority, any prompting should be carried out with care so as not to take away from student ownership or unintentionally narrow future thinking. Thus, facilitation guides should be viewed as a resource but not a directive. For example, guides could provide suggestions on the timing of potential questions or details and language related to specific disciplinary ideas.

Formal STEM learning environments, in contrast, are typically characterized as being more symbolically complex, wherein learners are expected to recall specific content knowledge and solve problems that have one correct answer [39]. In the search for predetermined solutions, student thinking often remains siloed. Moreover, the structured, sequential, evaluative nature of formal school settings [13] works against personal authority. To enhance student learning and promote transdisciplinary learning, we encourage formal educators to consider ways to promote behavioral and affective modes of learning.

Project-based learning [45] is promoted as one way to promote content integration in schools and provide opportunities for students to engage in disciplinary practices (i.e., to act like a mathematician, scientist, or engineer). However, to realize this potential and move beyond interdisciplinary to transdisciplinary thinking, we offer a few suggestions. First, rather than serving as a culminating task (i.e., an end-of-unit assessment) in which students apply previously learned knowledge and skills, projects can occur prior to explicit instruction. Providing students with opportunities to grapple with ill-structured problems can lead to pragmatic active experimentation and contextually rich concrete experiences the teacher can leverage. Finally, we urge formal educators to honor students’ informal language and avoid the rush to provide precise vocabulary, formal definitions, and canonical understandings of mathematics or science that may stifle students during active experiential learning.

6. Limitations and Future Research

There are several limitations with regard to the four learning experiences we analyzed that should be acknowledged. First, some may argue that grounding the analysis within engineering design tasks, purported as an “ideal integrator” [24], may limit our observations of students’ transdisciplinary thinking and ability to generalize to other STEM-related tasks, such as scientific inquiry tasks. Future research should attend to this as a potential way to compare and contrast the affordances and hindrances of a wider variety of task designs. Second, our analysis did not include a variety of nonformal contexts, such as museums or community centers (e.g., Boys and Girls Club). Again, future research should expand to consider a range of nonformal contexts. Such research might also investigate the role of parents and nonformal educators in shaping students’ transdisciplinary thinking in productive or nonproductive ways. Finally, our analysis primarily focused on the verbal statements and reasoning of students. We contend that the addition of embodiment (e.g., gestures) and the manipulation of objects and materials as components of our analysis will enhance how we observe and interpret students’ transdisciplinary thinking within ill-structured STEM problems in nonformal learning environments.

7. Conclusions

The purpose of this paper was to illustrate students’ transdisciplinary thinking during nonformal STEM-focused learning experiences. Our analytic framework, which targets student claim making, provides researchers with tools to operationalize this approach in a variety of learning situations [42]. Based on our analysis, we provided recommendations for educators in both nonformal and formal settings. In nonformal spaces, we suggest creating more robust facilitation guides that include potential student responses and targeted prompts for students to actively reflect on their emerging claims, evidence, and reasoning. Within school settings, we encourage teachers to allow students to grapple with ill-structured problems prior to a unit of instruction. Finally, we urge educators across both settings to honor students’ informal language and experiential knowledge. The significance of our research lies in the continued possibilities for and challenges to promoting transdisciplinary thinking both outside of and within school contexts. As a field, we encourage scholars, researchers, educators, and curriculum developers to consider the potential role of nonformal environments in supporting and enhancing STEM thinking within the larger STEM ecosystem.