1. Introduction
Daily practice at universities in Sweden and all over the world in 2020–2021 abruptly changed from regular teaching to online teaching due to the COVID-19 pandemic [
1]. Teaching online requires knowledge of new ways to engage, and these cannot be compared to traditional interactions for learning [
2,
3]. This can be a challenge because it involves managing tools, students, time, and spaces in new ways and also being able to promote new ways of social interaction and the orchestration of relations [
4]. It is widely accepted that interaction is important for developing interpersonal connections and conceptual understandings, but it occurs differently in online contexts than in face-to-face settings [
2]. In research, the importance of developing positive and supportive teacher–student relationships (TSR) has become a growing field (see, for example, [
4,
5,
6,
7,
8]). This relationship has a major impact on students’ academic performance [
8].
The relationship between the teacher and students can be understood as a process of communication to support learning [
9]. From a relational perspective, the learning is not in the individual or the collective. Instead, the learning appears in the gap between students and the teacher. This gap should not be conquered and should be seen as the place to enable learning interactions [
9].
Nevertheless, exploring university teacher relational competence is an unexplored field [
10], and there is limited research examining the pedagogical aspects of online teaching in general [
11]. Furthermore, research characterizing the practice of university lecturers in mathematics education is limited [
12,
13].
In this pilot study, the focus is to explore and visualize a university mathematics teacher’s digital relational communication competence during her first (online) meeting with ten pre-service special educators in mathematics. The focus of the study is on the teacher’s relational communication competence in online teaching in daily practice. Relational communication competence refers to the capability to communicate verbally and nonverbally by using a language that is understandable and contributes to the meaning, creation, and progression of knowledge [
5].
The following research question is addressed:
To examine what is said during the online seminar, Halliday’s [
14] Systemic Functional Linguistics is adopted to visualize what the text is about, who it is addressed to, and the structure of the text. To explore how it is said, Burgoon and Hobbler’s [
15] framework is used involving facial expressions, body language, and paralanguage. Nevertheless, relations cannot be examined without considering the context of culture since it influences learning and communication processes [
7,
14]. In the
Section 2, the context of the culture in mathematics education will be further discussed.
2. Context of Culture in Mathematics Education
There are issues concerning the goal of mathematics education, where some researchers want teachers to put more emphasis on the learning of rules, definitions, and proof [
16,
17], whereas other researchers want teachers to concentrate on cultural and/or social issues in mathematics to understand the broader perspective around how mathematical knowledge is developed within society [
18,
19]. When considering that knowledge is developed in society, it becomes evident that context is important because it includes assumptions about how individuals learn [
19]. Several researchers stress the importance of connecting mathematics to the real world, but studies [
20,
21,
22] show that in standard textbooks, the connection between the mathematical content and students’ everyday experiences is limited. This is problematic because mathematical textbooks are extensively used in many countries [
23,
24,
25], including Sweden [
26] where the present study was conducted. Furthermore, in Sweden, the dominant practice during mathematics lessons is students working individually in their mathematical textbooks [
26]. Furthermore, activating pupils´ prior knowledge before working with specific mathematical content is essential [
27]. Prior knowledge means that the reader is familiar with the content of the text and thus can integrate new information being learned into their prior knowledge structures to create meaning, which can contribute to understanding the relationship between what they already know, and the new information being learned [
27].
Oral communication in mainstream mathematics classrooms is often characterized by teacher talk, which involves explaining by giving directions, procedures, and explaining and correcting mistakes [
28]. This type of communication usually entails little student-to-student talk or student-to-teacher talk. Another common approach is the IRE pattern, or initiation–response–evaluation [
29], where the teacher initiates a question, a student responds, and the teacher evaluates something that they already know the answer to, for example, “What is 23 + 12?”. The answer often involves a number or word but without the students elaborating or explaining their ideas [
30]. These types of questions are known as closed and generate one correct answer already known by the teacher [
31]. Open questions, however, generate many possible alternatives and usually demand deeper thinking, but they are not commonly used in mathematics [
31]. The teacher’s choice of questions, thus contributes to shaping the classroom environment and the cognitive opportunities offered to students [
32], but the questions also give a signal of what mathematics is about.
Another aspect of the context in mathematics education, which also has widespread consensus, is the view that language has an important role in mathematics learning [
33] Thus, learning a subject involves learning the specific language of the subject [
34,
35]. In mathematics, the texts are usually multimodal, where individual meanings of the vocabulary, symbols, and illustrations need to be separated and sometimes combined to understand the text [
33,
36]. This can be problematic when students work individually in the textbook because then it is up to each student to create their own understanding of mathematics from reading the mathematical textbook.
Furthermore, a mathematical operation can be illustrated as concrete, half concrete, half abstract, and/or abstract [
37]. Concrete, for example, uses blocks to solve 3 + 4; half concrete uses illustrations of blocks; half abstract uses lines instead of symbols; and abstract uses symbols for numbers. According to Duval [
33], students’ learning in mathematics occurs during the transformation of different representations. This is supported by the results from several studies of students with special needs in mathematics [
38,
39,
40,
41,
42], that working with different representations supported the students’ meaning-making in mathematics.
However, in Sweden, how to support students with special needs in mathematics is not communicated in the national curriculum [
43]. Therefore, it is up to each school to interpret how the teaching for students with special needs in mathematics shall be performed.
Research Concerning Mathematics Teaching at the University Level
Research on the practice of university lecturers in mathematics education is limited [
12,
13]. Furthermore, studies examining the daily teaching practice of mathematics teachers at university barely exist. In the existing studies, the focus has been on how university students have perceived the mathematical content being taught or examining university students’ perceptions of what mathematics education consists of. In Skog’s study [
44] of pre-service teachers in mathematical courses, the results showed that the students aligned with mathematics with a focus on superficial learning and high-speed calculations (textbook-based learning). Pedagogical practice [
13] in higher education in mathematics barely exists, in both traditional and online classrooms. However, in Masilo’s [
45] study, 37 university students’ experience with an online Geometry Education course showed that the teacher’s presence became essential for students learning during online meetings by creating videos, podcasts, and blogs, fostering students to watch material online and participate for evaluation support.
Nevertheless, several researchers stress the importance of high-quality TSR for students’ social and academic development (see, for example, [
6,
7,
46]). Scandinavian research often includes discussions on ways teachers can act to enhance positive relationships and how they can develop relational competence [
7,
46], but studies examining TSR in regular and online courses in daily practice in mathematics courses at university levels do not exist.
3. Theoretical Perspectives
To theoretically inform this study, the relational perspective is used concerning digital relational competence. Relational competence can be used to define teachers’ capability to build positive relationships with students during interactions [
5]. In several studies, the importance of teachers’ relational competence, i.e., building positive and supportive relationships with students, has been stated as essential for students’ learning [
4,
5,
6,
7,
8].
This relationship can be understood as a process of communication to support learning [
9]. Thereby, it involves the teacher’s capability to communicate verbally and nonverbally, so attunement arises in relation to the student [
5]. However, one critique of research on teacher–student relations and teachers’ relational competence is the lack of theoretical frameworks [
6,
10]. Furthermore, few studies have been conducted to examine teachers’ relational competence in online teaching, which is the focus of this study. Nevertheless, two studies have examined TSR in online teaching but are not specific to mathematics. In Wiklund-Engblom’s [
4] interview study of nine upper secondary teachers, the teachers describe their distance teaching and how it enables them to meet their students’ different needs. Two theoretical frameworks are used in the study: self-regulated learning and teachers’ digital relational competence. One conclusion was that students’ achievements are more in focus in the digital context than in regular teaching and that this causes anxiety; consequently, an important part of digital relational competence is about designing for psychological safety.
Song et al. [
47] conducted questionary study among 534 undergraduate students in a communication course to compare their learning in face-to-face teaching and in online teaching. Statistical analysis involving descriptive statistics and correlations was conducted. The result showed that the students emphasize that teachers revealing personal information is more important for TSR in online courses for the students’ learning than in regular teaching.
However, in research, the qualities of TSR are seldom discussed or examined [
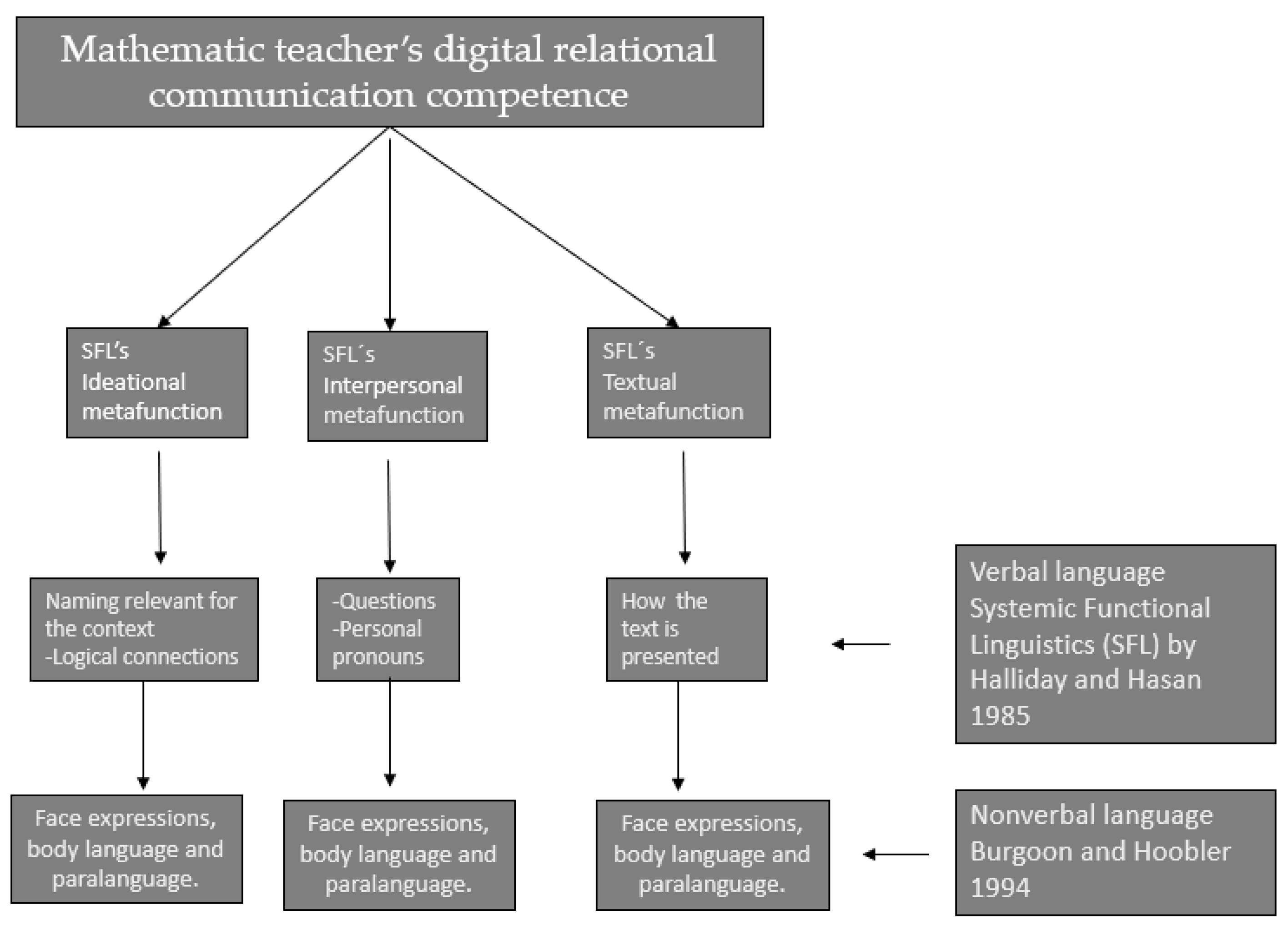
10]. In this study, the teacher’s digital relational competence refers to the teacher’s communication competence to build positive TSR in daily practice. To examine what is said (verbal and written communication), Systemic Functional Linguistics (SFL) is used to visualize teachers’ and students’ communication at the clause level.
3.1. Systemic Functional Linguistics—Verbal and Written Communication
SFL is a linguistic perspective that views language as a resource that people use to accomplish a purpose by expressing meanings in context [
14]. The language is viewed as a system of meaning which can be analyzed at the clause level to understand how contexts are reflected in participants’ linguistic choices.
According to Halliday’s terminology, each text is about something (the ideational metafunction), is addressed to someone (the interpersonal metafunction), and is based on the text structure (the textual metafunction).
Ideational metafunction refers to what is happening in a text and involves examining the naming of objects relevant to the context and logical connections, and in this study focuses on logical relationships of meaning by examining the use of conjunctions [
48].
This study concerns mathematical words and concepts that are important for understanding the mathematical content fraction of division.
Interpersonal metafunction involves participants and how semiotic resources enact personal and social relationships with other people surrounding us. These relationships can be visualized by examining the “voice” by identifying the use of personal pronouns, interrogative, imperative, and modal verbs in texts [
49].
Textual metafunction refers to how the text is presented and whether it is coherent [
14]. In mathematics, it usually means multimodal texts, i.e., texts where words are integrated with illustrations and/or symbols.
SFL has previously been put forward as a suitable tool when studying spoken or written texts in mathematics classrooms [
34,
49]. For example, in Herbel-Eisenmann’s [
49] study involving a linguistics analysis of a 64-page middle school mathematics textbook, the “voice”, or the interpersonal function of the text, was explored. The analysis showed that the style of the text was authoritative through the use of commands (imperative) usually involving “use”, “write”, “draw”, and “find”, with few opportunities for the students to explain their thinking. However, SFL does not consider nonverbal communication, i.e., how the words are expressed into concern, which is essential since nonverbal communication enhances the linguistic meaning of expressions [
15,
50].
3.2. Nonverbal Communication
Nonverbal language enhances linguistic meaning by guiding what is being said and visualizing the transmitter’s feelings, attitude, and values [
15,
50]. The main channels of nonverbal communication are facial expressions, body language, and paralanguage [
15].
Six commonly accepted facial expressions are identified: happiness, surprise (curiosity), anger, disgust, sadness, and fear [
50]. Body language includes expressions such as gestures, body positions, and gaze [
50]. Gestures, which are usually conscious and intentional movements expressed with hands or arms, can be used for commanding, showing agreement, own effects, and when replying, for example, by nodding [
51].
Paralanguage is another type of nonverbal language which refers to pronunciation and pauses [
52]. For example, when the speaker wants to highlight something special in their utterance, important word(s) are emphasized. Pauses can be an important utility in interactions since they can indicate time for reflection but can also suggest uncertainty [
53].
Another important aspect concerning nonverbal communication is what the listeners (the receivers) do when someone is talking because this has a significant influence on how the speaker composes his or her talk [
54]. An active listener looks at the speaker and gives feedback, for example, by nodding.
4. Materials and Methods
In this study, the interaction between a university teacher and a class of 10 pre-service special educator teachers in mathematics during an online seminar is explored. This was the first time the teacher and the students met. The seminar was 2 h and 45 min in length and was divided into two parts with a 20-min break in between. The first part lasted for 95 min and the second part for 70 min. The seminar’s focus concerned the learning goals “on an in-depth level with adequate words and concepts able to describe and discuss students’ concept development in mathematics”.
4.1. Materials
In this study, video recordings were used to visualize interactions between students and the teacher. This made it possible to visualize images of actual places and be able to examine not only the verbal language, but also nonverbal aspects such as gesture, gaze, facial expression, and tone of voice [
55]. To be able to take nonverbal language into concern is essential when examining a teacher’s relational competence [
46] since it provides meaning to the words being said or presented.
In this study, ethical guidelines for the Humanities and Social Sciences set out by the Swedish Research Council [
56] were followed. Before the seminar, the students were informed both orally and in writing about the research. Those wanting to participate in the study completed a consent letter and this resulted in 9 students out of 10 agreeing to participate. However, one of the students who had agreed was unable to participate with the video due to needing to care for her infant. Therefore, data collection involved 8 students and the teacher. The student who did not agree to participate did not have her camera on and was assigned a number instead of her name.
At the seminar, Zoom was used, which is a web-based program allowing multiple people to interact with each other with video and audio, giving users the ability to react in real time. However, only one participant at a time can talk. Furthermore, a chat function and a function for groupings, so-called breakout rooms, and the ability to share documents are included in this program.
In this study, all of the students and the teacher were familiar with zoom when the study was conducted since all teaching since March 2020 had been mostly online, using zoom as a teaching tool.
At the present seminar, the teacher was visible for the PowerPoint presentation all of the time (the teacher’s upper body was shown to the left of the presentation). The teacher could also interact by pointing at different parts in her PowerPoint presentation. This is a function available in Zoom. Thus, the students could follow the teacher’s verbal and nonverbal language. The students were interacting using their own video cameras and both nonverbal and verbal language but also their names were visible to the teacher. During the seminar, two video cameras were utilized to follow the interactions that took place. One video camera recorded only the teacher and the other video camera recorded both the students and the teacher from the computer screen using Zoom’s recording feature. This resulted in four films, two with only the teacher that lasted for 95 and 70 min and two with the teacher and the students that also lasted for 95 and 70 min.
4.2. Approach
Initially, the filmed material was observed several times and then transcribed with a focus on the verbal language to establish an overall picture of the type of interactions that appeared. Suitable video corpus and systematic sampling from the data were then identified by using content analysis, which is a research method for making valid and replicable inferences by coding and interpreting texts concerning the content in the communication [
57]. Thirteen sequences were identified as suitable involving the mathematical content: division of fractions, young children’s experiences of number sense, subitizing, cardinal numbers, multilinguistic, equal sign, different operations such as division and subtraction, priority rules, algorithms, methods in operations, everyday knowledge connected to mathematics, and fractions. A preliminary analysis of TSR patterns was conducted. These sequences were analyzed verbally and nonverbally to explore the mathematics teacher’s relational competence. One episode was then chosen to illustrate a significant pattern that occurred during the seminar between a student and the teacher. Focusing on a significant pattern is inspired by Aspelin’s [
58] approach and has been used in both face-to-face teachings and in online teaching when examining teachers’ relational competence. In short, the characteristic pattern first involved a mathematical task that the student should solve, followed by a discussion of how they solved the task. Potential issues for solving the task were then discussed based on the teacher’s and the students’ previous experiences with students with special needs in mathematics. Finally, fruitful teaching connected to the specific task was then discussed.
Analysis
In this study, micro-analysis is used, which involves in-depth analysis. Micro-analysis has previously been used when examining TSR in daily practice (see, for example, [
58,
59]). Using micro-analysis is based on Scheff’s [
60] approach, which can provide a conscientious exploration of interaction in single episodes. As mentioned before, the micro-analysis in this study focused on an episode that was selected because of its characteristic pattern found in the interactions. Nevertheless, the in-depth analysis needs to be connected to well-defined theory/theories.
To analyze the teacher’s digital relational competence, with a focus on the communication competence, the verbal language—what is said—at a deeper level, Halliday’s [
14] three metafunctions are used. Ideational metafunction is based on naming and refers to important concepts and/or words to understand a piece of content, i.e., what the seminar is about, such as number sense, and logical connections involving logical relationships of meaning. Interpersonal metafunction investigates the choice of questions/imperatives, personal pronouns, and modal verbs being used by the teacher. Textual metafunction refers to how the teacher presents the text and whether it is coherent. In mathematics, this usually means multimodal texts.
The other part being analyzed is the nonverbal language because thoughts, feelings, and experiences are reflected in bodily expressions mediated together with the spoken language [
15]. In this study, nonverbal language refers to facial expressions, body language [
50], and paralanguage, i.e., pronunciation and pauses [
52,
53]. In
Figure 1, the analysis tool is visualized.
The digital context was analyzed by examining limitations and opportunities for TSR in the interaction. Nevertheless, the students’ and teacher’s cameras on their computers did not register everything that was happening during the seminar, only what the video cameras were faced to, which influence the analysis since it only focus on what the cameras and microphones recorded. Furthermore, only one person could talk at a time, which also influenced the interaction in the seminar.
6. Discussion
Examinations of daily practices at the university level in mathematics education barely exist [
12,
13], and due to the pandemic, teaching since 2020 has been primarily online [
1,
54]. Nevertheless, when universities lose their spatial environment, the context changes and leads to unwritten rules being renegotiated and gives the university environment a new context which probably influences TSR.
Yet, the teacher–student relationship at university is an under-researched field [
10], and online teaching at university with regard to teacher–student relationships has not been further explored, except by Wiklund-Engblom [
4] and Song et al. [
47]. However, these studies do not study the interactions that actually emerged in the courses between the teacher and students. Instead, they involve students’ or teachers’ experiences and perceptions of TSR online.
In this pilot study, the aim was to explore a university mathematics teacher’s digital relational communication competence in an online seminar with ten pre-service special educators in mathematics by examining the verbal and nonverbal language in a selected episode that emerged. A micro-analysis was conducted to visualize the interaction. This approach has previously been used when examining relational competence [
58,
59], but not in online teaching. Relational competence in this study refers to providing supportive and positive teacher–student relationships, which several researchers stress as essential for students’ learning (see, for example, [
4,
5,
7,
9,
47]). This relationship can be understood as a communication process to support learning, where verbal and nonverbal language are considered [
9]. Furthermore, in this study, relational communication competence refers to the capability to communicate verbally and nonverbally by using a language that is understandable and contributes to meaning-making and the progression of knowledge [
5,
46]. Nevertheless, one critique of the research on teacher–student relations and teachers’ relational competence is a lack of theoretical frameworks [
6,
10]. In this study, to manifest the teacher’s digital relational communication competence, Halliday’s Systemic Functional Linguistics [
14] was used to visualize the verbal language. Using SFL, language is viewed as a system of meaning, which can be analyzed at the clause level to understand how contexts are reflected in participants’ linguistic choices. SFL has previously been used when examining texts in mathematics [
34,
49]. To examine how the verbal language is spoken and received, nonverbal language is connected to SFL’s metafunctions: ideational, interpersonal, and textual (see
Figure 1). Nonverbal language in this study refers to facial expressions, gestures, and paralanguage [
15,
50,
51,
52] since nonverbal language enhances the linguistic meaning of expressions [
15,
50,
53].
6.1. How a Mathematics Teacher’s Digital Relational Communication Competence Can Be Manifested
This section is divided into analyses of SFL’s metafunctions: ideational, interpersonal, and textual.
6.1.1. Ideational Metafunction
Ideational metafunction contributed to visualizing the context to the interaction by examining important words (naming) [
14,
48] used in the sequence connected to the mathematical content fraction of division. Learning the mathematics content is a matter of learning to communicate properly inside the discipline where mathematical concepts and words have a central role [
36]. Concerning naming, attunement, both in verbal and nonverbal language, was raised between the student and the teacher concerning the problem of focusing too much on the procedures and rules in mathematics education since it is challenging for students to grasp, and especially for those with special needs in mathematics. Instead, connecting to pupils’ everyday context before showing the procedure was highlighted by both the student and the teacher as essential for students to grasp the mathematical content. This agreement was also shown nonverbally by the teacher and student by nodding, smiling, and pointing at one another.
Connection to the students’ context before showing the procedure is in line with what some researchers [
18,
19] stress as the core of teaching mathematics, but this contrasts with what other researchers [
16,
17] state as the most important part. However, research shows that the connection to students’ everyday knowledge in standard mathematics textbooks is vague [
20,
21,
22]. This is problematic since mathematical textbooks are extensively used in several countries [
23,
24,
25,
26], and in Sweden, where this study was conducted, mathematics textbooks have a central role [
26]. Complementary materials are thus needed to connect the mathematical content to the pupils’ everyday knowledge so mathematics can become useful and thereby meaningful. This also involves activating the students’ prior knowledge, which is essential for their learning. Prior knowledge can then be connected to the new knowledge being learned, which is essential for developing their knowledge [
27].
The conjunction “but” appeared in both the teacher’s and the students’ utterances, and both times were emphasized to indicate importance [
52]. “But” in the teacher’s utterance contributed to changing the perspective from the students’ thinking like a mathematician to instead thinking as a mathematics special educator, where the focus becomes successful teaching when supporting students in need of understanding the division of fractions. “But” was also used by the students and was concerned with pupils needing to have time perception. The teacher became silent and looked up at the ceiling, pausing, appearing to express uncertainty, which is also one of the purposes of pauses [
53]. Conjunctions refer to SFL´s ideational metafunction [
14,
48] and refer to visualizing relationships of meaning.
Furthermore, the teacher’s nonverbal language contributed to visualizing her engagement with the mathematical content and context in the interaction, but also her curiosity to explore the students’ thinking in mathematics. The teacher visualized pupils’ frustration from her own experiences concerning fractions through facial expressions and gestures. According to Song et al. [
47], being personal is a fruitful way to develop supportive and positive relations with students.
6.1.2. Interpersonal Metafunction
SFL´s interpersonal metafunction refers to who is taking part: the roles and relationships among participants [
14,
48]. In this study, the questions and personal pronouns are in focus. During the seminar, several questions were posed by the teacher.
The teacher gave direction during the seminar by posing questions where the common approach in mathematics IRE (initiation–response–evaluation) [
29] barely existed. Some of these questions were open, and some were closed during the seminar. In this study, the closed questions had the function of checking whether the students agreed to some of the teacher’s statements. Another type of closed question referred to clarification and was used when examining whether the teacher had understood a student’s thoughts correctly. Several open-ended questions were posed during the seminar and referred to exploring, i.e., involving students’ thinking or reasoning [
31]. This is not a common approach in a mathematics context [
28,
29,
31]. These questions led to fruitful discussions about supporting pupils’ understanding of the division of fractions where the students were invited to participate. The teachers’ choice of questions is essential because they contribute to shaping the classroom environments and the cognitive opportunities offered to students [
32], but they also give a signal of what mathematics is about. Furthermore, the opening questions become essential to make the students active involving their thinking and experiences in mathematics. Connecting something personal to the teaching, such as letting the students talk about their own experience with the mathematical content, can make students more involved. This can be seen as a positive consequence of students having a chance to express their identity and then being offered to show a personal part of themselves. Using opening questions and inclusive imperative often involve deeper thinking [
31], but they are not common in mathematics teaching.
Nonverbal language also became important, especially when the teacher asked a question: she smiled at the screen. Smiling occurred several times when the teacher asked questions, where her facial expressions also visualized her curiosity and interest in students’ answers. Smiling is important since it is considered an entry gate to communication [
50]. The teacher used pauses when posing questions—referring to paralanguage [
52]—aiming to help the student reflect, and when the teacher was uncertain and tried to understand, which is the purpose of pauses [
53].
Furthermore, to build supportive TSR, the teacher addressed the students directly by using personal pronouns, such as “you” (singular) and “you” (plural), and by pointing at the student(s). She also related the content to common everyday experiences using the personal pronouns “we” and “our”. The teacher also related the content to her own experience by using the personal pronoun “I”. By being personal, the students gained insight into the fact that the teacher has her own experiences, feelings, and engagement about the mathematical content being discussed. According to Song et al. [
47], being personal is a successful path in developing relations with students.
6.1.3. Textual Metafunction
The textual metafunction refers to the construction of a text (in whatever form) and to the formation of whole entities that are communicatively meaningful [
48]. Working with the language in mathematics is essential since it is complex and often multimodal, consisting of numbers, symbols, illustrations. These semiotic resources are sometimes understood separately and sometimes combined to understand the mathematical content being expressed [
33,
36]. Attunement was raised between the teacher and student concerns using different representations for fractions to support pupils’ understanding.
This is also supported in other studies [
33]; according to Duval [
33], learning in mathematics occurs during transformation between different representations of a concept. Thus, one essential aim in teaching should be to empower students to deal decisively with different situations, which means being able to make connections between different representations in mathematics. Thus, the teaching of mathematics should contain many representations, but guidance is also needed to visualize the connections between them. Furthermore, the teacher specifically mentioned concrete working as essential. According to the results in several studies [
38,
39,
40,
41,
42], it is a fruitful approach, especially when working with pupils with special needs in mathematics.
Additionally, the student presented an interesting and uncommon type of concrete representation of fractions, and she used gestures to clarify and describe parts of a fraction.
6.2. TSR in Online Teaching
Digital orchestration of social interactions requires knowledge of new ways to engage, and these cannot be compared to traditional interactions for learning [
14]. Hence, relational competence becomes even more important while designing didactically for learning in online teaching [
2]. Limited research has previously examined online teaching in university mathematics courses. However, in Masilo’s [
45] study, the students stated the importance of the teacher being present in the online course in mathematics, which referred to evaluation support and creating videos and podcasts connected to the mathematical content to help the students grasp the mathematical content. However, teacher–student relation (TSR) in daily practice was not examined, as in this study.
In this study, the computer program Zoom was used, which is a web-based program allowing multiple people to interact with each other with audio and video. Both the teacher and the students in this study were familiar with Zoom and used it since March 2020.
During the seminar, the students and the teacher saw each other on the screen. Seeing each other benefits the interactions. This can be linked to the importance of having access to nonverbal language, which reveals feelings, attitudes, and values [
15,
50]. Nonverbal language can also reveal important clues if the students and the teacher are actively listening. This is important because how the listener responds both in the verbal and nonverbal language influence how the teacher and student constitute their talk [
54] and thereby influence TSR. The teacher created an open climate for discussions where the students could participate verbally, raising their hands, but also by writing in the chat.
Furthermore, the teacher invited the students to participate by pointing at the screen when she posed questions. Furthermore, pointing at the screen was also used when showing agreement, which was used by both the teacher and students. The teacher also invited the students to participate in the discussion by smiling and leaning against the screen.
The teacher could see who was speaking since the students’ names were integrated into their pictures. Thus, the teacher could be personal and mention the students by name, which is important in building positive and supportive TSR according to Song et al. [
47].
6.3. Conclusions
Establishing future-oriented structures for online learning and devising a more efficient and effective educational environment due to experiences from teaching during the COVID-19 pandemic seems important since online teaching will most likely influence future teaching at universities [
61].
In this pilot study, a theoretical framework is suggested to manifest a mathematics university teacher’s digital relational competence using SFL, a linguistic perspective that views language as a resource that people use to accomplish a purpose by expressing meanings in context [
14]. Systemic Functional Linguistics constitute an essential part that contributes to showing the structure of a language within a specific discipline. This is stressed by Schleppegrell [
35] as essential because “Learning the language of a new discipline is a part of learning the new discipline; in fact, the language and learning cannot be separated” (p. 140). The choice of questions and use of personal pronouns contributed to visualizing the relationship between the teacher and students and was formed from SFL´s interpersonal metafunction. Open questions become important where the students should reflect and reason, which involves deeper thinking in mathematics. The students then related to their own experiences and thereby showed a more personal part of themselves. Relating to experiences contributes to activating the students’ prior knowledge in the area division of fractions. That the teacher revealed personal information but also asked the students to reveal personal information positively influenced TSR. This indicates that mathematics teachers should consider talking more about themselves and personalizing the teaching materials in online teaching but also ask the students about their personal experience to build positive and supportive relationships between the teacher and students.
SFL’s ideational were used to visualize the choice of words employed for context and textual metafunctions visualize the kind of communication that appeared and communication, respectively. Working with different representations and also relating to pupils’ everyday knowledge were stressed as essential in mathematics.
Connected to all metafunctions, nonverbal language becomes important to visualize how the verbal language was expressed, i.e., which message is sent, involving facial expressions, paralanguage, and gestures. Gestures and facial expressions were used, for example, when expressing agreement, to describe and clarify concepts and provide authenticity of feelings. Using paralanguage highlighted important parts of the interaction and provided time for reflection but was also used to express uncertainty.
However, in online teaching, technical aspects open up both opportunities and limitations for TSR. For example, the student and teacher can communicate in many different ways, both in oral and written text (in the chat) and by gestures, but also by sharing documents. When the students and the teacher have their cameras on, their feelings, attitudes, and values are shown, which influence TSR. Furthermore, the teacher can be personal by calling the students by name when inviting them to participate in discussions or replying to a student’s question or utterance since the students’ names are visible on the screen.
Nevertheless, when the students do not have their cameras on, bodily gestures are lost, creating disruptions in interactions. Thereby, communication is enhanced by having the camera on, as these gestures can be conveyed and received to a greater extent. The picture can also be frozen because of poor internet connection, which negatively influences the interaction. Another limitation but also an opportunity for TSR in online teaching at universities in mathematics is the size of the student group, the students’ and teachers’ level of knowledge and security with technology, as well as time and resources in the course.
6.4. Implications for Practice and Future Research
In this pilot study, a teacher’s digital relational communication competence in mathematics was examined by using micro-analysis. Although the micro-analysis was based on interaction patterns in the seminar, I cannot claim that the result is typical for TSR in online teaching in mathematics at the university level. However, what this study presents is an analysis tool to examine TSR in daily practice by exploring how a mathematical relational competence in mathematics can be manifested. The analysis tool presented in the paper can contribute to visualizing important aspects in the interactions with students in online mathematics teaching concerning TSR. Therefore, the research in mathematics at the university level can expand to not only involve examineexamine how the students have perceived the mathematical content being taught [
12,
13] or students’ perceptions of what mathematics education consists of [
44]. This analysis tool can thus become useful for mathematics teachers to promote professional development in another dimension of teaching in mathematics.
It seems that future teaching at universities will more or less involve online meetings.
A comparison between TSR in daily practice in online teaching and in daily face-to-face meetings in university mathematics courses by using microanalysis would be interesting to explore further concerning fruitful interactions for TSR. Examining TSR in other areas would also be interesting. However, the context differs in different areas and thus needs to be considered because this influences the communication and students’ learning processes, and thereby TSR [
7,
14].
Furthermore, how to support pupils with special needs in mathematics in Sweden is not communicated in the national curriculum [
43], and it is up to each school to interpret how the teaching for these students in mathematics will be performed. In this study, attunement appeared between the teacher and student concerning fruitful teaching for students with special needs by relating students’ everyday knowledge before showing procedures and using different representations to develop pupils’ conceptual understanding. Further research is suggested to explore successful teaching for pupils with special needs in mathematics to help them grasp the mathematical content.