Cognitive Training in the Domain of Mathematics for Potentially Gifted Children in Primary School
Abstract
1. Introduction
1.1. Cognitive Training
1.2. Executive Functioning
1.3. Cognitive Training in Arithmetical Problem Solving
1.4. The Current Study
2. Materials and Methods
2.1. Participants
2.2. Design and Procedure
2.3. Instruments
2.3.1. Intelligence and Development 2 (IDS-2) IQ Screener
2.3.2. Digit Span Wechsler Intelligence Scale for Children-V-NL
2.3.3. Picture Span Wechsler Intelligence Scale for Children-V-NL
2.3.4. Metacognition Questionnaire
2.3.5. Cognitive Training Programme
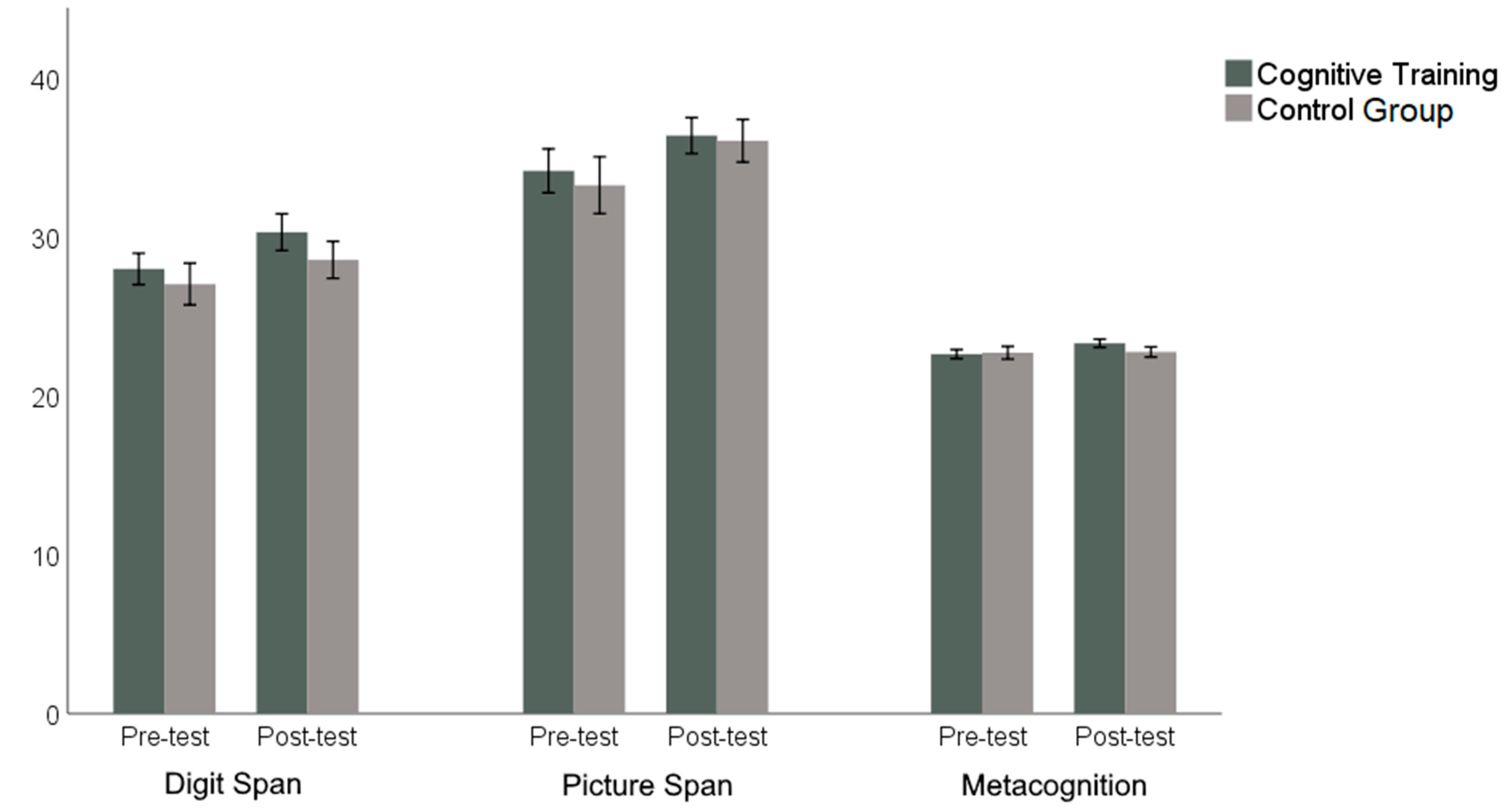
3. Results
3.1. Training Effectiveness: Progression from Pre-Test to Post-Test
3.2. Role of IQ Score in Working Memory and Metacognition Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Arithmetical metacognition | Distinguishing between different arithmetic problems; identifying the characteristics of an arithmetic problem | The trainer starts with a general explanation of categories and how problems can be categorised. Then, children discuss how arithmetic problems can be categorised. Children fill in a diagram with possible arithmetic categories and their characteristics. At last, children are guided on reflecting on how this diagram can help them with arithmetical problem solving |
| Working memory | Listening span task with a secondary task (3–7 sentences) | Children listen to a series of short sentences. For each sentence, they have to recall the last word, write it down in the same order and write down whether the sentences are true or false. The difficulty of the task increases from 3 to 7 words to recall. |
| Arithmetical problem-solving component | Categorising different arithmetic problems by their structure | The trainer starts by explaining the fourth step in the problem-solving heuristic. Then, children are presented with five arithmetic problems that they need to solve individually according to the first four steps of the problem-solving heuristic. |
References
- De Boer, G.C.; Minnaert, A.E.M.G.; Kamphof, G. Gifted Education in the Netherlands. J. Educ. Gift. 2013, 36, 133–150. [Google Scholar] [CrossRef]
- Crepeau-Hobson, F.; Bianco, M. The identification of gifted students with learning disability. J. Learn Disabil. 2013, 46, 304–316. [Google Scholar]
- Koshy, V.; Pinheiro-Torres, C. ‘Are we being de-gifted, Miss?’ Primary school gifted and talented co-ordinators’ responses to the Gifted and Talented Education Policy in England. Br. Educ. Res. J. 2012, 39, 953–978. [Google Scholar] [CrossRef][Green Version]
- Subotnik, R.F.; Olszewski-Kubilius, P.; Worrell, F.C. Rethinking Giftedness and Gifted Education. Psychol. Sci. Publ. Int. 2011, 12, 3–54. [Google Scholar] [CrossRef] [PubMed]
- Vogelaar, B.; Bakker, M.; Hoogeveen, L.; Resing, W.C.M. Dynamic testing of gifted and average-ability children’s analogy problem solving: Does executive functioning play a role? Psychol. Sch. 2017, 54, 837–851. [Google Scholar] [CrossRef]
- Brody, L.E.; Mills, C.J. Gifted Children with Learning Disabilities: A Review of the Issues. J. Learn Disabil. 1997, 30, 282–296. [Google Scholar] [CrossRef]
- Reis, S.M.; Baum, S.M.; Burke, E. An Operational Definition of Twice-Exceptional Learners. Gift Child. Q. 2014, 58, 217–230. [Google Scholar] [CrossRef]
- Martin, M.; Clare, L.; Altgassen, A.M.; Cameron, M.H.; Zehnder, F. Cognition-based interventions for healthy older people and people with mild cognitive impairment. Cochrane Database Syst. Rev. 2011, 1, 1–39. [Google Scholar] [CrossRef]
- Leung, P.; Orgeta, V.; Orrell, M. The effects on carer well-being of carer involvement in cognition-based interventions for people with dementia: A systematic review and meta-analysis. Int. J. Geriatr. Psych. 2017, 32, 372–385. [Google Scholar] [CrossRef]
- Carretti, B.; Caldarola, N.; Tencati, C.; Cornoldi, C. Improving reading comprehension in reading and listening settings: The effect of two training programmes focusing on metacognition and working memory. Br. J. Educ. Psychol. 2013, 84, 194–210. [Google Scholar] [CrossRef]
- Cornoldi, C.; Carretti, B.; Drusi, S.; Tencati, C. Improving problem solving in primary school students: The effect of a training programme focusing on metacognition and working memory. Br. J. Educ. Psychol. 2015, 85, 424–439. [Google Scholar] [CrossRef] [PubMed]
- Weissheimer, J.; Fujii, R.C.; Souza, J.G.M. The effects of cognitive training on executive functions and reading in typically-developing children with varied socioeconomic status in Brazil. Ilha Desterro J. Lan. Lit. Engl. Cult. Stud. 2019, 72, 85–100. [Google Scholar] [CrossRef]
- Christopher, M.E.; Miyake, A.; Keenan, J.M.; Pennington, B.; DeFries, J.C.; Wadsworth, S.J.; Willcutt, E.; Olson, R.K. Predicting word reading and comprehension with executive function and speed measures across development: A latent variable analysis. J. Exp. Psychol. Gen. 2012, 141, 470–488. [Google Scholar] [CrossRef] [PubMed]
- Baten, E.; Praet, M.; Desoete, A. The relevance and efficacy of metacognition for instructional design in the domain of mathematics. ZDM Math Educ. 2017, 49, 613–623. [Google Scholar] [CrossRef]
- Schneider, W.; Artelt, C. Metacognition and mathematics education. ZDM Math Educ. 2010, 42, 149–161. [Google Scholar] [CrossRef]
- Cornoldi, C.; Caponi, B.; Focchiatti, R.; Lucangeli, D.; Todeschini, M.; Falco, G. Mathematics and Metacognition; Centro Studi Erickson: Torento, Italy, 1995. [Google Scholar]
- Titz, C.; Karbach, J. Working memory and executive functions: Effects of training on academic achievement. Psychol. Res. 2014, 78, 852–868. [Google Scholar] [CrossRef]
- Hohn, R.L.; Frey, B. Heuristic Training and Performance in Elementary Mathematical Problem Solving. J. Educ. Res. 2002, 95, 374–380. [Google Scholar] [CrossRef]
- Fuchs, L.S.; Fuchs, D.; Prentice, K.; Burch, M.; Hamlett, C.L.; Owen, R.; Schroeter, K. Enhancing third-grade student’ mathematical problem solving with self-regulated learning strategies. J. Educ. Psychol. 2003, 95, 306–315. [Google Scholar] [CrossRef]
- Rueda, M.R.; Cómbita, L.M.; Pozuelos, J.P. Cognitive training in childhood and adolescence. In Cognitive training: An Overview of Features and Applications, 2nd ed.; Strobach, T., Karbach, J., Eds.; Springer International Publishing AG: Cham, Switzerland, 2020; Volume 2, pp. 141–158. [Google Scholar] [CrossRef]
- Bürki, C.N.; Ludwig, C.; Chicherio, C.; De Ribaupierre, A. Individual differences in cognitive plasticity: An investigation of training curves in younger and older adults. Psychol. Res. 2014, 78, 821–835. [Google Scholar] [CrossRef]
- Foster, J.L.; Harrison, T.L.; Hicks, K.L.; Draheim, C.; Redick, T.S.; Engle, R.W. Do the effects of working memory training depend on baseline ability level? J. Exp. Psychol. Learn. Mem. Cogn. 2017, 43, 1677–1689. [Google Scholar] [CrossRef]
- Swanson, H.L.; Beebe-Frankenberger, M. The Relationship Between Working Memory and Mathematical Problem Solving in Children at Risk and Not at Risk for Serious Math Difficulties. J. Educ. Psychol. 2004, 96, 471–491. [Google Scholar] [CrossRef]
- Jaeggi, S.M.; Buschkuehl, M.; Jonides, J.; Perrig, W.J. Improving fluid intelligence with training on working memory. Proc. Natl. Acad. Sci. USA. 2008, 105, 6829–6833. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Wang, C.; Zhao, Q.; Yang, L.; Buschkuehl, M.; Jaeggi, S.M. The malleability of executive function in early childhood: Effects of schooling and targeted training. Dev Sci. 2018, 22, e12748. [Google Scholar] [CrossRef] [PubMed]
- Schubert, T.; Strobach, T.; Karbach, J. New directions in cognitive training: On methods, transfer, and application. Psychol. Res. 2014, 78, 749–755. [Google Scholar] [CrossRef]
- Diamond, A. Executive functions. Ann. Rev. Psychol. 2013, 64, 135–168. [Google Scholar] [CrossRef]
- Scionti, N.; Cavallero, M.; Zogmaister, C.; Marzocchi, G.M. Is cognitive training effective for improving executive functions in preschoolers? A systematic review and meta-analysis. Front. Psychol. 2020, 10, 1–23. [Google Scholar] [CrossRef]
- Lucangeli, D.; Tressoldi, P.E.; Cendron, M. Cognitive and Metacognitive Abilities Involved in the Solution of Mathematical Word Problems: Validation of a Comprehensive Model. Contemp Educ Psychol. 1998, 23, 257–275. [Google Scholar] [CrossRef]
- Desoete, A.; De Craene, B. Metacognition and mathematics education: An overview. ZDM Math Educ. 2019, 51, 565–575. [Google Scholar] [CrossRef]
- Träff, U. The contribution of general cognitive abilities and number abilities to different aspects of mathematics in children. J. Exp. Child. Psychol. 2013, 116, 139–156. [Google Scholar] [CrossRef]
- Passolunghi, M.C.; Pazzaglia, F. Individual differences in memory updating in relation to arithmetic problem solving. Learn Ind. Differ. 2004, 14, 219–230. [Google Scholar] [CrossRef]
- Holmes, J.; Gathercole, S.E.; Dunning, D.L. Adaptive training leads to sustained enhancement of poor working memory in children. Dev. Sci. 2009, 12, F9–F15. [Google Scholar] [CrossRef] [PubMed]
- Alloway, T.P.; Alloway, R.G. Investigating the predictive roles of working memory and IQ in academic attainment. J. Exp. Child. Psychol. 2010, 106, 20–29. [Google Scholar] [CrossRef] [PubMed]
- Nelwan, M.; Vissers, C.; Kroesbergen, E.H. Coaching positively influences the effects of working memory training on visual working memory as well as mathematical ability. Neuropsychologia 2018, 113, 140–149. [Google Scholar] [CrossRef] [PubMed]
- Van der Stel, M.; Veenman, M.V.J. Metacognitive skills and intellectual ability of young adolescents: A longitudinal study from a developmental perspective. Eur. J. Psychol. Educ. 2013, 29, 117–137. [Google Scholar] [CrossRef]
- Yu, K.C.; Fan, S.C.; Lin, K.Y. Enhancing students’ problem-solving skills through context-based learning. Int. J. Sci. Math Educ. 2014, 13, 1377–1401. [Google Scholar] [CrossRef]
- Lai, Y.; Zhu, X.; Chen, Y.; Li, Y. Effects of Mathematics Anxiety and Mathematical Metacognition on Word Problem Solving in Children with and without Mathematical Learning Difficulties. PLoS ONE 2015, 10, e0130570. [Google Scholar] [CrossRef]
- Wexler, B.E.; Iseli, M.; Leon, S.; Zaggle, W.; Rush, C.; Goodman, A.; Esat Emal, A.; Bo, E. Cognitive Priming and Cognitive Training: Immediate and Far Transfer to Academic Skills in Children. Sci. Rep. 2016, 6, 1–9. [Google Scholar] [CrossRef]
- Sobkow, A.; Fulawka, K.; Tomczak, P.; Zjawiony, P.; Traczyk, J. Supplemental Material for Does Mental Number Line Training Work? The Effects of Cognitive Training on Real-Life Mathematics, Numeracy, and Decision Making. J. Exp. Psychol. Appl. 2019, 25, 372–385. [Google Scholar] [CrossRef]
- Snyder, K.E.; Nietfeld, J.L.; Linnenbrink-Garcia, L. Giftedness and metacognition. Gift Child. Q. 2011, 55, 181–193. [Google Scholar] [CrossRef]
- Carr, M.; Alexander, J.; Schwanenflugel, P. Where gifted children do and do not excel on metacognitive tasks. Roeper Rev. 1996, 18, 212–217. [Google Scholar] [CrossRef]
- Rodríguez-Naveiras, E.; Verche, E.; Hernández-Lastiri, P.; Montero, R.; Borges, Á. Differences in working memory between gifted or talented students and community samples: A meta-analysis. Psicothema 2019, 31, 255–262. [Google Scholar]
- Kontostavlou, E.Z.; Drigas, A. Executive functions training and giftedness. Retos 2022, 43, 1005–1014. [Google Scholar] [CrossRef]
- Berg, D.H.; McDonald, P.A. Differences in mathematical reasoning between typically achieving and gifted children. J. Cogn. Psychol. 2018, 30, 281–291. [Google Scholar] [CrossRef]
- Grob, A.; Hagmann-von Arx, P. IDS-2.Intelligentie en Ontwikkelingsschalen voor Kinderen en Jongeren: Verantwoordingen Psychometrie; Hogrefe: Amsterdam, The Netherands, 2018; Dutch translation by Ruiter, S.; Visser, L.; Timmerman, M. [Google Scholar]
- Hendriks, M.P.H.; Ruiter, S. WISC-V-NL: Technische Handleiding, Dutch revision; Pearson: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Sihotang, R.O.; Hutagalung, E.E. Metacognition skills of the gifted and talented students. J. Phys. Conf. Ser. 2020, 1521, 032017. [Google Scholar] [CrossRef]
- Oppong, E.; Shore, B.M.; Muis, K.R. Clarifying the Connections Among Giftedness, Metacognition, Self-Regulation, and Self-Regulated Learning: Implications for Theory and Practice. Gift Child. Q. 2018, 63, 102–119. [Google Scholar] [CrossRef]
- Kornmann, J.; Zettler, I.; Kammerer, Y.; Gerjets, P.; Trautwein, U. What characterises children nominated as gifted by teachers? A closer consideration of working memory and intelligence. High Abil. Stud. 2015, 26, 75–92. [Google Scholar] [CrossRef]
- Alloway, T.P.; Elsworth, M. An investigation of cognitive skills and behavior in high ability students. Learn Ind. Differ. 2012, 22, 891–895. [Google Scholar] [CrossRef]
- Veenman, M.V.J.; Kok, R.; Blöte, A.W. The relation between intellectual and metacognitive skills in early adolescence. Instr. Sci. 2005, 33, 193–211. [Google Scholar] [CrossRef]
| Metacognitive Beliefs | Working Memory | Problem-Solving Components | |
|---|---|---|---|
| Session 1 | Discussion of the importance of attention for problem solving | Listening span task without a secondary task | Understanding the wording of the problem: focus on relevant information |
| Session 2 | Discussion of the role of self-efficacy in problem solving | Listening span task with a secondary task (2–6 sentences) | Understanding the wording of the problem: focus on irrelevant information |
| Session 3 | Discussion of the importance of working memory in problem solving | See session 2 | A mental representation of the problem: building up a visual representation of the problem to insert and connect new information |
| Session 4 | Distinguishing between different maths problems; identifying the characteristics of a maths problem | Listening span task with a secondary task (3–7 sentences) | Classify different maths problems by their structure |
| Session 5 | Discussion of how that problem can be solved using different procedures | See session 4 | Identifying the phases that lead to the solution |
| Session 6 | Using mistakes to improve problem-solving performance | Listening span task with a secondary task (3–8 sentences) | Producing plans for solving a given problem |
| Session 7 | The importance of intrinsic motivation | See session 6 | Solving problems: the importance of choosing the proper operations and performing them in the right order |
| Session 8 | The importance of factors that negatively affect school attainment, particularly in mathematics (e.g., anxiety) | See session 6 | The importance of monitoring problem-solving activities |
| Wilk’s λ | F | p | ηp2 | |
|---|---|---|---|---|
| Multivariate effects | ||||
| Measurement | 0.57 | 21.73 | <0.001 | 0.43 |
| Measurement × Condition | 0.93 | 2.23 | 0.090 | 0.07 |
| Univariate effects | ||||
| Digit Span | ||||
| Measurement | 31.26 | <0.001 | 0.26 | |
| Measurement × Condition | 1.34 | 0.251 | 0.02 | |
| Picture Span | ||||
| Measurement | 28.50 | <0.001 | 0.25 | |
| Measurement × Condition | 0.38 | 0.539 | 0.004 | |
| Metacognition | ||||
| Measurement | 7.51 | 0.007 | 0.08 | |
| Measurement × Condition | 5.59 | 0.020 | 0.06 |
| Cognitive Training | Control Group | ||||
|---|---|---|---|---|---|
| Pre-Test | Post-Test | Pre-Test | Post-Test | ||
| Digit Span | M | 28.00 | 30.32 | 27.05 | 28.58 |
| (SD) | (0.53) | (0.55) | (0.60) | (0.61) | |
| Picture Span | M | 34.18 | 36.40 | 33.28 | 36.08 |
| (SD) | (0.74) | (0.58) | (0.82) | (0.65) | |
| Metacognition | M | 22.64 | 23.32 | 22.73 | 22.78 |
| (SD) | (0.16) | (0.14) | (0.18) | (0.15) | |
| Pre-test | Post-test | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Digit Span | Picture Span | Metacognition | Digit Span | Picture Span | Metacognition | |||||||
| Variable | B (SE) | β | B (SE) | β | B (SE) | β | B (SE) | β | B (SE) | β | B (SE) | β |
| Constant | 20.47 (3.34) | 19.55 (4.28) | 24.60 (1.01) | 21.40 (3.28) | 21.80 (3.56) | 23.22 (0.86) | ||||||
| IDS score | 0.07 (0.03) | 0.22 * | 0.13 (0.04) | 0.33 ** | −0.02 | −0.20 | 0.07 (0.03) | 0.23 * | 0.14 (0.03) | 0.40 *** | −0.004 (0.01) | −0.05 |
| Condition | 1.49 (0.80) | 0.19 | −0.31 (0.86) | −0.04 | 0.54 (0.21) | −0.27 * | ||||||
| R2 | 0.046 | .109 | 0.040 | 0.093 | 0.158 | 0.071 | ||||||
| F | 4.37 * | 11.07 ** | 3.69 | 4.59 * | 8.34 *** | 3.39 * | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Vreeze-Westgeest, M.G.J.; Vogelaar, B. Cognitive Training in the Domain of Mathematics for Potentially Gifted Children in Primary School. Educ. Sci. 2022, 12, 127. https://doi.org/10.3390/educsci12020127
de Vreeze-Westgeest MGJ, Vogelaar B. Cognitive Training in the Domain of Mathematics for Potentially Gifted Children in Primary School. Education Sciences. 2022; 12(2):127. https://doi.org/10.3390/educsci12020127
Chicago/Turabian Stylede Vreeze-Westgeest, Mirjam G. J., and Bart Vogelaar. 2022. "Cognitive Training in the Domain of Mathematics for Potentially Gifted Children in Primary School" Education Sciences 12, no. 2: 127. https://doi.org/10.3390/educsci12020127
APA Stylede Vreeze-Westgeest, M. G. J., & Vogelaar, B. (2022). Cognitive Training in the Domain of Mathematics for Potentially Gifted Children in Primary School. Education Sciences, 12(2), 127. https://doi.org/10.3390/educsci12020127






