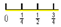Analysis of Problem Posing Using Different Fractions Meanings

Abstract

The aim of this work is to study the knowledge that 11 to 12-year-old pupils have about the different meanings of fractions. For this purpose, an investigation about the ability that 11 to 12-year-old pupils have with fraction problems through problem posing is performed. In particular, we analyze if they pose different types of problems depending on the provided help and if they are able to solve the problems they pose. To do so, after making a classification about types of fractions problems, an instrument is designed to see if students are able to invent and solve problems with different conditions (no reference at all, reference to an image, reference to a graphic representation, and reference to an operation). The analysis of results shows that most of the students properly solve what they invent, and points out that they tend to pose part-whole and part-set problems, even when the given reference suggests another type of problem.

1. Introduction

Several authors support and demonstrate that there exists a relationship between the ability to pose problems and the ability to solve them, since the former ones have a positive influence on the latter ones. Thus, according these results, it is necessary implement problem posing results in schools to improve the mathematical competence of students [1,2,3]. In fact, some regulations that establishes the basic curriculum for Primary Education, as for instance in Spain [4], emphasize the importance of problem solving to develop the mathematical competence. However, unexpectedly, problem posing is a task that is not usually carried out at schools [2,5,6,7].

In addition, fractions are difficult mathematical content since they can have different uses of meanings depending on the context [8,9,10]. Fractions take different meanings across different contexts and therefore different types of problems and situations [9,11] and its treatment requires different strategies [7,10,12], in particular, the use of different graphical representations.

This work focuses on analyzing the ability of primary school students to pose problems that include a fraction in their formulation. In particular, taking into account different studies about types of fraction problems [8,13,14,15], a classification was made regarding the different meanings or context of the problem. Actually, based on this classification, the purpose of this paper is to analyze 6th grade-pupils’ ability in posing problems related to fractions in order to know if pupils tend to formulate problems of a specific type. For this challenge, pupils were asked to pose and solve different problems (Part-whole, Part-set, Division of two numbers and Rational number), providing different types of references (no reference at all, visual reference or written reference).

The purpose of this study is to study if pupils tend to formulate problems of a specific type, if they pose different types of problems depending on the provided reference and if they are able to solve the problems they pose.

Specifically, we face this purpose for 6th grade pupils by means of the following research objectives:

• To determine the ability of pupils in posing problems related to fractions (RO1);
• To examine the ability that pupils have in solving problems when posing them (RO2);
• To analyze the predilection on the type of problem posed. That is, if pupils tend to formulate problems of a specific type or context (RO3);
• To study the effectiveness of the provided references. That is, if the type of given reference helps pupils to pose and solve a problem and if the given reference evokes the formulation of a specific type of fraction problem (RO4).

2. Theoretical Framework

The methodology carried out here in this paper is guided by a theoretical framework, which influences the study’s design. Specifically, this foundation has been divided into two different parts: problem posing and fraction problems.

2.1. Problem Posing

Various authors point out that problem solving is as important as problem posing, since pupils who are able to pose problems usually know how to solve them. Nevertheless, when they are able to solve, they may not be able to pose problems [1,16,17].

In fact, a close relation between problem posing and solving is stated since problem posing is an important tool to give indications about problem solving and to improve pupils’ comprehension and mathematical knowledge [2,18].

Concretely, problem posing has several benefits for the teaching-learning of mathematics such as [1,16,18]:

• Problem posing can increase the mathematical knowledge, since the task of creating or formulating a new problem allows the pupils to establish relationships between the different phases of problem solving [19]. In fact, thanks to problem posing, pupils reach complex reflection levels, reaching a reasoning stage that makes the construction of mathematical knowledge possible [20]. Moreover, problem posing allows avoidance or overcoming mathematical mistakes coming from the operative phase of problem resolution since pupils choose the proper information and data to operate later in the problem [21];
• Problem posing tasks also contribute to the development of pupils’ curiosity and motivation [3,16] and decreases pupils’ fear and anxiety towards mathematics, contributing the development of responsible and favorable attitudes [18,21];
• Other studies establish a very positive and direct relationship between the task of problem posing and the creativity of pupils since fluency, flexibility and originality are proper features when formulating problems [18];
• Finally, problem posing is a great evaluation task for teachers, since it allows them to see pupils’ mathematical knowledge, to analyze their processes of reasoning and to assess their conceptual development [17].

Therefore, due to all these positive aspects of problem posing, this task should be implemented at schools. However, it has not been addressed as a part of many mathematics curricula [2,5,6,7] and there has not been enough research related to how to develop these kinds of tasks probably due by the common belief that the main purpose of problems is focused on the result not on the process.

Some authors propose different methods to implement the task of inventing problems. Those methods normally consist of formulating a problem under some given conditions such as a representation, a required context or a specific operation for solving the problem, or reformulating a new problem from a given one by changing some data [22,23].

According to this, a classification about how to present a problem posing task is presented in Stoyanova [23]. This classification is based on: free situations, where pupils do not have any restriction to pose the problem; middle-structured situations, where pupils have to pose a problem similar to another given one; and structured situations, where pupils have to reformulate a given problem by altering its data.

Another classification is made in Christou et al. [22], based on the nature of the information given to the pupils when the task is proposed. Regarding this, problem posing tasks can be: posing a problem freely; posing a problem from a given response; posing a problem from some given information; posing a problem considering a given situation; and posing a problem which can be solved with a given operation.

In view of this work, the proposed method is based on considering those proposals [22,23] and the type of references of information given to the pupils when they are asked to pose a problem. Specifically, the following tasks are designed:

• No reference: pupils should pose a problem freely, but including a fraction in the formulation;
• Visual reference: pupils are given an image or a graphic representation (as normally appear in primary schools books and resources) from which they should pose a related problem. These references are used with the objective of evoking a specific type of fractions problems;
• Written reference: pupils are given an operation with fractions and they should formulate a problem that could be solved using this operation.

2.2. Fractions Problems

In recent decades, many researchers in the education community have been deeply concerned about the basic mathematical knowledge related to fractions in general [24,25,26,27] and about the fraction problem posing in particular [28,29,30,31].

Regarding this, Castro [1] stated that some teachers and current resources focus on the teaching of fractions when presenting a fraction as the relation between two numbers known as numerator and denominator. The denominator represents the total of equal portions, which the unit has been divided into, while the numerator represents the number of portions that have been taken. According to this, pupils’ learning is focused on representing only a notion of fraction, but it is not applied with context or with different meanings [1].

Despite this consideration, Kieren [8,32,33] established that, to build the knowledge about fractions students must recognize several intuitive meanings or uses. That is, fractions take different meanings across different contexts [11,32,33] and therefore different types of problems and situations, and its treatment requires different teaching strategies [12], such as, different graphical representations.

Learning and thinking about the fraction meanings is constrained by the identification of the unit and by the symbolic or graphical representations of the meanings. On one hand, students have difficulties on recognizing the importance of the unit because they do not realise that the unit is different in every context [14,34,35].

On the other hand, the understanding of fraction concepts also requires working with representations of the meanings. In this sense, the most common graphical representations are the area, set, and number line representations. Some studies have showed that these graphical representations create different challenges to students for the identification of the unit and consequently of the fraction meaning [11,12,33].

Therefore, to have an adequate knowledge of fractions, it is important to have an understanding of the different meanings of fractions and connections among them, the unit in different contexts, and the graphical representations.

These meanings are: quotient, ratio, multiplicative operator and measurement [8]. In addition, Perera & Valdemorós in [15] mentioned one more intuitive meaning, which is the part-whole relation used as basis to build the other four previously established. It should be noted that understanding a fraction as a part-whole is different if the whole is continuous, as a rectangle, or discrete, as a set of objects. In this way, this meaning will be presented as two separated ones.

Then, taken those approaches into account, several meanings of fractions can be distinguished [5,15].

• Part-whole with continuous unit (PW): This is the most basic and frequent fraction meaning. It refers to a whole divided into equal parts and indicates the relation that exists between a number of parts and the total.
• Part-whole with discrete unit or part-set meaning (PS): This meaning considers a unit formed by disjointed elements, that is, a set or group of items that is divided into subgroups with equal number of items in each of them.
• Quotient: This meaning is applied in contexts of distribution, when a whole or magnitude is equally distributed or divided into a number of parts of the same or different magnitude. In this way, two related but different submeanings can be established:
• Division of two numbers (D2N), when the whole and the parts have different units, that is, they are different magnitudes. Then, it is possible to consider the fraction as a non-exact division that is not necessarily done, but simply indicated [13].
• Rational number (RN), when the whole and the parts are referred to the same magnitude. Then, this meaning relates the idea of fraction with that of decimal numbers.
• Ratio: Other meaning is stated when two quantities, of the same or different type, are compared without giving an idea of number. This use of the fractions presents difficulties on many pupils, since this notion is normally shown as a calculation, corresponding to an algorithm, without being supported by graphic representations. Due to these difficulties, in this study this meaning is not considered, because it is not in the scope of 6th course of primary school where this study is set out.
• Operator: In this meaning, the fraction acts over a quantity through operations of division and multiplication, in order to transform this quantity in a new one. This meaning is associated with part-set one since the operation is always performed in a set. As occurs with the meaning of the fraction as a ratio, this meaning is many times seen as an algorithm without representing and understanding it.
• Measurement: Finally, this meaning arises from comparing two magnitudes, where one of them is the model taken to measure, and the other one is the one to be measured. Commonly, this meaning is confused with the idea of fraction as a rational number when using measurement units. For instance, 0.75 liters of water do not represent a fraction as a measurement, because $\frac{3}{4}$ liter is the capacity of the bottle, not a part from the whole, as it is a bottle whose capacity is 1 liter and is filled up its $\frac{3}{4}$.

In

Table 1. Examples of different meanings of fractions.

Meaning	Statement	Graphic Representation
Part-whole (PW)	“Mary has eaten $\frac{1}{8}$ of the pizza”
Part-set (PS)	“ $\frac{2}{6}$ of the colors are blue”
Division of two number (D2N)	“Each child receives $\frac{2}{3}$ pieces of chocolate.”
Rational number (RN)	“A bottle of $\frac{3}{4}$ l of capacity.”
Ratio	“Compare the quantity of cases and pencils” $\frac{\mathrm{pencilcases}}{\mathrm{pencils}}$ = $\frac{4}{18}$ = $\frac{2}{9}$”
Operator	“Take $\frac{3}{4}$ from 12 cakes”
Measurement	“The bottle is full up to $\frac{2}{3}$ of its total capacity”

, some examples of the different meanings are shown to better understand each of the meanings.

In particular, in this work, several meanings of fraction have been studied, namely: Part-whole with continuous unit, part-whole with discrete unit, quotient and measurement, since they are the most used at schools. The meaning of a fraction as a ratio has not been included to avoid confusing pupils with the meaning of quotient, since the ratio is usually taught in upper grades. Besides, the meaning of a fraction as an operator has been also excluded because this type of fractions problems is usually included in the meaning part-whole with discrete units, since they refer to a part taken from a group, so they will be considered in that meaning.

Therefore, the classification specifically done and used for this work is the following one:

• Part-whole: This meaning is equivalent to the part-whole with continuous unit. An example of this type of problems could be “My brother has eaten $\frac{2}{3}$ and my father $\frac{1}{4}$. Which fraction of pizza is remaining?”
• Part-set: This meaning is equivalent to the part-whole with discrete unit. An example of this type of problems could be “Mary has 25 sweets and she gives $\frac{2}{5}$ of sweets to her best friend, Kate. How many sweets does Kate have?”
• Division of two numbers: This meaning is equivalent to the quotient when numerator and denominator have different unit. An example of this type of problems could be “A teacher has 4 pieces of chocolate and he wants to divide them up his 12 pupils. How many pieces of chocolate will each pupil receive?”
• Rational number: This meaning is equivalent to the quotient when numerator and denominator share the same unit, that is they work as a magnitude and the fraction is related to a decimal number. An example of this type of problems could be “In a perfumery there are 30 liters of perfume and the workers have to distribute them into bottles of $\frac{3}{4}$ liters. How many bottles will be needed?”

This classification jointly with the described method of problem posing based on the different provided reference, have been used as a basis of the instrument developed in the methodological design of this research, described in the following item.

3. Methodology

The methodology used on this study is a quantitative analysis based on the task of problem posing in pupils from 6th grade of Primary Education.

After this, all the student productions were analyzed to classify every posed problem regarding if they were well invented or not and if they were well solved or not. Furthermore, the context of the statements of these posed problems were analyzed distinguishing the type of fraction meaning that the student used.

3.1. Participants

The participants that took part in this investigation were 50 European pupils from 6th grade of Primary Education, so they were 11 and 12 years old. The study was carried out just when students finished their instructions about fractions. Pupils were asked to pose some problems in different sessions, for this reason, the number of collected tasks for every problem can vary depending on the availability.

In this study it is not any discrimination or ethical disregard for learners and it does not suppose any detrimental effects for them.

3.2. Instrument

As mentioned before, to carry out this research, an instrument for posing problems was developed according to the revised theoretical framework. This instrument consists of some tasks to request that the pupils pose problems with several types of references (no reference at all, visual reference and written reference), to check if the given reference suggested a specific type of problem. The students were also asked for solving the problems they have invented in order to see if there is a relation between the ability to pose and the ability to solve such problems.

Concretely, the requested tasks were the described in

Table 2. Method designed for the problem posing instrument.

Nr	Task	Reference Given	Type of Reference	Type of Problem Expected
1	Invent a problem that includes at least a fraction in its statement. Then, solve it. Explain or draw whatever you need to do the task.		None	Any meaning
2	Invent a problem of fractions related to the following image. Then, solve it. Explain or draw whatever you need to do the task.		Visual reference: image	Part-whole
3	Invent a problem of fractions related to the following image. Then, solve it. Explain or draw whatever you need to do the task.		Visual reference: image	Part-set
4	Invent a problem of fractions related to the following image. Then, solve it. Explain or draw whatever you need to do the task.		Visual reference: image	Division of two numbers
5	Invent a problem of fractions related to the following image. Then, solve it. Explain or draw whatever you need to do the task.		Visual reference: image	Rational number
6	Invent a problem of fractions related to the following graphic representation. Then, solve it. Explain or draw whatever you need to do the task.		Visual reference: graphic representation	Part-whole
7	Invent a problem of fractions related to the following graphic representation. Then, solve it. Explain or draw whatever you need to do the task.		Visual reference: graphic representation	Part-whole
8	Invent a problem of fractions related to the following graphic representation. Then, solve it. Explain or draw whatever you need to do the task.		Visual reference: graphic representation	Part-set
9	Invent a problem of fractions related to the following graphic representation. Then, solve it. Explain or draw whatever you need to do the task.		Visual reference: graphic representation	Rational number
10	Invent a problem of fractions related to the following operation. Then, solve it. Explain or draw whatever you need to do the task	$\frac{3}{4}$–$\frac{2}{3}$	Written reference:Operation	Any meaning

:

Table 2 also shows the different types of help or references given that have been used for each task and the type of meaning of the fraction that is expected to suggest.

Concretely, in Activity 1, there is no reference at all, so pupils should pose a problem freely; they only know that it should include a fraction. Thus, there is not a specific type expected, which allows the teacher to check which meaning the pupils tend to give to the fractions.

In Activities 2, 3, 4 and 5, pupils are given visual reference; they should pose a problem related to the image given in each case expecting to evoke a part-whole problem in Activity 2, a part-set problem in Activity 3, a division of two numbers problem in Activity 4, and a unit of measurement problem in Activity 5.

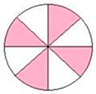
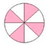
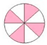
In Activities 6, 7, 8 and 9, pupils are also given visual help, but with graphic representations instead of images. Activities 6 and 7 are different in relation to the shape of the graphic representation; the first one is rectangular while the second one is circular. Both are expected to suggest a part-whole problem, but they have been designed with different shapes to know if pupils have any stereotype when representing a fraction. In Activity 8, the graphic representation is expected to suggest a part-set problem, and the one included in Activity 9, is expected to suggest a unit of measurement problem.

Finally, in Activity 10, pupils should pose a problem that can be solved with a given operation. It is not expected to suggest a certain type, but the operation is to give pupils written help instead of visual help.

4. Results and Discussion

After collecting the student´s productions, each problem was classified into 3 different criteria: “well invented” (when the problem is have sense and can be solved using mathematical connections), “wrongly invented” (when statement has not sense or is uncompleted or cannot be solved) or “not invented”. From the “well invented” problems, a new subcategory was established among “well solved” and “wrongly solved” if once the student pose the problem they know how to solve it.

Table 3. Percentage of well and wrongly invented problems and well and wrongly solved problems for each activity of the instrument.

Activity	Well Invented	Well Solved (*)	Wrongly Solved (*)	Wrongly Invented	Not Invented	Total
1 No help	67.3%	66.7%	33.3%	32.7%	0%	49
2	66.7%	78.6%	21.4%	33.3%	0%	21
3	42.2%	73.7%	26.3%	55.6%	2.2%	45
4	52.2%	70.8%	29.2%	43.5%	4.3%	46
5	36.9%	52.9%	47.1%	60.9%	2.2%	46
6	56.5%	80.8%	19.2%	39.2%	4.3%	46
7	54.2%	69.2%	30.8%	45.8%	0%	24
8	61.2%	63.3%	36.7%	34.7%	4.1%	49
9	11.1%	60.0%	40.0%	73.3%	15.6%	45
10 operation	26.5%	61.5%	38.5%	65.3%	8.2%	49
TOTAL	46.2%	68.5%	31.5%	49.3%	4.5%	420

^(*) Note that these percentages are calculated from the total of well invented problems.

shows the percentages of problems classified into each type. These percentages are in relation to the total number of problems collected of each activity, a number that varies depending on the activity since not all the tasks were done by the same number of students.

Apart from this, if problems were or were not well invented and solved, problems were also classified into “part-whole”, “part-set”, “division of two numbers” or “unit of measurement” depending on the meaning of the fraction in the formulation posed by the students, and classified as “no fractions” if it was not a problem of fractions.

Table 4. Percentage of each type of fraction meaning in the problems invented.

Activity	Expected	PW	PS	D2N	RN	Others	TOTAL
1 No help	FREE	38.8%	42.9%	0%	6.1%	12.2%	49
2	PW	85.7%	4.8%	0%	0%	9.5%	21
3	PS	0%	72.7%	6.8%	0%	20.5%	44
4	D2N	0%	$\overline{50.0}\%$	27.3%	0%	22.7%	44
5	RN	2.2%	$\overline{33.3}\%$	15.6%	11.1%	37.8%	45
6	PW	54.5%	20.5%	0%	0%	25.0%	44
7	PW	75.0%	4.2%	0%	0%	20.8%	24
8	PS	0%	78.7%	0%	0%	21.3%	47
9	RN	2.6%	13.2%	0%	15.8%	$\overline{}68.4\%$	38
10 operation	FREE	42.2%	26.7%	0%	11.1%	20.0%	45
TOTAL		24.9%	38.7%	5.5%	4.7%	$\overline{26.2}\%$	401

PW: part-whole; PS: part-set; D2N: division of two numbers; RN: Rational number.

shows this classification when the student poses a statement related to fractions even if it was well invented or not. This is because now the objective should be analyzed if the type of given condition evoked the fraction meaning expected, even if the formulation of the problem was not completed but included some information that allowed the teacher to see the meaning that the pupil had given to the fraction. Thus, the percentages in Table 4 are associated with the total invented problem (well and wrongly invented together).

As can be observed in Table 4, some relevant percentages are marked. The results where the posed problem coincide with the type of help provided are underlined. On the other hand, the percentages, which correspond to other different type of problem to the expected from the given help, are overlined.

From our results in Table 3, we can observe that almost the 50% of the total of problems collected are well invented, and, in almost all the activities, there is a high percentage of pupils who solve the problem properly, after having invented it well. In other words, most of the problems which are well-invented are well solved too, since they represent more than 60% of well posed problems.

Regarding if the type of given reference helps pupils to pose a problem, Table 3 points out that the most helpful reference for posing problems are the references given in Activities 1 (where no reference is included) and 2 (which included an image of a pizza) since their percentages were around 67%. On the contrary, the less useful reference were those given in Activities 9 (which included a numerical line) and 10 (which included an operation). These had the higher percentages of wrongly invented problems, around 70%. These two activities are also the ones with a higher percentage of non-invented problems, between 8 and 15.

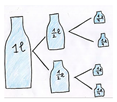
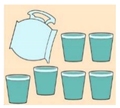
About if the type of given reference lets pupils also solve the problem, Table 3 points out that the most helpful references for solving problems are those corresponding to activities 2 (which included an image of a pizza) and 6 (which included a rectangular graphic representation). It is interesting to highlight that both activities were intended to suggest a part-whole problem. On the contrary, the activity with a higher percentage of wrongly solved problems is Activity 5, which included an image of glasses and a jar.

Concerning if the given reference evokes the formulation of a specific type of fraction problem, Table 4 shows that, when pupils have no help and, therefore, any meaning of the fraction can be expected, the preferred types are part-whole and part-set problems, since both percentages together are equal to 80%.

On one hand, the visual reference used to suggest part-whole and part-set problems has given very good results. Actually, as their percentages were nearly 80%, this type of help seems useful for pupils. It is important to note that no difference has arisen between images related to real life or graphic representations since both have had very similar results. Nevertheless, in the case of graphic representations, the circular shape has had better results than the rectangular one, with a difference of 20%.

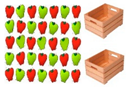
On the other hand, the visual references used to evoke rational number of division of two number meanings were not successful at all. In fact, the given reference in Activity 9, numerical line, was not useful for pupils, since the type of problem expected, which was rational number, obtained a percentage of 15%, and the higher percentage of problems posed were not about fractions (68%). Something similar occurred with Activity 5 (which included an image of glasses and a jar) and was also expected to suggest a rational number problem. In this case, the most repeated type of problems was part-set (33%) and nearly the 40% of problems where not about fractions. Finally, Activity 4, which included an image of apples and two boxes, was expected to suggest a problem of division of two numbers. However, it had better results in part-set problems, because the image of the apples is similar to the image of sweets used to evoke the part-set meaning. Only the 27% of pupils invented a problem of the type expected, but the 50% of them posed a part-set problem.

Therefore, the effectiveness of every given reference regarding the level of success in inventing and the evocating type of problem is sum up as follows.

• Pizza: Great invention, great part-whole evocation as expected.
• Set of points: Great invention, great part-set evocation as expected.
• Circular graph: Good invention, great part-whole evocation as expected.
• Rectangular graph: Good invention, good PW evocation as expected and also some part-set evocation.
• Set of candies: Medium level of invention, great part-set evocation as expected.
• Apples and boxes: Medium invention and evokes division of two number notion as expected but also part-set due the similarity of the reference.
• Number line: Difficult to invent but evokes rational number type as expected.
• Jar: Low level of invention but does not evoke rational number type as expected.

5. Conclusions

According to the RO1 of this work, which is to determine the pupils’ ability in problem posing, the first conclusion is that there is around a 50% success rate for problem posing in 6th grade pupils. Like others studies suggested [28,29,30,31], this study shows some difficulties on fraction problem posing indicating a lack of conceptual understanding of fundamental mathematics probably due by the fact that problem posing tasks are not addressed at the schools [2,5,6,7].

Regarding to RO2, we can conclude that most pupils (70%) have a high ability to solve problems when posing them. That is, they are able to solve what they invent, confirming what several prestigious authors ([1,2,16,17,18]) said about the positive influence of problem posing on problem solving.

Apart from the ability in problem posing, the predilection on the type of problem that pupils have posed was also studied (RO3). Concerning that, it was proven that pupils preferred types as part-whole and part-set even when the given reference was expected to suggest another type of problem or any specific type. However, other types of problems are rarely posed. Consequently, the notions on division of two numbers and rational number are less intuitive for them. This is probably because, in the school, part-whole and part-set meanings are the first ones studied for presenting fractions and therefore those are the two main meanings that pupils know better. This result is aligned with previous studies, which agree with the idea of considering those fraction meanings as the most appropriated for introducing fractions at school [14,33,34,35].

In relation to the effectiveness of the provided references (RO4), it is shown that the most intuitive graphical representations posing part-whole problems are circular area representations such as pizzas, cakes or simply a circular graph. Similarly, images or graphs related to sets are more useful for part-set problems as was previously expected. However, graphs and images provided for inducing division of two numbers or rational number uses are not intuitive at all. Furthermore, inventing these kinds of problems, for whichever given reference, is very unusual at this level. On the other hand, these area representations also seems more helpful when solving problems. Then, apart from the fact that the use of images as pizza and cakes are prototypic images used at the schools, those results suggest that the model of areas is appropriate for teaching those meanings [14].

Finally, two suggestions are important to take into account from this research: in accordance with other previous approaches [16,21,36], it is important to implement general problem posing tasks at schools and fraction problem posing tasks in particular since they have a positive influence on the development of the mathematical competence. Secondly, to overcome pupil’s difficulties on fractions, this work suggests that it is necessary to introduce more helpful images, graphics, tasks and resources in the pupils’ instruction, in order to they get a better understanding of those fraction meanings that present more difficulties.