Abstract
Teacher professional learning occurs across various contexts. Previous studies on teacher learning and changes in practice have focused on either classroom contexts or learning communities outside of school, but have rarely investigated teacher learning across multiple contexts. Investigating teacher learning across the double contexts of classroom and learning community has presented methodological challenges. In response, this paper proposes the suitability of adopting a socio-cultural development framework to further the analytical approach to such challenges. Using the framework, this paper considers the case study of a middle school mathematics teacher who resolved a problem of teaching practice through interacting with other members of the community of practice where they build shared goals and knowledge. This paper contributes to the field by expanding the scope of research on teacher learning across these two contexts, in which problem of practice becomes conceptual resources that the teacher uses in her teaching practice.
1. Introduction
Teachers learn in various contexts, including by participating in school-sponsored professional development (PD) programmes or university-organised PD sessions, and by making commitments to teacher-organised professional learning communities (PLCs) [1,2]. They also learn through their own teaching—by engaging in their teaching or interacting with students, amongst other factors [3,4]. Teachers’ motivations for learning may vary, but one of the most important motivations is to improve their teaching practice, which is critical not only for students’ learning, but also for professional development. Thus, teacher learning is deeply connected with classroom teaching, since one of its ultimate goals is to devise better ways to help students learn core competencies including knowledge, skills, values, and attitudes.
In recent decades, much research has been conducted on teacher learning in PLCs (e.g., [5,6,7]). PLCs function as important settings for teachers to learn about teaching, content, and students. They offer opportunities for improving teaching competency as well as professional development through collaboration [8,9,10]. Teachers learn as they participate in organised social activities, as such PLC participation can greatly help teachers improve their instructional practice. Through interaction with other teachers, resources, and various environments, teachers reproduce and reorganise their conceptions of the world and their knowledge, rendering them ‘communities of practice’ [11,12]. Teachers form communities of practice when they gather with shared goals (e.g., improving teaching practice or student outcomes) and engage in activities to achieve these goals. Such communities can also form in various contexts: Out-of-school courses, teacher associations, sponsored workshops, and professional development sessions [13].
Although PLCs are critical for teacher learning and enhanced teaching practice, literature has rarely examined the connection between PLCs and changes in teaching practice. This study explores how teachers learn and change across PLCs and classrooms using a socio-cultural development framework. The theoretical framework is proposed in this article, and it is claimed that it enables investigation of changing teachers’ practices across classroom and PLC environments, where teachers can access professional learning opportunities and conceptual resources created in socially organised activities. The case study of a middle school teacher is explored through the socio-cultural development theoretical framework, with a problem of practice as a mediator to connect two different contexts.
2. Literature Review
2.1. Teacher Learning across the Contexts of PLCs and Classrooms
Studies of teacher PLCs in school contexts have been conducted in reaction to traditional PD workshops, which are often considered de-contextualised from the classroom context [14]. Traditional PD workshops outside school communities, such as university-led workshops, often provide only subject-matter or pedagogical knowledge that may not naturally translate into changes in teaching practice. In response, some studies of teacher communities have focused on teacher PLCs in school contexts [6,7,15,16]. They addressed the importance of teaching communities at the school level because schools are where teachers work; that is, teacher learning and development should be contextualised in their work environments. These studies have helped us understand the mechanisms of teacher PLCs, including the reasons underlying their formation and their roles in supporting sustainable teacher learning [7,17].
The key features of teacher PLCs’ formation, development, and sustainment are to: (a) Establish norms and collegial collaboration, (b) focus on students’ academic performance as an evaluative tool to adjust instruction, (c) access knowledge resources, (d) share responsibility for student success, and (e) participate in ongoing and frequent discussions on teaching and methods for improvement [6,7,17,18]. Additionally, when teachers feel comfortable in gathering to discuss ideas or share knowledge from their experiences, one can say that they partake in a community of practice. In communities of practice, teachers share their difficulties, observe each other’s teaching, receive feedback, and establish mutual accountability for student success [12].
In this line of research on teacher learning in a community of practice, Horn and Little [19] investigated how teachers’ collegial conversation routines attributed to the formation and sustainment of teacher PLCs. Through two case studies, they argued that collegial discussions provide important conceptual resources. Specifying the roles of resources in fostering teacher learning, Horn [16] identified the following conversational resource types: (a) Reform artefacts—reform slogans, curricula, or assessment tools that aid teacher practice; (b) classification systems—categories whose discussion allows teachers to increase their understanding of the underlying pedagogical assumptions; and (c) rendering of classroom interaction—teaching rehearsals that allow teachers to learn their practice through interaction. In addition to teaching rehearsals, various resources were used to bridge two contexts, including video-stimulated recalls (e.g., [1,20,21]), discursive recalls (e.g., teaching replays and rehearsals in [19]), students’ written or oral works (e.g., [22,23]), and dilemma cases from classroom teaching (e.g., [16,24]).
These studies address the important role of resources in connecting classroom practice with PD or PLC activities to improve teachers’ instruction and enhance their learning. For example, using students’ work samples can provide teachers with tools for developing students’ identities as mathematical thinkers. The use of resources can also shift teachers’ participation in PD practices [23]. Classroom cases such as teaching replays and rehearsals, allow teachers to consider classroom features that they had previously overlooked [25]. Teachers also develop their professional vision by participating in video clubs where video-clips are the tools making connections between teacher learning and classroom practice [20,21].
Teachers have opportunities to investigate problems of practice or teaching dilemmas by engaging in discussions or other socially organised activities in PLC meetings [3,26]. They initially solve problems of practice theoretically, as they reflect on and attend to the problems of practice and anticipate other problems of practice in the next teaching [27], and develop rich conceptual resources that they can utilise in the classroom [5]. These conceptual resources give teachers pedagogical insights that may reorganise their knowledge, and can then implement reconstructed knowledge and insights in their teaching. This process is repeated as the teacher engages in and across two communities of practice. Although teachers live in multiple communities of practice, such as their classrooms and schools, and in communities outside school (e.g., workshops, professional development, and university courses), in this paper I focus specifically on classrooms and the PLC meetings, as the work and learning environments are the two most salient communities for teachers attempting to improve their practice. As illustrated in the case study, a teacher who shared real-class dilemmas with members of her PLC experienced mediation by the group and reformulation of the dilemma, transforming it to become a conceptual recourse of that PLC. In this paper, the conceptual resources created by building on teaching dilemmas or problems of practice represented in various types of resources act as mediators to study teacher learning within and across these contexts.
2.2. Situative Perspective and Multiple Units of Analysis
Several studies have adopted a situative perspective to investigate teacher learning, as situative learning theory expounds upon three aspects of cognition [11,28,29,30]. First, cognition is situated in the social context in which ordinary cultural practices or social activities occur. Second, knowledge and learning process are social, resulting from long-term group interactions and enculturation into communities’ thinking processes. Finally, cognition is distributed across people and tools, enabling groups to accomplish cognitive tasks that individual members could not perform alone [31]. These aspects posit the activity system or collective practices in a community of practice as the unit of analysis.
The situative perspective provides a tool to analyse how people within communities of practice learn from engaging in social activities or ‘shared practices’ [32], p. 111, and co-construct knowledge. Additionally, it addresses how newcomers experience ‘becoming full participants in a sociocultural practice’ [11], p. 29, situating their incorporation as a process of moving from peripheral to full participation. This theoretical perspective provides a tool to explore how teachers use PLCs to enhance their learning and later apply their knowledge to future teaching. However, when we consider an individual teacher’s change in practice as his/her learning and development in and from engaging in shared practices, Kazemi and Hubbard’s study [2] forms the limited scholarship that suggests tracing how individual teachers’ improvement in teaching practice resulting from PLC learning translates into classroom practice. However, to date there are few studies that combine multiple analytical methods.
Rogoff argues that multiple views cannot be analysed simultaneously [33,34]. Rogoff describes dynamic human development on three planes [33]: Apprenticeship on the community plane involving active participation with others in a culturally organized activity; guided participation on the interpersonal plane involving mutual involvement of individuals in socioculturally structured collective activities, and participatory appropriation on the individual plane, where individuals change their understanding of and responsibility for activities through their participation. Participation in community activities and interaction with others in routine, tacit, and explicit collaboration prepares individuals for future participation in similar events. She argues that when we take a unit of analysis as a reformulation of the relation between the individual and the social and cultural environment, it preserves the essence of the events of interest.
Rogoff later elaborates on what she termed the transformation-of-participation perspective, suggesting a detailed approach to children’s development in cultural activities [34]. She argues that human development is a process whereby people transform through their participation in their communities’ cultural activities. However, these three planes of analysis—community, interpersonal, and individual—form a cultural process of changing participation in which all children participate in their communities’ sociocultural activities. When individuals are the focus of analysis, they are brought to the foreground, and interpersonal or cultural contexts become part of the background. In contrast, when examining interpersonal relationships, relationships among peers or teachers come to the fore, while other aspects fall back. The same logic applies when focusing on cultural institutions. Information on cultural elements comes to the fore, while details pertaining to individuals and their relationships fall into the background. This offers the mechanism of change one would use to examine content from multiple analytical views, but is not a coordination of multiple units of analysis.
Cobb and Bowers, however, suggest alternative approaches to classroom-based research and instructional design, focusing on the reflexive relationship between theory and practice [29]. They emphasise the importance of analysing both individuals’ modes of participation and communal practices, and argue that “coordinating a focus on both individual and collective activity is an integral part of their [teachers’] classroom-based practice in that it has allowed us [teachers] to be more effective when supporting students’ mathematical development over extended periods of time” [29], p. 10. They suggest the coordination of multiple units of analysis involving collective activity, and individuals’ reasoning while participating in communal practices, and the reflexive relationship between students’ reasoning and communal practices. Thus, the coordination of multiple units of analysis is possible. This paper therefore adopts the socio-cultural development framework built upon socio-cultural perspectives on human development, enabling not only analysis of social activities, but also the ability to trace individual teachers’ cognitive development through dialectic interactions in socially organised activities.
2.3. Theoretical Framework: Socio-Cultural Developmental Framework
In his anthropological studies on human development, Saxe [35] provides an analytical framework for coordinating multiple analytical perspectives by discussing the historical relationship between forms and functions of collective practices. He argues that his socio-cultural developmental analytic framework consisted of microgenetic, sociogenetic, and ontogenetic developments is to derive an understanding of the interplay between cultural and developmental cognitive processes.
In considering historical analyses on form–function relations in collective practices with cognitive-developmental treatments on the dynamics of historical stability and change, he developed case studies for historical change in collective practices in the Oksapmin communities of Papua New Guinea, focusing on economic change in mathematically related concepts and the word fu. The Oksapmin people counted by assigning particular numbers to body parts, with fu indicating that all body parts were counted. Today, however, the word fu is used to refer to twice its original numerical designation. The analysis of historical change due to economic exchange and of changes in individual practice related to mathematics and fu represents a diachronic analysis of shifting word forms and meanings in collective practice. Saxe considered the interrelated actions of customers and clerks engaged in joint activity and how the dynamic of collective practices evolved from the local to regional level over time. These analyses of form–function relationships in dynamic collective practices have implications for the study of the dynamic cognitive development of individuals engaged in cultural practices over time. These studies have focused on three strands of development observed in the analysis of how individuals create and accomplish goals that are relevant to the study of dynamic cognitive development: Microgenetic development, “regularities in moment-to-moment constructions” [35] (p. 209); sociogenetic development, “regularities in the propagation of forms or functions as the form-function relations are reproduced and altered within a community” [35] (p. 210); and ontogenetic development, “trajectories in individuals’ development” over time [35] (p. 210).
The analysis of fu’s form–function relationship provides insight into the study of teacher cognitive development through interpersonal interactions. Such analysis provides a framework for analysing the form–function relationships of the conceptual resources that teachers create and synthesise via participation in PLCs to resolve teaching dilemmas from their classrooms.
2.4. Research Questions
The literature review showed that most studies on teacher learning in PD or PLC settings are unidirectional. Many studies of teacher learning have investigated how and what teachers learn from their participation in PD, from either a situative or an individual cognitive perspective. At present, however, the literature lacks detailed analyses of teacher learning, which establish a clear link between what they have learned in PD courses or in PLC settings and how their learning applied to their improved teaching practices. To fill this gap, this article examines a teacher’s professional growth and change in practice with mediators—problems of practice in her classroom, but which become conceptual resources in PLC—using a socio-cultural developmental framework. To achieve the aim of investigating teacher learning with a clear link between two settings of PD/PLC and classroom practice, this study particularly answers the following research questions:
- (1)
- How do problems of practice become conceptual resources for teacher learning?
- (2)
- How does a teacher implement the transformed conceptual resources in her classroom teaching?
3. Methods
3.1. Data Collection
Data collection for this study was undertaken during a five week-long summer school session in 2012 with one participant teacher, Ms. M, as part of a larger project, whose goal was to investigate the relationship between teaching practice and students’ robust understanding of algebra. Ms. M was a middle school teacher in an urban district in California, U.S. At the time of the observation, she had 15 years teaching experience, comprising five years teaching 8th-grade algebra and 10 years teaching elementary school (mostly 4th and 5th grade), and was well-known as a highly proficient teacher in the school district. The session ran for a total of five weeks during the summer, with classes held four days per week for approximately two hours per day. The teacher’s goals for the session were to engage students in non-typical algebraic problem solving, and in the final week to prepare students for 8th-grade algebra.
3.2. Data Sources
Data were collected through video-taped classroom observations, field notes, audio-taped teacher–researcher meetings, and teacher interviews. All everyday classroom observations over the five weeks were video recorded using two cameras: One on the teacher at the rear of the classroom, and the other on students. The participant teacher and researchers met twice a week to share reflections and provide support through planning lessons together and working on mathematics and pedagogical strategies, among other methods. Two audio-recorded interviews were conducted with the teacher. One was a longer interview (20–30 min) at the beginning of the summer session to understand the teacher’s goals for the classes and her conceptions of the instructional aspects of mathematics teaching. The research team also interviewed the teacher at the end of the summer session to reflect on the programme. Other interviews were shorter (7–10 min) and were conducted daily before and after class. The purpose of these interviews was to understand the teacher’s goals for the day and what she anticipated instructionally, with a greater focus on students’ difficulties.
3.3. Data Analysis
All recordings examined were transcribed by the author. The transcripts were coded [36] to identify the teacher’s knowledge-in-practice [37] and problem of practice. Once three corresponding codes of knowledge-in-practice were generated, they were applied to the whole corpus. For this study, the episodes of problem of practice were tagged, and PLC meetings regarding a particular episode were transcribed as supplemental data.
In this study, one episode was selected to investigate how a problem of teaching practice was brought up; and resolved and transformed into conceptual resources as the teacher interacted with other PLC members. A single case study [38] was used to illustrate how to trace individual teacher’s learning and change using the socio-cultural development framework with qualitative analysis.
As indicated in the literature review section, a mediator was necessary to trace teacher learning in different contexts using the socio-cultural development framework. To analyse this case study, I used the problems of teaching practice as the mediator between classroom practice and PD, and exploring how the problems of teaching practice become a conceptual resource for teacher learning. To utilise the socio-cultural developmental framework, I drew on three units of analysis for this case study: (a) The dimension of cognitive development of an individual teacher, Ms. M; (b) the interpersonal dimension, focusing on how the individual teacher interacted with other members of the PD team, and (c) the dimension of interplay between individual(s) and the mediator, the problem of teaching practice, as the individual accomplished her goals over time. The analysis traced how the problem of teaching practice evolved to become a conceptual resource.
4. Findings
4.1. Problems of Teaching Practice
During the summer sessions and interviews, Ms. M’s knowledge-in-practice was shown to be highly proficient [37]. In week 4, Ms. M encountered a problem of teaching practice (teaching dilemma) when she introduced a problem that was challenging to 7th grade students, the 52-card pick up problem:
“A deck of cards was dropped on the floor. Naoko may have picked up none, one, 52, or any number in between. How many different combinations of cards could she have picked up?”
On the first day of the lesson, Ms. M introduced the problem, but students failed to grasp its meaning, struggling to understand the problem itself. A simple approach to solve the problem could be 52C1 + 52C2 + 52C3 + …52C51 + 52C52 = . There are also several approaches to solve the problem including this summation of the combination, using Pascal’s triangle, and using possibility—each card has two choices of taking or not-taking, and there are 52 cards total, but null set, so that the possibility is However, the problem itself was challenging to 7th grade students even though Ms. M’s teaching goal with this problem was for students to figure out patterns making the complicated problem easier. It was hard for her students to make sense of what the situation of the question meant, and they were confused with the numbers (e.g., Ace, King, Queen, and numbers) and figures (e.g., diamond, heart, clover, and spade) of cards to understand the situation. She explained the problem situation to make students understand and ended the lesson with asking students to think about the problem by the next day.
On the second day, as her teaching goal revealed in the interview and classroom observation, Ms. M had her students try to approach the 52-card problem using one of the problem-solving strategies, ‘solving an easier problem’. She made the 52-card problem into a 10-card problem:
“Ten cards are dropped on the floor. Bruce (Bruce was a stuffed tiger on the corner of the classroom, and it was used not only for this problem, but also for encouraging students to have persistence in solving math problems [37,39].) may have eaten one, 10, or any number of cards in between. How many different combinations of cards could he have eaten?”
Despite her attempt to simplify the problem, the students still struggled with the concept of combinations with 10 cards. Thus, Ms. M began listing the cards (A, 1, 2, …, 9) and each combination of picking them up, such as ‘Bruce eats no cards, Bruce eats one card, Bruce eats two cards…’. However, Ms. M’s approach in her lesson was not useful to solve the problem in a successful way, so the students failed to see the patterns of the possibilities or combinations. Figure 1 was re-drawn to clarify the strategy on the whiteboard that, and depicts the classroom discussion of this approach.
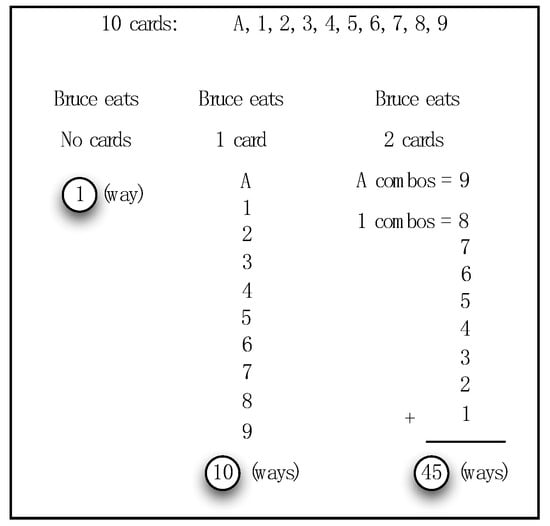
Figure 1.
Classroom discussion of the 10 card problem led by Ms. M unsuccessfully.
This mode was unsuccessful for figuring out the pattern of 210, leading Ms. M to eventually end up on the problem on that day of the lesson although Ms. M still encouraged students to solve the problem successfully in the next day rather than just giving up solving the problem (More detailed descriptions of the episodes were written in [37]).
4.2. Transformation of Problems of Practice into Conceptual Resources
The problem itself was, of course, challenging to middle school students, as it consisted of a concept of combination. Having this problem in the class was also challenging to her, as a teacher, to make middle school students explore the complex mathematical concept. Ms. M reflected on this teaching dilemma or a problem of teaching practice in the interview right after finishing this class teaching as follows:
“Ms. M: Well, today was kind of making a mess day. And I’m hoping that we can clean it up next week. I think there are some, I was surprised at, um, I was surprised at how difficult today’s 10-card pick up was. So, I’m letting go of my 52-cards pick up. And wanting to do 10-card pick up.One tricky thing that I talked to you about earlier is that, when I, I had an idea to give them to warm up that was easier than the problem of the week. Partly because I wanted to see what they could do on their own. But, by giving them an easier problem, it’s sort of became, um, less evident that they could solve an easier problem than the easier problem that I give them.… (ellipsis)But next week, I think we really need to go back and do the 10-cards pick up again and I would really like to build it up not starting with ten cards, but starting with one card, and then two cards, and then three cards, and, and building it up. Because the pattern right now we have, we have pattern, we have one, ten, and forty-five. That’s all we have right now. And it’s not pretty to them. So, um, we need to revisit this problem and deal with it on Monday, which I think it will be good.”
The problem of practice from her perspective was that Ms. M thought that reducing the number from 52 cards to 10 cards would help implant the idea of making an easier problem, which was one of problem-solving strategies, but the approach of seeing it as starting from 1 card, 2 cards, then 3 cards and so on did not build a pattern of all combinations, 210. She brought this 52-card pick up problem to the teacher–researcher conversation space, a PLC setting, both before teaching the 52-card problem and after the second day of teaching the problem, where it became a teaching dilemma—the problem of teaching practice.
PLC meetings were usually a place for Ms. M to reflect on her teaching of previous days and to plan for the next class. At the first PLC meeting regarding teaching the 52-card problem, Ms. M and other members of the PLC discussed how to teach the problem in the best way as she planned to teach it to implement a problem-solving strategy. Other members, mostly researchers of mathematics education, presented three different ways of approaching the problem stated above: (1) A simple combinatory equation, 52C1 + 52C2 + 52C3 + …52C51 + 52C52 = ; (2) using a Pascal’s triangle strategy from 0 card to 52 cards; and (3) using a concept of possibility—each card has two choices of taking or not-taking, and there are 52 cards total, but null set, so that the possibility is . During the meeting, there were opportunities for Ms. M to investigate the mathematical concept in a deeper way, but it did not yet become conceptual resources as shown in the following audio-recorded meeting transcript excerpt:
“Ms. M: This is solving a simpler version of problem week, so that was what I envision this being approach. And because there are a lot of possibilities, there are 52 cards and many things that card could be, 52 things card could be, so.Researcher (R)1: To clarify the problem, does it mean Naoko can pick one at once, and there are 52 kinds of cards?R2: Right, you’re on the way to prove in the very complex combinatorial identity, which is the way I first approach to this problem, and then, when, you know, there is an easy way.Ms. M: And I don’t know the way.R2: Oh, okay.Ms. M: What was your first thought?R2: First thought was combinatory. Sum of quotients of factorials (ways to pick up 1 card, ways to pick up 2 cards, … ways to pick up 52 cards).Second thought was 252 −1. Basic question at play: How many subsets does a set of n elements have? Notice that every time you add an element, you double the number of subsets. But the card problem doesn’t count the null set, so subtract 1.Ms. M: Well, what I will show to students is the patterns of Pascal’s triangle that I introduced last week in class.R1: And, well, there is another way to approach this problem. We can choose the first card or not, and also can choose the second card or not, and so on. Then, we have 252 cases. And then, we can subtract one case, null set.Ms. M: Okay, but I don’t understand the way.”
Ms. M and PLC members also had a conversation about how challenging the problem was, and it involved some rather complex mathematics. Ms. M responded that her class may not need to go into the deeper mathematics, and she had a way to deal with it—making the problem easier as provided in the textbook. That is, she planned to use Pascal’s triangle with a smaller number than 52 which was provided in the textbook in her teaching.
In sum, researchers provided three approaches to solve the problem, but she simply planned to use a problem-solving strategy. Even though there were professional learning opportunities for her to utilize it in her teaching in these mathematical discussions in the PLC, but these did not become conceptual resources that she could use in her teaching at this point. This, in turn, became a problem of practice in her teaching of the 52-cards pick up problem, as her leading classroom discussion at the second day of teaching with this problem was unsuccessful (Figure 1).
After teaching the 52-cards pick up problem unsuccessfully, she had to teach the lesson the following day with no PLC meeting in between. Thus, Ms. M had an emergent personal conversation with a member of the PLC, who facilitated the conversation by eliciting Ms. M’s initial thoughts on the problem and its challenging aspects, and helped her re-organise her understanding of the mathematical concepts. This can be considered as a PLC meeting, as members of a community of practice gathered and shared a goal—to teach the mathematics problem successfully—and engaged in activities to achieve the goal [11,12].
As this meeting was not a regular meeting that we were usually prepared for with audio-recording, but an impromptu meeting, the original conversation was not recorded. Instead, immediately after the conversation, the member who facilitated the conversation reflected on what they had discussed and how they resolved the problem of teaching practice, and this reflection was audio-recorded. Below is an excerpt from the community member—the facilitator’s reflection on the conversation:
“We discussed how she (Ms. M) was seeing the problem and how to organise her thinking. She was seeing it as starting from one card, then two, then three, etc., and she was also seeing the pattern of doubling. We then discussed how we could explain why the pattern was doubling, and how to organise the students’ answers.We drew out several tables of combinations and looked at what changed when an additional card was added. We looked at several ways to organise her thinking. The students were thinking about ways to pick up one card, two cards, etc., in the context of 10 cards. She realised that it was easier to start with all combinations of one card, then build to all combinations of two cards etc.In showing the doubling, her goal was to help the students make sense of the problem, to organise their lists so that they could see that they still had the original list, plus each combination in the original list with the new card added in. Thus, through recursion, we were able to establish this formula and since the problem does not allow for the null pick-up case, the final formula is . We were clear that students could do this without understanding how to explicitly generate each of the subsets.”
During this personal conversation, the problem of teaching practice, which she noticed that her class’s ways of seeing the pattern with 10 cards was not helpful to solve the 52 cards problem or even 10 cards problem successfully, finally transformed into a conceptual resource. In this impromptu meeting, in contrast to the previous PLC meeting described above, Ms. M tried to fully investigate the structure and concept of the mathematics and to reorganize the students’ ways of thinking. She drew out tables of the combinations based on the students’ ideas, and she noticed a better approach to the problem—starting with all combinations of each card. She also investigated with the researcher how to make students access the concept of the combinations and drew a formula of .
The previous PLC meeting may also provide her professional opportunities to learn, and it could be connected to this impromptu meeting, so this aspect should be further investigated. To answer the first research question, fully engaging in the socially organised discussion between two members (or other members) helped the problem of practice finally become conceptual resources, including mathematical concepts and pedagogical approaches to the concept [37], that Ms. M could utilise it in her next day’s teaching. By discussing the problem of practice with others, various conceptual resources (e.g., content knowledge of and pedagogical approaches to this concept) were created and shared during the process of reproducing the participant teacher’s knowledge. The conceptual resources were finally accessed and used by Ms. M when she made a connection from shared goals and knowledge among members of the community of practice to her problems of teaching practice.
4.3. Use of Conceptual Resources in Classroom Teaching
On the following day, Ms. M took a different approach to the 52-card problem. She gave students 10 fixed cards (i.e., A, 1, 2, …, 9) and began with all combinations of one card to pick-up, two cards to pick-up, and so on, as she had learned from the conversation with the researcher. Her students were finally able to figure out the patterns and formula of the combination, and that the final answer to the problem was . The excerpt below describes how Ms. M used the conceptual resources so that led the classroom discussion of the card pick up problem successfully.
“Ms. M: Let’s see if we can make sense of that. Has anybody got the list for the four cards?(Students raised hands and Ms. M quietly checked their answers in their notebooks.)Ms. M: Nice, nice. How many did you end up with? (Two students raised hands.)Okay, so we have two people, JL and JD so far, who have 16 possibilities for four cards. Isn’t that what the prediction was?All right. So, I want to propose something to you. So, show me eye both in the where I’m pointing, please.Okay, so when we have three cards, we could pick up none, but what happens if we add 4 to this? What happens if we add 4 to nothing? What happens if we add 4 with an Ace?So, you used to have an Ace with the 2, and now you can have an Ace, 2, and the 4.Now you can have… [A, 2, 3, 4] (Ms. M writes A, 2, 3, 4), Ace with the 3?Now you can have… [A, 3, 4] (Ms. M writes A, 3, 4).We used to have a 2 and a 3? (Ms. M writes 2, 3, 4).We used to have a 3. (Ms. M writes 3, 4).Total number of possibilities?Yeah, now, we have enough cases of both to really see a pattern.You got it is going to be 16 and it is. (…)We have 2 possibilities, 4 possibilities, 8 possibilities, 16 possibilities, 32 possibilities, and then what?Student: There are 64 possibilities.Ms. M: 64 possibilities, possible thing you could have eaten?Students: Yeah.Ms. M: I’d like to get some justification for that. Where does 64 come from? I’d like to hear from DC, please.DC: Uhm, 32 plus 32.Ms. M: She said, 32 plus 32. So, back to this pattern, your discover earlier of the two plus plus two is four, the four plus four is eight. That eight plus eight is sixteen. The sixteen plus sixteen is thirty-two. Thirty-two plus thirty-two is sixty-four, and what? Comes next with CR.CR: So, for the seven cardsMs. M: Yes, please.CR: 128.(Ms. M then facilitated whole class discussion on how to arrive at a power of 2 and express it in an abbreviated way.)”
Ms. M accomplished the goals for both her teaching and learning using the conceptual resources. The observation also helped ascertain how the mediator transformed instructional dilemmas into successful teaching practices. Answering the second research question, the classroom observation enabled us to understand how Ms. M used applied conceptual resources or re-organised knowledge from PLC to her teaching. Additionally, the interrelated discussions of two members of the community engaged in joint activity and Ms. M’s cognitive development with achieving the goal were observed.
5. Summary and Conclusions
Ms. M was regarded as a highly proficient teacher in her school district, and she intentionally chose the 52-cards pick up problem to teach how making an easier problem strategy works to solve more complicated problem. However, the 52-cards pick up problem itself was challenging both to the middle school students and to Ms. M, the teacher. Not having a profound understanding of the mathematical idea, it became a problem of practice or teaching dilemma while teaching it to the 7th grade students. We also observed how the problem of teaching practice could or could not become conceptual resources in two different learning community meetings.
The problem of practice was challenging to her, but ultimately it could be a good opportunity for her to make and access conceptual resources about this problem of teaching practice. By engaging in discussions or other socially organized activities in the PLC meetings, members of the community of practice developed rich conceptual resources that Ms. M could utilise in the classroom. That is, the problem of practice could become a conceptual resource for Ms. M to think various ways of solving the combinatory problem and to learn to teach complex mathematical concept to younger students, when she made a connection between the problem of the teaching practice and shared goals and knowledge among other members of community of practice.
In terms of cognitive development, these resources give the teacher pedagogical insights and reorganize her knowledge. The teacher then implements the reconstructed knowledge and insights in her teaching so that she could accomplish the goal. This process is repeated as the teacher engages in and across two Communities of Practices. This can be illustrated in Figure 2, in which “a teacher” highlighted dilemmas or problems of practice from daily classroom teaching that she wanted to share with members of her teacher learning community or PD sessions. Although teachers live in multiple communities of practice, such as their classrooms and schools, and in communities outside school (e.g., workshops, professional development, and university courses), in this figure I focus specifically on classrooms and the PLC involving PD sessions, as the work and learning environments are the two most salient communities for a teacher attempting to improve his/her practice.
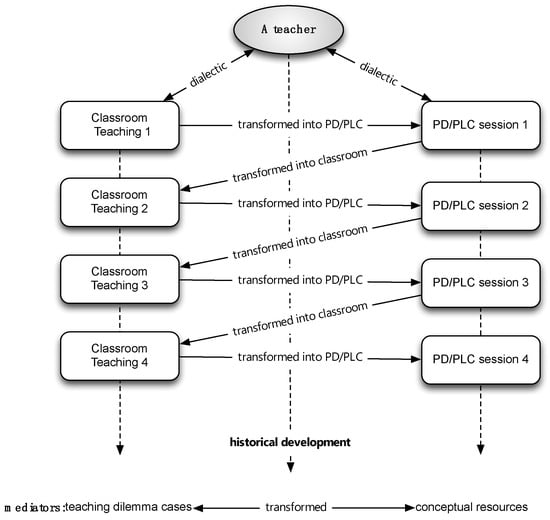
Figure 2.
Teacher learning across PD/PLC (Professional Development/Professional Learning Communities) and classroom contexts using mediators.
The dotted arrows at the bottom of Figure 2 refer to the teacher’s learning and developmental trajectory, situated in each context. Learning and development occur over time, and they are situated in either the teacher’s classroom settings or PLC/PD sessions. That is, the phenomenon of teacher learning through ongoing PD sessions and PLC meetings is not unidirectional but, rather, dialectic: Teacher learning and the work of teaching are intertwined. Investigating two research questions in this study required a new approach to teacher learning, and it provides a possibility of teacher learning across these two contexts by connecting them with a mediator—a problem of teaching practice becoming conceptual resources—to coordinate multiple perspectives.
6. Discussion and Future Direction
Ms. M presented her teaching dilemma in terms of her lack of familiarity with the subject matter and student learning, which was then discussed with others in the learning community. Through communal discussions to resolve the dilemma, conceptual resources were created and shared by reconstructing the teachers’ knowledge. This illustrated the potential of the application of a sociocultural development approach to the social propaganda of forms or functions, focusing on how the teaching dilemma became a conceptual resource in the process of communication between the teacher and PLC members. Ms. M was then able to apply these conceptual resources to her teaching practice. Using classroom observations, her instructions were analysed to ascertain how the conceptual resources transformed instructional dilemmas into successful teaching practices (i.e., the microgenetic development approach).
The gap between the two contexts was bridged when Ms. M transformed her dilemma through participation in the learning community. The methodology used in this study also allows longitudinal aspects to be analysed in future research, and enabling the researchers to re-visit Ms. M’s teaching in both similar and different lessons in subsequent years, and to trace the development of her instructional strategies and knowledge. These new developments could be observed by tracing the transformative relationships between the teaching dilemma and conceptual resources across contexts due to microgenetic and sociogenetic processes (i.e., the ontogenetic development approach). This coordinated approach has yielded the possibility of investigating teacher development and learning within and across multiple contexts, so that we can trace how learning is transformed into instructional practice and how instructional practices are transformed into learning resources within a learning community, shedding light on the investigation into the mechanisms of teacher learning and development bridging classrooms and learning communities.
Further studies tracing how teaching dilemmas are discussed in PD/PLC will provide valuable contributions to the field, as will studying the trajectory of this approach in the learning community and its deployment in the classroom. Methodologically, we should conduct careful observations not only of PLCs, but also of classroom instruction, and analyse these aspects using multiple coordinated units of analysis, which may prove challenging as the data for analysis can be substantial. Thus, although teacher learning linked to classroom practice is more complicated than student learning in classroom contexts alone, the analytical approach proposed provides us with valuable insights into teacher learning across contexts. When we examine how teachers grow as they participate in either classrooms or learning communities, coordinating multiple foci of analysis facilitates understanding the links between the two contexts. We can perform: (a) Fine-grained analyses of the development of individual teachers’ goal-oriented construction; (b) analyses of collective practices—how individuals interact in the process of accomplishing their goals—over time, and (c) analyses of how individuals and socially organized activities interplay across multiple contexts. Moreover, the foregrounded approach can be changed based on the research purposes. The next step is to conduct further empirical studies to follow up on this suggestion.
Further research on teacher learning in PLCs where teaching practice is linked to learning activity is required. Due to the necessity for teachers to bridge their learning in PD/PLC and classroom, this article suggests linking these contexts not only for research, but also for practice, by using different types of teaching dilemma cases (e.g., interview, video-clips, students’ work, or lesson plans) as effective mediators for teachers to plan, implement, and reflect on classroom teaching in PD or PLC contexts.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted according to the guidelines of the Declaration of Helsinki, and approved by the Institutional Review Board (or Ethics Committee) of University of California, Berkeley, protocol number 2010-01-492 (02/02/2010).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data sharing is not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Borko, H.; Jacobs, J.; Eiteljorg, E.; Pittman, M.E. Video as a tool for fostering productive discussions in mathematics professional development. Teach. Teach. Educ. 2008, 24, 417–436. [Google Scholar] [CrossRef]
- Kazemi, E.; Hubbard, A. New directions for the design and study of professional development: Attending to the coevolution of teachers’ participation across contexts. J. Teach. Educ. 2008, 59, 428–441. [Google Scholar] [CrossRef]
- Lampert, M. Teaching Problems and the Problems of Teaching; Yale University Press: New Haven, CT, USA, 2001. [Google Scholar]
- Sherin, M.G. When teaching becomes learning. Cogn. Instr. 2002, 20, 119–150. [Google Scholar] [CrossRef]
- Horn, I.S.; Kane, B.D. Opportunities for professional learning in mathematics teacher workgroup conversations: Relationships to instructional expertise. J. Learn. Sci. 2015, 24, 373–418. [Google Scholar] [CrossRef]
- Little, J.W. Locating learning in teachers’ communities of practice: Opening up problems of analysis in records of everyday work. Teach. Teach. Educ. 2002, 18, 917–946. [Google Scholar] [CrossRef]
- McLaughlin, M.W.; Talbert, J.E. Professional Communities and the Work of High. School Teaching; University of Chicago Press: Chicago, IL, USA, 2001. [Google Scholar]
- DuFour, R.; Fullan, M. Cultures Built to Last: Systemic PLCs at Work; Solution Tree Press: Bloomington, IN, USA, 2012. [Google Scholar]
- Hord, S.M. Learning Together, Leading Together: Changing Schools through Professional Learning Communities; Teachers College Press & NSDC: New York, NY, USA, 2004. [Google Scholar]
- Lieberman, A.; Miller, L. Teachers in Professional Communities: Improving Teaching and Learning; Teachers College Press: New York, NY, USA, 2008. [Google Scholar]
- Lave, J.; Wenger, E. Situated Learning: Legitimate Peripheral Participation; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Wenger, E. Communities of Practice: Learning, Meaning, and Identity; Cambridge University Press: New York, NY, USA, 1998. [Google Scholar]
- Grossman, P.; Wineburg, S.; Woolworth, S. What Makes Teacher Community Different from a Gathering of Teachers? (Occasional Paper); University of Washington, Centre for the Study of Teaching and Policy: Seattle, WA, USA, 2000. [Google Scholar]
- Wilson, S.M.; Berne, J. Teacher learning and the acquisition of professional knowledge: An examination of research on contemporary professional development. Rev. Res. Educ. 1999, 24, 173–209. [Google Scholar] [CrossRef]
- Grossman, P.; Wineburg, S.; Woolworth, S. Toward a theory of teacher community. Teach. Coll. Rec. 2001, 103, 942–1012. [Google Scholar] [CrossRef]
- Horn, I.S. Learning on the job: A situated account of teacher learning in high school mathematics departments. Cogn. Instr. 2005, 23, 207–236. [Google Scholar] [CrossRef]
- McLaughlin, M.W.; Talbert, J.E. Building School-Based Teacher Learning Communities: Professional Strategies to Improve Student Achievement; Teachers College Press: New York, NY, USA, 2006. [Google Scholar]
- Talbert, J.E. Professional learning communities at the crossroads: How systems hinder or engender change. In Second International Handbook of Educational Change; Hargreaves, A., Lieberman, A., Fullan, M., Hopkins, D., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 2010; pp. 555–571. [Google Scholar]
- Horn, I.S.; Little, J.W. Attending to problems of practice: Routines and resources for professional learning in teachers’ workplace interactions. Am. Educ. Res. J. 2010, 47, 181–217. [Google Scholar] [CrossRef]
- Sherin, M.G.; Han, S.Y. Teacher learning in the context of a video club. Teach. Teach. Educ. 2004, 20, 163–183. [Google Scholar] [CrossRef]
- van Es, E.A.; Sherin, M.G. How different video club designs support teachers in “learning to notice”. J. Comput. Teach. Educ. 2006, 22, 125–135. [Google Scholar]
- Gearhart, M.; Saxe, G.B. When teachers know what students know: Integrating mathematics Assessment. Theory Pract. 2004, 43, 304–313. [Google Scholar] [CrossRef]
- Kazemi, E.; Franke, M.L. Teacher learning in mathematics: Using student work to promote collective inquiry. J. Math. Teach. Educ. 2004, 7, 203–235. [Google Scholar] [CrossRef]
- Lin, P.J. On enhancing teachers’ knowledge by constructing cases in classrooms. J. Math. Teach. Educ. 2002, 5, 317–349. [Google Scholar] [CrossRef]
- Horn, I.S. Teaching replays, teaching rehearsals, and re-visions of practice: Learning from colleagues in a mathematics teacher community. Teach. Coll. Rec. 2010, 112, 225–259. [Google Scholar]
- Ball, D.L.; Cohen, D.K. Developing practice, developing practitioners: Toward a practice-based theory of professional education. Teaching as the Learning Profession: Handbook of Policy and Practice; Sykes, G., Darling-Hammond, L., Eds.; Jossey Bass: San Francisco, CA, USA, 1999; pp. 3–32. [Google Scholar]
- Kim, H.; Metzger, M.; Heaton, R.M. Teacher planning sessions as professional opportunities to learn: An elementary mathematics teacher ’s re-conceptualization of instructional triangles. Int. J. Sci. Math. Educ. 2020, 18, 1207–1227. [Google Scholar] [CrossRef]
- Borko, H.; Peressini, D.; Romagnano, L.; Knuth, E.; Willis-Yorker, C.; Wolley, C.; Hovermill, J.; Masarik, K. Teacher education does matter: A situative view of learning to teach secondary mathematics. Educ. Psychol. 2000, 35, 196–206. [Google Scholar] [CrossRef]
- Cobb, P.; Bowers, J. Cognitive and situated learning perspectives in theory and practice. Educ. Res. 1999, 28, 4–15. [Google Scholar] [CrossRef]
- Greeno, J.G. Situative research relevant to standards for school mathematics. A Research Companion to Principles and Standards for School Mathematics; Kilpatric, J., Martin, W.G., Schifter, D., Eds.; National Council of Teachers of Mathematics: Reston, VA, USA, 2003; pp. 304–332. [Google Scholar]
- Putnam, R.T.; Borko, H. What do new views of knowledge and thinking have to say about research on teacher learning? Educ. Res. 2000, 29, 4–15. [Google Scholar] [CrossRef]
- Levine, T.H. Tools for the study and design of collaborative teacher learning: The affordances of different conceptions of teacher community and activity theory. Teach. Educ. Q. 2010, 37, 109–130. [Google Scholar]
- Rogoff, B. Observing sociocultural activity on three planes: Participatory appropriation, guided participation, and apprenticeship. In Sociocultural Studies of Mind; Wertsch, J.V., del Rio, P., Alvarez, A., Eds.; Cambridge University Press: Cambridge, UK, 1995; pp. 139–164. [Google Scholar]
- Rogoff, B. The Cultural Nature of Human Development; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Saxe, G.B. Cultural Development of Mathematical Ideas: Papua New Guinea Studies; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Miles, M.B.; Huberman, A.H. Qualitative Data Analysis: An Expanded Sourcebook; Sage Publications: Thousand Oaks, CA, USA, 1994. [Google Scholar]
- Kim, H. Pedagogical knowledge, pedagogical content knowledge, and content knowledge for teaching mathematics: How do they shape a proficient teachers’ practice when teaching new content. In Proceedings of the 12th International Congress on Mathematical Education, Seoul, Korea, 8−15 July 2012. [Google Scholar]
- Yin, R.K. Case Study Research: Design and Methods, 4th ed.; Sage publications, Inc.: Thousand Oaks, CA, USA, 2009; Volume 5. [Google Scholar]
- Menanix, S.E. Teaching for a Growth Mindset: How Contexts and Professional Identity Shift Decision-Making. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2015. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).