A Visual Approach for Solving Problems with Fractions
Abstract
:1. Introduction
2. Visual Approaches to Problem Solving
3. Problem Solving and Rational Numbers
3.1. Discussing the Concept of Rational Number
3.2. Visual Strategies for Solving Problems with Fractions
3.3. Some Potentialities of Visual Solutions
4. Method
5. Preliminary Results and Discussion
5.1. Task 4
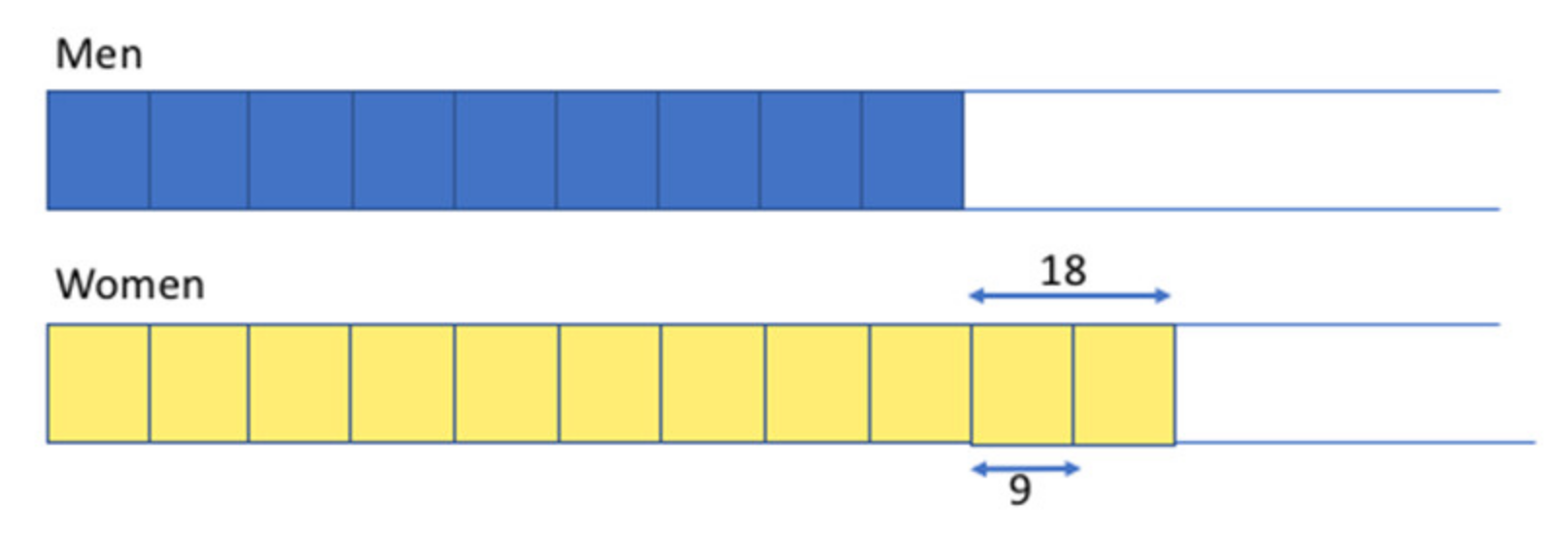
5.2. Task 5
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A


References
- Moss, J.; Case, R. Developing children’s understanding of the rational numbers: A new model and an experimental curriculum. J. Res. Math. Educ. 1999, 30, 122–147. [Google Scholar] [CrossRef] [Green Version]
- Pólya, G. How to Solve it: A New Aspect of Mathematical Method; Princeton University Press: Princeton, NJ, USA, 1945. [Google Scholar]
- Presmeg, N. Creative advantages of visual solutions to some non-routine mathematical problems. In Proceedings of the Problem@Web International Conference: Technology, Creativity and Affect in Mathematical Problem Solving, Faro, Portugal, May 2014; Carreira, S., Amado, N., Jones, K., Jacinto, H., Eds.; Universidade do Algarve: Faro, Portugal, 2014; Available online: https://sapientia.ualg.pt/handle/10400.1/3750 (accessed on 12 October 2021).
- Vale, I.; Pimentel, T.; Barbosa, A. The power of seeing in problem solving and creativity: An issue under discussion. In Broadening the Scope of Research on Mathematical Problem Solving: A Focus on Technology, Creativity and Affect; Amado, N., Carreira, S., Jones, K., Eds.; Springer: Cham, Switzerland, 2018; pp. 243–272. [Google Scholar]
- Tripathi, P.; Case, R. Developing mathematical understanding through multiple representations. Math. Teach. Middle Sch. 2008, 13, 438–445. [Google Scholar] [CrossRef]
- National Council of Teachers of Mathematics. Principles to Actions: Ensuring Mathematical Success for All; NCTM: Reston, VA, USA, 2014. [Google Scholar]
- Stylianou, D.; Silver, E. The role of visual representations in advanced mathematical problem solving: An examination of expert-novice similarities and differences. Math. Think. Learn. 2004, 6, 353–387. [Google Scholar] [CrossRef]
- Bruner, J. Toward a Theory of Instruction; Harvard University Press: Cambridge, MA, USA, 1966. [Google Scholar]
- Behr, M.; Harel, G.; Post, T.; Lesh, R. Rational number, ratio and proportion. In Handbook on Research of Teaching and Learning; Grouws, D., Ed.; McMillan: New York, NY, USA, 1992; pp. 296–333. [Google Scholar]
- Lesh, R.; Post, T.; Behr, M. Representations and translations among representations in mathematics learning and problem solving. In Problems of Representation in the Teaching and Learning of Mathematics; Javier, C., Ed.; Erlbaum: Hilsdale, MI, USA, 1987; pp. 33–40. [Google Scholar]
- Vale, I.; Barbosa, A. The importance of seeing in mathematics communication. J. Eur. Teach. Educ. Netw. 2017, 12, 49–63. [Google Scholar]
- Arcavi, A. The role of visual representations in the learning of mathematics. Educ. Stud. Math. 2003, 52, 215–241. [Google Scholar] [CrossRef]
- Woleck, K.R. Listen to their pictures: An investigation of children’s mathematical drawings. In The Roles of Representation in School Mathematics, 2001 Yearbook; Cuoco, A.A., Curcio, F.R., Eds.; NCTM: Reston, VA, USA, 2001; pp. 215–227. [Google Scholar]
- Krutetskii, V.A. The Psychology of Mathematical Abilities in Schoolchildren; University of Chicago Press: Chicago, IL, USA, 1976. [Google Scholar]
- Bailey, D.H.; Hoard, M.K.; Nugent, L.; Geary, D.C. Competence with fractions predicts gains in mathematics achievement. J. Exp. Child Psychol. 2012, 113, 447–455. [Google Scholar] [CrossRef] [Green Version]
- Pinto, H. O Desenvolvimento do Sentido da Multiplicação e da Divisão de Números Racionais. Ph.D. Thesis, Instituto de Educação da Universidade de Lisboa, Lisboa, Portugal, 2011. [Google Scholar]
- Behr, M.; Lesh, R.; Post, T.; Silver, E. Rational number concepts. In Acquisition of Mathematics Concepts and Processes; Lesh, R., Landau, M., Eds.; Academic Press: New York, NY, USA, 1983; pp. 92–126. [Google Scholar]
- Kieren, T. On the mathematical, cognitive and instructional foundations of rational numbers. In Number and Measurement: Papers from a Research Workshop; Lesh, R., Bradbard, D., Eds.; ERIC/SMEAC: Columbus, OH, USA, 1976; pp. 101–144. [Google Scholar]
- Lamon, S.J. Rational numbers and proportional reasoning: Toward a theoretical framework for research. In Second Handbook of Research on Mathematics Teaching and Learning, National Council of Teachers of Mathematics; Lester, F.K., Ed.; Information Age Publishing: Charlotte, NC, USA, 2007; pp. 629–668. [Google Scholar]
- Van den Heuvel-Panhuizen, M. The didactical use of models in realistic mathematics education: An example from a longitudinal trajectory on percentage. Educ. Stud. Math. 2003, 54, 9–35. [Google Scholar] [CrossRef]
- Cramer, K.; Wyberg, T. Efficacy of Different Concrete Models for Teaching the Part-Whole Construct for Fractions. Math. Think. Learn. 2009, 11, 226–257. [Google Scholar] [CrossRef]
- Owens, D.T. Study of the relationship of area concept and learning concepts by children in grades three and four. In Recent Research on Number Concepts, National Council of Teachers of Mathematics; Kieren, T.E., Ed.; ERIC/SMEAC: Columbus, OH, USA, 1980; pp. 629–668. [Google Scholar]
- Siegler, R.S.; Thompson, C.A.; Schneider, M. An Integrated Theory of Whole Number and Fractions Development. Cognitive Psychol. 2011, 62, 273–296. [Google Scholar] [CrossRef]
- Ng, S.F.; Lee, K. The model method: Singapore children’s tool for representing and solving algebraic word problems. J. Res. Math. Educ. 2009, 40, 282–313. [Google Scholar] [CrossRef]
- Beckman, S. Solving algebra and other story problems with simple diagrams: A method demonstrated in grade 4-6 texts used in Singapore. Math. Educ. 2004, 14, 42–46. [Google Scholar]
- Gravemeijer, K. What makes mathematics so difficult, and what can we do about it? In Educação Matemática: Caminhos e Encruzilhadas; Santos, L., Canavarro, A.P., Brocardo, J., Eds.; APM: Lisboa, Portugal, 2005; pp. 83–101. [Google Scholar]
- D’Ambrosio, B.S.; Mewborn, D.S. Children’s constructions of fractions and their implications for classroom instruction. J. Res. Math. Educ. 1994, 8, 150–161. [Google Scholar] [CrossRef]
- Uttal, D.H.; O’Doherty, K.; Newland, R.; Hand, L.L.; DeLoache, J. Dual Representation and the Linking of Concrete and Symbolic Representations. Child Dev. Perspect. 2009, 3, 156–159. [Google Scholar] [CrossRef]
- Opfer, J.; Siegler, R. Development of quantitative thinking. In The Oxford Handbook of Thinking and Reasoning; Holyoak, K., Morrison, R., Eds.; Oxford University Press: Oxford, UK, 2012; pp. 585–605. [Google Scholar]
- Gates, P. Social class and the visual in mathematics. In Proceedings of the 8th MES Conference, Portland, OR, USA, 21–26 June 2015; Mukhopadhyay, S., Greer, B., Eds.; Portland State University: Portland, OR, USA, 2015. [Google Scholar]
- Singapore Math. Challenging Word Problems; Marshall Cavandish Education: Hougang, Singapore, 2011. [Google Scholar]
- Vale, I.; Barbosa, A. Mathematical problems: The advantages of visual strategies. J. Eur. Teach. Educ. Netw. 2018, 32, 23–33. [Google Scholar]
- Erickson, F. Qualitative Methods in Research on Teaching. In Handbook of Research on Teaching; Wittrockk, M., Ed.; MacMillan: New York, NY, USA, 1986; pp. 119–161. [Google Scholar]
- Miles, M.; Huberman, A. Qualitative Data Analysis; Sage Publications: Newbury Park, CA, USA, 1994. [Google Scholar]



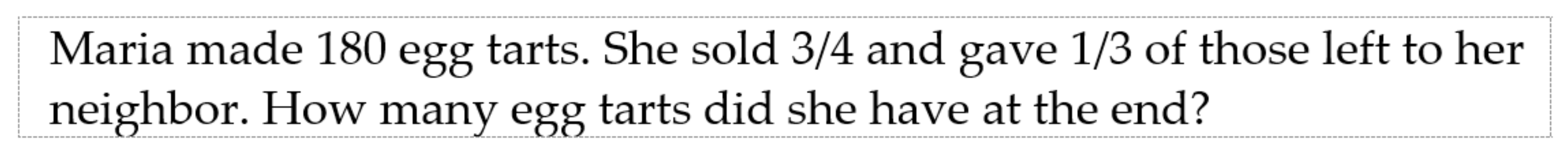
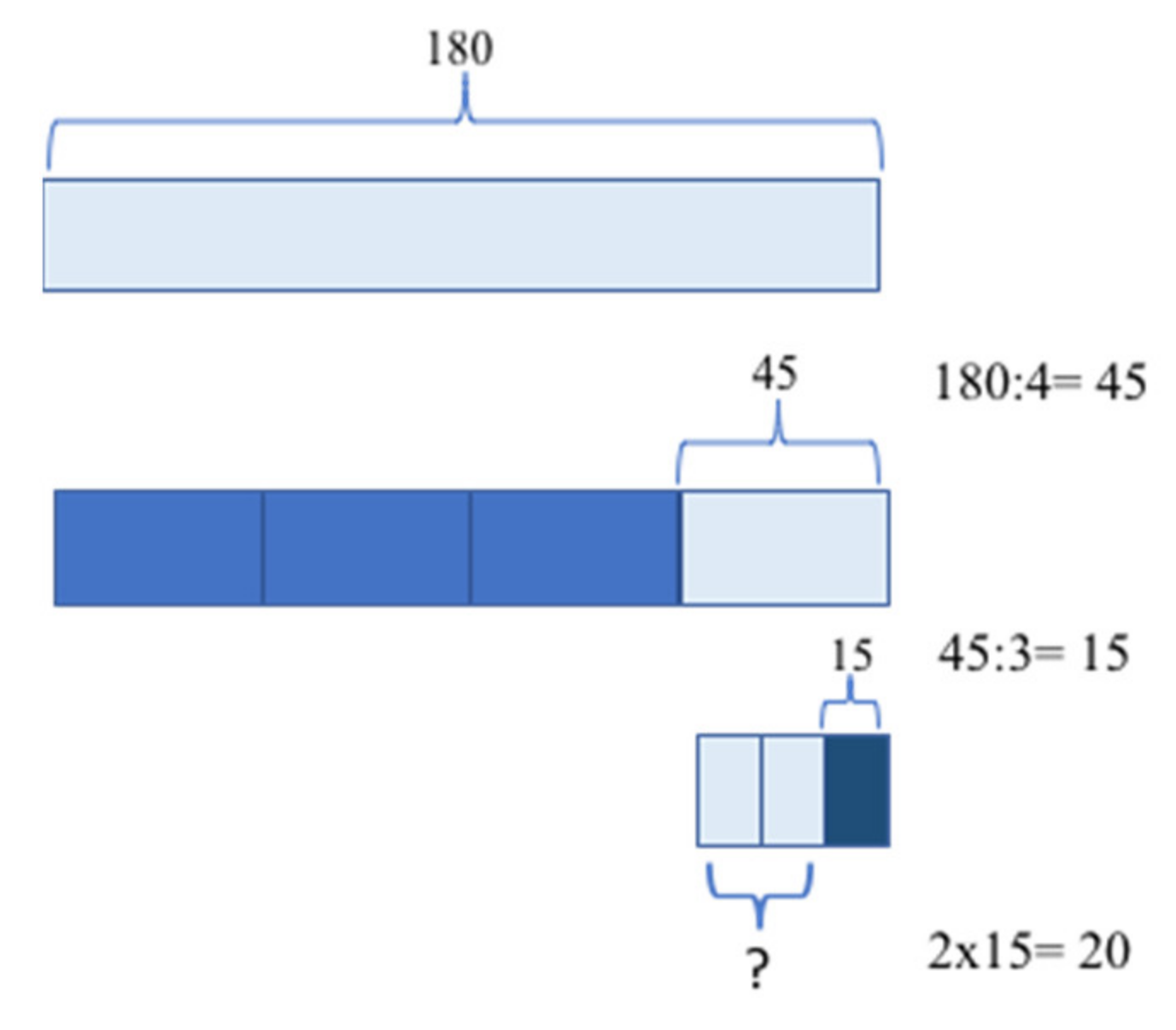

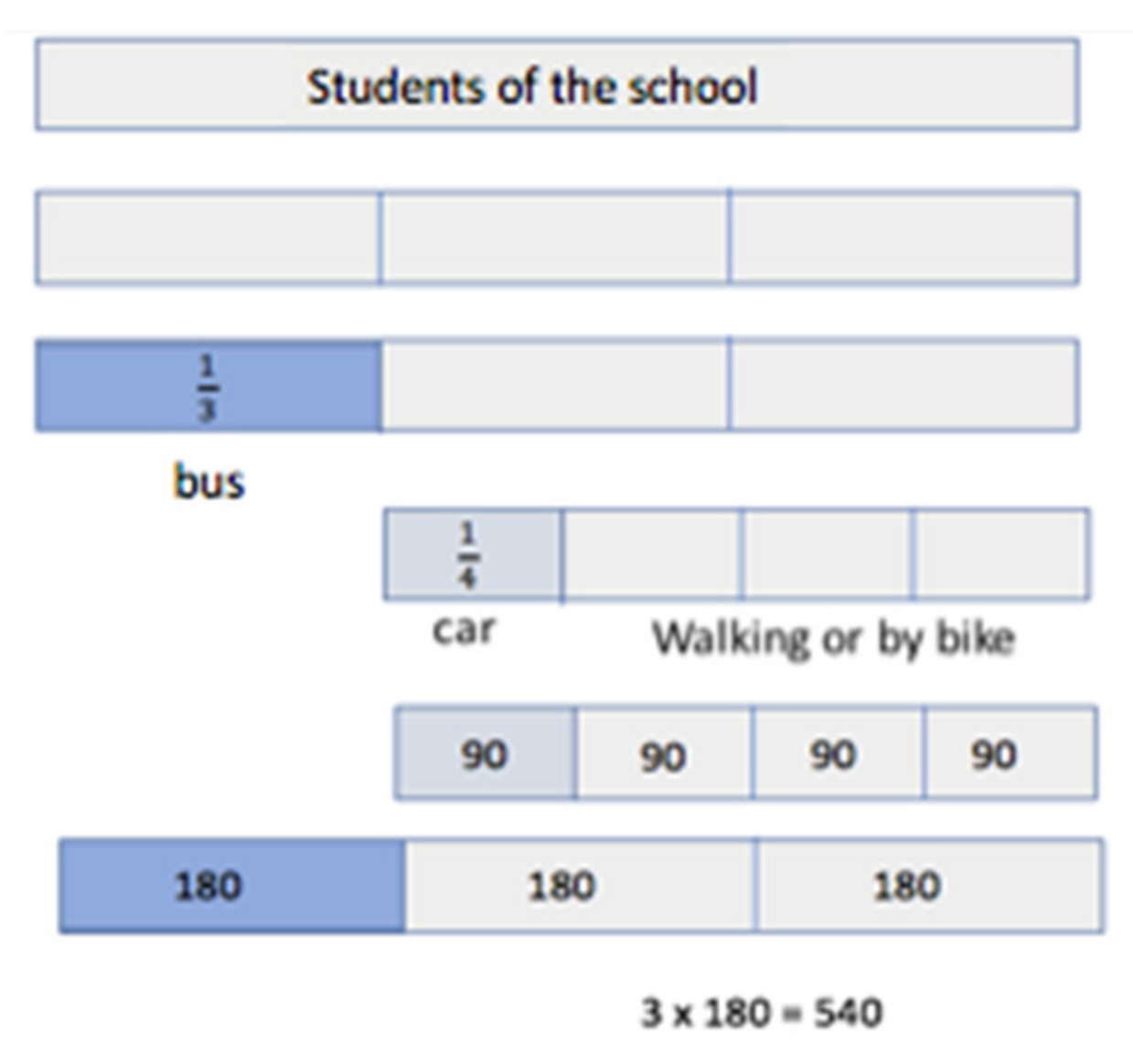
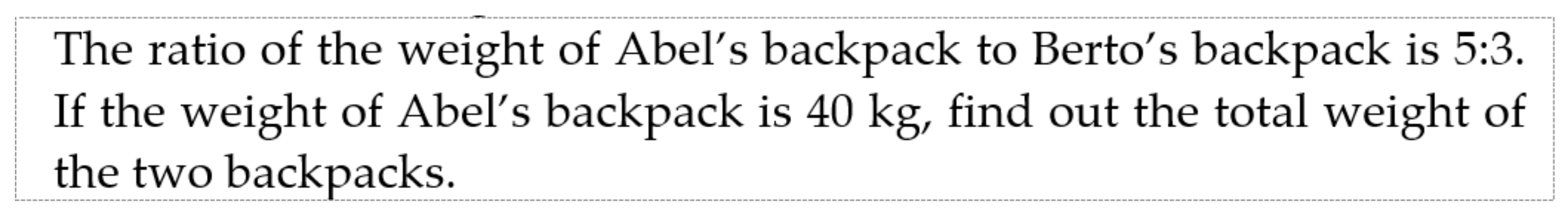

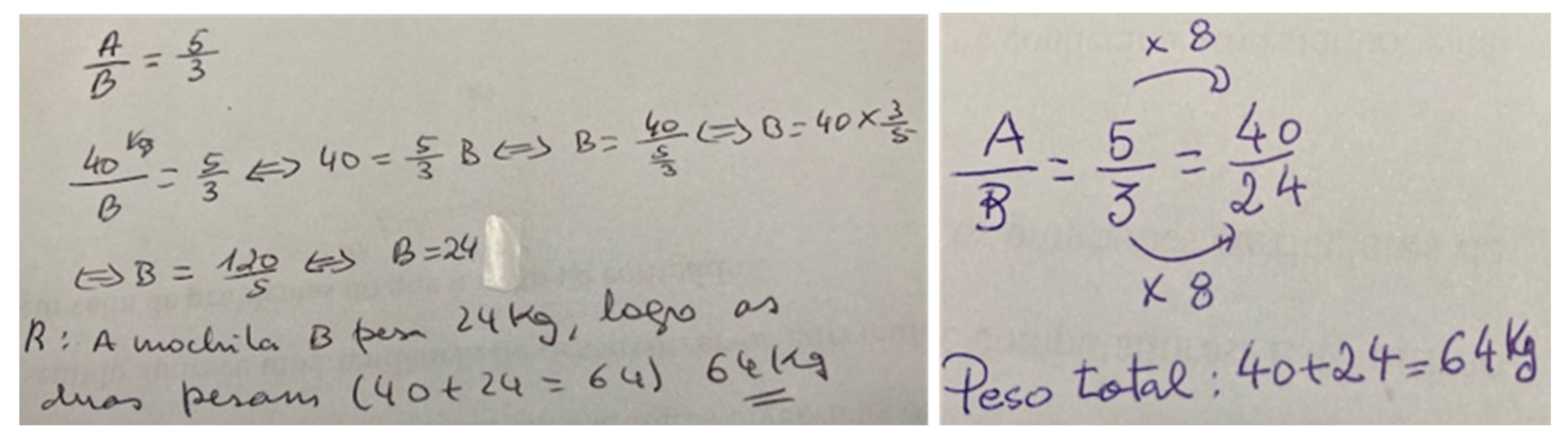





| Before | After | ||||
|---|---|---|---|---|---|
| Problem/Task | Visual Strategies (%) | Non-Visual Strategies (%) | Problem/Task | Visual Strategies (%) | Non-Visual Strategies (%) |
| 1 | 62.5 | 37.5 | 1 | 33 | 67 |
| 2 | 11.1 | 88.9 | 2 | 100 | 0 |
| 3 | 50 | 50 | 3 | 75 | 25 |
| 4 | 10 | 90 | 4 | 36.4 | 63.6 |
| 5 | 0 | 100 | 5 | 44.4 | 55.6 |
| Total | 26.7 | 73.3 | Total | 57.8 | 42.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barbosa, A.; Vale, I. A Visual Approach for Solving Problems with Fractions. Educ. Sci. 2021, 11, 727. https://doi.org/10.3390/educsci11110727
Barbosa A, Vale I. A Visual Approach for Solving Problems with Fractions. Education Sciences. 2021; 11(11):727. https://doi.org/10.3390/educsci11110727
Chicago/Turabian StyleBarbosa, Ana, and Isabel Vale. 2021. "A Visual Approach for Solving Problems with Fractions" Education Sciences 11, no. 11: 727. https://doi.org/10.3390/educsci11110727
APA StyleBarbosa, A., & Vale, I. (2021). A Visual Approach for Solving Problems with Fractions. Education Sciences, 11(11), 727. https://doi.org/10.3390/educsci11110727






