A Theoretical Model for the Development of Mathematical Talent through Mathematical Creativity
Abstract
1. Introduction
Mathematical giftedness is the name we shall give to a unique aggregate of mathematical abilities that opens up the possibility of successful performance in mathematical activity (or with school children in mind, the possibility of a creative mastery of the subject).[9] (p. 77)
Talent that has not yet been developed or evidenced; that is, the potential exists to develop and demonstrate it, but due to one or more factors have been unable to manifest it in action schemes.[12] (p. 27, translation by the author)
- What type of activities foster developing creativity and, hence, mathematical talent?
- What theoretical model allows us to best analyse creative mathematical activity?
- What institutional conditions propel the development of creative mathematical activity?
2. Theoretical Framework
2.1. Definitions: Institution, Praxeology, and Levels of Complexity
2.2. Mathematical Creativity
“(a) the process that results in unusual (novel) and/or insightful solution(s) to a given problem or analogous problems, and/or (b) the formulation of new questions and/or possibilities that allow an old problem to be regarded from a new angle requiring imagination”.(p. 24)
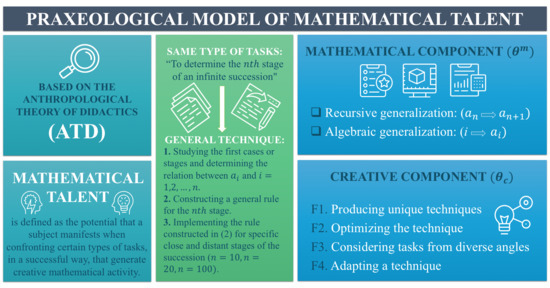
2.3. Praxeological Model of Mathematical Talent (PMMT)
- F1. Producing unique techniques: Faced with a novel task, distinct steps are produced without following a specific routine. Exploring the task presented in relation to that which is already known generates new ideas and leads to constructing new techniques, all guided by the assignment.
- F2. Optimizing the technique: Evaluating a range of possible routes that allow performance of the task, then choosing the “optimal” one as a function of the number of steps and mathematical knowledge involved. This may mean constructing a general rule (verbal, iconic, or alphanumeric) instead of using a series of drawings to determine the properties of an unknown stage in a figural sequence.
- F3. Considering tasks from diverse angles: This means analysing the task without restricting it to a certain domain (such as algebra, geometry, discrete mathematics, etc.), or discipline (physics, chemistry, visual arts, etc.), either by producing steps that permit task execution (recognizing the knowledge that motivated the subject to follow a certain path or to change direction), or generating diverse techniques to perform the same task.
- F4. Adapting a technique: This entails identifying the functioning, scope, and limits of a technique produced in order to implement it on another task after certain modifications. First, the technique must be validated (that is, verifying that its steps make it possible to do what is proposed); second, it needs to be adapted and, perhaps, improved while solving another task.
2.4. Implementing the Praxeological Model
- Studying the first cases or stages and determining the relation between and
- Constructing a general rule for the stage.
- Implementing the rule constructed in (2) for specific close and distant stages of the succession (.
3. The Study
3.1. The Setting and Characteristics of the Institution
3.2. Didactic Design of the MC
4. Results
4.1. Problem Situation 2: Origami Cubes
- Task 2.1: Determine the number of cubes required to construct any stage of the sequence (different sequences of origami cubes were presented).
- Task 2.2: Construct three stages using the origami cubes following a pattern.
| Technique | |
|---|---|
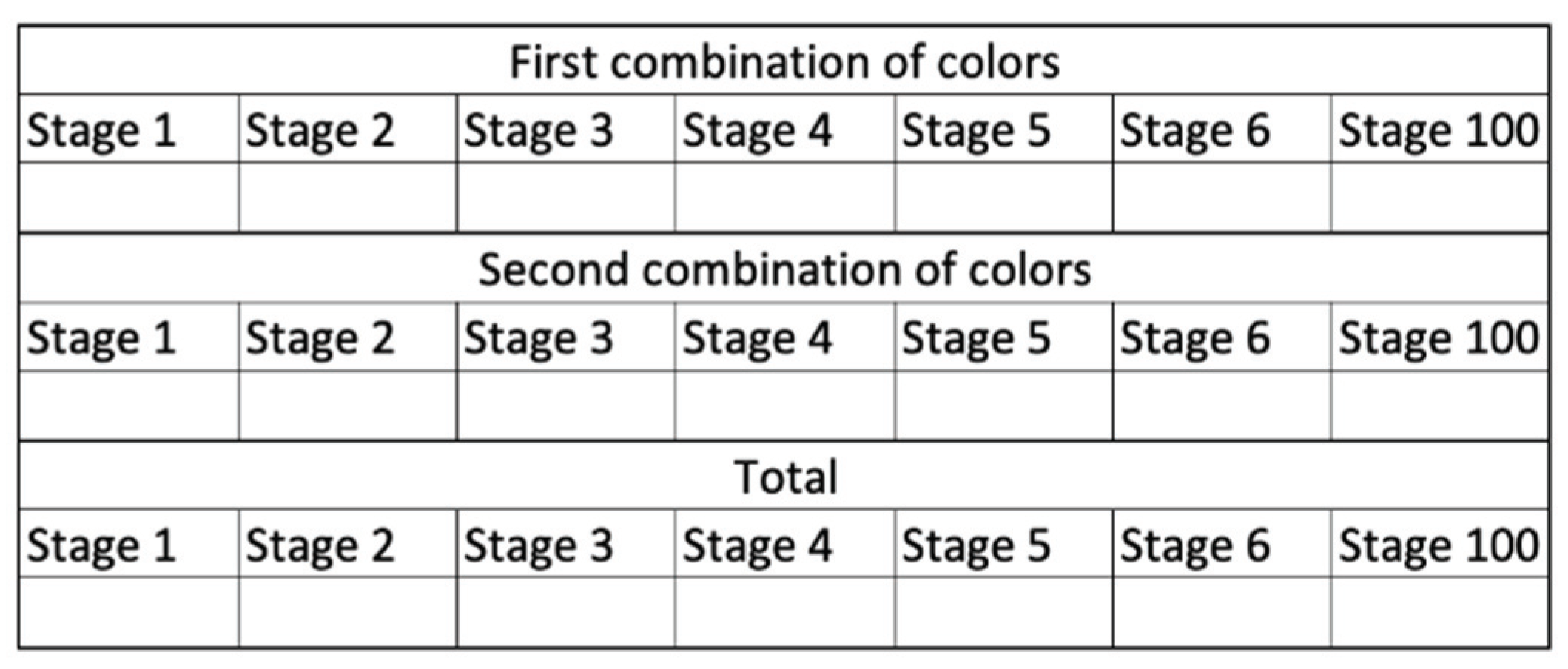
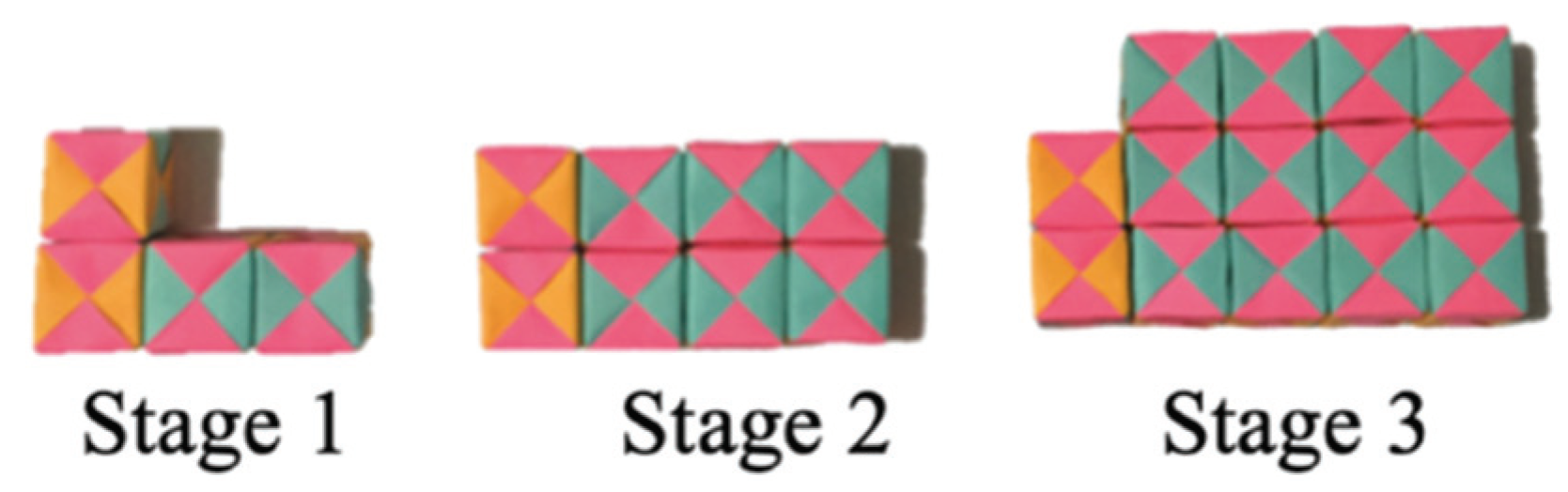
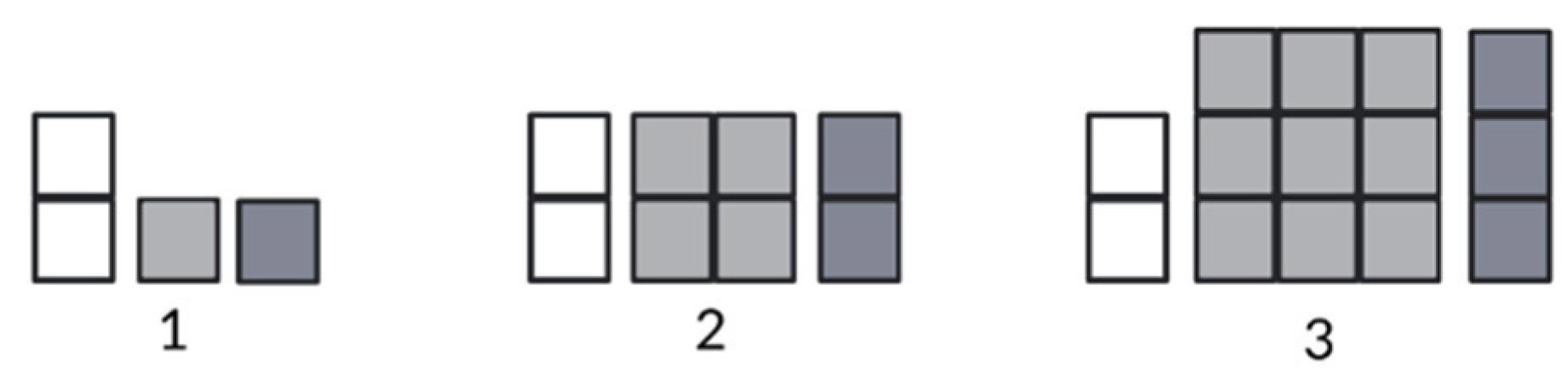
| Step 1. Determine that the first combination (orange/pink) remains unchanged, and place the number 2 in the first combination up to stage 100 (Figure 2). Step 2. Count the cubes in the second combination (blue/pink) and write the numbers 2, 6 and 12, respectively, in the first three cells. Step 3. Identify a pattern based on the stages given and make drawings with squares to represent the cubes for stages 4, 5 and 6 in the two combinations (Figure 3). Step 4: Based on the drawing of stage 6, they made drawings of the increments for n = 7, n = 8, n = 9 and n = 10 (Figure 3). Next they counted and made the sums. Step 5: To obtain the result for stage 100, they multiplied the number of cubes of stage 10 by 10. The instructor asked them to prove this ‘rule of 3’ for stage 9 based on stage 3. After doing so, they abandoned this technique. Later, they returned to their attempt to count the number of cubes using drawings. | On the first three stages, they explored other close ones using drawings, but could not determine a recursive rule per se. They optimized the technique by changing from drawing the complete figure to drawings that show only the increments (F2). They tried to optimize (F2) by adapting a school technique called ‘the rule of 3’ to determine case 100, but failed to solve the task. |
| Technique | Technologies and |
|---|---|
| Step 1. Same as for pair A. Step 2. Same as for pair A. Step 3. Based on the initial stages of the second combination, they determined that stage 1 has 2 cubes, stage 2 has cubes, and stage 3 has cubes. They then departed from the material and made a sum to determine the number of cubes in stage 4: cubes. Step 4. Based on this algebraic rule, they attempted to implement this for , proposing the operation: however, they were unsuccessful in calculating the operation or optimizing their technique. | Based on the initial stages, they constructed an algebraic rule for distant stages as follows: They optimized the technique (F2) by setting the cubes aside and focusing on the sum required to determine the number of cubes in the second combination. |
| Technique | Technologies and |
|---|---|
| Step 1. Same as for pair A. Step 2. They related the origami cubes in combination two to the floors of a building, observing that ‘In stage 1 there are 2 columns of 1 floor, in stage 2 there are 3 columns of 2 floors, in stage 3 there are 4 columns of 3 floors’. Step 3. They determined that stage 4 of combination two has 5 columns of 4 floors. Using this recursive rule, they completed the row of combination two up to stage 100: 101 columns by 100 floors: . Step 4. They noted that in the table (Figure 2) only 2 cubes must be added to the total number of cubes in combination two (Figure 4). They then calculated the sum that corresponds to the total up to stage 100, which is Step 5. Upon the instructor’s indication, they determined another technique to solve the task by identifying that ‘squares’ are formed in combination two and calculating their respective area; that is, for the first stage, a square, for the second, a square, and for the third, a square. They then proposed that to each calculation of the product they needed to add 1 to the first term, 2 to the second, and 3 to the third (Figure 5). They concluded that: ‘the number of the stage is multiplied twice, the new stage is added, and then 2 from the other combination is added’. | Based on the initial stages, they determined an algebraic rule with two equivalent patterns of construction: . To optimize the technique, they generated a novel technique using a known reference; namely, a building to represent the cubes (F1, F2, F4). They produced two different techniques to perform the same task (F3). |
| Technique | Technologies and |
|---|---|
| Step 1. By manipulating the material, they determined that a row of 3 cubes was added between the stage 1 and stage 2 pyramids, and that a row of 4 cubes was added between the stage 2 and stage 3 pyramids (Figure 7). Step 2. Next, they determined that a row of five cubes had to be added below pyramid 4 and, similarly, a row of six cubes had to be added below pyramid 5. Step 3. They determined that calculating the number of cubes of any pyramid of this sequence required totalling the number of cubes of the previous pyramid and the stage + 1 (Figure 8). Using this rule, they constructed a list up to stage . | Based on the initial stages, they determined the following recursive generalization: θ1: They optimized the technique of counting into a recursive technique (F2). |
4.2. Problem Situation 4: Intersections and Regions
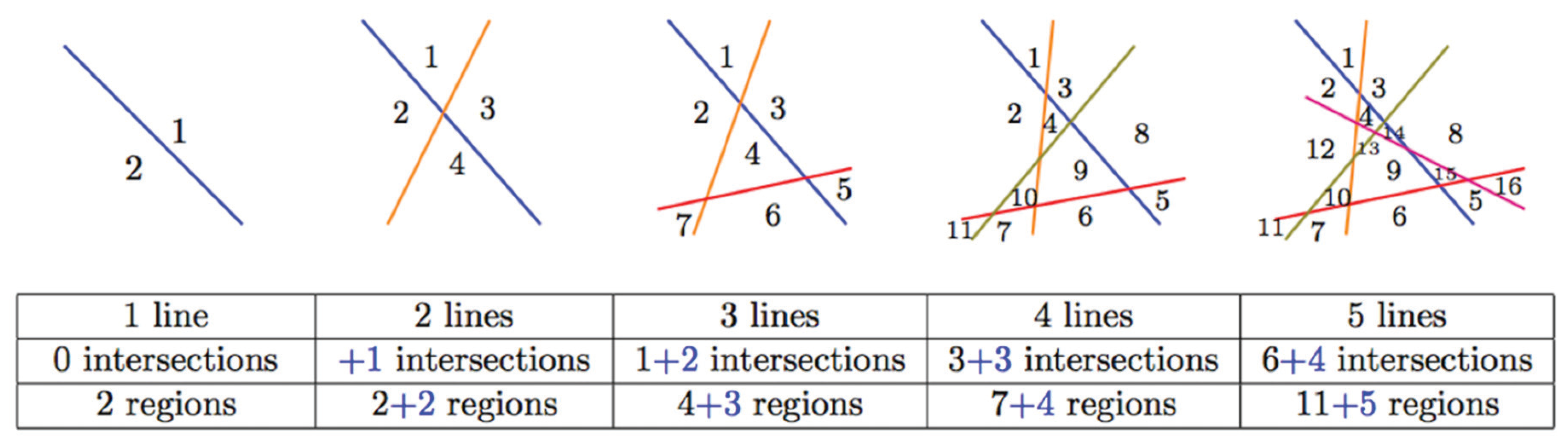
- Determine the number of regions into which a plane is divided by non-parallel lines, where an intersection can only be formed by two lines.
- Task 4.1: Determine the number of intersections formed on the plane when any number of non-parallel lines are placed and only two lines can form an intersection.
- Task 4.2: Determine the number of regions formed on the plane when any number of non-parallel lines are placed and only two lines can form an intersection.
| Technique | Technologies and |
|---|---|
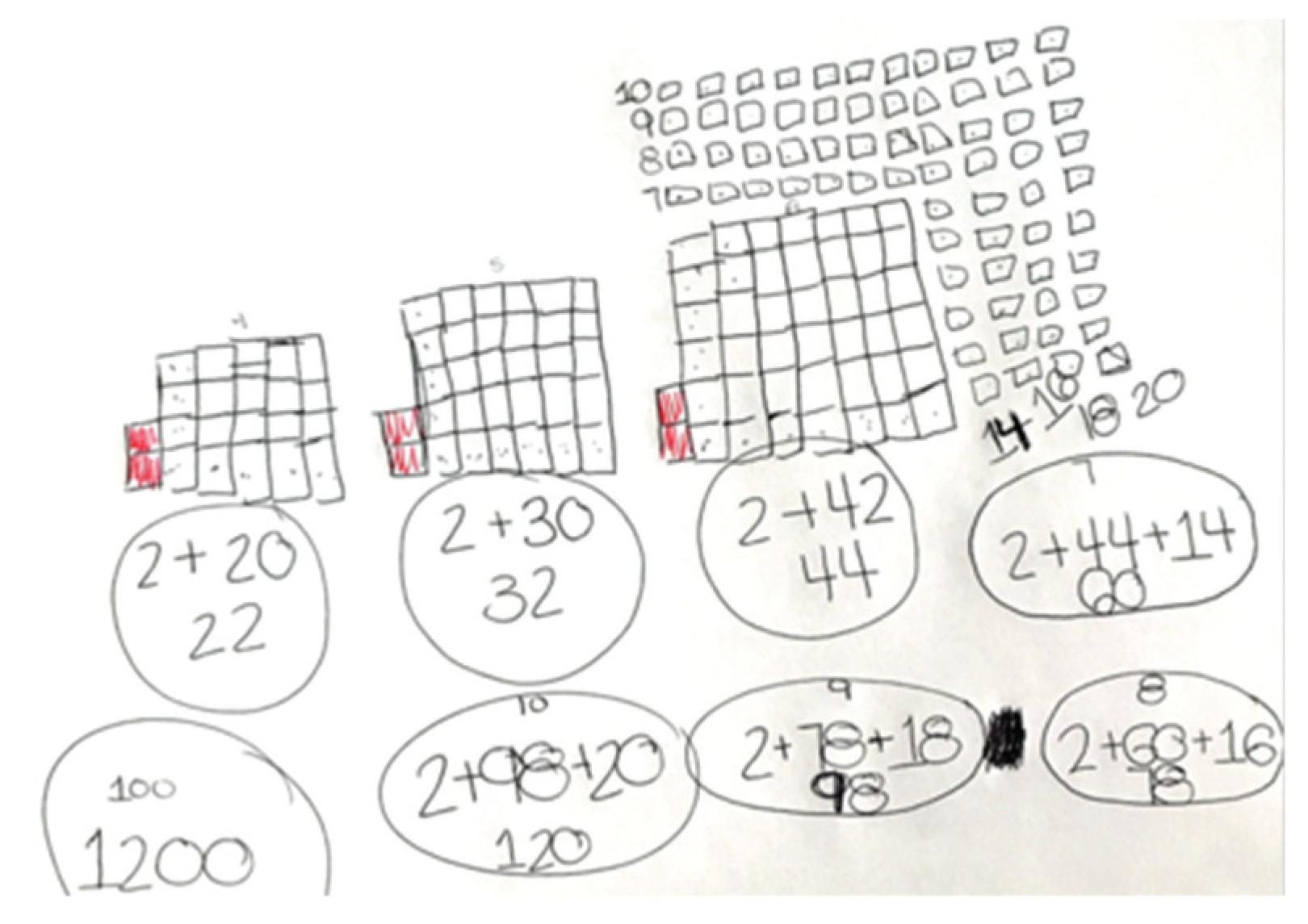
| Step 1. They used the tangible material to count the intersections for the first 6 lines, but failed to consider the non-visible intersections. The instructor pointed out this error, which led to step 2. Step 2. They made drawings of the lines on a blank sheet (Figure 11) to count all the intersections more systematically. This allowed them to count all the intersections formed by drawing seven lines. Step 3. They constructed a recursive process for the first 8 lines: 6 lines generate 15 intersections ; 7 lines produce 21 lines . Hence, 8 lines should give intersections. They verified the number of intersections by following the conditions on the list (Figure 11) and then used this technique to reach 20 lines. Step 4. They made several attempts to find a rule based on the relation between the number of lines and the number of intersections of the stage , and tested their proposed rules with the information for stage 4, but did not succeed in establishing an algebraic rule. | Taking the first 6 stages as the base, they considered a relation of dependence between and , and, later, the recursive rule: . They optimized their technique by passing from the drawings to constructing a recursive rule (F2). They attempted to optimize their recursive technique and find a rule of algebraic generalization (F2). They also applied the verification technique presented previously (F4). |
| Technique | and |
|---|---|
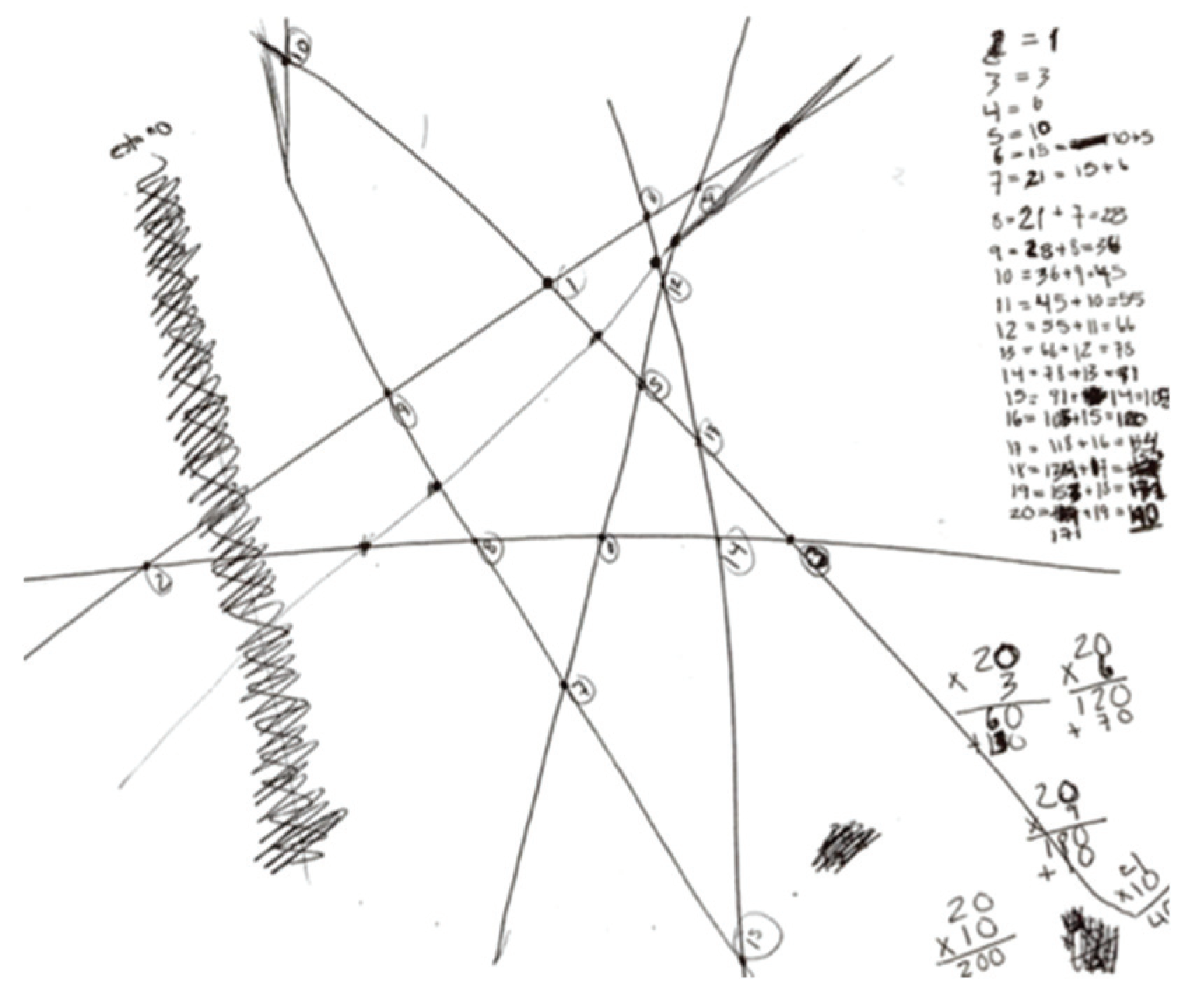
| Step 1. Using the tangible material, they counted the number of intersections for the first 5 stages, including the intersections that do not appear visually (Figure 5). Step 2. They constructed a recursive process for the first 8 lines based on the differences between stages and that is: with 2 lines, one intersection; with 3 lines, intersections; with 4 lines, intersections; with 5 lines, intersections; and with 6 lines intersections; so with 7 lines the number of intersections will be the same as with 6 lines plus 6: intersections, and with 8 lines the number will be the same as with 7 lines plus 7: intersections (Figure 12). Step 3. They identified that the technique associated with the pyramid task (Figure 4) can be applied to solve the intersection task, as well, though they recalled that the earlier task was not solved. Step 4. They determined which task is solved by adding up consecutive positive whole numbers, such that . Step 5. They related a famous technique from Carl Friedrich Gauss (Hayes, 2006) to add up the first consecutive positive numbers (Figure 13) that the instructor had mentioned briefly in the first session. Step 6. They determined the value of the sum by forming pairs between the 10 initial and 10 final numbers, as shown here: until they obtained Finally, they stated that this process must be repeated up to the number 50, but that this technique is not effective for any number of lines stipulated, so they continued trying to come up with an algebraic rule. Step 7. The instructor asked them to perform the same activity, but with 20 lines. This led to the following conclusion: taking away one (leaving 19), dividing by two (leaving 9.5), taking only the 9 (the whole part) and multiplying (making 180) plus the one in the half, leaves 190 intersections. Step 8: They verified this technique with one member’s results for 20 lines and then implemented it for 100 lines: , taking 49, multiplying it by 100, and adding 50 from the half to obtain the result of 4,950 intersections. | Based on the first 5 cases, they considered a relation of dependence between and that led to the recursive rule: . They constructed two rules of algebraic generalization for lines: They optimized their technique by passing from the tangible material to a recursive rule. They recognized the applicability of a technique based on considering three types of tasks: the intersection task, the pyramid task, and the task of the sum of the first 100 positive whole numbers (F3, F4). They adapted Gauss’ technique for the first 10 whole positive numbers for the sum of the first 99 numbers (F4). They optimized the technique of adding pairs and constructed a rule of algebraic generalization (F2). |
| Technique | Technologies and |
|---|---|
| Step 1. Using the tangible material, they counted the number of intersections for the first 6 lines, after arranging them so that all intersections were visible. Step 2. Same as pair B, but followed this rule up to 18 lines. Based on this step, they proposed their own techniques, which were discussed at a couple different moments. Step 3. (Member 1). With the goal of detecting a pattern that would allow her/him to construct an algebraic rule, he continued to apply this recursive rule up to 55 lines (Figure 14). Step 3. (Member 2). This student related the technique associated with the pyramid cube task (Figure 4), realizing that it could be used to solve the intersection task. This student showed the instructor a sheet where –on his own initiative– he had resolved the pyramid cube task using the recursive rule one-by-one up to . He mentioned that the numbers are the same, but ‘go two behind’; that is, ‘If the number of lines here is five, there it would be pyramid 3’. Though this student recognized that this new task is solved using pyramid 98, he continued to search for a more direct way. Step 4. (Member 1). Once this student had a sufficient number of cases (55 lines), he identified a pattern based on ‘tens’ (10, 20, 30, 40…). He explained the process on the blackboard (Figure 15): ‘The way in which it is possible to reach 45 is by multiplying 10 × 5—the half– and subtracting 5 to reach 45. I made it to 50 this way, one-by-one and verified it [algebraic rule] for 20, 30 and 40, and it worked; for example, for 20 I obtained 190, because it’s 20 × 10, which is half of 20 minus 10, and that gives 190. I did the same with 30, 40… up to 100. What I did was 100 × 50 minus 50, which is half. That gave me 4950”. | Based on the first 6 cases, they structured a relation of dependence between and , and later constructed the recursive rule: . They constructed a rule of algebraic generalization to find the number of intersections of lines: . They optimized their technique by passing from the tangible material to a recursive rule (F2). Member 2 recognized the applicability of a technique with respect to two task types: pyramid cubes and line intersections. He identified the similarities and differences between the tasks in order to implement the technique (F3, F4). Member 1 optimized his recursive technique and produced a unique technique based on ‘tens’. He verified that this new technique worked for other cases (F1, F2). |
5. Discussion
6. Conclusions and Future Research
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Singer, F.M.; Sheffield, L.J.; Freiman, V.; Brandl, M. Research on and Activities for Mathematically Gifted Students, 1st ed.; ICME-13 Topical Surveys; Springer Open: New York, NY, USA, 2016. [Google Scholar]
- Greenes, C. Identifying the gifted student in mathematics. Arith. Teach. 1981, 28, 14–17. [Google Scholar]
- Miserandino, D.; Subotnik, R.; Ou, K. Identifying and nurturing mathematical talent in urban school setting. J. Second. Gifted Educ. 1995, 6, 245–257. [Google Scholar]
- Ficici, A.; Siegle, D. International teachers’ judgment of gifted mathematics student characteristics. Gifted Talented Int. 2008, 23, 23–38. [Google Scholar] [CrossRef]
- Miller, R. Discovering Mathematical Talent; ERIC Digest No. E482; Council for Exceptional Children: Reston, VA, USA, 1990. [Google Scholar]
- Sheffield, L. The Development of Gifted and Talented Mathematics Students and the National Council of Teachers of Mathematics Standards, 1st ed.; Diane Publishing: Collingdale, PA, USA; University of Connecticut: Mansfield, CT, USA, 1994. [Google Scholar]
- Renzulli, J.S. The three-ring definition of giftedness: A developmental model for promoting creative productivity. In Conceptions of Giftedness, 2nd ed.; Sternberg, R.J., Davidson, J.E., Eds.; Cambridge University Press: New York, NY, USA, 2005; Volume 2, pp. 246–280. [Google Scholar]
- Kattou, M.; Kontoyianni, K.; Pitta-Pantazi, D.; Christou, C. Connecting mathematical creativity to mathematical ability. ZDM Math. Educ. 2013, 45, 167–181. [Google Scholar] [CrossRef]
- Krutetskii, V.A. The Psychology of Mathematical Abilities in Schoolchildren; University of Chicago Press: Chicago, IL, USA, 1976. [Google Scholar]
- Leikin, R. Giftedness and High Ability in Mathematics. In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer: Dordrecht, The Netherlands, 2014; pp. 247–251. [Google Scholar]
- Benavides, M. Caracterización de Sujetos con Talento en Resolución de Problemas de Estructura Multiplicativa [Characterization of Subjects with Talent in Solving Problems of Multiplicative Structure]. Ph.D. Thesis, Universidad de Granada, Granada, Spain, 2008. [Google Scholar]
- Villarraga, M.; Martínez, P.; Benavides, M. Hacia la definición del término talento [Towards the definition of the talent term]. In La Educación de Niños con Talento en Iberoamérica; Benavides, M., Maz, A., Castro, E., Blanco, R., Eds.; Trineo S.A.: Santiago, Chile, 2004; pp. 25–35. [Google Scholar]
- Boaler, J. Mathematical Mindsets; Jossey-Bass: San Francisco, CA, USA, 2016. [Google Scholar]
- Vale, I.; Pimentel, T. Mathematical challenging tasks in elementary grades. In Proceedings of the 7th Congress of the European Society for Research in Mathematics Education; Pytlak, M., Rowland, T., Swoboda, E., Eds.; ERME: Rzeszow, Poland, 2011; pp. 1154–1164. [Google Scholar]
- Kozlowski, J.; Chamberlin, S.; Eric, M. Factors that Influence Mathematical Creativity. Math Enthus. 2019, 16, 505–540. [Google Scholar]
- Leikin, R. The education of mathematically gifted students: Some complexities and questions. Math Enthus. 2011, 8, 167–188. [Google Scholar]
- Diezmann, C.M.; Watters, J.J. The importance of challenging tasks for mathematically gifted students. Gifted Talented Int. 2002, 17, 76–84. [Google Scholar] [CrossRef]
- Sriraman, B. Mathematical giftedness, problem solving, and the ability to formulate generalizations. J. Second. Gifted Educ. 2003, 14, 151–165. [Google Scholar] [CrossRef]
- Mann, E.L. Creativity: The essence of mathematics. J. Educ. Gifted 2006, 30, 236–262. [Google Scholar] [CrossRef]
- Singer, F.M.; Ellerton, N.; Cai, J. Problem-Posing Research in Mathematics Education: New Questions and Directions. Educ. Stud. Math. 2013, 83, 1–7. [Google Scholar] [CrossRef]
- Leikin, R. Teaching the mathematically gifted. Gifted Educ. Int. 2010, 27, 161–175. [Google Scholar] [CrossRef]
- Koshy, V.; Ernest, P.; Casey, R. Mathematically gifted and talented learners: Theory and practice. Int. J. Math. Educ. Sci. Technol. 2009, 40, 213–228. [Google Scholar] [CrossRef][Green Version]
- Diezmann, C.M.; Waiters, J.J. Catering for mathematically gifted elementary students: Learning from challenging tasks. Gifted Child Today 2000, 23, 14–52. [Google Scholar] [CrossRef]
- McClure, L.; Piggott, J. Meeting the Needs of Your Most Able Pupils: Mathematics, 1st ed.; David Fulton Publishers: London, UK, 2007. [Google Scholar]
- Elia, I.; van den Heuvel-Panhuizen, M.; Kolovou, A. Exploring Strategy Use and Strategy Flexibility in Non-Routine Problem Solving by Primary School High Achievers in Mathematics. ZDM Math. Educ. 2009, 41, 605–618. [Google Scholar] [CrossRef]
- Sriraman, B. The characteristics of mathematical creativity. ZDM Math. Educ. 2009, 41, 13–27. [Google Scholar] [CrossRef]
- Tan, L.S.; Lee, S.S.; Ponnusamy, L.D.; Koh, E.R.; Tan, K.C.K. Fostering Creativity in the Classroom for High Ability Students: Context Does Matter. Educ. Sci. 2016, 6, 36. [Google Scholar] [CrossRef]
- Brody, L. The study of exceptional talent. High Ability Stud. 2005, 16, 87–96. [Google Scholar] [CrossRef]
- Dimitriadis, C. Developing mathematical ability in primary school through a ‘pull-out’ programme: A case study. Education 2011, 39, 467–482. [Google Scholar] [CrossRef]
- Kennard, R. Providing for Mathematically Able Children in Ordinary Classrooms. Gifted Educ. Int. 1998, 13, 28–35. [Google Scholar] [CrossRef]
- Johnson, D.T. Teaching Mathematics to Gifted Students in a Mixed-Ability Classroom; ERIC Digest No. E594; Council for Exceptional Children: Reston, VA, USA, 2000. [Google Scholar]
- Van Tassel-Baska, J. Myth 12: Gifted programs should stick out like a sore thumb. Gifted Child Q. 2009, 53, 266–268. [Google Scholar] [CrossRef]
- Oktaç, A.; Roa-Fuentes, S.; Rodríguez, M. Equity issues concerning gifted children in mathematics: A perspective from México. In Mapping Equity and Quality in Mathematics Education; Atweh, B., Graven, M., Secada, W., Valero, P., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 351–364. [Google Scholar]
- Bosch, M.; Chevallard, Y.; García, F.J.; Monaghan, J. Working with the Anthropological Theory of the Didactic in Mathematics Education: A Comprehensive Casebook, 1st ed.; Routledge: London, UK; New York, NY, USA, 2019. [Google Scholar]
- Levav-Waynberg, A.; Leikin, R. The role of multiple solution tasks in developing knowledge and creativity in geometry. J. Math. Behav. 2012, 31, 73–90. [Google Scholar] [CrossRef]
- Vale, I.; Pimentel, T.; Cabrita, I.; Barbosa, A.; Fonseca, L. Pattern problem solving tasks as a mean to foster creativity in mathematics. In Proceedings of the 36th Conference of the International Group for the Psychology of Mathematics Education; Tso, T.Y., Ed.; PME: Taipei, Taiwan, 2012; Volume 4, pp. 171–178. [Google Scholar]
- Kattou, M.; Christou, C.; Pitta-Pantazi, D. Mathematical creativity or general creativity? In Proceedings of the 9th Congress of European Research in Mathematics Education; Krainer, K., Vondrová, N., Eds.; Charles University in Prague: Prague, Czech Republic, 2015; pp. 1016–1023. [Google Scholar]
- Castela, C.; Romo-Vázquez, A. Des mathématiques a l’automatique: Étude deseffets de transposition sur la transformée de Laplace dans la formation des ingénieurs [From mathematics to automatic: Study of transposition effects on the Laplace transform in engineering education]. Rech. Didact. Math. 2011, 31, 79–130. [Google Scholar]
- Chevallard, Y. Introducing the anthropological theory of the didactic: An attempt at a principled approach. Hiroshima J. Math. Educ. 2019, 12, 71–114. [Google Scholar]
- Sriraman, B. Are mathematical giftedness and mathematical creativity synonyms? A theoretical analysis of constructs. J. Second. Gifted Educ. 2005, 17, 20–36. [Google Scholar] [CrossRef]
- Radford, L. Layers of generality and types of generalization in pattern activities. PNA 2010, 4, 37–62. [Google Scholar]
- Rivera, F.D. Visual templates in pattern generalization activity. Educ. Stud. Math. 2010, 73, 297–328. [Google Scholar] [CrossRef]
- Rivera, F. Teaching and Learning Patterns in School Mathematics: Psychological and Pedagogical Considerations; Springer: New York, NY, USA, 2013. [Google Scholar]
- Vergel, R. Generalización de patrones y formas de pensamiento algebraico temprano [Generalization of patterns and forms of early algebraic thinking]. PNA 2015, 9, 193–215. [Google Scholar]
- Bosch, M.; Chevallard, Y. La sensibilite´ de l’activité mathématique aux ostensifs [The sensitivity of mathematical activity to ostensives]. Rech. Didact. Math 1999, 19, 77–124. [Google Scholar]
- Sriraman, B.; Lee, K.H. The Elements of Creativity and the Giftedness in Mathematics, 1st ed.; Sense Publishers: Leiden, The Netherlands, 2011. [Google Scholar]
- Bicknell, B. Parental Roles in the Education of Mathematically Gifted and Talented Children. Gifted Child Today 2014, 37, 83–93. [Google Scholar] [CrossRef]
- Feldhusen, J.F. Beyond general giftedness: New ways to identify and educate gifted, talend, and precocious youth. In Rethinking Gifted Education; Borland, J., Ed.; Teacher College Press: New York, NY, USA, 2003; pp. 34–45. [Google Scholar]
- Chaachoua, H.; Bessot, A.; Romo-Vázquez, A.; Castela, C. Developments and functionalities in the praxeological model. In Working with the Anthropological Theory of the Didactic: A Comprehensive Casebook, 1st ed.; Bosch, M., Chevallard, Y., García, F.J., Monaghan, J., Eds.; Routledge: London, UK, 2019; pp. 41–60. [Google Scholar]







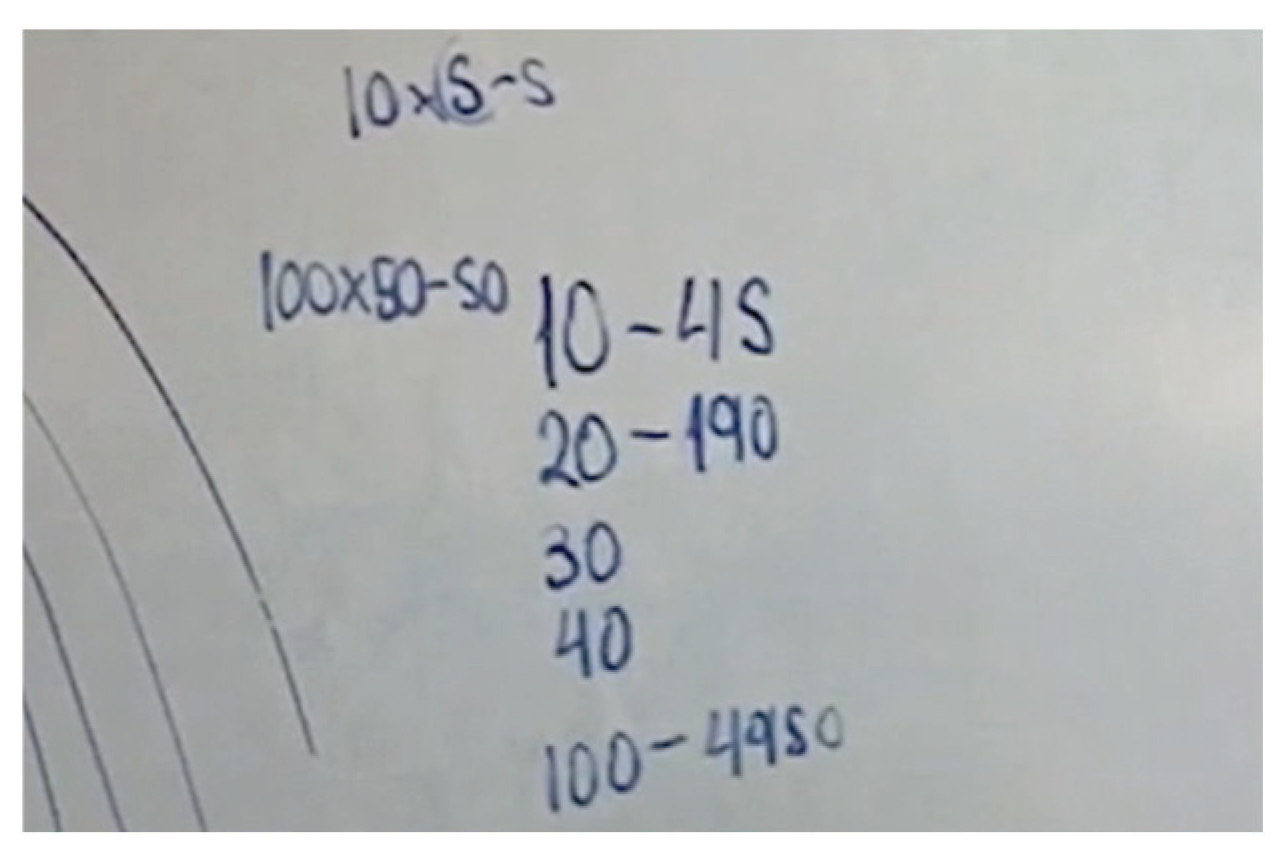
| 5th Grade | 6th Grade | |||
|---|---|---|---|---|
| Sex | 10 Years | 11 Years | 12 Years | Total |
| Female | 2 | 8 | 2 | 12 |
| Male | 3 | 8 | 3 | 14 |
| Total | 5 | 16 | 5 | 26 |
| Problem Situation | Tasks |
|---|---|
| 1. Sierpiński’s triangle | Task 1.1: Determine the change in the number of triangles while building Sierpiński’s triangle. Task 1.2: Determine changes in the area while building Sierpiński’s triangle. Task 1.3: Determine changes of the perimeter while building Sierpiński’s triangle. |
| 2. Origami cubes | Task 2.1: Determine the number of cubes required to construct any stage of the sequence (different sequences of origami cubes were presented). Task 2.2: Construct three stages using the origami cubes following a pattern. |
| 3. Tables and chairs | Task 3.1: Determine the number of chairs that can be arranged at any number of tables. Task 3.2: Determine the number of squares required to build any stage of the sequence. Task 3.3: Determine the number of shaded squares required to construct any image. |
| 4. Intersections and regions | Task 4.1: Determine the number of intersections formed on a plane when any number of non-parallel lines are placed but only two lines can form an intersection. Task 4.2: Determine the number of regions formed on a plane when any number of non-parallel lines are placed but only two lines can form an intersection. |
| 5. Tower of Hanoi | Task 5.1: Determine the minimum number of movements with any number of disks. |
| 6. Folding paper | Task 6.1: Determine the total thickness of the folded sheet for any number of folds. Task 6.2: Determine the surface area of the sheet for any number of folds. Task 6.3: Determine the perimeter of the surface of the sheet for any number of folds. |
| Term | Combination Pink/Orange | Combination Pink/Blue | Total Cubes | Increase of Cubes between Stages |
|---|---|---|---|---|
| 1 | 2 | |||
| 2 | 2 | |||
| 3 | 2 | |||
| 4 | 2 | 20 | 22 | |
| Lines | Increase of Regions | |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | 11 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barraza-García, Z.M.; Romo-Vázquez, A.; Roa-Fuentes, S. A Theoretical Model for the Development of Mathematical Talent through Mathematical Creativity. Educ. Sci. 2020, 10, 118. https://doi.org/10.3390/educsci10040118
Barraza-García ZM, Romo-Vázquez A, Roa-Fuentes S. A Theoretical Model for the Development of Mathematical Talent through Mathematical Creativity. Education Sciences. 2020; 10(4):118. https://doi.org/10.3390/educsci10040118
Chicago/Turabian StyleBarraza-García, Zeidy M., Avenilde Romo-Vázquez, and Solange Roa-Fuentes. 2020. "A Theoretical Model for the Development of Mathematical Talent through Mathematical Creativity" Education Sciences 10, no. 4: 118. https://doi.org/10.3390/educsci10040118
APA StyleBarraza-García, Z. M., Romo-Vázquez, A., & Roa-Fuentes, S. (2020). A Theoretical Model for the Development of Mathematical Talent through Mathematical Creativity. Education Sciences, 10(4), 118. https://doi.org/10.3390/educsci10040118