Pre-Service Teachers’ Declarative Knowledge of Wave-Particle Dualism of Electrons and Photons: Finding Lexicons by Using Network Analysis
Abstract
1. Introduction
2. Theoretical Underpinnings: Lexicons of Declarative Knowledge
3. Research Design and Sample
3.1. Tasks and Their Contexts
3.2. Data Collection and Handling
3.3. Research Questions
- RQ1. What kinds of lexicons do pre-service teachers use for electrons and photons?
- RQ2. What are the lexicons shared by at least a pair of pre-service teachers?
4. Methods: Construction and Analysis of Lexical Networks and Lexicons
4.1. Text Analysis
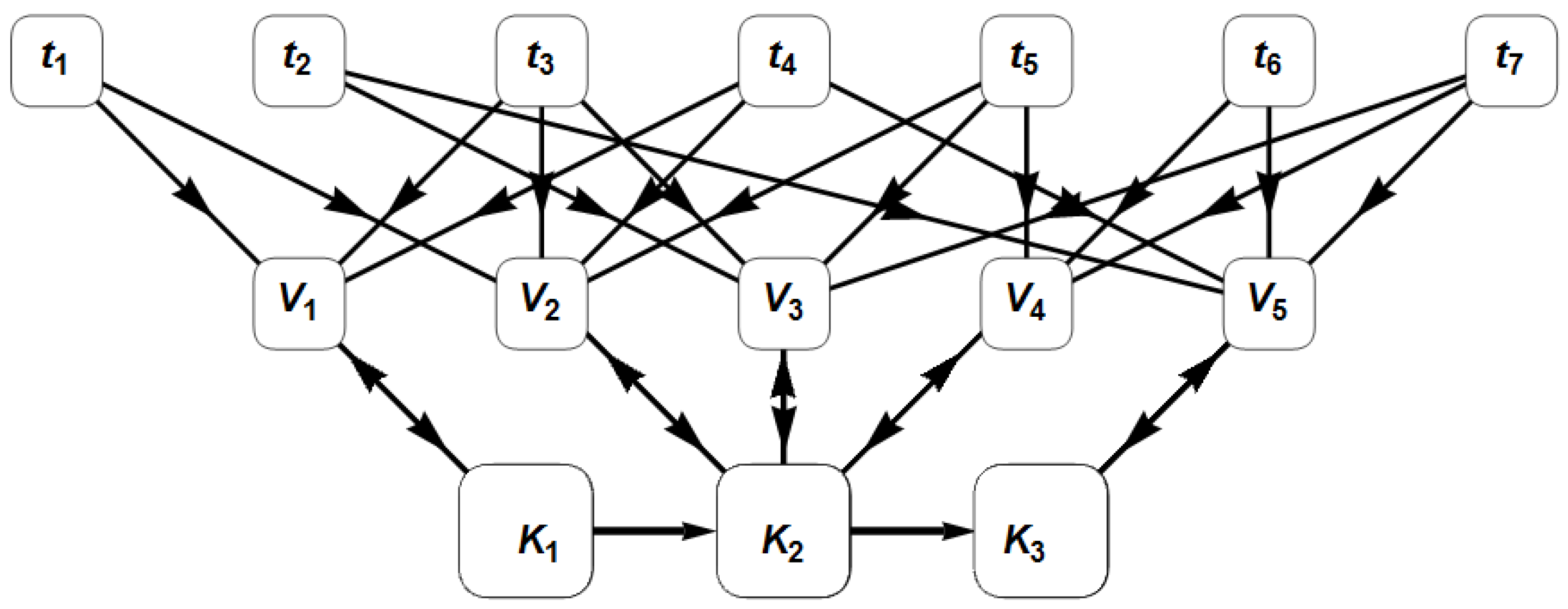
4.2. Construction of Lexical Network
4.3. Lexicons
5. Results
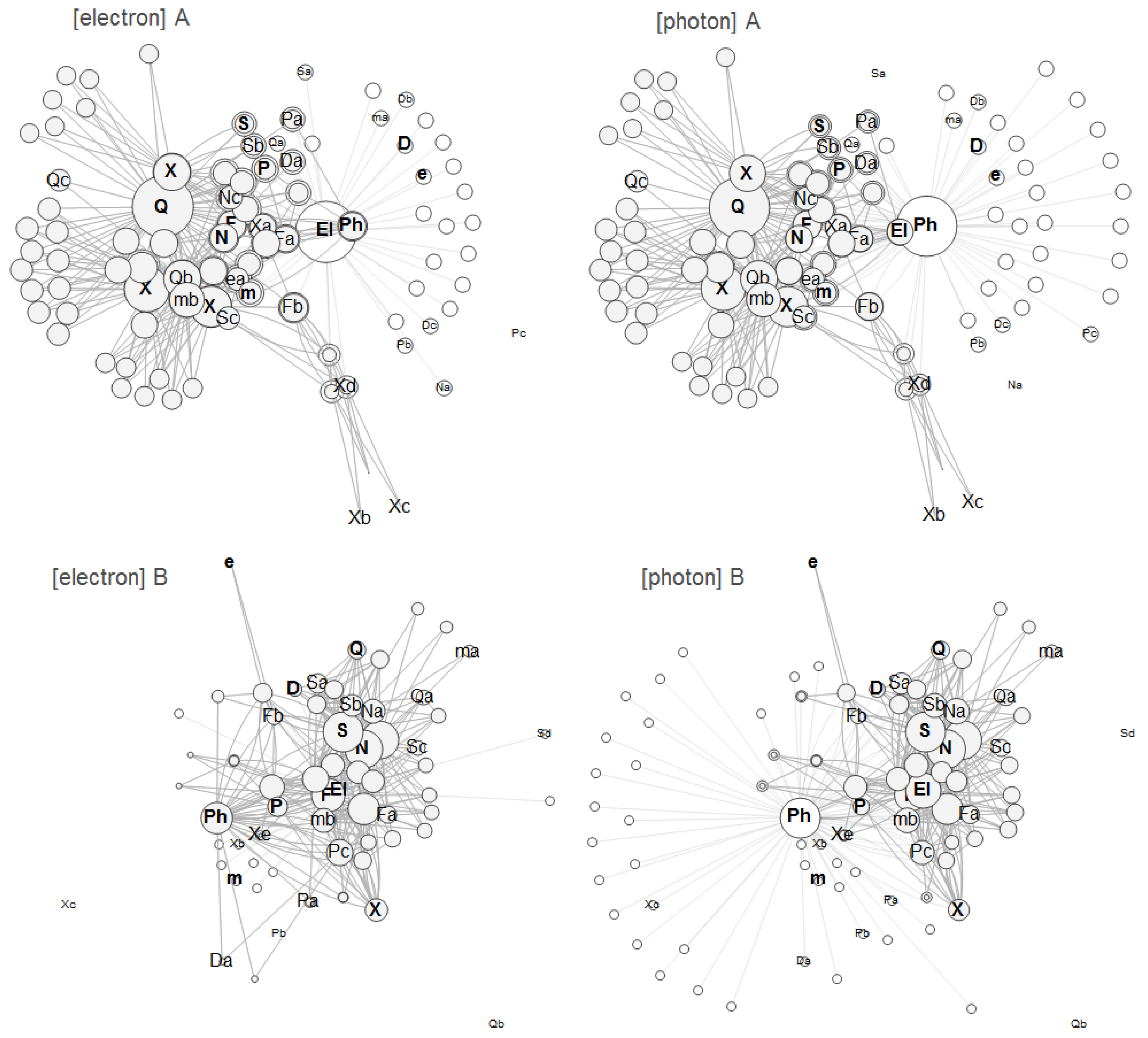
5.1. Lexicons
5.2. Shared Lexicons
5.3. Relevance and Reliability
6. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Excerpt | Pruned | Key Words and Terms |
|---|---|---|
| Although photons do not arrive at the same time, we observe an interference pattern forming of single spots. | Photon double-slit experiment form single hit interference pattern of photons | - photon double-slit experiment - photon - single hit - interference pattern |
| This indicates the particle nature of light. | [Photon double-slit experiment and single hits] indicate that light has particle nature. | - photon double-slit experiment - single hit - light - particle nature |
| Property | ||||||||
|---|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | |
| W | P | D | E | Q | S | Xp | Xe | |
| Wave | Particle | Dualism | Energy | Quantization | Stochastic | DSE photon | DSE electr | |
| wave | particle | dual model | energy | quantization | probability | DSE photon | DSE electron | |
| wave motion | particle nature | single hit | intensity | quantum | Probability distribution | young-experiment | young- experiment | |
| wave property | mass | radiation energy | field quantum | Probability wave | ||||
| wave nature | charge | kinetic energy | light quantum | wave-function | ||||
| interference | light particle | work function | radiation quantum | born-rule | ||||
| EM wave | electron flow | light energy | quantum hypothesis | hit distribution | ||||
| EM field | elastic collision | linear momentum | uncertainty relation | |||||
| K1 | In the Young double-slit experiment the wave entering the slit changes so that both slits act as the source of a wave. The resulting new wave interferes. The wave with same phase strengthen and with the different phases weaken each other. This results in a minima and maxim in the interference pattern on the detection screen. The interference pattern found in the double-slit experiment is still explained by the wave model of light. |
| K2 | The principle of the double-slit experiment can be applied in a new experiment with the low intensity light. In the experiment, the intensity of the light is reduced to such an extent that it is possible to think of the photon as opposed to the Young’s experiment. |
| K3 | Finally, in the double-slit experiment the interference pattern is formed but the pattern is found to be based on the individual hits. The classical wave model is not able to explain and the experiment is a clear proof of the particle nature of the light. The probability of photon detection locations is described by the wave function. |
| K4 | Light is not really the wave nor the particle but both models describe light. Depending on the situation, light can be interpreted as electromagnetic wave motion or as photons which are massless particles. |
| K5 | The wave function combines the particle model and the wave model. In the wave-particle dualism particles are reduced as momentarily and locally existing quanta. The wave motion becomes the wave function that regulates the probability of the photon observation. The wave function itself has no detectable physical properties. |
| K6 | In the previous didactic reconstruction of the photon phenomenon, the double-slit experiment resulted in the wave-particle dualism type of the quantum model of the photon. |
| K7 | Louis de Broglie put forward a hypothesis that the wave-particle dualism is the nature of all the fundamental entities of nature. The idea of dividing energy quantum into particles and waves should be discarded. The wave-particle dualism does not only concern photons. |
| K8 | According to the classical model, the electron is small particle that is identifiable and localised. The movement of the particle follows basic laws of the classical mechanics and their behavior in interaction situations can be predicted by the classical physics. The mass and the charge and the linear momentum and energy are localized on the location indicated by the particle location vector. |
| K9 | The interference pattern is observed in the double-slit experiment for the weak electron beam. In this case the interference pattern consists of individual hits. From this, it can be concluded that the electron must have both particle nature and wave nature. In the double-slit experiment the geometry of the slit and the de Broglie law make the probability distribution of the individual hit of the electron predictable |
| K10 | The wave nature of the electron can only be detected as interference phenomena such as for example in the double-slit experiment. The wave related to the electron is the probability wave represented by the wave function. The square of the wave function indicates the probability distribution of the presence of the electron. It is also noteworthy that the wave function is not the same as in the case of photon. |
| K11 | Based on the double-slit experiment the electron has both the particle nature and wave nature. The combination of the particle nature and the wave nature results in the wave-particle dualism that applies to the electron. The particle is the field quantum which is detected only in interactions and does not exist as individuals. The probability distribution expressed by the wave function also follows the uncertainty principle. |
Appendix B
Appendix C
| Category | Description in Original Reference | Lexicons (min.) | |
|---|---|---|---|
| Ayene | cat I | Classical wave and intuitive model | SC |
| et al. [1] | cat II | Mixed model | QS,FDQ,FPDQ |
| cat III | Incipient Quantum model | QSX, QS | |
| Mannila | Clas-M | Classical (hybrid) model | SC |
| et al. [5] | Traj-M | Trajectory-based model | QS,PDQ,FDQ |
| Stat-M | Statistical/ensemble model | QS,QSX,FPDQ | |
| Quant-M | Fully quantum model | QFX, QSX | |
| Cheong | I | Introductory physics course | QS,FDQ,FPDQ,PDQ |
| & Song [6] | U | Undergraduate quantum mechanics | QSX,QS,FPDQ |
| G | Graduate quantum mechanics | QFX |
References
- Ayene, M.; Krick, J.; Damitie, B.; Ingerman, A.; Thacker, B. A Holistic Picture of Physics Student Conceptions of Energy Quantization, the Photon Concept, and Light Quanta Interference. Int. J. Sci. Math. Educ. 2018, 17, 1049–1070. [Google Scholar] [CrossRef]
- Didiş, N.; Eryilmaz, A.; Erkoç, S. Investigating students’ mental models about the quantization of light, energy, and angular momentum. Phys. Rev. Spec. Top-Ph. 2014, 10, 020127. [Google Scholar] [CrossRef]
- Henriksen, E.K.; Angell, C.; Vistnes, A.I.; Bungum, B. What Is Light? Students’ Reflections on the Wave-Particle Dualism of Light and the Nature of Physics. Sci. Educ. 2018, 27, 81–111. [Google Scholar] [CrossRef]
- McKagan, S.B.; Perkins, K.K.; Wieman, C.E. Design and validation of the Quantum Mechanics Conceptual Survey. Phys. Rev. Spec. Top-Ph. 2010, 6, 020121. [Google Scholar] [CrossRef]
- Mannila, K.; Koponen, I.T.; Niskanen, J.A. Building a picture of students’ conceptions of wave- and particle-like properties of quantum entities. Eur. J. Phys. 2002, 23, 45–53. [Google Scholar] [CrossRef]
- Cheong, Y.W.; Song, J. Different Levels of the Meaning of Wave-Particle Duality and a Suspensive Perspective on the Interpretation of Quantum Theory. Sci. Educ. 2014, 23, 1011–1030. [Google Scholar] [CrossRef]
- Yun, E.; Park, Y. Extraction of scientific semantic networks from science textbooks and comparison with science teachers’ spoken language by text network analysis. Int. J. Sci. Educ. 2018, 40, 2118–2136. [Google Scholar] [CrossRef]
- Chi, M.T.H.; Ohlsson, S. Complex Declarative Learning. In Cambridge Handbook of Thinking and Reasoning; Holyoak, K.J., Morrison, R.G., Eds.; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Koponen, I.T.; Nousiainen, M. Concept networks in learning: Finding key concepts in learners’ representations of the interlinked structure of scientific knowledge. J. Complex. Netw. 2014, 2, 187–202. [Google Scholar] [CrossRef]
- Koponen, I.T.; Nousiainen, M. Concept networks of students’ knowledge of relationships between physics concepts: Finding key concepts and their epistemic support. Appl. Netw. Sci. 2018, 3, 14. [Google Scholar] [CrossRef]
- Koponen, I.T.; Nousiainen, M. Pre-Service Teachers’ Knowledge of Relational Structure of Physics Concepts: Finding Key Concepts of Electricity and Magnetism. Educ. Sci. 2019, 9, 18. [Google Scholar] [CrossRef]
- Neiles, K.Y.; Todd, I.; Bunce, D.M. Establishing the Validity of Using Network Analysis Software for Measuring Students’ Mental Storage of Chemistry Concepts. J. Chem. Educ. 2016, 93, 821–831. [Google Scholar] [CrossRef]
- Kubsch, M.; Nordine, J.; Neumann, K.; Fortus, D.; Krajcik, J. Probing the Relation between Students’ Integrated Knowledge and Knowledge-in-Use about Energy using Network Analysis. Eurasia J. Math. Sci. T 2019, 15, 1728. [Google Scholar] [CrossRef]
- Evans, V. How words Mean: Lexical Concepts, Cognitive Models, and Meaning Construction. Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Evans, V. Lexical concepts, cognitive models and meaning-construction. Cogn Linguist 2006, 17, 491–534. [Google Scholar] [CrossRef]
- Kuhn, T.S. The Road since Structure; University of Chicago Press: Chicago, IL, USA, 2000. [Google Scholar]
- Hoyningen-Huene, P. Systematicity: The Nature of Science; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Gattei, S. Thomas Kuhn’s Linguistic Turn and the Legacy of Logical Empiricism; Routledge: Oxon, UK, 2016. [Google Scholar]
- Clariana, R.B.; Wallace, P.E.; Godshalk, V.M. Deriving and measuring group knowledge structure from essays: The effects of anaphoric reference. Educ. Teach. Res. Dev. 2009, 57, 725–737. [Google Scholar] [CrossRef]
- Clariana, R.B. Deriving Individual and Group Knowledge Structure from Network Diagrams and from Essays. In Digital Knowledge Maps in Education: Technology-Enhanced Support for Teachers and Learners; Ifenthaler, D., Hanewald, R., Eds.; Springer: New York, NY, USA, 2014; pp. 117–130. [Google Scholar]
- Derman, A.; Eilks, I. Using a word association test for the assessment of high school students’ cognitive structures on dissolution. Chem. Educ. Res. Pract. 2016, 17, 902–913. [Google Scholar] [CrossRef]
- Langacker, R.W. Grammar and Conceptualization; Mouton de Gruyter: Berlin, Germany, 1999. [Google Scholar]
- Müller, R.; Wiesner, H. Teaching quantum mechanics on an introductory level. Am. J. Phys. 2002, 70, 200–209. [Google Scholar] [CrossRef]
- Hobson, A. There are no particles, there are only fields. Am. J. Phys. 2012, 81, 211–223. [Google Scholar] [CrossRef]
- Estrada, E. The Structure of Complex Networks: Theory And Applications; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
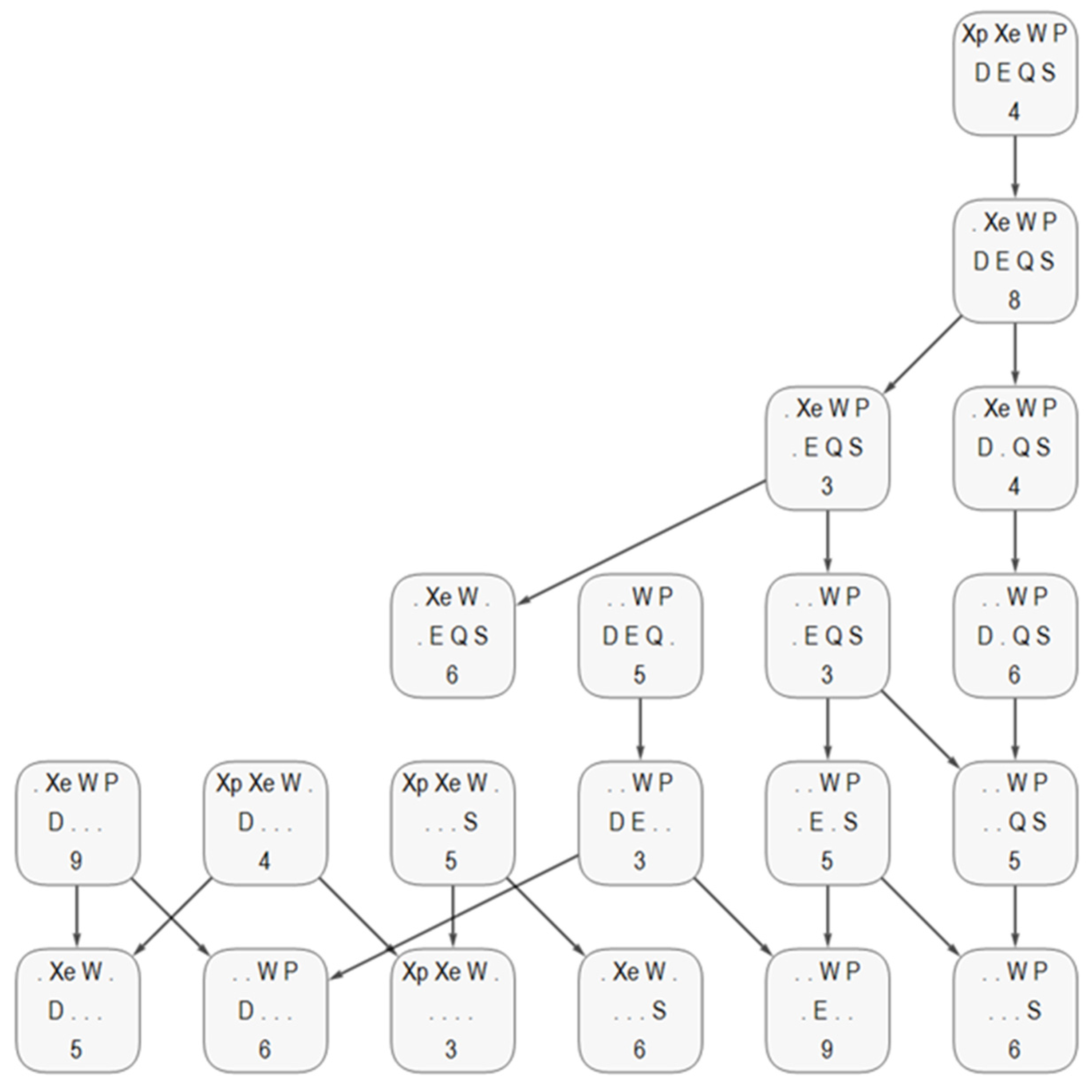
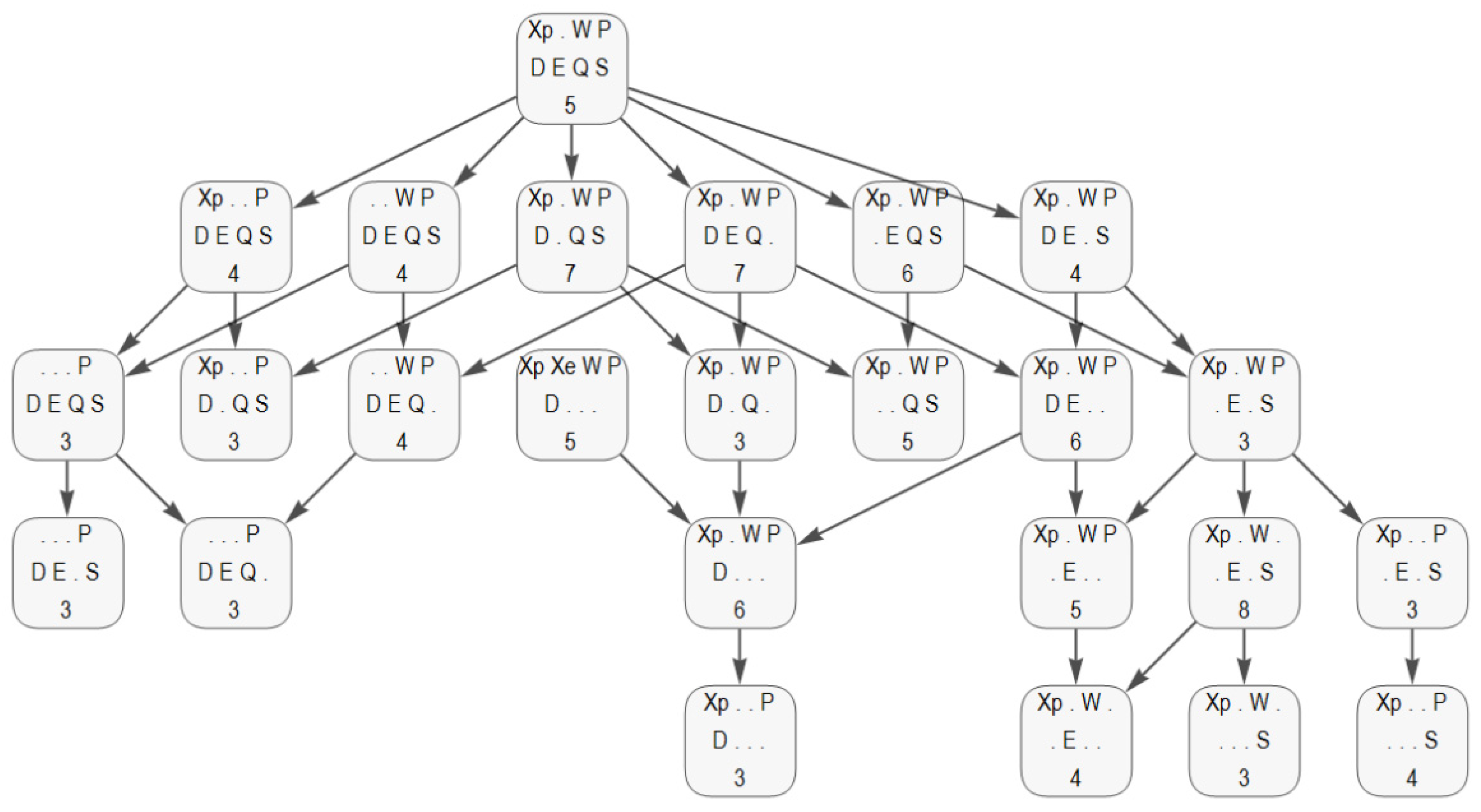
| Property |
|---|
| Wave and/or field-properties |
| Particle properties |
| Dualism |
| Energy related properties |
| Quanta and quantization |
| Stochastic and probabilistic properties |
| Properties related to double-slit experiment for photons |
| Properties related to double-slit experiment for electrons |
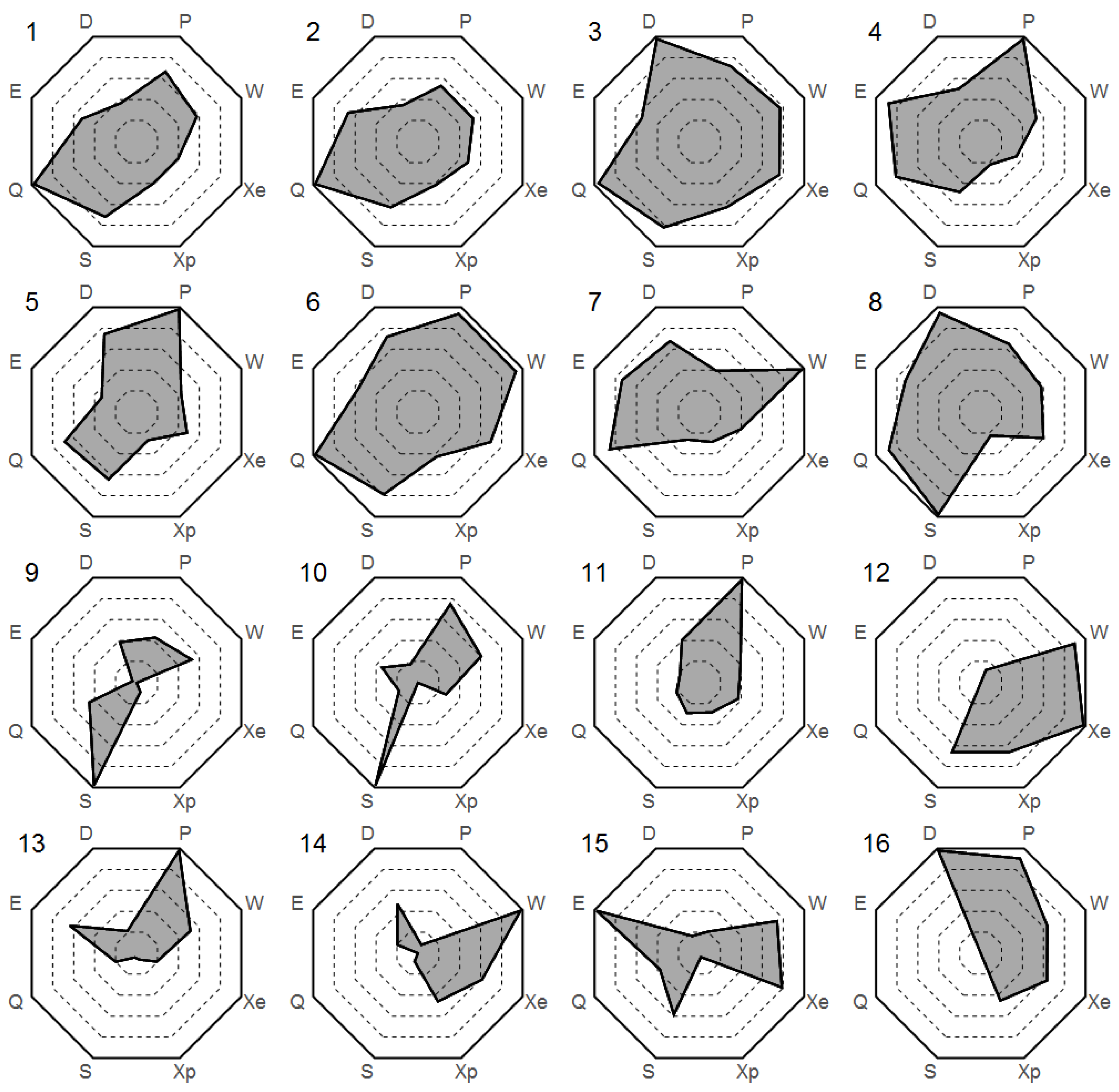
| Level | A: L=8,7 | B: L=6 | C: L=5,4 | D: L=5,4 | G: L=4,3 |
|---|---|---|---|---|---|
| Name | QFX Quant. Full+X | QSX Quant., Stats+X | QS Quant., Stats. | FDQ Field, D+Quant | SC: SemiClas. |
| Type Cases | 1-3,6 | 3,5,6,11 | 1-3,5,6,8,15 | 1-3,6,8,15 | |
| Type Cases | 1-8 | 4,5,15 | 1-3,5,6,8,15 | ||
| Type Cases | 1,2,4 |
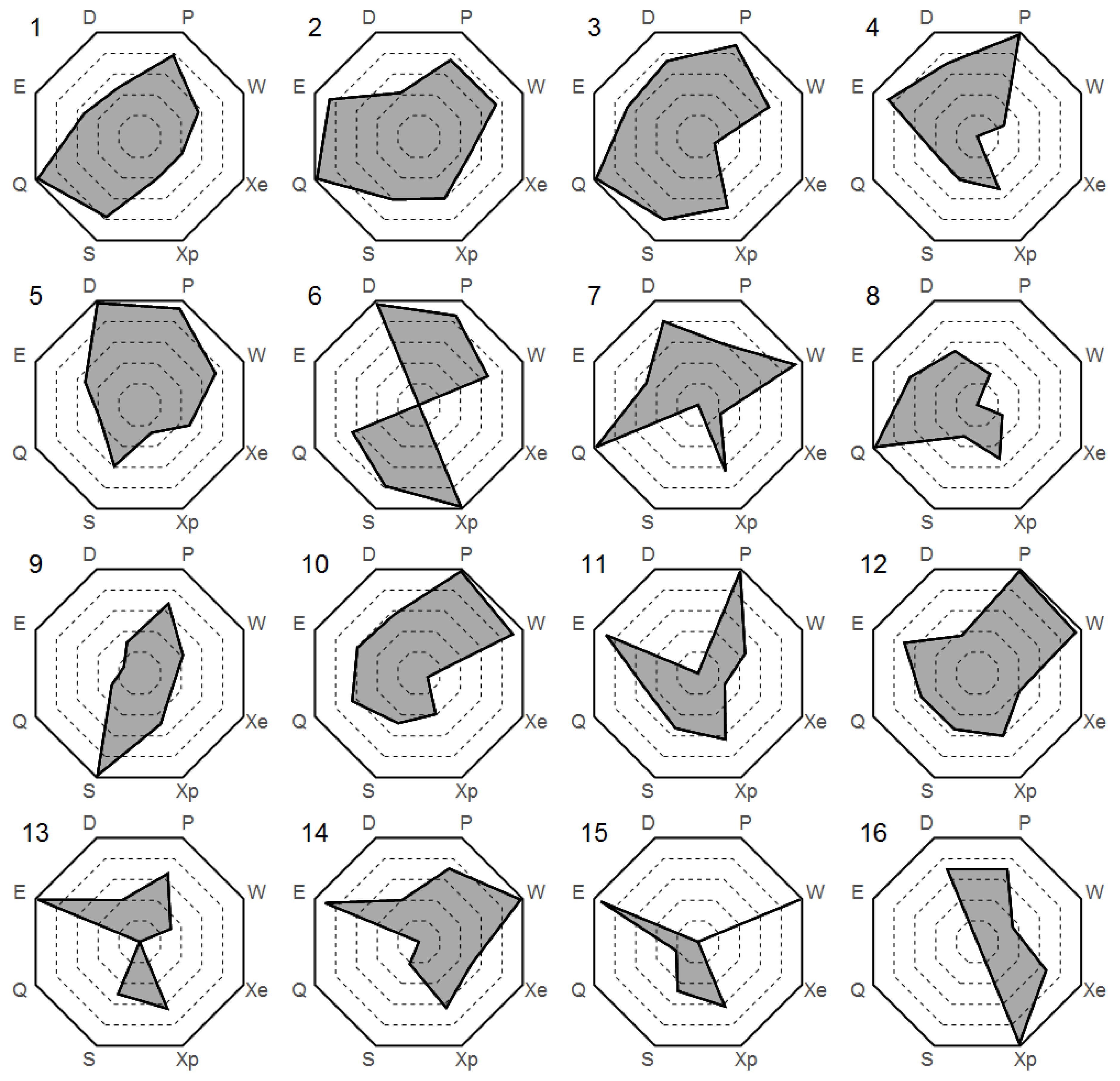
| Level | A: L=8,7 | B: L=6,5 | C: L=6,5 | D: L=6,5 | G: L=5-3 |
|---|---|---|---|---|---|
| Name | QFX Quant. Full+X | QSX Quant, Stats+X | FPDQ Quant, Dual. | PDQ Quant, Particle | SC SemiClas. |
| Type Cases | 1-3,10-12 | 1-3,5,10 | 2-4,8 | ||
| Type Cases | 1-3,5,6,10,12 | 1-3,6,9-12 | 1-4,7,10,12 | 2,4,6,8,14 | |
| Type Cases | 4,5-7,9,10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nousiainen, M.; Koponen, I.T. Pre-Service Teachers’ Declarative Knowledge of Wave-Particle Dualism of Electrons and Photons: Finding Lexicons by Using Network Analysis. Educ. Sci. 2020, 10, 76. https://doi.org/10.3390/educsci10030076
Nousiainen M, Koponen IT. Pre-Service Teachers’ Declarative Knowledge of Wave-Particle Dualism of Electrons and Photons: Finding Lexicons by Using Network Analysis. Education Sciences. 2020; 10(3):76. https://doi.org/10.3390/educsci10030076
Chicago/Turabian StyleNousiainen, Maija, and Ismo T. Koponen. 2020. "Pre-Service Teachers’ Declarative Knowledge of Wave-Particle Dualism of Electrons and Photons: Finding Lexicons by Using Network Analysis" Education Sciences 10, no. 3: 76. https://doi.org/10.3390/educsci10030076
APA StyleNousiainen, M., & Koponen, I. T. (2020). Pre-Service Teachers’ Declarative Knowledge of Wave-Particle Dualism of Electrons and Photons: Finding Lexicons by Using Network Analysis. Education Sciences, 10(3), 76. https://doi.org/10.3390/educsci10030076





