2. Literature Review
Insight into the agglomeration economies is not new and may at least be traced to Alfred Marshall, though in the context of positive externalities of larger markets (
Marshall 1920). Newer literature is showing a tendency toward very slowly rediscovering this neglected effect for a secondary purpose of measuring economic shock effects and impacts of declining demand in one sector on another sector. Regarding the analyses of statistical associations between overall macroeconomic variables and transportation categories, the usual approach tests the direction of the transportation sector to the macroeconomy. The approach in this paper was open to the direction of causation.
Vukić et al. (
2021) used an input–output approach to analyze the impact of transportation on the Croatian economy, coming to the conclusion that multiplying effects existed.
Dobes and Leung (
2015) came to the conclusion that such multiplier effects are mostly exaggerated. For an overview of possible positive effects on other transportation categories, see
Jugović et al. (
2011). Our analysis does not cover the economic grounds for the plunge in shipping activity after the economic crisis of 2008. For a recent analysis of this topic, see
Jerebić and Pavlin (
2018). For a comprehensive analysis of the transportation sector, see
Gwilliam and Mackie (
2017). Dobes and Leung go back to the Marshallian agglomeration economies and increasing external economies of scale resulting from reduced transport costs by imperfectly competitive industries, enabling them to increase their output, to increase supply of labor, and thereby increase GDP. These agglomeration economies are the consequence of larger specialization and division of labor. Thus, an increase in population would likely lead to a more than proportionate increase in social welfare (
Dobes and Leung 2015). Agglomeration effects are also the point of interest for
Graham (
2007).
Graham (
2007) developed an econometric model to investigate the relationship between the density of economic activity and productivity for different sectors of the UK economy, finding positive externalities from increasing urban densities. That population distributions determine total transport costs for manufacturing firms is also recognized by
Kilkenny (
1995).
Del Rio-Chanona et al. (
2020) provide quantitative predictions of first-order supply and demand shocks for the US economy associated with the COVID-19 pandemic at the level of individual occupations and industries. They came to the conclusion that these shocks would threaten around 20 per cent of the US economy’s GDP, jeopardize 23 per cent of jobs, and reduce total wage income by 16 per cent. Their severe shock scenario predicted a 67% decline in the demand for the transportation and warehousing (including air, rail, and transit) sector.
Baker et al. (
2020) found an increase in consumer spending at the early stage of the pandemic due to stockpiling, and sharp declines in the subsequent weeks, with public transportation and air travel seeing the largest impacts.
Concerning the effects of long-time planning in transportation infrastructure on the overall economy, a case study of Tatarstan is worth mentioning as it provides an overview of possibilities a large-scale logistics center (LC) carrying out integrated logistics (information, storage, and transport) has for a local economy (
Gafurov et al. 2014).
Hammes (
2013) studied the factors affecting the choice of projects to be included in the National Transport Infrastructure Plan for 2010–2021 in Sweden, controlling for CBA results, finding no evidence for the hypothesis that large agglomerations are in any way discriminated against. This is once again commensurate to the Marshallian hypothesis of agglomeration effects. Continuing on long-time transportation infrastructure planning,
Laird and Venables (
2017) concluded that major transport investment is frequently made in terms of impact on economic performance, mostly cost–benefit analysis broadened by a set of other economic mechanisms creating the risk of legitimizing incommensurable effects. Appraisal frameworks need to capture all relevant impacts, and there is a need for context-specific appraisals with due care.
The industrial technological spillovers on transportation industry were analyzed by
Tsekouras et al. (
2016). They adopted a metafrontier framework and tested it with a Panel General Method of Moments on Air, Land and Water data, on the transportation industries of seventeen European countries for the period of 1999–2006. They found that path dependence is a major determinant of the productive performance of European transportation systems with divergence and clustering processes present (
Tsekouras et al. 2016).
Alstadt et al. (
2012) analyzed the effects of transportation system improvements on economic growth and productivity by changing access to markets and connectivity. Their study demonstrated the impact of various transportation projects on business concentration and productivity, but indirectly, via a two-step process by econometric models testing the relationship between access and connectivity characteristics of local areas and relative levels of business productivity, job concentration, and export base. Their results confirmed that different types of access are relevant to different industry sectors. As a consequence, the productivity and agglomeration of a given industry in a given area can be related to more than one dimension of accessibility. These results can have important implications for estimating the wider economic benefits of transportation investment and suggest the need for complex multimodal transportation project proposal appraisals (
Alstadt et al. 2012).
As may be seen from the above, the literature in this specific field is scarce and sparse. Thus, we hope our analysis may improve the state of knowledge in the field and commence some desired discussion in the future. Our analysis mostly focuses on the statistical associations between the overall industry and the transportation industry, as well as its constituent sectors. It was our desire to identify potential multiplier effects, but in contrast to other studies, with regard to the direction of causality and concentrating on changes.
3. Data and Methods
We used sectoral data for the non-financial business economy value added at factor costs in million euro according to the NACE nomenclature from B-J and L-N, and especially C: Manufacturing as independent variables to test several conjectures about statistical associations with the transportation sector categories: air, land, and water separately, as well as with the cumulative transportation sector (H: transportation and storage) as a dependent variable. We used the yearly data for Croatia in the period from 2008 to 2015 (
Croatian Bureau of Statistics 2018;
European Commission 2017). Our goal was to investigate the dependence of the transportation sector value added on other industry sectors’ value added. Firstly, we correlated the natural logarithms of the cumulative sectoral and transport category data. Afterwards, we constructed a panel of data by splitting the cumulative data into groups based on enterprise sizes (size classes according to the number of employees: 0–9, 10–49, 50–249, and 250+ employees). Panel data analysis is useful to obtain consistent estimates in the presence of omitted variables (
Baltagi 2005;
Wooldridge 2002). We pooled the data into a stacked form, by grouping the data belonging to a single variable into a single column. Then, we tested the variables for unit roots in individual intercepts and trends. The performed tests were the Levin, Lin, and Chu
t-test, and Breitung t-statistics with the null hypothesis assuming common unit root processes, as well as the Im, Pesaran, and Shin W-statistics, Augmented Dickey–Fuller/Fisher Chi-square, and Phillips–Perron/Fisher Chi-square statistics, where the null hypothesis assumes individual unit root processes. Subsequently, if the individual time series exhibits unit roots, i.e., non-stationarities, the time series needs to be first-differenced, and the process repeated on the residuals until weak stationarity (without normality) is reached. We also conducted a preliminary Granger “causality” test on first-differenced data with a lag = 1, to eliminate the falsified conjectures about possible causalities. We also calculated a correlation matrix of first-differenced data on all variables to eliminate those correlations having plausible grounds for multicollinearity. We tested, with the Hausman test, whether or not individual cross-section components in terms of enterprise sizes may have an impact on the overall results. A central assumption of the Hausman test is that the random effects are uncorrelated with the explanatory variables. It tests whether we should be using a random effects or a fixed effects estimation. Panel ordinary least squares are usually biased and inconsistent because of unobserved heterogeneity in the data. One of the ways to circumvent this problem is to use first differencing. This does not eliminate only the unobserved heterogeneity that does not vary across time but does vary across the cross-section variable instead, but it also eliminates the idiosyncratic error. For all practical purposes, we decided to use a panel estimated generalized least square (EGLS) with cross-sectional weights. This method is used to control for heteroscedasticity or auto-correlation problems, with good results and high significance most of the time. All data were first differenced, except where explicitly natural logarithms were used. For additional information on the used statistical tests, please consult
Baltagi (
2005) as well as
Wooldridge (
2002). For all statistical purposes, including both statistical hypothesis testing, as well as inferential coefficient estimation, a significance level of
p < 0.01 was used. All statistical analyses were performed in the Eviews statistical software package (
EViews 2015).
4. Results and Discussion
Descriptive statistics is necessary for the choice of further statistical tests. If the dataset does not tend to be strongly stationary (normally distributed) or at least weak stationary (without any structural breaks in level or trend), logarithms to achieve linearity and normality, or first differences to achieve at least weak stationarity, will have to be used for inference testing. We initiate our analysis by showing the descriptive statistics for the data at hand (
Table 1).
Table 1 shows the usual descriptive metrics of mean, median, standard deviation, and the Jarque–Bera test results. The Jarque–Bera test is used as a benchmark for the normal distribution. The limit value is usually set at around 7, whereby distributions having the value greater than 7 are not normally distributed.
From the descriptive statistics’ Jarque–Bera test results, we may conclude that most of the variables have a close to a normal distribution, except for land transportation that with a Jarque–Bera index of 49.72 is significantly higher than the borderline 7.00. Thus, for most variables, parametric tests are acceptable without the use of logarithms to achieve linearity, but for some of them we need to take the natural logarithm of the data.
For purposes of identifying possible multicollinearity or linearly non-independent variables, a correlation matrix between all analyzed variables is needed.
Table 2 shows the correlation matrix of first-differenced variables of interest. We first differenced the variables as the paper in general deals with the changes in variables, and to control for strong non-stationarity (non normal distribution) but also weak non-stationarity (in level and trend). The correlation matrix shows a strong statistical association between the growth of the industrial sector and the transportation sector taken cumulatively, as well as by individual categories (
Table 2).
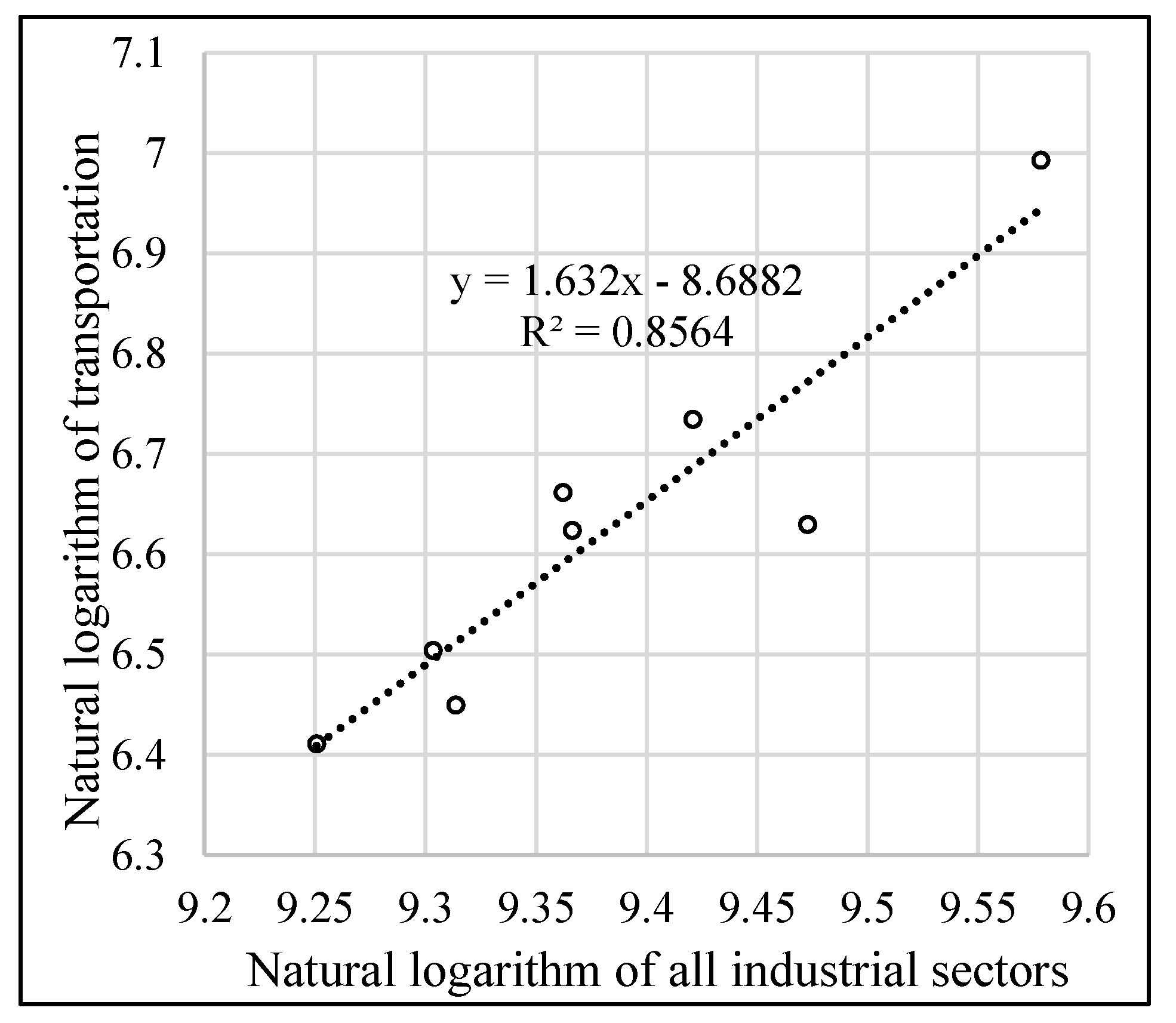
We now proceed to the diagrammatic correlation analysis between the transportation sector and its categories and the industry, with the manufacturing taken separately. By correlating logarithms of scalars, we look at the statistical association between the states of the world, and get the coefficient of direction from the equation (
Figure 1 and
Figure 2).
Figure 1 and
Figure 2 show a similar behavior of the manufacturing sector compared to the industrial sector. Both are elastic, meaning a 1% increase in industrial and manufacturing production is associated with a more than 1% increase in the demand for transportation services. This is not unexpected, as the manufacturing sector, because of division of labor, indispensably and incrementally requires transportation services.
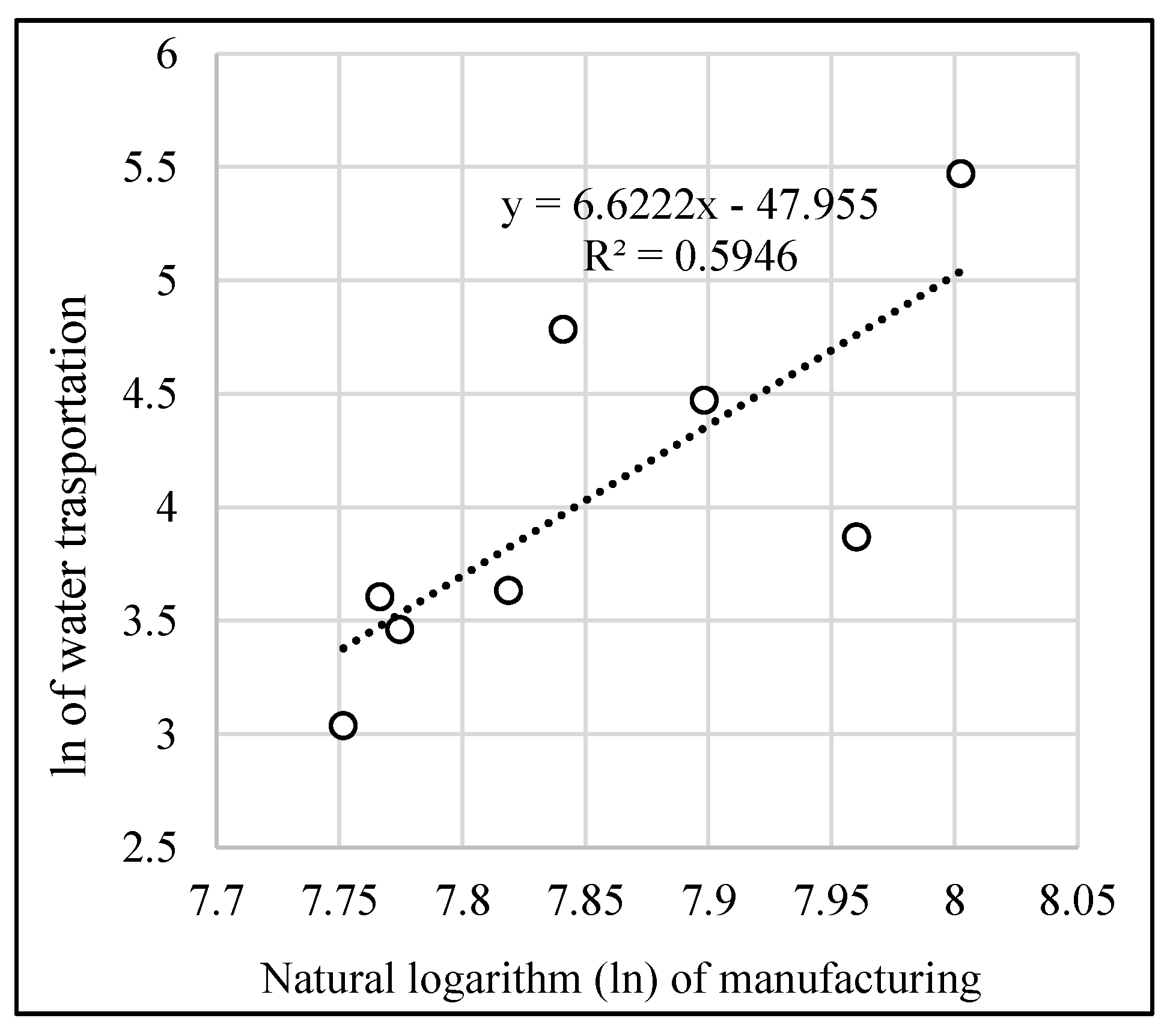
The relation between all industrial sectors and water transportation is shown in
Figure 3. The vector parameter is in this case 0.8, half of total transportation.
Regarding
Figure 3 and
Figure 4, one particular feature in
Figure 4 is striking: the value of the vector parameter between manufacturing and water transport. With 6.62, its value is manifold the values of other three correlations. This could be explained by the role of shipping in the transportation of manufactured goods. Manufactured goods are mostly containerized and shipped, explaining the relationship between the two variables.
Before proceeding to the statistical inferential analysis, we tested the variables for their stationarity. Stationarity in both its strong and weak form is an important precondition of time series if parametric tests are to be used. Strong stationarity means statistical normal distribution, and weak stationarity means the absence of structural breaks in level or trend. Structural breaks of any kind are incommensurable with parametric tests. That is why several different panel unit root tests are used simultaneously to prevent possible mistakes in the rejection of non-stationarities.
The augmented Dickey–Fuller test, for most of the variables, shows their non-stationarity. For illustration purposes, the tables for borderline cases of interest including total industrial production and transportation are shown (
Table 3 and
Table 4).
The unit root test confirms the null hypothesis of the panel not being stationary in level or in trend. Only the Phillips–Perron/Fisher Chi-square test points to the possible lack of unit roots, but this test is not as strict as the others. The non-stationarity in level is most certainly due to a sudden fall in industrial production of all sectors during the global 2008–2009 crisis, and the non-stationarity in trend is a consequence of prolonged negative economic trends afterwards. We test for non-stationarities in all variables but we only show the results for the transportation sector as an example of the test (
Table 4).
The results of the panel unit root tests unequivocally show all data is non-stationary. Consequently, we decided to first-difference all variables. When we correlate first-differenced variables, we look at statistical associations between changes in variables
Table 5 shows the results of the Granger “causality” test.
The results cannot disprove the possible causal relationship between overall industry and the transportation sector.
We then had to decide whether to use the fixed or the random effects panel analysis. For this purpose, we conducted the Hausman test for model misspecification in panel data analysis. The Hausman test looks for a correlation between the errors and the regressors in the model. The null hypothesis is that there is no correlation between the two. In case of failure to reject the null hypothesis, a random effects model is the preferred model in terms of efficiency and consistency of its estimators of true population parameters (
Stephanie 2017).
The results of the Hausman test (Chi-square statistic: 9.376,
p = 0.002) show that we can reject the null hypothesis of the viability of a random effects test equation and that we are dealing with cross-section fixed effects (R
2 = 0.954, F-statistic = 140.022,
p < 0.001). We used the fixed effects approach (cross-section weights) and additionally differenced the variables for full stationarity. An additional fact gained from differencing can be used in the description of the results: differenced dependent and independent variables in inferential analysis may be used as statistical associations between changes. Thus, if the Granger “causality” test by falsification determined the probable direction of causality, and first differencing eliminated the autoregression, the remaining results are more probable than not to show the “true causality” (
Stephanie 2017).
Therefore, we proceeded with panel EGLS tests for industrial production and transportation categories (
Table 6).
From the panel EGLS test statistics summary (
Table 6), it is evident that there is a statistically significant relationship between the industrial production variables (total industry and manufacturing) and the transportation sector (land, water, and air). There is though, one notable exception in the panel EGLS (
Table 6, row 7): a not statistically significant correlation between industrial production and air transportation. We explain this by the fact that in Croatia, as a tourist destination, air traffic’s primary role is passenger transport. Nevertheless, if we look back at
Table 2, row 2 and 3, showing the Granger “causality” test correlating industry and manufacturing with air transport, the connection suddenly reappears. This is because the Granger “causality” test correlates not only the time lagged dependent variable against the independent, but also against itself, eliminating in this way the autoregressive component of the dependent variable from the equation. All industrial sectors, including manufacturing, have a strong statistical association with the transportation sector. Although the transportation sector includes industries providing transportation of passengers and cargo, warehousing and storage for goods, other modes of transportation as well as connected services and utilities, we analyzed air, land, and water, as they are representative of moving industrial and manufacturing produce. The analyzed modes were statistically associated to industrial and manufacturing production. Unfortunately, the data are for the period 2008–2015 only, whereby Croatia ended the recession only during Q4/2014–Q2/2015. The data, when taken by the value of the vector parameters, show a potential for growth in the transportation sector, and especially because of steady growth in manufacturing. Manufactured products are usually containerized, and this is the primary reason for high statistical association between the rise in the value added of manufacturing, the value added in shipping, water transportation, and the number of twenty-foot equivalent units (TEUs).
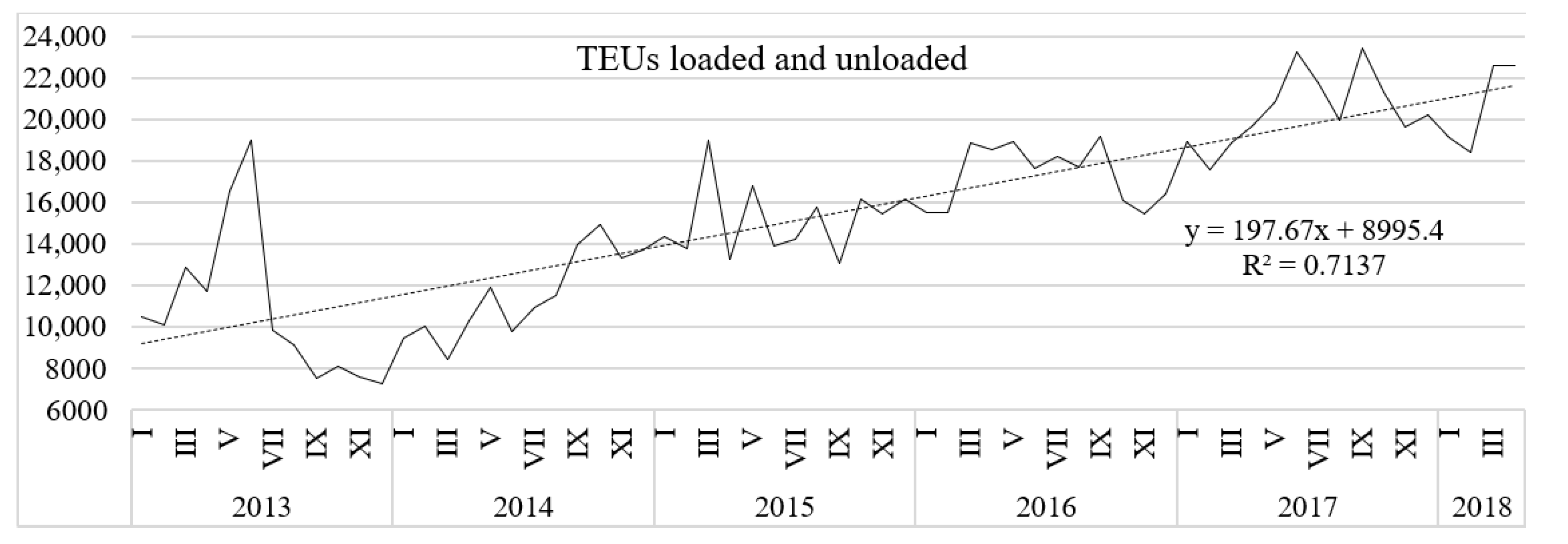
Figure 5 shows a positive trend in loaded and unloaded twenty-foot equivalent units (TEUs) at Croatian ports (
Croatian Bureau of Statistics 2018;
European Commission 2017).
In addition to the cargo in transition, the most prominent growth factor is the manufacturing industry. For every unit of growth in manufacturing, there are six units of growth in the water transportation category of the transportation sector. Even after differencing the non-stationary trends, the change in manufacturing shows the highest parameter coefficient and the highest coefficient of determination (R2 = 0.511) among the analyzed factors. This is fully commensurate with economic theory and the size of the Croatian economy. The smaller an economy, the larger the share of international trade in its gross national product. In other words, the smaller an economy, the larger the positive effects of the division of labor on the transport sector relative to its size. In addition to that, we should not forget Croatia’s geographic position and the ability of docking even the largest deep-sea container ships.
5. Conclusions
Economic development is as much dependent on the transportation sector and its categories (air, land, and water) as on the industry in general and the manufacturing sector in particular. As an economy develops, so does its division of labor through specialization. The more it specializes, the more it transports domestically and abroad. Thus, economic development, represented by economic growth, should have a progressive statistical association with the transportation sector and its categories (air, land, and water). In this communication, we analyzed the statistical associations between the aforementioned sectors and categories of value added data for the Croatian economy between 2008 and 2015. We used several statistical methods at our disposal. Firstly, we correlated the logarithms of the variables to test for statistical associations between scalars (states of the world). Secondly, we used panel EGLS with cross-section weights on differenced variables to test for statistical associations between changes in the variables. In all cases, the results showed statistically significant correlations and coefficients of determination at p < 0.05 level. We conclude there is a statistically significant relationship between domestic industrial and manufacturing sectors and the transportation sector and its categories, with the Granger causality tests pointing to a direction going from the industrial and manufacturing sectors to the transportation sector and its categories, a relationship fully commensurate with the economic theory of development. Nevertheless, looking at the parameter coefficients, this relationship is not as strong as one would expect. The lack of any causality going from the development of the transportation sector to the development of the overall economy and manufacturing, since one would expect an autoregressive relationship, may be due to lacking investments into transportation infrastructure, especially rail. This research, though, has one strong limitation: it does not look into Croatia’s position as a shipping hub for surrounding countries. This prospect is also severely challenged by the lack of investments in railway infrastructure, a major infrastructural bottleneck for the transportation of containerized manufactured produce, both domestic and foreign, both for domestic consumption and just in transition. We anxiously await the data of increased transportation and its influence on the economic development once the major railway routes are modernized.