Growth Dynamics, Multiple Equilibria, and Local Indeterminacy in an Endogenous Growth Model of Money, Banking and Inflation Targeting ^†

Abstract

We develop an overlapping generations monetary endogenous growth (generated by productive public expenditures) model with inflation targeting, characterized by relocation shocks for young agents, which in turn generates a role for money (even in the presence of the return-dominating physical capital) and financial intermediaries. Based on this model, we show that growth dynamics emerge with a S-shaped growth path producing three equilibria. The low and high-growth equilibria are stable, but locally indeterminate, while the medium-growth equilibrium is unstable. Since, government expenditure is productive in our model, a higher inflation-target would translate into higher growth, but under multiple equilibria, this is not necessarily always the case.

1. Introduction

Introducing (non-interest bearing) money in general equilibrium models with single or multiple assets that yield non-negative nominal interest rate is, understandably, not straightforward. In this regard, multiple modelling approaches exist to motivate the role of money in such models; for example, money in the production function, money in the utility, cash-in-advance, shopping time, money search, mandatory cash reserve requirements (see Walsh 2017 for a detailed discussion of these models). Following Diamond and Dybvig (1983), an alternative approach to create a role of currency for transactions in general equilibrium models, even if money is dominated in the rate of return, is based on spatial separation and limited communication. In this context, economic agents are subject to random relocation (liquidity preference) shocks, and fiat money is the only asset available to relocating agents for smoothing consumption at the new location, since they would have given up their claims on returns to capital that they held at their old location.

By modelling money in this manner, a number of recent studies have analyzed the effects of traditional monetary policies, i.e., money growth rate and cash-reserve requirements (which the financial intermediaries in the model are subjected to), and fiscal policy on growth, inflation and welfare in endogenous growth models (see for example, Espinosa-Vega and Yip 1996, 1999, 2002; Gupta 2007; Bose et al. 2007; Ghosh and Neanidis 2017). Against this backdrop, our paper aims to build on this line of theoretical set-up of incorporating money, by introducing, for the first time in this literature, a monetary authority that targets the inflation rate rather than the money growth rate, given the growing importance of inflation-targeting across the world.1

Specifically speaking, we develop an overlapping generations (OLG) monetary endogenous growth (due to public expenditures in the firms’ production function) model with inflation-targeting, characterized by relocation shocks for young agents, which in turn generates a role for money (even in the presence of the return-dominating physical capital) and financial intermediaries. Given this model, we show that growth dynamics emerge, with the growth path being S-shaped. On one hand, this results in three equilibria, with the low and high-growth equilibria being stable, but both of which are found to be locally indeterminate. On the other hand, the medium-growth equilibrium is unstable. Since, government expenditure is productive in our model, a higher inflation-target would translate into higher growth, but under multiple equilibria, an increase in the inflation-target is not necessarily going to be growth-enhancing at the medium-growth unstable equilibrium, which cannot be ruled out due to indeterminancy of the two other stable equilibria.

Our paper, in the process, also adds to the recent literature of monetary endogenous growth OLG models with money being modelled either through the cash-in-advance constraint or cash-reserve requirements of banks, that has shown the existence of growth dynamics, multiple equilibria (with possibility of chaos), and local indeterminacy (see for example, Gupta and Vermeulen 2010; Gupta 2011; Kudoh 2013; Gupta and Stander 2018). However, unlike these papers, which rely on an ad hoc approach of modelling financial intermediaries, we are able to provide a solid reasoning of the existence of banks based on the liquidity shock characterizing our model. Further, in our framework, we are also able to analyze growth dynamics and the impact of changes in the inflation-target by accommodating for the existence of unofficial financial markets, which are widely witnessed within the financial system of many developing economies (see Gupta 2008, 2009; Goswami and Gupta 2009, and references cited therein for detailed discussion in this regard).

At this stage, it is important for us to highlight in greater detail, in terms of the structure of the model, as to how our paper differs from the closely related studies of Gupta and Vermeulen (2010), Kudoh (2013), and Gupta and Stander (2018). To create growth dynamics in their models, Gupta and Vermeulen (2010) and Gupta and Stander (2018) had to respectively introduce probability of survival as a function of private and public investment, and lagged inputs respectively, while Kudoh (2013) had to rely on lump-sum, rather than income taxation. In terms of introducing money, Kudoh (2013) used an ad hoc cash-in-advance model while the other two papers introduced cash-reserve requirements that the banks need to hold, though, unlike us without providing proper microfoundation to the existence of banks. While these studies, like in our paper also produces multiple equilibria and indeterminancy, our paper does the same in the context of an inflation targeting monetary authority, by without having to introduce additional features (like, endogenous probability of death, lagged input, or lump-sum tax) in a more realistic model of money and financial intermediation. While our model does not produce chaotic growth dynamics as in the papers of Gupta and Vermeulen (2010), Kudoh (2013), and Gupta and Stander (2018), we are able to incorporate an important feature of developing economies in our model in the form of unofficial financial markets. In sum, our framework caters to both developed and developing inflation targeting economies, with proper microfounadtions for an explicit role of money, and a motivation for the existence of a banking system required to intermediate capital. In sum, our model is more general than the works of Gupta and Vermeulen (2010), Kudoh (2013), and Gupta and Stander (2018). Having said this, future work within our framework would need us to incorporate features to produce chaotic dynamics, which in turn have been shown to be present in data associated with economic growth, as pointed out by Kříž and Knězáčková (2014).

The remainder of the paper proceeds as follows: Section 2 outlines the economic environment. Section 3 develops the benchmark version of the monetary endogenous growth OLG model, while Section 4 provides several extensions of benchmark model, with which we analyze growth dynamics, as well as, impact of the changes in the inflation target. Section 5 offers some concluding remarks.

2. The Economic Environment

The economy has four principal agents, namely two-period lived overlapping generations consumers, financial intermediaries (banks), firms and an infinitely-lived government. There exists an infinite sequence of two-period-lived overlapping generations, besides, an initial old generation. At each date $t=0,1,2\dots$, young agents are assigned to one of two symmetric locations (indexed by $j=1,2$). Without loss of generality, each location is assumed to contain a continuum of young agents with unit mass. In each location, an individual firm produces a perishable consumption good $\left(y_t\right)$ by employing physical capital $\left(k_t\right)$, labour $\left(n_t\right)$ and a publicly-provided intermediate input $\left(g_t\right)$. Formally, the production function is as follows:

$$y_t=A{k}_t^{\alpha }{\left(n_t{g}_t\right)}^{1-\alpha }$$

(1)

where $A>0$ is a technology parameter, $0<\alpha (1-\alpha )<1$ is the elasticity of output with respect to capital and labour or productive government expenditure, respectively.

The firms’ unit of capital at time $t+1$ is acquired out of forgoing a unit of the consumption good at time t. Note that (1) is subject to constant returns to scale in k and n whereas there are increasing returns to scale in all the three inputs, k, n and g. As in Bencivenga and Smith (1991, 1992), we assume that there are no retail markets for capital such that each firm uses only its own capital in production. Following Barro (1990), we assume that g is non-rival and non-excludable and that each firm takes the level of g as given while solving its own optimization problem. As such, (1) exhibits private diminishing returns. We also assume that except for the initial old, agents have no endowment of capital or consumption goods.

We assume that all young agents are ex ante identical and are endowed with one unit of labour which they supply inelastically in time t and earn a real wage, $w_t$. They retire when old and only care about old-age consumption and as such they save all of the time t wage income. We have that $c_{it}$ is the age i consumption of a representative agent of generation time t such that the life-time utility is defined by a preference function of the form

$$U\left(c_{1t},c_{2t}\right)=ln\left(c_{2t}\right)$$

(2)

As pointed out above, young agents are assigned to two symmetric locations (indexed by $j=1,2$) at each time period, t. At the beginning of each period, agents are completely separated by location and all transactions in goods, labour and assets are conducted in autarky within each location. The source of differences among young agents emanate from their locations ex post. In each of the two locations, a fraction $0<\sigma <1$ of young agents are randomly relocated to the other location. The probability of relocation $\sigma$, is constant across periods, identically and independently distributed ($i.i.d$) across agents and is known to all agents.

The economy is populated by a finite number of banks that are regarded as being cooperative entities set up by an alliance of young-age consumers. By design, banks can exploit the law of large numbers whereas individuals cannot. Hence, if banks exist then all savings will be intermediated, as detailed in Diamond and Dybvig (1983). Banks accept deposits, $D_t$ from young-age consumers at each time period t and use them to acquire two primary assets available in the economy: fiat money, $M_t$, and capital, $k_t$. These two assets are created in order to maximize young-age consumers’ lifetime utility given by (2). Similar to the spatial separation form of OLG models of Townsend (1987), Champ et al. (1996), Espinosa-Vega and Yip (1996) and Gupta (2007), our model set-up implies that the stock of nominal money, $M_t$, is the only asset available to relocating young agents for consumption at the new location as they would have given up their claims on returns to their capital.

The government, which is assumed to be infinitely-lived and made up of only the inflation-targeting monetary wing for the sake of simplicity and without loss of generality, purchases $g_t$ units of consumption goods. Government expenditure is assumed to be a productive factor in the firms’ production function. Government’s productive consumption expenditure is wholly financed by seigniorage (inflation tax).

3. The Benchmark Model

Below we present the optimized solutions of the various agents in the economy, with details of the derivation provided in Appendix A.

3.1. Factor Markets

If we take the real wage, $w_t$, real rental of capital, $r_t$ and public capital, $g_t$ to be parametric, then the firms’ profit maximization implies that factors are rewarded according to their respective marginal productivities. Formally,

$$n_t:w_t=(1-\alpha )A{\left(\frac{k_t}{n_t}\right)}^{\alpha }{g}_t^{1-\alpha }$$

(3)

(3) represents the optimal hiring decision for a firm. The firm will hire labour up to a point whereby the marginal product of labour is equal to the real wage and

$$k_t:r_t=\alpha A{k_t}^{\alpha -1}{\left(n_t{g}_t\right)}^{1-\alpha }$$

(4)

3.2. Financial Intermediaries

By design, financial intermediaries can exploit the law of large numbers whereas individuals cannot. Thus if banks exist then all savings are intermediated. Young agents deposit their wage income, $w_t$ at each date t which, in turn, is used by banks to acquire primary assets: money and capital. When banks hold fiat money, $M_t$, supplied inelastically by the government and the old, they receive a return of

$$\frac{P_t}{P_{t+1}}=\frac{1}{{\mathsf{\Pi }}_{t+1}}=R_t^m$$

(5)

where where $P_t$ denotes the economy’s price level at time t and $P_{t+1}$ is the time $t+1$ price level. ${\mathsf{\Pi }}_{t+1}$ is the gross rate of inflation. On the other hand, banks receive $r_{t+1}$ on their investment in capital. Finally, $R_t^a$ and $R_t^s$ are the returns paid by the banks to agents that have been relocated and those that remain at the original location, respectively.

In this model, fiat money is the only means of smoothing consumption in the face of relocation. Banks’ portfolio problem amounts to maximizing the welfare of young agents taking into account the fact that some of their customers can be suddenly relocated. To that end, banks hold fiat money and thus in essence fulfil a liquidity provision role in the economy.

Further, to satisfy the needs of customers that remain at the original location, banks invest in capital. They choose $q_t$, the fraction of their assets held as capital, that is, $q_t=\frac{k_{t+1}}{w_t}$, to maximize the expected lifetime utility of a representative depositor. Formally,

$$\underset{0\le q_t\le 1}{max}V=ln\left(w_t\right)+\sigma ln\left[R_t^a\right]+(1-\sigma )ln\left[R_t^s\right]$$

(6)

subject to two resource constraints. First, there exists $\sigma$ relocated agents, who must be provided with fiat money. This is accomplished with the bank’s holdings of fiat money. Since the return paid to each unit of fiat money is $\frac{1}{{\mathsf{\Pi }}_{t+1}}$, the following condition must hold:

$$\sigma R_t^a=(1-q_t)R_t^m$$

(7)

Whenever $R_t^a$ dominates the return on fiat money, all savings are channelled through financial intermediaries and the only relevant asset choice problem is the one depicted above in Equation (6). So the $(1-\sigma )$ agents that remain at the original location will be paid through the banks’ investment in physical capital. By diversifying their capital investments, banks ensure themselves one unit of capital at time $t+1$ for one unit of deposit made at time t. Given the time $t+1$ rental rate of capital as $r_{t+1}$, $R_t^s$ must satisfy the second resource constraint:

$$(1-\sigma )R_t^s=q_t{r}_{t+1}$$

(8)

The solution to maximizing problem (6) subject to (7) and (8) is given by:

$$q_t=q=(1-\sigma )$$

(9)

3.3. Government

The government’s budget constraint at time t, in real per-capita terms, is:

$$g_t=\frac{M_t-M_{t-1}}{P_t}$$

(10)

We deliberately ignore taxes to keep our model simple without affecting the main results. The government coordinates operations of the central bank, which serves the government’s interests. The government, through the central bank, conducts an inflation targeting framework with a goal to maintain price stability.

With ${\mathsf{\Omega }}_t$ defined as the period t gross growth rate of the economy at time t, ${\mathsf{\Pi }}_t$ as the time t gross inflation and that in this model’s monetary regime, the government targets inflation such that ${\mathsf{\Pi }}_t=\widehat{\mathsf{\Pi }}$, the government’s budget constraint, in real terms, can be expressed as

$$g_t=m_t\left(1-\frac{1}{{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}\right)$$

(11)

3.4. Household’s Portfolio Decisions

The portfolio optimization problem of the young agent is as follows. At each time point, young agents allocate their entire savings, $w_t$ in the forms of real bank deposits, $d_t$, real money balances, $m_t$ and capital, $k_t$. Defining ${\psi }_1$, ${\psi }_2$ and $(1-{\psi }_1-{\psi }_2)$ as the fraction of savings held as, $d_t$, $m_t$ and $k_t$, respectively, young agents solve the following problem:

$$\underset{{\psi }_1,{\psi }_2}{max}ln\left[w_t\right]+\sigma ln\left[{\psi }_1{R}_t^a+{\psi }_2{R}_t^m\right]+(1-\sigma )ln\left[{\psi }_1{R}_t^s+{\psi }_2{R}_t^m+(1-{\psi }_1-{\psi }_2)r_{t+1}\right]$$

(12)

Assuming that $r_{t+1}>R_t^m$, that is, capital return dominates real balances, ${\psi }_2=0$. In other words, the money holdings by young savers are implicit in their holding of bank deposits exclusively. Solving (12) under the condition that ${\psi }_2=0$, the optimal solution for ${\psi }_1$ is given as follows:

$${\psi }_1=\frac{\sigma \left(r_{t+1}\right)}{r_{t+1}-R_t^s}$$

(13)

with $r_{t+1}\ge R_t^s$. Given that the upper limit of $R_t^s$ is $r_{t+1}$, whenever $r_{t+1}=R_t^s$, ${\psi }_1=1$.

3.5. Equilibrium

• Given $w_t$, $R_t^a$, $R_t^s$, ${\mathsf{\Pi }}_{t+1}$ and $r_{t+1}$, a bank chooses $q_t$ to maximize expected lifetime utility of the depositor, (6), subject to (7) and (8).
• Given $w_t$, $R_t^a$, $R_t^s$, ${\mathsf{\Pi }}_{t+1}$ and $r_{t+1}$, young agents maximize their utility (2), by choosing ${\psi }_1$ with ${\psi }_2=0$ .
• Given $g_t$, $w_t$ and $r_{t+1}$, firms maximize profits and (3) and (4) holds.
• Money market equilibrium conditions: $\frac{M_t}{P_t}=m_t=(1-q_t)w_t$ is satisfied for all $t\ge 0$.
• The loanable funds market equilibrium condition: $k_t=q_t{w}_t$ is satisfied for all $t\ge 0$.
• The goods market equilibrium condition requires: $c_{2t}+k_t+g_t=A{k}_t^{\alpha }{\left(g_t{n}_t\right)}^{(1-\alpha )}$ is satisfied for all $t\ge 0$.
• The labour market equilibrium condition: $n_t=1$ for all $t\ge 0$.
• The government budget constraint (10) is balanced on a period by period basis.
• $d_t$, $r_{t+1}$ and $P_t$ must be positive at all dates with $r_{t+1}>R_t^m$.

3.6. Steady-State Growth

Assuming that there are no legal restrictions on financial intermediaries, then ${\psi }_1=1$ in equilibrium and all primary asset holdings are intermediated such that

$$k_{t+1}=q_t{w}_t$$

(14)

Substituting (11) into (3) and using the money market equilibrium, the government budget constraint and $q=1-\sigma$, we obtain the gross growth rate of the economy to be

$${\mathsf{\Omega }}_{t+1}=\frac{k_{t+1}}{k_t}=(1-\sigma ){\left(A(1-\alpha )\right)}^{\frac{1}{\alpha }}{\left[\sigma \left(1-\frac{1}{{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}\right)\right]}^{\frac{1-\alpha }{\alpha }}$$

(15)

Going by (15), the economy’s growth rate at time $t+1$, i.e., ${\mathsf{\Omega }}_{t+1}$ is a function of the same at time t, i.e., ${\mathsf{\Omega }}_t$, and hence, this economy will have transitional dynamics. Note if the monetary authority followed a traditional money growth rule, i.e., say $M_t={\mu }_t{M}_{t-1}$, with $\mu$ being the gross growth rate of nominal money balances, then the growth path would be: ${\mathsf{\Omega }}_{t+1}=\frac{k_{t+1}}{k_t}=(1-\sigma ){\left(A(1-\alpha )\right)}^{\frac{1}{\alpha }}{\left[\sigma \left(1-\frac{1}{{\mu }_t}\right)\right]}^{\frac{1-\alpha }{\alpha }}$, i.e., there would be no growth dynamics. In other words, the inflation-targeting behaviour of the central bank is what produces the growth dynamics in our model.

4. The Model with Compulsory Reserve Requirements

In this section, we subject banks to compulsory cash reserve requirements that are administered by the government. We follow Bencivenga and Smith (1992), Espinosa-Vega and Yip (1996) and Gupta (2007) in setting the obligatory reserve requirement as a cap on the portion of banks’ portfolio that can be held as capital. This implies that we restrict (9) to $\overline{q}<(1-\sigma )$, where $\overline{q}$ represents the obligatory reserve requirement.

In an environment with binding reserve requirements, banks are limited to set the fraction of their portfolio held as capital to $0\le \overline{q}\le (1-\sigma )$. In this set up, (13), which equates ${\psi }_1$ to 1, may not hold. The implication of this is that banks will not be in a position to intermediate all the primary assets. The mandatory reserve requirements can be so severe to the extent that ${\psi }_1<1$. In that case, some investments would have to be financed internally. In the face of obligatory reserve requirements, the benchmark model resource constraints given by (7) and (8) change to

$$\sigma R_t^a=\frac{(1-\overline{q})}{{\mathsf{\Pi }}_{t+1}}>\frac{1}{{\mathsf{\Pi }}_{t+1}}$$

(16)

$$(1-\sigma )R_t^s=\overline{q}{r}_{t+1}<r_{t+1}$$

(17)

Even though banks are subjected to a repressive financial sector in the form of binding reserve requirements, from (13) and (17) we can establish the interval within which the government can facilitate that all agents be able to intermediate their entire savings through banks. Specifically, we can have ${\psi }_1=1$ if and only if ${(1-\sigma )}^2\le \overline{q}\le (1-\sigma )$.

In the case whereby banks are restricted to invest a fraction, $\overline{q}$ of their deposits into capital, the economy’s time $t+1$ gross growth rate (${\mathsf{\Omega }}_{t+1}$) is given by

$${\mathsf{\Omega }}_{t+1}=\overline{q}{\left(A(1-\alpha )\right)}^{\frac{1}{\alpha }}{\left[(1-\overline{q})\left(1-\frac{1}{{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}\right)\right]}^{\frac{1-\alpha }{\alpha }}$$

(18)

We proceed to analyse the growth dynamics of the model with compulsory reserve requirements. According to (18), the economy’s growth dynamics are centred on the relationship between ${\mathsf{\Omega }}_{t+1}$ and ${\mathsf{\Omega }}_t$, in that ${\mathsf{\Omega }}_{t+1}=f\left({\mathsf{\Omega }}_t\right)$. In this paper, we assume that the parameter values of $\overline{q}$, A, $\alpha$, and $\widehat{\mathsf{\Pi }}$ are such that the model will always produce steady-state(s).2 There is a positive relationship between ${\mathsf{\Omega }}_{t+1}$ and ${\mathsf{\Omega }}_t$ in that an increase in ${\mathsf{\Omega }}_t$ leads to an increase in the reserve-augmented seigniorage revenue for the government. This increases the ratio of real government expenditure to the real wage, $\frac{g_t}{w_t}=(1-q_t)\left(1-\frac{1}{{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}\right)$, and hence a higher gross growth rate, ${\mathsf{\Omega }}_{t+1}$ emanating from higher government productive expenditure. The model’s possible growth path(s), including the position and equilibrium, is (are) dependent on the values of parameters A, $\overline{q}$, $\alpha$ and $\widehat{\mathsf{\Pi }}$, given ${\mathsf{\Omega }}_t$. The relationship between ${\mathsf{\Omega }}_{t+1}$ and ${\mathsf{\Omega }}_t$ can be inferred from the first derivative of ${\mathsf{\Omega }}_{t+1}$ with respect to (w.r.t) ${\mathsf{\Omega }}_t$ and is

$$\frac{\partial {\mathsf{\Omega }}_{t+1}}{\partial {\mathsf{\Omega }}_t}=\overline{q}{(1-\overline{q})}^{\frac{1-\alpha }{\alpha }}{A}^{\frac{1}{\alpha }}\frac{{(1-\alpha )}^{\frac{1+\alpha }{\alpha }}}{\alpha {\mathsf{\Omega }}_t^2\widehat{\mathsf{\Pi }}}{\left(1-\frac{1}{{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}\right)}^{\frac{1-2\alpha }{\alpha }}$$

(19)

According to (19), $\frac{\partial {\mathsf{\Omega }}_{t+1}}{\partial {\mathsf{\Omega }}_t}>0$. This confirms that (18) is an increasing function in that an increase in ${\mathsf{\Omega }}_t$ is associated with an increase in ${\mathsf{\Omega }}_{t+1}$. The curvature of the gross growth path represented by (18) is dependent on the value of the parameter $\alpha$. To show this, we proceed to compute the second derivative of ${\mathsf{\Omega }}_{t+1}$ w.r.t ${\mathsf{\Omega }}_t$ and is given by

$$\frac{{\partial }^2{\mathsf{\Omega }}_{t+1}}{{\partial }^2{\mathsf{\Omega }}_t}=\overline{q}{(1-\overline{q})}^{\frac{1-\alpha }{\alpha }}{A}^{\frac{1}{\alpha }}\frac{{(1-\alpha )}^{\frac{1+\alpha }{\alpha }}}{\alpha {\mathsf{\Omega }}_t^3\widehat{\mathsf{\Pi }}}{\left(1-\frac{1}{{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}\right)}^{\frac{1-3\alpha }{\alpha }}\left[\frac{1}{\alpha {\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}-2\right]$$

(20)

From (20), the curvature of (18) is dependent on the value of $\alpha$ that can be derived from the last part of the right-hand-side of (20) in square-brackets, which is $\left[\frac{1}{\alpha {\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}-2\right]$. For values of $\alpha$>$\frac{1}{2{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}$, (20) is negative, implying that the slope of the tangent line to (18) is decreasing as ${\mathsf{\Omega }}_t$ increases. Next, for $\alpha$<$\frac{1}{2{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}$, (20) is positive, thus the slope of the tangent line to (18) increases as ${\mathsf{\Omega }}_t$ increases. Now the inflection point occurs when $\alpha$ = $\frac{1}{2{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}$, or alternatively at ${\mathsf{\Omega }}_t$ = $\frac{1}{2\alpha \widehat{\mathsf{\Pi }}}$. Given this, Figure 1 plots the resultant growth path for ${\mathsf{\Omega }}_{t+1}$ as a function of ${\mathsf{\Omega }}_t$. Note that, when ${\mathsf{\Omega }}_t$ is equal one, i.e., zero net growth, ${\mathsf{\Omega }}_{t+1}$ will be non-zero, with the positive vertical intercept of the f locus being $\overline{q}{\left(A(1-\alpha )\right)}^{\frac{1}{\alpha }}{\left[(1-\overline{q})\left(1-\frac{1}{\widehat{\mathsf{\Pi }}}\right)\right]}^{\frac{1-\alpha }{\alpha }}$.

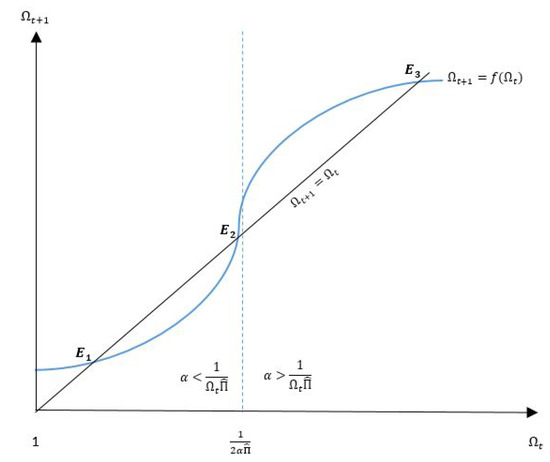
Figure 1. Growth Dynamics with Compulsory Reserve Requirements.

As can be seen, the S-shaped growth path depicted in Figure 1 produces multiple equilibria; three to be specific. The low and high-growth equilibria are stable under perfect foresight, since the f loci intersects the 45 degree line from above, while the the medium-growth equilibrium is unstable, as the f loci intersects the 45 degree line from below. Furthermore, although $k_{t-1}$ is a state variable and cannot jump, ${\mathsf{\Omega }}_t=\frac{k_t}{k_{t-1}}$ is not a state variable and, hence, can jump. This resultant jump then implies that there are infinitely many rational expectations paths to the low- and high-growth stable equilibria from any initial given value for $k_1$. Hence, the stable equilibria in this economy suffers from local indeterminacy, as there is still asymptotic convergence to the balanced growth path. It must be noted that, the equilibria at which the economy is likely to reside is conditional on $\alpha$.

Finally note that depending on whether the level of the reserve requirement is $(1-\sigma )$ or ${(1-\sigma )}^2$, there are two alternative gross growth rate paths for ${\mathsf{\Omega }}_{t+1}$:

$${\mathsf{\Omega }}_{t+1}^1={(1-\sigma )}^2{\left(A(1-\alpha )\right)}^{\frac{1}{\alpha }}{\left[(1-{(1-\sigma )}^2)\left(1-\frac{1}{{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}\right)\right]}^{\frac{1-\alpha }{\alpha }}$$

(21)

and

$${\mathsf{\Omega }}_{t+1}^2=(1-\sigma ){\left(A(1-\alpha )\right)}^{\frac{1}{\alpha }}{\left[\sigma \left(1-\frac{1}{{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}\right)\right]}^{\frac{1-\alpha }{\alpha }}$$

(22)

We can show that for ${\sigma }^2-3\sigma +2⪌1$, or alternatively, for $\sigma ⪌\frac{3-\sqrt{5}}{2}$, we have ${\mathsf{\Omega }}_{t+1}^2⪌{\mathsf{\Omega }}_{t+1}^1$. The other root of $\sigma$ is obtained from ${\sigma }^2-3\sigma +2=1$ or ${\sigma }^2-3\sigma +1=0$ and $\frac{3+\sqrt{5}}{2}>1$, hence implausible.

4.1. The Model with Different Inflation Targets

Next we analyze the growth dynamics with binding reserve requirements and different inflation targets, focusing on the relationship between ${\mathsf{\Omega }}_{t+1}$ and $\widehat{\mathsf{\Pi }}$ as given by (18). The target inflation, $\widehat{\mathsf{\Pi }}$, determines the position of the gross growth path. Going by (18), the impact of increasing (lowering) $\widehat{\mathsf{\Pi }}$ is to move the $t+1$ gross growth curve up (down), which is understandable, given that seigniorage-financed government expenditure is productive. Formally, we infer the relationship between ${\mathsf{\Omega }}_{t+1}$ and $\widehat{\mathsf{\Pi }}$ from the first derivative of ${\mathsf{\Omega }}_{t+1}$ w.r.t $\widehat{\mathsf{\Pi }}$ and is

$$\frac{\partial {\mathsf{\Omega }}_{t+1}}{\partial \widehat{\mathsf{\Pi }}}=\overline{q}{(1-\overline{q})}^{\frac{1-\alpha }{\alpha }}{A}^{\frac{1}{\alpha }}\frac{{(1-\alpha )}^{\frac{1+\alpha }{\alpha }}}{\alpha {\mathsf{\Omega }}_t{\widehat{\mathsf{\Pi }}}^2}{\left(1-\frac{1}{{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}\right)}^{\frac{1-2\alpha }{\alpha }}$$

(23)

According to (23), $\frac{\partial {\mathsf{\Omega }}_{t+1}}{\partial \widehat{\mathsf{\Pi }}}>0$, and hence an increasing function of $\widehat{\mathsf{\Pi }}$. The resulting upward movement in the growth path following an increase in the inflation-target is illustrated in Figure 2 below by the dashed curves.3

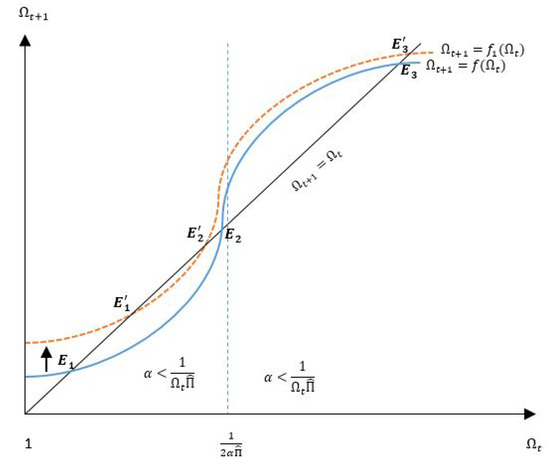
Figure 2. Growth Dynamics with Different Inflation Targets.

The policy implication of this result is that even if seigniorage-financed government expenditure is productively used, an increase in the inflation-target might not yield growth-enhancing effects, with the outcome being conditional on the threshold value of $\alpha$, i.e., $\frac{1}{2{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}$. If $\alpha$, i.e., the elasticity of per capita output w.r.t per capita stock falls below the threshold, a higher inflation-target will not increase growth at the medium-growth equilibrium. Put differently, too much weight on productive public input (i.e., higher value of $(1-\alpha )$) at the cost of private capital, could in fact reduce growth, given that in the presence of indeterminacy in the model, the high-growth stable equilibrium is not necessarily an obvious choice made by the agents in the economy. In other words, increasing the inflation target to segenerate more seigniorage-based revenue to be used productively, is not necessarily a growth-enhancing policy decision, and depends crucially on the elasticity of per capita output w.r.t per capita stock. Naturally, policymakers need to have a precise estimates for the elasticity parameters of the production function.

4.2. The Model with an Unofficial Financial Market (UFM)

Most developing economies’ financial markets are largely shallow, not organized and characterized by active and competitive UFMs, as discussed in Gupta (2008, 2009), Goswami and Gupta (2009).4 These UFMs play a greater financial intermediation role in developing economies, compared to the official banking system. This is so since UFMs are not subjected to reserve requirement policies. In cases where banks are subjected to stringent reserve requirement policies, then only a part of the capital formation is done through the official banking system, i.e., we have ${\psi }_1<1$, indicating high reserve requirements, in particular, whenever $\overline{q}<{(1-\sigma )}^2$. When reserve requirements are very high, young agents will only save ${\psi }_1=\frac{\sigma \left(r_{t+1}\right)}{r_{t+1}-R_t^s}$ with banks and the remaining in the UFM. This can be considered a rational decision considering that UFMs are free of any reserve requirements. Given that UFMs exist in developing economies, we analyse the growth dynamics in this context. Using (9) and (13), we have

$${\psi }_1=\frac{\sigma \left(1-\sigma \right)}{1-\sigma -\overline{q}}$$

(24)

where $\overline{q}\in (0,{(1-\sigma )}^2)$. In the presence of UFMs, the size of investment in physical capital stock is given by

$$k_{t+1}=\left[(1-\sigma )(1-{\psi }_1)+{\psi }_1\overline{q}\right]w_t$$

(25)

The first term on the right-hand-side of the expression represents the size of the self-financed capital investment while the second term gives the investment by financial intermediaries. Using (3), (11), (24) and (25) and the fact that only market equilibrium and government budget constraint hold, we can derive the expression for the gross rate of growth as follows:

$${\mathsf{\Omega }}_{t+1}^c={(1-\sigma )}^2{\left(A(1-\alpha )\right)}^{\frac{1}{\alpha }}{\left[(1-\overline{q})\left(1-\frac{1}{{\mathsf{\Omega }}_t^c\widehat{\mathsf{\Pi }}}\right)\right]}^{\frac{1-\alpha }{\alpha }}$$

(26)

Comparing with (18) when no UFM exists, the economy’s growth path with a UFM will yield similar growth dynamics. In other words, our theoretical results tend to carry over, and are robust to whether we are analyzing a developed inflation targeting economy or an underdeveloped one, with the latter characterized by UFM.

5. Conclusions

In this paper, we develop an overlapping generations monetary endogenous growth model with an inflation-targeting central banker. Growth is endogenized by incorporating government expenditure into the production function, while relocation shocks on young agents generate a role for money, even in the presence of the return-dominating asset of physical capital, and financial intermediaries. Given this framework, we show that growth dynamics arise, with a S-shaped growth path yielding three-equilibria. In particular, we obtain a stable low- and high-growth equilibria and one unstable medium-growth equilibrium. In addition, the stable equilibria are found to be locally indeterminate. Since government expenditure is productive in our model, a higher inflation-target would translate into higher growth, but under multiple equilibria, an increase in the inflation target is not necessarily found to be growth-enhancing at the medium-growth unstable equilibrium, which the economy could always choose due to the issue of indeterminancy. Finally, realizing that developing economies are characterized by unofficial financial markets, we also account for this feature in our model as an extension. We find that even under this augmentation of the model, our basic results continue to be robust.

Appendix A.1. Optimization Solution for Banks

Banks choose $q_t$ to maximize the expected lifetime utility of the representative young-age depositor

$$\underset{0\le q_t\le 1}{max}V=ln\left(w_t\right)+\sigma ln\left[R_t^a\right]+(1-\sigma )ln\left[R_t^s\right]$$

(A5)

subject to

$$\sigma R_t^a=(1-q_t)R_t^m$$

(A6)

$$(1-\sigma )R_t^s=q_t{r}_{t+1}$$

(A7)

Given (A6) and (A7), we can then re-write (A5) as follows

$$\underset{0\le q_t\le 1}{max}V=ln{w}_t+\sigma ln\left[\frac{(1-q_t)R_t^m}{\sigma }\right]+(1-\sigma )ln\left[\frac{q_t{r}_{t+1}}{(1-\sigma )}\right]$$

(A8)

where $R_t^m$ and $r_{t+1}$ are taken to be given. The solution to this problem is given by

$$R_t^a:{\lambda }_t=-\frac{\sigma }{1-q_t}$$

$$R_t^s:{\lambda }_t=-\frac{1-\sigma }{q_t}$$

Hence,

$$q_t=q=(1-\sigma )$$

(A9)

Appendix A.2. Optimization Solutions for Young-Age Consumer

The portfolio optimization problem of the young agent is as follows. At each time point, young agents allocate their entire savings, $w_t$ in the forms of real bank deposits, $d_t$, real money balances, $m_t$ and capital, $k_t$. Defining ${\psi }_1$, ${\psi }_2$ and $(1-{\psi }_1-{\psi }_2)$ as the fraction of savings held as, $d_t$, $m_t$ and $k_t$ respectively, young agents solve the following problem:

$$\underset{{\psi }_1,{\psi }_2}{max}ln{w}_t+\sigma ln\left[{\psi }_1{R}_t^a+{\psi }_2{R}_t^m\right]+(1-\sigma )ln\left[{\psi }_1{R}_t^s+{\psi }_2{R}_t^m+(1-{\psi }_1-{\psi }_2)r_{t+1}\right]$$

(A10)

Assuming that capital returns dominate real balances such that $r_{t+1}>R_t^m$ and hence ${\psi }_2=0$, solving (A10) under this assumption gives the optimality solution for ${\psi }_1$ as

$$\frac{\sigma }{{\psi }_1}+\frac{(1-\sigma )(R_t^s-r_{t+1})}{\psi {}_1{R}_t^s+\left(r_{t+1}\right)(1-{\psi }_1)}=0$$

$$\sigma \left[\psi {}_1{R}_t^s+\left(r_{t+1}\right)(1-{\psi }_1)\right]+{\psi }_1\left[(1-\sigma )(R_t^s-r_{t+1})\right]=0$$

$$\sigma \psi {}_1{R}_t^s+\sigma r_{t+1}-\sigma {\psi }_1{r}_{t+1}+{\psi }_1{R}_t^s-\sigma {\psi }_1{R}_t^s-{\psi }_1{r}_{t+1}+\sigma {\psi }_1{r}_{t+1}=0$$

$$\sigma r_{t+1}+{\psi }_1{R}_t^s-{\psi }_1{r}_{t+1}=0$$

$${\psi }_1=\frac{\sigma \left(r_{t+1}\right)}{r_{t+1}-R_t^s}$$

(A11)

with $r_{t+1}\ge R_t^s$. Since the upper limit of $R_t^s$ is $r_{t+1}$, it implies that when $r_{t+1}=R_t^s$, ${\psi }_1=1$.

Appendix A.3. Steady-State Growth and Inflation

In the absence of any legal restrictions on the financial intermediaries, in equilibrium, ${\psi }_1=1$ and all primary asset holdings are intermediated. That is

$$k_{t+1}=q_t{w}_t$$

(A12)

From (3), we have $w_t=(1-\alpha )A{\left(\frac{k_t}{n_t}\right)}^{\alpha }{g}_t^{1-\alpha }$ and the fact that $q=1-\sigma$ and that in equilibrium $n_t=1$ implies that

$$k_{t+1}=(1-\sigma )(1-\alpha )A{k}_t^{\alpha }{g}_t^{1-\alpha }$$

(A13)

From (11), we have $g_t=m_t\left(1-\frac{1}{{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}\right)$, and given the money market equilibrium $\frac{M_t}{P_t}=m_t=(1-q_t)w_t$, we can express $g_t$ as

$$g_t=(1-q_t)w_t\left(1-\frac{1}{{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}\right)$$

$$g_t=(1-q_t)(1-\alpha )A{k}_t^{\alpha }{g}_t^{1-\alpha }\left(1-\frac{1}{{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}\right)$$

which simplifies to

$$g_t={\left[(1-q_t)(1-\alpha )A{k}_t^{\alpha }\left(1-\frac{1}{{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}\right)\right]}^{\frac{1}{\alpha }}$$

(A14)

Plugging this expression for $g_t$ back into (A13), we have

$$k_{t+1}=(1-\sigma )(1-\alpha )A{k}_t^{\alpha }{\left[{\left((1-q_t)(1-\alpha )A{k}_t^{\alpha }\left(1-\frac{1}{{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}\right)\right)}^{\frac{1}{\alpha }}\right]}^{1-\alpha }$$

$$k_{t+1}=(1-\sigma )(1-\alpha )A{k}_t^{\alpha }{\left[(1-q_t)(1-\alpha )A{k}_t^{\alpha }\left(1-\frac{1}{{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}\right)\right]}^{\frac{1-\alpha }{\alpha }}$$

$$k_{t+1}=(1-\sigma )(1-\alpha )A{k}_t^{\alpha }{(1-q_t)}^{\frac{1-\alpha }{\alpha }}{(1-\alpha )}^{\frac{1-\alpha }{\alpha }}{A}^{\frac{1-\alpha }{\alpha }}{k}_t^{1-\alpha }{\left(1-\frac{1}{{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}\right)}^{\frac{1-\alpha }{\alpha }}$$

and simplifying and dividing both sides by $k_t$, we have

$${\mathsf{\Omega }}_{t+1}=\mathsf{\Omega }=\frac{k_{t+1}}{k_t}=(1-\sigma ){\left(A(1-\alpha )\right)}^{\frac{1}{\alpha }}{\left[\sigma \left(1-\frac{1}{{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}\right)\right]}^{\frac{1-\alpha }{\alpha }}$$

(A15)

Appendix A.4. The Model with Compulsory Reserve Requirements

The obligatory reserve requirement is defined as a cap on the portion of banks’ portfolio that can be held as capital such that we restrict (9) to $\overline{q}<(1-\sigma )$, where $\overline{q}$ represents the obligatory reserve requirement. In this case, banks are limited to set the fraction of their portfolio held as capital to $0\le \overline{q}\le (1-\sigma )$. In this set up, (13) may not hold.

In the presence of obligatory reserve requirements, the benchmark model resource constrains given by (7) and (8) change to

$$\sigma R_t^a=\frac{(1-\overline{q})}{{\mathsf{\Pi }}_{t+1}}>\frac{1}{{\mathsf{\Pi }}_{t+1}}$$

(A16)

$$(1-\sigma )R_t^s=\overline{q}{r}_{t+1}<r_{t+1}$$

(A17)

That the consolidated government can facilitate that all agents to intermediate all their savings through the banks in the presence of binding reserve requirements imply that we can have ${\psi }_1=1$ if and only if ${(1-\sigma )}^2\le \overline{q}\le (1-\sigma )$.

In the case whereby banks are restricted to invest a fraction, $\overline{q}$ of their deposits into capital, the economy’s gross growth rate (${\mathsf{\Omega }}_{t+1}$) is given by

$${\mathsf{\Omega }}_{t+1}=\overline{q}{\left(A(1-\alpha )\right)}^{\frac{1}{\alpha }}{\left[(1-\overline{q})\left(1-\frac{1}{{\mathsf{\Omega }}_t\widehat{\mathsf{\Pi }}}\right)\right]}^{\frac{1-\alpha }{\alpha }}$$

(A18)