Homogeneity of Determinants in the Financial Sector and Investment in EU Countries
Abstract
1. Introduction
2. Literature Review
3. Data and Methods
- Are homogeneous financial markets and investment activities in the European Union countries that are members of the EMU the same as those that are not members of the EMU?
- Are the European Union’s financial markets and investment activity homogeneous within the Visegrad Group countries?
- Are EU countries different in terms of financial markets and investment activity?
- Does GDP per capita (PPS) depend on the volume of loans to non-financial institutions in the European Union?
- Does GDP per capita (PPS) depend on the volume of investment in the EU countries?
- The status of debt securities (Debt_securities_NEF) held by non-financial corporations.
- Loan status (Debt_NF, debt_C) held by the non-financial corporations and households’ sectors.
- Net flows of debt securities (Credit_flows_securities_NF) to non-financial corporations.
- Net credit flows (Credit_flows_NF, Credit_flows_C) to non-financial businesses and households.
- The development of the sum of all financial sector liabilities (Total_liabilities), which includes currency and deposits, debt securities, loans, equity and investment fund shares, insurance, pension and standardized guarantee schemes, financial derivatives and employee stock options and other liabilities of financial institutions.
- Developments of all liabilities of financial institutions (Liabilities_FI) include money market funds, collective investment funds, financial intermediaries other than insurance corporations and pension funds, auxiliary financial institutions, captive finance institutions and money lenders, insurance companies, and pension funds.
- Development of all central bank liabilities (Liabilities_CB).
- Gross household investment (Investment_C) is defined as gross fixed capital formation divided by gross disposable income adjusted for changes in net equity of households in pension funds reserves. Household investment mainly consists of purchases and renovation of dwellings.
- The rate of gross investment of non-financial corporations (Investment_NF) is defined as gross fixed capital formation divided by gross value added. This ratio relates the investment of non-financial corporations in fixed assets (buildings, machinery, etc.) to the added value generated during the production process.
- The Maastricht long-term interest rate criterion (EMU) is used as a convergence criterion for the European Monetary Union in the area of long-term interest rates (gross government bond yields on the secondary market with an average residual maturity of around 10 years).
- Foreign direct investment (FDI_in) from the international investment category is carried out by a foreign entity (direct investor) purchasing an entity in the domestic economy for the purpose of earning a profit, while a direct investor controls at least 10% of the entity’s capital. For the comparability of economies of different sizes, FDI inward data is expressed as a share of the reporting country’s GDP.
- Foreign direct investment (FDI_out) from the international investment category is made by the domestic entity (direct investor) purchasing an entity in a foreign economy for the purpose of making a profit, while the direct investor controls at least 10% of the foreign entity’s capital. For the comparability of economies of different sizes, FDI outward data is expressed as a share of the reporting country’s GDP.
- The capital account (CA) includes all transactions related to capital transfers and the acquisition or assignment of unproduced non-financial assets. The capital account together with the current and financial accounts form the balance of payments. It is expressed as a percentage of GDP. Financial flows are referred to as credit items, debit items, and balance. This indicator is based on balance of payments data provided to Eurostat by EU Member States.
- International investment position (Balance_portf_I) is a statistical statement showing at some point the value and composition of: financial assets of residents of the given economy, which are claims on non-residents and gold held as reserve assets; financial liabilities of residents of the economy to non-residents. The difference between the foreign financial assets and the liabilities of a given economy can be positive or negative. The indicator is expressed in millions of national currency units and is based on Eurostat’s balance of payments statistics.
- Gross domestic product per capita in purchasing power standard (GDP_capita_PPS) is a measure of economic performance. It represents the added value of all manufactured goods and services. The GDP per capita index expressed in purchasing power standard is in relation to the EU-28 average of 100. If a country-specific index is higher than 100, it means that its GDP per capita is higher than the EU-28 average and vice versa. The figures are given in the purchasing power standard—a common currency which wipes out differences in price levels between countries, allowing a comparison of GDP between countries rather than over time
4. Results
4.1. Correlation Analysis
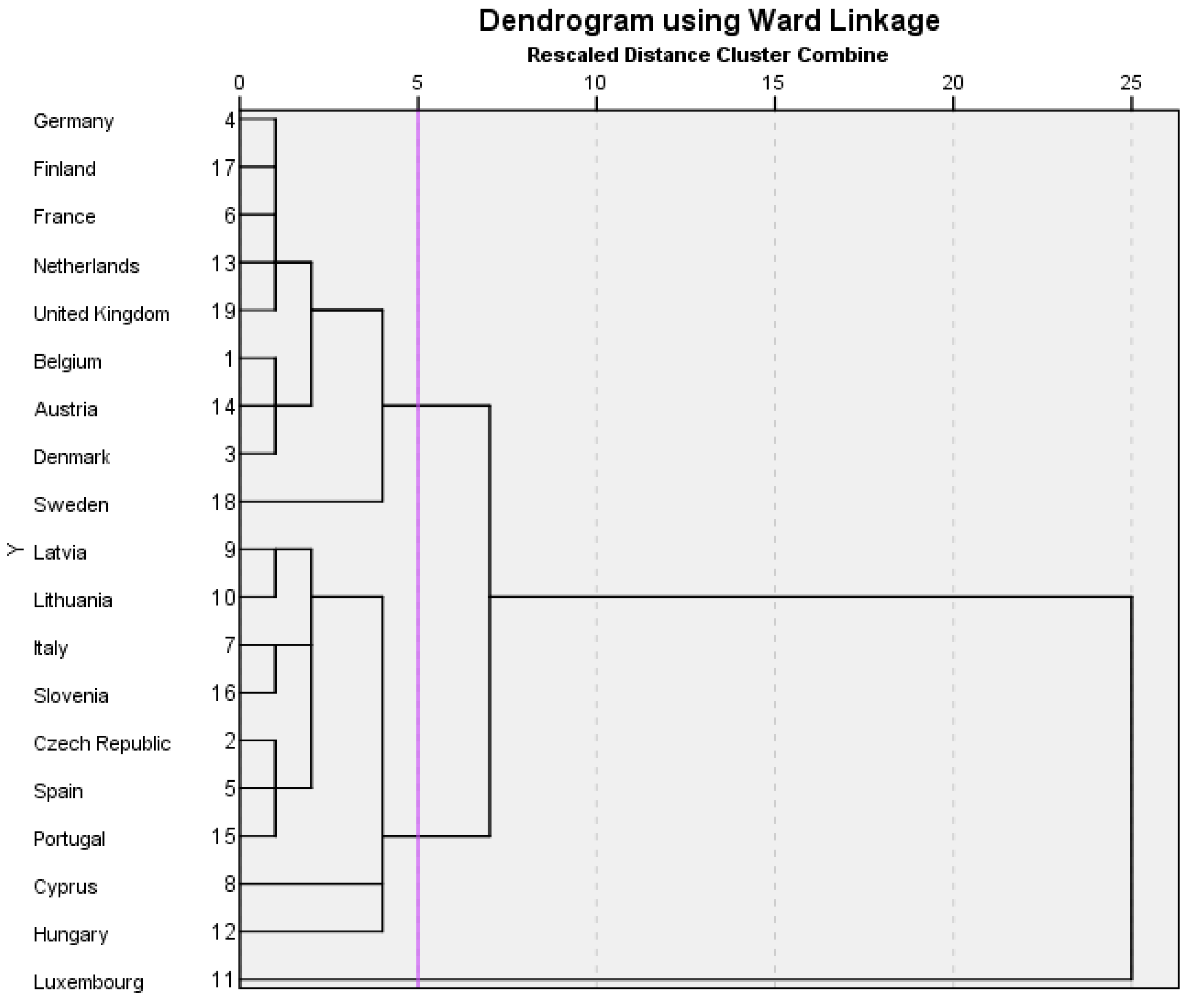
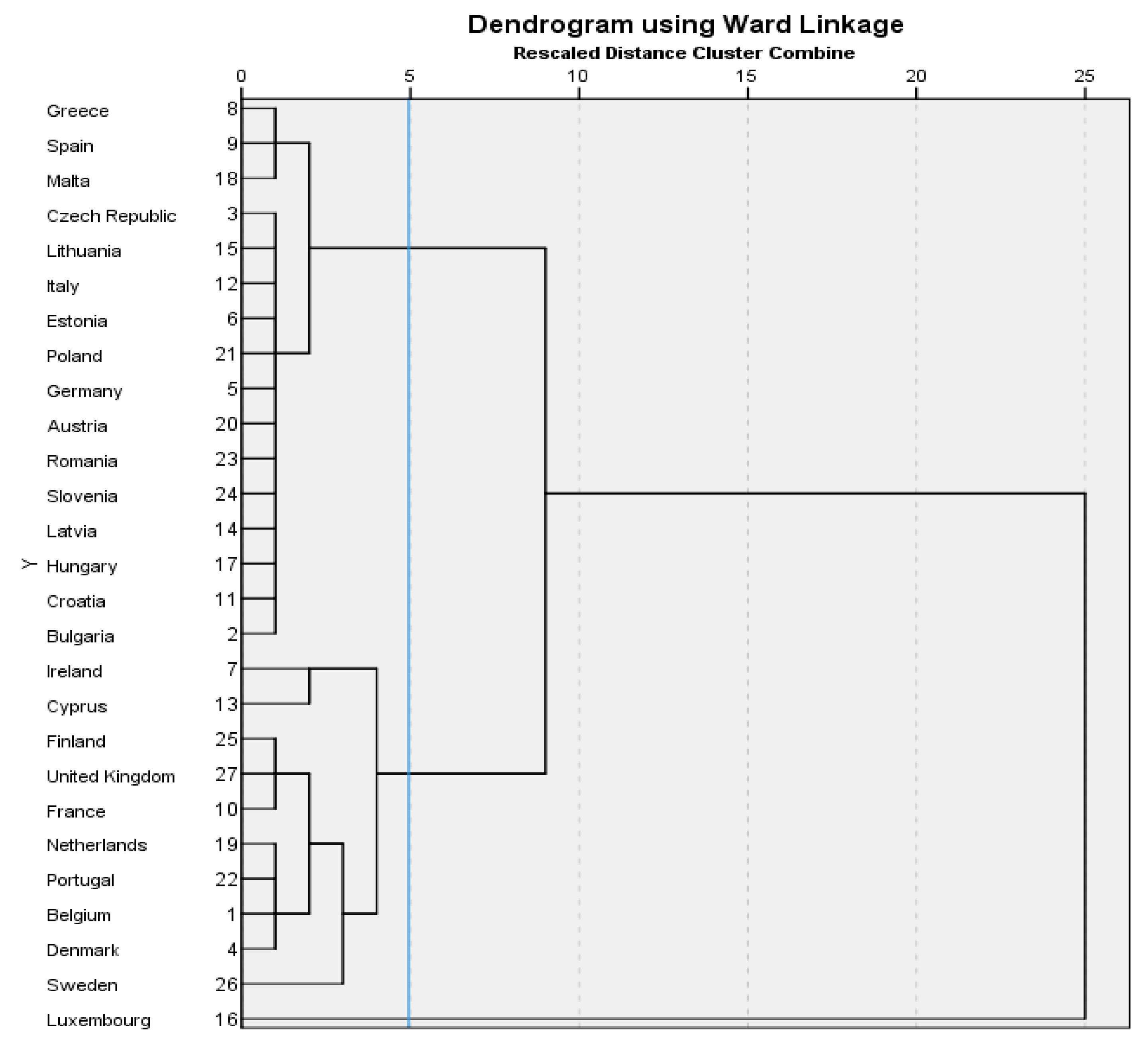
4.2. Cluster Analysis
- Cluster 1: Germany, Finland, France, the Netherlands, the United Kingdom, Belgium, Austria, Denmark and Sweden;
- Cluster 2: Latvia, Lithuania, Italy, Slovenia, the Czech Republic, Spain, Portugal, Cyprus, Hungary;
- Cluster 3: Luxembourg.
- Cluster 1: Greece, Spain, Malta, the Czech Republic, Lithuania, Italy, Estonia, Poland, Germany, Austria, Romania, Slovenia, Latvia, Hungary, Croatia, Bulgaria;
- Cluster 2: Ireland, Cyprus, Finland, the United Kingdom, France, the Netherlands, Portugal, Belgium, Denmark, Sweden;
- Cluster 3: Luxembourg.
- Cluster 1: Denmark, Austria, Belgium, France, Spain, Sweden, the Czech Republic, Slovakia and Cyprus
- Cluster 2: Latvia, Lithuania and Portugal;
- Cluster 3: Germany, Finland, the Netherlands, Italy, the United Kingdom, Slovenia;
- Cluster 4: Hungary;
- Cluster 5: Luxembourg.
5. Discussion
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
| Country | Debt_NF, % in GDP | Investment_C, % | GDP_capita_PPS, volume index EU28 = 100 | Country | Debt_NF, % in GDP | Investment_C, % | GDP_capita_PPS, volume index EU28 = 100 |
|---|---|---|---|---|---|---|---|
| Belgium | 112.60 | 10.11 | 117.00 | Luxembourg | 200.70 | 9.99 | 253.00 |
| Czech Republic | 31.30 | 9.03 | 89.00 | Hungary | 51.20 | 6.79 | 68.00 |
| Denmark | 65.90 | 8.50 | 128.00 | Netherlands | 128.00 | 11.01 | 128.00 |
| Germany | 40.90 | 9.70 | 124.00 | Austria | 61.20 | 8.68 | 127.00 |
| Estonia | 61.20 | 8.35 | 79.00 | Portugal | 75.70 | 5.16 | 77.00 |
| Spain | 75.20 | 5.43 | 92.00 | Slovenia | 46.20 | 6.09 | 85.00 |
| France | 61.40 | 9.42 | 104.00 | Slovakia | 47.10 | 7.69 | 76.00 |
| Italy | 60.30 | 8.27 | 96.00 | Finland | 65.40 | 11.32 | 109.00 |
| Cyprus | 208.30 | 10.22 | 85.00 | Sweden | 85.10 | 6.24 | 121.00 |
| Latvia | 60.70 | 4.83 | 67.00 | United Kingdom | 65.90 | 6.29 | 105.00 |
| Lithuania | 32.30 | 6.47 | 78.00 |
References
- Akbar, Saeed, Shafiqur Rehman, and Phillip Ormrod. 2013. The impact of recent financial shocks on the financing and investment policies of UK private firms. International Review of Financial Analysis 26: 59–70. [Google Scholar] [CrossRef]
- Al-Fawwaz, Abdulrahman. 2018. Foreign Direct Investment and Economic Stability: The case of Arab Peninsula. Advances in Social Sciences Research Journal 5: 200–13. [Google Scholar] [CrossRef]
- Amore, Mario Daniele, Cédric Schneider, and Alminas Žaldokas. 2013. Credit supply and corporate innovation. Journal of Financial Economics 109: 835–55. [Google Scholar] [CrossRef]
- Arouri, Mohamed El Hedi, Duc Khuong Nguyen, and Kuntara Pukthuanthong. 2012. An international CAPM for partially integrated markets: theory and empirical evidence. Journal of Banking and Finance 36: 2473–493. [Google Scholar] [CrossRef]
- Artl, Josef, Markéta Artlová, and Eva Rublíková. 2002. Analýza ekonomických časových řad s příklady. Praha: Skripta VŠE. [Google Scholar]
- Azzimonti, Marina, Eva de Francisco, and Vincenzo Quadrini. 2014. Financial Globalization, Inequality, and the Rising Public Debt. American Economic Review 104: 2267–302. [Google Scholar] [CrossRef]
- Baldwin, Richard, Henrik Braconier, and Rikard Forshid. 2005. Multinationals, endogenous growth, and technological spillovers: theory and evidence. Review of International Economics 13: 945–63. [Google Scholar] [CrossRef]
- Barro, R. J., and X. Sala-i-Martin. 1995. Economic Growth. Cambridge: McGraw-Kill. [Google Scholar]
- Battiston, Stefano, J. Doyne Farmer, Andreas Flache, Diego Garlaschelli, Andrew G. Haldane, Hans Heesterbeek, Cars Hommes, Carlo Jaeger, Robert May, and Marten Scheffer. 2016. Complexity theory and financial regulation. Science 351: 818–19. [Google Scholar] [CrossRef]
- Bekaert, Geert, Campbell Harvey, Christian Lundblad, and Stephan Siegel. 2011. What segments equity markets? Review of Financial Studies 24: 3847–890. [Google Scholar] [CrossRef]
- Bekaert, Geert, Michael Ehrmann, Marcel Fratzscher, and Arnaud Mehl. 2014. Global crises and equity market contagion. Journal of Finance 69: 2597–649. [Google Scholar] [CrossRef]
- Bernanke, Ben S., and Gertler Mark. 1995. Inside the Black Box: The Credit Channel of Monetary Policy Transmission. Journal of Economic Perspectives, American Economic Association 9: 27–48. [Google Scholar] [CrossRef]
- Braggion, Fabio, and Steven Ongena. 2013. A Century of Firm—Bank Relationships: Did Banking Sector Deregulation Spur Firms to Add Banks and Borrow More? CEPR Discussion Papers. [Google Scholar] [CrossRef][Green Version]
- Campello, Murillo, John R. Graham, and Campbell Harvey. 2010. The real effects of financial constraints: Evidence from a financial crisis. Journal of Financial Economics 97: 470–87. [Google Scholar] [CrossRef]
- Cerny, Philip G. 1994. The Dynamics of Financial Globalization: Technology, Market Structure, and Policy Response. Policy Sciences 27: 319–42. [Google Scholar] [CrossRef]
- Chambet, Anthony, and Rajna Gibson. 2008. Financial integration, economic instability and trade structure in emerging markets. Journal of International Money and Finance 27: 654–75. [Google Scholar] [CrossRef]
- Coad, Alexander, and Werner Hölzl. 2010. Firm Growth: Empirical Analysis. WIFO Working Papers 361. [Google Scholar]
- Custódio, Cláudia, Miguel A. Ferreira, and Luís Laureano. 2013. Why are US firms using more short-term debt? Journal of Financial Economics 108: 182–212. [Google Scholar] [CrossRef]
- De Mitri Stefania, Gobbi Giorgio, and Sette Enrico. 2010. Relationship lending in a financial turmoil. Temi di discussione (Economic working papers), Economic Research and International Relations Area. [Google Scholar] [CrossRef]
- Dewally, Michaël, and Yingying Shao. 2014. Liquidity crisis, relationship lending and corporate finance. Journal of Banking Finance 39: 223–39. [Google Scholar] [CrossRef]
- Duan, Qi, Yong Wei, and Zhiping-Chen Ying. 2014. Relationship between the benchmark interest rate and a macroeconomic indicator. Economic Modelling 38: 220–26. [Google Scholar] [CrossRef]
- Duarte, Leandro do Rosário Viana, Yin Kedong, and Li Xuemei. 2017. The Relationship between FDI, Economic Growth and Financial Development in Cabo Verde. International Journal of Economics and Finance 9: 132. [Google Scholar] [CrossRef][Green Version]
- Dwenger, Nadja, Frank M. Fossen, and Martin Simmler. 2015. From Financial to Real Economic Crisis: Evidence from Individual Firm-Bank Relationships in Germany. Discussion Papers. Berlin: Free University Berlin, School of Business & Economics. [Google Scholar]
- Eurostat. 2019. Statistics. Luxembourg: Eurostat. [Google Scholar]
- Festus, Kandenge. 2011. Public and Private Investment and Economic Growth in Namibia (1970–2005). BOJE: Botswana Journal of Economics 7: 2–15. [Google Scholar]
- Gaiotti, Eugenio. 2013. Credit availability and investment: Lessons from the “great recession”. European Economic Review 59: 212–27. [Google Scholar] [CrossRef]
- Gopalan, Radhakrishnan, Gregory F. Udell, and Vijay Yerramilli. 2011. Why Do Firms Form New Banking Relationships? Journal of Financial and Quantitative Analysis 46: 1335–365. [Google Scholar] [CrossRef]
- Gros, Daniel. 2014. Investment as the Key to Recovery in the Euro Area? CEPS Policy Briefs, November 18, 326. [Google Scholar]
- Guitiérrez, Ester, and Sebastián Lozano. 2012. Competing risks analysis of the duration of federal target funds rates. Computers Operations Research 39: 785–91. [Google Scholar] [CrossRef]
- Hachem, Kinda. 2011. Relationship lending and the transmission of monetary policy. Journal of Monetary Economics 58: 590–600. [Google Scholar] [CrossRef]
- Helleiner, Eric. 1995. Explaining the globalization of financial markets: Bringing states back in. Review of International Political Economy 2: 315–41. [Google Scholar] [CrossRef]
- Helleiner, Eric, Stefano Pagliari, and Irene Spagna. 2018. Governing the World’s Biggest Market: The Politics of Derivatives Regulation after the 2008 Crisis. Oxford: Oxford University Press. [Google Scholar]
- Ioannidou, Vasso, and Steven Ongena. 2010. “Time for a Change”: Loan Conditions and Bank Behavior when Firms Switch Banks. Journal of Finance American Finance Association 65: 1847–877. [Google Scholar]
- Jimenez, Gabriel, Steven Ongena, Jose-Luis Peydro, and Jesus Saurina. 2012. Credit Supply and Monetary Policy: Identifying the Bank Balance-Sheet Channel with Loan Applications. American Economic Review, American Economic Association 102: 2301–326. [Google Scholar] [CrossRef]
- Kahle, Kathleen M., and Rene M. Stulz. 2011. Financial Policies, Investment, and the Financial Crisis: Impaired Credit Channel or Diminished Demand for Capital? Fisher College of Business Working Pape. [Google Scholar] [CrossRef][Green Version]
- Keynes, John Maynard. 1963. Obecná teorie zaměstnanosti, úroku a peněz. Praha: Nakladatelství ČSAV. [Google Scholar]
- Kose, Ayhan, Eswar Prasad, and Marco Terrones. 2009. Does financial globalization promote risk sharing? Journal of Development Economics 89: 258–70. [Google Scholar] [CrossRef]
- Kritikos, Alexander. 2014. Entrepreneurs and their impact on jobs and economic growth. IZA World of Labor. [Google Scholar] [CrossRef]
- Leary, Mark. 2009. Bank Loan Supply, Lender Choice, and Corporate Capital Structure. Journal of Finance, American Finance Association 64: 1143–85. [Google Scholar] [CrossRef]
- Lemmon, Michael, and Michael R. Roberts. 2010. The Response of Corporate Financing and Investment to Changes in the Supply of Credit. Journal of Financial and Quantitative Analysis 45: 555–87. [Google Scholar] [CrossRef]
- Lin, Tom. 2014. The new financial industry. Alabama Law Review 65: 567–623. [Google Scholar]
- Mandishekwa, Robson. 2014. Causality between Economic Growth and Investment in Zimbabwe. Journal of Economics and Sustainable Development 5: 136. [Google Scholar]
- Meloun, Milan, Jiří Militký, and Martin Hil. 2012. Statistická analýza vícerozměrných dat v příkladech. Praha: Academia Praha. [Google Scholar]
- Nerlove, Marc. 1983. Expectations, Plans, and Realizations in Theory and Practice. Econometric Society 51: 1251–79. [Google Scholar] [CrossRef]
- Nishant Dass, Jayant R. Kale, and Vikram Nanda. 2015. Trade Credit, Relationship-specific Investment, and Product Market Power. Review of Finance 19: 1867–923. [Google Scholar] [CrossRef]
- Panetta, Fabio, and Federico M. Signoretti. 2010. Credit demand and supply in Italy during the financial crisis. Questioni di Economia e Finanza (Occasional Papers) Economic Research and International Relations Area. [Google Scholar] [CrossRef]
- Ponticelli, Jacopo, and Leonardo S. Alencar. 2016. Court Enforcement, Bank Loans, and Firm Investment: Evidence from a Bankruptcy Reform in Brazil. The Quarterly Journal of Economics 131: 1365–413. [Google Scholar] [CrossRef]
- Samuelson, Paul, and William Nordhaus. 2007. Ekonomie: 18. vydání. Praha: NS Svoboda. [Google Scholar]
- Thompson, Grahame. 2017. Time, trading and algorithms in financial sector stability. New Political Economy 22: 1–11. [Google Scholar] [CrossRef]
- Underhill, Geoffrey. 2015. The emerging post-crisis financial architecture: The path-dependency of ideational adverse selection. The British Journal of Politics and International Relations 17: 461–93. [Google Scholar] [CrossRef]
- Verman, Reetu, and Edgar Wilson. 2005. A multivariate Analysis of Savings, Investment and Growth in India. Economics Working Papers. Wollongong: School of Economics, University of Wollongong. [Google Scholar]
- Voutsinas, Konstantinos, and Richard A. Werner. 2011. Credit supply and corporate capital structure: Evidence from Japan. International Review of Financial Analysis 20: 320–34. [Google Scholar] [CrossRef]
- Zhang, Kevin Honglin. 2001. How does foreign direct investment affect economic growth in China? Economics of Transition 9: 679–93. [Google Scholar] [CrossRef]


| Area | Abbreviation | Variable | Unit of Measure |
|---|---|---|---|
| Financial sector | Debt_securities_NF | Private sector debt: debt securities of non-financial institutions, consolidated | in % GDP |
| Debt_NF | Private sector debt: loans to non-financial institutions, consolidated | in % GDP | |
| Debt_C | Private sector debt: household loans, consolidated | in % GDP | |
| Credit_flow_securities_NF | Credit flow in the private sector: debt securities of non-financial institutions, consolidated | in % GDP | |
| Credit_flows_NF | Credit flows in the private sector: loans to non-financial institutions, consolidated | in % GDP | |
| Credit_flows_C | Credit flows in the private sector: household credit, consolidated | in % GDP | |
| Liabilities_FI | Liabilities of financial institutions, consolidated | in % GDP | |
| Liabilities_CB | Central bank liabilities, consolidated | in % GDP | |
| Total_liabilities | Total financial sector liabilities, consolidated | in % GDP | |
| Investment activity | Investment_C | Household investment rate | % |
| Investment_NF | Investment rate of non-financial corporations | % | |
| EMU | EMU convergence criteria | % | |
| FDI_in | Level of foreign direct investment (FDI) in the given economy | in millions | |
| FDI_out | Level of foreign direct investment (FDI) directed out of the given economy | in millions | |
| CA | Capital account | in % GDP | |
| Balance_portf_I | Portfolio investment balance | in millions | |
| GDP_ capita_ PPS | Gross domestic product per capita in purchasing power standard | Volume index, EU28 = 100 |
| The Observed Relationship | Indicator 1 | Indicator 2 | Result |
|---|---|---|---|
| Relationship 1 | Debt_NF | Investment_NF | 0.192943 |
| Relationship 2 | Debt_C | Investment_C | 0.351116 |
| Relationship 3 | Credit_flows_NF | Investment_NF | −0.01687 |
| Relationship 4 | Credit_flows_C | Investment_C | 0.187758 |
| Relationship 5 | GDP_capita_PPS | Debt_NF | 0.571182 |
| Relationship 6 | GDP_capita_PPS | Debt_C | 0.370495 |
| Relationship 7 | GDP_capita_PPS | Investment_NF | 0.005208 |
| Relationship 8 | GDP_capita_PPS | Investment_C | 0.462431 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urbankova, E.; Krizek, D. Homogeneity of Determinants in the Financial Sector and Investment in EU Countries. Economies 2020, 8, 14. https://doi.org/10.3390/economies8010014
Urbankova E, Krizek D. Homogeneity of Determinants in the Financial Sector and Investment in EU Countries. Economies. 2020; 8(1):14. https://doi.org/10.3390/economies8010014
Chicago/Turabian StyleUrbankova, Erika, and David Krizek. 2020. "Homogeneity of Determinants in the Financial Sector and Investment in EU Countries" Economies 8, no. 1: 14. https://doi.org/10.3390/economies8010014
APA StyleUrbankova, E., & Krizek, D. (2020). Homogeneity of Determinants in the Financial Sector and Investment in EU Countries. Economies, 8(1), 14. https://doi.org/10.3390/economies8010014





