Time-Varying Risk Aversion and the Profitability of Carry Trades: Evidence from the Cross-Quantilogram †
Abstract
1. Introduction
2. Methodology: The Cross-Quantilogram
3. Data and Empirical Findings
3.1. Data
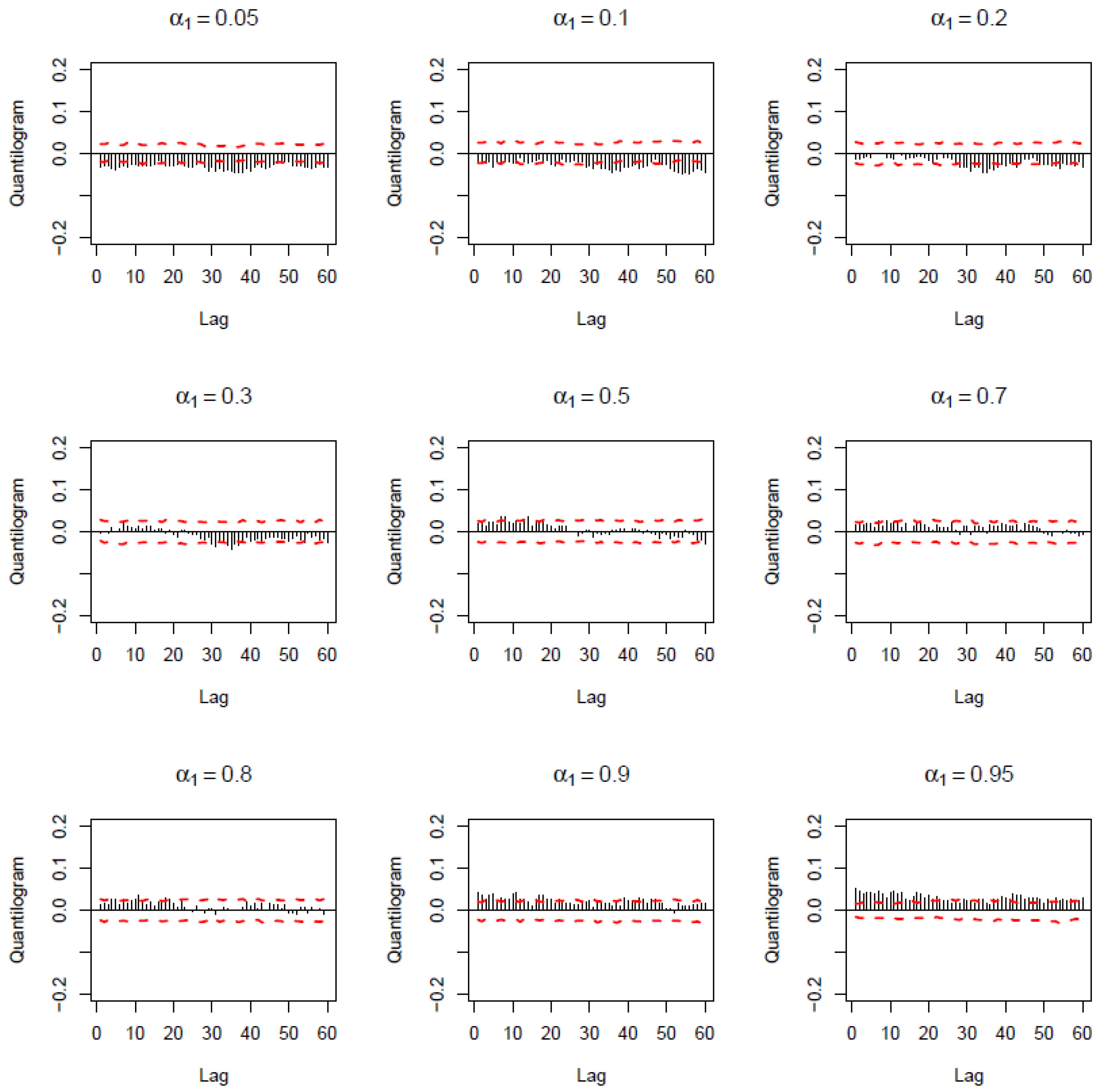
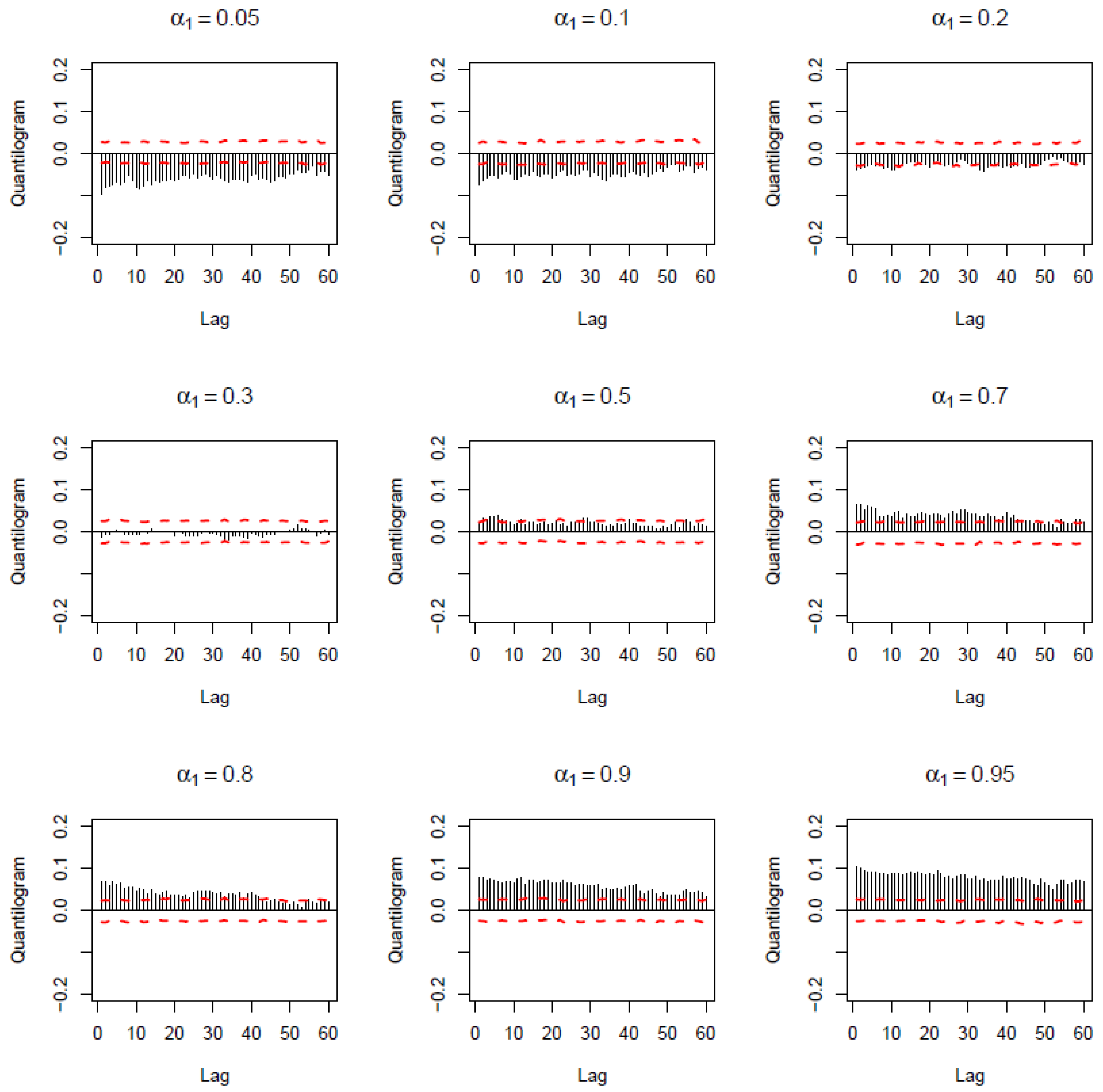
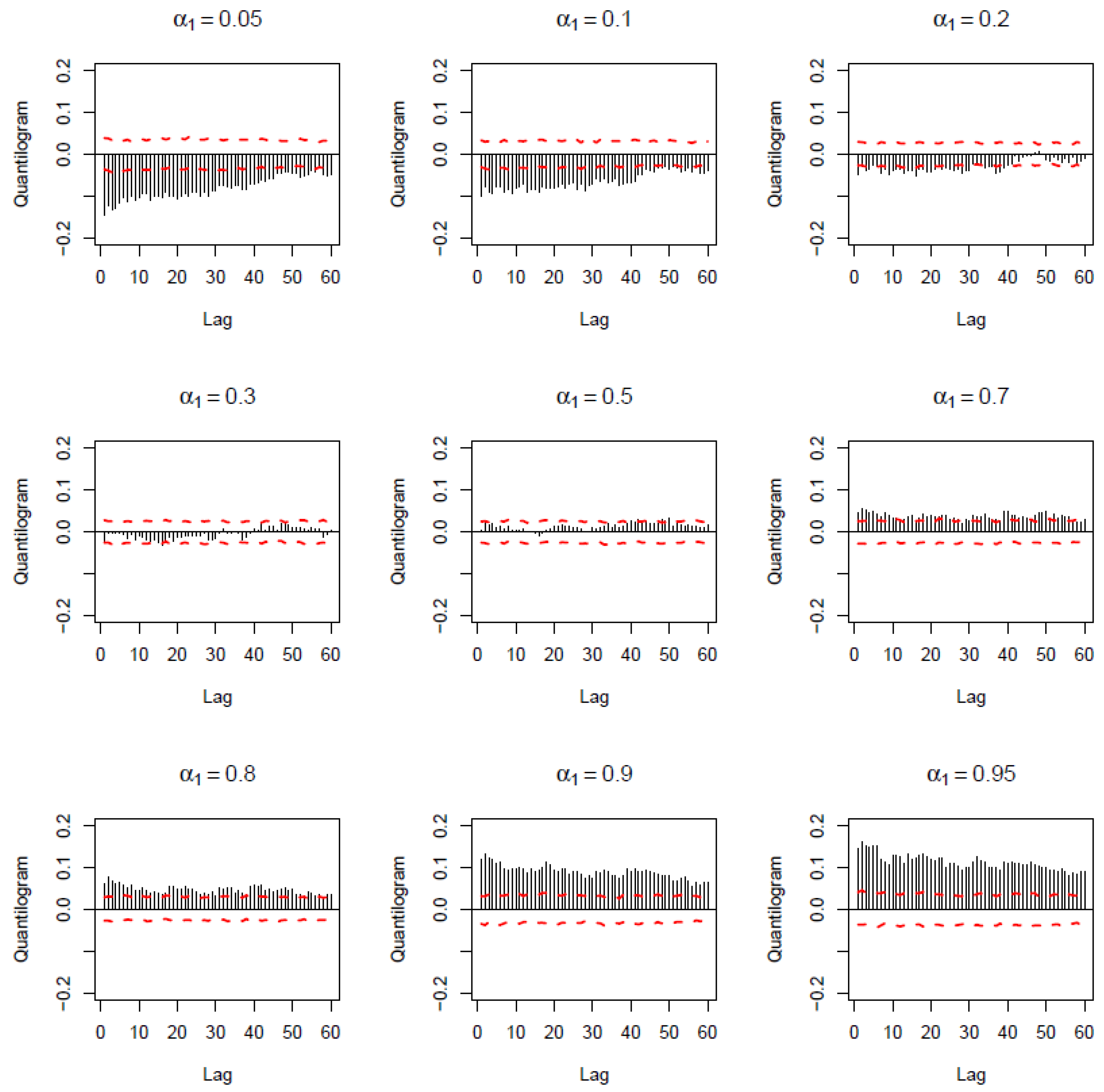
3.2. Empirical Findings
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
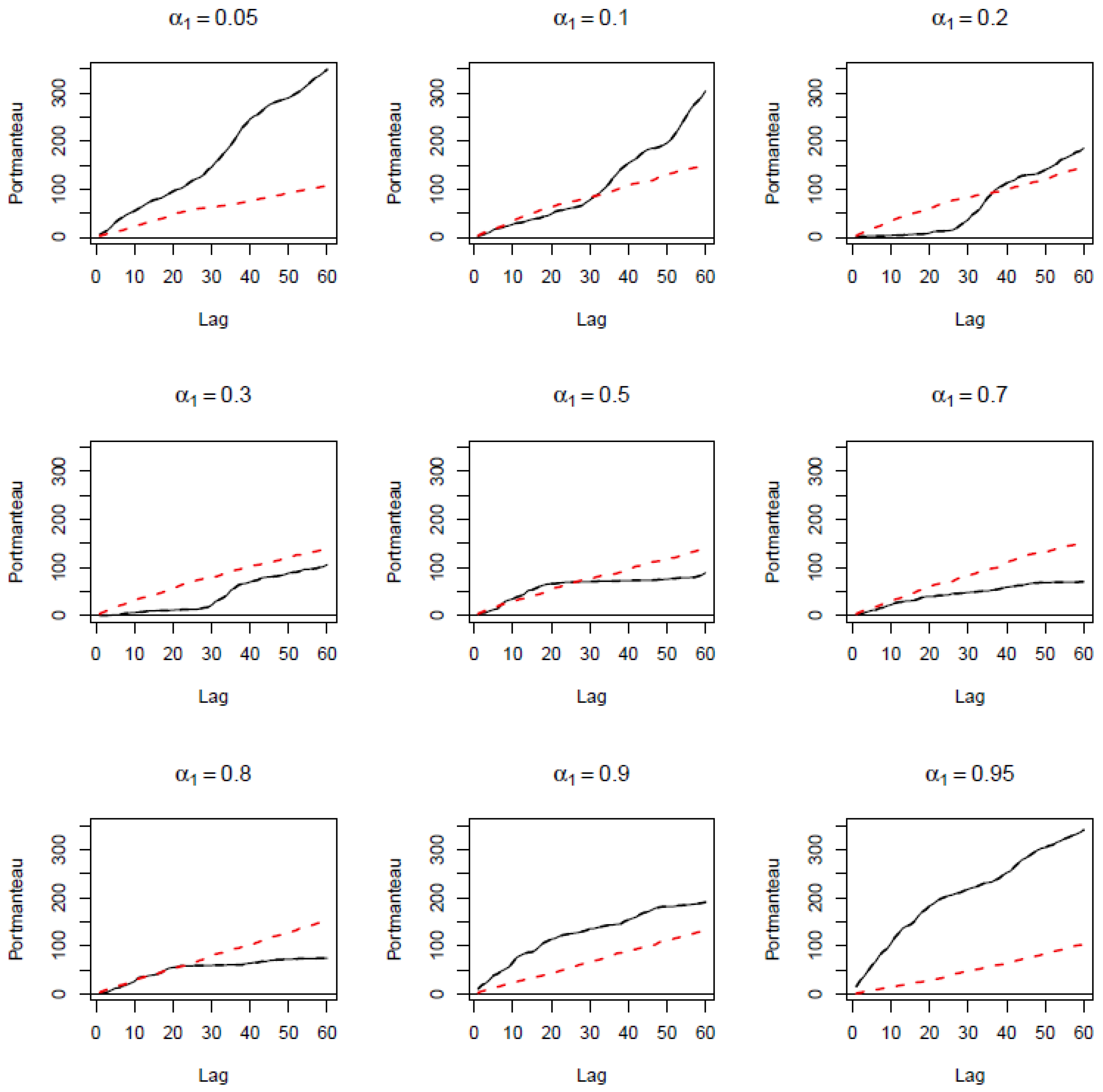
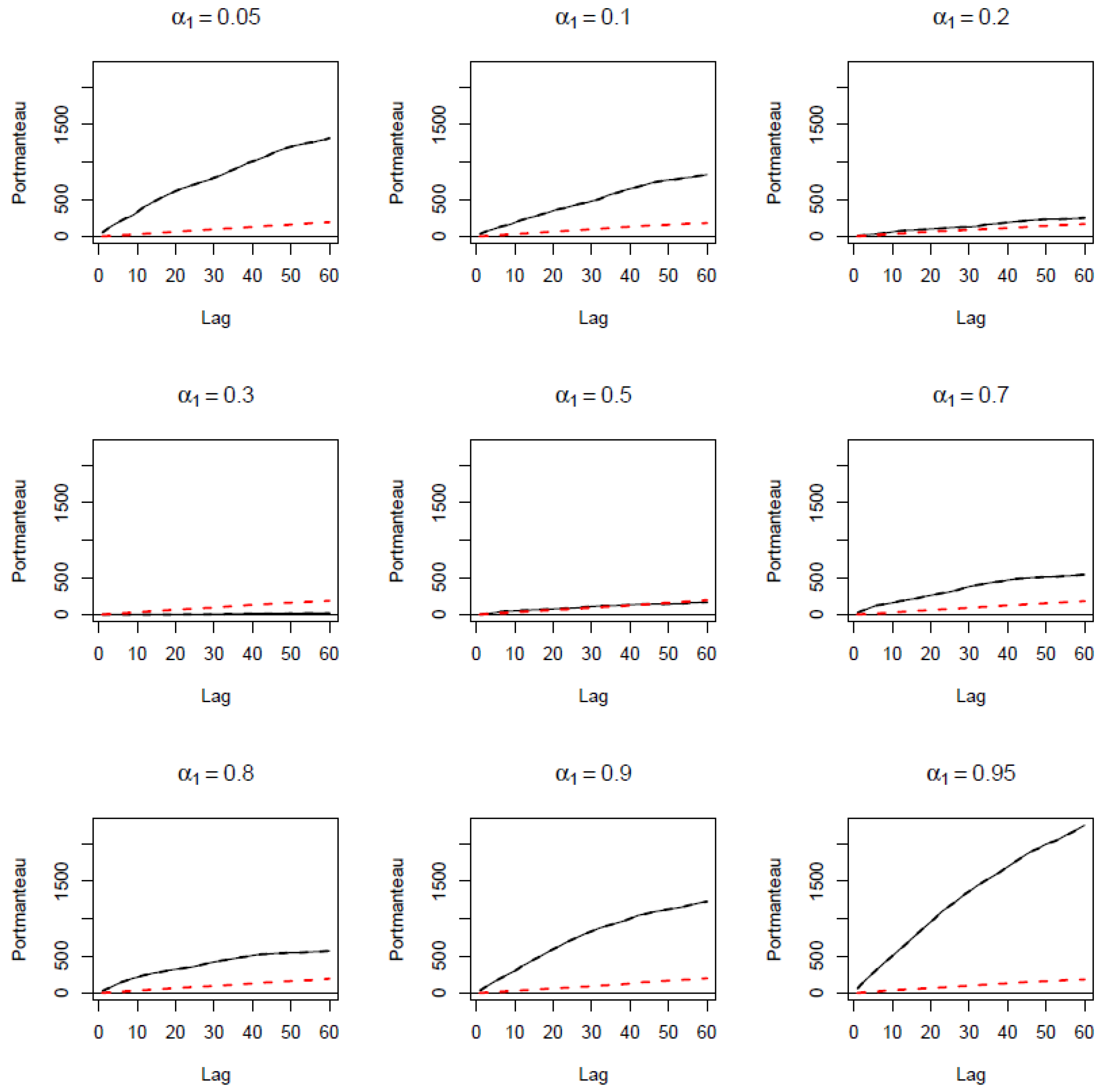
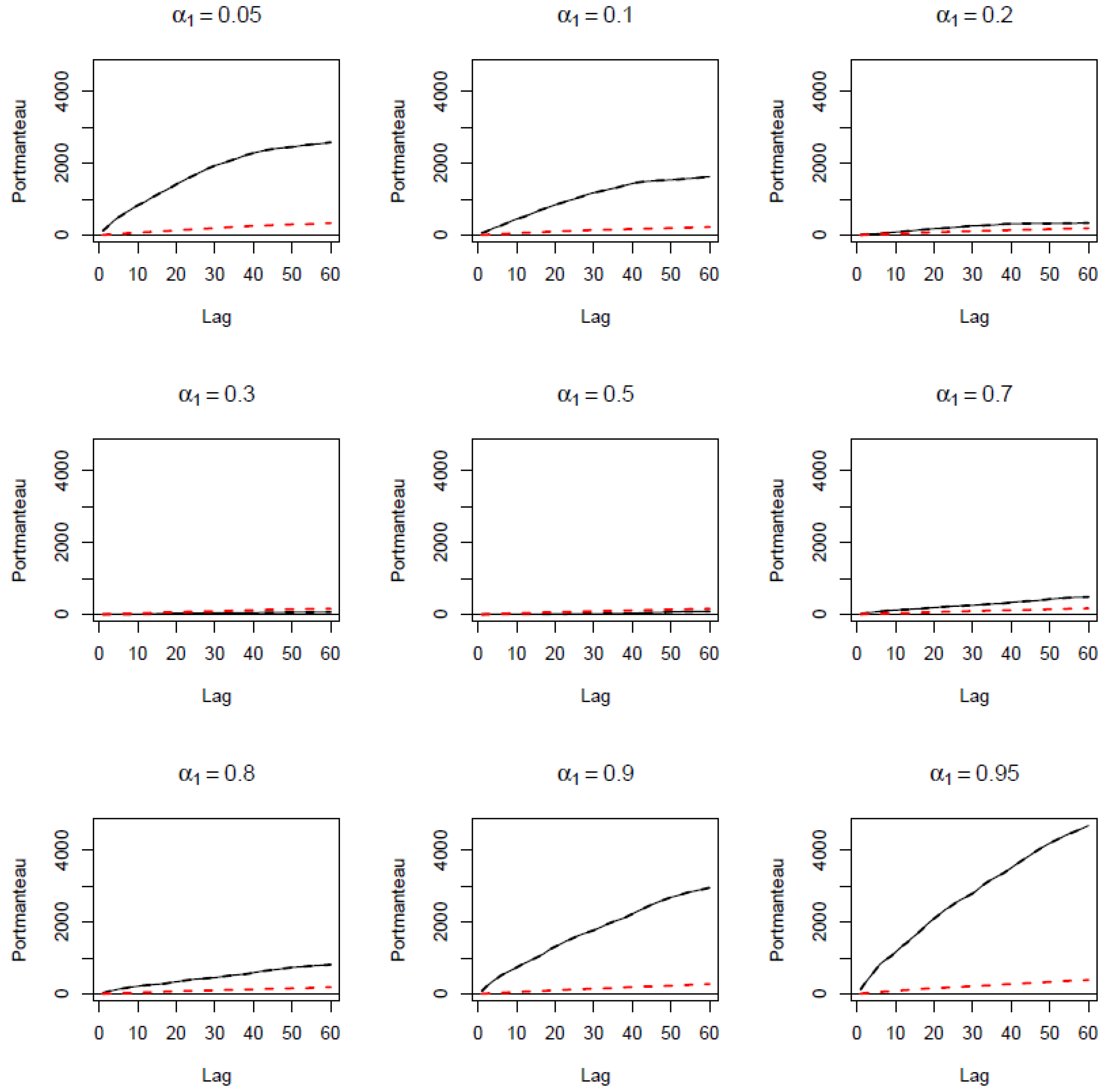
Appendix A
References
- Ang, Andrew, and Joseph Chen. 2002. Asymmetric Correlations of Equity Portfolios. Journal of Financial Economics 63: 443–94. [Google Scholar] [CrossRef]
- Baillie, Richard T., and Sanders S. Chang. 2011. Carry trades, momentum trading and the forward premium anomaly. Journal of Financial Markets 14: 441–64. [Google Scholar] [CrossRef]
- Bekaert, Geert, Eric C. Engstrom, and Nancy R. Xu. 2017. The Time Variation in Risk Appetite and Uncertainty. Columbia Business School Research Paper No. 17–108. New York: Columbia Business School, Columbia University. Available online: https://www8.gsb.columbia.edu/cbs-directory/node/30648/preview (accessed on 27 February 2020).
- Breitung, Jörg, and Bertrand Candelon. 2006. Testing for short- and long-run causality: A frequency-domain approach. Journal of Econometrics 132: 363–78. [Google Scholar] [CrossRef]
- Brunnermeier, Markus K., Stefan Nagel, and Lasse H. Pedersen. 2009. Carry Trades and Currency Crashes. In NBER Macroeconomics Annual 2008. Edited by Daron Acemoglu, Kenneth Rogoff and Michael Woodford. Chicago: University of Chicago Press, vol. 23, pp. 313–47. [Google Scholar]
- Burnside, Craig, Martin Eichenbaum, and Sergio Rebelo. 2007. The Returns to Currency Speculation in Emerging Markets. American Economic Review Papers and Proceedings 97: 333–38. [Google Scholar] [CrossRef]
- Burnside, Craig, Martin Eichenbaum, and Sergio Rebelo. 2008. Carry trade: The gains of diversification. Journal of the European Economic Association 6: 581–88. [Google Scholar] [CrossRef]
- Christiansen, Charlotte, Angelo Ranaldo, and Paul Söderlind. 2011. The Time-Varying Systematic Risk of Carry Trade Strategies. Journal of Financial and Quantitative Analysis 46: 1107–25. [Google Scholar] [CrossRef]
- Chung, Jaehun, and Yongmiao Hong. 2007. Model-free evaluation of directional predictability in foreign exchange markets. Journal of Applied Econometrics 22: 855–89. [Google Scholar] [CrossRef]
- Daviou, Agustin, and Florentina Paraschiv. 2014. Investor behavior under changing market volatility. The Journal of Investing 23: 96–113. [Google Scholar] [CrossRef]
- Demirer, Riza, Konstantinos Gkillas, Rangan Gupta, and Christian Pierdzioch. 2019. Time-varying risk aversion and realized gold volatility. North American Journal of Economics and Finance 50: 101048. [Google Scholar] [CrossRef]
- Dietrich, Felix. 2018. The Effect of Risk Changes on Carry Trade Returns and Speculative Behavior. Working paper (July 29, 2018). St. Gallen: University of St. Gallen. [Google Scholar]
- Diks, Cees, and Valentyn Panchenko. 2006. A new statistic and practical guidelines for nonparametric Granger causality testing. Journal of Economic Dynamics & Control 30: 1647–69. [Google Scholar]
- Egbers, Tom, and Laurens Swinkels. 2015. Can implied volatility predict returns on the currency carry trade? Journal of Banking & Finance 59: 14–26. [Google Scholar]
- Han, Heejoon, Oliver Linton, Tatsushi Oka, and Yoon-Jae Whang. 2016. The cross-quantilogram: Measuring quantile dependence and testing directional predictability between time series. Journal of Econometrics 193: 251–70. [Google Scholar] [CrossRef]
- Hassani, Hossein, Anatoly Zhigljavsky, Kerry Patterson, and A. Soofi. 2010. A comprehensive causality test based on the singular spectrum analysis. In Causality in Science. Edited by Phyllis McKay Illari, Federica Russo and Jon Williamson. Oxford Scholarship Online. Oxford: Oxford University Press, chp. 18. pp. 379–406. [Google Scholar] [CrossRef]
- Jeong, Kiho, Wolfgang K. Härdle, and Song Song. 2012. A consistent nonparametric test for causality in quantile. Econometric Theory 28: 861–87. [Google Scholar] [CrossRef]
- Koenker, Roger, and Gilbert Bassett. 1978. Regression quantiles. Econometrica 46: 33–50. [Google Scholar] [CrossRef]
- Linton, Oliver, and Yoon-Jae Whang. 2007. The quantilogram: With an application to evaluating directional predictability. Journal of Econometrics 141: 250–82. [Google Scholar] [CrossRef]
- Menkhoff, Lukas, Lucio Sarno, Maik Schmeling, and Andreas Schrimpf. 2012. Carry trades and global foreign exchange volatility. Journal of Finance 67: 681–718. [Google Scholar] [CrossRef]
- Péguin-Feissolle, Anne, Birgit Strikholm, and Timo Teräsvirta. 2013. Testing the Granger noncausality hypothesis in stationary models of unknown functional form. Communications in Statistics: Simulation and Computation 42: 1063–87. [Google Scholar] [CrossRef]
- Plantin, Guillaume, and Hyun Song Shin. 2011. Carry Trades, Monetary Policy and Speculative Dynamics. Centre for Economic Policy Research (CEPR) Discussion Papers No. DP8224. Washington: SSRN. Available online: https://ssrn.com/abstract=1758433 (accessed on 27 February 2020).
- Sugihara, George, Robert May, Hao Ye, Chih-hao Hsieh, Ethan Deyle, Michael Fogarty, and Stephan Munch. 2012. Detecting causality in complex ecosystems. Science 338: 496–500. [Google Scholar] [CrossRef] [PubMed]
- Wang, Changyun. 2004. Futures trading activity and predictable foreign exchange market movements. Journal of Banking & Finance 28: 1023–41. [Google Scholar]
| 1 | The risk aversion index is stationary by design, while the log-return of the G10CHI ensures its stationarity, as per the requirement of using mean-reverting series for the cross-quantilogram estimation. Complete details of standard unit root tests conducted on the two variables are available upon request. |
| 2 | The data can be downloaded from: https://www.nancyxu.net/risk-aversion-index. |
| 3 | The data are available for download from: https://index.db.com/dbiqweb2/home.do?redirect=productpagelist®ion=ALL®ionHidden=ALL&assetClass=FX&assetClassHidden=FX&returnStream=ALL&returnStreamHidden=ALL. |
| 4 | As part of preliminary analysis, we conducted a wide variety of linear and nonlinear (nonparametric) conditional mean-based test of causality. In particular, the standard linear Granger causality test produced a test-statistic of 14.80, with a p-value of 0.00; the nonlinear tests of Diks and Panchenko (2006) had a test statistic of 2.14, with a p-value of 0.02; and the various nonlinear tests of Péguin-Feissolle et al. (2013) based on unknown functional forms, i.e., General Taylor-based, Semi-Additive Taylor-based, P-General Taylor-based, and Artificial Neural Network (ANN)-based had test statistics of 20.02, 10.24, 20.02, and 20.41, respectively, with all having p-values of 0.00. Naturally, all these tests rejected the null of no-Granger causality from risk aversion to carry trade returns. Further, the nonparametric Singular Spectrum Analysis (SSA)-based test of Hassani et al. (2010) yielded a value of 0.46 (i.e., <1), again suggesting predictive content of risk aversion for carry trade returns. Moreover, the nonparametric Convergent Cross Mapping (CCM) test of Sugihara et al. (2012) showed that carry trade returns has greater cross map skills to risk aversion than it is the other way round, thus confirming that risk aversion does indeed cause carry trade returns. Complete details of these tests are available upon request from the authors. Finally, the frequency-domain Granger causality test of Breitung and Candelon (2006) showed that risk aversion has predictive content for carry trade returns at a cycle length of less than 4 days, then at a cycle length of beyond 5 days, i.e., basically at short-, medium-, and long-horizons. While these conditional mean-based tests are helpful, they are silent about the causal relationship contingent on the state of these two variables, as well as of the sign of the impact, unlike our more powerful cross-quantilogram approach. |
| 5 | The lack (weak evidence) of predictability around the median of the carry trade returns was also confirmed based on the quantiles (of the carry trade returns)-based causality test of Jeong et al. (2012). Complete details of these results are available upon request from the authors. |
| 6 | This pattern of negative relationship at lower quantiles and positive signs at higher quantiles relative to the median was also confirmed by the exceedance correlations of Ang and Chen (2002), complete details of which are available upon request from the authors. |
| 7 | Robustness checks based on the G10 Currency Future Harvest, G10 Currency Harvest and Global Currency Harvest indexes in US dollars and Euro (derived from the same data source reported in Footnote 2) yield qualitatively similar results. Moreover, as suggested by an anonymous referee, we conducted our analysis for the G10CHI returns for subsamples covering from the start to 2007, and from 2007 to the end. Not surprisingly, we found that while the pattern of directional predictability remains the same, the effects are way stronger in the second subsample—a result that makes perfect sense, as the latter period corresponds to heightened risk aversion in the wake of the global financial crisis. Understandably, our full-sample results are driven by the post-crisis period. Complete details of these results are available upon request from the authors. |
| Statistics | G10CHI Return (%) | Risk Aversion Index |
|---|---|---|
| Mean | 0.0274 | 2.7018 |
| Median | 0.0557 | 2.5312 |
| Maximum | 6.0717 | 27.1459 |
| Minimum | −8.0140 | 2.2310 |
| Std. Dev. | 0.6337 | 0.8310 |
| Skewness | −1.0322 | 13.7736 |
| Kurtosis | 17.7566 | 305.1085 |
| Jarque-Bera | 54,986.7400 | 22,792,372.0000 |
| p-value | 0.0000 | 0.0000 |
| Observations | 5944 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demirer, R.; Gupta, R.; Hassani, H.; Huang, X. Time-Varying Risk Aversion and the Profitability of Carry Trades: Evidence from the Cross-Quantilogram. Economies 2020, 8, 18. https://doi.org/10.3390/economies8010018
Demirer R, Gupta R, Hassani H, Huang X. Time-Varying Risk Aversion and the Profitability of Carry Trades: Evidence from the Cross-Quantilogram. Economies. 2020; 8(1):18. https://doi.org/10.3390/economies8010018
Chicago/Turabian StyleDemirer, Riza, Rangan Gupta, Hossein Hassani, and Xu Huang. 2020. "Time-Varying Risk Aversion and the Profitability of Carry Trades: Evidence from the Cross-Quantilogram" Economies 8, no. 1: 18. https://doi.org/10.3390/economies8010018
APA StyleDemirer, R., Gupta, R., Hassani, H., & Huang, X. (2020). Time-Varying Risk Aversion and the Profitability of Carry Trades: Evidence from the Cross-Quantilogram. Economies, 8(1), 18. https://doi.org/10.3390/economies8010018








