Embedding Preference Uncertainty for Environmental Amenities in Climate Change Economic Assessments: A “Random” Step Forward
Abstract
1. Introduction
“… Even if the climate damages in the DICE model used in the numerical exercise above are doubled to account for a wider range of nonmarket impacts, following the results in the Stern Review, we would argue that these impacts are still comparatively low …”
“We believe that it is exactly the nonmarket effects of climate change that are the most worrisome. If we focus on the risk for catastrophes, as Weitzman suggests, then we believe the main effect of climate change will not be to stop growth in conventional manufacturing, but rather to damage our ability to enjoy some vital ecosystem services …”
2. Framing the Problem of Future Preference Uncertainty
3. Methodology
3.1. Model Considerations
- WTP0 is the present WTP for an environmental good or service.
- WTPt is the future WTP for the environmental good or service at time t.
- α is the growth rate of the WTP value for the environmental good or service.
- t is the time in years (assuming that α and discount rates are expressed on a yearly basis).
3.1.1. Income Growth
- Y is the income.
- WTP is the willingness to pay amount.
3.1.2. Environmental Scarcity
3.1.3. Substitution Elasticity between Natural and Man-Made Capitals
3.1.4. Changing Preferences
3.2. Model Formation
- In case of perfect substitution between man-made and environmental assets, the effect of scarcity on WTP values is negligible and the non-market damages are estimated in consumption;
- In case of weak substitution, the effect on WTP values is captured via the depletion factor, as discussed below.
- g is growth rate of income expressed as percentage change from previous year.
- ω is the income elasticity of WTP.
- αtot is the total growth rate of WTP.
- αinc is the income growth factor.
- αsc is the environmental depletion (or scarcity) factor.
- αpr is the changing preferences factor.
- θ(0) is the sum of αinc + αsc at time 0.
- k is the drift that reflects future preferences.
- εt is a random component estimated by σW(t).
- The income elasticity of WTP (ω)
- The income or growth rate (g) on an annual basis
- The WTP elasticity of demand (λ)
- The environmental depletion rate (q) on an annual basis
- The preferences factor (αpr), which is expressed by k
- The volatility (σ) for the stochastic term
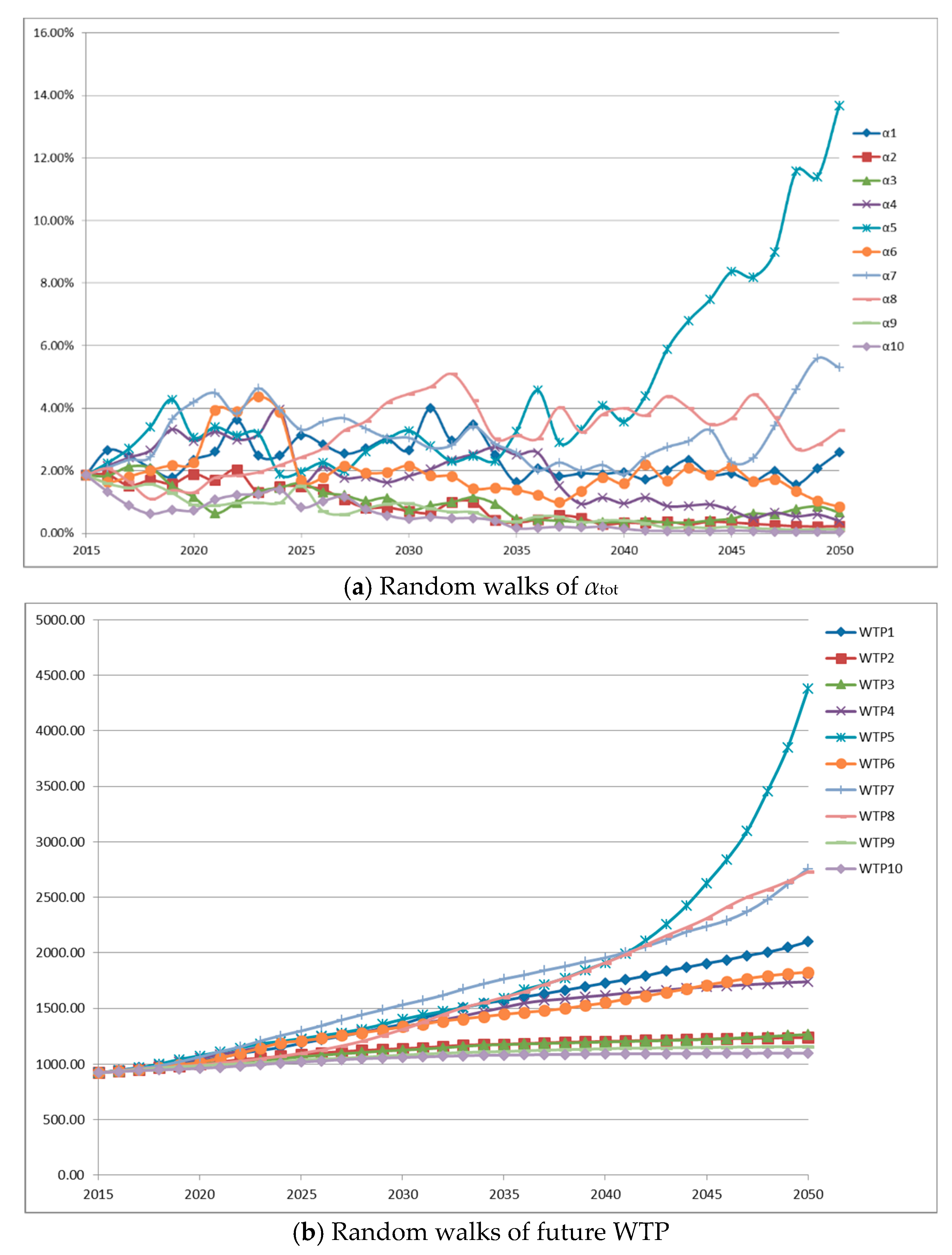
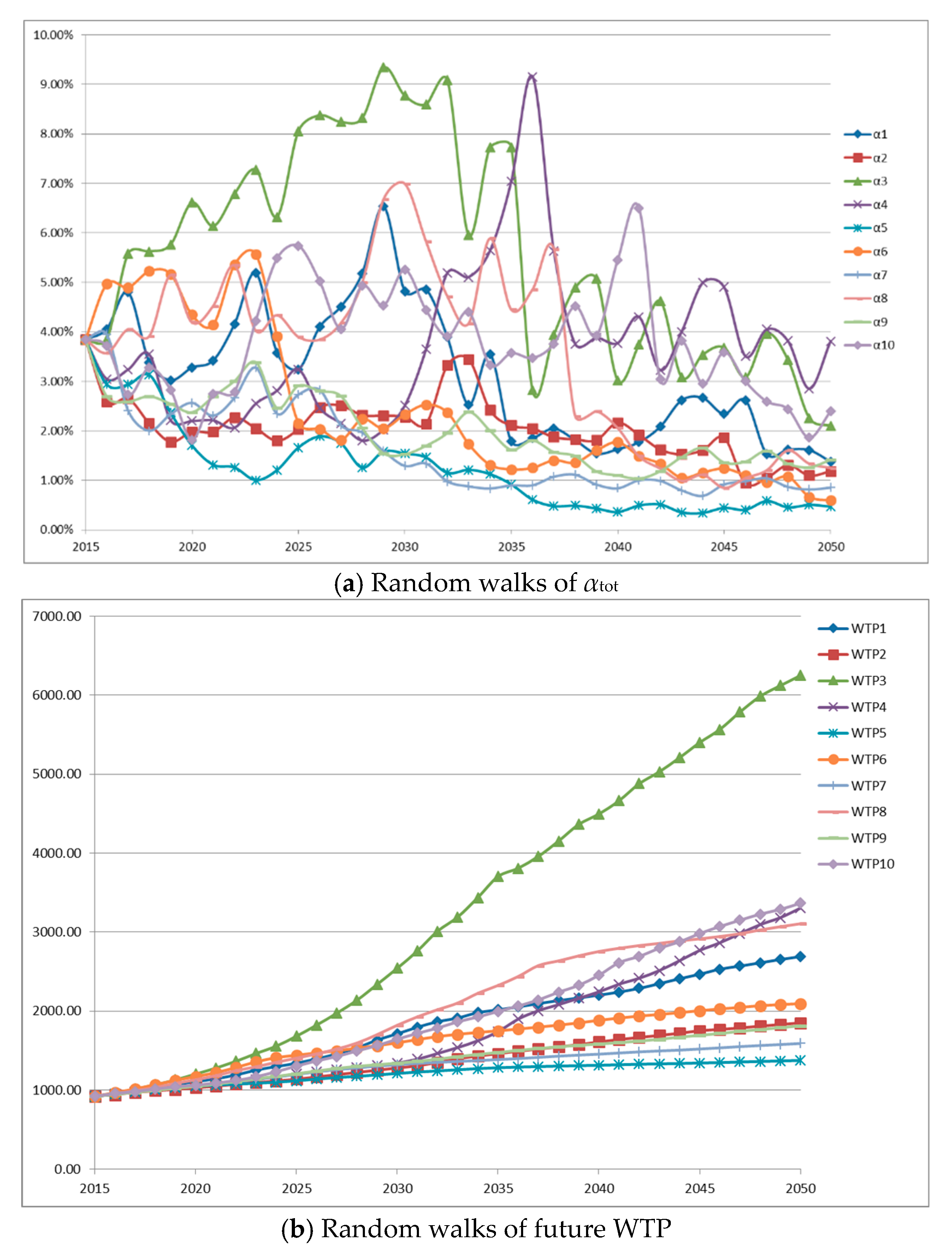
4. An Illustrative Example
4.1. Input Parameters
- Scenario A: Unchanged preferences. In this case the ratio WTP2050/WTP2015 equals to 1 and, consequently, the average (annual) preferences factor is zero.
- Scenario B: Green preferences. In this case the ratio WTP2050/WTP2015 is assumed to be 2 and, consequently, the annual preferences factor is 1.98%.
- Scenario C: Materialistic preferences. In this case the ratio WTP2050/WTP2015 is assumed to be 0.5 and, consequently, the annual preferences factor is −1.98%.
4.2. Present Value of WTP Ignoring αtot
- PVtot is the total present value of WTP for recreation per ha of forest land (i.e., 922 €2015).
- WTPt is the annual WTP for recreation per ha of forest land at time t.
- s is the social discount rate.
- t is the time in years.
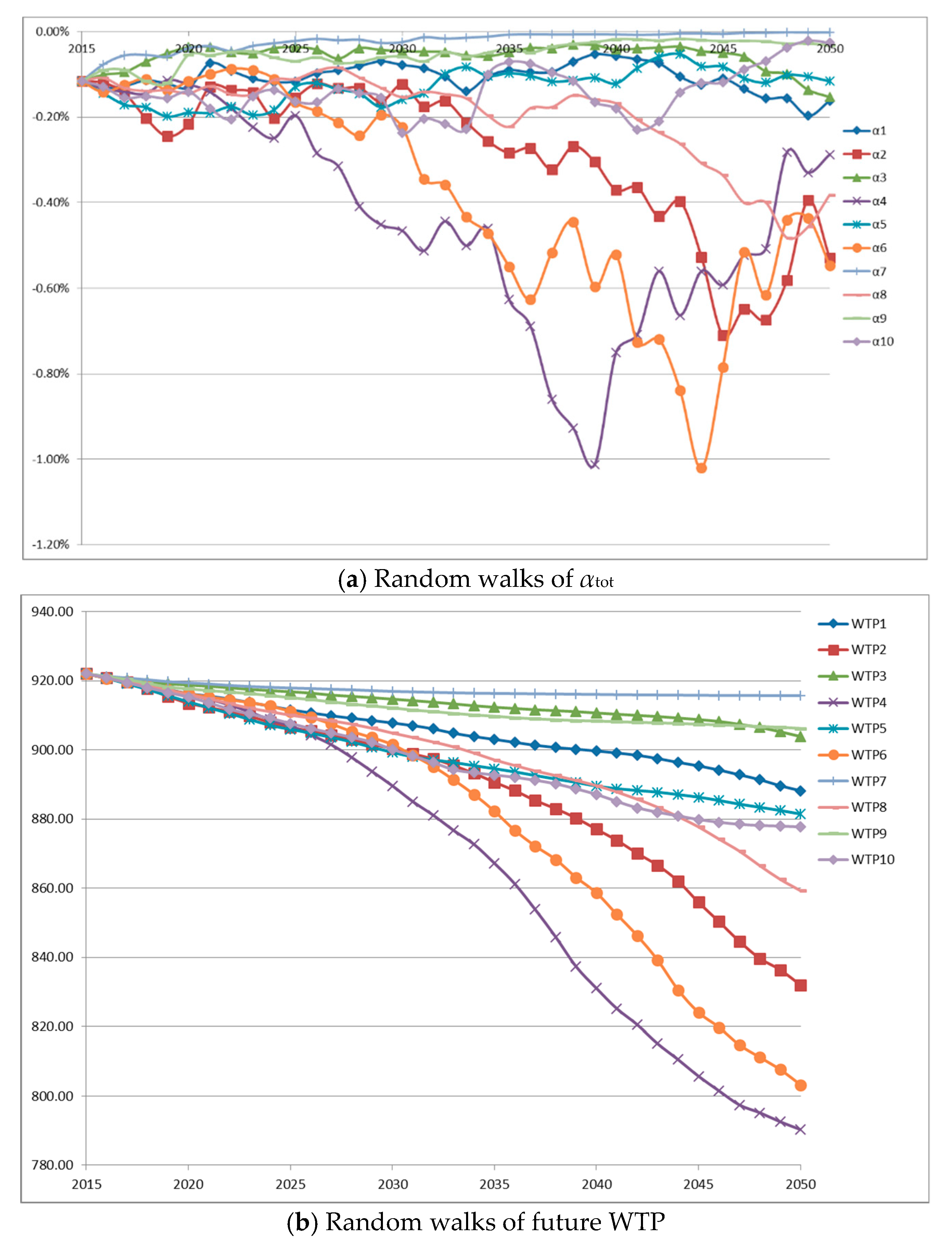
4.3. Present Value of WTP Considering αtot
4.3.1. Scenario A: Unchanged Preferences
4.3.2. Scenario B: Green Preferences
4.3.3. Scenario C: Materialistic Preferences
4.4. Discussion of Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ackerman, Frank, and Elizabeth A. Stanton. 2013. Climate Economics. The State of the Art. Oxford and New York: Routledge. [Google Scholar]
- Anderson, Mark W., Mario Teisl, and Caroline Noblet. 2012. Giving voice to the future in sustainability: Retrospective assessment to learn prospective stakeholder engagement. Ecological Economics 84: 1–6. [Google Scholar] [CrossRef]
- Arbués, Fernando, María Ángeles García-Valiñas, and Roberto Martínez-Espiñeira. 2003. Estimation of residential water demand: A state-of-the-art review. Journal of Socio-Economics 32: 81–102. [Google Scholar] [CrossRef]
- Arrow, Kenneth J., William R. Cline, Karl-Goran Maler, Mohan Munasinghe, Ray Squitier, and Joseph E. Stiglitz. 1996. Intertemporal equity, discounting, and economic efficiency. In Climate Change 1995: Economic and Social Dimensions of Climate Change, Contribution of Working Group III to the Second Assessment Report of the Intergovernmental Panel on Climate Change. Edited by James P. Bruce, Hoesung Lee and Erik F. Haites. Cambridge: Cambridge University Press. [Google Scholar]
- Le Kama, Alain Ayong, and Katheline Schubert. 2004. Growth, Environment and Uncertain Future Preferences. Environmental and Resource Economics 28: 31–53. [Google Scholar] [CrossRef]
- Bacchetta, Philippe, and Eric Van Wincoop. 2007. Random walk expectations and the forward discount puzzle. American Economic Review 97: 346–50. [Google Scholar] [CrossRef]
- Balint, Tomas, Francesco Lamperti, Antoine Mandel, Mauro Napoletano, Andrea Roventini, and Alessandro Sapio. 2017. Complexity and the Economics of Climate Change: A Survey and a Look Forward. Ecological Economics 138: 252–65. [Google Scholar] [CrossRef]
- Barbier, Edward B., Stefan Baumgärtner, Kanchan Chopra, Christopher Costello, Anantha Duraiappah, Rashid Hassan, Ann Kinzig, Markus Lehman, Unai Pascual, Stephen Polasky, and et al. 2009. The valuation of ecosystem services, Chapter 18. In Biodiversity, Ecosystem Functioning, and Human Wellbeing: An Ecological and Economic Perspective. Edited by Shahid Naeem, Daniel E. Bunker, Andy Hector, Michel Loreau and Charles Perrings. Oxford: Oxford University Press, pp. 248–62. [Google Scholar]
- Baum, Seth D., and William E. Easterling. 2010. Space-time discounting in climate change adaptation. Mitigation and Adaptation Strategies for Global Change 15: 591–609. [Google Scholar] [CrossRef]
- Baumgärtner, Stefan, Alexandra Klein, Denise Thiel, and Klara Winkler. 2015. Ramsey Discounting of Ecosystem Services. Environmental and Resource Economics 61: 273–96. [Google Scholar] [CrossRef]
- Bergstrom, Theodore C., and Robert P. Goodman. 1973. Private demands for public goods. American Economic Review 63: 280–96. [Google Scholar]
- Besley, Timothy, and Torsten Persson. 2019. The Dynamics of Environmental Politics and Values. Journal of the European Economics Association 17: 993–1024. [Google Scholar] [CrossRef]
- Borcherding, Thomas, and Robert Deacon. 1972. Demand for services of non-federal governments. American Economic Review 62: 891–901. [Google Scholar]
- Borges, Maria Rosa. 2011. Random walk tests for the Lisbon stock market. Applied Economics 43: 631–39. [Google Scholar] [CrossRef]
- Bosello, Francesco. 2014. The role of economic modelling for climate change mitigation and adaptation strategies. In Routledge Handbook of the Economics of Climate Change Adaptation. Edited by Anil Markandya, Ibon Galarraga and Elisa Sainz de Murieta. Abingdon: Routledge. [Google Scholar]
- Boyd, James, and Spencer Banzhaf. 2007. What are ecosystem services? The need for standardized environmental accounting units. Ecological Economics 63: 616–26. [Google Scholar] [CrossRef]
- Cline, William R. 1992. The Economics of Global Warming. Washington: Institute for International Economics. [Google Scholar]
- Dalhuisen, Jasper M., Raymond J. G. M. Florax, Henri L. F. de Groot, and Peter Nijkamp. 2003. Price and income elasticities of residential water demand: A meta-analysis. Land Economics 79: 292–308. [Google Scholar] [CrossRef]
- Dasgupta, Partha. 2008. Discounting climate change. Journal of Risk and Uncertainty 37: 141–69. [Google Scholar] [CrossRef]
- Dasgupta, Partha, and Eric Maskin. 2005. Uncertainty and hyperbolic discounting. American Economic Review 95: 1290–99. [Google Scholar] [CrossRef]
- Dasgupta, Partha, Karl-Göran Mäler, and Scott Barrett. 1999. Intergenerational equity, social discount rates, and global warming. In Discounting and Intergenerational Equity. Edited by Paul R. Portney and John P. Weyant. Washington: Resources for the Future. [Google Scholar]
- de Groot, Rudolf, Luke Brander, Sander van der Ploeg, Robert Costanza, Florence Bernard, Leon Braat, Mike Christie, Neville Crossman, Andrea Ghermandi, Lars Hein, and et al. 2012. Global estimates of the value of ecosystems and their services in monetary units. Ecosystem Services 1: 50–61. [Google Scholar] [CrossRef]
- Drupp, Moritz A., and Martin C. Hänsel. 2018. Relative Prices and Climate Policy: How the Scarcity of Non-Market Goods Drives Policy Evaluation. Economics Working Papers 2018-01. Kiel: Christian-Albrechts-University of Kiel, Department of Economics. Available online: https://www.econstor.eu/bitstream/10419/174361/1/1012760782.pdf (accessed on 15 December 2015).
- Fama, Elugene F. 1965. Random walks in stock market prices. Financial Analysts Journal 21: 55–59. [Google Scholar] [CrossRef]
- Fisher, Anthony C., and John V. Krutilla. 1975. Resource conservation, environmental preservation, and the rate of discount. Quarterly Journal of Economics 89: 358–70. [Google Scholar] [CrossRef]
- Fisher, Brendan, R. Kerry Turner, and Paul Morling. 2009. Defining and classifying ecosystem services for decision making. Ecological Economics 68: 643–53. [Google Scholar] [CrossRef]
- Flores, Nicholas E., and Richard T. Carson. 1997. The Relationship between the Income Elasticities of Demand and Willingness to Pay. Journal of Environmental Economics and Management 33: 287–95. [Google Scholar] [CrossRef]
- Freeman, Myrick, III. 2003. The Measurement of Environmental and Resource Values: Theory and Methods, 2nd ed.Washington: Resources for the Future. [Google Scholar]
- Gay, Carlos, and Francisco Estrada. 2010. Objective probabilities about future climate are a matter of opinion. Climatic Change 99: 27–46. [Google Scholar] [CrossRef]
- Gollier, Christian. 2007. Comment intégrer le risque dans le calcul économique. Revue d’ Économie Politique 117: 209–23. [Google Scholar] [CrossRef]
- Gollier, Christian. 2008. Discounting with fat-tailed economic growth. Journal of Risk and Uncertainty 37: 171–86. [Google Scholar] [CrossRef]
- Gollier, Christian. 2017. Valuation of Natural Capital Under Uncertain Substitutability. TSE Working Paper No. TSE−813. Available online: http://publications.ut-capitole.fr/24094/1/Gollier_24094.pdf (accessed on 12 December 2015).
- Gollier, Christian, and Martin L. Weitzman. 2010. How Should the Distant Future be Discounted When Discount Rates are Uncertain? Economics Letters 107: 350–53. [Google Scholar] [CrossRef]
- Goulder, Lawrence H., and Donald Kennedy. 1997. Valuing ecosystem: Philosophical bases and empirical methods. In Nature’s Services: Societal Dependence on Natural Ecosystems. Edited by Gretchen. C. Daily. Washington: Island Press, pp. 23–48. [Google Scholar]
- Gravelle, Hugh, and Dave Smith. 2000. Discounting for Health Effects in Cost Benefit and Cost Effectiveness Analysis. Centre for Health Economics Technical Paper Series 20. York: University of York. [Google Scholar]
- Groom, Ben, Cameron Hepburn, Phoebe Koundouri, and David Pearce. 2005. Declining discount rates: The long and the short of it. Environmental and Resource Economics 32: 445–93. [Google Scholar] [CrossRef]
- Grüne-Yanoff, Till, and Sven Ove Hansson. 2009. Preference Change. Approaches from Philosophy, Economics and Psychology. Heidelber: Springer. [Google Scholar]
- H.M. Treasury. 2003. The Green Book: Appraisal and Evaluation in Central Government. London: The Stationery Office. [Google Scholar]
- H.M. Treasury. 2009. Accounting for the Effects of Climate Change: Supplementary Green Book Guidance. Available online: https://www.gov.uk/government/uploads/ system/uploads/attachment_data/file/191501/Accounting_for_the_effects_of_climate_change.pdf (accessed on 17 December 2015).
- Harr, Milton E. 1987. Reliability-Based Design in Civil Engineering. New York: McGraw-Hill. [Google Scholar]
- Heal, G. 2009. The economics of climate change: A post-Stern perspective. Climatic Change 96: 275–97. [Google Scholar] [CrossRef]
- Hein, Lars, Kris van Koppen, Rudolf S. de Groot, and Ekko C. van Ierland. 2006. Spatial scales, stakeholders and the valuation of ecosystem services. Ecological Economics 57: 209–28. [Google Scholar] [CrossRef]
- Hertzler, Greg. 2007. Adapting to Climate Change and Managing Climate Risks by Using Real Options. Australian Journal of Agricultural Research 58: 985–92. [Google Scholar] [CrossRef]
- Hewitt, Julie A., and W. Michael Hanemann. 1995. A Discrete-continuous Choice Approach to Residential Water Demand under Block Rate Pricing. Land Economics 71: 173–92. [Google Scholar] [CrossRef]
- Hoel, Michael, and Thomas Sterner. 2007. Discounting and relative prices. Climatic Change 84: 265–80. [Google Scholar] [CrossRef]
- Hof, Andries F., Chris W. Hope, Jason Lowe, Michael D. Mastrandrea, Malte Meinshausen, and Detlef P. van Vuuren. 2012. The benefits of climate change mitigation in integrated assessment models: The role of the carbon cycle and climate component. Climatic Change 113: 897–917. [Google Scholar] [CrossRef]
- Hökby, Stina, and Tore Söderqvist. 2003. Elasticities of Demand and Willingness to Pay for Environmental Services in Sweden. Environmental and Resource Economics 26: 361–83. [Google Scholar] [CrossRef]
- Horowitz, John K. 2002. Preferences in the future. Environmental and Resource Economics 21: 241–59. [Google Scholar] [CrossRef]
- Hotelling, Harold. 1931. The Economics of Exhaustible Resources. Journal of Political Economy 39: 139–75. [Google Scholar] [CrossRef]
- Hultman, Magnus, Azadeh Kazeminia, and Vahid Ghasemi. 2015. Intention to visit and willingness to pay premium for ecotourism: The impact of attitude, materialism, and motivation. Journal of Business Research 68: 1854–61. [Google Scholar] [CrossRef]
- Jacobsen, Jette Bredahl, and Nick Hanley. 2009. Are there income effects on global willingness to pay for biodiversity conservation? Environmental and Resource Economics 43: 137–60. [Google Scholar] [CrossRef]
- Jacobsen, Jette Bredahl, Thomas Hedemark Lundhede, and Bo Jellesmark Thorsen. 2013. The effects of current income and expected change in future income on stated preferences for environmental improvements. Journal of Forest Economics 19: 206–19. [Google Scholar] [CrossRef]
- Janssen, Marco A., and Wander Jager. 2001. Fashions, habits and changing preferences: Simulation of psychological factors affecting market dynamics. Journal of Economic Psychology 22: 745–72. [Google Scholar] [CrossRef]
- Jaynes, Edwin T. 1957. Information theory and statistical mechanics. The Physical Review 106: 620–30. [Google Scholar] [CrossRef]
- Kaplow, Louis, and David Weisbach. 2011. Discount rates, social judgments, individuals’ risk preferences, and uncertainty. Journal of Risk and Uncertainty 42: 125–43. [Google Scholar] [CrossRef]
- Kidd, Quentin, and Aie-Rie Lee. 1997. Postmaterialist values and the environment: A critique and reappraisal. Social Science Quarterly 78: 1–15. [Google Scholar]
- Kilbourne, William, and Gregory Pickett. 2008. How materialism affects environmental beliefs, concern, and environmentally responsible behavior. Journal of Business Research 61: 885–93. [Google Scholar] [CrossRef]
- Kontogianni, Areti, Gary W. Luck, and Michalis Skourtos. 2010. Valuing ecosystem services on the basis of service-providing units: A promising solution to the ‘endpoint problem’ in stated preference approaches. Ecological Economics 69: 1479–87. [Google Scholar] [CrossRef]
- Kontogianni, Areti, Christos H. Tourkolias, Dimitris Damigos, and Michalis Skourtos. 2013. Assessing sea level rise costs and adaptation benefits under uncertainty in Greece. Environmental Science & Policy 37: 61–78. [Google Scholar]
- Kopp, Robert E., and Bryan K. Mignone. 2012. The U.S. government’s social cost of carbon estimates after their first two years: Pathways for improvement. Economics 6: 2012–15. [Google Scholar] [CrossRef]
- Kriström, Bengt, and Pere Riera. 1996. Is the income elasticity of environmental improvements less than one? Environmental & Resource Economics 7: 45–55. [Google Scholar]
- Krysiak, Frank C., and Daniela Krysiak. 2006. Sustainability with Uncertain Future Preferences. Environmental & Resource Economics 33: 511–31. [Google Scholar]
- Lamb, Laura. 2019. Changing preferences for environmental protection: Evidence from volunteer behaviour. International Review of Applied Economics 33: 384–401. [Google Scholar] [CrossRef]
- Lebègue, Danièl, Philippe Hirtzman, and Luc. Baumstark. 2005. Commissariat Général du Plan, Le prix du Temps et la Décision Publique: Révision du Taux d’Actualisation Public. Paris: Documentation Française. [Google Scholar]
- Lee, Christine, Claire Schlemme, Jessica Murray, and Robert Unsworth. 2015. The cost of climate change: Ecosystem services and wildland fires. Ecological Economics 116: 261–69. [Google Scholar] [CrossRef]
- Linquiti, Peter, and Nicholas Vonortas. 2012. The value of flexibility in adapting to climate change: A real options analysis of investments in coastal defense. Climate Change Economics 3: 1250008-1/28. [Google Scholar] [CrossRef]
- Loewenstein, George, and David Schkade. 2003. Wouldn’t it be nice? Predicting future feelings. In Foundations of Hedonic Psychology: Scientific Perspectives on Enjoyment and Suffering. Edited by Daniel Kahneman, Ed Diener and Norbert Schwarz. New York: Russell Sage Foundation. [Google Scholar]
- MacInnis, Deborah J., Vanessa M. Patrick, and Choong Whan Park. 2005. Looking through the crystal ball: The role of affective forecasting and misforecasting in consumer behaviour. Review of Marketing Research 2: 43–79. [Google Scholar]
- Martini, Chiara, and Silvia Tiezzi. 2014. Is the environment a luxury? An empirical investigation using revealed preferences and household production. Resource and Energy Economics 37: 147–67. [Google Scholar] [CrossRef]
- Masur, Jonathan S., and Eric A. Posner. 2011. Climate regulation and the limits of cost-benefit analysis. California Law Review 99: 1557–600. [Google Scholar]
- Metcalf, Gilbert, and James Stock. 2015. The Role of Integrated Assessment Models in Climate Policy: A User’s Guide and Assessment; Discussion Paper 2015-68. Cambridge: Harvard Project on Climate Agreements. Available online: http://belfercenter.ksg.harvard.edu/files/dp68_metcalf-stock.pdf (accessed on 5 January 2016).
- Mishra, Srikanta. 2002. Assigning Probability Distributions to Input Parameters of Performance Assessment Models. SKB Technical Report TR-02-11. Stockholm: Svensk Kärnbränslehantering AB. [Google Scholar]
- Mun, Johnathan. 2006. Real Options Analysis—Tools and Techniques for Valuing Strategic Investments and Decisions, 2nd ed.Hoboken: John Wiley & Sons, Inc. [Google Scholar]
- Neumayer, Eric. 1999. Global warming: Discounting is not the issue, but substitutability is. Energy Policy 27: 33–43. [Google Scholar] [CrossRef]
- Newell, Richard G., and William A. Pizer. 2003. Discounting the distant future: How much do uncertain rates increase valuations? Journal of Environmental Economics and Management 46: 52–71. [Google Scholar] [CrossRef]
- Noblet, Caroline L., Mark W. Anderson, and Mario F. Teisl. 2015. Thinking past and thinking future: An empirical test of the effects of retrospective assessment on future preferences. Ecological Economics 114: 180–87. [Google Scholar] [CrossRef][Green Version]
- Nordhaus, William D. 1997. Discounting in economics and climatic change: An editorial comment. Climate Change 37: 315–28. [Google Scholar] [CrossRef]
- Nordhaus, William D. 2007. The Stern Review on the economics of climate change. Journal of Economic Literature 45: 686–702. [Google Scholar] [CrossRef]
- Nunes, Paulo A. L. D., and Jeroen C. J. M. van den Bergh. 2001. Economic Valuation of Biodiversity: Sense or Nonsense? Ecological Economics 39: 203–22. [Google Scholar] [CrossRef]
- O’Neill, Brian. 2010. Multi-century scenario development and socioeconomic uncertainty. In Improving the Assessment and Valuation of Climate Change Impacts for Policy and Regulatory Analysis: Modeling Climate Change Impacts and Associated Economic Damages; Washington: U.S. Environmental Protection Agency and U.S. Department of Energy. Available online: https://yosemite.epa.gov/ee/epa/eerm.nsf/vwAN/EE-0564-115.pdf/$file/EE-0564-115.pdf (accessed on 30 November 2015).
- OECD. 2012a. Medium and Long-Term Scenarios for Global Growth and Imbalances; OECD Economic Outlook 2012. Paris: OECD. Available online: http://www.oecd.org/berlin/50405107.pdf (accessed on 5 December 2015).
- OECD. 2012b. Environmental Outlook to 2050: The Consequences of Inaction. Key Findings on Biodiversity; Paris: OECD. Available online: http://www.oecd.org/env/indicators-modelling-outlooks/biodiversitychapteroftheoecdenvironmentaloutlookto2050theconsequencesofinaction.htm (accessed on 5 December 2015).
- OECD. 2015. Inflation (CPI). Paris: OECD. Available online: https://data.oecd.org/price/inflation-cpi.htm (accessed on 5 December 2015).
- Parry, Martin, Nigel Arnell, Tony McMichael, Robert Nicholls, Pim Martens, Sari Kovats, Matthew Livermore, Cynthia Rosenzweig, Ana Iglesias, and Gunther Fischer. 2001. Millions at risk: Defining critical climate change threats and targets. Global Environmental Change-Human and Policy Dimensions 11: 181–83. [Google Scholar] [CrossRef]
- Pattanayak, Subhrendu K., Julia M. Wing, Brooks M. Depro, George Van Houtven, Paul De Civita, David M. Stieb, and Bryan Hubbell. 2002. International Health Benefits Transfer Application Tool: The Use of PPP and Inflation Indices. Final Report, Prepared for Economic Analysis and Evaluation Division, Office of Policy Coordination and Economic Analysis Policy and Planning Directorate, Healthy Environments and Consumer Safety Branch. Ottawa: Health Canada. [Google Scholar]
- Pearce, David. 2003. Conceptual Framework for Analysing the Distributive Impacts of Environmental Policies. Paper presented at the OECD Environment Directorate Workshop on the Distribution of Benefits and Costs of Environmental Policies, Paris, France, March 4–5. [Google Scholar]
- Pesando, James. 1979. On the random walk characteristics of short- and long-term interest rates in an efficient market. Journal of Money, Credit and Banking 11: 457–66. [Google Scholar] [CrossRef]
- Pindyck, Robert S. 2013. Climate Change Policy: What Do the Models Tell Us? Journal of Economic Literature 51: 860–72. [Google Scholar] [CrossRef]
- Pingali, Prabhu, Anaka Aiyar, Mathew Abraham, and Andaleeb Rahman. 2019. Managing climate change risks in food systems. In Transforming Food Systems for a Rising India. Palgrave Studies in Agricultural Economics and Food Policy. Cham: Palgrave Macmillan. [Google Scholar]
- Pint, Ellen M. 1999. Household Responses to Increased Water Rates during the California Drought. Land Economics 75: 246–66. [Google Scholar] [CrossRef]
- PricewaterhouseCoopers. 2015. The World in 2050—Will the Shift in Global Economic Power Continue? Available online: https://www.pwc.com/gx/en/issues/the-economy/assets/world-in-2050-february-2015.pdf (accessed on 15 December 2015).
- Rosenberger, R. Randall S., and Tom D. Stanley. 2010. Publication Selection of Recreation Demand Price Elasticity: A Meta-Analysis. Available online: https://www.hendrix.edu/uploadedFiles/Departments_and_Programs/Business_and_Economics/AMAES/MAER%202010%20AR%20Rosenberger%20Stanley%20090110.pdf (accessed on 17 December 2015).
- Scalas, Enrico. 2006. The application of continuous-time random walks in finance and economics. Physica A: Statistical Mechanics and its Applications 362: 225–39. [Google Scholar] [CrossRef]
- Scarborough, Helen. 2010. Decomposing the social discount rate. Paper presented at the AARES Conference, Adelaide, Australia, February 10–12; Available online: http://ageconsearch.umn.edu/bitstream/59156/2/Scarborough,%20Helen.pdf (accessed on 30 November 2015).
- Shafer, Glenn, and Vladimir Vovk. 2001. Game Theoretic Probability in Finance. In Probability and Finance: It’s Only a Game! New York: Wiley, pp. 201–36. [Google Scholar]
- Shannon, Claude E. 1948. A mathematical theory of communication. The Bell System Technical Journal 27: 379–423, 623–56. [Google Scholar] [CrossRef]
- Smith, Graham. 2002. Tests of the Random Walk Hypothesis for London Gold Prices. Applied Economics Letters 9: 671–74. [Google Scholar] [CrossRef]
- Stern, Nicholas H. 2008. The economics of climate change. American Economic Review 98: 1–37. [Google Scholar] [CrossRef]
- Stern, Nicholas H., and Cabinet Office—HM Treasury. 2007. The Stern Review of the Economics of Climate Change. Cambridge: Cambridge University Press. [Google Scholar]
- Sterner, Thomas, and U. Martin Persson. 2008. An Even Sterner Review: Introducing Relative Prices into the Discounting Debate. Review of Environmental Economics and Policy 2: 61–76. [Google Scholar] [CrossRef]
- Summers, Lawrence, and Richard Zeckhauser. 2008. Policymaking for posterity. Journal of Risk and Uncertainty 37: 115–40. [Google Scholar] [CrossRef][Green Version]
- TEEB. 2010. The Economics of Ecosystems and Biodiversity: Ecological and Economic Foundation. London: Earthscan. [Google Scholar]
- Thomas, John F., and Geoffrey J. Syme. 1988. Estimating residential price elasticity of demand for water: A contingent valuation approach. Water Resources Research 24: 1847–57. [Google Scholar] [CrossRef]
- Thunström, Linda, Jonas Nordström, and Jason F. Shogren. 2015. Certainty and overconfidence in future preferences for food. Journal of Economic Psychology 51: 101–13. [Google Scholar]
- Traeger, Christian P. 2007. Theoretical Aspects of Long-Term Evaluation in Environmental Economics. Ph.D. thesis, University of Heidelberg, Heidelberg, Germany, October 27. Available online: http://www.ub.uni-heidelberg.de/archiv/7049 (accessed on 12 December 2015).
- Traeger, Christian P. 2011. Sustainability, limited substitutability, and non-constant social discount rates. Journal of Environmental Economics and Management 62: 215–28. [Google Scholar] [CrossRef]
- Vale, Petterson Molina. 2016. The changing climate of climate change economics. Ecological Economics 121: 12–19. [Google Scholar] [CrossRef]
- van der Ploeg, Sander, and Rudolf S. de Groot. 2010. The TEEB Valuation Database—A Searchable Database of 1310 Estimates of Monetary Values of Ecosystem Services. Wageningen: Foundation for Sustainable Development. [Google Scholar]
- van Vuuren, Detlef P., Jason Lowe, Elke Stehfest, Laila Gohar, Andries F. Hof, Chris Hope, Rachel Warren, Malte Meinshausen, and Gian-Kasper Plattner. 2011. How well do integrated assessment models simulate climate change? Climatic Change 104: 255–85. [Google Scholar] [CrossRef]
- Warren, Rachel, Michael Mastrandrea, Chris Hope, and Andries Hof. 2010. Variation in the climatic response to SRES emissions scenarios in integrated assessment models. Climatic Change 102: 671–785. [Google Scholar] [CrossRef]
- Watkiss, Paul, and Chris Hope. 2011. Using the social cost of carbon in regulatory deliberations. WIREs Climate Change 2: 886–901. [Google Scholar] [CrossRef]
- Weisbach, David A., and Cass R. Sunstein. 2008. Climate Change and Discounting the Future: A Guide for the Perplexed. Harvard Law School Program on Risk Regulation Research Paper No. 08-12. Washington: AEI Center for Regulatory and Market Studies. [Google Scholar] [CrossRef]
- Weitzman, Martin L. 2007. A Review of the Stern Review on the Economics of Climate Change. Journal of Economic Literature 45: 703–24. [Google Scholar] [CrossRef]
- Woodward, Merrilyn, Ben Gouldby, Zoran Kapelan, Soon-Thiam Khu, and Ian Townend. 2011. Real options in flood risk management decision making. Journal of Flood Risk Management 4: 339–49. [Google Scholar] [CrossRef]
- World Bank. 2009. Mainstreaming Adaptation to Climate Change in Agriculture and Natural Resources Management Projects, Guidance Note 7, Annex 12. Environment Department. Available online: http://climatechange.worldbank.org/climatechange/content/note-7-evaluate-adaptation-economic-analysis (accessed on 5 December 2015).
- World Bank. 2011. Climate Change and Fiscal Policy: A Report for APEC, Office of the Chief Economist, East Asia and Pacific Region. Available online: http://www-wds.worldbank.org/external/default/WDSContentServer/WDSP/IB/2011/02/01/000333038_20110201000150/Rendered/PDF/565630REV0ESW010Policy01Jan13112011.pdf (accessed on 5 December 2015).
- World Bank. 2015. PPP Conversion Factor, GDP (LCU per International $). Available online: http://data.worldbank.org/indicator/PA.NUS.PPP?page=4 (accessed on 5 January 2016).
- Worthington, Andrew C., and Mark Hoffman. 2008. An empirical survey of residential water demand modelling. Journal of Economic Surveys 22: 842–71. [Google Scholar] [CrossRef]
- Yoo, James, Silvio Simonit, Ann Kinzig, and Charles Perrings. 2014. Estimating the Price Elasticity of Residential Water Demand: The Case of Phoenix, Arizona. Applied Economic Perspectives and Policy 36: 333–50. [Google Scholar] [CrossRef]
- Yu, Xiaohua, Zhifeng Gao, and Yinchu Zeng. 2014. Willingness to pay for the “Green Food” in China. Food Policy 45: 80–87. [Google Scholar] [CrossRef]
| No. of Estimates | Mean | Median | St.Dev. | Min | Max | |
|---|---|---|---|---|---|---|
| Provisioning services | 9 | 671 | 450 | 867 | 121 | 1593 |
| 1 Food | 2 | 299 | 299 | 422 | 0 | 597 |
| 2 Water | 3 | 191 | 121 | 123 | 118 | 333 |
| 3 Raw materials | 4 | 181 | 31 | 322 | 2 | 662 |
| 4 Genetic resources | ||||||
| 5 Medicinal resources | ||||||
| 6 Ornamental resources | ||||||
| Regulating services | 13 | 491 | 367 | 584 | 105 | 1212 |
| 7 Air quality regulation | ||||||
| 8 Climate regulation | 6 | 152 | 34 | 241 | 7 | 624 |
| 9 Disturbance moderation | ||||||
| 10 Regulation of water flows | ||||||
| 11 Waste treatment | 3 | 7 | 0 | 13 | 0 | 22 |
| 12 Erosion prevention | 1 | 5 | 5 | 5 | 5 | |
| 13 Nutrient cycling | 1 | 93 | 93 | 93 | 93 | |
| 14 Pollination | ||||||
| 15 Biological control | 2 | 235 | 235 | 330 | 1 | 469 |
| Habitat services | 10 | 862 | 171 | 1342 | 51 | 3573 |
| 16 Nursery service | ||||||
| 17 Genetic diversity | 10 | 862 | 171 | 1342 | 51 | 3573 |
| Cultural services | 26 | 990 | 139 | 2644 | 1 | 10028 |
| 18 Esthetic information | ||||||
| 19 Recreation | 25 | 989 | 138 | 2644 | 1 | 10027 |
| 20 Inspiration | ||||||
| 21 Spiritual experience | ||||||
| 22 Cognitive development | 1 | 1 | 1 | 1 | 1 | |
| TOTAL | 58 | 3013 | 1127 | 5437 | 278 | 16406 |
| Statistics | PV Ignoring αtot | Scenario A | Scenario B | Scenario C |
|---|---|---|---|---|
| Mean | 72,200 | 93,950 | 131,070 | 70,300 |
| Median | 64,480 | 85,850 | 116,020 | 64,120 |
| St. Dev. | 44,320 | 56,160 | 81,480 | 43,820 |
| Minimum | 1550 | 2440 | 5150 | 210 |
| Maximum | 194,610 | 278,180 | 392,360 | 209,340 |
| Mean Std. Error | 1400 | 1780 | 2580 | 1390 |
| Percentiles | PV Ignoring αtot | Scenario A | Scenario B | Scenario C |
|---|---|---|---|---|
| 100% | 1550 | 2440 | 5150 | 210 |
| 90% | 18,740 | 26,830 | 34,280 | 17,820 |
| 80% | 29,950 | 41,610 | 54,290 | 28,830 |
| 70% | 40,530 | 54,970 | 73,030 | 39,480 |
| 60% | 52,470 | 69,840 | 93,270 | 52,120 |
| 50% | 64,470 | 85,840 | 115,940 | 64,120 |
| 40% | 78,710 | 101,450 | 142,830 | 76,170 |
| 30% | 95,220 | 122,910 | 170,350 | 89,940 |
| 20% | 113,400 | 144,690 | 205,080 | 107,210 |
| 10% | 136,680 | 173,690 | 250,550 | 134,890 |
| 0% | 194,610 | 278,180 | 392,360 | 209,340 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skourtos, M.; Damigos, D.; Kontogianni, A.; Tourkolias, C.; Hunt, A. Embedding Preference Uncertainty for Environmental Amenities in Climate Change Economic Assessments: A “Random” Step Forward. Economies 2019, 7, 107. https://doi.org/10.3390/economies7040107
Skourtos M, Damigos D, Kontogianni A, Tourkolias C, Hunt A. Embedding Preference Uncertainty for Environmental Amenities in Climate Change Economic Assessments: A “Random” Step Forward. Economies. 2019; 7(4):107. https://doi.org/10.3390/economies7040107
Chicago/Turabian StyleSkourtos, Michalis, Dimitris Damigos, Areti Kontogianni, Christos Tourkolias, and Alistair Hunt. 2019. "Embedding Preference Uncertainty for Environmental Amenities in Climate Change Economic Assessments: A “Random” Step Forward" Economies 7, no. 4: 107. https://doi.org/10.3390/economies7040107
APA StyleSkourtos, M., Damigos, D., Kontogianni, A., Tourkolias, C., & Hunt, A. (2019). Embedding Preference Uncertainty for Environmental Amenities in Climate Change Economic Assessments: A “Random” Step Forward. Economies, 7(4), 107. https://doi.org/10.3390/economies7040107






