Delinquency and Default in USA Student Debt as a Proportional Response to Unemployment and Average Debt per Borrower
Abstract
1. Introduction
2. Literature Review
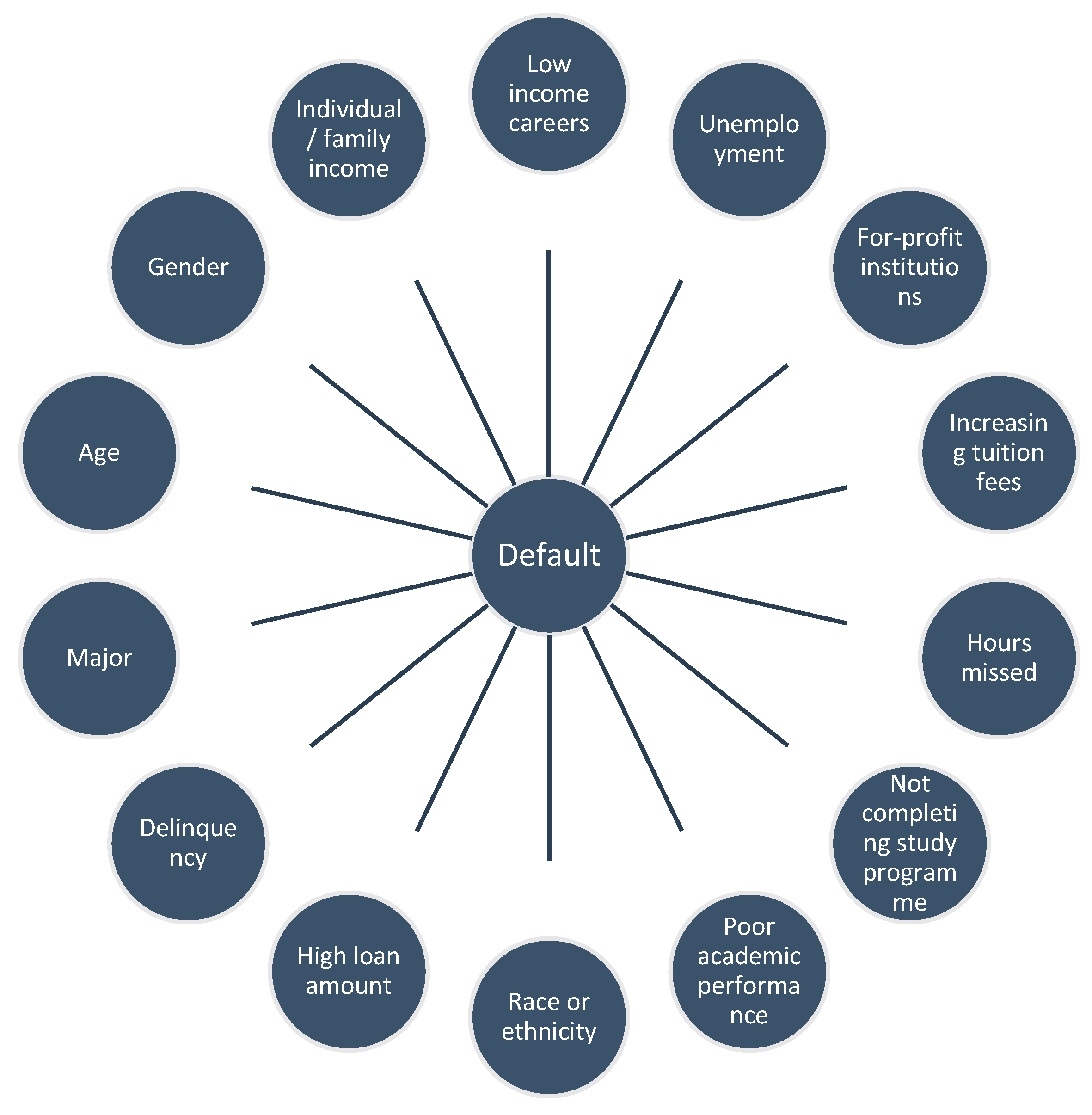
2.1. Student Characteristics and Default
2.2. Institutional Characteristics and Default
2.3. Enrolment and Default
2.4. Income Level and Default
2.5. Unemployment, Debt and Default
3. Methodology
4. Data
5. Tests and Diagnostics for Panel Data
6. Empirical Results and Discussion
6.1. Empirical Results—Econometric First Approach
6.2. Empirical Results—Econometric Second Approach: FRM Models
6.3. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Avery, Christopher, and Sarah Turner. 2012. Student loans: Do college students borrow too much—Or not enough? The Journal of Economic Perspectives 26: 165–92. [Google Scholar] [CrossRef]
- Baum, Sandy, and Marie O’Malley. 2003. College on credit: How borrowers perceive their education debt. Journal of Student Financial Aid 33: 1. [Google Scholar]
- Breusch, Trevor S., and Adrian R. Pagan. 1980. The Lagrange multiplier test and its applications to model specification in econometrics. The Review of Economic Studies 47: 239–53. [Google Scholar] [CrossRef]
- Brown, Meta, Andrew Haughwout, Donghoon Lee, Joelle Scally, and Wilbert van der Klaauw. 2015. Measuring Student Debt and its Performance. In Student Loans and the Dynamics of Debt. Edited by Brad Hershbein and Kevin M. Hollenbeck. Kalamazoo: W.E. Upjohn Institute for Employment Research, pp. 37–52. [Google Scholar] [CrossRef]
- Cellini, Stephanie Riegg, and Rajeev Darolia. 2015. College costs and financial constraints: Student borrowing at for-profit institutions. In Student Loans and the Dynamics of Debt. Edited by Brad Hershbein and Kevin M. Hollenbeck. Kalamazoo: W.E. Upjohn Institute for Employment Research, pp. 137–74. [Google Scholar]
- Chakrabarti, Raji, Andrew Haughwout, Donghoon Lee, Joelle Scally, and Wilbert van der Klaauw. 2017. Press Briefing on Household Debt, with Focus on Student Debt. April 3, 2017. New York: Federal Reserve Bank of New York. Available online: https://www.newyorkfed.org/medialibrary/media/press/PressBriefing-Household-Student-Debt-April32017.pdf (accessed on 7 February 2019).
- Choy, Susan P., Xiaojie Li, and C. Dennis Carroll. 2006. Dealing with Debt: 1992–93 Bachelor’s Degree Recipients 10 Years Later. Washington, DC: US Department of Education, National Center for Education Statistics, Institute of Education Sciences. [Google Scholar]
- Christman, Dana E. 2000. Multiple realities: Characteristics of loan defaulters at a two-year public institution. Community College Review 27: 16–32. [Google Scholar] [CrossRef]
- Deming, David J., Claudia Goldin, and Lawrence F. Katz. 2012. The for-profit postsecondary school sector: Nimble critters or agile predators? Journal of Economic Perspectives 26: 139–64. [Google Scholar] [CrossRef]
- Doornik, Jurgen A., and Henrik Hansen. 2008. An omnibus test for univariate and multivariate normality. Oxford Bulletin of Economics and Statistics 70: 927–39. [Google Scholar] [CrossRef]
- Dynarski, Mark. 1994. Who defaults on student loans? Findings from the national postsecondary student aid study. Economics of Education Review 13: 55–68. [Google Scholar] [CrossRef]
- Elliott, William, and IlSung Nam. 2013. Is student debt jeopardizing the short-term financial health of US households? Federal Reserve Bank of St. Louis Review 95: 405–24. [Google Scholar]
- Flint, Thomas A. 1997. Predicting student loan defaults. The Journal of Higher Education 68: 322–54. [Google Scholar] [CrossRef]
- Goodell, John W. 2016. Do for-profit universities induce bad student loans? The Quarterly Review of Economics and Finance 61: 173–84. [Google Scholar] [CrossRef]
- Guan, Weihua. 2003. From the help desk: Bootstrapped standard errors. The Stata Journal 3: 71–80. [Google Scholar] [CrossRef]
- Han, Byung-Suk, Hyoung-Goo Kang, and Sang-Gyung Jun. 2015. Student loan and credit risk in Korea. Economics Letters 135: 121–25. [Google Scholar] [CrossRef]
- Hardin, James W., and Joseph M. Hilbe. 2013. Generalized Estimating Equations, 2nd ed. Boca Raton: Chapman and Hall/CRC. [Google Scholar]
- Harrast, Steven A. 2004. Undergraduate Borrowing: A Study of Debtor Students and Their Ability to Retire Undergraduate Loans. Journal of Student Financial Aid 34: 21–37. [Google Scholar]
- Haughwout, Andrew, Donghoon Lee, Joelle Scally, and Wilbert van der Klaauw. 2015. Student Loan Borrowing and Repayment Trends. Report, April 16, 2015. New York: Federal Reserve Bank of New York. [Google Scholar]
- Herr, Elizabeth, and Larry Burt. 2005. Predicting student loan default for the University of Texas at Austin. Journal of Student Financial Aid 35: 2. [Google Scholar]
- Ionescu, Felicia. 2009. The federal student loan program: Quantitative implications for college enrollment and default rates. Review of Economic Dynamics 12: 205–31. [Google Scholar] [CrossRef][Green Version]
- Ionescu, Felicia, and Nicole Simpson. 2016. Default risk and private student loans: Implications for higher education policies. Journal of Economic Dynamics and Control 64: 119–47. [Google Scholar] [CrossRef]
- Knapp, Laura Greene, and Terry G. Seaks. 1992. An analysis of the probability of default on federally guranteed student loans. The Review of Economics and Statistics 74: 404–11. [Google Scholar] [CrossRef]
- Krishnan, Karthik, and Pinshuo Wang. 2018. The Cost of Financing Education: Can Student Debt Hinder Entrepreneurship? Management Science. [Google Scholar] [CrossRef]
- Liang, Kung-Yee, and Scott L. Zeger. 1986. Longitudinal data analysis using generalized linear models. Biometrika 73: 13–22. [Google Scholar] [CrossRef]
- Lochner, Lance, and Alexander Monge-Naranjo. 2004. Education and default incentives with government student loan programs. NBER Working Paper, 8815. [Google Scholar]
- Looney, Adam, and Constantine Yannelis. 2015. A crisis in student loans? How changes in the characteristics of borrowers and in the institutions they attended contributed to rising loan defaults. Brookings Papers on Economic Activity 2015: 1–89. [Google Scholar] [CrossRef]
- Looney, Adam, and Constantine Yannelis. 2018. Borrowers with Large Balances: Rising Student Debt and Falling Repayment Rates. Washington, DC: Brookings Institution. [Google Scholar]
- Monge-Naranjo, Alexander. 2014. Recent trends in student loans: More loans and higher balances. Federal Reserve Bank of St. Louis Economic Synopses 2: 014. [Google Scholar] [CrossRef]
- Mooney, Christopher F., Christopher L. Mooney, Christopher Z. Mooney, Robert D. Duval, and Robert Duvall. 1993. Bootstrapping: A Nonparametric Approach to Statistical Inference. No. 94–95. Newcastle upon Tyne: Sage. [Google Scholar]
- Papke, Leslie E., and Jeffrey M. Wooldridge. 1996. Econometric methods for fractional response variables with an application to 401(k) plan participation rates. Journal of Applied Econometrics 11: 619–32. [Google Scholar] [CrossRef]
- Papke, Leslie E., and Jeffrey M. Wooldridge. 2008. Panel data methods for fractional response variables with an application to test pass rates. Journal of Econometrics 145: 121–33. [Google Scholar] [CrossRef]
- Pesaran, Mohammad Hashem. 2004. General Diagnostic Tests for Cross Section Dependence in Panels. Cambridge Working Papers in Economics 0435. Cambridge: Faculty of Economics, University of Cambridge. [Google Scholar]
- Pesaran, Mohammad Hashem. 2006. Estimation and inference in large heterogeneous panels with a multifactor error structure. Econometrica 74: 967–1012. [Google Scholar] [CrossRef]
- Pinto, Mary Beth, and Phylis M. Mansfield. 2006. Financially at-risk college students: An exploratory investigation of student loan debt and prioritization of debt repayment. Journal of Student Financial Aid 36: 22–32. [Google Scholar]
- Podgursky, Michael, Mark Ehlert, Ryan Monroe, Donald Watson, and John Wittstruck. 2002. Student loan defaults and enrollment persistence. Journal of Student Financial Aid 32: 27–42. [Google Scholar]
- Raheli, Hossein, Rassul Mohammad Rezaei, Mehri Raei Jadidi, and Hassan Ghasemi Mobtaker. 2017. A two-stage DEA model to evaluate sustainability and energy efficiency of tomato production. Information Processing in Agriculture 4: 342–50. [Google Scholar] [CrossRef]
- Ramalho, Esmeralda A., Joaquim JS Ramalho, and Pedro D. Henriques. 2010. Fractional regression models for second stage DEA efficiency analyses. Journal of Productivity Analysis 34: 239–55. [Google Scholar] [CrossRef]
- Ramsey, James Bernard. 1969. Tests for specification errors in classical linear least-squares regression analysis. Journal of the Royal Statistical Society. Series B (Methodological) 31: 350–71. [Google Scholar] [CrossRef]
- Rothstein, Jesse, and Cecilia Elena Rouse. 2011. Constrained after college: Student loans and early-career occupational choices. Journal of Public Economics 95: 149–63. [Google Scholar] [CrossRef]
- Sánchez, Juan M., and Lijun Zhu. 2015. Student Loan Delinquency: A Big Problem Getting Worse? Economic Synopses 2015: 7. [Google Scholar] [CrossRef][Green Version]
- Schmeiser, Maximilian, Christiana Stoddard, and Carly Urban. 2016. Student loan information provision and academic choices. American Economic Review 106: 324–28. [Google Scholar] [CrossRef]
- Steiner, Matt, and Natali Teszler. 2003. The Characteristics Associated with Student Loan Default at Texas A and M University. Austin, TX. January. Available online: http://www.trelliscompany.org/wp-content/uploads/2017/02/TAMU_Default_Study.pdf (accessed on 14 March 2019).
- Stinebrickner, Ralph, and Todd Stinebrickner. 2008. The effect of credit constraints on the college drop-out decision: A direct approach using a new panel study. American Economic Review 98: 2163–84. [Google Scholar] [CrossRef]
- University of Michigan. 2018. University of Michigan: Consumer Sentiment [UMCSENT], Retrieved from FRED, Federal Reserve Bank of St. Louis. Available online: https://fred.stlouisfed.org/series/UMCSENT (accessed on 3 February 2018).
- Volkwein, James Fredericks, and Alberto F. Cabrera. 1998. Who defaults on student loans? The effects of race, class, and gender on borrower behavior. In Condemning Students to Debt: College Loans and Public Policy. Edited by Richard Fossey and Mark Bateman. New York: Teachers College Press. [Google Scholar]
- Volkwein, J. Fredericks, and Bruce P. Szelest. 1995. Individual and campus characteristics associated with student loan default. Research in Higher Education 36: 41–72. [Google Scholar] [CrossRef]
- Volkwein, J. Fredericks, Bruce P. Szelest, Alberto F. Cabrera, and Michelle R. Napierski-Prancl. 1998. Factors associated with student loan default among different racial and ethnic groups. The Journal of Higher Education 69: 206–37. [Google Scholar] [CrossRef]
- Webber, Karen L., and Sharon L. Rogers. 2014. Student loan default: Do characteristics of four-year institutions contribute to the puzzle? Journal of Student Financial Aid 44: 99–124. [Google Scholar]
- Wolla, Scott A. 2014. The Rising Cost of College: Tuition, Financial Aid, and Price Discrimination. Page One Economics Newsletter 2014: 1–4. [Google Scholar]
- Woo, Jennie H. 2002. Factors Affecting the Probability of Default: Student Loans in California. Journal of Student Financial Aid 32: 5–23. [Google Scholar]
- Wooldridge, Jeffrey M. 2013. Introductory Econometrics: A Modern Approach. Boston: Cengage Learning. [Google Scholar]
| Breusch–Pagan and Doornik–Hansen Tests | |||
|---|---|---|---|
| Homoskedasticity | Normality | ||
| Statistics | F(1,398) = 29.64 *** | (2) = 3.082 | |
| Pesaran and Wooldridge Tests | |||
| Cross-section Independence | No Serial Correlation | ||
| Statistics | N(0,1) = 50.18 *** | F(1,49) = 85.975 *** | |
| Ramsey Test | |||
| Omitted Variables | |||
| Statistics | F(3,38) = 1.28 | ||
| Variable | VIF | ||
| ln(fstress) | 1.83 | ||
| ln(adb) | 3.84 | ||
| ln(unem) | 2.29 | ||
| ln(cs) | 3.08 | ||
| ln(unem) × reg2 | 2.03 | ||
| ln(unem) × reg3 | 2.40 | ||
| ln(unem) × reg4 | 2.76 | ||
| Mean VIF | 2.60 | ||
| Breusch–Pagan test for random effects | |||
| Random effects vs. OLS | |||
| Statistics | Chibar2(01) = 385.48 *** | ||
| Dependent Variable is Def | Linear Random Effects-GLS Model | Probit Binomial Model | Logit Binomial Model | ||
|---|---|---|---|---|---|
| Estimate | Estimate | Average Marginal | Estimate | Average Marginal | |
| (Standard Error) | (Standard Error) | (Standard Error) | (Standard Error) | (Standard Error) | |
| ln(unem) | 0.00455 *** | 0.020162 *** | 0.003507 *** | 0.03679 *** | 0.003287 *** |
| (0.0012) | (0.0074) | (0.0012) | (0.0014) | (0.0013) | |
| ln(adb) | 0.038937 *** | 0.19870 *** | 034562 *** | 0.382477 *** | 0.034177 *** |
| (0.0100) | (0.0568) | (0.0097) | (0.1102) | (0.0097) | |
| ln(cs) | 0.094105 *** | 0.540503 *** | 0.094014 *** | 1.0407 *** | 0.092995 *** |
| (0.0134) | (0.0704) | (0.0126) | (10.360) | (0.0126) | |
| ln(fstress) | 0.01703 *** | - | - | - | - |
| (0.0045) | |||||
| reg1 * ln(unem) | 0.009813 *** | 0.147453 *** | 0.025647 *** | 0.286813 *** | 0.025628 *** |
| (0.0020) | (0.02633) | (0.0047) | (0.0518) | (0.0048) | |
| reg2 * ln(unem) | 0.006361 *** | 0.122116 *** | 0.021240 *** | 0.233516 *** | 0.020866 *** |
| (0.0019) | (0.0255) | (0.0045) | (0.0495) | (0.0045) | |
| reg3 * ln(unem) | −0.004389 ** | 0.071810 *** | 0.012490 *** | 0.146015 *** | 0.013047 *** |
| (0.0023) | (0.0269) | (0.0047) | (0.0523) | (0.0047) | |
| reg4 * ln(unem) | Omitted | 0.094510 *** | 0.016439 *** | 0.187621 *** | 0.016765 *** |
| (0.0263) | (0.0046) | (0.0513) | (0.0046) | ||
| Constant | −0.54521 *** | −4.84710 *** | −9.0525 *** | ||
| (0.0450) | (0.257) | (0.509) | |||
| # Observations | 400 | 400 | 400 | 400 | 400 |
| # States | 50 | 50 | 50 | 50 | 50 |
| 0.4896 | |||||
| 531.48 *** | 603.16 *** | 553.73 *** | |||
| Specification Test | One-Part Model | Two-Part Model-GFRM II | ||||||
|---|---|---|---|---|---|---|---|---|
| Logit | Probit | Logit | Probit | |||||
| Model 1 | Model 2 | Model 1 | Model 2 | Model 1 | Model 2 | Model 1 | Model 2 | |
| RESET test | 6.509 *** | 4.916 ** | 8.014 *** | 3.877 ** | 5.709 ** | 5.733 ** | 7.143 *** | 4.577 ** |
| GOFF-I test | 7.788 *** | 4.521 ** | 5.930 ** | 4.552 ** | 6.906 *** | 5.34 ** | 5.171 ** | 5.301 ** |
| GOFF-II test | 3.227 * | 6.040 ** | 9.726 ***- | 3.372 * | 2.648 * | 6.941 *** | 8.775 *** | 4.035 ** |
| P Test | ||||||||
| H1: FRM II–Logit | 37.147 *** | 0.432 | 35.66 *** | 0.226 | ||||
| H1: FRM II–Probit | 34.30 *** | 0.003 | 32.82 *** | 0.056 | ||||
| H1: FRM II–Loglog | 10.90 *** | 8.330 *** | 8.605 *** | 7.571 *** | 9.965 *** | 9.230 *** | 7.762 *** | 8.395 *** |
| H1: FRM II–Cloglog | 1.997 | 3.656 ** | 7.022 *** | 1.460 | 1.518 | 4.453 ** | 6.141 ** | 1.974 |
| One-Part Model | Two-Part Model-GFRM II | |||||||
| Loglog | Cloglog | Loglog | Cloglog | |||||
| Model 1 | Model 2 | Model 1 | Model 2 | Model 1 | Model 2 | Model 1 | Model 2 | |
| RESET test | 18.478 *** | 1.306 | 1.352 | 8.116 *** | 17.26 *** | 1.681 | 0.995 | 9.201 *** |
| GOFF-I test | 0.547 | 8.756 *** | 19.28 *** | 0.329 | 9.877 *** | |||
| GOFF-II test | 20.536 *** | 0.926 | 1.252 | |||||
| P Test | ||||||||
| H1: FRM II–Logit | 23.910 *** | 0.091 | 0.053 | 13.01 *** | 22.53 *** | 0.015 | 0.006 | 14.15 *** |
| H1: FRM II–Probit | 18.346 *** | 0.084 | 1.361 | 12.91 *** | 17.07 *** | 0.218 | 1.030 | 14.06 *** |
| H1: FRM II–Loglog | 1.723 | 18.45 *** | 1.376 | 19.60 *** | ||||
| H1:FRM II–Cloglog | 17.136 *** | 0.241 | 15.82 *** | 0.087 | ||||
| 1.352 | ||||||||
| Variables | One-Part Models | Two-Part Models–Second Part | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Logit | Cloglog | Logit | Probit | Loglog | Cloglog | |||||||
| Model 1 | Model 2 | Model 1 | Model 2 | Model 1 | Model 2 | Model 1 | Model 2 | Model 1 | Model 2 | Model 1 | Model 2 | |
| Ln Unemp | 0.72498 | 0.56442 | 0.714818 | 0.430817 | 0.430377 | 0.555790 | ||||||
| (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | |||||||
| Ln Consent | 4.1849 | 3.47629 | 3.3550 | 2.69794 | 4.11833 | 3.41889 | 2.48705 | 2.07142 | 2.44960 | 2.13408 | 3.29949 | 2.64841 |
| (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | |
| Ln StudLoan | 0.45470 | 0.32198 | 0.456299 | 0.282758 | 0.315330 | 0.324207 | ||||||
| (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | |||||||
| Ln FedFund | 0.21001 | 0.140725 | 0.16276 | 0.098352 | 0.206927 | 0.1382437 | 0.124222 | 0.083950 | 0.123363 | 0.096257 | 0.160409 | 0.096487 |
| (0.00) *** | (0.00) *** | (0.00) *** | (0.017) ** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.019) ** | |
| Ln FedFund12 | −0.47782 | −0.386794 | −0.38829 | −309652 | −0.471323 | −0.381190 | −0.28751 | −0.228414 | −0.272293 | −0.224709 | −0.382974 | −0.304826 |
| (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | |
| Region1 × Ln Unemp | 1.10069 | 0.904759 | 1.09451 | 0.651306 | 0.628539 | 0.899260 | ||||||
| (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | |||||||
| Region2 × Ln Unemp | 0.66666 | 0.527119 | 0.661803 | 0.401305 | 0.4058867 | 0.522815 | ||||||
| (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | |||||||
| Region3 × Ln Unemp | 0.090182 | 0.005711 | 0.077027 | 0.052234 | 0.1287208 | 0.0054921 | ||||||
| (0.584) | (0.964) | (0.639) | (0.600) | (0.230) | (0.964) | |||||||
| Region4 × Ln Unemp | 0.38483 | 0.310101 | 0.380502 | 0.231298 | 0.241940 | 0.305699 | ||||||
| (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | |||||||
| Region1 × Ln StudLoan | 0.7788 | 0.570535 | 0.781294 | 0.478170 | 0.522313 | 0.574361 | ||||||
| (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | |||||||
| Region2 × Ln StudLoan | 0.648943 | 0.457115 | 0.651841 | 0.403390 | 0.455813 | 0.4613107 | ||||||
| (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | |||||||
| Region3 × Ln StudLoan | 0.533799 | 0.339007 | 0.533100 | 0.333980 | 0.416123 | 0.340367 | ||||||
| (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | |||||||
| Region4 × Ln StudLoan | 0.614946 | 0.429088 | 0.618155 | 0.383997 | 0.441950 | 0.433428 | ||||||
| (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | |||||||
| Constant | −21.910 | −20.7485 | −17.694 | −16.1810 | −21.6425 | −20.5164 | −13.1288 | −12.4903 | −12.8187 | −12.7431 | −17.4776 | −15.9932 |
| (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | (0.00) *** | |
| Observations | 765 | 765 | 765 | 765 | 764 | 764 | 764 | 764 | 764 | 764 | 764 | 764 |
| R2 | 0.3898 | 0.52767 | 0.38579 | 0.521970 | 0.382689 | 0.52576 | 0.380290 | 0.525543 | 0.374636 | 0.52880 | 0.383142 | 0.51968 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuinhas, J.A.; Moutinho, V.; Silva, E. Delinquency and Default in USA Student Debt as a Proportional Response to Unemployment and Average Debt per Borrower. Economies 2019, 7, 100. https://doi.org/10.3390/economies7040100
Fuinhas JA, Moutinho V, Silva E. Delinquency and Default in USA Student Debt as a Proportional Response to Unemployment and Average Debt per Borrower. Economies. 2019; 7(4):100. https://doi.org/10.3390/economies7040100
Chicago/Turabian StyleFuinhas, José Alberto, Victor Moutinho, and Estefano Silva. 2019. "Delinquency and Default in USA Student Debt as a Proportional Response to Unemployment and Average Debt per Borrower" Economies 7, no. 4: 100. https://doi.org/10.3390/economies7040100
APA StyleFuinhas, J. A., Moutinho, V., & Silva, E. (2019). Delinquency and Default in USA Student Debt as a Proportional Response to Unemployment and Average Debt per Borrower. Economies, 7(4), 100. https://doi.org/10.3390/economies7040100






