Assessing Regional Economic Performance in the Southern Thailand Special Economic Zone Using a Vine-COPAR Model
Abstract
:1. Introduction
2. Methodology
2.1. Vine Copula Models
C and D Vine Copulas
2.2. VAR Model
2.3. Granger Causality
3. Data and Empirical Results
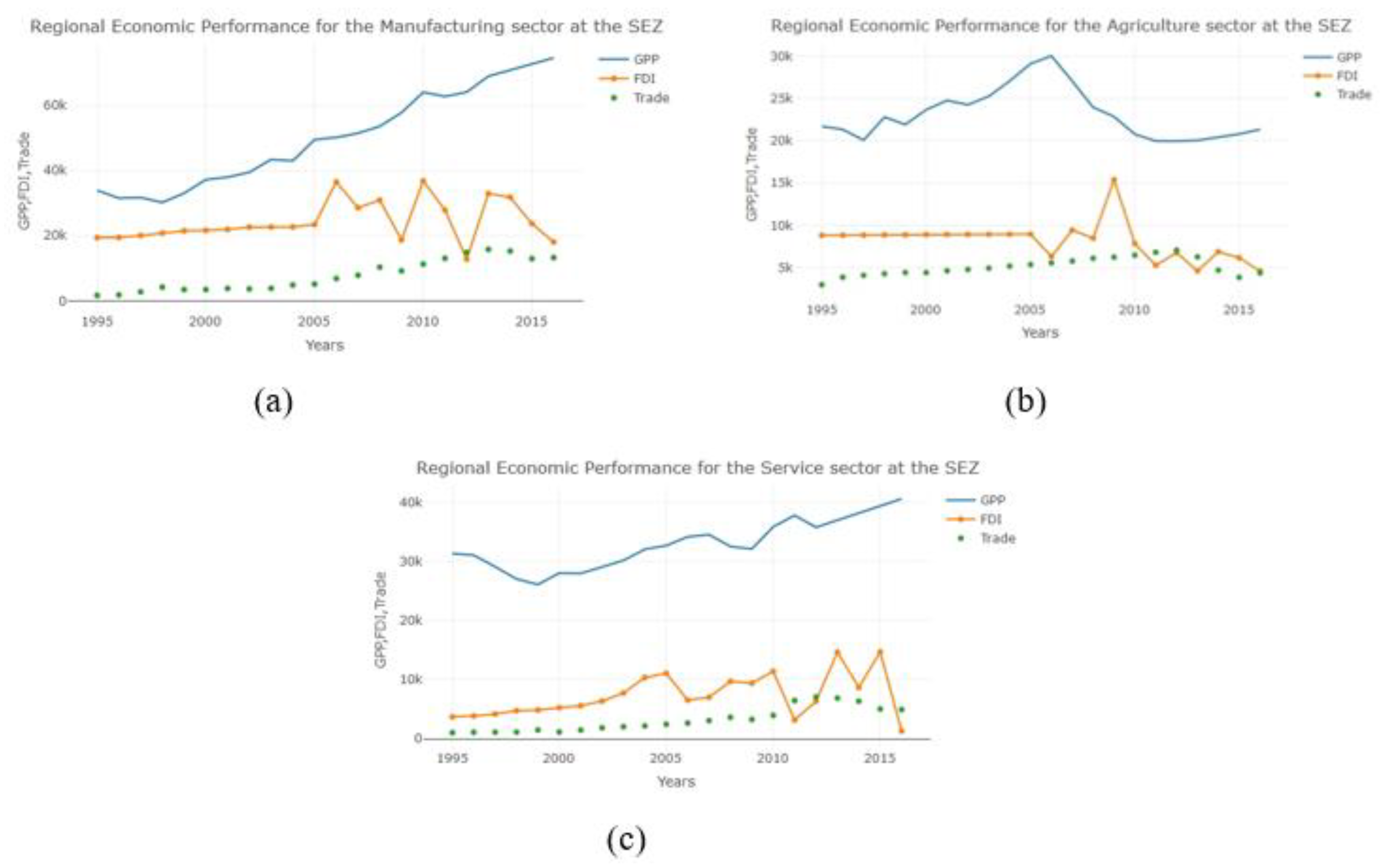
3.1. Data
3.2. Empirical Results
3.2.1. CD-Vine COPAR Models
3.2.2. Evaluation of the Performance of the Prediction Models
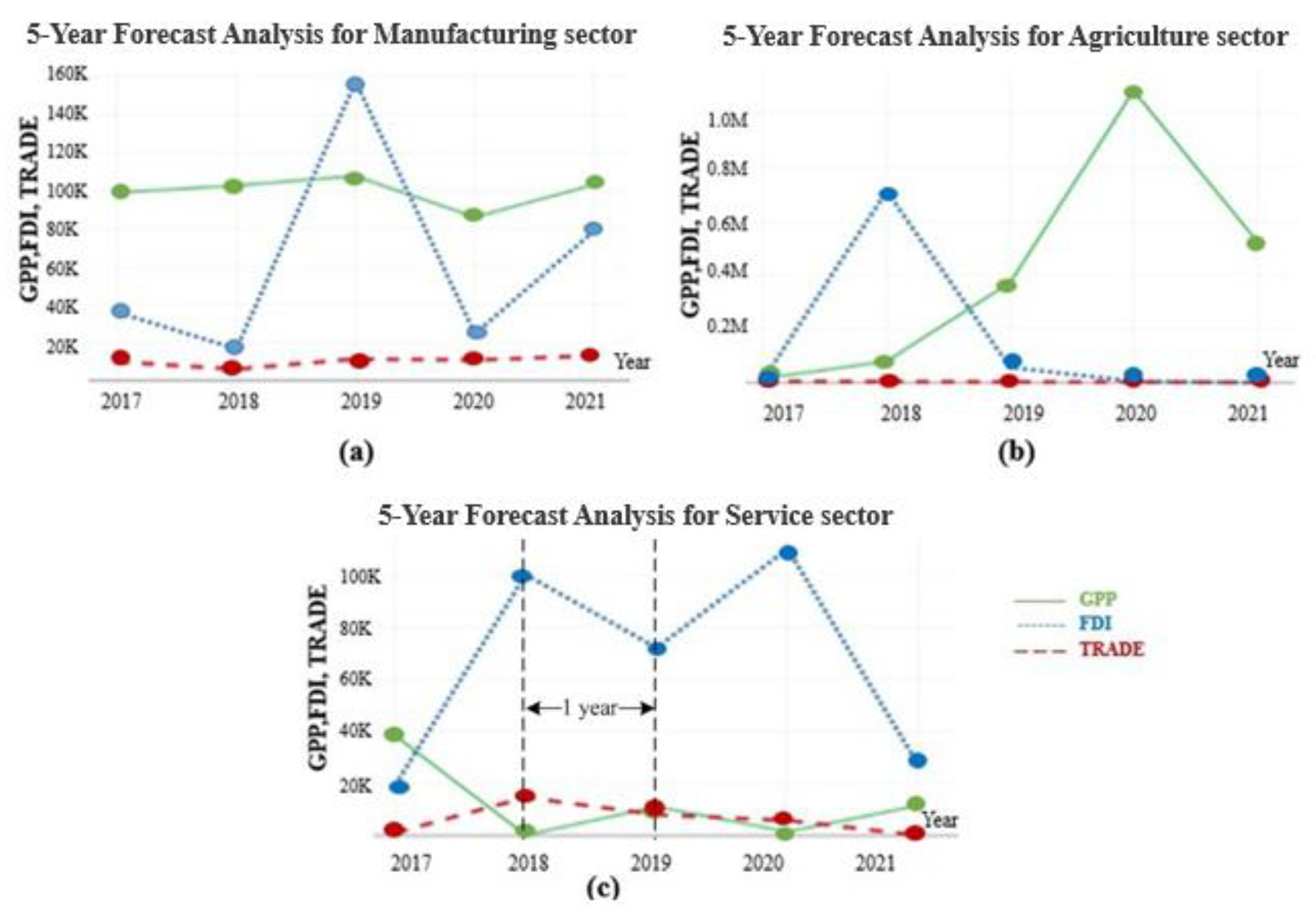
3.2.3. The Prediction of the SEZ’s Economic Performance for the Next Five Years
3.2.4. Vine COPAR-Based Granger Causality
4. Conclusions and Policy Implications
- (1)
- The appropriate specification for a forecasting method using a Vine-COPAR model provides better results than a single time series, since evaluating more dependence structures leads to more accurate predictions. Moreover, the Vine-COPAR based Granger causality can accommodate high-order moment causality and this approach thus provides effective long-run performance.
- (2)
- For five-year forecast (2017–2021), the FDI and TRADE appeared to be the important contributions towards the SEZ. However, GPP and FDI displayed sharp fluctuations, and TRADE behaved constantly. Therefore, the government should encourage their competitiveness and maintain continuity of foreign investment and trade policies.
- (3)
- Granger causality and bidirectional causality existed among GPP, FDI and TRADE in all sectors.
Author Contributions
Funding
Conflicts of Interest
References
- Ascani, Andrea, Riccardo Crescenzi, and Simona Iammarino. 2012. Reginal Economic Development: A Review. Working Paper. European Community’s Seventh Framework Programme FP7-SSH -2010.2.2-1 (266834). London, UK: European Commission. [Google Scholar]
- Brechmann, Eike Christian, and Claudia Czado. 2015. COPAR—Multivariate time series modeling using the COPula AutoRegressive model. Journal Applied Stochastic Models in Business and Industry Archive 31: 495–514. [Google Scholar] [CrossRef]
- Brechmann, Eike Christian, and Ulf Schepsmeier. 2013. Modeling Dependence with C-and D-Vine Copulas: The R Package CDVine. Journal of Statistical Software 52: 1–27. [Google Scholar] [CrossRef]
- Cherdchom, Parinya, Paratta Prommin, and Arisara Romyen. 2016. Growth of Small and Meduim Enterprises under Special Economic Development Zone: Case Study Sadao District Songkhla Province. Research Report. Songkhla: Faculty of Economics, Prince of Songkhla University. [Google Scholar]
- Lau, Chi-Keung Marco. 2010. Convergence across the United States: Evidence from Panel ESTRA Unit root Test. International Advances in Economic Research 16: 52–64. [Google Scholar] [CrossRef]
- Ehling, Manfred, and Thomas Körner. 2015. Handbook on Data Quality Assessment Methods and Tools. Wiesbaden: Eurostat. [Google Scholar]
- Engle, Robert F., and Clive WJ Granger. 1987. Cointegration and Error Correction: Representation, Estimation and Testing. Econometrica 55: 251–76. [Google Scholar] [CrossRef]
- Government Public Relations Department. 2016. Sothern Situation: Special Economic Zones in the Deep South to Help Improve Local Economy. Available online: http://nwnt.prd.go.th/nnt_en/Southern%20Situation/article9.php (accessed on 20 April 2018).
- Hamilton, James D. 1994. Time Series Analysis. Princeton: Princeton University Press. [Google Scholar]
- Ho, Owen C. H. 2004. Determinants of Foreign Direct Investment in China. Paper presented at the 16th Annual Conference of the Association for Chinese Economics Studies, Australia (ACESA), Brisbane, Australia, July 19–20. [Google Scholar]
- Joe, Harry. 1996. Families of m-Variate Distributions with Given Margins and m(m−1)/2 Bivariate Dependence Parameters. In Distributions with Fixed Marginals and Related Topics. Edited by Ludger Ruschendorf, Berthold Schweizer and Michael D. Taylor. Hayward: Institute of Mathematical Statistics, pp. 120–41. [Google Scholar]
- Lucas, Robert E., Jr. 1988. On the mechanics of economic development. Journal of Monetary Economics 22: 3–42. [Google Scholar] [CrossRef]
- Lütkepohl, Helmut. 2005. New Introduction to Multiple Time Series Analysis. Berlin: Springer. [Google Scholar]
- Nelson, Charles R., and Charles R. Plosser. 1982. Trends and Random Walks in Macroeconomic Time Series: Some Evidence and Implications. Journal of Monetary Economics 10: 130–52. [Google Scholar] [CrossRef]
- Pecican, Eugen S. 2010. Forecasting based on open var model. Romanian Journal of Economic Forecasting 1: 59–69. [Google Scholar]
- Pindyck, Rober S., and Daniel L. Rubinfeld. 1997. Econometric Models and Economic Forecasts. New York: McGraw-Hill. [Google Scholar]
- Romer, Paul M. 1986. Increasing returns and long-run growth. Journal of Political Economy 94: 1002–37. [Google Scholar] [CrossRef]
- Sklar, A. 1959. Fonctions de repartition ‘a n dimensionset leurs marges. Publications de l’Institut Statistique de l’Université de Paris 8: 229–31. [Google Scholar]
- Slaper, Timothy. 2014. Measuring the Economic Performance of Regions: Creative Destruction and Economic Dynamism. Indiana Business Review. Bloomington: Indiana Business Research Center. [Google Scholar]
- The World Bank. 2017. Special Economic Zones: An Operational Review of Their Impacts. CIIP Competitive Industries and Innovation Program. Washington: The Office of the Publisher of the World Bank Group. [Google Scholar]
- Tsay, Ruey S. 2002. Analysis of Financial Time Series. New York: Wiley. [Google Scholar]
- Pan, Wei-Hwa, and Xuan-Thang Ngo. 2016. Endogenous growth theory and regional performance: The moderating effects of Special Economic Zones. Communist and Post-Communist Studies 49: 113–22. [Google Scholar] [CrossRef]
| SEZ Economic Performance | Manufacturing | Agriculture | Service | |||
|---|---|---|---|---|---|---|
| C−Vine COPAR | D−Vine COPAR | C−Vine COPAR | D−Vine COPAR | C−Vine COPAR | D−Vine COPAR | |
| pair−copula 1 | 5.470 (12 = Joe) | 4.682 (12 = Joe) | −0.010 (12 = rotated Clayton) | −0.042 (12 = rotated Clayton) | 0.510 (12 = Gaussian) | −0.411 (12 = Gaussian) |
| 1.221 (13 = rotated Joe) | −2.303 (23 = Frank) | 1.581 (13 = Rotated Joe) | −1.046 (23 = rotated Gumbel) | 0.486 (13 = Frank) | −1.024 (23 = Frank) | |
| −4.583 (231 = Frank) | 1.276 (132 = Clayton) | −16.812 (231 = Frank) | −0.164 (132 = Gaussian) | −0.954 (231 = Frank) | −0.388 (132 = Gaussian) | |
| Kendall’s tau | 0.700 | 0.660 | −2.516 | −0.020 | 0.340 | 0.221 |
| 0.380 | −0.243 | 0.245 | −0.044 | 0.054 | −0.046 | |
| −0.430 | 0.389 | −0.823 | −0.105 | −0.410 | −0.267 | |
| tail dependence 2 | [0,0.865] | [0,0.840] | [0,0] | [0,0] | [0,0] | [0,0] |
| [0,0.567] | [0,0] | [0.450,0] | [0,0] | [0,0] | [0,0] | |
| [0,0] | [0.581,0] | [0,0] | [0,0] | [0,0] | [0,0] | |
| AIC | 76.254 | 59.125 | 100.422 | 135.718 | 111.162 | 131.362 |
| Vine−COPAR(p) 3 | D−Vine COPAR (3) | C−Vine COPAR (3) | C−Vine COPAR (2) | |||
| Manufacturing | Agriculture | Service | ||||
|---|---|---|---|---|---|---|
| Accuracy | D-Vine COPAR | Classical VAR | C-Vine COPAR | Classical VAR | C-Vine COPAR | Classical VAR |
| RMSE | 0.679 | 0.685 | 0.998 | 1.024 | 1.140 | 1.145 |
| MAE | 0.480 | 0.482 | 1.106 | 1.219 | 0.808 | 0.829 |
| BOOTSTRAP with D-Vine COPAR 1 | BOOTSTRAP with C-Vine COPAR 1 | BOOTSTRAP with C-Vine COPAR 1 | ||||
| RMSE | 0.674 | 0.992 | 1.134 | |||
| Null Hypothesis | Statistics | Manufacturing | Agriculture | Service |
|---|---|---|---|---|
| FDI does not Granger-cause GPP | LR test | 13.406 | 0.367 | 22.287 |
| p-value | 0.004 *** | 0.947 | 5.683 × 10−5 *** | |
| Trade does not Granger-cause GPP | LR test | 0.361 | 4.368 | 24.438 |
| p-value | 0.948 | 0.224 | 2.023 × 10−5 *** | |
| GPP does not Granger-cause FDI | LR test | 17.956 | 3.714 | 23.443 |
| p-value | 0.000 *** | 0.294 | 3.265 × 10−5 *** | |
| TRADE does not Granger-cause FDI | LR test | 10.301 | 13.814 | 19.852 |
| p-value | 0.016 ** | 0.003 *** | 0.000 | |
| GPP does not Granger-cause TRADE | LR test | 2.924 | 34.975 | 23.205 |
| p-value | 0.404 | 1.233 × 10−7 *** | 3.660 × 10−5 *** | |
| FDI does not Granger-cause TRADE | LR test | 3.550 | 33.741 | 23.930 |
| p-value | 0.314 | 2.247 × 10−7 *** | 2.583 × 10−5 *** |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romyen, A.; Liu, J.; Sriboonchitta, S.; Cherdchom, P.; Prommee, P. Assessing Regional Economic Performance in the Southern Thailand Special Economic Zone Using a Vine-COPAR Model. Economies 2019, 7, 30. https://doi.org/10.3390/economies7020030
Romyen A, Liu J, Sriboonchitta S, Cherdchom P, Prommee P. Assessing Regional Economic Performance in the Southern Thailand Special Economic Zone Using a Vine-COPAR Model. Economies. 2019; 7(2):30. https://doi.org/10.3390/economies7020030
Chicago/Turabian StyleRomyen, Arisara, Jianxu Liu, Songsak Sriboonchitta, Parinya Cherdchom, and Paratta Prommee. 2019. "Assessing Regional Economic Performance in the Southern Thailand Special Economic Zone Using a Vine-COPAR Model" Economies 7, no. 2: 30. https://doi.org/10.3390/economies7020030
APA StyleRomyen, A., Liu, J., Sriboonchitta, S., Cherdchom, P., & Prommee, P. (2019). Assessing Regional Economic Performance in the Southern Thailand Special Economic Zone Using a Vine-COPAR Model. Economies, 7(2), 30. https://doi.org/10.3390/economies7020030





