Chronicle of a Failure Foretold: 2017 Rector Election at Ghent University

Abstract

After more than half a year of elections (yielding three voting stages and nine voting rounds), the 2017 Rector election at Ghent University (Belgium) resulted in a victory for the duo leading all nine voting rounds, and in a resounding defeat for the electoral system. Significant regulation changes were needed in order to break the institutional deadlock in which Ghent University found itself. In this paper, we follow the timeline of the election and dissect what went wrong in the election planning.

1. Some Preliminary Notions on Majority Decisions

Since Rousseau published his acclaimed book ‘Du Contrat Social’ (Rousseau 1762), countless discussions on the (non)existence of the ‘general will’ built up the field of social choice, whose main goal is to identify what is best for this general will. Associated with the search for what is best, a collective will often find itself with the need of reaching a collective decision by calling an election. Although very early election systems can be traced back to Ancient Greece (and even to some small bands of primitive hunter-gatherers), it is considered that the fundaments for election systems were established after the stimulating discussion between Borda (1781) and Condorcet (1785) about the appropriate election system for new members of the French Academy of Sciences. It is a couple of centuries later that Arrow points out his despairing impossibility theorem Arrow (1963): in case there are more than three candidates, there is no election system that satisfies some basic and deeply-expected properties. Fortunately, things become easier when selecting among only two candidates.

Simple majority decision is one of the most widespread and studied methods for selecting among two candidates (Fishburn 1970; Inada 1969; May 1952; Sen 1966). A candidate is said to defeat another candidate by simple majority if the number of voters who prefer the former candidate to the latter one is greater than the number of voters who prefer the latter candidate to the former one. In the two-candidate setting, it assures that a winner will be proclaimed letting aside the scenario of a tie (which is impossible when the number of voters is odd and unlikely when the number of voters is large). In case more than two candidates are considered, the method of simple majority might result in the famous voting paradox in which a majority cycle could arise (Condorcet 1785).

A closely related concept is that of absolute majority (Fishburn 1973), where a candidate is said to defeat another candidate by absolute majority if the number of voters who prefer the former candidate to the latter one is greater than half of the number of voters. Note that, in case no abstention is allowed, both simple majority and absolute majority coincide. However, when voters are allowed to abstain from voting, the proclamation of a winner by absolute majority is no longer assured even in a two-candidate election.

Although simple and absolute majority probably are the most common examples of majority decisions, other types of majorities have also called the attention of social choice theorists. The strongest type of majority is that of unanimous majority (Fishburn 1973). A candidate is said to defeat another candidate by unanimous majority if every voter prefers the former candidate to the latter one. Note that the proclamation of a winner is rarely assured under the unanimous majority decision. In between the notions of absolute majority and unanimous majority lie the so-called qualified majorities (Ferejohn and Grether 1974). Qualified majorities require the proportion of voters who prefer the former candidate to the latter one to be greater than or equal to a certain quota $\alpha$ (where $\alpha \in [0.5,1]$), fixed before the election. Note that any $\alpha <\frac{r+1}{2r}$ (where r is the number of voters) corresponds to absolute majority and $\alpha =1$ corresponds to unanimous majority. Finally, the last type of majorities discussed here is that of majorities based on difference of votes (García-Lapresta and Llamazares 2001; Llamazares 2006). This type of majorities lies in between the notions of simple majority and unanimous majority, and requires the difference between the number of voters who prefer the former candidate to the latter one and the number of voters who prefer the latter candidate to the former one to be greater than or equal to a fixed threshold $t\in \{1,\dots ,r\}$. Note that $t=1$ corresponds to simple majority and $t=r$ corresponds to unanimous majority.

2. The Context of the 2017 Rector Election at Ghent University

Ghent University was founded on 9 October 1817, physician Jean-Charles Van Rotterdam being the first Rector of the institution. In the year of its 200-year anniversary, a new Rector election took place. The election was ruled by the regulations issued by the Board of Governors on 10 February 2017 (as an amend of the special decree dated 26 June 1991 relating to Ghent University and the University Centre of Antwerp). In the following, we summarize the most important aspects of the considered regulations (originally written in Dutch).

As stated in Articles 7 and 8 of stated regulations, the candidatures had to be listed as a duo, i.e., one candidate for the position of Rector and one candidate for the position of Vice-Rector. It was a requirement for the duo to be a gender-balanced pair of full professors at Ghent University that could not reach the age of 66 years during the course of their (potential) four-year mandate.

The electoral college consisted of four groups of voters (Article 4): professional staff (ZAP), assistant academic staff (AAP), administrative and technical staff (ATP) and students (STU). All members of the electoral college had to be invited to vote via a link to the election application on the intranet sent to their personal Ghent University e-mail address. The personal link mentioned could only be accessed during the election period. A voter could decide whether to vote for one of the duos or to vote ‘blanco’. It comes without saying that all votes were strictly confidential.

The percentage of votes for each of the duos had to be computed in each category of the electoral college. Then, the percentages of votes had to be aggregated by applying the following weights for the different categories (Article 12): $0.67$ for ZAP, $0.085$ for AAP, $0.085$ for ATP and $0.16$ for STU. After computing the aggregated percentage for each duo, the duo reaching a (weighted) two-thirds majority of the votes had to be proclaimed the winner (Article 13). Note that a two-thirds weighted majority was a requirement regardless of how many duos presented their candidature. If no duo reached the required two-thirds weighted majority, then a second voting round had to be organised. The regulations clearly stated that up to five voting rounds had to be conducted until a duo reached a two-thirds weighted majority. In case the fifth round concluded without a winning duo, Article 16 stated that the voting rounds were terminated, and that the election procedure had to be restarted.

Talking in terms of majority decisions, we can see that the considered method requiring a two-thirds (weighted) majority is a weighted version of what some call supermajority, i.e., a qualified majority with $\alpha =\frac{2}{3}$. Note that a problem the chosen election system needs to face is the increasing difficulty of reaching the chosen quota $\alpha =\frac{2}{3}$ as the number of candidates increases. Fortunately, as will be discussed later, the number of candidatures turned out to be only two in each of the voting rounds. Nevertheless, as we will also discuss later, the changes in the regulations solved this potential problem by considering the common plurality with runoff in which the two candidates with the most votes are compared by simple majority in a second voting round (Richelson 1980).

3. A Failure Foretold

3.1. First Voting Stage

On 17 March, the candidatures for the 2017 Rector election were officially announced. The announced duos were Rik Van de Walle and Mieke Van Herreweghe (RM) and Guido Van Huylenbroeck and Sarah De Saeger (GS).

The planned schedule for the first voting stage was the following:

(i)

First voting round: From Wednesday 19 April (9:00 a.m.) to Friday 21 April (12:00 p.m.).

(ii)

Second voting round (if necessary): From Wednesday 26 April (9:00 a.m.) to Friday 28 April (12:00 p.m.).

(iii)

Third voting round (if necessary): From Wednesday 3 May (9:00 a.m.) to Friday 5 May (12:00 p.m.).

(iv)

Fourth voting round (if necessary): From Monday 8 May (9:00 a.m.) to Tuesday 9 May (12:00 p.m.).

(v)

Fifth voting round (if necessary): From Thursday 11 May (9:00 a.m.) to Friday 12 May (12:00·p.m.).

After the first-voting-round counting on Friday 21 April, no duo reached the fixed two-thirds weighted majority. Although there was a significant difference in support between both duos ($57.76\%$ of the votes for RM opposed to $36.20\%$ of the votes for GS), the leading duo actually was considerably far from the fixed quota.

The second voting round surely was meant to be a critical moment in the first voting stage. The difference in support between both duos in the first voting round hinted that GS would probably be unable to reach a two-thirds weighted majority. It was unsure whether sufficient voters would switch their votes deciding to support the leading duo in order to avoid an election deadlock. The results of the second voting round were not promising. The percentage of abstentions decreased (from $6.05\%$ to $4.44\%$) and the turnout significantly increased (from 11,084 to 13,922), but the support for RM only increased up to $59.62\%$. After the second round, three more voting rounds were conducted (all first-cycle voting results are provided in

Table 1. Results of the first voting stage.

Round	Turnout	RM	GS	Blanco
First	11,084	$57.76\%$	$36.20\%$	$6.05\%$
Second	13,922	$59.62\%$	$35.94\%$	$4.44\%$
Third	14,445	$58.18\%$	$35.95\%$	$5.86\%$
Fourth	12,021	$58.69\%$	$34.11\%$	$7.19\%$
Fifth	14,544	$58.10\%$	$32.57\%$	$9.32\%$

1) but the support for RM no longer increased beyond that of the second voting round while the abstentions kept increasing round after round.

Although foreseen after the results of the third voting round and the questionable choice of voting system, the first voting stage ended with the fifth voting round not yielding a duo carrying the required support. Together with the results of the first voting stage, a brief statement appeared on the election website: “New candidates can present themselves from Monday 29 May (9:00 a.m.) until Wednesday 31 May (12:00 p.m.)” (News Bulletin of Ghent University 2017, 12 May 2017). Despite RM clearly being ahead their adversary, no duo could be proclaimed Rector and Vice-Rector with the then-current regulations.

3.2. Second Voting Stage

It was not until 31 May that the duos for the second voting stage were officially announced. Leading duo RM appeared as the only candidate. At the same time, some controversial modifications in the Rectoral team structure were announced:

“After lengthy deliberations and starting from reciprocal trust that has been built up step by step, we have arrived at a common programme that contains the most important elements of our original programmes and that we can all fully embrace. We are convinced that the implementation of this programme would be very beneficial to our university and to the UGhentians” (News Bulletin of Ghent University 2017, 31 May 2017).

“The explicit desire—expressed by us and by many other people—to bring visions together, to let us all come together and to realise an ambitious project has led to the question of expanding the rectoral team. We make a plea for the possibility to appoint extra vice-rectors at our university (which by the way has long been possible at other Flemish universities), who would become full members of the rectoral team, together with the elected rector and vice-rector” (News Bulletin of Ghent University 2017, 31 May 2017).

In particular, the proposal was to appoint five Vice-Rectors instead of one2, former Rector/Vice-Rector candidates Guido Van Huylenbroeck and Sarah De Saeger being two of the proposed Vice-Rectors. Quoting a message by GS privately sent to the corporate e-mail address of the electorate, “A request to the board of governors and the parlement has been formulated to create the possibility (also in a decree) to appoint extra vice-rectors. If, against all expectations, this proves to be impossible, Rik and Mieke have engaged themselves to take us on board of their rectoral team be it with other titles.”

The planned schedule for the second voting stage was the following:

(i)

First voting round: From Monday 19 June (8:00 a.m.) to Tuesday 20 June (8:00 a.m.).

(ii)

Second voting round (if necessary): From Wednesday 21 June (8:00 a.m.) to Thursday 22 June (8:00 a.m.).

(iii)

Third voting round (if necessary): From Friday 23 June (8:00 a.m.) to Saturday 24 June (8:00 a.m.).

(iv)

Fourth voting round (if necessary): From Monday 26 June (8:00 a.m.) to Tuesday 27 June (8:00 a.m.).

(v)

Fifth voting round (if necessary): From Wednesday 28 June (8:00 a.m.) to Thursday 29 June (8:00 a.m.).

The result of the first-voting-round counting on Tuesday 20 June was indeed surprising: RM remained at $58.62\%$ of the votes, $41.38\%$ of the votes being abstentions. Not even an increasing turnout (from 8560 to 10,391) and support (from $58.62\%$ to $60.34\%$) in the second voting round prevented RM to announce their withdrawal before the start of the third voting round (all second-cycle voting results are provided in

Table 2. Results of the second voting stage.

Round	Turnout	RM	Blanco
First	8560	$58.62\%$	$41.38\%$
Second	10,391	$60.34\%$	$39.66\%$

3). The same day of the withdrawal announcement, an official announcement appeared on the election website: “The Board of Governors of Ghent University will now establish the further course of the elections” (News Bulletin of Ghent University 2017, 22 June 2017).

One could conjecture that the problem in this voting stage was not the election system itself; instead, the popular exasperation towards the new proposal of Rectoral team was to be blamed. Anyway, the 2017 Rector election at Ghent University reached a deadlock starting 22 June.

3.3. Third Voting Stage

On 16 August, it was announced that “new elections for a rector and vice-rector will be held in September. The Board of Governors has adapted the election regulations” (News Bulletin of Ghent University 2017, 16 August 2017). Mainly, the new regulations stopped counting abstentions towards the majority decision, reduced the number of voting rounds in the voting stage, and reduced the required quota to a (strict)4 one-half weighted majority in the last voting round of the voting stage. More precisely, the new regulations distinguish three cases: (a) there were more than two duos as candidates; (b) there were two duos as candidates; (c) there was only one duo as a candidate. In the first case, the first voting round would be conducted as in the previous voting stages; in a potential second round, only the two most voted duos would be compared and required to have a two-thirds weighted majority (without counting abstentions); and, in a potential third round, the quota would be reduced to a one-half weighted majority (without counting abstentions). In the second case, the first voting round would be conducted as in the previous voting stages; and, in a potential second round, the quota would be reduced to a one-half weighted majority (without counting abstentions). In the third case, the votes would be either yes, no, or abstention, and it would be required to reach a two-thirds weighted majority in the first round and a one-half weighted majority in the potential second round (without counting abstentions).

The planned schedule for the third voting stage was the following:

(i)

First voting round: From Monday 18 September (8:00 a.m.) to Tuesday 19 September (8:00 a.m.).

(ii)

Second voting round (if necessary): From Thursday 21 September (8:00 a.m.) to Friday 22 September (8:00 a.m.).

(iii)

Third voting round (if necessary): From Monday 25 September (8:00 a.m.) to Tuesday 26 September (8:00 a.m.).

On 25 August, the candidatures for the last voting stage were announced. The announced duos were the already-acquainted RM and the new duo Karin Raeymaeckers and Patrick De Baets (KP).

Adding a little bit more of drama to the elections, the day of the counting of the first voting round, Sas van Rouveroij—chairman of the election commission—announced the cancellation of the voting round: “Today, the proverbial Murphy’s law has hit. [...] A technical failure has caused the election email of Karin and Patrick not to be sent to all intended recipients. The principle of equality is particularly important in this—all students and staff are entitled to the same communication—hence this unanimous decision of the electoral commission, in which all ranks are represented” (News Bulletin of Ghent University 2017, 19 September 2017). Apparently, due to a technical defect, the campaign message of RM reached 61,187 voters while the campaign message of KP reached only 13,507 voters. A new schedule was announced:

(i)

First voting round: From Thursday 21 September (8:00 a.m.) to Friday 22 September (8:00 a.m.).

(ii)

Second voting round (if necessary): From Monday 25 September (8:00 a.m.) to Tuesday 26 September (8:00 a.m.).

The first recount yielded no duo carrying a two-thirds weighted majority, but RM presented a comfortable lead ($60.25\%$ against $39.75\%$). Interestingly, it was the first time in the whole election that RM did not win in all the categories of the electoral college: KP carried $51.58\%$ of the student vote in opposition to the $48.42\%$ carried by RM.

This same day at 3:00 p.m. it was announced that KP had decided to withdraw their candidature, and that there would be only one candidate in the second voting round. It was also reminded that “Votes cast for the one team that is left shall be either yes, no or abstention”. Finally, on Tuesday 26 September, RM obtained the required one-half weighted majority in the last round of the voting stage, thus being elected as the new Rector and Vice-Rector. All third-cycle voting results are provided in

Table 3. Results of the third voting stage (with abstentions).

Round	Turnout	RM	KP	No	Blanco
First	8171	$57.40\%$	$37.81\%$	-	$4.79\%$
Second	7945	$67.95\%$	-	$26.75\%$	$5.30\%$

and

Table 4. Results of the third voting stage (without abstentions).

Round	Turnout	RM	KP	No
First	7710	$60.25\%$	$39.75\%$	-
Second	7515	$71.74\%$	-	$28.26\%$

5.

4. A Further Analysis of the Voting System

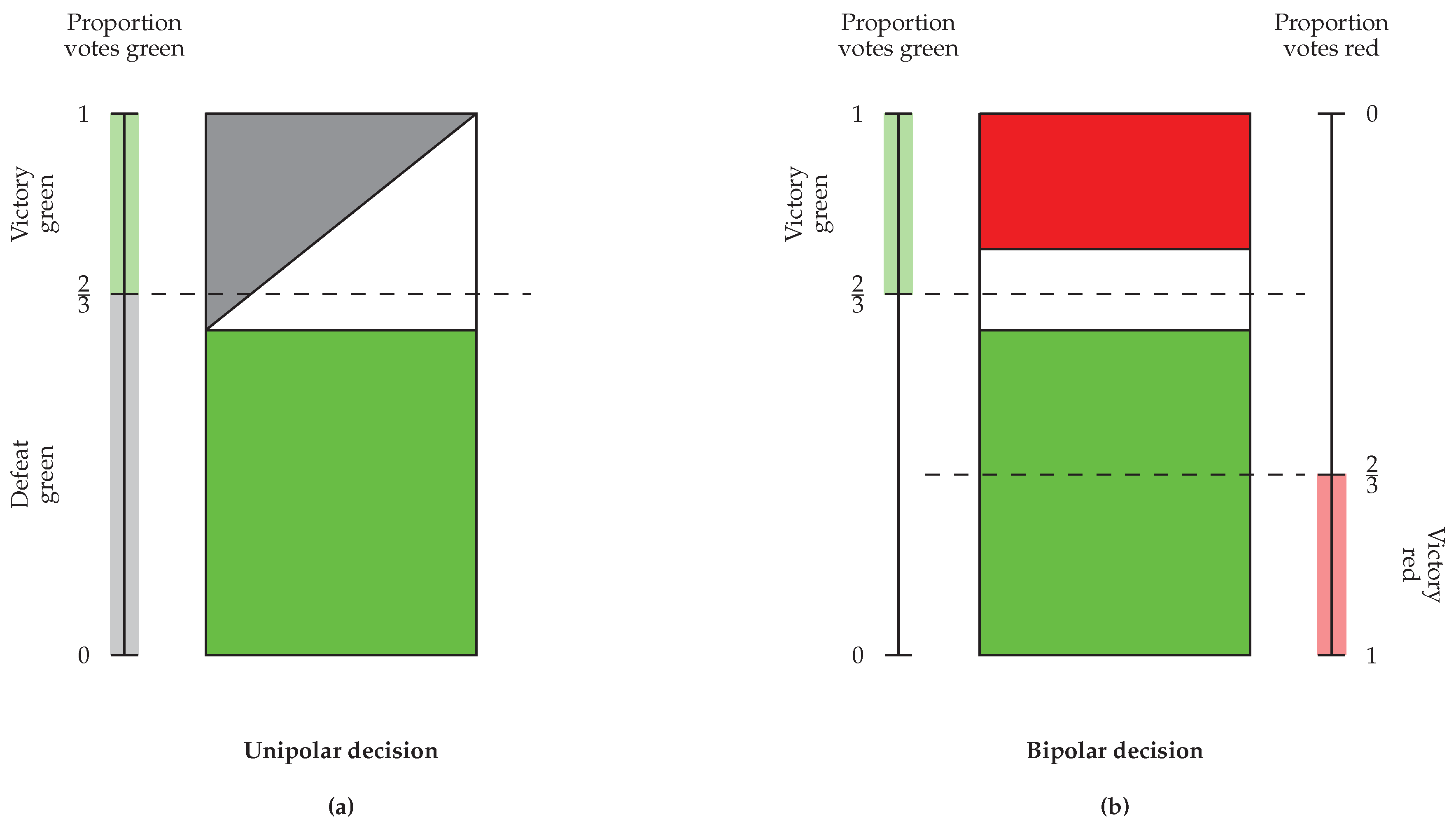
In the eighteenth century, Rousseau (1762) already encouraged the use of qualified majorities or majorities based on difference of votes for important decisions: “The more the deliberations are important and serious, the more the opinion that carries should approach unanimity.” Mostly, these deliberations are linked to a unipolar decision, i.e., one votes for or against a unique given option. For instance, ‘do you agree with duo x being appointed as Rector and Vice-Rector?’. In these cases, the fact that the candidate’s proclamation is not supported by the chosen majority decision is understood as a defeat of the candidate.

In case there are two candidates, the deliberations are linked to a bipolar decision, i.e., one votes for either one or another option among two given ones. For instance, ‘do you prefer duo x or duo y being appointed as Rector and Vice-Rector?’. These differences between the semantics of a unipolar decision and a bipolar decision are illustrated in Figure 1. In a bipolar decision, the proclamation of a winner may turn cumbersome if one requires a (moderately) large quota/threshold. Naturally, it holds that the larger the quota/threshold, the higher the chance of the election procedure reaching a deadlock. Furthermore, one could note that the fact that a certain duo reaches a large quota/threshold does not mean that the duo is seen by the electorate as a good option for the Rectorship— neither does it mean that the other duo is not. Only relative information on how both candidates are positioned w.r.t. each other is available. Of course, the use of a moderately-large quota/threshold might be justified in order to add some stability that may prevent the outcome to be susceptible to small changes in the votes (for instance, the result of a simple majority decision could ultimately depend on just one undecided voter). Unfortunately, the use of a large quota/threshold inevitably leads to a reduced decisive spectrum of election results. In national elections, this problem is normally avoided by allowing for coalitions between parties, but, obviously, this solution is simply not possible in a Rector election.

A potential solution for avoiding an electoral deadlock could be to fix a small (but non-negligible) quota/threshold. This will result in a ‘guarantee’ of a winner being selected after some voting rounds, while not electing a candidate that has just one more vote than its adversary. Subsequently, the proclamation (or not) of this winner could confront a (for instance) two-thirds majority voting procedure since it is now indeed a unipolar decision. In Figure 2, we illustrate an example of this two-stage procedure in which a $52\%$-majority (without counting abstentions) is required at the first stage and the winning candidate is then confronted to a two-thirds majority voting at the second stage. In the general setting in which there are more than two candidates, only the first stage is to be adapted by considering a ranking rule for elections with more than two candidates, e.g., the plurality rule (a small threshold could also be fixed).

A more elegant solution would require to totally reformulate the semantics of the election in an approval-voting fashion (Brams and Fishburn 1983). Instead of ‘which candidate do you prefer?’, the question to be asked would now be ‘which candidates do you approve?’. The bipolar question would then turn into two (or more, depending on the number of candidates) unipolar questions. However, quoting Balinski and Laraki (2014) on approval voting, “why limit the judgment to accept/not accept or pass/fail?” In the following section, we propose a potential procedure for the next Rector elections: Balinski and Laraki’s Majority Judgment (Balinski and Laraki 2007, 2010).

5. A Proposal for Upcoming Elections

Social choice theory is a field full of paradoxes (Nurmi 1999), probably Arrow’s and Condorcet’s paradoxes being the two most famous ones. On the one hand, Arrow’s paradox states that, in an election with at least three candidates, it is possible for a candidate to win, yet with the same set of rank-order preferences a second candidate wins when a third candidate withdraws. A famous interpretation of this paradox is often attributed to philosopher Sidney Morgenbesser (Hausman 2011): “After finishing dinner, Sidney Morgenbesser decides to order dessert. The waitress tells him he has two choices: apple pie and blueberry pie. Sidney orders the apple pie. After a few minutes the waitress returns and says that they also have cherry pie at which point Morgenbesser says: In that case I’ll have the blueberry pie”. Although this anecdote technically concerns individual decisions rather than collective decisions, we could illustrate the point in a similar manner by considering three friends that are offered apple pie and blueberry pie, initially vote and decide to order the apple pie and, after being offered the cherry pie, decide to order the blueberry pie instead. As silly as this sounds, Arrow’s impossibility theorem (Arrow 1963) proves that there is no natural method6 that avoids this paradox7, leaving aside dictatorships.

On the other hand, Condorcet’s paradox states that, in an election with at least three candidates, the transitivity of the voters’ preferences does not imply the transitivity of the majority rule. Coming back to the example of the pies, one could understand this paradox with the following example. Alice’s favourite pie is apple pie, but she sure does prefer blueberry pie to cherry pie. Bob has always liked berries, thus, he would rather eat a blueberry pie, or, in case this is not possible, a cherry pie. A third diner, Carol, has expressed her desire of enjoying a cherry pie, but she would actually be fine with the house-special apple pie. Inconveniently, when choosing which desert to share, they realize that they collectively prefer the apple pie to the blueberry pie, the blueberry pie to the cherry pie, and the cherry pie to the apple pie. Thus, they forget about sharing, and just proceed to order one piece of each. We conclude that, although each voter expresses transitive preferences, cycles might (and often do!) appear in the collective preference.

Balinski and Laraki (2007) recently advocated for totally restructuring the form in which we understand and perform voting systems: “[...] if Arrow’s and Condorcet’s paradoxes are to be avoided, then the traditional model and paradigm must be abandoned. [...] Not only do rank-order inputs not permit voters to express themselves as they wish, but they are the culprits that lead to all of the impossibilities and incompatibilities” (Balinski and Laraki 2014). They proposed a method called Majority Judgment Balinski and Laraki (2010) that proceeds as follows. First, a common language of grades (labels in a linearly ordered scale) needs to be agreed upon. Afterwards, each of the voters is required to evaluate each of the candidates independently according to this common language of grades. Then, for each candidate x, the grades are ordered in an increasing manner. We denote by $s_i^x$ the i-th greatest grade assigned to candidate x. Subsequently, the majority value is computed for each candidate x, i.e., the sequence

$${\mathit{m}}^x=(s_t^x,s_{t+1}^x,s_{t-1}^x,s_{t+2}^x,s_{t-2}^x,\dots ,s_{2t-1}^x,s_1^x),$$

if there is an odd number of voters $r=2t-1$, or

$${\mathit{m}}^x=(s_t^x,s_{t-1}^x,s_{t+1}^x,s_{t-2}^x,s_{t+2}^x,\dots ,s_{2t-2}^x,s_1^x),$$

if there is an even number of voters $r=2t-2$. Finally, candidates are lexicographically ordered8 according to their majority values by ranking a candidate x ahead of a candidate y if the value at the first position at which ${\mathit{m}}^x$ and ${\mathit{m}}^y$ differ is greater in ${\mathit{m}}^x$ than in ${\mathit{m}}^y$. Note that two candidates can only be tied if they have the same grades.

Example 1.

Consider the list of grades used by OpinionWell poll during the French 2012 presidential election (Balinski and Laraki 2014):

$$\mathit{Outstanding}\succ \mathit{Excellent}\succ \mathit{Very}\mathit{Good}\succ \mathit{Good}\succ \mathit{Acceptable}\succ \mathit{Poor}\succ \mathit{To}\mathit{reject}.$$

Consider that there are five voters and three candidates x, y and z. Candidate x received two times the grade Outstanding and three times the grade Excellent; candidate y received one time the grade Outstanding, three times the grade Excellent and one time the grade Very good; candidate z received two times the grade Very Good and three times the grade Good.

The ordered grades assigned to each candidate are thus the following ones:

$$\begin{array}{cc}\hfill {\mathit{s}}^x& =(\mathit{Outstanding},\mathit{Outstanding},\mathit{Excellent},\mathit{Excellent},\mathit{Excellent}),\hfill \\ \hfill {\mathit{s}}^y& =(\mathit{Outstanding},\mathit{Excellent},\mathit{Excellent},\mathit{Excellent},\mathit{Very}\mathit{good}),\hfill \\ \hfill {\mathit{s}}^z& =(\mathit{Very}\mathit{good},\mathit{Very}\mathit{good},\mathit{Good},\mathit{Good},\mathit{Good}).\hfill \end{array}$$

Thus, the majority values for each candidate are the following ones:

$$\begin{array}{cc}\hfill {\mathit{m}}^x& =(\mathit{Excellent},\mathit{Excellent},\mathit{Outstanding},\mathit{Excellent},\mathit{Outstanding}),\hfill \\ \hfill {\mathit{m}}^y& =(\mathit{Excellent},\mathit{Excellent},\mathit{Excellent},\mathit{Very}\mathit{good},\mathit{Outstanding}),\hfill \\ \hfill {\mathit{m}}^z& =(\mathit{Good},\mathit{Good},\mathit{Very}\mathit{good},\mathit{Good},\mathit{Very}\mathit{good}).\hfill \end{array}$$

Since x has a greater grade than y at the third position (first position at which ${\mathit{m}}^x$ and ${\mathit{m}}^y$ differ) and a greater grade than z at the first position (first position at which ${\mathit{m}}^x$ and ${\mathit{m}}^z$ differ), we conclude that candidate x should be proclaimed the winner according to the method of Majority Judgment.

The number of advantages of this method over classical ones based on ranking is substantial. From a practical point of view, the method of Majority Judgment is easy to understand for the voters and, unlike many classical methods based on ranking, its implementation is computationally friendly even for a large electorate. From a theoretical point of view, both Arrow’s and Condorcet’s paradoxes are assured to be avoided, and among other properties, it is proved to be fairly resistant to manipulation. Moreover, in case of elections with only two candidates, which was the actual case of the Rector elections at Ghent University, provides a(n arguably) more natural outcome than the simple majority rule since “the method of majority decision takes no account of intensities of preference, and it is certainly arguable that what matters is not merely the number who prefer x to y and the number who prefer y to x, but also by how much each prefers one alternative to the other” (Sen 1970). Indeed, as suggested by Balinski and Laraki, in the next Rector elections at Ghent University, we might need to judge, rather than vote.

6. Conclusions

One hundred and fifty-nine days passed from the first voting round of the Rector elections at Ghent University to the last one, and we wonder whether this time lapse could have been greatly reduced just by considering a more suitable electoral system. The requirement of the two-thirds weighted majority proved to be too strong, while the ultimate restriction to a one-half weighted majority seems to be an ‘ad hoc’ solution just trying to assure the end of the electoral deadlock. We conjecture that the use of a two-stage voting procedure in which a candidate is selected in a first voting stage subsequently being confronted to a two-thirds (weighted) majority voting in a second voting stage probably would have reduced the election time lapse considerably (and would have reduced voters’ fatigue towards the election). In addition, the use of Majority Judgment in future elections is strongly encouraged by the authors.