Does Oil Price Drive World Food Prices? Evidence from Linear and Nonlinear ARDL Modeling
Abstract
:1. Introduction
2. Literature Review
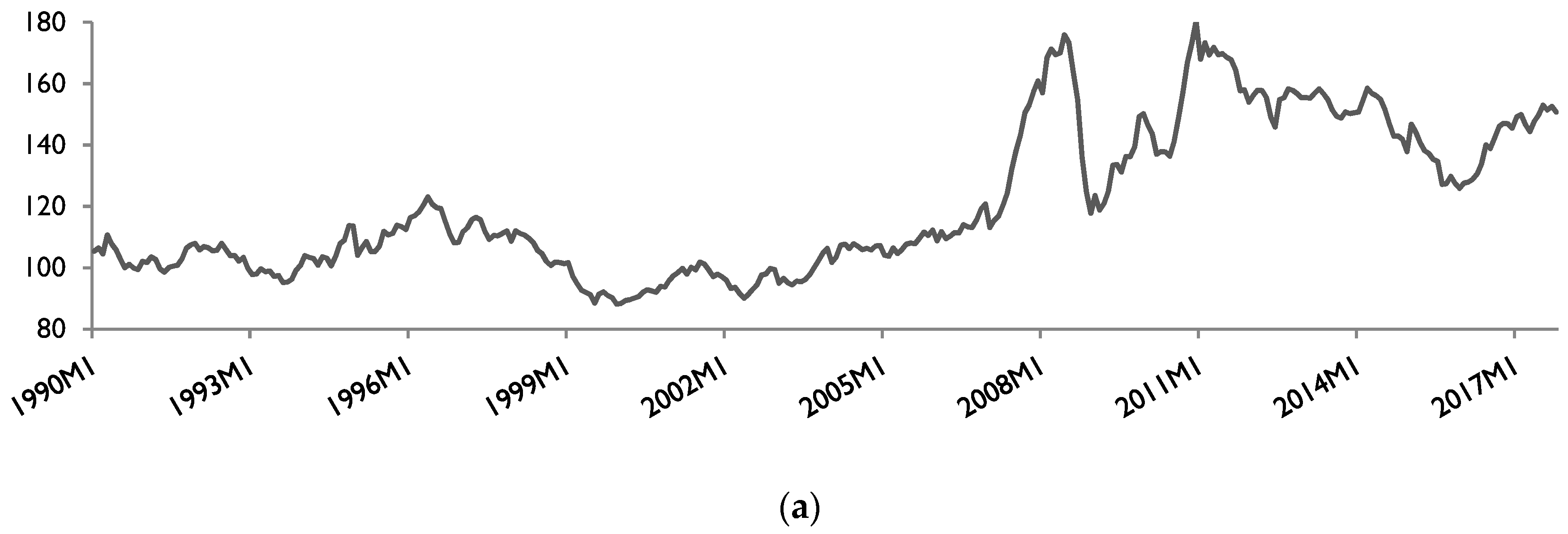
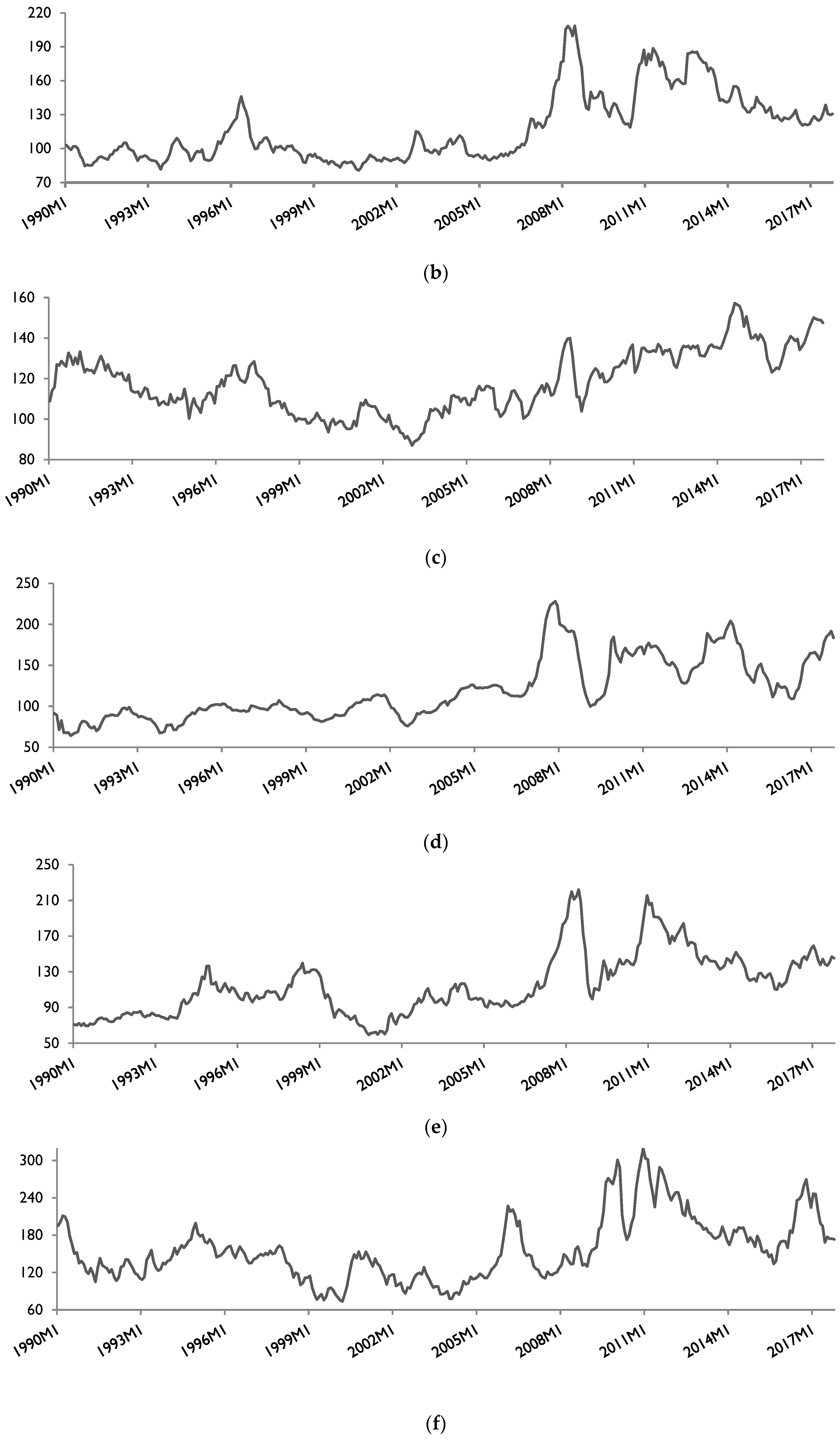
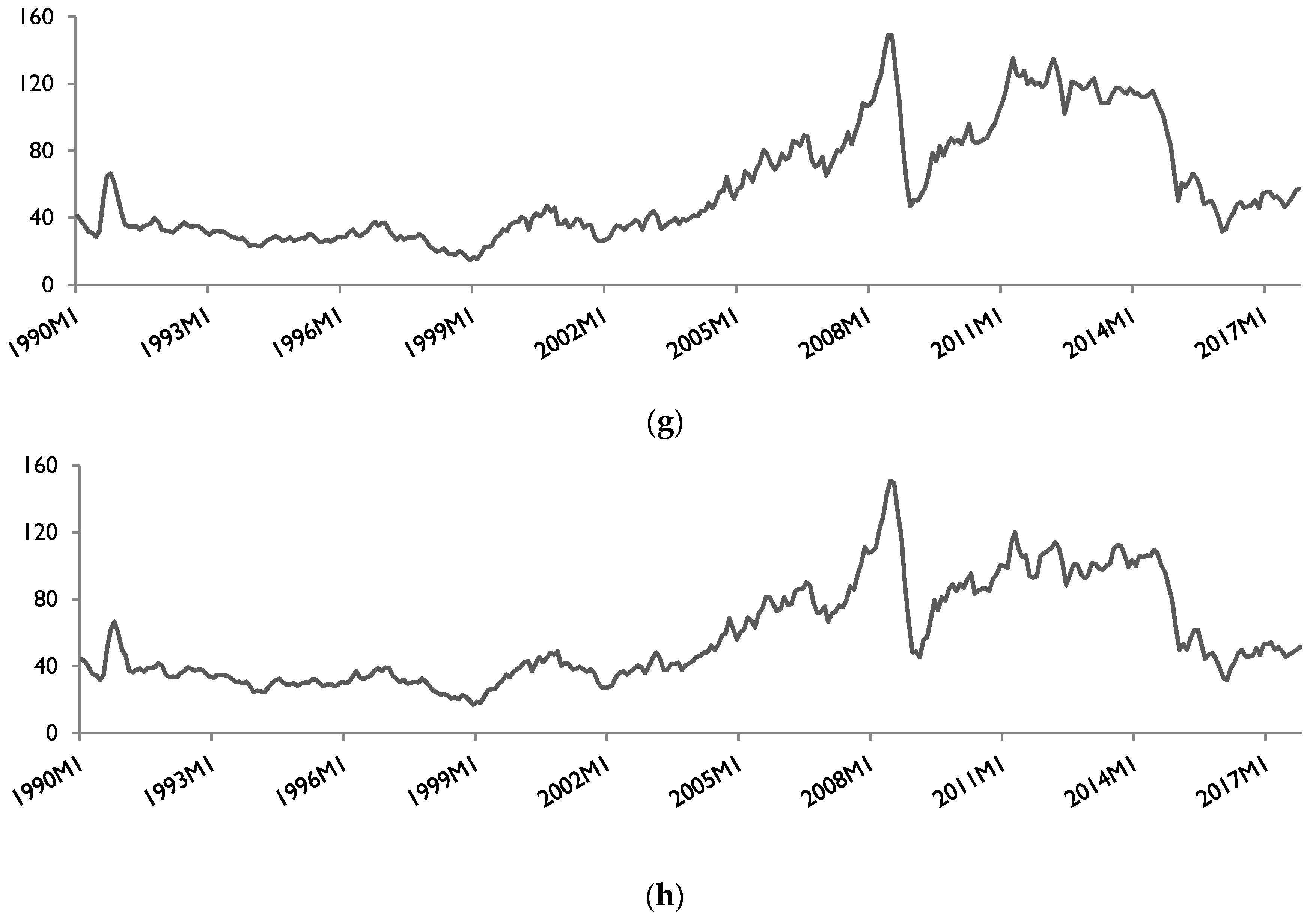
3. Data Issues
4. The Empirical Methodology
5. Empirical Results
5.1. Results of Unit Root Tests
5.2. Linear ARDL Estimates
5.3. Nonlinear ARDL Estimates
6. Managerial Implications
7. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Abbott, Philip C., Christopher Hurt, and Wallace E. Tyner. 2008. What’s Driving Food Prices? Issue Reports 37951. Oak Brook: Farm Foundation. [Google Scholar]
- Abbott, Philip C., Christopher Hurt, and Wallace E. Tyner. 2009. What’s Driving Food Prices? March 2009 Update. Issue Reports 48495. Oak Brook: Farm Foundation. [Google Scholar]
- Abdulai, Awudu. 2000. Spatial price transmission and asymmetry in the Ghanaian maize market. Journal of Development Economics 63: 327–49. [Google Scholar] [CrossRef]
- Ajmi, Ahdi Noomen, Ghassen El-montasser, Shawkat Hammoudeh, and Duc Khuong Nguyen. 2014. Oil prices and MENA stock markets: New evidence from nonlinear and asymmetric causalities during and after the crisis period. Applied Economics 46: 2167–77. [Google Scholar] [CrossRef]
- Apergis, Nicholas, and Anthony Rezitis. 2011. Food price volatility and macroeconomic factors: Evidence from GARCH and GARCH-X estimates. Journal of Agricultural and Applied Economics 43: 95–110. [Google Scholar] [CrossRef]
- Asfaha, T. A., and Andre Jooste. 2007. The effect of monetary changes on relative agricultural prices. Agrekon 46: 460–74. [Google Scholar] [CrossRef]
- Balcombe, Kelvin, and George Rapsomanikis. 2008. Bayesian estimation and selection of nonlinear vector error correction models: The case of sugar–ethanol oil nexus in Brazil. American Journal of Agricultural Economics 90: 658–68. [Google Scholar] [CrossRef]
- Banerjee, Anindya, Juan Dolado, and Ricardo Mestre. 1998. Error-correction mechanism tests for cointegration in a single-equation framework. Journal of Time Series Analysis 19: 267–83. [Google Scholar] [CrossRef]
- Barnett, Richard C., David A. Bessler, and Robert L. Thompson. 1983. The money supply and nominal agricultural prices. American Journal of Agricultural Economics 65: 303–7. [Google Scholar] [CrossRef]
- Baumeister, Christiane, and Lutz Kilian. 2014. Do oil price increases cause higher food prices? Economic Policy 29: 691–747. [Google Scholar] [CrossRef] [Green Version]
- Büyükşahin, Bahattin, and Jeffrey H. Harris. 2011. Do speculators drive crude oil futures prices? Energy Journal 32: 167–202. [Google Scholar] [CrossRef]
- Campiche, Jody L., Henry L. Bryant, James W. Richardson, and Joe L. Outlaw. 2007. Examining the evolving correspondence between petroleum prices and agricultural commodity prices. Paper presented at American Agricultural Economics Association Annual Meeting, Portland, OR, USA, July 29–August 1. [Google Scholar]
- Chen, Sheng-Tung, Hsiao-I Kuo, and Chi-Chung Chen. 2010. Modeling the relationship between the oil price and global food prices. Applied Energy 87: 2517–25. [Google Scholar] [CrossRef]
- Claudio, Araujo, Catherine Araujo-Bonjean, and Johny Egg. 2010. Choc pétrolier externe et performance des marchés des céréales: le marché du mil au Niger. Revue d’économie du développement 18: 47–70. [Google Scholar]
- Coronado, Semei, Omar Rojas, Rafael Romero-Meza, Apostolos Serletis, and Leslie Verteramo Chiu. 2018. Crude oil and biofuel agricultural commodity prices. In Uncertainty, Expectations and Asset Price Dynamics. Edited by Fredj Jawadi. Basel: Springer International Publishing, pp. 107–23. [Google Scholar]
- Deaton, Angus, and Guy Laroque. 1992. On the behaviour of commodity prices. The Review of Economic Studies 59: 1–23. [Google Scholar] [CrossRef]
- Dickey, David A., and Wayne A. Fuller. 1981. Likelihood ratio statistics for autoregressive time series with a unit root. Econometrica 49: 1057–72. [Google Scholar] [CrossRef]
- Diks, Cees, and Valentyn Panchenko. 2006. A new statistic and practical guidelines for nonparametric Granger causality testing. Journal of Economic Dynamics and Control 30: 1647–69. [Google Scholar] [CrossRef]
- Elliott, Graham, Thomas J. Rothenberg, and James H. Stock. 1996. Efficient Tests for an Autoregressive Unit Root. Econometrica 64: 813–36. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations (FAO). 2009. The State of Agricultural Commodity Markets, High Food Prices and Food Crisis—Experiences and Lessons Learned. Rome: FAO. [Google Scholar]
- Food Security Information Network. 2018. Global Report on Food Crises 2018. Rome: World Food Programme. [Google Scholar]
- Fowowe, Babajide. 2016. Do oil prices drive agricultural commodity prices? Evidence from South Africa. Energy 104: 149–57. [Google Scholar] [CrossRef]
- Gregory, Allan W., and Bruce E. Hansen. 1996. Residual-based tests for cointegration models with regime shifts. Journal of Econometrics 70: 99–126. [Google Scholar] [CrossRef]
- Hamilton, James D. 1988. Are the macroeconomic effects of oil-price change symmetric? A Comment. Carnegie Rochester Conference Series on Public Policy 28: 369–78. [Google Scholar] [CrossRef]
- Hamilton, James D. 1996. This is what happened to the oil price-macroeconomy relationship. Journal of Monetary Economics 38: 215–20. [Google Scholar] [CrossRef]
- Harri, Ardian, Lanier Nalley, and Darren Hudson. 2009. The relationship between oil, exchange rates, and commodity prices. Journal of Agricultural and Applied Economics 41: 501–10. [Google Scholar] [CrossRef]
- Hoover, Kevin D. 2001. Causality in Macroconomics. Cambridge: Cambridge University Press. [Google Scholar]
- Ibrahim, Mansor H. 2015. Oil and food prices in Malaysia: A nonlinear ARDL analysis. Agricultural and Food Economics 3: 1–14. [Google Scholar] [CrossRef]
- Johansen, Soren. 1988. Statistical analysis of cointegration vectors. Journal of Economic Dynamics and Control 12: 231–54. [Google Scholar] [CrossRef]
- Johansen, Soren. 1991. Estimation and hypothesis testing of cointegration vectors in Gaussian vector autoregressive models. Econometrica 59: 1551–80. [Google Scholar] [CrossRef]
- Koirala, Krishna H., Ashok K. Mishra, Jeremy M. D’Antoni, and Joey E. Mehlhorn. 2015. Energy prices and agricultural commodity prices: Testing correlation using copulas method. Energy 81: 430–36. [Google Scholar] [CrossRef]
- Kripfganz, Sebastian, and Daniel C. Schneider. 2016. ardl: Stata module to estimate autoregressive distributed lag models. Paper presented at Stata Conference, Chicago, IL, USA, July 29. [Google Scholar]
- Lagi, Marco, Yavni Bar-Yam, Karla Z. Bertrand, and Yaneer Bar-Yam. 2015. Accurate market price formation model with both supply-demand and trend-following for global food prices providing policy recommendations. Proceedings of the National Academy of Sciences 112: E6119–28. [Google Scholar] [CrossRef]
- Mills, Terence C. 1991. Nonlinear time series models in economics. Journal of Economic Surveys 5: 215–42. [Google Scholar] [CrossRef]
- Narayan, Seema, and Paresh Kumar Narayan. 2007. Understanding asymmetries in macroeconomic aggregates: The case of Singapore. Applied Economics Letters 14: 905–8. [Google Scholar] [CrossRef]
- Nazlioglu, Saban. 2011. World oil and agricultural commodity prices: Evidence from nonlinear causality. Energy Policy 39: 2935–43. [Google Scholar] [CrossRef]
- Nazlioglu, Saban, and Ugur Soytas. 2011. World oil prices and agricultural commodity prices: Evidence from an emerging market. Energy Economics 33: 488–96. [Google Scholar] [CrossRef]
- Pal, Debdatta, and Subrata K. Mitra. 2017. Time-frequency contained co-movement of crude oil and world food prices: A wavelet-based analysis. Energy Economics 62: 230–39. [Google Scholar] [CrossRef]
- Pal, Debdatta, and Subrata K. Mitra. 2018. Interdependence between crude oil and world food prices: A detrended cross correlation analysis. Physica A: Statistical Mechanics and its Applications 492: 1032–44. [Google Scholar] [CrossRef]
- Pala, Aynur. 2013. Structural Breaks, Cointegration, and Causality by VECM Analysis of Crude Oil and Food Price. International Journal of Energy Economics and Policy 3: 238–46. [Google Scholar]
- Paris, Anthony. 2018. On the link between oil and agricultural commodity prices: Do biofuels matter? International Economics 155: 48–60. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, Yongcheol Shin, and Richard J. Smith. 2001. Bounds testing approaches to the analysis of level relationships. Journal of Applied Econometrics 16: 289–326. [Google Scholar] [CrossRef] [Green Version]
- Rapsomanikis, George, David Hallam, and Piero Conforti. 2003. Market integration and price transmission in selected food and cash crop markets of developing countries: Review and applications. In Commodity Market Review 2003–2004. Rome: FAO. [Google Scholar]
- Reboredo, Juan C. 2012. Do food and oil prices co-move? Energy Policy 49: 456–67. [Google Scholar] [CrossRef]
- Saghaian, Sayed H. 2010. The impact of the oil sector on commodity prices: Correlation or causation? Journal of Agricultural and Applied Economics 42: 477–85. [Google Scholar] [CrossRef]
- Salisu, Afees A., Kazeem O. Isah, Oluwatomisin J. Oyewole, and Lateef O. Akanni. 2017. Modelling oil price-inflation nexus: The role of asymmetries. Energy 125: 97–106. [Google Scholar] [CrossRef]
- Scherer, Frederic M., and David Ross. 1990. Industrial Market Structure and Economic Performance, 3rd ed. Boston: Houghton Mifflin. [Google Scholar]
- Schmidhuber, Josef, and Francesco N. Tubiello. 2007. Global food security under climate change. Proceedings of the National Academy of Sciences 104: 19703–8. [Google Scholar] [CrossRef]
- Schwarz, Gideon. 1978. Estimating the dimension of a model. The Annals of Statistics 6: 461–64. [Google Scholar] [CrossRef]
- Sek, Siok Kun. 2017. Impact of oil price changes on domestic price inflation at disaggregated levels: Evidence from linear and nonlinear ARDL modeling. Energy 130: 204–17. [Google Scholar] [CrossRef]
- Shin, Yongcheol, Byungchul Yu, and Matthew Greenwood-Nimmo. 2014. Modelling asymmetric cointegration and dynamic multipliers in an ARDL framework. In Festschrift in Honor of Peter Schmidt. Edited by Robin C. Sickles and William C. Horrace. New York: Springer Science and Business Media. [Google Scholar]
- Tatom, John A. 1988. Are the macroeconomic effects of oil price changes symmetric? Carnegie-Rochester Conference Series on Public Policy 28: 325–68. [Google Scholar] [CrossRef]
- Tiwari, Aviral Kumar, Rabeh Khalfaoui, Sakiru Adebola Solarin, and Muhammad Shahbaz. 2018. Analyzing the time-frequency lead–lag relationship between oil and agricultural commodities. Energy Economics 76: 470–94. [Google Scholar] [CrossRef]
- Toda, Hiro Y., and Taku Yamamoto. 1995. Statistical inference in vector autoregressive with possibly integrated processes. Journal of Econometrics 66: 225–50. [Google Scholar] [CrossRef]
- Wheeler, Tim, and Joachim von Braun. 2013. Climate change impacts on global food security. Science 341: 508–13. [Google Scholar] [CrossRef]
- Wong, K. Kai Seng, and Mad Nasir Shamsudin. 2017. Impact of crude oil price, exchange rates and real GDP on Malaysia’s food price fluctuations: Symmetric or Asymmetric? International Journal of Economics and Management 11: 259–75. [Google Scholar]
- Zhang, Zan, Su-Ling Tsai, and Tsangyao Chang. 2017. New evidence of interest rate pass-through in Taiwan: A Nonlinear Autoregressive Distributed Lag Model. Global Economic Review 46: 129–42. [Google Scholar] [CrossRef]
- Zivot, Eric, and Donald W. K. Andrews. 1992. Further evidence of great crash, the oil price shock and unit root hypothesis. Journal of Business and Economic Statistics 10: 251–70. [Google Scholar]
| 1 | According to Hoover (2001), the Simpson Paradox refers to “a number of situations in which statistical dependencies that are consistent in subpopulations disappear or are reversed in whole populations” (Hoover 2001, p. 19). |
| 2 | See Shin et al. (2014) for more details. |
| 3 | See Dickey and Fuller (1981), Elliott et al. (1996) and Zivot and Andrews (1992) for details on the construction of unit root tests. |
| 4 | The statistical software Eviews 10 was used to perform unit root tests. |
| 5 | The computations were done in Stata 14 using the ARDL command for Stata (ardl) written by Kripfganz and Schneider (2016). |
| 6 | The computations were done in Stata 14 using the nonlinear ARDL command for Stata (nardl) written by Marco Sunder and retrieved from Matthew Greenwood-Nimmo’s webpage. |
| ADF | ERS | ZA | ||||||
|---|---|---|---|---|---|---|---|---|
| Level | 1st Diff. | Level | 1st Diff. | Level | Break Date | 1st Diff. | Break Date | |
| lnBrent | −2.641 | −14.000 *** | 8.464 | 0.277 *** | −3.831 | 2004M07 | −14.197 *** | 1999M01 |
| lnWTI | −2.732 | −13.506 *** | 7.816 | 0.204 *** | −4.093 | 2003M10 | −8.364 *** | 1999M01 |
| lnFPI | −2.453 | −14.476 *** | 10.513 | 0.190 *** | −5.084 ** | 2007M02 | −8.362 *** | 2008M07 |
| lnMPI | −2.162 | −16.695 *** | 9.839 | 0.561 *** | −5.398 ** | 2001M10 | −5.346 *** | 2003M04 |
| lnDPI | −3.716 ** | −12.777 *** | 4.491 ** | 0.217 *** | −4.503 | 2007M02 | −12.960 *** | 2007M12 |
| lnCPI | −2.965 | −13.253 *** | 6.481 * | 0.223 *** | −5.334 ** | 2007M05 | −13.487 *** | 2008M03 |
| lnVOPI | −3.565 ** | −7.008 *** | 3.129 *** | 0.348 *** | −4.259 | 2007M04 | −7.616 *** | 2001M06 |
| lnSPI | −3.521 ** | −14.145 *** | 7.922 | 0.184 *** | −4.714 | 2009M01 | −14.277 *** | 2011M01 |
| Variable | Brent Crude Oil | WTI Crude Oil | ||||
|---|---|---|---|---|---|---|
| Coefficient | t-Statistic | p-Value | Coefficient | t-Statistic | p-Value | |
| Dependent variable: ΔFPI | ||||||
| Constant | 0.115 *** | 2.68 | 0.008 | 0.102** | 2.53 | 0.012 |
| lnFPIt−1 | −0.032 *** | −2.86 | 0.005 | −0.029 *** | −2.78 | 0.006 |
| lnOPt−1 | 0.310 *** | 4.03 | 0.000 | 0.347 *** | 3.71 | 0.000 |
| ΔlnFPIt−1 | 0.243 *** | 4.56 | 0.000 | 0.242 *** | 4.53 | 0.000 |
| ΔlnOPt−1 | 0.009 ** | 2.58 | 0.010 | 0.010 ** | 2.51 | 0.012 |
| Cointegration test statistics | FPSS = 4.240 tBDM = −2.857 | FPSS = 4.076 tBDM = −2.781 | ||||
| Dependent variable: ΔMPI | ||||||
| Constant | 0.163 *** | 2.75 | 0.006 | 0.101 * | 1.73 | 0.085 |
| lnMPIt−1 | −0.043 *** | −3.18 | 0.002 | −0.028 ** | −2.13 | 0.034 |
| lnOPt−1 | 0.252 *** | 3.53 | 0.001 | 0.314 ** | 2.31 | 0.021 |
| ΔlnOPt−1 | 0.010 *** | 3.49 | 0.001 | 0.034 * | 1.85 | 0.065 |
| ΔlnOPt−1 | − | − | - | 0.056 *** | 3.01 | 0.003 |
| Cointegration test statistics | FPSS = 7.416 ** tBDM = −3.180 * | FPSS = 3.878 tBDM = −2.127 | ||||
| Dependent variable: ΔDPI | ||||||
| constant | 0.147 *** | 3.76 | 0.000 | 0.133 *** | 3.55 | 0.000 |
| lnDPIt−1 | −0.046 *** | −4.01 | 0.000 | −0.044 *** | −3.89 | 0.000 |
| lnOPt−1 | 0.414 *** | 5.14 | 0.000 | 0.455 *** | 4.83 | 0.000 |
| ΔlnDPIt−1 | 0.496 *** | 10.40 | 0.000 | 0.497 *** | 10.39 | 0.000 |
| ΔlnOPt−1 | 0.019 *** | 3.16 | 0.002 | 0.020 *** | 3.01 | 0.003 |
| Cointegration test statistics | FPSS = 8.040 *** tBDM = −4.010 *** | FPSS = 7.570 ** tBDM = −3.890 *** | ||||
| Dependent variable: ΔCPI | ||||||
| Constant | 0.152 *** | 3.13 | 0.002 | 0.137 *** | 2.98 | 0.003 |
| lnCPIt−1 | −0.043 *** | −3.29 | 0.001 | −0.041 *** | −3.23 | 0.001 |
| lnOPt−1 | 0.326 *** | 3.80 | 0.000 | 0.360 *** | 3.53 | 0.000 |
| ΔlnCPIt−1 | 0.326 *** | 6.25 | 0.000 | 0.325 *** | 6.22 | 0.000 |
| ΔlnOPt−1 | 0.014** | 2.50 | 0.013 | 0.014** | 2.43 | 0.016 |
| Cointegration test statistics | FPSS = 5.405 * tBDM = −3.287 ** | FPSS = 5.226 * tBDM = −3.231 ** | ||||
| Dependent variable: ΔVOPI | ||||||
| Constant | 0.143 *** | 3.08 | 0.002 | 0.136 *** | 2.97 | 0.003 |
| lnVOPIt−1 | −0.037 *** | −3.10 | 0.002 | −0.035 *** | −3.01 | 0.003 |
| lnOPt−1 | 0.234 * | 1.78 | 0.076 | 0.238 | 1.53 | 0.126 |
| ΔlnVOPIt−1 | 0.343 *** | 6.33 | 0.000 | 0.343 *** | 6.32 | 0.000 |
| ΔlnVOPIt−2 | −0.140 ** | −2.45 | 0.015 | −0.141 ** | −2.47 | 0.014 |
| ΔlnVOPIt−4 | 0.173 *** | 3.19 | 0.002 | 0.172 *** | 3.16 | 0.002 |
| ΔlnOPt−1 | 0.008 | 1.44 | 0.151 | 0.008 | 1.27 | 0.205 |
| Cointegration test statistics | FPSS = 4.956 * tBDM = −3.099 * | FPSS = 4.721 tBDM = −3.011 * | ||||
| Dependent variable: ΔSPI | ||||||
| Constant | 0.194 *** | 3.03 | 0.003 | 0.180 *** | 2.82 | 0.005 |
| lnSPIt−1 | −0.052 *** | −3.52 | 0.000 | −0.051 *** | −3.50 | 0.001 |
| lnOPt−1 | 0.336 ** | 2.49 | 0.013 | 0.375 ** | 2.40 | 0.017 |
| ΔlnSPIt−1 | 0.262 *** | 4.94 | 0.000 | 0.260 *** | 4.92 | 0.000 |
| ΔlnOPt−1 | 0.017 ** | 2.12 | 0.035 | 0.019 *** | 2.82 | 0.005 |
| Cointegration test statistics | FPSS = 6.253 ** tBDM = −3.522 ** | FPSS = 6.214 ** tBDM = −3.497 ** | ||||
| Variable | Brent Crude Oil | WTI Crude Oil | ||||
|---|---|---|---|---|---|---|
| Coefficient | t-Statistic | p-Value | Coefficient | t-Statistic | p-Value | |
| Dependent variable: ΔFPI | ||||||
| Constant | 0.211 *** | 3.58 | 0.000 | 0.201 *** | 3.46 | 0.001 |
| lnFPIt−1 | −0.045 *** | −3.57 | 0.000 | −0.043 *** | −3.45 | 0.001 |
| 0.007 * | 1.78 | 0.077 | 0.007 * | 1.77 | 0.078 | |
| 0.005 | 1.34 | 0.180 | 0.005 | 1.32 | 0.187 | |
| ΔlnFPIt−1 | 0.171 *** | 3.13 | 0.002 | 0.167 *** | 3.03 | 0.003 |
| ΔlnFPIt−2 | 0.106 * | 1.93 | 0.055 | 0.105 * | 1.90 | 0.058 |
| Δ | −0.020 | −0.70 | 0.484 | −0.028 | −0.90 | 0.370 |
| Δ | 0.089 *** | 3.18 | 0.002 | 0.104 *** | 3.50 | 0.001 |
| Cointegration test statistics | FPSS = 4.408 tBDM = −3.565 ** | FPSS = 4.152 tBDM = −3.451 * | ||||
| Long-run asymmetric coefficients | = 0.158 ** = −0.126 | = 0.172 ** = −0.134 | ||||
| Long and short-run asymmetry tests | = 5.705 ** = 2.918 * | = 7.065 *** = 2.256 | ||||
| Dependent variable: ΔMPI | ||||||
| Constant | 0.138 ** | 2.01 | 0.045 | 0.126 * | 1.86 | 0.064 |
| lnMPIt−1 | −0.028 ** | −1.98 | 0.049 | −0.026 * | −1.81 | 0.071 |
| 0.006 | 1.53 | 0.127 | 0.006 | 1.61 | 0.108 | |
| 0.005 | 1.27 | 0.204 | 0.006 | 1.33 | 0.185 | |
| ΔlnMPIt−5 | −0.131 ** | −2.45 | 0.015 | −0.134 ** | −2.52 | 0.012 |
| Δ | 0.040 | 1.23 | 0.219 | 0.040 | 1.23 | 0.219 |
| Δ | 0.060 * | 1.81 | 0.071 | 0.057 * | 1.66 | 0.099 |
| Δ | 0.083 *** | 2.63 | 0.009 | 0.079 ** | 2.37 | 0.018 |
| Cointegration test statistics | FPSS = 2.247 tBDM = −1.976 | FPSS = 2.343 tBDM = −1.808 | ||||
| Long-run asymmetric coefficients | = 0.210 = −0.195 | = 0.253 = −0.231 | ||||
| Long and short-run asymmetry tests | = 0.428 = 3.152 * | = 0.711 = 3.659 * | ||||
| Dependent variable: ΔDPI | ||||||
| Constant | 0.368 *** | 4.99 | 0.000 | 0.395 *** | 5.23 | 0.000 |
| lnDPIt−1 | −0.081 *** | −4.99 | 0.000 | −0.087 *** | −5.22 | 0.000 |
| 0.019 *** | 2.73 | 0.007 | 0.022 *** | 2.97 | 0.003 | |
| 0.015 ** | 2.12 | 0.035 | 0.018 ** | 35 | 0.020 | |
| ΔlnDPIt−1 | 0.289 *** | 5.59 | 0.000 | 0.280 *** | 5.43 | 0.000 |
| ΔlnDPIt−2 | 0.192 *** | 3.66 | 0.000 | 0.194 *** | 3.72 | 0.000 |
| Δ | −0.028 | −0.56 | 0.578 | −0.082 | −51 | 0.131 |
| Δ | 0.067 | 1.40 | 0.163 | 0.121 ** | 36 | 0.019 |
| Cointegration test statistics | FPSS= 8.308 *** tBDM = −4.986 *** | FPSS = 9.113 *** tBDM = −5.216 *** | ||||
| Long-run asymmetric coefficients | = 0.235 ** = −0.189 ** | = 0.262 *** = −0.210 *** | ||||
| Long and short-run asymmetry tests | = 13.21 *** = 0.742 | = 18.63 *** = 2.723 * | ||||
| Dependent variable: ΔCPI | ||||||
| Constant | 0.274 *** | 4.17 | 0.000 | 0.259 *** | 4.02 | 0.000 |
| lnCPIt−1 | −0.058 *** | −4.11 | 0.000 | −0.056 *** | −3.96 | 0.000 |
| 0.015 ** | 2.43 | 0.020 | 0.015 ** | 41 | 0.016 | |
| 0.013 ** | 2.10 | 0.037 | 0.014 ** | 2.08 | 0.039 | |
| ΔlnCPIt−1 | 0.283 *** | 5.22 | 0.000 | 0.289 *** | 5.30 | 0.000 |
| ΔlnCPIt−2 | 0.120 ** | 2.19 | 0.029 | 0.113 ** | 2.05 | 0.041 |
| Δ | −0.068 | −1.48 | 0.140 | −0.049 | −1.01 | 0.315 |
| Δ | 0.095 ** | 2.20 | 0.028 | 0.102 ** | 2.22 | 0.027 |
| Δ | −0.081 * | −1.86 | 0.064 | −0.089 * | −1.95 | 0.052 |
| Cointegration test statistics | FPSS = 5.653 * tBDM =−4.113 *** | FPSS = 5.279 * tBDM = −3.964 *** | ||||
| Long-run asymmetric coefficients | = 0.256 *** = −0.235 ** | = 0.279 *** = −0.254 ** | ||||
| Long and short-run asymmetry tests | = 1.727 = 1.609 | = 2.240 = 0.699 | ||||
| Dependent variable: ΔVOPI | ||||||
| Constant | 0.230 *** | 3.79 | 0.000 | 0.213 *** | 3.53 | 0.000 |
| lnVOPIt−1 | −0.049 *** | −3.72 | 0.000 | −0.046 *** | −3.50 | 0.001 |
| 0.001 | 0.22 | 0.822 | 0.002 | 03 | 0.741 | |
| −0.001 | −0.15 | 0.878 | −0.0003 | .04 | 0.965 | |
| ΔlnVOPIt−1 | 0.339 *** | 6.20 | 0.000 | 0.343 *** | 6.26 | 0.000 |
| ΔlnVOPIt−2 | −0.162 *** | −2.81 | 0.005 | −0.164 *** | −2.81 | 0.005 |
| ΔlnVOPIt−3 | −0.162 *** | −2.81 | 0.005 | 0.098 * | 1.71 | 0.089 |
| ΔlnVOPIt−4 | − | − | 0.161 *** | 2.91 | 0.004 | |
| Δ | −0.041 | −0.69 | 0.494 | −0.041 | −0.65 | 0.514 |
| Δ | 0.173 *** | 3.06 | 0.002 | 0.185 *** | 07 | 0.002 |
| Δ | 0.113 * | 1.86 | 0.064 | 0.094 | 48 | 0.139 |
| Cointegration test statistics | FPSS = 4.794 * tBDM = −3.794 ** | FPSS = 4.215 tBDM = −3.501 ** | ||||
| Long-run asymmetric coefficients | = 0.032 = 0.024 | = 0.053 = 0.008 | ||||
| Long and short-run asymmetry tests | = 5.127 ** = 4.171 ** | = 5.106 ** = 1.462 | ||||
| Dependent variable: ΔSPI | ||||||
| Constant | 0.277 *** | 3.73 | 0.000 | 0.269 *** | 3.64 | 0.000 |
| lnSPIt−1 | −0.056 *** | −3.78 | 0.000 | −0.055*** | −3.72 | 0.000 |
| 0.012 | 1.21 | 0.277 | 0.014 | 31 | 0.192 | |
| 0.010 | 0.94 | 0.347 | 0.012 | 02 | 0.307 | |
| ΔlnSPIt-1 | 0.262 *** | 4.94 | 0.000 | 0.262 *** | 4.92 | 0.000 |
| Δ | −0.099 | −1.13 | 0.258 | −0.041 | .44 | 0.661 |
| Δ | 0.244 *** | 2.97 | 0.003 | 0.189 ** | 18 | 0.030 |
| Cointegration test statistics | FPSS = 4.859 * tBDM = −3.783 ** | FPSS = 4.719 tBDM = −3.718 ** | ||||
| Long-run asymmetric coefficients | = 0.220 = −0.190 | = 0.254 = −0.219 | ||||
| Long and short-run asymmetry tests | = 0.936 = 0.974 | = 1.176 = 0.168 | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zmami, M.; Ben-Salha, O. Does Oil Price Drive World Food Prices? Evidence from Linear and Nonlinear ARDL Modeling. Economies 2019, 7, 12. https://doi.org/10.3390/economies7010012
Zmami M, Ben-Salha O. Does Oil Price Drive World Food Prices? Evidence from Linear and Nonlinear ARDL Modeling. Economies. 2019; 7(1):12. https://doi.org/10.3390/economies7010012
Chicago/Turabian StyleZmami, Mourad, and Ousama Ben-Salha. 2019. "Does Oil Price Drive World Food Prices? Evidence from Linear and Nonlinear ARDL Modeling" Economies 7, no. 1: 12. https://doi.org/10.3390/economies7010012
APA StyleZmami, M., & Ben-Salha, O. (2019). Does Oil Price Drive World Food Prices? Evidence from Linear and Nonlinear ARDL Modeling. Economies, 7(1), 12. https://doi.org/10.3390/economies7010012





