Stock Prices of Renewable Energy Firms: Are There Asymmetric Responses to Oil Price Changes?
Abstract
1. Introduction
2. Models and Methods
3. Data
4. The Results
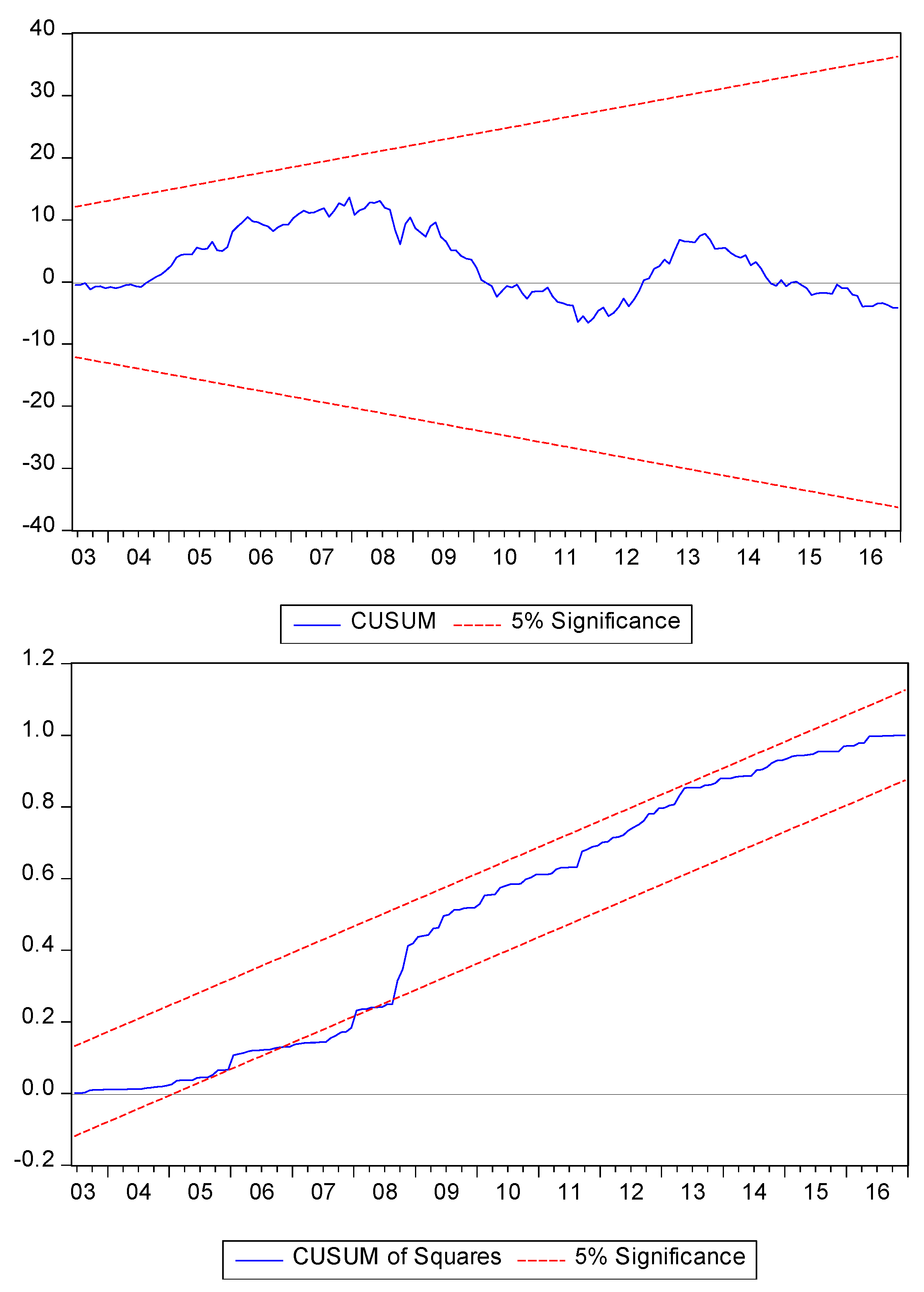
5. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Baek, Jungho. 2007. The J-curve and the U.S.-Canada forest products trade. Journal of Forest Economics 13: 245–58. [Google Scholar] [CrossRef]
- Baek, Jungho, and Hyun Seok Kim. 2013. Is economic growth good or bad for the environment? Empirical evidence from Korea. Energy Economics 36: 744–49. [Google Scholar] [CrossRef]
- Baek, Jungho, and Won W. Koo. 2009. Assessing exchange rate sensitivity of U.S. bilateral agricultural trade. Canadian Journal of Agricultural Economics 57: 187–203. [Google Scholar] [CrossRef]
- Baek, Jungho, and Dominique Pride. 2014. On the income-nuclear energy-CO2 emissions nexus revisited. Energy Economics 43: 6–10. [Google Scholar] [CrossRef]
- Bahmani-Oskooee, Mohsen, and Jungho Baek. 2015. Further evidence on Orcutt’s hypothesis using Korean-US commodity data. Applied Economics Letters 22: 717–24. [Google Scholar] [CrossRef]
- Basher, Syed A., and Perry Sadorsky. 2006. Oil price risk and emerging stock markets. Global Finance Journal 17: 224–51. [Google Scholar] [CrossRef]
- Bekhet, Hussain Ali, and Ali Matar. 2013. Co-integration and causality analysis between stock market prices and their determinates in Jordan. Economic Modelling 35: 508–14. [Google Scholar] [CrossRef]
- Bondia, Ripsy, Sajal Ghosh, and Kakali Kanjilal. 2016. International crude oil prices and the stock prices of clean energy and technology companies: Evidence from non-linear cointegration tests with unknown structural breaks. Energy 101: 558–65. [Google Scholar] [CrossRef]
- Broadstock, David C., Hong Cao, and Dayong Zhang. 2012. Oil shocks and their impact on energy related stocks in China. Energy Economics 34: 1888–95. [Google Scholar] [CrossRef]
- Chaudhuri, Kausik, and Samuel Smiles. 2004. Stock market and aggregate economic activity: Evidence from Australia. Applied Financial Economics 14: 121–29. [Google Scholar] [CrossRef]
- Cong, Rong-Gang, Yi-Ming Wei, Jian-Lin Jiao, and Ying Fan. 2008. Relationships between oil price shocks and stock market: An empirical analysis from China. Energy Policy 36: 3544–53. [Google Scholar] [CrossRef]
- Cummins, Mark, Oonagh Garry, and Claire Kearney. 2014. Price discovery analysis of green equity indices using robust asymmetric vector autoregression. International Review of Financial Analysis 35: 261–67. [Google Scholar] [CrossRef]
- Cunado, Juncal, and Fernando Perez de Gracia. 2014. Oil price shocks and stock market returns: Evidence for some European countries. Energy Economics 42: 365–77. [Google Scholar] [CrossRef]
- Fang, Chung-Rou, and Shih-Yi You. 2014. The impact of oil price shocks on the large emerging countries’ stock prices: Evidence from China, India and Russia. International Review of Economics & Finance 29: 330–38. [Google Scholar]
- Ghosh, Sajal. 2009. Import demand of crude oil and economic growth: Evidence from India. Energy Policy 37: 699–702. [Google Scholar] [CrossRef]
- Irene Henriques, Perry Sadorsky. 2008. Oil prices and the stock prices of alternative energy companies. Energy Economics 30: 998–1010. [Google Scholar] [CrossRef]
- Huang, Roger D., Ronald W. Masulis, and Hans R. Stoll. 1996. Energy shocks and financial markets. Journal of Futures Markets: Futures, Options, and Other Derivative Products 16: 1–27. [Google Scholar] [CrossRef]
- Humpe, Andreas, and Peter Macmillan. 2009. Can macroeconomic variables explain long-term stock market movements? A comparison of the US and Japan. Applied Financial Economics 19: 111–19. [Google Scholar] [CrossRef]
- Iwata, Hiroki, Keisuke Okada, and Sovannroeun Samreth. 2010. Empirical study on the environmental Kuznets curve for CO2 in France: The role of nuclear energy. Energy Policy 38: 4057–63. [Google Scholar] [CrossRef]
- Jalil, Abdul, and Syed F. Mahmud. 2009. Environment Kuznets curve for CO2 emissions: A cointegration analysis for China. Energy Policy 37: 5167–72. [Google Scholar] [CrossRef]
- Johansen, Søren, and Katarina Juselius. 1990. Maximum likelihood estimation and inference on cointegration—With applications to the demand for money. Oxford Bulletin of Economics and Statistics 52: 169–210. [Google Scholar] [CrossRef]
- Kang, Wensheng, Ronald A. Ratti, and Kyung Hwan Yoon. 2015. The impact of oil price shocks on the stock market return and volatility relationship. Journal of International Financial Markets, Institutions and Money 34: 41–54. [Google Scholar] [CrossRef]
- Kilian, Lutz, and Cheolbeom Park. 2009. The impact of oil price shocks on the US stock market. International Economic Review 50: 1267–87. [Google Scholar] [CrossRef]
- Kumar, Surender, Shunsuke Managi, and Akimi Matsuda. 2012. Stock prices of clean energy firms, oil and carbon markets: A vector autoregressive analysis. Energy Economics 34: 215–26. [Google Scholar] [CrossRef]
- Kyritsis, Evangelos, and Apostolos Serletis. 2017. Oil Prices and the Renewable Energy Sector. Discussion papers 2017/15. Bergen, Norway: Department of Business and Management Science, Norwegian School of Economics. [Google Scholar]
- Managi, Shunsuke, and Tatsuyoshi Okimoto. 2013. Does the price of oil interact with clean energy prices in the stock market? Japan and the World Economy 27: 1–9. [Google Scholar] [CrossRef]
- Masih, Rumi, Sanjay Peters, and Lurion De Mello. 2011. Oil price volatility and stock price fluctuations in an emerging market: Evidence from South Korea. Energy Economics 33: 975–86. [Google Scholar] [CrossRef]
- Papapetrou, Evangelia. 2001. Oil price shocks, stock market, economic activity and employment in Greece. Energy Economics 23: 511–32. [Google Scholar] [CrossRef]
- Park, Jungwook, and Ronald A. Ratti. 2008. Oil price shocks and stock markets in the US and 13 European countries. Energy Economics 30: 2587–608. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, Yongcheol Shin, and Richard J. Smith. 2001. Bounds testing approaches to the analysis of level relationships. Journal of Applied Econometrics 16: 289–326. [Google Scholar] [CrossRef]
- Pilinkus, Donatas. 2010. Macroeconomic indicators and their impact on stock market performance in the short and long run: The case of the Baltic States. Technological and Economic Development of Economy 16: 291–304. [Google Scholar] [CrossRef]
- Reboredo, Juan C. 2015. Is there dependence and systemic risk between oil and renewable energy stock prices? Energy Economics 48: 32–45. [Google Scholar] [CrossRef]
- Reboredo, Juan C., Miguel A. Rivera-Castro, and Andrea Ugolini. 2017. Wavelet-based test of co-movement and causality between oil and renewable energy stock prices. Energy Economics 61: 241–52. [Google Scholar] [CrossRef]
- Reynolds, Douglas B., and Jungho Baek. 2012. Much ado about Hotelling: Between the ideas of Hubbert. Energy Economics 34: 162–70. [Google Scholar] [CrossRef]
- Sadorsky, Perry. 1999. Oil price shocks and stock market activity. Energy Economics 21: 449–69. [Google Scholar] [CrossRef]
- Sadorsky, Perry. 2012. Correlations and volatility spillovers between oil prices and the stock prices of clean energy and technology companies. Energy Economics 34: 248–55. [Google Scholar] [CrossRef]
- Sari, Ramazan, Bradley T. Ewing, and Ugur Soytas. 2008. The relationship between disaggregate energy consumption and industrial production in the United States: An ARDL approach. Energy Economics 30: 2302–13. [Google Scholar] [CrossRef]
- Shin, Yongcheol, Byungchul Yu, and Matthew Greenwood-Nimmo. 2014. Modelling asymmetric cointegration and dynamic multipliers in a nonlinear ARDL framework. In Festschrift in Honor of Peter Schmidt. New York: Springer, pp. 281–314. [Google Scholar]
- Shin, Chul, Jungho Baek, and Eunnyeong Heo. 2018. Do oil price changes have symmetric or asymmetric effects on Korea’s demand for imported crude oil? Energy Sources, Part B: Economic, Planning and Policy 13: 6–12. [Google Scholar] [CrossRef]
- Stambuli, Benedict Baraka. 2013. Price and income elasticities of oil Demand in Tanzania: An autoregressive approach. Business Management Dynamics 3: 75–83. [Google Scholar]
- Tappen, Samuel, and Jungho Baek. 2016. Can oil tax policy change exploration levels? Empirical evidence from Alaska oil legislation. Energy Sources Part B: Economics, Planning and Policy 11: 1055–60. [Google Scholar] [CrossRef]
- Umekwe, Maduabuchi, and Jungho Baek. 2017. Do oil prices really matter to U.S. shale oil production? Energy Sources, Part B: Economics, Planning, and Policy 12: 268–74. [Google Scholar] [CrossRef]
- Wang, Yudong, Chongfeng Wu, and Li Yang. 2013. Oil price shocks and stock market activities: Evidence from oil-importing and oil-exporting countries. Journal of Comparative Economics 41: 1220–39. [Google Scholar] [CrossRef]
| 1 | Since the pioneering work by Pesaran et al. (2001), the ARDL approach has been one of the most widely used methods in many fields of empirical research. Some examples include the following: Baek (2007), Baek and Koo (2009), and Bahmani-Oskooee and Baek (2015) for international trade; Sari et al. (2008); Ghosh (2009), Reynolds and Baek (2012), Stambuli (2013), Tappen and Baek (2016), and Shin et al. (2018) for energy economics; Jalil and Mahmud (2009), Iwata et al. (2010), Baek and Kim (2013), and Baek and Pride (2014) for environmental economics; and Chaudhuri and Smiles (2004), Humpe and Macmillan (2009), Pilinkus (2010), and Bekhet and Matar (2013) for financial markets. |
| 2 | Changes in stock prices of renewable energy are more likely to react to higher oil prices. When high oil prices are expected to be maintained, for example, people are motivated to seek out alternative energy sources like solar and wind power, which increasingly compete with fossil fuels, thereby resulting in a surge in the price of alternative energy stocks. Although falling oil prices may swing away from people's attention from renewable sources, concerns about greenhouse-gas emissions are still likely to encourage the development of alternatives, thereby mitigating a drop in the price of alternative energy stocks. Accordingly, an asymmetrical price response would make some sense on the stock prices of renewable energy firms. To the best of our knowledge, Kyritsis and Serletis (2017) is perhaps the only study considering the asymmetrical effects of oil prices when examining the topic. Using a GARCH model, they show that oil price fluctuations have little effect on renewable stock prices so that the asymmetrical effects do not exist. |
| 3 | It is important to note that the ARDL approach has certain econometric advantages in comparison to standard cointegration methods (i.e., Johansen and Juselius 1990). First, the ARDL can be used irrespective of whether the regressors are I(0) or I(1); hence, this method does not require the same order of integration among variables and pre-testing unit roots. Second, since an error-correction model (ECM) can be derived from the ARDL via a simple linear transformation, it is a very convenient tool to estimate the short- and long-run parameters of the model simultaneously. Third, the ARDL is more robust and performs better for finite sample size (small sample size) than conventional cointegration methods. |
| 4 | It is worth emphasizing that the short- and long-run estimates in Equation (4) are econometrically meaningful; a cointegration relationship should hold among the selected variables. For this, the null of the nonexistence of the long-run relationship, namely θ0 = θ1 = θ2 = θ3 = θ4 = 0 is tested. This can be implemented using an F-test with two sets of asymptotic critical values tabulated by Pesaran et al. (2001) in which a lower critical value assumes to be I(0) regressor and an upper value assumes to be I(1). This is why the ARDL is called a bounds testing procedure. If the calculated F-statistic lies outside the upper critical level of the critical bounds, the null can be rejected, indicating that the variables are cointegrated. |
| 5 | Although NEX can be collected from September 1999, the NYSE Arca Tech 100 Index can only be traced back to January 2002. For this reason, we compile the data starting from January 2002. |
| 6 | The error correction coefficient is negative and very significant, providing confirming evidence of cointegration (Panel C). |
| Mean | Standard Deviation | Min | Max | |
|---|---|---|---|---|
| sprt | 199.869 | 78.956 | 95.280 | 455.190 |
| copt | 67.074 | 26.764 | 19.720 | 133.880 |
| sptt | 1104.542 | 496.679 | 385.730 | 2153.540 |
| intt | 3.347 | 1.084 | 5.280 | 1.500 |
| Panel A: Short-Run Coefficient Estimates | ||||
|---|---|---|---|---|
| Independent Variables | Dependent Variable: sprt | |||
| Lag Order | ||||
| 0 | 1 | 2 | 3 | |
| Δ(sprt) | 0.076 | |||
| (1.556) | ||||
| Δ(POSt) | 0.243 | |||
| (2.914) ** | ||||
| Δ(NEGt) | 0.116 | 0.026 | −0.152 | |
| (1.652) * | (0.366) | (−2.349) ** | ||
| Δ(sptt) | 1.202 | |||
| (17.231) ** | ||||
| Δ(intt) | −0.019 | |||
| (−1.096) | ||||
| Panel B: Long-Run Coefficient Estimates | ||||
| POSt | NEGt | sptt | intt | Constant |
| 0.037 | 0.143 | 1.579 | 0.696 | −8.252 |
| (0.111) | (0.430) | (1.677) * | (3.066) ** | (−1.310) |
| Panel C: Diagnostic Statistics | ||||
| ect−1 | LM | Wald-S | Wald-L | Adj. R2 |
| −0.036 | 8.433 | 4.176 | 0.507 | 0.692 |
| (−1.947) ** | (0.750) | (0.041) ** | (0.476) | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, D.; Baek, J. Stock Prices of Renewable Energy Firms: Are There Asymmetric Responses to Oil Price Changes? Economies 2018, 6, 59. https://doi.org/10.3390/economies6040059
Lee D, Baek J. Stock Prices of Renewable Energy Firms: Are There Asymmetric Responses to Oil Price Changes? Economies. 2018; 6(4):59. https://doi.org/10.3390/economies6040059
Chicago/Turabian StyleLee, Donggyu, and Jungho Baek. 2018. "Stock Prices of Renewable Energy Firms: Are There Asymmetric Responses to Oil Price Changes?" Economies 6, no. 4: 59. https://doi.org/10.3390/economies6040059
APA StyleLee, D., & Baek, J. (2018). Stock Prices of Renewable Energy Firms: Are There Asymmetric Responses to Oil Price Changes? Economies, 6(4), 59. https://doi.org/10.3390/economies6040059






