Export-Led Growth, Global Integration, and the External Balance of Small Island Developing States
Abstract
1. Introduction
1.1. Related Research
1.2. Aims and Contribution
1.3. Study Area
2. Methodology
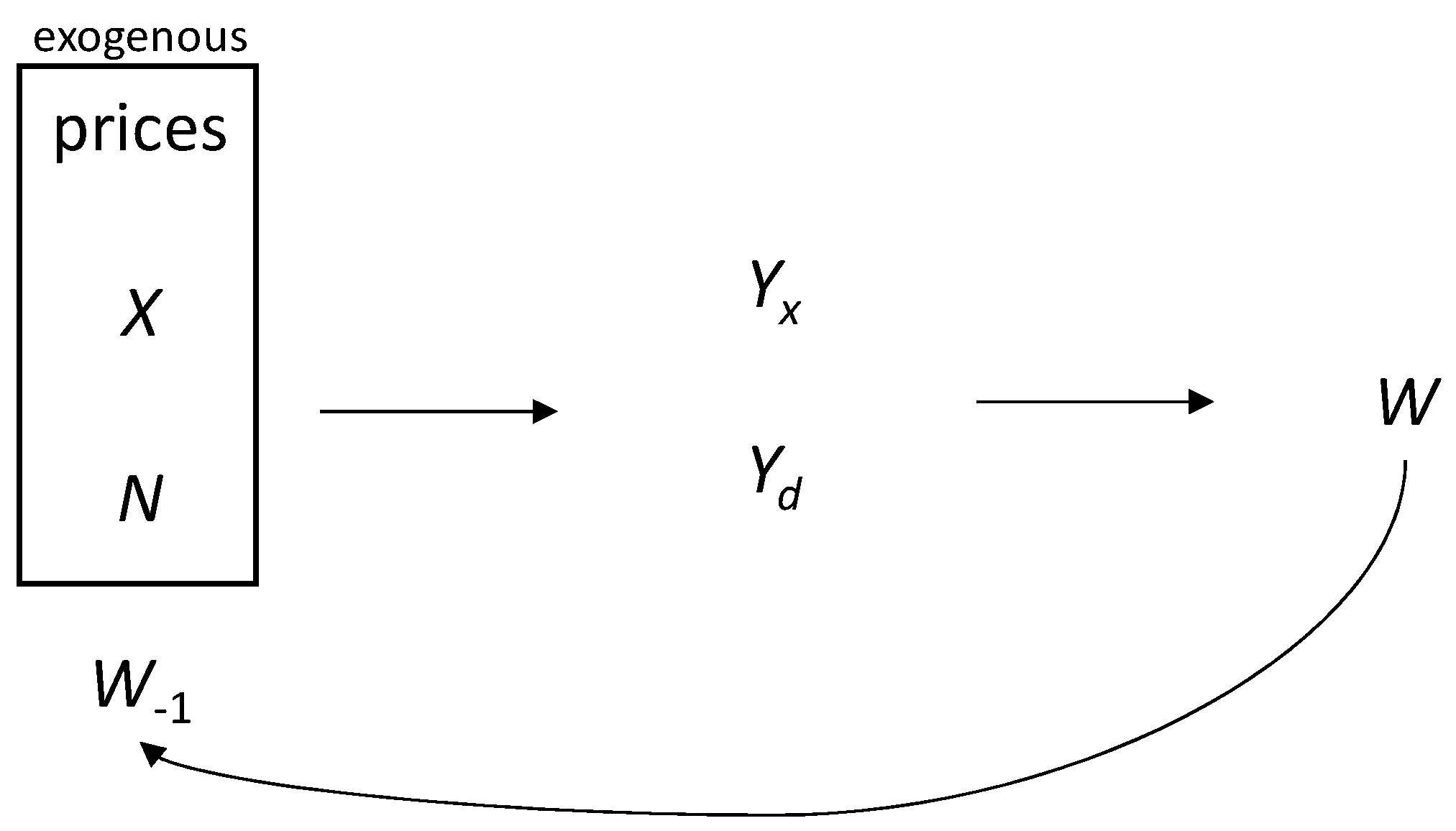
2.1. Prices
2.2. Gross Domestic Product (GDP) in the Two-Sector Model
2.3. Consumption in the Two-Sector Model
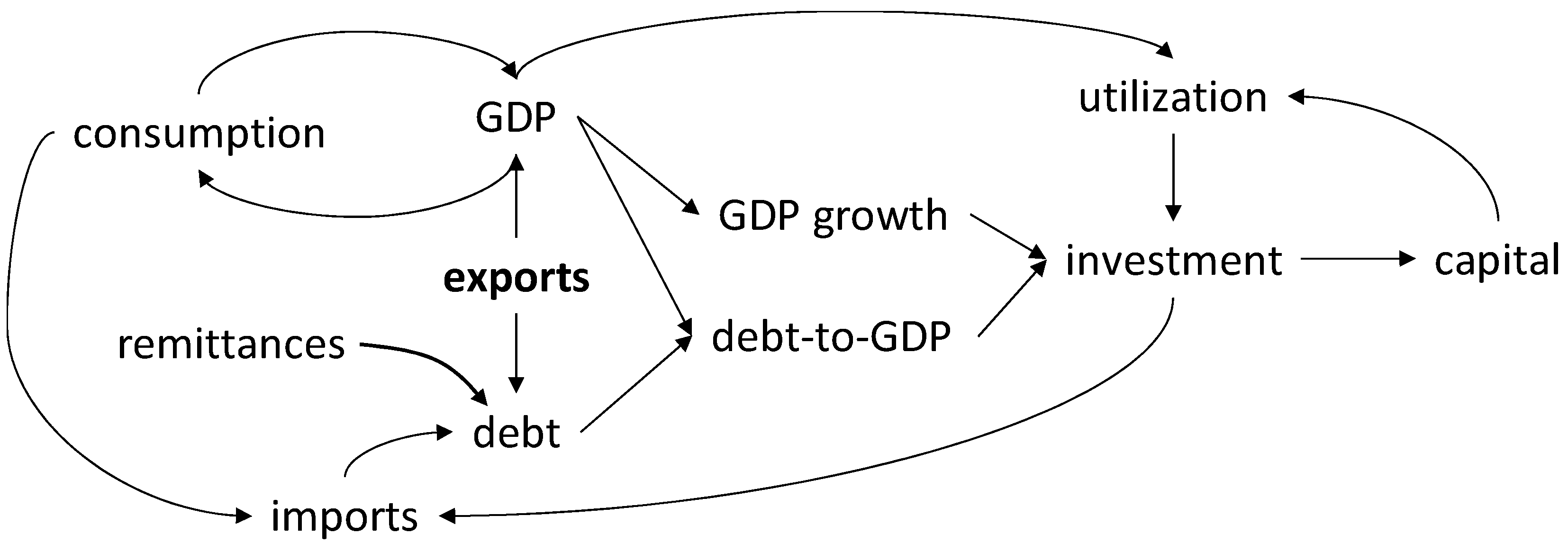
2.4. The Aggregated One-Sector Model
2.5. Balance of Payments, Debt and Investment
2.6. Calibration
2.6.1. GDP and Imports
2.6.2. Investment and Debt
3. Results
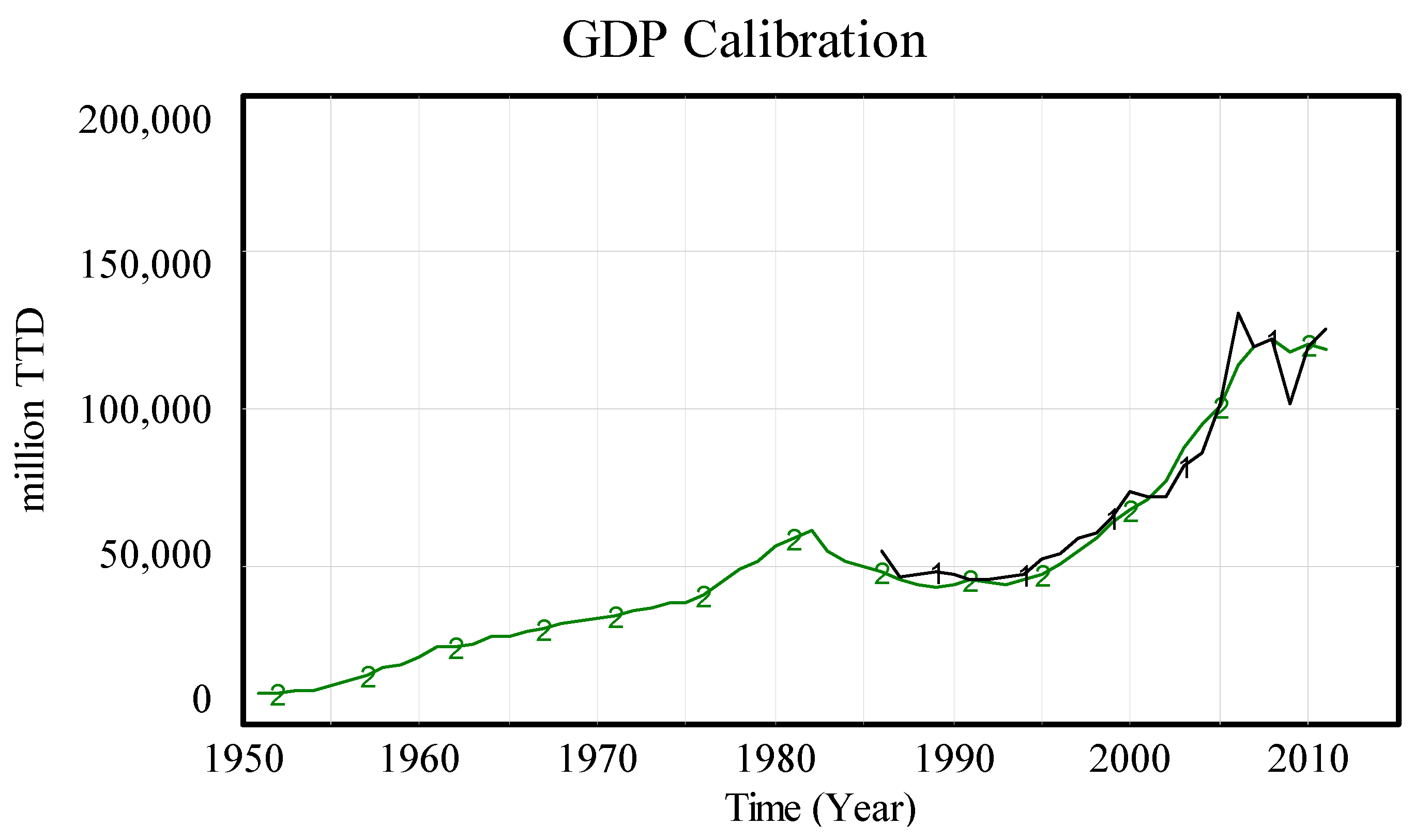
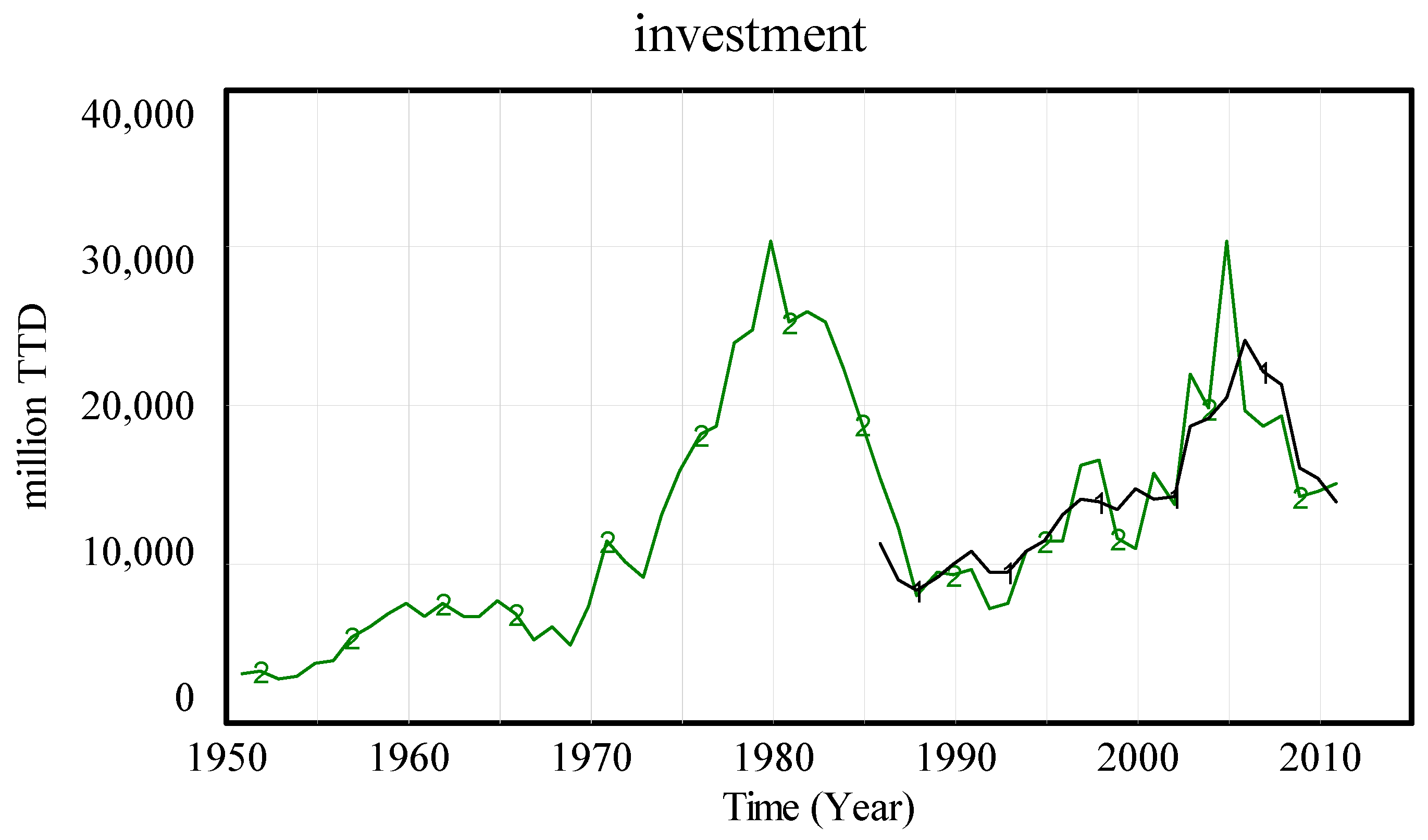
3.1. Goodness-of-Fit
3.2. Parameter Estimates
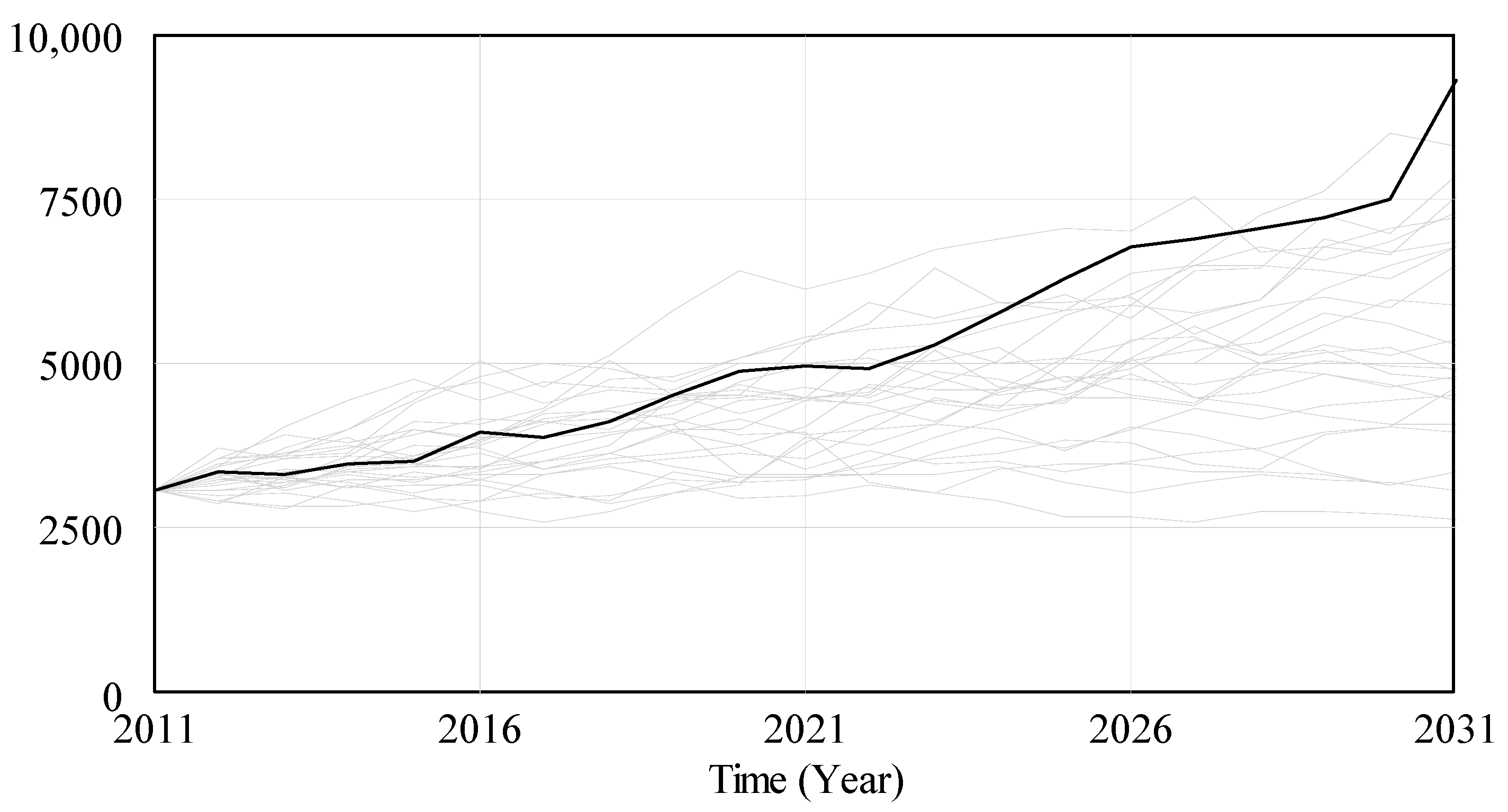
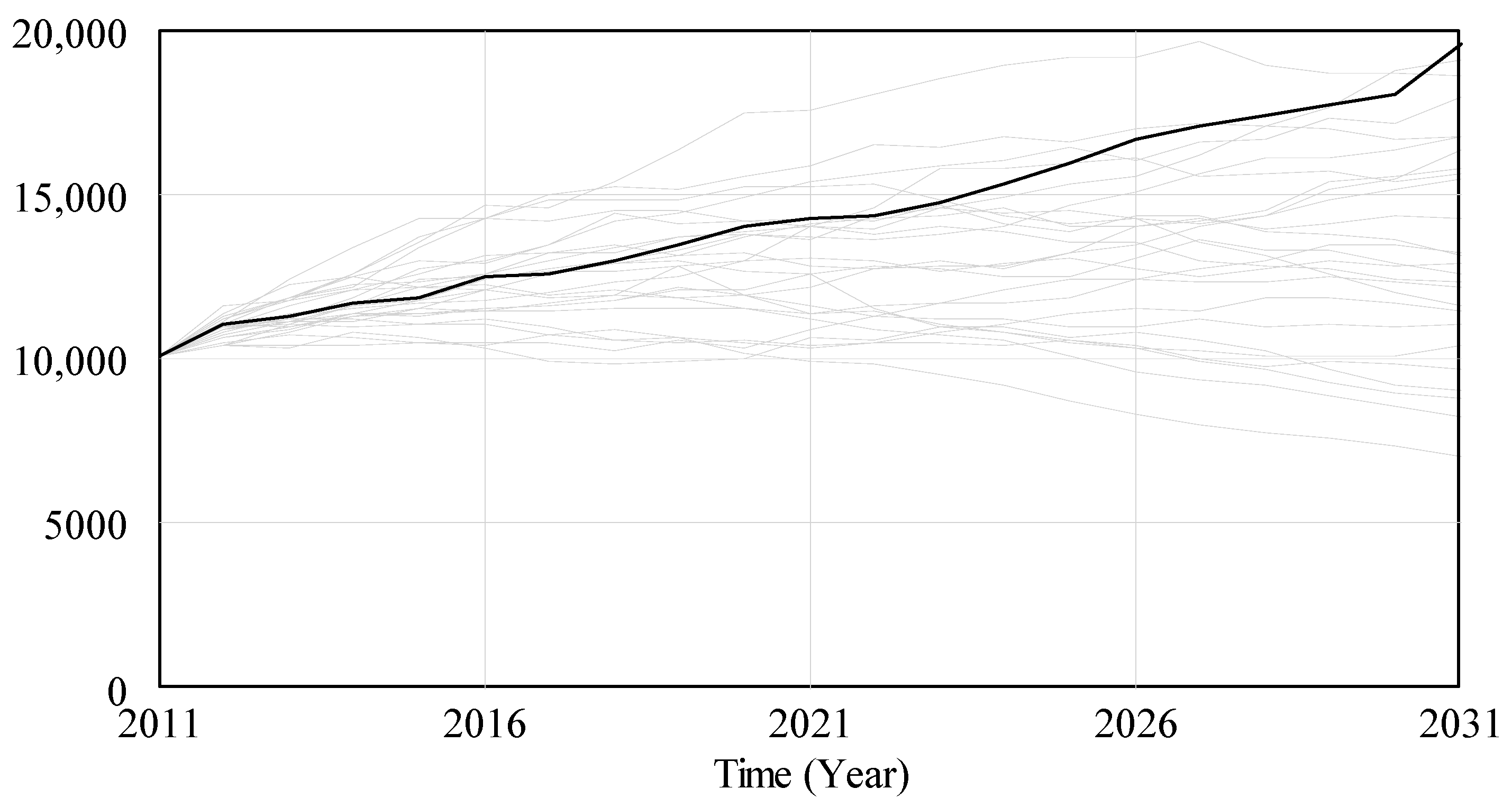
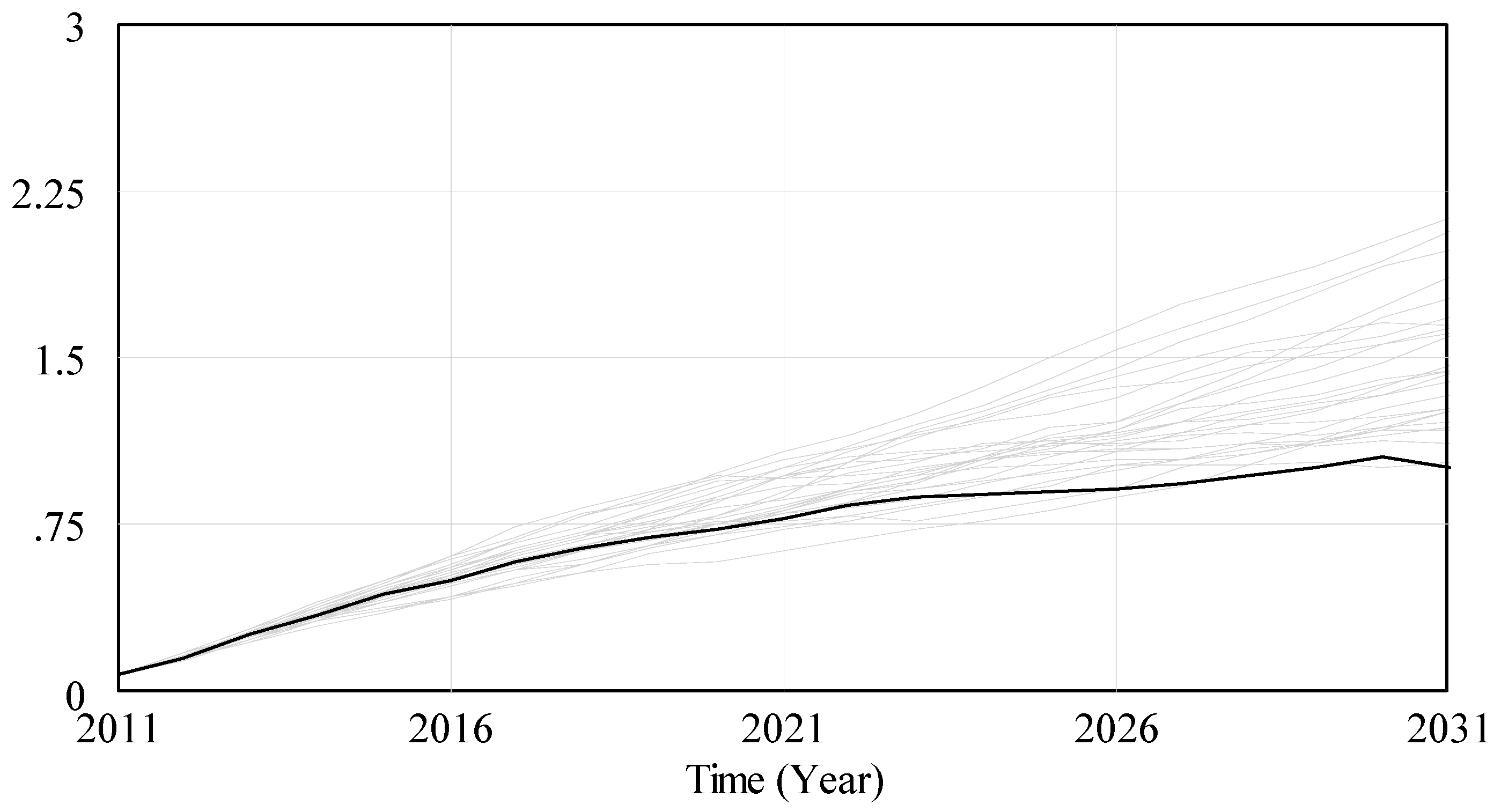
3.3. Simulations
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aghion, Philippe, Peter Howitt, and Cecilia García-Peñalosa. 1998. Endogenous Growth Theory. Cambridge: MIT Press. [Google Scholar]
- Alleyne, Antonio, and Brian M. Francis. 2017. Globalisation and International Competitiveness: The Future of the Caribbean Require Reform Changes. SSRN Scholarly Paper ID 2956746. Rochester: Social Science Research Network. Available online: http://papers.ssrn.com/abstract=2956746 (accessed on 8 November 2015).
- Armstrong, Harvey, and Robert Read. 1995. Western European Micro-States and EU Autonomous Regions: The Advantages of Size and Sovereignty. World Development 23: 1229–45. [Google Scholar] [CrossRef]
- Bates, Samuel, and Valérie Angeon. 2015. Promoting the Sustainable Development of Small Island Developing States: Insights from Vulnerability and Resilience Analysis. Région et Développement 42: 15–29. [Google Scholar]
- Best, Lloyd A. 1968. Outlines of a Model of Pure Plantation Economy. Social and Economic Studies 17: 283–326. Available online: http://www.jstor.org/stable/27856339 (accessed on 23 June 2015).
- Boopsingh, Trevor M., and Gregory McGuire, eds. 2014. From Oil to Gas and Beyond: A Review of the Trinidad and Tobago Model and Analysis of Future Challenges. Lanham: University Press of America. [Google Scholar]
- Briguglio, Lino. 1995. Small Island Developing States and Their Economic Vulnerabilities. World Development 23: 1615–32. [Google Scholar] [CrossRef]
- Bruce, Carlton J., and Cherita Girvan. 1972. The Open Petroleum Economy: A Comparison of Keynesian and Alternative Formulations. Social and Economic Studies 21: 125–52. Available online: http://www.jstor.org/stable/27856525 (accessed on 8 August 2015).
- Chenery, Hollis B. 1975. The Structuralist Approach to Development Policy. The American Economic Review 65: 310–16. Available online: http://www.jstor.org/stable/1818870 (accessed on 4 November 2014).
- Cohen, Avi J., and Geoffrey C. Harcourt. 2003. Retrospectives: Whatever Happened to the Cambridge Capital Theory Controversies? Journal of Economic Perspectives 17: 199–214. Available online: http://www.jstor.org/stable/3216846 (accessed on 27 August 2012). [CrossRef]
- Demas, William G. 2009. The Economics of Development in Small Countries: With Special Reference to the Caribbean. Kingston and St. Michael: University of the West Indies Press. First published 1965. [Google Scholar]
- Drakes, Crystal, Timothy Laing, Eric Kemp-Benedict, and Adrian Cashman. 2016. Caribbean Scenarios 2050. CERMES Technical Report, 84. Cave Hill, Barbados: Centre for Resource Management and Environmental Studies, University of the West Indies. [Google Scholar]
- Ebi, Kristie L., Tom Kram, Detlef P. van Vuuren, Brian C. O’Neill, and Elmar Kriegler. 2014. A New Toolkit for Developing Scenarios for Climate Change Research and Policy Analysis. Environment: Science and Policy for Sustainable Development 56: 6–16. [Google Scholar] [CrossRef]
- ECLAC. 2003. Progress Made in the Implementation of the CARICOM Single Market and Economy. LC/CAR/G.770. Port of Spain: Economic Commission for Latin America and the Caribbean, United Nations. [Google Scholar]
- ECLAC. 2009. Economic Growth in the Caribbean. LC/CAR/L.244. Port of Spain: Economic Commission for Latin America and the Caribbean, United Nations. [Google Scholar]
- Feenstra, Robert C., Robert Inklaar, and Marcel P. Timmer. 2015. The next Generation of the Penn World Table. American Economic Review 105: 3150–82. [Google Scholar] [CrossRef]
- Felipe, Jesus, and John S. L. McCombie. 2001. The CES Production Function, the Accounting Identity, and Occam’s Razor. Applied Economics 33: 1221–32. [Google Scholar] [CrossRef]
- Felipe, Jesus, and John McCombie. 2006. The Tyranny of the Identity: Growth Accounting Revisited. International Review of Applied Economics 20: 283–99. [Google Scholar] [CrossRef]
- Felipe, Jesus, and John S. L. McCombie. 2013. The Aggregate Production Function and the Measurement of Technical Change: “Not Even Wrong”. Cheltenham: Edward Elgar. [Google Scholar]
- Figueroa, Mark. 1996. The Plantation School and Lewis: Contradictions, Continuities and Continued Caribbean Relevance. Social and Economic Studies 45: 23–49. Available online: http://www.jstor.org/stable/27866101 (accessed on 23 June 2015).
- Fisher, Franklin M. 2005. Aggregate Production Functions—A Pervasive, but Unpersuasive, Fairytale. Eastern Economic Journal 31: 489–91. Available online: http://www.jstor.org/stable/40326426 (accessed on 17 December 2017).
- Foley, Duncan K., and Thomas R. Michl. 1999. Growth and Distribution. Cambridge: Harvard University Press. [Google Scholar]
- Forrester, Jay W., and Peter M. Senge. 1980. Tests for Building Confidence in System Dynamics Models. System Dynamics, TIMS Studies in Management Sciences 14: 209–28. [Google Scholar]
- Gibson, Bill. 2003. An Essay on Late Structuralism. In Development Economics and Structuralist Macroeconomics: Essays in Honor of Lance Taylor. Edited by Amitava Krishna Dutt and Jaime Ros. Cheltenham: Edward Elgar, pp. 52–76. Available online: http://www.uvm.edu/~wgibson/Research/tay.pdf (accessed on 3 November 2014).
- Girvan, Cherita, and Norman Girvan. 1970. Multinational Corporations and Dependent Underdevelopment in Mineral-Export Economies. Social and Economic Studies 19: 490–526. Available online: http://www.jstor.org/stable/27856449 (accessed on 8 August 2015).
- Girvan, Norman. 2006. Caribbean Dependency Thought Revisited. Canadian Journal of Development Studies/Revue Canadienne d’études Du Développement 27: 328–52. [Google Scholar] [CrossRef]
- Graham, Alan K. 1976. Parameter Formulation and Estimation in System Dynamics Models. Paper presented at the 1976 International Conference on System Dynamics Method, Geilo, Norway, August 8–15; pp. 541–80. [Google Scholar]
- Guillaumont, Patrick. 2009. An Economic Vulnerability Index: Its Design and Use for International Development Policy. Oxford Development Studies 37: 193–228. [Google Scholar] [CrossRef]
- Hausmann, Ricardo, and Bailey Klinger. 2009. Policies for Achieving Structural Transformation in the Caribbean. Discussion Paper 2, Private Sector Development Discussion Paper. Washington, DC, USA: Inter-American Development Bank. [Google Scholar]
- Holder, Carlos, and DeLisle Worrell. 1985. A Model of Price Formation for Small Economies: Three Caribbean Examples. Journal of Development Economics 18: 411–28. [Google Scholar] [CrossRef]
- Homer, Jack B. 2012. Partial-Model Testing as a Validation Tool for System Dynamics. System Dynamics Review 28: 281–94. [Google Scholar] [CrossRef]
- Hussain, Mohammed Nureldin. 2006. The Implications of Thirlwall’s Law for Africa’s Development Challenges. In Growth and Economic Development: Essays in Honour of A.P. Thirlwall. Edited by Philip Arestis, John McCombie and Roger Vickerman. Cheltenham: Edward Elgar Publishing Limited. [Google Scholar]
- Kraay, Aart, and William Easterly. 1999. Small States, Small Problems? Washington, DC: The World Bank. Available online: http://elibrary.worldbank.org/doi/book/10.1596/1813-9450-2139 (accessed on 19 January 2016).
- Kuznets, Simon. 1960. Economic Growth of Small Nations. In Economic Consequences of the Size of Nations. Edited by Austin E. Robinson. London: Palgrave Macmillan, pp. 14–32. [Google Scholar] [CrossRef]
- Lee, Frederic S. 1999. Post Keynesian Price Theory. Cambridge: Cambridge University Press. [Google Scholar]
- Lenferna, Georges Alexandre. 2018. Can We Equitably Manage the End of the Fossil Fuel Era? Energy Research & Social Science 35: 217–23. [Google Scholar] [CrossRef]
- Lewis, W. Arthur. 1954. Economic Development with Unlimited Supplies of Labour. The Manchester School 22: 139–91. [Google Scholar] [CrossRef]
- Lewis, W. Arthur. 1979. The Dual Economy Revisited. The Manchester School 47: 211–29. [Google Scholar] [CrossRef]
- Lewis, W. Cris. 1976. Export Base Theory and Multiplier Estimation: A Critique. The Annals of Regional Science 10: 58–70. [Google Scholar] [CrossRef]
- Lewis-Bynoe, Denny, ed. 2014. Building the Resilience of Small States: A Revised Framework. London: Commonwealth Secretariat. [Google Scholar]
- Lin, Justin Yifu, ed. 2012. New Structural Economics: A Framework for Rethinking Development and Policy. Washington, DC: The World Bank. Available online: http://elibrary.worldbank.org/doi/book/10.1596/978-0-8213-8955-3 (accessed on 7 October 2015).
- Martinez-Moyano, Ignacio J., and George P. Richardson. 2013. Best Practices in System Dynamics Modeling. System Dynamics Review 29: 102–23. [Google Scholar] [CrossRef]
- McGlade, Christophe, and Paul Ekins. 2015. The Geographical Distribution of Fossil Fuels Unused When Limiting Global Warming to 2 °C. Nature 517: 187–90. [Google Scholar] [CrossRef] [PubMed]
- McKenzie, Rex A. 2005. Structuralist Approaches to Social & Economic Development in the English Speaking Caribbean. Paper presented at the 6th Annual SALISES Conference on Governance, Institutions and Economic Growth: Reflections on Sir Arthur Lewis’ Theory of Economic Growth, Mona, Jamaica, March 17; Available online: http://eprints.kingston.ac.uk/36115/ (accessed on 7 April 2018).
- Means, Gardiner. 1964. The Corporate Revolution in America. Springfield: Collier Books. [Google Scholar]
- Milner, Chris, and Tony Westaway. 1993. Country Size and the Medium-Term Growth Process: Some Cross-Country Evidence. World Development 21: 203–11. [Google Scholar] [CrossRef]
- Moss, Richard H., Jae A. Edmonds, Kathy A. Hibbard, Martin R. Manning, Steven K. Rose, Detlef P. van Vuuren, Timothy R. Carter, Seita Emori, Mikiko Kainuma, Tom Kram, and et al. 2010. The next Generation of Scenarios for Climate Change Research and Assessment. Nature 463: 747–56. [Google Scholar] [CrossRef] [PubMed]
- North, Douglass C. 1955. Location Theory and Regional Economic Growth. Journal of Political Economy 63: 243–58. Available online: http://www.jstor.org.ezproxy.library.tufts.edu/stable/1825076 (accessed on 21 March 2018). [CrossRef]
- Nurse, Leonard A., Roger F. McLean, John Agard, Lino P. Briguglio, Virginie Duvat-Magnan, Netatua Pelesikoti, Emma Tompkins, and Arthur Webb. 2014. Small Islands. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part B: Regional Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel of Climate Change. Edited by Vicente R. Barros, Christopher B. Field, David Jon Dokken, Michael D. Mastrandrea, Katharine J. Mach, T. Eren Bilir, Monalisa Chatterjee, Kristie L. Ebi, Yuka Otsuki Estrada, Robert C. Genova and et al. Cambridge and New York: Cambridge University Press, pp. 1613–54. [Google Scholar]
- Ocampo, José Antonio. 2003. Structural Dynamics and Economic Growth in Developing Countries. Santiago: United Nations Economic Commission for Latin America and the Caribbean (ECLAC). [Google Scholar]
- Ocampo, José Antonio, Codrina Rada, and Lance Taylor. 2013. Growth and Policy in Developing Countries: A Structuralist Approach. New York: Columbia University Press. [Google Scholar]
- Oliva, Rogelio. 2003. Model Calibration as a Testing Strategy for System Dynamics Models. European Journal of Operational Research 151: 552–68. [Google Scholar] [CrossRef]
- O’Neill, Brian C., Elmar Kriegler, Kristie L. Ebi, Eric Kemp-Benedict, Keywan Riahi, Dale S. Rothman, Bas J. van Ruijven, Detlef P. van Vuuren, Joern Birkmann, Kasper Kok, and et al. 2017. The Roads Ahead: Narratives for Shared Socioeconomic Pathways Describing World Futures in the 21st Century. Global Environmental Change 42: 169–80. [Google Scholar] [CrossRef]
- O’Neill, Brian C., Elmar Kriegler, Keywan Riahi, Kristie L. Ebi, Stephane Hallegatte, Timothy R. Carter, Ritu Mathur, and Detlef P. Vuuren. 2014. A New Scenario Framework for Climate Change Research: The Concept of Shared Socioeconomic Pathways. Climatic Change 122: 387–400. [Google Scholar] [CrossRef]
- Phelps Brown, E. H. 1957. The Meaning of the Fitted Cobb-Douglas Function. The Quarterly Journal of Economics 71: 546–60. [Google Scholar] [CrossRef]
- Powell, J. D. Michael. 1964. An Efficient Method for Finding the Minimum of a Function of Several Variables without Calculating Derivatives. The Computer Journal 7: 155–62. [Google Scholar] [CrossRef]
- Rosenstein-Rodan, N. Paul. 1943. Problems of Industrialisation of Eastern and South-Eastern Europe. The Economic Journal 53: 202–11. Available online: http://www.jstor.org/stable/2226317 (accessed on 12 August 2010).
- Rothman, Dale S., Patricia Romero-Lankao, Vanessa J. Schweizer, and Beth A. Bee. 2014. Challenges to Adaptation: A Fundamental Concept for the Shared Socio-Economic Pathways and Beyond. Climatic Change 122: 495–507. [Google Scholar] [CrossRef]
- Samuelson, Paul A. 1966. A Summing Up. The Quarterly Journal of Economics 80: 568–83. [Google Scholar] [CrossRef]
- Seers, Dudley. 1964. The Mechanism of an Open Petroleum Economy. Social and Economic Studies 13: 233–42. Available online: http://www.jstor.org/stable/27853782 (accessed on 8 August 2015).
- Setterfield, Mark, ed. 2002. The Economics of Demand-Led Growth: Challenging the Supply-Side Vision of the Long Run. Cheltenham and Northampton: Edward Elgar. [Google Scholar]
- Shaikh, Anwar. 1974. Laws of Production and Laws of Algebra: The Humbug Production Function. The Review of Economics and Statistics 56: 115–20. [Google Scholar] [CrossRef]
- Solow, Robert M. 1956. A Contribution to the Theory of Economic Growth. The Quarterly Journal of Economics 70: 65–94. [Google Scholar] [CrossRef]
- Sraffa, Piero. 1962. Production of Commodities: A Comment. The Economic Journal 72: 477–79. [Google Scholar] [CrossRef]
- Stanton, Elizabeth A., Frank Ackerman, and Sivan Kartha. 2009. Inside the Integrated Assessment Models: Four Issues in Climate Economics. Climate and Development 1: 166–84. [Google Scholar] [CrossRef]
- Sterman, John D. 1984. Appropriate Summary Statistics for Evaluating the Historical Fit of System Dynamics Models. Dynamica 10: 51–66. [Google Scholar]
- Storm, Servaas. 2015. Structural Change. Development and Change 46: 666–99. [Google Scholar] [CrossRef]
- Strobl, Eric. 2012. The Economic Growth Impact of Natural Disasters in Developing Countries: Evidence from Hurricane Strikes in the Central American and Caribbean Regions. Journal of Development Economics 97: 130–41. [Google Scholar] [CrossRef]
- Stubbs, Richard. 1999. War and Economic Development: Export-Oriented Industrialization in East and Southeast Asia. Comparative Politics 31: 337–55. [Google Scholar] [CrossRef]
- Taylor, Lance. 1989. Stabilization and Growth in Developing Countries: A Structuralist Approach. Chur: Taylor & Francis. [Google Scholar]
- Taylor, Lance, ed. 1990. Socially Relevant Policy Analysis: Structuralist Computable General Equilibrium Models for the Developing World. Cambridge: MIT Press. [Google Scholar]
- Taylor, Lance. 2004. Reconstructing Macroeconomics: Structuralist Proposals and Critiques of the Mainstream. Cambridge: Harvard University Press. [Google Scholar]
- Thirlwall, Anthony Philip. 1979. The Balance of Payments Constraint as an Explanation of International Growth Rate Differences. BNL Quarterly Review 32: 45–53. [Google Scholar]
- Thirlwall, Anthony Philip. 2011. Balance of Payments Constrained Growth Models: History and Overview. PSL Quarterly Review 64: 307–51. Available online: http://papers.ssrn.com/abstract=2049740 (accessed on 13 March 2015).
- UN DESA. 2015. World Population Prospects: The 2015 Revision. New York: United Nations, Department of Economic and Social Affairs, Population Division. [Google Scholar]
- Van Vuuren, Detlef P., Elmar Kriegler, Brian C. O’Neill, Kristie L. Ebi, Keywan Riahi, Timothy R. Carter, Jae Edmonds, Stephane Hallegatte, Tom Kram, Ritu Mathur, and et al. 2014. A New Scenario Framework for Climate Change Research: Scenario Matrix Architecture. Climatic Change 122: 373–86. [Google Scholar] [CrossRef]
- Williams, Ewart. 2012. Review of the Heritage and Stabilisation Fund (HSF). Paper presented at the Revenue Management in Hydrocarbon Economies, University of the West Indies, St. Augustine, Trinidad and Tobago, June 21; Available online: http://sta.uwi.edu/conferences/12/revenue/documents/GovernorPresentationReviewHSFUWIJune21.pdf (accessed on 23 March 2015).
- WTTC. 2018a. Travel & Tourism Economic Impact 2018 Barbados. London: World Travel and Tourism Council. [Google Scholar]
- WTTC. 2018b. Travel & Tourism Economic Impact 2018 Jamaica. London: World Travel and Tourism Council. [Google Scholar]
| 1 | Bates and Angeon (2015) criticize both Briguglio and Guillaumont’s measures and offer support to Kraay and Easterly. They point out that being small and an island are not determinate, and raise concern that financial support to small island states could reward poor decisions. They argue that the SIDS category is artificial, in that “islandness” does not confer a particular additional vulnerability that cannot be offset by good policy. They contrast in particular Singapore with the Bahamas, arguing that Singapore followed a “smart strategy” for development, while the Bahamas did not. Although we believe their arguments to have some merit, they did not alter our conclusion. As we have already noted, the bulk of the literature acknowledges that being a small island is not determinate. Furthermore, we would challenge the assumption that smart strategies can be unambiguously identified ab initio. Poor choices can sometimes be foreseen and avoided, but it is difficult to say which of several promising strategies will ultimately succeed. Finally, we point out that the history of Singapore and the Bahamas are quite distinct. As argued by Stubbs (1999), war or the threat of war enabled the emergence of strong states throughout East and South-east Asia. In this view, the comparative peacefulness of the Americas made it is harder to impose unpleasant sacrifices in the interest of long-run development. |
| 2 | These are separate, but reinforcing points. Fisher showed that an aggregate production function cannot be defined, and the Cambridge Capital Controversies undermined the claim that factors are paid for their marginal contribution to output. The question then arises as to why the neoclassical growth model appears to work anyway. The answer is that statistical tests are in fact confirming an accounting identity, not testing the model. |
| 3 | Arguably, gross national income (GNI) is more relevant than GDP in a model focusing on externally-oriented production in which a significant portion of the capital in the export sector is foreign-owned. However, the available data are insufficient to test and calibrate such a model. |
| 4 | |
| 5 | In Thirlwall’s model the elasticity applies to all imports, not only consumption goods. |
| 6 | Vensim DSS version 6.4E (http://www.vensim.com). Model code is available upon request. |
| 7 | The variable in the public data set is listed in parentheses. |
| 8 | These statistics are for the time period 1975–2008. The augmented Dickey–Fuller and Phillips–Perron tests failed to reject a unit root for the time series of log exports. |
| 9 | This is made explicit in the Lotofen declaration: http://www.lofotendeclaration.org/. |
| R2 | Adj R2 | DW | MAPE | Theil | |||
|---|---|---|---|---|---|---|---|
| Um | Uv | Uc | |||||
| Barbados | |||||||
| GDP | 0.85 | 0.76 | 0.45 | 3.1 | 0.06 | 0.03 | 0.91 |
| Investment | 0.79 | 0.70 | 1.03 | 8.9 | 0.00 | 0.08 | 0.92 |
| Imports | 0.94 | 0.93 | 1.77 | 4.4 | 0.00 | 0.27 | 0.73 |
| Jamaica | |||||||
| GDP | 0.85 | 0.76 | 0.85 | 3.9 | 0.20 | 0.00 | 0.80 |
| Investment | 0.92 | 0.89 | 1.07 | 4.8 | 0.00 | 0.04 | 0.96 |
| Debt | 0.93 | 0.92 | 1.26 | 10.7 | 0.00 | 0.21 | 0.78 |
| Imports | 0.69 | 0.64 | 0.69 | 8.2 | 0.00 | 0.35 | 0.64 |
| Trinidad and Tobago | |||||||
| GDP | 0.96 | 0.94 | 1.45 | 5.8 | 0.04 | 0.02 | 0.93 |
| Investment | 0.63 | 0.45 | 1.78 | 15.4 | 0.00 | 0.23 | 0.77 |
| Imports | 0.93 | 0.92 | 2.00 | 7.4 | 0.01 | 0.00 | 0.99 |
| Parameter | Barbados | Jamaica | Trinidad and Tobago |
|---|---|---|---|
| g0 | 0.017 | 0.046 | 0.040 |
| gu | 0.101 | 0.282 | 0.048 |
| gd | 0.017 | 0.013 | 0.001 |
| v* | 1.889 | 0.644 | 2.000 |
| m0 | 0.177 | 0.000 | 0.420 |
| εm | −0.123 | −2.802 | −3.000 |
| cx | 0.000 | 0.000 | 0.000 |
| sw | 0.000 | 0.034 | 0.468 |
| ωx | 0.400 | 0.372 | 0.400 |
| ωd | 0.700 | 0.700 | 0.699 |
| axd | 0.189 | 0.250 | 0.202 |
| adx | 0.250 | 0.500 | 0.250 |
| mx | 0.250 | 0.237 | 0.170 |
| md | 0.082 | 0.196 | 0.032 |
| i | 0.070 | 0.012 | 0.028 |
| ρK | 0.000 | 0.003 | pre-’97 0.081 post-’97 0.048 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kemp-Benedict, E.; Drakes, C.; Laing, T.J. Export-Led Growth, Global Integration, and the External Balance of Small Island Developing States. Economies 2018, 6, 35. https://doi.org/10.3390/economies6020035
Kemp-Benedict E, Drakes C, Laing TJ. Export-Led Growth, Global Integration, and the External Balance of Small Island Developing States. Economies. 2018; 6(2):35. https://doi.org/10.3390/economies6020035
Chicago/Turabian StyleKemp-Benedict, Eric, Crystal Drakes, and Timothy J. Laing. 2018. "Export-Led Growth, Global Integration, and the External Balance of Small Island Developing States" Economies 6, no. 2: 35. https://doi.org/10.3390/economies6020035
APA StyleKemp-Benedict, E., Drakes, C., & Laing, T. J. (2018). Export-Led Growth, Global Integration, and the External Balance of Small Island Developing States. Economies, 6(2), 35. https://doi.org/10.3390/economies6020035






