Money and Pay-As-You-Go Pension

Abstract

This paper presents examination of how a pension policy affects income growth and the inflation rate in a utility model. Even if the contribution rate of pension increases because of an aging society, an aging society increases income growth and the inflation rate. Moreover, this paper presents examination of the optimal growth rate of the money supply. Because of the pension policy, the optimal growth rate of money stock changes. This result is intuitive because a pay-as-you-go pension changes capital accumulation. Therefore, the income growth rate should be changed to raise the welfare of all generations.

1. Introduction

In an aging society with fewer children, pension sustainability is an important topic. With pay-as-you-go pension systems, funds paid by younger people are distributed to older people as pensions in a single period. Therefore, the presence of fewer children implies a decrease in the number of working people in the future. The per-capita pension burden on younger people becomes greater or the per-capita pension benefit for older people becomes smaller.

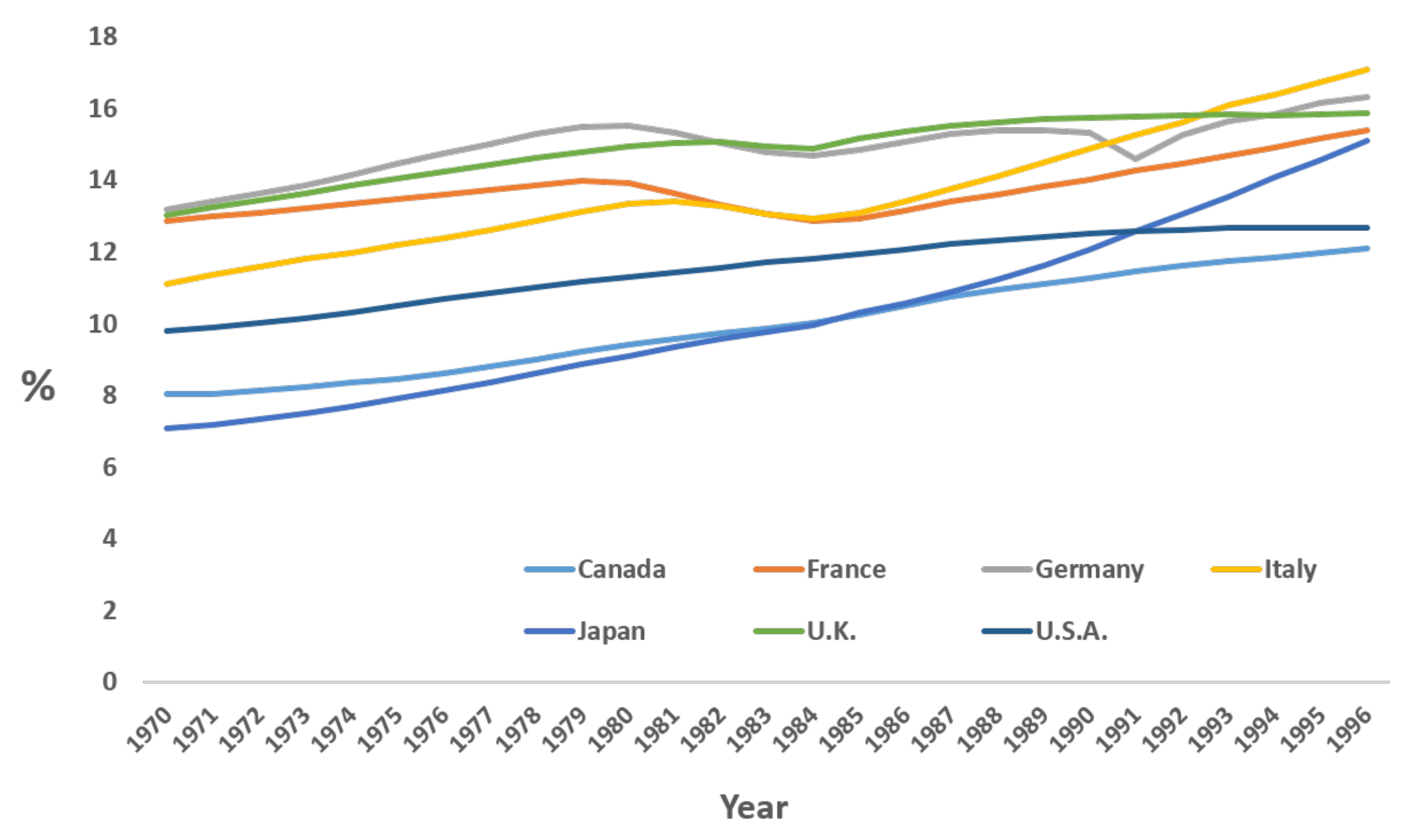
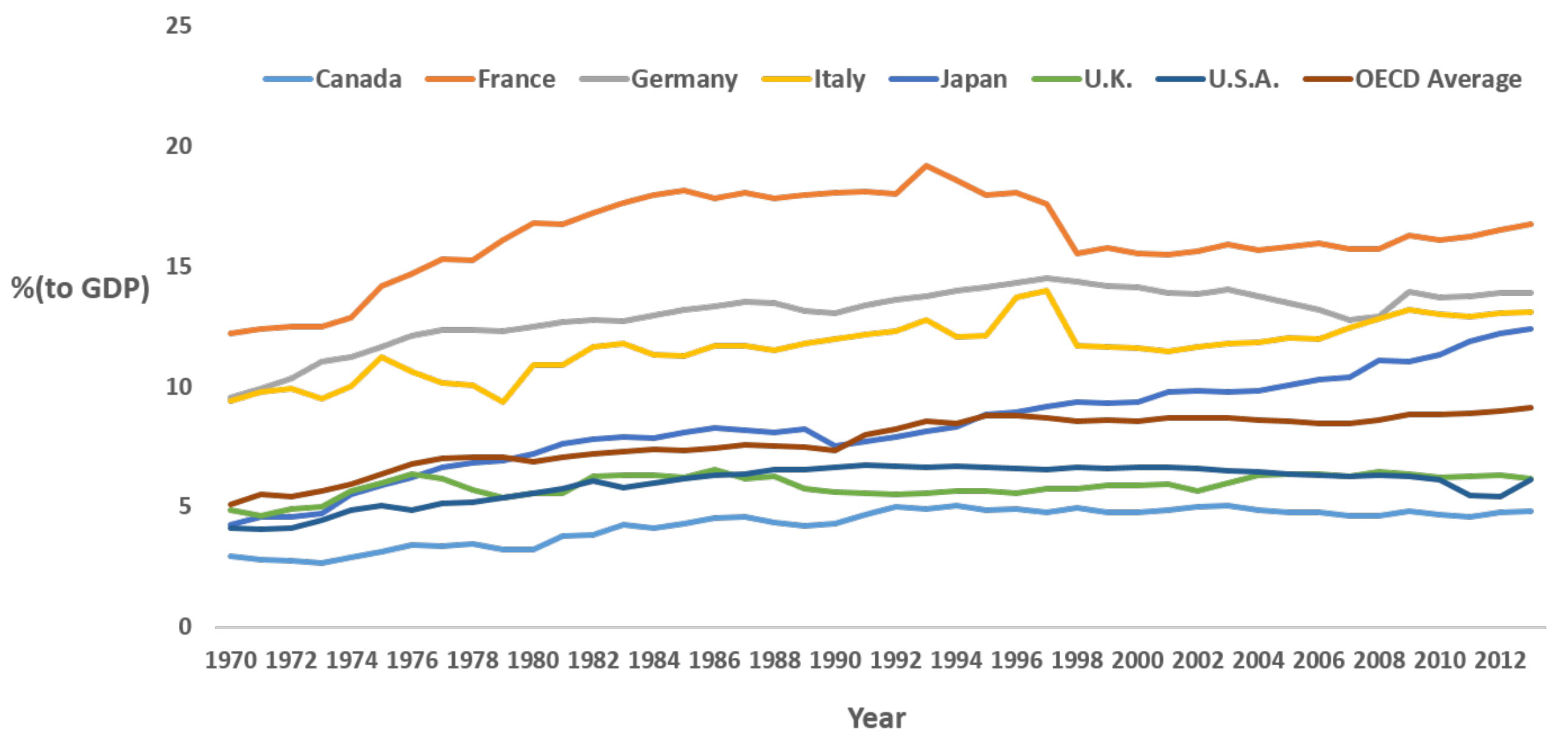
Figure 1 shows the elderly population rates of some OECD countries. As presented there, the elderly population rate continues to increase. Because of an increase in the elderly population rate, younger people must pay for their government to provide a social security system that includes programs such as public pensions and medical services. As presented in Figure 2, social security contributions continue to increase in some OECD countries. Especially, in Japan, which has the highest elderly population rate in the world, social security contributions are increasing sharply.

To maintain the pension benefit, the government must raise the pension contribution rate: The burden for younger people should be raised. However, without increasing the contribution rate, the pension benefit can be raised. Fanti and Gori (2010) report that a decrease in the contribution rate for pensions raises the pension benefit because capital accumulation is facilitated by increased saving. As shown by the overlapping-generations model, a pay-as-you-go pension reduces savings, thereby inhibiting capital accumulation. A decrease in the contribution rate increases capital accumulation. Consequently, the wage rate increases. The government can collect sufficient revenue to provide pension benefits.

Other means of increasing the pension benefit without increasing the burden for younger people might be used. A child-care policy such as a child allowance might be used. van Groezen et al. (2003) derive that a child allowance can raise fertility. An increase in fertility increases the future number of working people. Therefore, the pension sustainability is strong. Abío et al. (2004) and Fenge and Meier (2005) consider an incentive policy by which the pension benefit depends on the number of children in the household. This policy has a positive effect on population growth.

As these related studies have demonstrated, some means exist to maintain or raise pension benefits in an aging society with fewer children society. However, other policies can be considered for pensions: monetary policies. An increase in the money supply raises the Gross Domestic Product (GDP) because the interest rate decreases and the investment is facilitated in the short run. In the long run, an increase in money supply raises the inflation rate. Individuals reduce the money stock and increase the investment in capital stock, which is regarded as a portfolio re-balance effect. This paper sets an endogenous growth model with money in a utility and pay-as-you-go pension and examines how a decrease in the population growth affects the income growth rate and the inflation rate.

These analyses were conducted to examine how the pension policy affects income growth and the inflation rate in the money in the utility model to evaluate the policy mentioned above. The results obtained through this study are presented as follows. Even if the pension contribution rate increases because of an aging society, an aging society increases the income growth per capita and the inflation rate. This shows that the negative effect of an increase in the contribution rate on the income growth rate is small. Moreover, this paper presents an examination of the optimal growth rate of the money supply. The optimal growth rate of money stock changes if the government provides the pension policy. This result is intuitive because a pay-as-you-go pension changes capital accumulation. Therefore the income growth rate should be changed to raise the welfare level for all generations.

Some studies have examined monetary policy. Mino and Shibata (1995) examine how monetary policy affects the income growth rate. In addition, Chang et al. (2013) describe their examination of how monetary policy affects the income growth rate and welfare in an endogenous growth model. Heer and Maußner (2012) refer to the effects on income inequality. De Gregorio (1993) and Bhattacharya et al. (2009) derive an optimal monetary policy.

As derived herein, Corneo and Marquardt (2000) and Ono (2010) demonstrate that a pay-as-you-go pension reduces the income growth rate, too. These papers do not assess monetary policy measures.

The author of Yakita (2006) sets an endogenous growth model with monetary policy and examines how increased life expectancy affects the income growth rate and the inflation rate. Depending on the parameter conditions, the effects of increased life expectancy on the income growth rate and the inflation rate are determined. However, the present analyses present derivation of the effect of a decrease in population growth in raising both the income growth and the inflation rate. An increase in life expectancy and a decrease in population growth have the same effect in terms of an aging effect. These two effects on the inflation rate and the income growth rate differ. Bhattacharya et al. (2009) derive that the zero inflation policy is not optimal. However, the analyses presented here derive the optimal level of the growth rate of money supply can be changed by a pay-as-you-go pension policy, which is not expressed in the related literature. No report of the relevant literature describes consideration of monetary policy in a pay-as-you-go pension model.

The remainder of this paper presents the following. Section 2 explains the model setting. Section 3 derives the equilibrium. Section 4 presents examination of the respective effects of fewer children on the income growth rate and the inflation rate. Section 5 derives the optimal growth rate of the money supply to maximize social welfare. Section 6 confirms the theoretical analysis with the numerical examples. The final section concludes this paper.

2. The Model

Agents of three types exist in this model economy: households, firms, and a government. This model economy is assumed as a two-period overlapping-generations model.

2.1. Household

Individuals in the household live in two periods: young and old. In any t period, younger people and the older people exist simultaneously. Younger people supply labor inelastically according to units of time. The individuals in the household care about consumption during the younger period $c_{1t}$, consumption in the older period $c_{2t+1}$, and the real money stock per capita $m_t$. These variables are assumed to be real variables. The utility function in this paper is assumed as the following log utility function with money in utility, as assumed by Sidrauski (1967); Walsh (2010) and others

$$u_t=\alpha \ln c_{1t}+(1-\alpha )\ln m_t+\rho \ln c_{2t+1},0<\alpha <1,0<\rho <1.$$

(1)

In that equation, $\alpha$ denotes the preference for money. Small $\alpha$ shows that the preference for money is large. In addition, $\rho$ denotes the discount factor. During the young period, households supply labor to obtain a real wage income $w_t$ and to pay the burden for public pension ${\tau }_t{w}_t$, where ${\tau }_t$ denotes the contribution rate for pension.1 In the older period, older people can receive a real pension benefit $Z_{t+1}$. Then, the budget constraint in the young period is

$$s_t=(1-{\tau }_t)w_t-c_{1t}-m_t,$$

(2)

where $s_t$ denotes the real savings.2 The budget constraint in the older period is

$$c_{2t+1}=(1+r_{t+1})s_t+\frac{m_t}{1+{\pi }_{t+1}}+Z_{t+1},$$

(3)

where $1+{\pi }_{t+1}$ and $1+r_{t+1}$ respectively denote the inflation rate between t and $t+1$ period and the real interest rate.3 Then, using (2) and (3), the lifetime budget constraint can be derived as

$$c_{1t}+\frac{c_{2t+1}}{1+r_{t+1}}=(1-{\tau }_t)w_t-\left(1-\frac{1}{(1+r_{t+1})(1+{\pi }_{t+1})}\right)m_t+\frac{Z_{t+1}}{1+r_{t+1}}.$$

(4)

The optimal allocations to maximize the utility function (1) subject to budget constraint (4) are derived as

$$c_{1t}=\frac{\alpha }{1+\rho }\left((1-{\tau }_t)w_t+\frac{Z_{t+1}}{1+r_{t+1}}\right)$$

(5)

$$c_{2t+1}=\frac{\rho (1+r_{t+1})}{1+\rho }\left((1-{\tau }_t)w_t+\frac{Z_{t+1}}{1+r_{t+1}}\right)$$

(6)

$$m_t=\frac{1-\alpha }{(1+\rho )\left(1-\frac{1}{(1+r_{t+1})(1+{\pi }_{t+1})}\right)}\left((1-{\tau }_t)w_t+\frac{Z_{t+1}}{1+r_{t+1}}\right).$$

(7)

We assume $(1+r_{t+1})(1+{\pi }_{t+1})>1$ to maintain positive demand for money stock.

2.2. Firms

This model includes the assumption of the final goods production function as the following equation:

$$Y_t=K_t^{\theta }{\left(A_t{L}_t\right)}^{1-\theta },0<\theta <1,$$

(8)

where $Y_t$ denotes final goods. Final goods $Y_t$ are produced by inputting capital stock $K_t$ and labor $L_t$. $A_t$ denotes productivity. Assuming a perfectly competitive market, the real wage rate $w_t$ and the real interest rate $1+r_{t+1}$ are given respectively as

$$w_t=(1-\theta )A_t{K}_t^{\theta }{\left(A_t{L}_t\right)}^{-\theta },$$

(9)

$$1+r_{t+1}=\theta K_t^{\theta -1}{\left(A_t{L}_t\right)}^{1-\theta }.$$

(10)

The capital stock is assumed to be depreciated in a single period. This paper presents consideration of a Romer type externality as explained by Romer (1986), i.e., $A_t=a\frac{K_t}{L_t}$ is assumed. This setting is given by Grossman and Yanagawa (1993). a denotes a positive parameter. Then, the wage rate and real interest rate are given as

$$w_t=(1-\theta )a^{1-\theta }{k}_t,$$

(11)

$$1+r_t=\theta a^{1-\theta },$$

(12)

where $k_t\equiv \frac{K_t}{L_t}$.

2.3. Government

The government supplies money at the rate of $\mu (>0)$. Assuming an aggregate money stock as $M_t$, then the money stock in the subsequent period is $M_{t+1}=(1+\mu )M_t$. $m_t$ is real money stock per capita. Actually, $m_t=\frac{M_t}{P_t{N}_t}$ can be obtained where $P_t$ denotes the price level in t period and $N_t$ denotes the total population size of younger people in t period. Then, the older population size is $N_{t-1}$ in t period. Assuming the population growth rate as $\frac{N_{t+1}}{N_t}=1+n$, then the dynamics of money stock $m_t$ is

$$m_{t+1}=\frac{1+\mu }{(1+{\pi }_{t+1})(1+n)}{m}_t.$$

(13)

The government can use seigniorage when issuing currency. The analyses in this paper subsume that seigniorage is used for non-productive government expenditures.

In addition to the money supply, the government runs a pay-as-you-go pension system. The government collects revenue from younger people at contribution rate ${\tau }_t$ and uses the proceeds to provide pension benefit $Z_t$ for older people. Now, considering balanced budget constraint, $Z_t$ is assumed as presented below:

$$Z_t=ϵw_t.$$

(14)

Therein, $ϵ$ represents the replacement rate of pension. The government collects tax revenue to provide fixed pension benefit $ϵw_t$, such as a defined benefit pension. Then, the pension benefit is $N_t{\tau }_t{w}_t=N_{t-1}ϵw_t$, i.e., the following equation is reduced as4

$$\tau =\frac{ϵ}{1+n}.$$

(15)

The analyses in this paper assume that the contribution rate is constant over time. The range of the contribution rate must be $0<\frac{ϵ}{1+n}<1$ not to be negative disposable income. Then, $ϵ$ should be in $0<ϵ<1+n$. The contribution must be pulled up to provide a fixed pension benefit if low fertility brings about a decrease in the population growth rate. This paper presents consideration of the defined benefit pension. Such an increase in the burden might occur in OECD countries. In Japan, the contribution rate for pensions continues increasing because of an aging society.5

3. Equilibrium

The equilibrium of this model economy can be specified by three market equilibria of the monetary market, labor market, and capital market. Because of the inelastic labor supply, $N_t=L_t$ and (11) provide the labor market equilibrium.

The capital market equilibrium is derived as $K_{t+1}=N_t{s}_t$, i.e., $(1+n)k_{t+1}=s_t$. $s_t$ is given as $s_t=(1-\tau )w_t-c_{1t}-m_t$. Then, with (5), (7), (11), (12), (14), and (15), the dynamics of capital stock per capita $k_t$ is derived as shown below:

$$\frac{k_{t+1}}{k_t}=\frac{\left(1+\rho -\alpha -\frac{1-\alpha }{1-\frac{1}{(1+r)(1+{\pi }_{t+1})}}\right)\left(1-\frac{ϵ}{1+n}\right)(1-\theta )a^{1-\theta }}{(1+n)(1+\rho )+\frac{ϵ(1-\theta )}{\theta }\left(\alpha +\frac{1-\alpha }{1-\frac{1}{(1+r)(1+{\pi }_{t+1})}}\right)}.$$

(16)

This paper presents consideration of the equilibrium of balanced growth path. Now, when the growth rate is defined as $1+g$ ($g>0$), both the growth rate of capital stock per capita $\frac{k_{t+1}}{k_t}$ given by (16) and that of $\frac{m_{t+1}}{m_t}$ given by (13) are equal to $1+g$.6 Considering (7), (9), (14), and (15), the ratio of $\frac{m_t}{k_t}$ is given as

$$\frac{m_t}{k_t}=\frac{1-\alpha }{(1+\rho )\left(1-\frac{(1+n)}{(1+r)(1+{\pi }_{t+1})}\right)}\left(\left(1-\frac{ϵ}{1+n}\right)(1-\theta )a^{1-\theta }+\frac{ϵ(1-\theta )(1+g)}{\theta }\right).$$

(17)

In the balanced growth path with constant inflation rate $\pi$, $\frac{m_t}{k_t}$ is also constant. Then, the growth rate of $\frac{m_{t+1}}{m_t}$ is $1+g$.

4. Society with Fewer Children

This section presents an examination of how fewer children, i.e., a decrease in population growth rate affects the income growth rate and inflation rate. The income growth rate $1+g$ and the inflation rate $\pi$ in balanced growth path are given as

$$1+g=\frac{\left(1+\rho -\alpha -\frac{1-\alpha }{1-\frac{1}{(1+r)(1+\pi )}}\right)\left(1-\frac{ϵ}{1+n}\right)(1-\theta )a^{1-\theta }}{(1+n)(1+\rho )+\frac{ϵ(1-\theta )}{\theta }\left(\alpha +\frac{1-\alpha }{1-\frac{1}{(1+r)(1+\pi )}}\right)},$$

(18)

$$1+g=\frac{1+\mu }{(1+\pi )(1+n)}.$$

(19)

Total differentiation of (18) and (19) by $g,\pi$, and n at the balanced growth path reduces the following equations as7

$$\begin{array}{c}\hfill \left(\begin{array}{cc}{\varphi }_1& -{\varphi }_2\\ 1& \frac{1+g}{1+\pi }\end{array}\right)\left(\begin{array}{c}\frac{dg}{dn}\\ \frac{d\pi }{dn}\end{array}\right)=\left(\begin{array}{c}{\varphi }_3\\ -\frac{1+g}{1+n}\end{array}\right),\end{array}$$

where

$$\begin{array}{lll}\hfill {\varphi }_1& =& (1+n)(1+\rho )+\frac{ϵ(1-\theta )}{\theta }\left(\alpha +\frac{1-\alpha }{1-\frac{1}{(1+r)(1+\pi )}}\right)>0,\hfill \\ \hfill {\varphi }_2& =& \frac{1-\alpha }{{\left(1-\frac{1}{(1+r)(1+\pi )}\right)}^2}\frac{1-\theta }{(1+r){(1+\pi )}^2}\left(\frac{1+g}{\theta }+a^{1-\theta }\left(1-\frac{ϵ}{1+n}\right)\right)>0,\hfill \\ \hfill {\varphi }_3& =& \left(1+\rho -\alpha -\frac{1-\alpha }{1-\frac{1}{(1+r)(1+\pi )}}\right)\frac{ϵ(1-\theta )a^{1-\theta }}{{(1+n)}^2}-(1+\rho )(1+g).\hfill \end{array}$$

The effects of decreased population growth (fewer children) on the income growth rate and inflation rate in the balanced growth path are

$$\frac{dg}{dn}=\frac{\frac{1+g}{1+\pi }{\varphi }_3-\frac{1+g}{1+n}{\varphi }_2}{det},$$

(20)

$$\frac{d\pi }{dn}=\frac{-\frac{1+g}{1+n}{\varphi }_1-{\varphi }_3}{det}<0,$$

(21)

where $det=\frac{1+g}{1+\pi }{\varphi }_1+{\varphi }_2>0$. The first term of ${\varphi }_3$ presents the positive effect of an increase in population growth on income growth. An increase in population growth reduces the burden of pensions for younger people. Then, the younger people can increase savings. Therefore, an increase in capital accumulation facilitates income growth in an increase in population growth n. However, the second term of ${\varphi }_3$ presents a negative effect of an increase in population growth on the income growth. An increase in population growth makes the population size large and reduces the capital stock per capita. Consequently, the income growth per capita $1+g$ is reduced. The positive effect on income growth shows the effect of a decrease in pension burdens. Without $ϵ$, an increase in population growth brings about negative effects on income growth.

With $ϵ=0$, it is obtained that ${\varphi }_3<0$ and $\frac{dg}{dn}<0$. However, with $ϵ=1+n$, it is obtained that ${\varphi }_3>0$ and $\frac{dg}{dn}=0$ because of $1+g=0$. Therefore, defining $F\left(ϵ\right)=\frac{1+g}{1+\pi }{\varphi }_3-\frac{1+g}{1+n}{\varphi }_2=0$, and assuming that $F\left(ϵ\right)$ is a monotonically increasing function of $ϵ$, $\frac{dg}{dϵ}$ is always negative in $0<ϵ<1+n$. The proof above reduces to the following proposition.

Proposition 1.

A decrease in population growth raises both the income growth rate and the inflation rate.

A decrease in population growth has the effect of increasing the capital stock per capita. Such a result is derived in related studies such as that of the Solow (1956) model. However, this paper includes discussion of two other effects. One effect is the pension burden. A decrease in population growth raises the pension burden for younger people because people of working generations decrease. The burden per capita must be pulled up when the government makes the level of pension benefit for older people constant if the working generations of people decrease. The other effect is the effect via the demand for money stock. As shown by ${\varphi }_2$, a decrease in population growth has the effect of an increase in the inflation rate.8 This effect decreases money demand and then savings to bring about increased capital accumulation. In addition to this effect, a decrease in population growth raises the capital stock per capita and then raises the income growth rate. This paper presents derivation that the positive effect on the income growth is greater than the negative effect brought about by an increase in the contribution rate.

Yakita (2006) examines life expectancy effects on the income growth rate and the inflation rate. An increase in life expectancy and a decrease in the population growth are substantially equivalent in terms of processes of an aging society with fewer children.9 Some results of this paper are same with Yakita (2006). A decrease in population growth, which brings about fewer children, increases the contribution rate to pensions. This decreases the capital accumulation. Also, the income growth per capita decreases. However, a decrease in population growth raises income growth directly because the capital stock per capita increases. This paper presents derivation that this effect is greater than the effect of an increase in contribution rate.

5. Monetary Policy

This section presents an examination of how monetary policy affects the income growth and inflation rate. Moreover, the following subsection presents an examination of welfare policy. Concretely, this paper presents an examination of how an increase in the growth rate of money stock $\mu$ affects social welfare.

5.1. Effect of Monetary Policy

This subsection presents effects of monetary policy on the income growth rate and the inflation rate. Total differentiation of (13) and (16) by $g,\pi$, and $\mu$ presents the following signs:

$$\frac{dg}{d\mu }=\frac{{\varphi }_2\frac{1+g}{1+\mu }}{det}>0,$$

(22)

$$\frac{d\pi }{d\mu }=\frac{{\varphi }_1\frac{1+g}{1+\mu }}{det}>0.$$

(23)

These results are intuitive. An increase in the money supply increases the inflation rate based on the ‘quantity theory of money’. An increase in the inflation rate decreases the demand for money stock. Then, households increase savings or investment for goods. Therefore, capital accumulation is facilitated.

5.2. Monetary Policy and Welfare

This subsection presents examination of whether an increase in the rate of supply can pull up social welfare or not. This paper assumes the following social welfare function as10

$$\begin{array}{ccc}\hfill W_t& =& \sum _{s=t}^{\infty }{\delta }^{s-t}{u}_s\hfill \\ & =& \frac{1+\rho }{1-\delta }\ln c_{1t}+\frac{\delta (1+\rho )}{{(1-\delta )}^2}\ln (1+g)+\frac{1-\alpha }{1-\delta }\ln \frac{1}{1-\frac{1}{(1+r)(1+\pi )}}\hfill \\ & +& \frac{1-\alpha }{1-\delta }\ln \frac{1-\alpha }{\alpha }+\frac{\rho }{1-\delta }\ln \frac{\rho (1+r)}{\alpha }.\hfill \end{array}$$

(24)

Total differentiation with respect to $W_t,g,\pi ,\mu$, we obtain $\frac{d{W}_t}{d\mu }$ as follows:

$$\begin{array}{ccc}\hfill \frac{d{W}_t}{d\mu }& =& \left(\frac{1+\rho }{1-\delta }\frac{1}{c_{1t}}\frac{d{c}_{1t}}{dg}+\frac{\delta (1+\rho )}{{(1-\delta )}^2}\frac{1}{1+g}\right)\frac{dg}{d\mu }-\frac{1-\alpha }{1-\delta }\frac{\frac{1}{(1+r){(1+\pi )}^2}}{1-\frac{1}{(1+r)(1+\pi )}}\frac{d\pi }{d\mu }\hfill \\ & =& \frac{\frac{1+g}{1+\mu }}{det}\left(\left(\frac{1+\rho }{1-\delta }\frac{1}{c_{1t}}\frac{d{c}_{1t}}{dg}+\frac{\delta (1+\rho )}{{(1-\delta )}^2}\frac{1}{1+g}\right){\varphi }_2-\frac{1-\alpha }{1-\delta }\frac{\frac{1}{(1+r){(1+\pi )}^2}}{1-\frac{1}{(1+r)(1+\pi )}}{\varphi }_1\right).\hfill \end{array}$$

(25)

The sign of $\frac{d{W}_t}{d\mu }$ is ambiguous. Without $ϵ$ and defining the parenthesis of (25) as $G\left(ϵ\right)$, the numerator of (25) is derived as11

$$G\left(0\right)=\left(\frac{\delta (1+\rho )}{{(1-\delta )}^2}\frac{1}{1+g}\right){\varphi }_2-\frac{\frac{1-\alpha }{(1+r){(1+\pi )}^2}}{1-\frac{1}{(1+r)(1+\pi )}}{\varphi }_1.$$

(26)

It is assumed that the optimal monetary policy is adopted at $ϵ=0$. Then, with $ϵ>0$, $G\left(ϵ\right)$ is given as

$$G\left(ϵ\right)=\left(\frac{1+\rho }{1-\delta }\frac{1}{c_{1t}}\frac{d{c}_{1t}}{dg}+\frac{\delta (1+\rho )}{{(1-\delta )}^2}\frac{1}{1+g}\right){\varphi }_2-\frac{\frac{1-\alpha }{(1+r){(1+\pi )}^2}}{1-\frac{1}{(1+r)(1+\pi )}}{\varphi }_1\ne 0.$$

(27)

Because of $\frac{1+\rho }{1-\delta }\frac{1}{c_{1t}}\frac{d{c}_{1t}}{dg}>0$ and because $ϵ$ reduces the income growth rate $1+g$, $G\left(ϵ\right)$ is not zero under the monetary policy such that $\frac{d{W}_t}{d\mu }=0$ at $ϵ=0$.12 That is, the money supply growth must be changed from $\frac{d{W}_t}{d\mu }\ne 0$ to $\frac{d{W}_t}{d\mu }=0$. Then, the following proposition can be established.

Proposition 2.

The government changes the growth rate of money to maximize social welfare if the government provides a pension policy.

Zero inflation policy is examined by Bhattacharya et al. (2009), who derive that zero inflation policy is not optimal because it does not maximize social welfare. This paper presents derivation that if the pension policy exists, the optimal growth rate of money supply increases for any inflation rate including zero inflation: even if the zero inflation policy should be adopted to maximize social welfare because of pension policy, the zero inflation policy is an inappropriate policy.13 Why does pension policy change the optimal growth rate of money? For instance, this paper explains the case of an increase in the optimal growth rate of money. A pay-as-you-go pension policy decreases capital accumulation, which reduces the income growth rate. A decrease in the income growth rate reduces the welfare of future generations. Therefore, an increase in the growth rate of the money supply must raise income growth. The households increase savings as real savings and decrease money as a means of saving, which promotes capital accumulation if the inflation rate rises. However, there is the negative effect of the inflation with promoting capital accumulation on the welfare. With small inflation rate ${\pi }_{t+1}$, the demand for real money stock $m_t$ is low as shown by (7). The utility from the demand for the money is low, too Therefore, too large level of inflation is not desirable.

6. Numerical Examples

This section examines the equilibrium with the numerical examples. The parameter setting are shown in

Table 1. Parameter setting.

$\alpha$	0.95
$\rho$	0.3
$\theta$	0.3
a	15
$1+n$	1
$1+\mu$	1.8

.

$\rho =0.3$ denotes the discount factor for the consumption in the old period. In developing countries, no population growth exists in the recent years and $n=0$. These parameters are based on de la Croix and Doepke (2003). $\theta$ denotes the capital income share and $\theta =0.3$ is set, considering the developed countries. $1+\mu =1.8$ is set. Then, the annual inflation rate is about $2\%$. To set $1+g=1$ for standardized, $\alpha =0.95$ and $a=15$ are set. Then, the interest rate $1+r=1.997$ are derived. This value means the about $2\%$ as the annual interest rate, which is consistent with the recent 30 years situation in Japan.

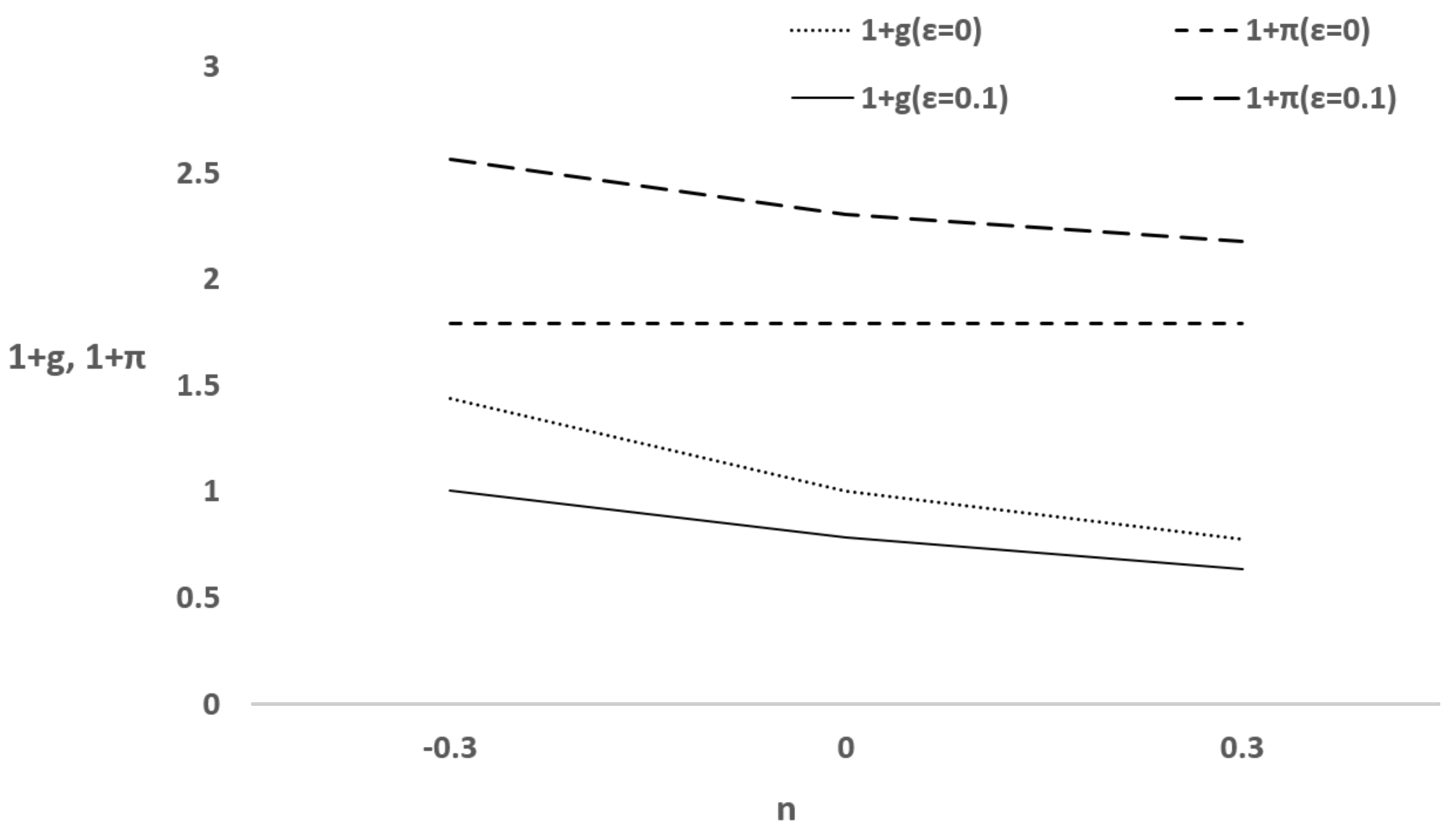
Figure 3 shows the results of numerical examples, which are consistent with the theoretical analysis shown by Proposition 1. An aging society brought about by a decrease in population growth raises the income growth rate $1+g$ and inflation rate $1+\pi$ in the case of $ϵ=0.1$. The results obtained by the theoretical analysis and the numerical example can explain the empirical results. Shirakawa (2012) shows the positive correlation between the population growth and inflation rate. This result is not same with the result obtained by this paper. However, MacMillan and Baesel (1990) shows the negative correlation between the population growth and inflation rate. This result is consistent with the results obtained by this paper.

This paper considers if the money supply rate changes, the correlation between the population growth and inflation rate changes. A decrease in money supply rate reduces the inflation rate as shown by this paper. Therefore, even if a decrease in the population growth rate raises the inflation rate, a decrease in money supply rate reduces the inflation rate and we can show the positive correlation between the population growth rate and the inflation rate thanks to money supply rate.

7. Conclusions

This paper presents an examination of how a decrease in population growth, as shown in an aging society with fewer children, affects income growth rate and the inflation rate in a balanced growth path in a model with money in utility and with a pay-as-you-go pension. An aging society with fewer children raises both the income growth rate and the inflation rate. The result obtained by this paper is same with the empirical research derived by MacMillan and Baesel (1990), which derives the negative correlation between population growth and inflation. On the other hand, Shirakawa (2012) shows the positive correlation. However, considering the money supply policy, the results obtained by this paper is not contradict with the empirical results obtained by Shirakawa (2012).

Public pensions have a negative effect on capital accumulation, as shown by numerous related studies. Therefore, the government should change a money supply to change capital accumulation and thereby maximize social welfare. This paper presents a derivation showing that optimal monetary policy depends on the pension policy.

Moreover, this paper demonstrates how an aging society should be considered. We can consider two cases: one for a decrease in population growth and the other for an increase in life expectancy as an aging society. These two cases are substantially equivalent to an aging society. However, the effects on income growth might be different between the two cases because of the direct effects on the inflation rate.