Labor Costs and Foreign Direct Investment: A Panel VAR Approach
Abstract
:1. Introduction
2. Data and Methodology
2.1. Data
2.2. Methodology
3. Empirical Results
| Fixed Effect | AB One Step System GMM | AB Two Step System GMM | Fixed Effect | AB One Step System GMM | AB Two Step System GMM | |
|---|---|---|---|---|---|---|
| Dependent Variable | 1 | 2 | 3 | 4 | 5 | 6 |
| fdpva | fdpva | fdpva | ulc | ulc | ulc | |
| L.fdpva | −0.246 ** (0.100) | 0.469 *** (0.146) | 0.530 *** (0.163) | 0.0156 ** (0.00737) | 0.0148 ** (0.00581) | 0.00962 ** (0.00479) |
| L2.fdpva | 0.0660 (0.101) | 0.265 ** (0.111) | 0.184 (0.134) | 0.000670 (0.00659) | 0.0113 * (0.00648) | 0.00571 (0.00653) |
| L.ulc | −0.938 (2.294) | 0.464 (3.915) | 1.195 (2.937) | 0.395 *** (0.0973) | 0.699 *** (0.219) | 0.703 * (0.373) |
| L2.ulc | 1.928 (1.973) | −0.112 (3.343) | −0.807 (2.483) | 0.348 ** (0.160) | 0.119 (0.184) | 0.123 (0.310) |
| Hansen Test | 0.648 | 0.648 | 0.476 | 0.476 | ||
| Difference Hansen Test | 0.307 | 0.307 | 0.563 | 0.563 | ||
| AB Test | 0.444 | 0.990 | 0.843 | 0.861 | ||
| Wald Test ulc | 0.108 | 0.577 | 0.743 | |||
| Wald Test fdpva | 0.038 | 0.034 | 0.089 |
| Fixed Effect | AB One Step System GMM | AB Two Step System GMM | Fixed Effect | AB One Step System GMM | AB Two Step System GMM | |
|---|---|---|---|---|---|---|
| Dependent Variable | 1 fdpva | 2 fdpva | 3 fdpva | 4 cml | 5 cml | 6 cml |
| L.fdpva | −0.221 ** (0.100) | −0.206 (0.295) | −0.265 (0.380) | −0.000461 (0.00337) | 0.00477 (0.00528) | 0.00443 (0.00726) |
| L2.fdpva | 0.086 (0.099) | −0.141 (0.266) | −0.147 (0.325) | 0.00107 (0.00343) | 0.00528 (0.00471) | 0.00177 (0.00599) |
| L.cml | 0.881 (0.295) | −0.774 (3.223) | −0.977 (3.655) | 0.948 *** (0.0912) | 0.942 *** (0.135) | 0.968 *** (0.172) |
| L2.cml | 0.561 (2.501) | 0.634 (3.225) | 0.847 (3.638) | 0.0639 (0.0905) | 0.0475 (0.0998) | 0.0695 (0.129) |
| Hansen Test | 0.266 | 0.266 | 0.279 | 0.279 | ||
| Difference Hansen Test | 0.491 | 0.491 | 0.356 | 0.356 | ||
| AB Test | 0.994 | 0.923 | 0.104 | 0.134 | ||
| Wald Test cml | 0.413 | 0.130 | 0.255 | |||
| Wald Test fdpva | 0.936 | 0.534 | 0.812 |
| Fixed Effect | AB One Step System GMM | AB Two Step System GMM | Fixed Effect | AB One Step System GMM | AB Two Step System GMM | |
|---|---|---|---|---|---|---|
| Dependent Variable | 1 | 2 | 3 | 4 | 5 | 6 |
| fdpva | fdpva | fdpva | ulc | ulc | ulc | |
| L.fdpva | 0.813 *** (0.0818) | 0.796 *** (0.145) | 0.908 *** (0.141) | −0.00713 (0.00605) | −0.00245 (0.0187) | −0.00139 (0.0253) |
| L2.fdpva | 0.000441 (0.0757) | 0.108 (0.142) | 0.0163 (0.0759) | 0.00414 (0.00561) | 0.00138 (0.0260) | 0.0007 (0.0292) |
| L.ulc | −0.175 (1.100) | −1.197 (0.760) | 0.0319 (1.129) | 0.996 *** (0.0806) | 0.859 *** (0.103) | 0.852 *** (0.130) |
| L2.ulc | 0.696 (1.007) | 0.464 (0.716) | −0.530 (1.051) | −0.186 ** (0.0745) | 0.128 (0.0903) | 0.133 (0.105) |
| Hansen Test | 0.753 | 0.753 | 0.358 | 0.358 | ||
| Difference Hansen Test | 0.450 | 0.450 | 0.780 | 0.780 | ||
| AB Test | 0.939 | 0.646 | 0.363 | 0.392 | ||
| Wald Test ulc | 0.537 | 0.113 | 0.504 | 0.989 | 0.997 | |
| Wald Test fdpva | 0.450 | 0.989 | 0.997 |
| Fixed Effect | AB One Step System GMM | AB Two Step System GMM | Fixed Effect | AB One Step System GMM | AB Two Step System GMM | |
|---|---|---|---|---|---|---|
| Dependent Variable | 1 | 2 | 3 | 4 | 5 | 6 |
| fdpva | fdpva | fdpva | cml | cml | cml | |
| L.fdpva | 0.796 *** (0.0827) | 0.685 (0.590) | 0.491 (0.352) | −0.000628 (0.00527) | 0.00297 (0.00713) | 0.00409 (0.00790) |
| L2.fdpva | 0.00272 (0.0758) | −0.0382 (0.181) | 0.00425 (0.113) | −0.00135 (0.00484) | 0.00163 (0.00644) | 0.00462 (0.00725) |
| L.cml | −0.995 (1.373) | 1.967 (5.421) | 0.614 (5.116) | 0.826 *** (0.0824) | 0.979 *** (0.143) | 0.877 *** (0.192) |
| L2.cml | 1.240 (1.436) | −1.835 (4.701) | −0.315 (4.607) | 0.169 * (0.0854) | 0.00974 (0.131) | 0.0790 (0.189) |
| Hansen Test | 0.486 | 0.486 | 0.380 | 0.380 | ||
| Difference Hansen Test | 0.683 | 0.683 | 0.857 | 0.857 | ||
| AB Test | 0.364 | 0.608 | 0.505 | 0.749 | ||
| Wald Test | 0.616 | 0.913 | 0.903 | 0.762 | 0.834 | 0.160 |
4. Conclusions
| ULC to FDI | FDI to ULC | CML to FDI | FDI to CML | |
|---|---|---|---|---|
| All sectors | Negative | None | Positive | Positive |
| Manufacturing | Negative | None | Positive | Positive |
| Finance | Negative | None | None | None |
| Industry | None | None | None | None |
| Construction | None | Positive | None | None |
Author Contributions
Conflicts of Interest
Appendix A
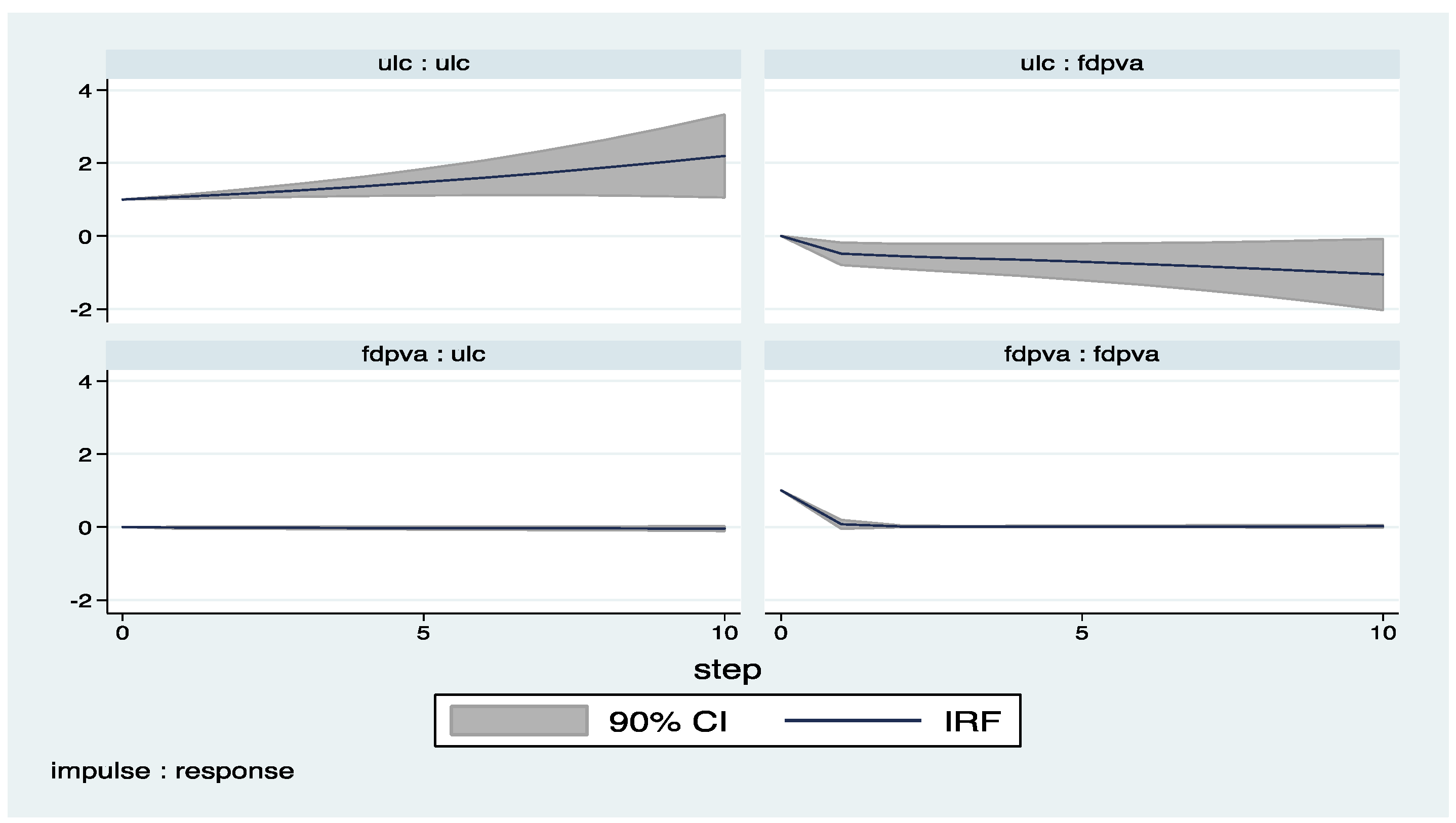
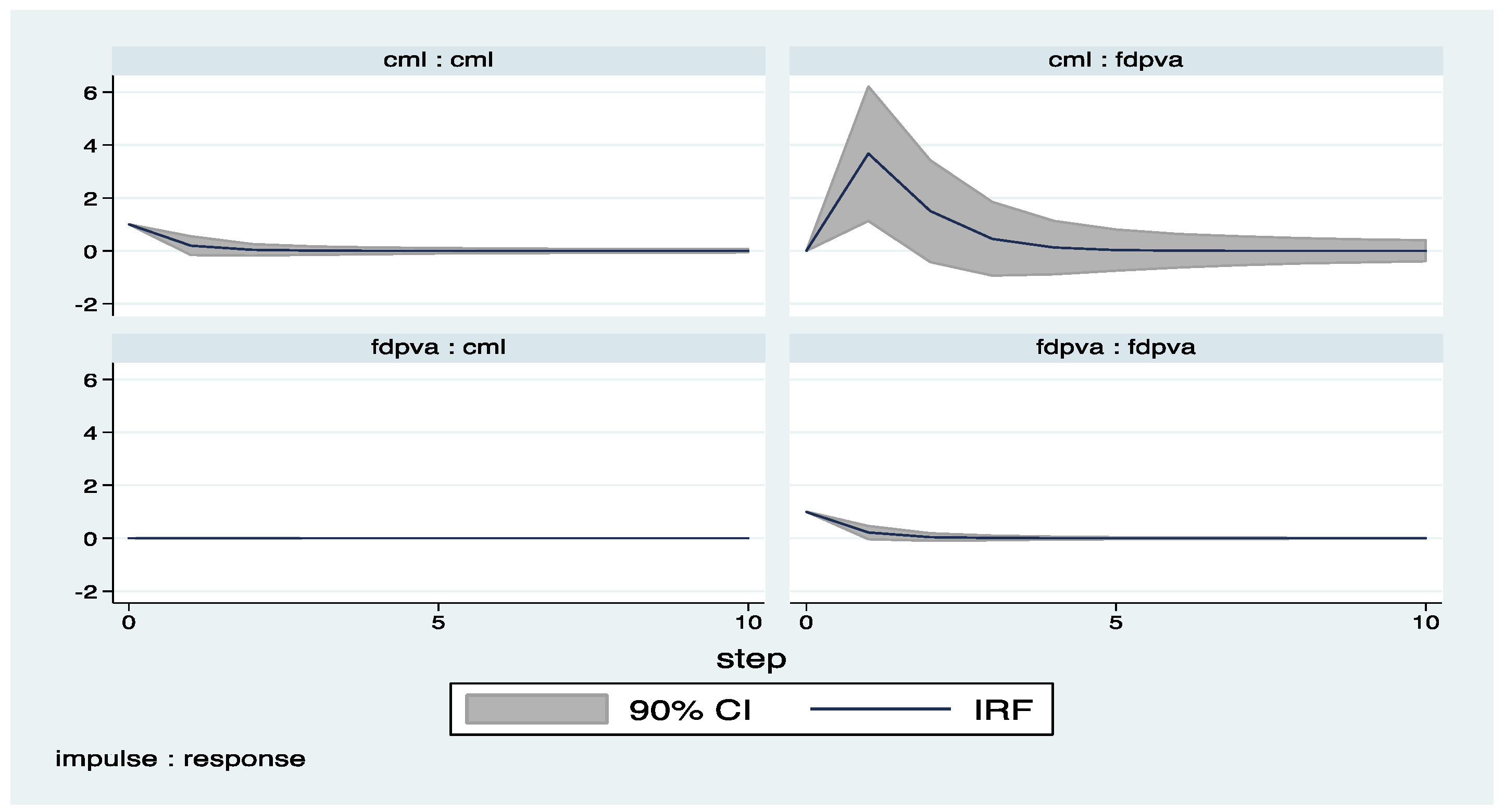
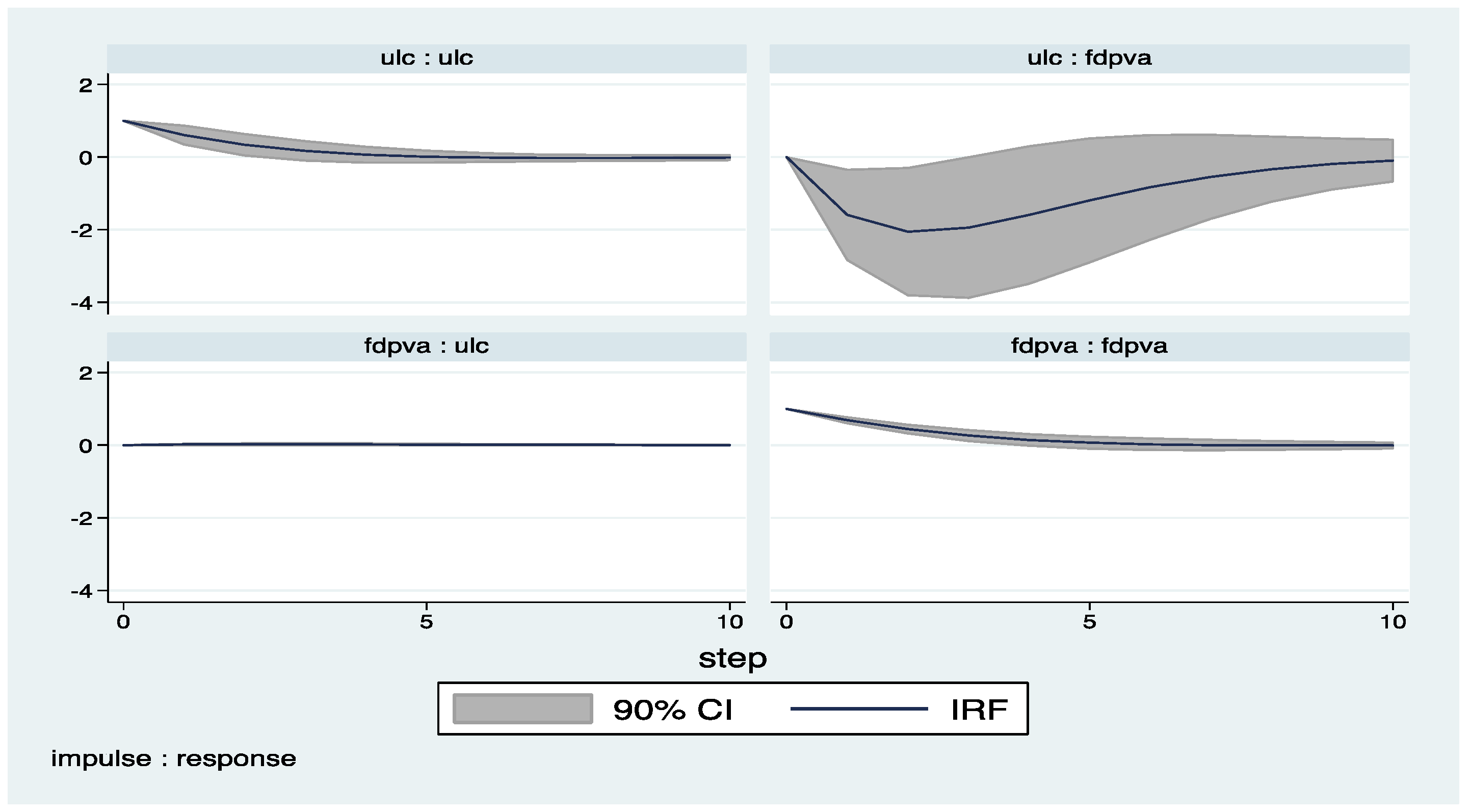
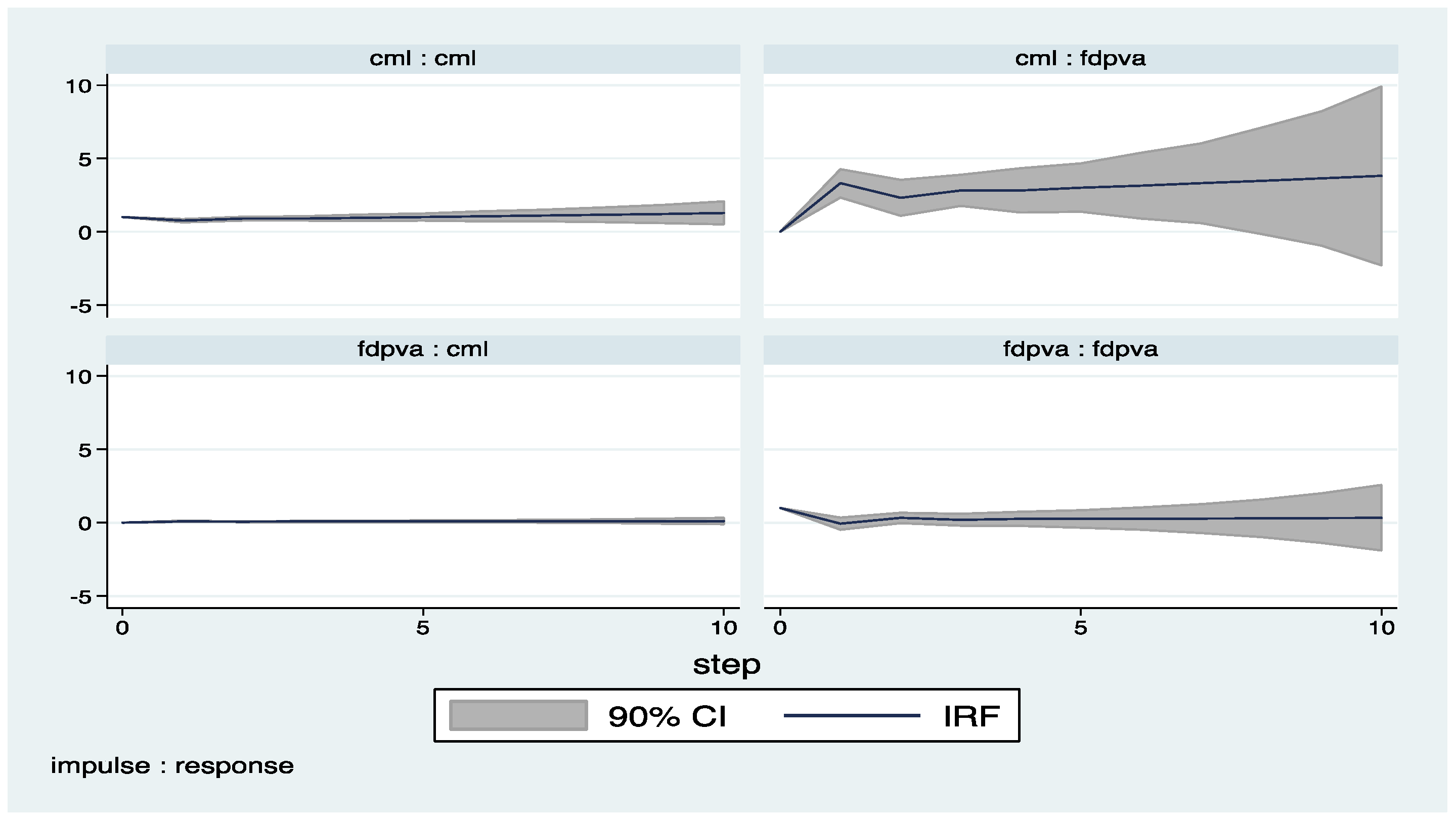
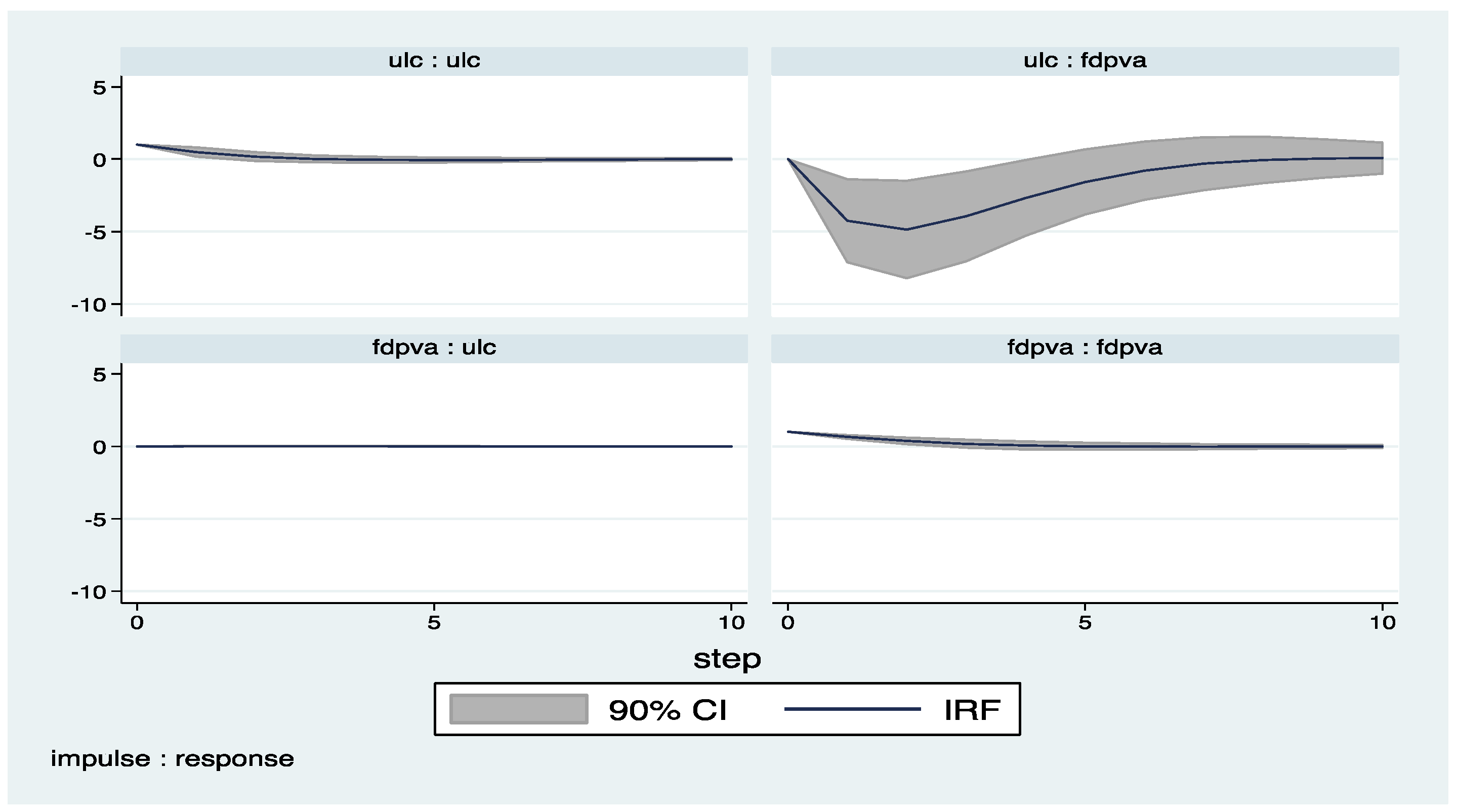
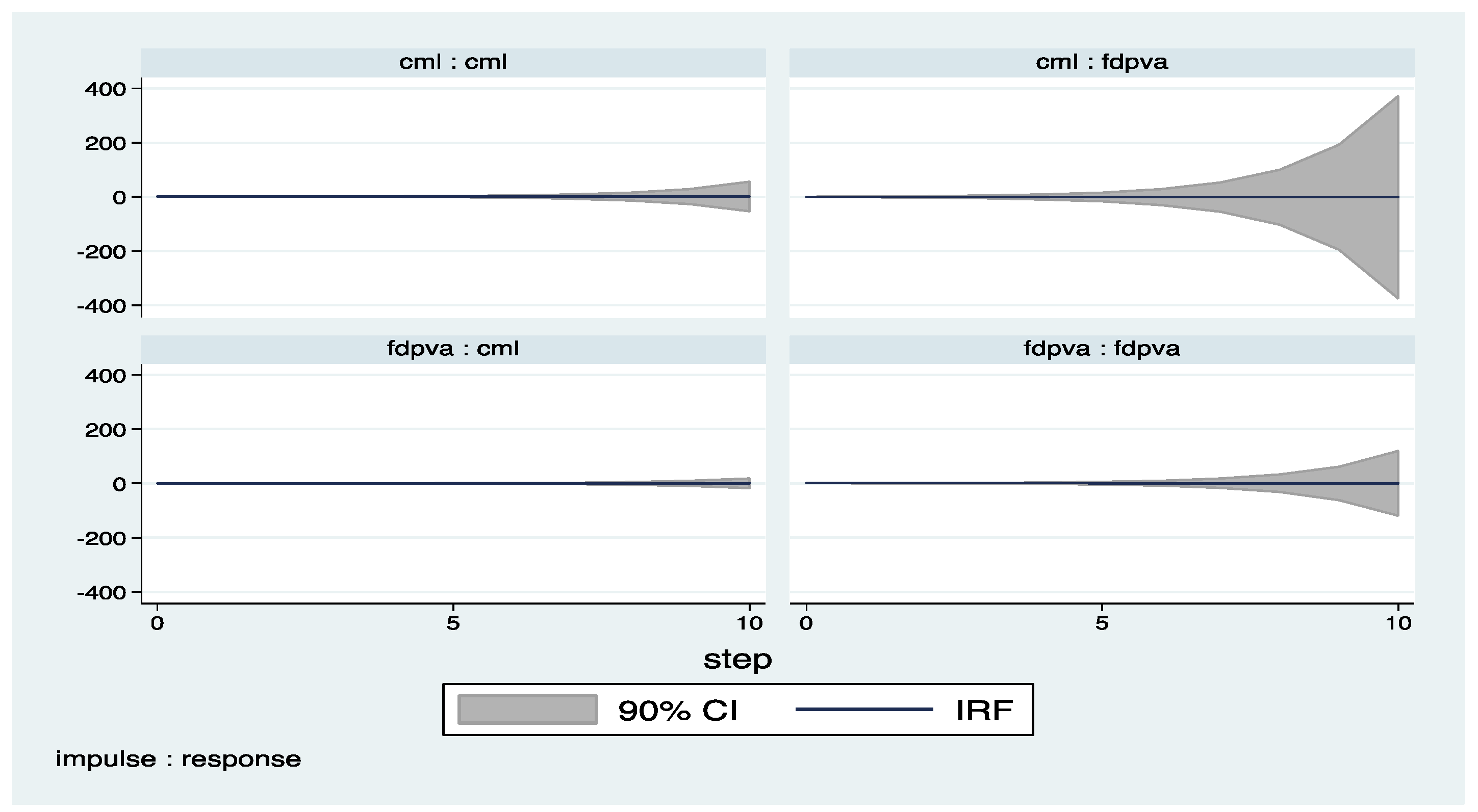
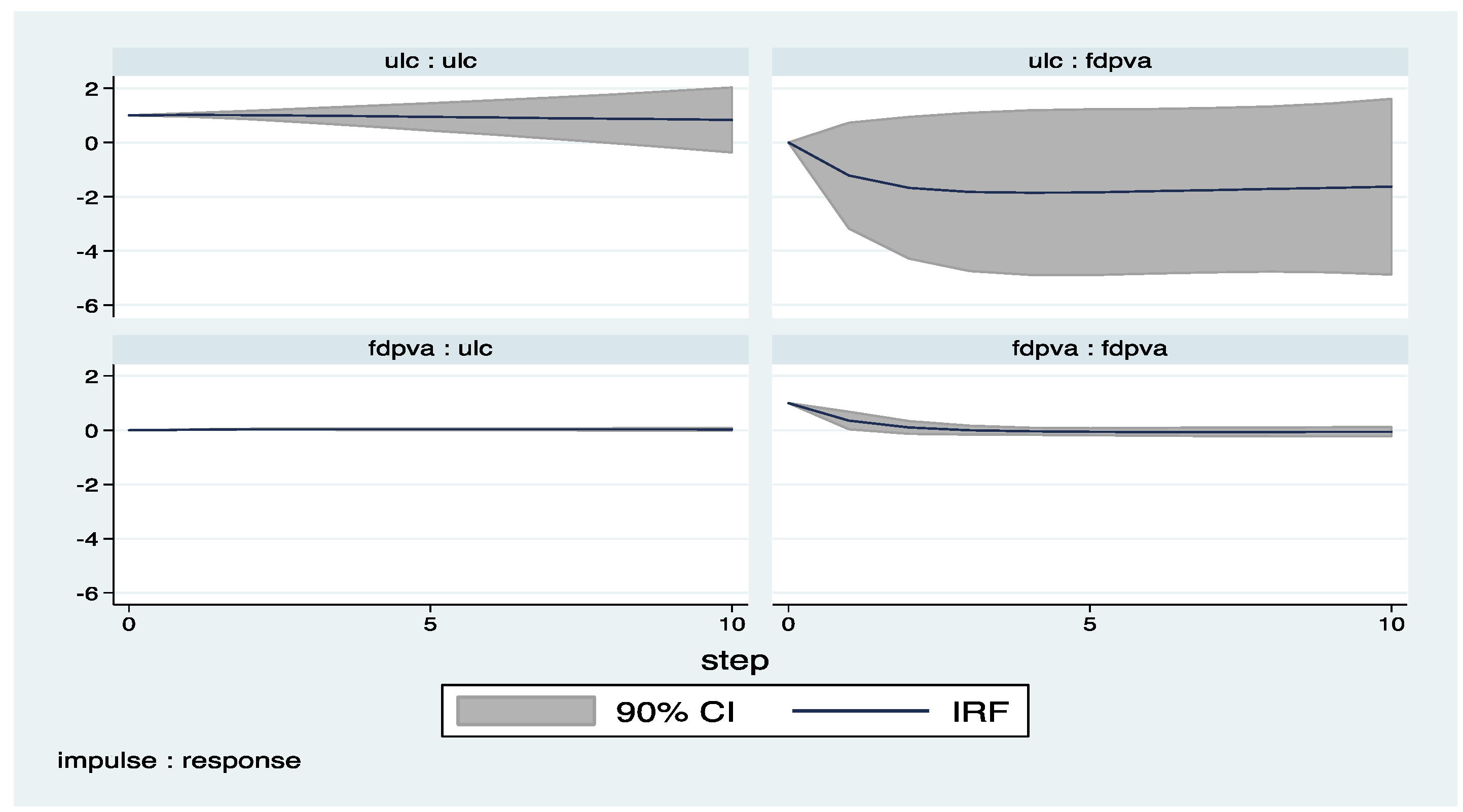
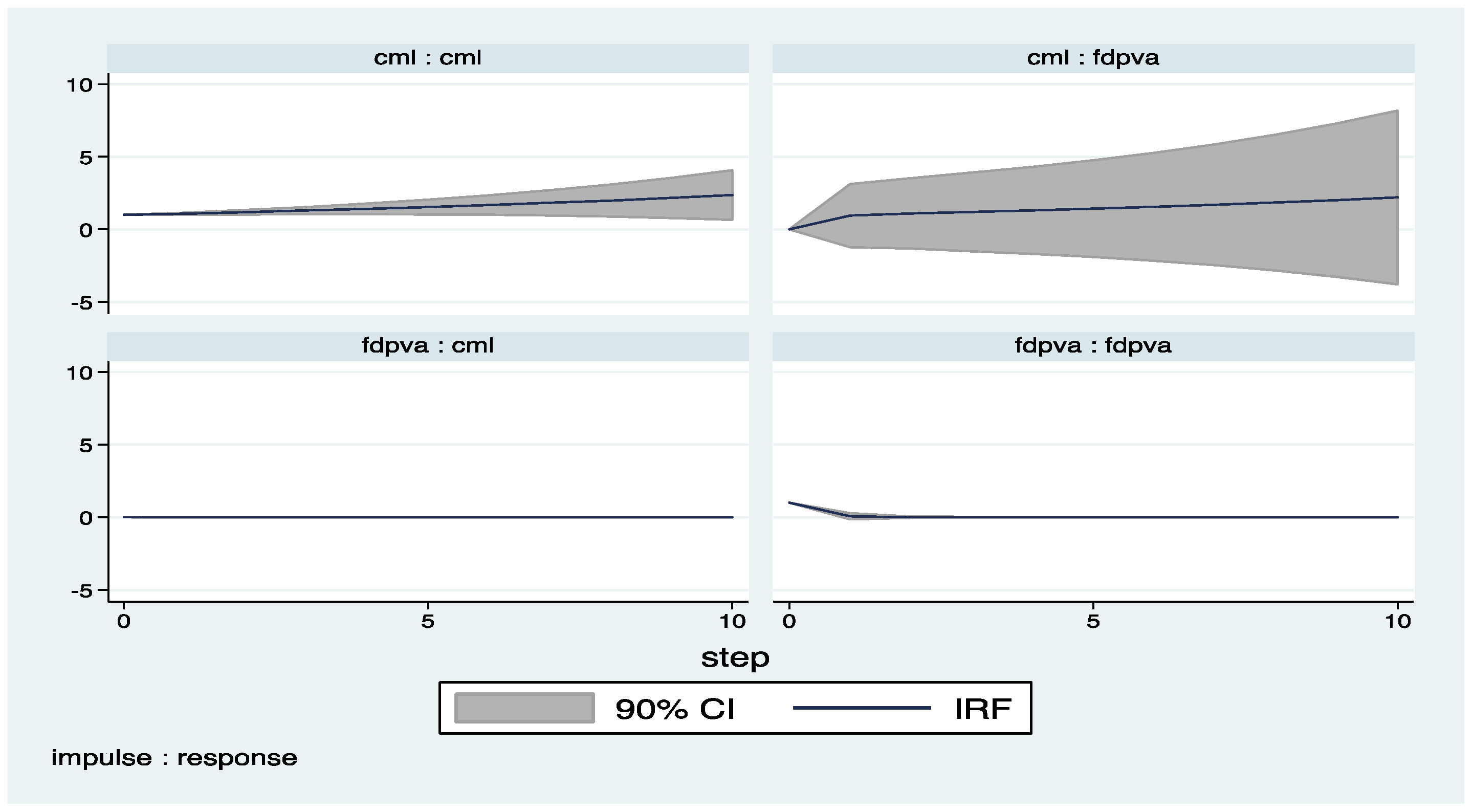
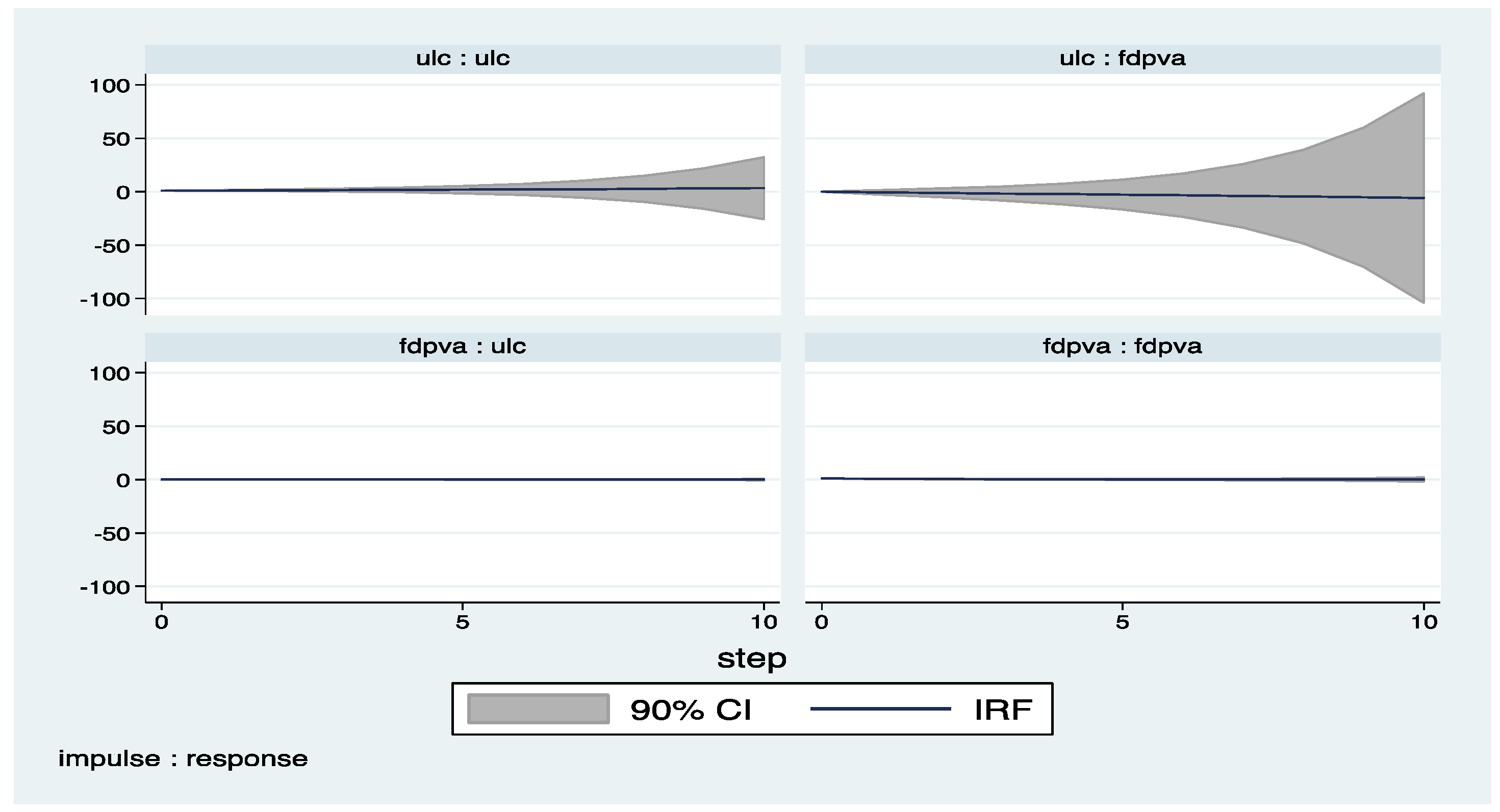
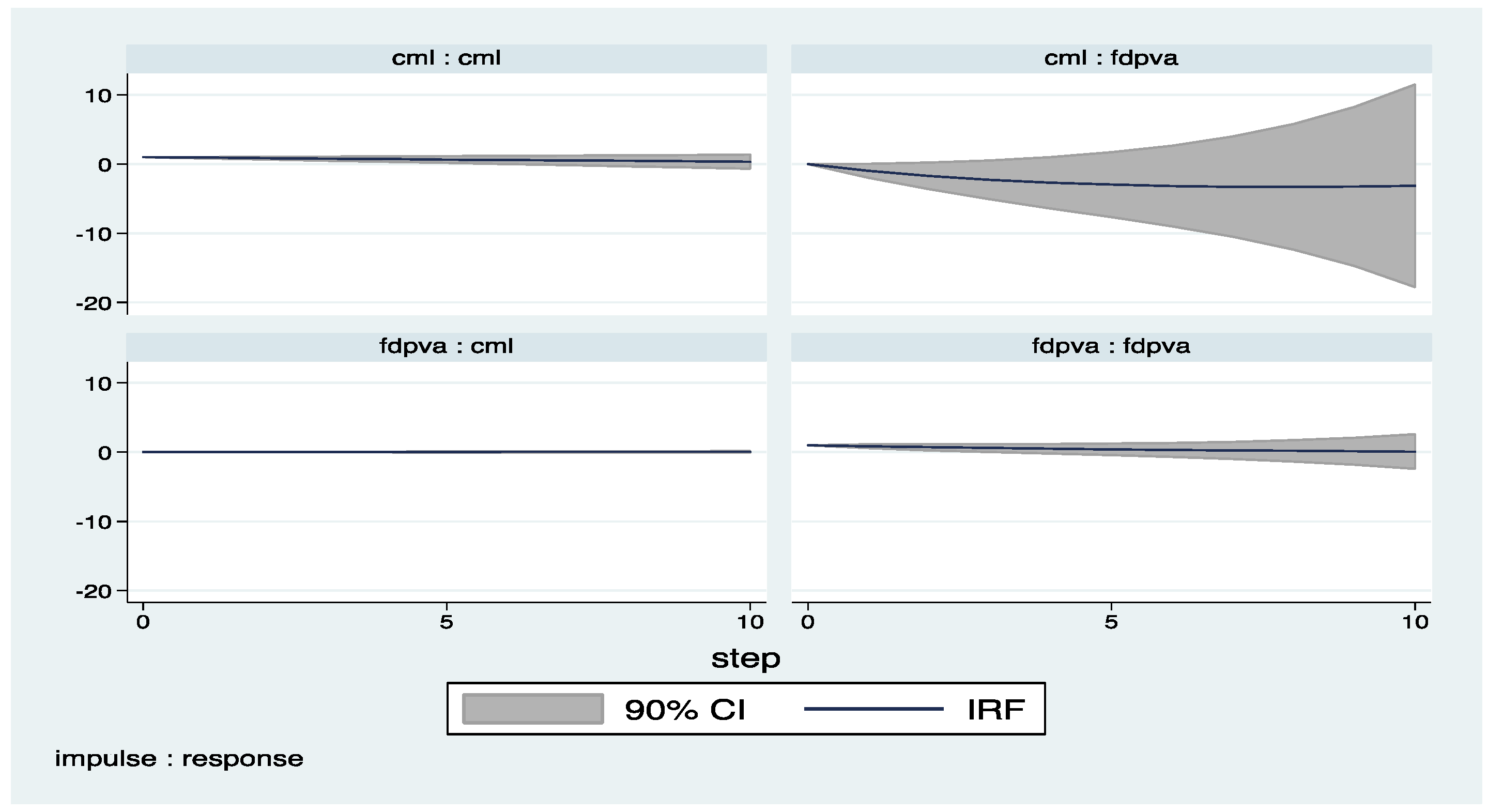
Appendix B (Exluding 2008–2009)
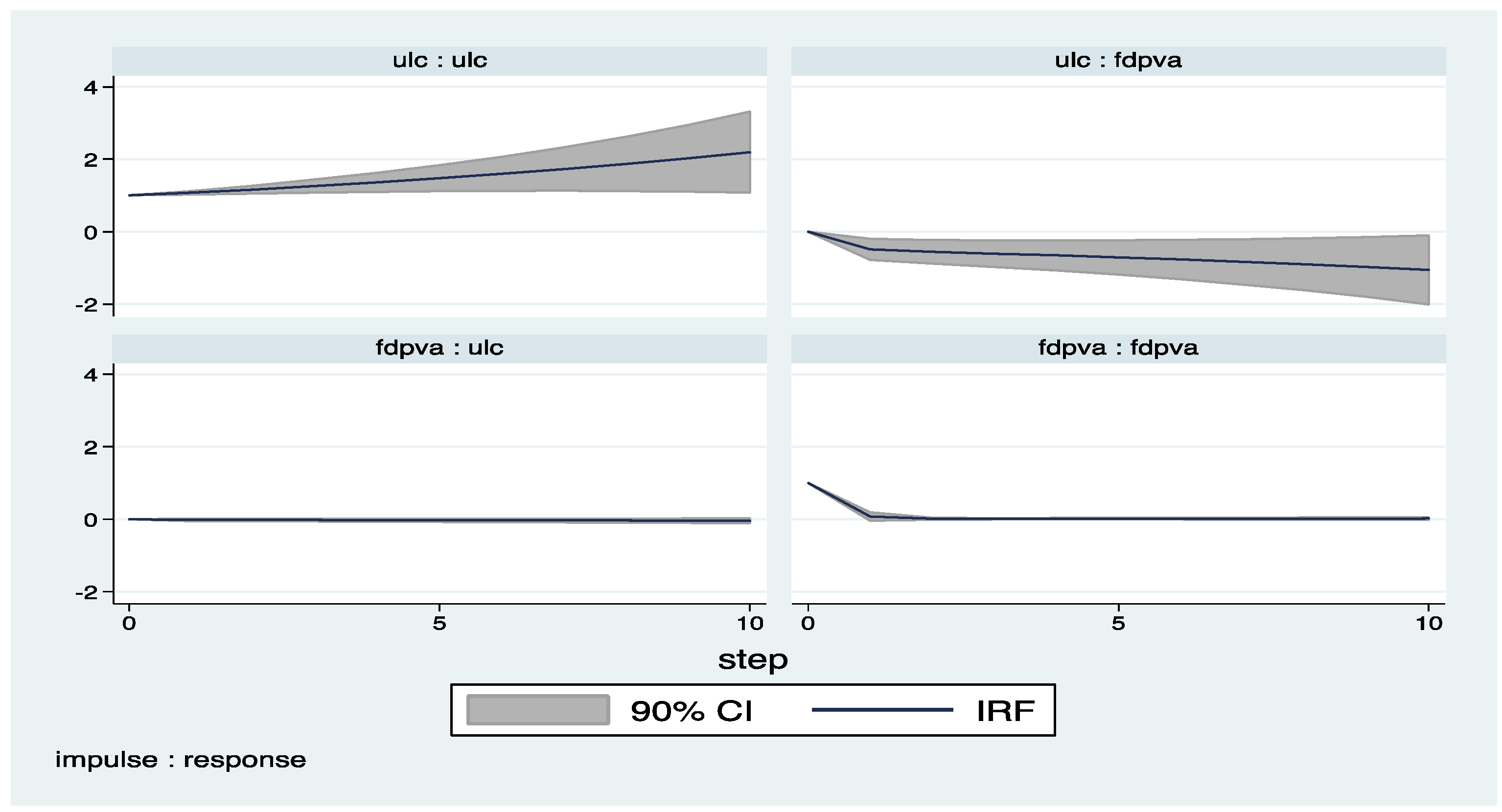
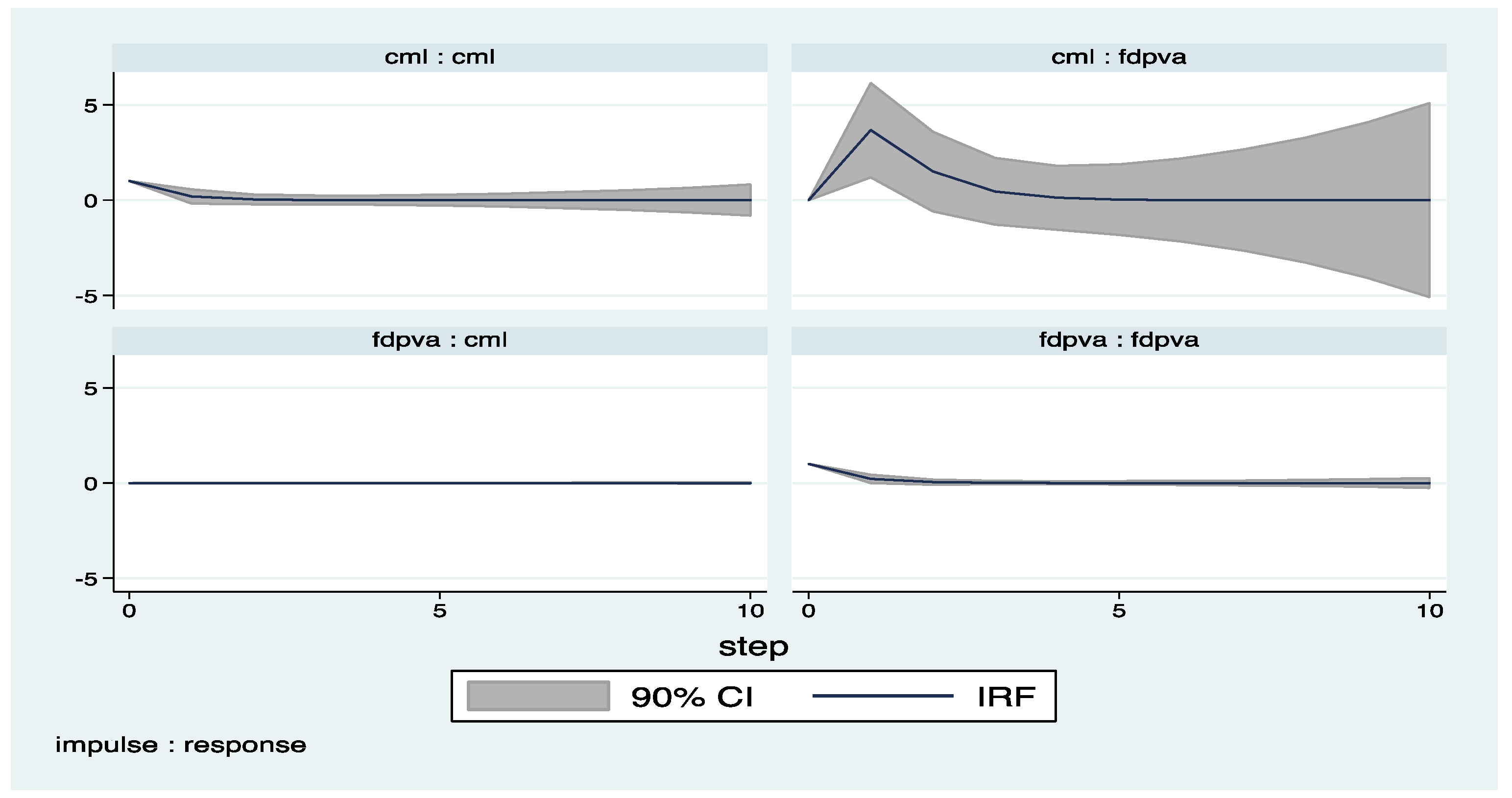
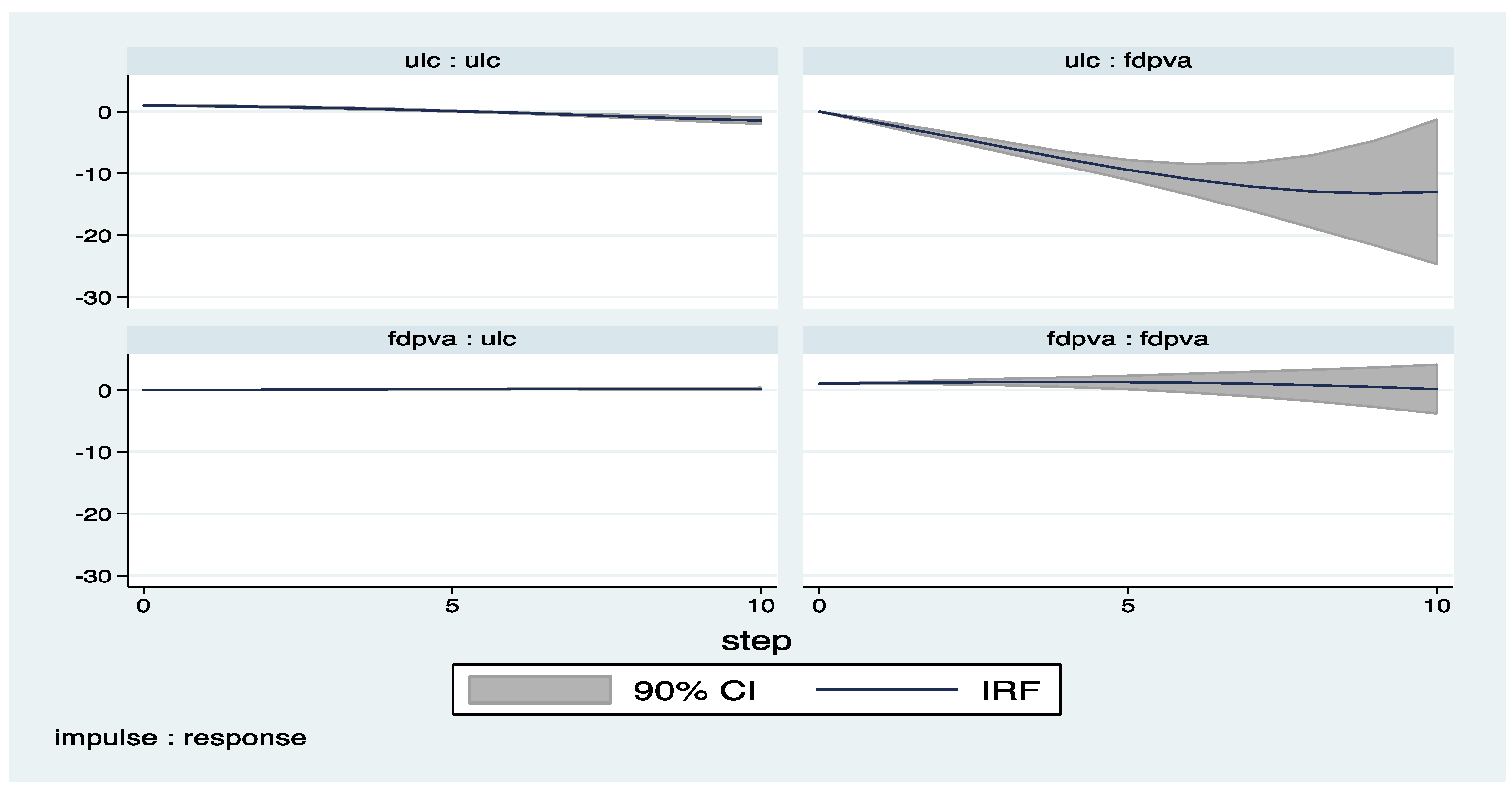

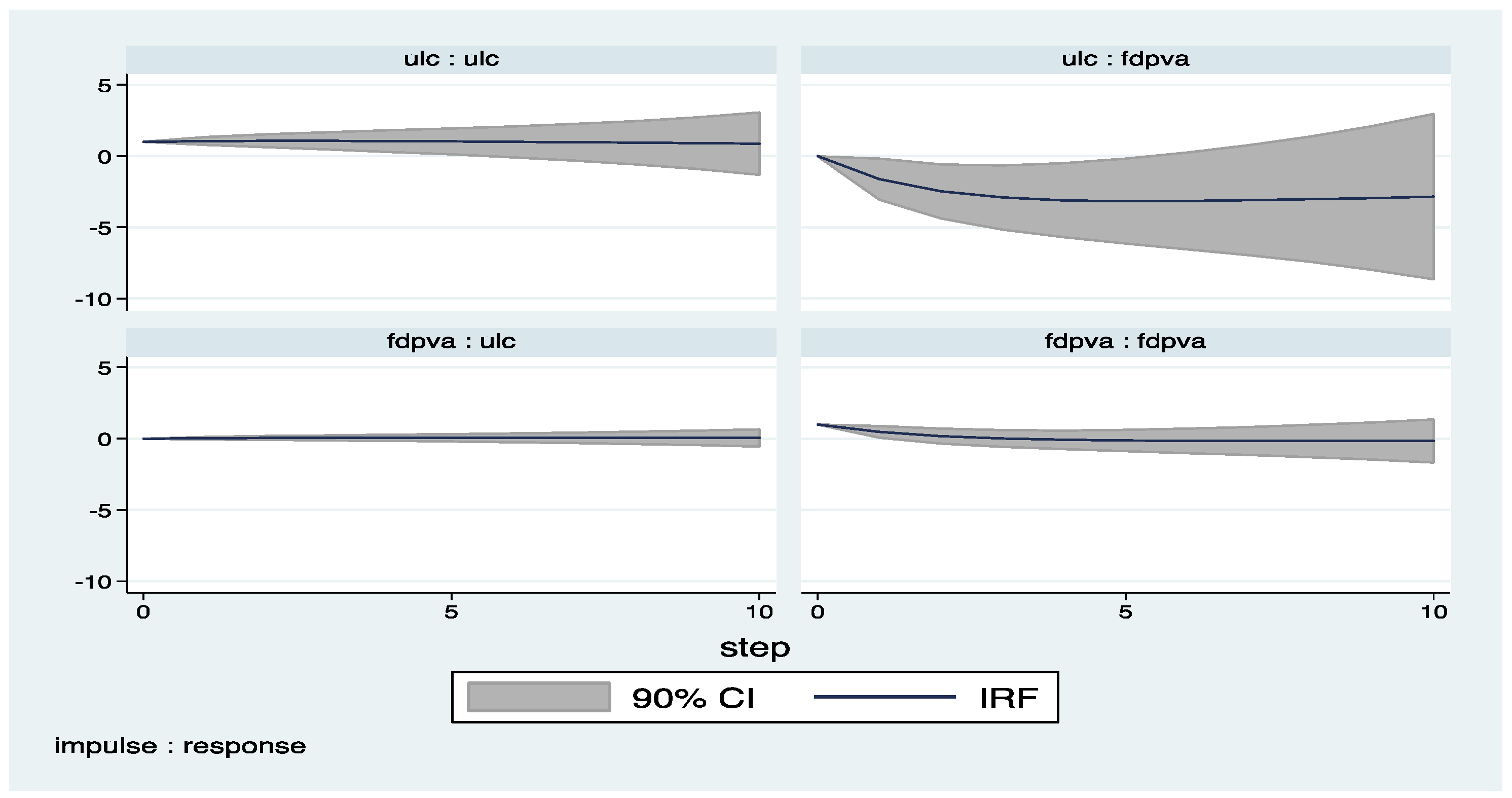
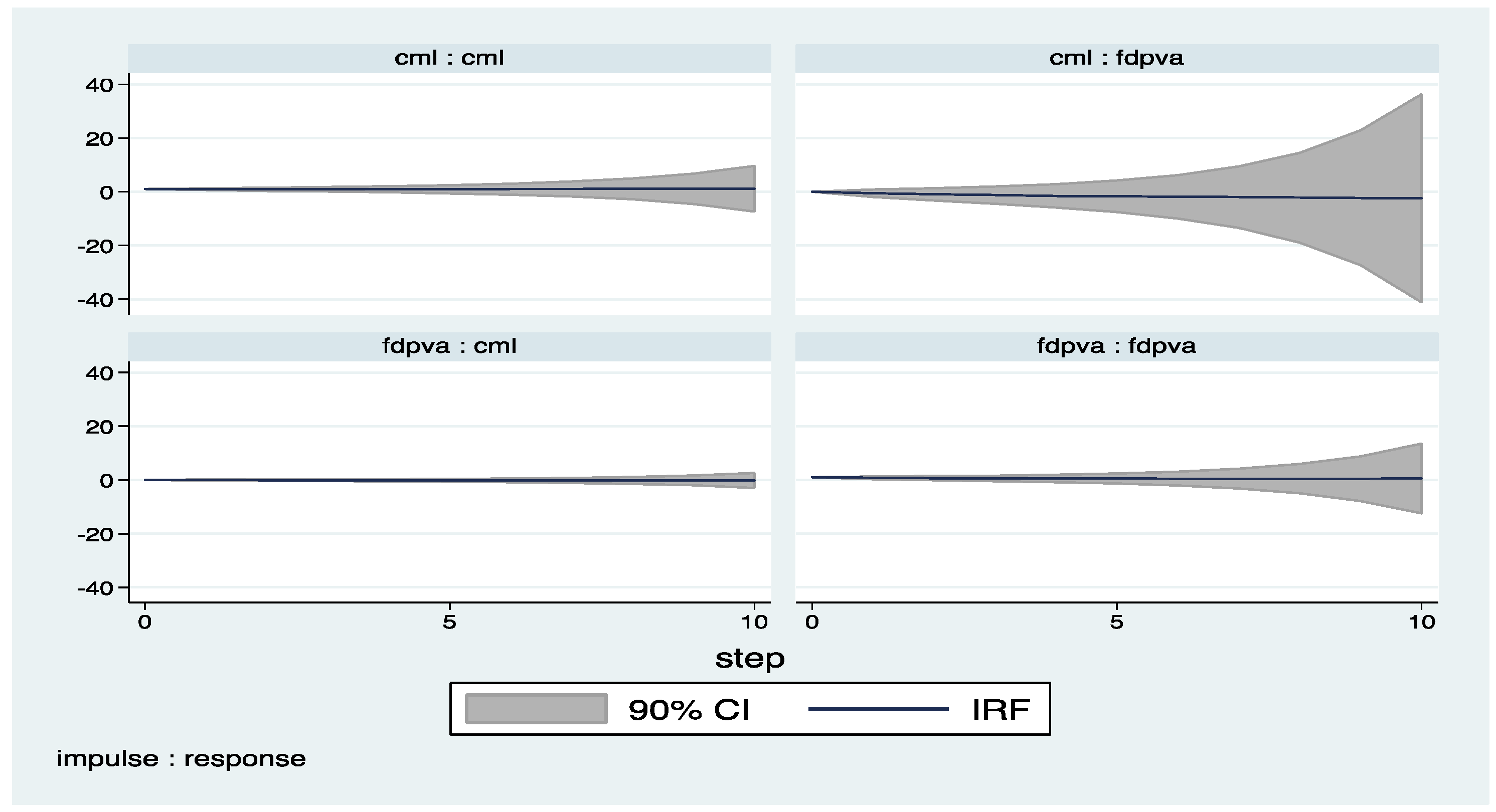
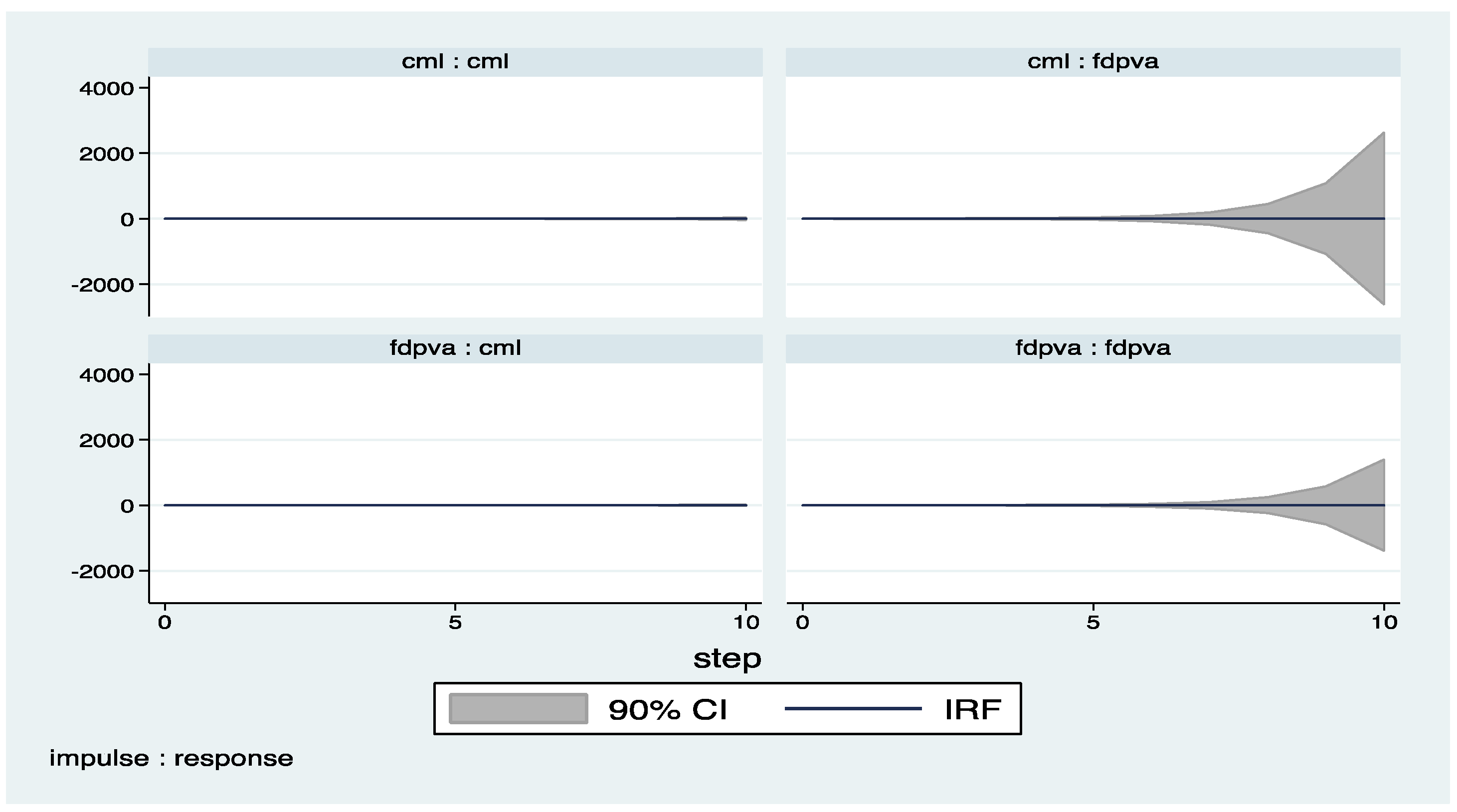
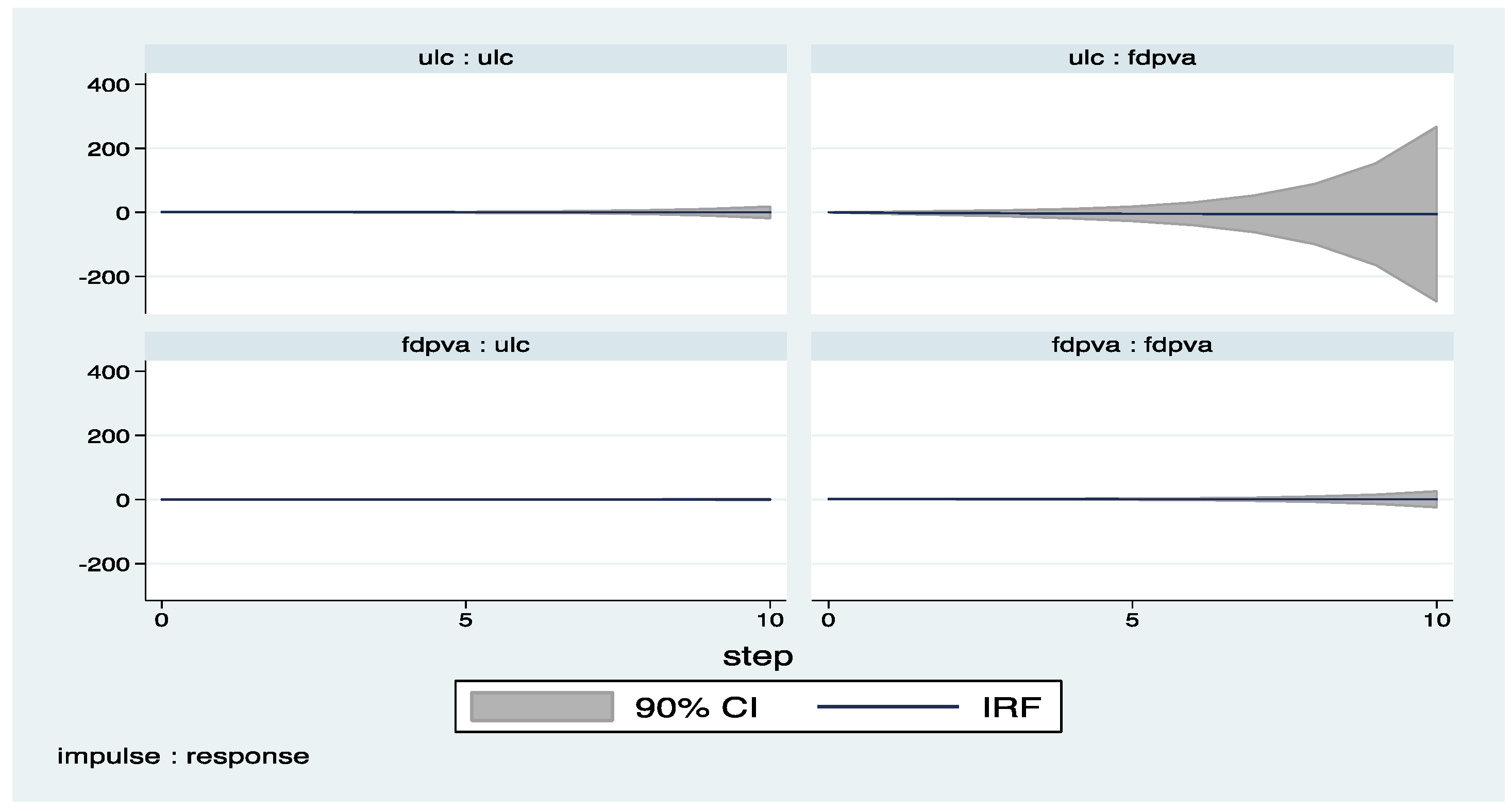

Appendix C. Country Classifications
References
- Abrigo, Michael R., and Inesa Love. 2015. Estimation of Panel Vector Autoregression in Stata: A Package of Programs. Available online: http://paneldataconference2015.ceu.hu/Program/Michael-Abrigo.pdf (accessed on 4 July 2017).
- Aitken, Brian J., Ann E. Harrison, and Robert E. Lipsey. 1996. Wages and foreign ownership: A comparative study of Mexico, Venezuela, and United States. Journal of International Economics 40: 345–71. [Google Scholar] [CrossRef]
- Almeida, Rita. 2007. The labor market effects of foreign owned firms. Journal of International Economics 72: 75–96. [Google Scholar] [CrossRef]
- Arellano, Manuel, and Stephen R. Bond. 1991. Some tests of specification for panel data: Monte Carlo evidence and an application to employment equations. Review of Economic Studies 58: 277–97. [Google Scholar] [CrossRef]
- Arellano, Manuel, and Olympia Bover. 1995. Another look at the instrumental variables estimation of error-components models. Journal of Econometrics 68: 29–51. [Google Scholar] [CrossRef]
- Baldwin, Robert E. 1995. The Effects of Trade and Foreign Direct Investment on Employment and Relative Wages. NBER Working Paper 5037. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Barry, Frank, Holger Görg, and Eric Strobl. 2005. Foreign direct investment and wages in domestic firms: Productivity spillovers vs. labor market crowding-out. International Journal of the Economics of Business 12: 67–84. [Google Scholar] [CrossRef]
- Blundell, Richard, and Stephen Bond. 1998. Initial conditions and moment restrictions in dynamic panel data models. Journal of Econometrics 87: 115–43. [Google Scholar] [CrossRef]
- Burke, James, and Gerald Epstein. 2001. Threat effects and the internationalization of production. Political Economy Research Institute Working Papers, No. 15. Available online: http://scholarworks.umass.edu/cgi/viewcontent.cgi?article=1009&context=peri_workingpapers (accessed on 16 September 2017).
- Campos, Nauro, and Yuko Kinoshita. 2003. Why Does FDI Go Where it Goes? New Evidence from the Transitional Economies. CEPR Discussion Paper No. 3984. Londra: Centre for Economic Policy Research. Available online: http://www.cepr.org/pubs/dps/DP3984.asp (accessed on 24 November 2016).
- Casu, Barbara, and Claudia Girardone. 2009. Testing the relationship between competition and efficiency in banking: A panel data analysis. Economics Letters 105: 134–37. [Google Scholar] [CrossRef]
- Chakrabarti, Avik. 2001. The Determinants of Foreign Direct Investment: Sensitivity Analyses of Cross-Country Regressions. Kyklos 54: 89–114. [Google Scholar] [CrossRef]
- Conyon, Martin, Sourafel Girma, Steve Thompson, and Peter Wrigh. 2002. The impact of foreign acquisition on wages and productivity in the U.K. Journal of Industrial Economics 50: 85–102. [Google Scholar] [CrossRef]
- Cragg, Michael Ion, and Mario Epelbaum. 1995. Why has wage dispersion grown in Mexico? Is it the incidence of reforms or the growing demand for skills? Journal of Development Economics 51: 99–116. [Google Scholar] [CrossRef]
- Crotty, James, Gerald Epstein, and Patricia Kelly. 1998. Multinational corporations in the neoliberal regime. In Globalization and Progressive Economic Policy. Edited by Gerald Epstein, Dean Baker and Robert Pollin. Cambridge: Cambridge University Press. [Google Scholar]
- Das, Satya P. 2002. Foreign direct investment and the relative wage in a developing economy. Journal of Development Economics 67: 55–77. [Google Scholar] [CrossRef]
- Driffield, Nigel, and Sourafel Girma. 2003. Regional FDI and wages spillovers: Evidence from the UK electronics industry. Oxford Bulletin of Economics and Statistics 65: 453–74. [Google Scholar] [CrossRef]
- Dunning, John. 1993. Multinational Enterprises and the Global Economy. Boston: Addison-Wesley Publishing Company. [Google Scholar]
- Eckel, Carsten. 2003. Fragmentation, efficiency-seeking FDI, and employment. Review of International Economics 11: 317–31. [Google Scholar] [CrossRef]
- Economou, Fotini, Chiristis Hassapis, Nikolaos Philippas, and Mike Tsionas. 2017. Foreign direct investment determinants in OECD and developing countries. Review of Development Economics 21: 527–42. [Google Scholar] [CrossRef]
- Feenstra, Robert C., and Gordon H. Hanson. 1996. Foreign investment, outsourcing and relative wages. In The Political Economy of Trade Policy: Papers in Honor of Jagdish Bhagwati. Edited by Gene Grossman, Douglas Irwin and Robert C. Feenstra. Cambridge: MIT Press, pp. 89–127. [Google Scholar]
- Feenstra, Robert C., and Gordon H. Hanson. 1997. Foreign direct investment and relative wages: Evidence from Mexico’s Maquiladoras. Journal of International Economics 42: 371–94. [Google Scholar] [CrossRef]
- Feliciano, Zadia M., and Robert E. Lipsey. 2006. Foreign ownership, wages, and wage changes in U.S. industries, 1987–1992. Contemporary Economic Policy 24: 74–91. [Google Scholar] [CrossRef]
- Gazaniol, Alexandre, and Catherine Laffineur. 2015. Does Outward Foreign Direct Investment Affect Domestic Real Wages? An Investigation Using French Micro-Data (No. 155). FIW Working Paper. Available online: http://www.fiw.ac.at/fileadmin/Documents/Publikationen/Working_Paper/N_155_Gazaniol_Laffineur.pdf (accessed on 16 September 2017).
- Girma, Sourafel, Holger Görg, and Erasmus Kersting. 2016. Which Boats are lifted by a Foreign Tide? Direct and Indirect Wage Effects of Foreign Ownership. Available online: http://econ.au.dk/fileadmin/Economics_Business/Research/TGF/DIEW2016/HGoerg.pdf (accessed on 13 September 2017).
- Gopinath, Munisamy, and Weiyan Chen. 2003. Foreign direct investment and wages: A cross country analysis. Journal of International Trade and Development 12: 285–309. [Google Scholar] [CrossRef]
- Harrison, Ann E. 2002. Has Globalization Eroded Labor’s Share? Some Cross-Country Evidence. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.198.9065&rep=rep1&type=pdf (accessed on 13 September 2017).
- Hartwig, Jochen. 2010. Is health capital formation good for long-term economic growth?—Panel Granger-causality evidence for OECD countries. Journal of Macroeconomics 32: 314–25. [Google Scholar] [CrossRef]
- Holtz-Eakin, Douglas, Whitney Newey, and Harvey S. Rosen. 1988. Estimating vector auto regressions with panel data. Econometrica 56: 1371–95. [Google Scholar] [CrossRef]
- Hsiao, Frank S. T., and Mei-Chu W. Hsiao. 2006. FDI, exports, and GDP in East and Southeast Asia—Panel data versus time-series causality analyses. Journal of Asian Economics 17: 1082–106. [Google Scholar] [CrossRef]
- Janicki, H., and P. V. Wunnava. 2004. Determinants of foreign direct investment: Empirical evidence from EU accession candidates. Applied Economics 36: 505–9. [Google Scholar] [CrossRef]
- Kónya, Laszio. 2006. Exports and growth: Granger-causality analysis on OECD countries with a panel data approach. Economic Modelling 23: 978–92. [Google Scholar] [CrossRef]
- Lemoine, Françoise. 1998. Integrating Central and Eastern Europe in the European Trade and Production Network. Working Paper 107. Available online: http://brie.berkeley.edu/publications/WP107.pdf (accessed on 16 September 2017).
- Lipsey, Robert E., and Fredrik Sjöholm. 2004. Foreign direct investment, education, and wages in Indonesian manufacturing. Journal of Development Economics 73: 415–22. [Google Scholar] [CrossRef]
- Lipsey, Robert E., and Fredrik Sjöholm. 2006. Foreign Firms and Indonesian Manufacturing Wages: An Analysis with Panel Data. Economic Development and Cultural Change 55: 201–21. [Google Scholar]
- OECD. 1993. Absolute Levels of Cost-Competitiveness: Methodological Aspects and Preliminary Estimates. Paris: OECD. [Google Scholar]
- Onaran, Özlem. 2009. Wage Share, Globalization and Crisis: The Case of the Manufacturing Industry in Korea, Mexico and Turkey. International Review of Applied Economics 23: 113–34. [Google Scholar] [CrossRef]
- Podrecca, Elana, and Gaetano Carmeci. 2001. Fixed investment and economic growth: New results on causality. Applied Economics 33: 177–82. [Google Scholar] [CrossRef]
- Pradhan, Rudra P., Mak B. Arvin, Neville R. Norman, and Samadran K. Bele. 2014. Economic growth and the development of telecommunications infrastructure in the G-20 countries: A panel-VAR approach. Telecommunications Policy 38: 634–49. [Google Scholar] [CrossRef]
- Rodrik, Dani. 1998. Capital Mobility and Labor. Cambridge: Harward University. [Google Scholar]
- Roodman, David. 2009. How to do xtabond2: An introduction to difference and system GMM in Stata. The Stata Journal 9: 86–136. [Google Scholar] [CrossRef]
- Ruane, Frances, and Ali Uğur. 2004. Foreign direct investment and productivity spillovers in Irish manufacturing industry: Evidence from firm level panel data. International Journal of Economics and Business 12: 53–66. [Google Scholar] [CrossRef]
- Schneider, Fredrich, and Bruno S. Frey. 1985. Economic and political determinants of foreign direct investment. World Development 13: 161–75. [Google Scholar] [CrossRef]
- UNCTAD. 2016. World Investment Report. New York and Geneva: UNCTAD. [Google Scholar]
- Vijayakumar, Narayanamurthy, Peruma Sridharan, and Kode Chandra S. Rao. 2010. Determinants of FDI in BRICS: A Panel Analysis. International Journal of Business Science and Applied Management 5: 1–13. [Google Scholar]
- Wei, Shang-Jin. 2000. How Taxing is Corruption on International Business. Review of Economics and Statistics 82: 1–11. [Google Scholar] [CrossRef]
- Wheeler, David, and Ashoka Mody. 1992. International Investment Location Decisions: The Case for U.S. Firms. Journal of International Economics 33: 57–76. [Google Scholar] [CrossRef]
- Windmeijer, Frank. 2005. A finite sample correction for the variance of linear two-step GMM estimators. Journal of Econometrics 126: 25–51. [Google Scholar] [CrossRef]
| 1 | Panel unit root tests provided in Table 1 are done in Stata (v. 12). Since the variables are not stationary at levels, the data is first differenced for further work. |
| 2 | All system GMM estimates are carried out by the Roodman’s ‘xtabond2’ command in Stata (v.12). The remaining results are available upon request. |
| 3 | Due to the heteroscedasticity problem in the one-step model, a robust-to-heteroscedasticity variance-covariance estimator is used. As such, the Sargan test statistics cannot be presented. |
| 4 | The impulse response functions with confidence intervals are derived by the help of pvar package by Abrigo and Love (2015). |
| 5 | The sectors are selected based on data availability. Industry includes the electricity sector. The labor cost indicators used in the analysis of manufacturing, construction, and finance are reflective exactly of labor costs in these sectors, whereas the labor cost indicator used in the analysis of the industry sector (i.e., electricity) makes use of what is labeled as the “business and/or industry” labor cost by the OECD. |
| 6 | Figures presented in Appendix B are produced by dropping the years of financial crisis (2008-2009), but there is no significant change on the results. |
| Observation | Mean | Standard Deviation | ||
|---|---|---|---|---|
| All | fdpva | 345 | 35.28 | 29.88 |
| cml | 345 | 19.18 | 7.26 | |
| ulc | 345 | 0.58 | 0.109 | |
| Manufacturing | fdpva | 255 | 49.81 | 44.7 |
| cml | 255 | 19.81 | 8.31 | |
| ulc | 255 | 0.616 | 0.11 | |
| Finance | fdpva | 225 | 59.54 | 70.6 |
| cml | 225 | 21.88 | 7.55 | |
| ulc | 225 | 0.57 | 0.13 | |
| Construction | fdpva | 270 | 5.30 | 5.53 |
| cml | 270 | 17.30 | 6.66 | |
| ulc | 270 | 0.66 | 0.17 | |
| Industry | fdpva | 195 | 33.19 | 38.65 |
| cml | 195 | 19.40 | 9.82 | |
| ulc | 195 | 0.53 | 0.13 |
| fdpva | cml | ulc | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Levin | IPS | ADF-Fisher Chi-square | PP-Fisher Chi-square | Levin | IPS | ADF-Fisher Chi-square | PP-Fisher Chi-square | Levin | IPS | ADF-Fisher Chi-square | PP-Fisher Chi-square | ||
| Panel A. Level | |||||||||||||
| All | Stat | 0.835 | 0.580 | 31.794 | −0.263 | 3.631 | −0.806 | 53.446 | 31.928 | 2.347 | 1.881 | 0.3871 | 33.526 |
| Prob | 0.7984 | 0.719 | 0.8739 | 0.396 | 0.999 | 0.210 | 0.110 | 0.870 | 0.990 | 0.970 | 0.650 | 0.821 | |
| Manufacturing | Stat | 1.906 | 0.717 | 32.884 | 45.285 | 2.790 | 3.197 | 31.560 | −0.794 | −0.437 | −0.671 | 0.625 | −0.284 |
| Prob | 0.971 | 0.763 | 0.617 | 0.138 | 0.997 | 0.999 | 0.679 | 0.2134 | 0.330 | 0.2511 | 0.734 | 0.388 | |
| Finance | Stat | −0.3396 | −1.005 | 30.301 | 38.758 | 0.604 | −0.840 | 31.414 | 25.539 | −0.285 | −0.447 | 37.918 | 0.795 |
| Prob | 0.367 | 0.158 | 0.450 | 0.131 | 0.727 | 0.200 | 0.305 | 0.698 | 0.387 | 0.327 | 0.151 | 0.786 | |
| Construction | Stat | 0.857 | 0.446 | 29.989 | 0.6273 | 1.936 | −0.902 | 36.020 | 28.412 | −0.971 | −0.748 | 36.735 | 0.765 |
| Prob | 0.804 | 0.672 | 0.568 | 0.734 | 0.973 | 0.183 | 0.285 | 0.648 | 0.165 | 0.220 | 0.258 | 0.777 | |
| Industry | Stat | −0.400 | −0.637 | 29.352 | 30.861 | 0.898 | −0.874 | 17.449 | 23.711 | 1.199 | −0.637 | 28.401 | −0.502 |
| Prob | 0.344 | 0.261 | 0.295 | 0.233 | 0.815 | 0.191 | 0.894 | 0.592 | 0.884 | 0.261 | 0.339 | 0.307 | |
| Panel B. First Difference | |||||||||||||
| All | Stat | −6.756 | −1.886 | 70.597 | 74.803 | −1.634 | −2.390 | 80.372 | 101.41 | −4.143 | −1.960 | 107.34 | 77.973 |
| Prob | 0.000 | 0.002 | 0.003 | 0.001 | 0.005 | 0.008 | 0.000 | 0.000 | 0.000 | 0.002 | 0.000 | 0.000 | |
| Manufacturing | Stat | −4.184 | −3.211 | 116.65 | 91.470 | −3.547 | −2.473 | 68.431 | 192.02 | −2.590 | −1.344 | 90.240 | 85.319 |
| Prob | 0.000 | 0.0000 | 0.000 | 0.000 | 0.000 | 0.006 | 0.000 | 0.000 | 0.004 | 0.008 | 0.000 | 0.000 | |
| Finance | Stat | −5.650 | −1.446 | 51.457 | 59.633 | −1.980 | −1.843 | 80.902 | 86.320 | −2.774 | −4.596 | 71.185 | 76.242 |
| Prob | 0.000 | 0.007 | 0.000 | 0.001 | 0.002 | 0.003 | 0.000 | 0.0000 | 0.002 | 0.000 | 0.000 | 0.000 | |
| Construction | Stat | −3.870 | −4.465 | 51.649 | 111.058 | −4.212 | −3.121 | 185.30 | 68.039 | −5.584 | −2.714 | 104.34 | 104.57 |
| Prob | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.003 | 0.000 | 0.000 | |
| Industry | Stat | −5.109 | −1.555 | 56.993 | 58.115 | −3.556 | −3.319 | 66.584 | 144.13 | −1.322 | −4.401 | 63.894 | 70.449 |
| Prob | 0.0000 | 0.00 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Fixed Effect | AB One Step System GMM | AB Two Step System GMM | Fixed Effect | AB One Step System GMM | AB Two Step System GMM | |
|---|---|---|---|---|---|---|
| Dependent Variable | 1 | 2 | 3 | 4 | 5 | 6 |
| fdpva | fdpva | fdpva | ulc | ulc | ulc | |
| L.fdpva | 0.024 | 0.930 *** | 0.953 *** | −0.008 | −0.014 | −0.011 |
| (0.037) | (0.113) | (0.103) | (0.013) | (0.012) | (0.01) | |
| L2.fdpva | 0.679 | 0.0358 | 0.0204 | −0.004 | 0.0121 | 0.0210 |
| (0.058) | (0.107) | (0.0992) | (0.014) | (0.0107) | (0.010) | |
| L.ulc | −1.284 | −1.204 ** | −1.255 * | −0.960 *** | 1.635 *** | 1.674 *** |
| (0.586) | (0.566) | (0.640) | (0.076) | (0.127) | (0.129) | |
| L2.ulc | −0.349 | 0.804 | 0.920 | 1.896 *** | −0.663 | −0.696 |
| (0.611) | (0.517) | (0.599) | (0.058) | (0.107) | (0.109) | |
| Hansen Test | 0.284 | 0.284 | 0.292 | 0.592 | ||
| Difference Hansen Test | 0.874 | 0.874 | 0.712 | 0.712 | ||
| AB Test | 0.618 | 0.690 | 0.570 | 0.297 | ||
| Wald Test ulc | 0.028 | 0.010 | 0.002 | |||
| Wald Test fdpva | 0.849 | 0.522 | 0.611 |
| Fixed Effect | AB One Step System GMM | AB Two Step System GMM | Fixed Effect | AB One Step System GMM | AB Two Step System GMM | |
|---|---|---|---|---|---|---|
| Dependent Variable | 1 | 2 | 3 | 4 | 5 | 6 |
| fdpva | fdpva | fdpva | cml | cml | cml | |
| L.fdpva | 0.406 (0.071) | 0.078 (0.124) | 0.0877 (0.153) | −0.011 (0.009) | 0.042 *** (0.010) | 0.0400 *** (0.0103) |
| L2.fdpva | −0.095 (0.057) | −0.148 (0.159) | −0.109 (0.181) | 0.038 *** (0.007) | 0.003 (0.723) | 0.005 (0.010) |
| L.cml | −0.484 (0.585) | 0.987 ** (0.546) | 0.864 (0.600) | 0.885 *** (0.072) | 0.658 *** (0.091) | 0.6457 *** (0.103) |
| L2.cml | 1.397 *** (1.941) | 1.393 *** (0.430) | 1.298 *** (0.487) | −0.176 (0.074) | 0.239 ** (0.102) | 0.2577 (0.107) |
| Hansen Test | 0.279 | 0.279 | 0.236 | 0.236 | ||
| Difference Hansen Test | 0.411 | 0.411 | 0.773 | 0.773 | ||
| AB Test | 0.297 | 0.490 | 0.495 | 0.493 | ||
| Wald Test cml | 0.000 | 0.000 | 0.0000 | |||
| Wald Test fdpva | 0.000 | 0.000 | 0.000 |
| Fixed Effect | AB One Step System GMM | AB Two Step System GMM | Fixed Effect | AB One Step System GMM | AB Two Step System GMM | |
|---|---|---|---|---|---|---|
| Dependent Variable | 1 | 2 | 3 | 4 | 5 | 6 |
| fdpva | fdpva | fdpva | ulc | ulc | ulc | |
| L.fdpva | 0.780 | 0.757 *** | 0.776 *** | 0.015 | −0.0349 | −0.0359 |
| (0.064) | (0.0821) | (0.0885) | (0.016) | (0.0271) | (0.0250) | |
| L2.fdpva | 0.065 (0.066) | 0.226 *** (0.0801) | 0.205 ** (0.085) | −0.007 (0.015) | 0.0167 (−0.0236) | 0.0177 (0.0225) |
| L.ulc | 0.721 (0.505) | −0.701 *** (0.237) | −0.688 (0.437) | 0.944 *** (0.054) | 0.530 *** (0.0817) | 0.530 *** (0.0844) |
| L2.ulc | −1.13 *** (0.481) | −0.827 ** (0.360) | −0.746 ** (0.296) | −0.124 ** (0.050) | 0.569 *** (0.220) | 0.562 ** (0.232) |
| Hansen Test | 0.393 | 0.393 | 0.481 | 0.481 | ||
| Difference Hansen Test | 0.326 | 0.326 | 0.797 | 0.797 | ||
| AB Test | 0.328 | 0.497 | 0.587 | 0.653 | ||
| Wald Test ulc | 0.036 | 0.015 | 0.039 | |||
| Wald Test fdpva | 0.281 | 0.143 | 0.146 |
| Fixed Effect | AB One Step System GMM | AB Two Step System GMM | Fixed Effect | AB One Step System GMM | AB Two Step System GMM | |
|---|---|---|---|---|---|---|
| Dependent Variable | 1 | 2 | 3 | 4 | 5 | 6 |
| fdpva | fdpva | fdpva | cml | cml | cml | |
| L.fdpva | 0.597 *** (0.086) | 0.425 *** (0.131) | 0.366 *** (0.128) | 0.035 *** (0.011) | 0.0379 *** (0.0125) | 0.0362 *** (0.0110) |
| L2.fdpva | 0.135 (0.089) | 0.110 (0.234) | 0.161 (0.195) | 0.002 (0.011) | −0.0025 (0.0323) | 0.007 (0.030) |
| L.cml | −0.974 (0.813) | 0.981 ** (0.459) | 0.986 ** (0.417) | 0.684 *** (0.104) | 0.006 (0.134) | 0.0124 (0.156) |
| L2.cml | 1.45 ** (0.7753) | −0.480 (0.527) | −0.476 (0.475) | 0.203 ** (0.100) | 0.937 *** (0.136) | 0.885 *** (0.120) |
| Hansen Test | 0.624 | 0.624 | 0.395 | 0.395 | ||
| Difference Hansen Test | 0.513 | 0.513 | 0.750 | 0.750 | ||
| AB Test | 0.234 | 0.268 | 0.061 | 0.067 | ||
| Wald Test cml | 0.063 | 0.000 | 0.000 | |||
| Wald Test fdpva | 0.030 | 0.000 | 0.001 |
| Fixed Effect | AB One Step System GMM | AB Two Step System GMM | Fixed Effect | AB One Step System GMM | AB Two Step System GMM | |
|---|---|---|---|---|---|---|
| Dependent Variable | 1 | 2 | 3 | 4 | 5 | 6 |
| fdpva | fdpva | fdpva | ulc | ulc | ulc | |
| L.fdpva | 0.859 (0.073) | 0.819 *** (0.0735) | 0.814 *** (0.076) | 0.005 (0.0098) | −0.0103 (0.0129) | −0.00776 (0.0108) |
| L2.fdpva | 0.078 *** (0.066) | 0.149 *** (0.0473) | 0.148 *** (0.050) | 0.0034 (0.016) | 0.00761 (0.00950) | 0.00704 (0.00970) |
| L.ulc | 1.082 (0.253) | −0.0706 (0.454) | −0.488 (0.488) | 0.709 *** (0.108) | 0.113 (0.128) | 0.126 (0.103) |
| L2.ulc | −1.806 *** (0.942) | −0.262 ** (0.126) | −0.306 * (0.165) | 0.403 *** (0.126) | 0.716 *** (0.110) | 0.735 *** (0.106) |
| Hansen Test | 0.299 | 0.299 | 0.277 | 0.277 | ||
| Difference Hansen Test | 0.507 | 0.507 | 0.568 | 0.568 | ||
| AB Test | 0.054 | 0.104 | 0.114 | 0.230 | ||
| Wald Test ulc | 0.007 | 0.001 | 0.007 | |||
| WaldTest fdpva | 0.763 | 0.653 | 0.719 |
| Fixed Effect | AB One Step System GMM | AB Two Step System GMM | Fixed Effect | AB One Step System GMM | AB Two Step System GMM | |
|---|---|---|---|---|---|---|
| Dependent Variable | 1 | 2 | 3 | 4 | 5 | 6 |
| fdpva | fdpva | fdpva | cml | cml | cml | |
| L.fdpva | 0.682 *** (0.0784) | 0.921 *** (0.0880) | 0.963 *** (0.0659) | 0.00147 (0.00914) | −0.000321 (0.00823) | 0.00140 (0.00915) |
| L2.fdpva | 0.0387 (0.0733) | 0.0831 (0.0696) | 0.0794 (0.0801) | 0.00547 (0.00739) | 0.00831 (0.0105) | 0.00743 (0.0107) |
| L.cml | 0.696 (0.561) | −0.328 (0.779) | −0.422 (0.657) | 0.999 *** (0.0320) | 0.943 *** (0.136) | 0.955 *** (0.213) |
| L2.cml | −0.391 (0.538) | −0.275 (0.566) | −0.348 (0.398) | 0.00161 (0.029) | 0.0585 (0.135) | 0.0458 (0.213) |
| Hansen Test | 0.651 | 0.651 | 0.439 | 0.439 | ||
| Difference Hansen Test | 0.738 | 0.738 | 0.645 | 0.645 | ||
| AB Test | 0.381 | 0.370 | 0.992 | 0.954 | ||
| Wald Test cml | 0.197 | 0.307 | 0.111 | |||
| Wald Test fdpva | 0.403 | 0.448 | 0.307 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bayraktar-Sağlam, B.; Sayek Böke, S. Labor Costs and Foreign Direct Investment: A Panel VAR Approach. Economies 2017, 5, 36. https://doi.org/10.3390/economies5040036
Bayraktar-Sağlam B, Sayek Böke S. Labor Costs and Foreign Direct Investment: A Panel VAR Approach. Economies. 2017; 5(4):36. https://doi.org/10.3390/economies5040036
Chicago/Turabian StyleBayraktar-Sağlam, Bahar, and Selin Sayek Böke. 2017. "Labor Costs and Foreign Direct Investment: A Panel VAR Approach" Economies 5, no. 4: 36. https://doi.org/10.3390/economies5040036
APA StyleBayraktar-Sağlam, B., & Sayek Böke, S. (2017). Labor Costs and Foreign Direct Investment: A Panel VAR Approach. Economies, 5(4), 36. https://doi.org/10.3390/economies5040036





