Accounting for Nonlinearity, Asymmetry, Heterogeneity, and Cross-Sectional Dependence in Energy Modeling: US State-Level Panel Analysis
Abstract
:1. Introduction
2. Methodology and Data
2.1. Econometric Issues
2.2. Modeling Issues
2.3. Data
3. Results and Discussion
3.1. Initial Results
3.2. Price Asymmetry
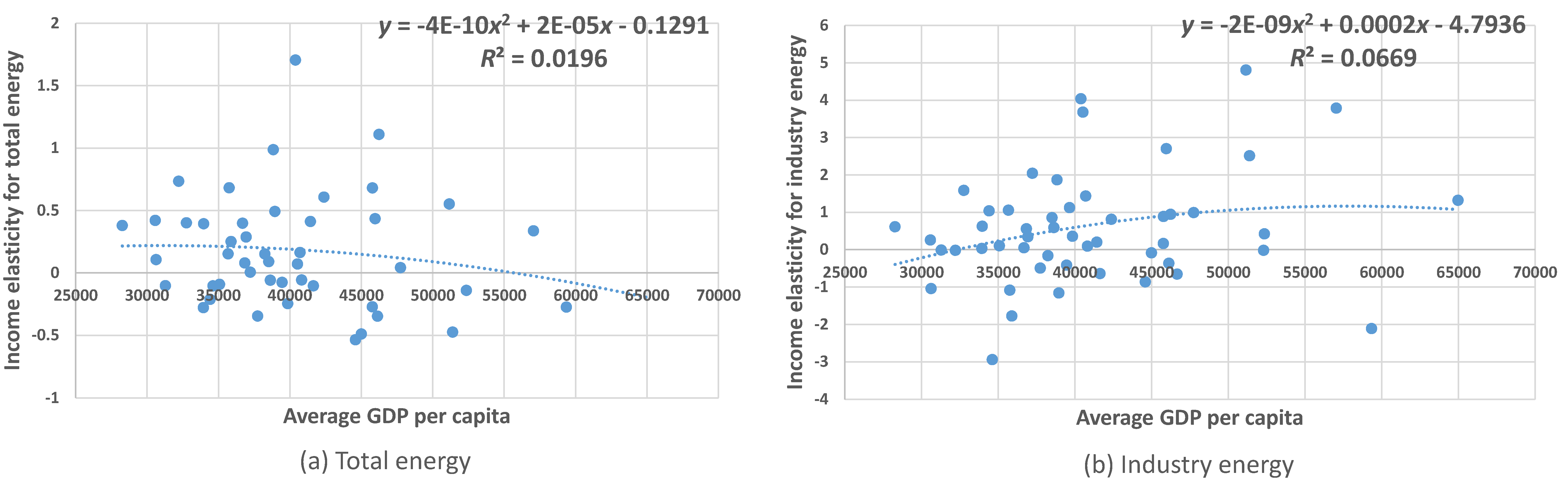
3.3. Nonlinear Income Elasticities
4. Summary
Acknowledgments
Conflicts of Interest
Appendix A
| Dependent Variable | Total Energy | Industrial Energy | Transport Energy | Residential Electricity | Commercial Electricity |
|---|---|---|---|---|---|
| Short Run | |||||
| LDV | 0.870 **** | 0.863 **** | 0.800 **** | 0.721 **** | 0.914 **** |
| GDP pc | 0.126 **** | 0.201 *** | 0.139 *** | 0.028 | 0.060 |
| Price | −0.021 **** | −0.029 *** | −0.029 **** | −0.060 **** | −0.035 *** |
| HDD | 0.127 **** | 0.157 **** | 0.049 ** | ||
| CDD | 0.023 **** | 0.072 **** | 0.051 **** | ||
| Long Run | |||||
| GDP pc | 0.971 **** | 1.466 *** | 0.699 **** | 0.102 | 0.692 * |
| Price | -0.159 *** | −0.214 ** | −0.148 **** | −0.215 **** | −0.410 *** |
| HDD | 0.980 **** | 0.564 **** | 0.569 * | ||
| CDD | 0.174 *** | 0.259 **** | 0.585 *** | ||
| Time Trends | |||||
| Time | −0.002 **** | −0.005 *** | −0.001 | 0.002 *** | 0.001 |
| Time-squared | 0.00005 **** | 0.0001 *** | 0.00004 * | 0.000 | −0.000 |
| Observations | 1248 | 1300 | 1300 | 1248 | 1248 |
| x-sections | 48 | 50 | 50 | 48 | 48 |
| CD (p) | 44.8 (0.00) | 31.8 (0.00) | 28.0 (0.00) | 47.0 (0.00) | 20.8 (0.00) |
References
- Agras, Jean, and Duane Chapman. 1999. A dynamic approach to the Environmental Kuznets Curve hypothesis. Ecological Economics 28: 267–77. [Google Scholar] [CrossRef]
- Beck, Nathaniel. 2008. Time-series—cross-section methods. In Oxford Handbook of Political Methodology. Edited by Janet Box-Steffensmeier, Henry Brady and David Collier. New York: Oxford University Press. [Google Scholar]
- Chudik, Alexander, and Hashem M. Pesaran. 2015. Common correlated effects estimation of heterogeneous dynamic panel data models with weakly exogenous regressions. Journal of Econometrics 188: 393–420. [Google Scholar] [CrossRef]
- Dergiades, Theologos, and Lefteris Tsoulfidis. 2008. Estimating residential demand for electricity in the United States, 1965–2006. Energy Economics 30: 2722–730. [Google Scholar] [CrossRef]
- Gately, Dermot, and Hillard G. Huntington. 2002. The asymmetric effects of changes in price and income on energy and oil demand. The Energy Journal 23: 19–55. [Google Scholar] [CrossRef]
- Graham, Daniel, and Stephen Glaister. 2002. The demand for automobile fuel: A survey of elasticities. Journal of Transport Economics and Policy 36: 1–26. [Google Scholar]
- Halicioglu, Ferda. 2007. Residential electricity demand dynamics in Turkey. Energy Economics 29: 199–210. [Google Scholar] [CrossRef]
- Holtedahl, Pernille, and Frederick Joutz. 2004. Residential electricity demand in Taiwan. Energy Economics 26: 201–24. [Google Scholar] [CrossRef]
- Hunt, Lester C., and David L. Ryan. 2015. Economic modelling of energy services: Rectifying misspecified energy demand functions. Energy Economics 50: 273–85. [Google Scholar] [CrossRef]
- Kao, Chihwa. 1999. Spurious regression and residual-based tests for cointegration in panel data. Journal of Econometrics 65: 9–15. [Google Scholar] [CrossRef]
- Kapetanios, George, M. Hashem Pesaran, and Takashi Yamagata. 2011. Panels with non-stationary multifactor error structures. Journal of Econometrics 160: 326–48. [Google Scholar] [CrossRef]
- Kenworthy, Jeffrey, and Felix Laube. 1999. Patterns of automobile dependence in cities: An international overview of key physical and economic dimensions with some implications for urban policy. Transportation Research Part A 33: 691–723. [Google Scholar] [CrossRef]
- Kiviet, F. Jan. 1995. On Bias, Inconsistency and Efficiency of Various Estimators in Dynamic Panel Data Models. Journal of Econometrics 68: 53–78. [Google Scholar] [CrossRef]
- Liddle, Brantley. 2009. Long-Run Relation among Transport Demand, Income, and Gasoline Price for the US. Transportation Research D: Transport and Environment 14: 73–82. [Google Scholar] [CrossRef]
- Liddle, Brantley. 2012. The systemic, long-run relation among gasoline demand, gasoline price, income, and vehicle ownership in OECD countries: Evidence from panel cointegration and causality modeling. Transportation Research D: Transport and Environment 17: 327–31. [Google Scholar] [CrossRef]
- Liddle, Brantley. 2013a. Urban density and climate change: A STIRPAT analysis using city-level data. Journal of Transport Geography 28: 22–29. [Google Scholar] [CrossRef]
- Liddle, Brantley. 2013b. The energy, economic growth, urbanization nexus across development: Evidence from heterogeneous panel estimates robust to cross-sectional dependence. The Energy Journal 34: 223–44. [Google Scholar] [CrossRef]
- Liddle, Brantley. 2015. What are the carbon emissions elasticities for income and population? Bridging STIRPAT and EKC via robust heterogeneous panel estimates. Global Environmental Change 31: 62–73. [Google Scholar] [CrossRef]
- Liddle, Brantley. 2017. Modeling Disaggregated Energy Consumption: Considering Nonlinearity, Asymmetry, and Heterogeneity by Analyzing US State-level Data. IAEE Energy Forum 1st Quarter 2017: 35–39. [Google Scholar]
- Lindmark, Magnus. 2004. Patterns of historical CO2 intensity transitions among high and low-income countries. Explorations in Economic History 41: 426–47. [Google Scholar] [CrossRef]
- Muller-Furstenberger, Georg, and Martin Wagner. 2007. Exploring the environmental Kuznets hypothesis: Theoretical and econometric problems. Ecological Economics 62: 648–60. [Google Scholar] [CrossRef]
- Narayan, Paresh, Russell Smyth, and Arti Prasad. 2007. Electricity consumption in G7 countries: A panel cointegration analysis of residential demand elasticities. Energy Policy 35: 4485–94. [Google Scholar] [CrossRef]
- Newman, Peter, and Jeffrey Kenworthy. 1989. Cities and Automobile Dependence: An International Sourcebook. Aldershot: Gower Technical. [Google Scholar]
- Pesaran, M. Hashem. 2004. General diagnostic tests for cross section dependence in panels. IZA. Discussion Paper No. 1240. Cambridge: Cambridge Working Papers in Economics. [Google Scholar]
- Pesaran, M. Hashem. 2006. Estimation and inference in large heterogeneous panels with a multifactor error structure. Econometrica 74: 967–1012. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem. 2007. A simple panel unit root test in the presence of cross-section dependence. Journal of Applied Econometrics 22: 265–312. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, and Ron Smith. 1995. Estimating long-run relationships from dynamic heterogeneous panel. Journal of Econometrics 68: 79–113. [Google Scholar] [CrossRef]
| 1 | As an anonymous reviewer suggested, breaks could be explicitly considered. However, only 26 time observations is likely insufficient for a robust consideration of endogenous breaks. Furthermore, since the data begins in 1987, the two most important energy-related events in the US—the two oil crises, dated 1973–1974 and 1979–1981—would lie outside the sample range. |
| 2 | As outlined in the table notes, some regressions included only a single lag because allowing for two lags produced highly insignificant results. |
| 3 | The Dynamic Common Correlated Effects Estimator of Chudik and Pesaran (2015) is implemented by STATA command xtdcce2, which was developed by Jan Ditzen. |
| 4 | While several papers have found a negative relationship between urban density and transport energy consumption (e.g., Newman and Kenworthy 1989; Kenworthy and Laube 1999; Liddle 2013a), in earlier work on the present dataset, (state-level) population density was not statistically significant for transport energy consumption (Liddle 2017). |
| 5 | Heating and cooling degree days’ data were not available for Alaska and Hawaii. |
| 6 | This estimator is implemented by STATA command xtlsdvc, which was developed by Giovanni Bruno. |
| 7 | This specification is estimated by using the pooled option in STATA command xtdcce2. |
| Variables | Observations | Mean | Std. Dev. | Min | Max |
|---|---|---|---|---|---|
| Total energy pc | 1350 | 374.1 | 171.3 | 171 | 1196 |
| Transport energy pc | 1350 | 100.7 | 39.7 | 48 | 403 |
| Industrial energy pc | 1350 | 140.4 | 125.0 | 18 | 706 |
| Residential electricity pc | 1350 | 4.4 | 1.2 | 1.9 | 7.4 |
| Commercial electricity pc | 1350 | 3.9 | 0.9 | 1.2 | 8.1 |
| GDP pc | 1350 | 41,059 | 9,600 | 20,511 | 75,694 |
| Cooling degree days | 1296 | 1,068 | 798 | 42 | 3,827 |
| Heating degree days | 1296 | 5,270 | 2,083 | 430 | 10,810 |
| Total energy price | 1350 | 12.7 | 5.8 | 5.1 | 40.3 |
| Transport energy price | 1350 | 13.8 | 7.3 | 5.3 | 31.0 |
| Industry energy price | 1350 | 8.8 | 5.3 | 2.1 | 56.3 |
| Commercial electricity price | 1350 | 27.2 | 9.5 | 12.2 | 109.4 |
| Residential electricity price | 1350 | 23.6 | 8.4 | 10.9 | 102.2 |
| Pesaran (2004) CD Test | Pesaran (2007) CIPS Test | |||
|---|---|---|---|---|
| Variables | Statistic | Abs. Corr. Coeff. | Specification W/O Trend | Specification W/Trend |
| Log total energy pc | 59.3 * | 0.52 | I(1) | I(1) |
| Log transport energy pc | 56.2 * | 0.44 | I(1) | I(1) |
| Log industrial energy pc | 58.6 * | 0.61 | I(1) | I(1) |
| Log residential electricity pc | 119.7 * | 0.77 | I(0) | I(1) |
| Log commercial electricity pc | 124.5 * | 0.77 | I(0) | I(1) |
| Log GDP pc | 163.2 * | 0.94 | I(1) | I(1) |
| Log cooling degree days | 78.2 * | 0.51 | I(0) | I(0) |
| Log heating degree days | 89.9 * | 0.57 | I(0) | I(0) |
| Log total energy price | 180.5 * | 0.99 | I(0) | I(1) |
| Log transport energy price | 181.4 * | 0.997 | I(0) | I(1) |
| Log industry energy price | 174.5 * | 0.96 | I(0) | I(1) |
| Log commercial electricity price | 147.4 * | 0.81 | I(1) | I(1) |
| Log residential electricity price | 156.2 * | 0.86 | I(1) | I(1) |
| Dependent Variable | Total Energy | Industrial Energy | Transport Energy | Residential Electricity | Commercial Electricity |
|---|---|---|---|---|---|
| Short-Run Elasticities | |||||
| LDV | 0.204 **** | 0.205 **** | 0.141 **** | −0.152 * | 0.280 **** |
| GDP pc | 0.177 *** | 0.560 *** | 0.255 *** | 0.290 *** | 0.178 |
| Price | −0.156 **** | −0.118 **** | −0.241 **** | −0.129 **** | −0.162 ** |
| HDD | 0.173 **** | 0.180 **** | 0.137 *** | ||
| CDD | 0.040 **** | 0.118 **** | 0.054 *** | ||
| Long-Run Elasticities | |||||
| GDP pc | 0.222 *** | 0.705 *** | 0.297 *** | 0.252 *** | 0.247 |
| Price | −0.196 **** | −0.148 **** | −0.280 **** | −0.112 **** | −0.224 ** |
| HDD | 0.217 **** | 0.156 **** | 0.190 *** | ||
| CDD | 0.050 **** | 0.103 **** | 0.075 *** | ||
| Pooled Coefficients | |||||
| Time | −0.000 | 0.005 | 0.001 | 0.006 **** | 0.001 |
| Time-squared | −0.0001 ** | −0.0002 * | 0.000 | −0.000 | 0.000 |
| Observations | 1202 | 1150 | 1250 | 1108 | 1202 |
| x-sections | 48 | 50 | 50 | 48 | 48 |
| CD (p) | −0.8 (0.43) | −0.6 (0.55) | −2.1 (0.04) | 2.8 (0.00) | 1.5 (0.14) |
| Dependent Variable | Total Energy | Industrial Energy | Transport Energy | Residential Electricity | Commercial Electricity |
|---|---|---|---|---|---|
| LDV | -0.018 | 0.172 | 0.009 | −0.026 | 0.150 * |
| GDP pc | 0.097 | 0.581 | 0.414 **** | 0.112 | 0.020 |
| Price up | −0.437 **** | −0.310 | −0.385 ** | -0.013 | 0.214 |
| Price down | −0.304 * | −0.544 *** | −0.699 **** | 7608 | −0.900 ** |
| Price high | −0.478 **** | 0.106 | −0.447 **** | −0.191 *** | 0.060 |
| HDD | 0.220 **** | 0.227 **** | 0.010 | ||
| CDD | 0.032 * | 0.113 **** | 0.062 ** | ||
| Observations | 1202 | 1150 | 1250 | 1202 | 1202 |
| x-sections | 48 | 50 | 50 | 48 | 48 |
| CD (p) | −1.1 (0.28) | −1.8 (0.07) | 0.9 (0.89) | 5.1 (0.00) | 2.1 (0.04) |
| Dependent Variable | Total Energy | Industrial Energy | Residential Electricity | Commercial Electricity |
|---|---|---|---|---|
| Heterogeneous Elasticities | ||||
| LDV | 0.369 **** | 0.367 **** | 0.091 ** | 0.334 **** |
| GDP pc | 0.178 *** | 0.281 | 0.140 *** | 0.101 |
| HDD | 0.163 **** | 0.242 **** | 0.098 * | |
| CDD | 0.030 *** | 0.133 **** | 0.052 ** | |
| Pooled Elasticities | ||||
| Price up | −0.067 *** | −0.397 **** | −0.039 | −0.002 |
| Price down | 0.039 | −0.126 ** | −0.130 **** | −0.292 **** |
| Price high | −0.031 **** | −0.164 **** | −0.037 *** | 0.061 * |
| Observations | 1202 | 1150 | 1108 | 1202 |
| x-sections | 48 | 50 | 48 | 48 |
| CD (p) | −0.7(0.48) | 14.5(0.00) | 11.1(0.00) | 6.3(0.00) |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liddle, B. Accounting for Nonlinearity, Asymmetry, Heterogeneity, and Cross-Sectional Dependence in Energy Modeling: US State-Level Panel Analysis. Economies 2017, 5, 30. https://doi.org/10.3390/economies5030030
Liddle B. Accounting for Nonlinearity, Asymmetry, Heterogeneity, and Cross-Sectional Dependence in Energy Modeling: US State-Level Panel Analysis. Economies. 2017; 5(3):30. https://doi.org/10.3390/economies5030030
Chicago/Turabian StyleLiddle, Brantley. 2017. "Accounting for Nonlinearity, Asymmetry, Heterogeneity, and Cross-Sectional Dependence in Energy Modeling: US State-Level Panel Analysis" Economies 5, no. 3: 30. https://doi.org/10.3390/economies5030030
APA StyleLiddle, B. (2017). Accounting for Nonlinearity, Asymmetry, Heterogeneity, and Cross-Sectional Dependence in Energy Modeling: US State-Level Panel Analysis. Economies, 5(3), 30. https://doi.org/10.3390/economies5030030






