The Relevance of Political Stability on FDI: A VAR Analysis and ARDL Models for Selected Small, Developed, and Instability Threatened Economies
Abstract
:1. Introduction
2. Literature Review
2.1. The Comparative Studies Explored
2.2. Selected Studies of Single Economies Explored
2.3. Summary of Literature Review and Implications
3. Methodology
3.1. Panel Model
3.2. Vector Auto Regression
3.3. ARDL Models
3.4. Methodological and Data Constraints
4. Discussion and Results
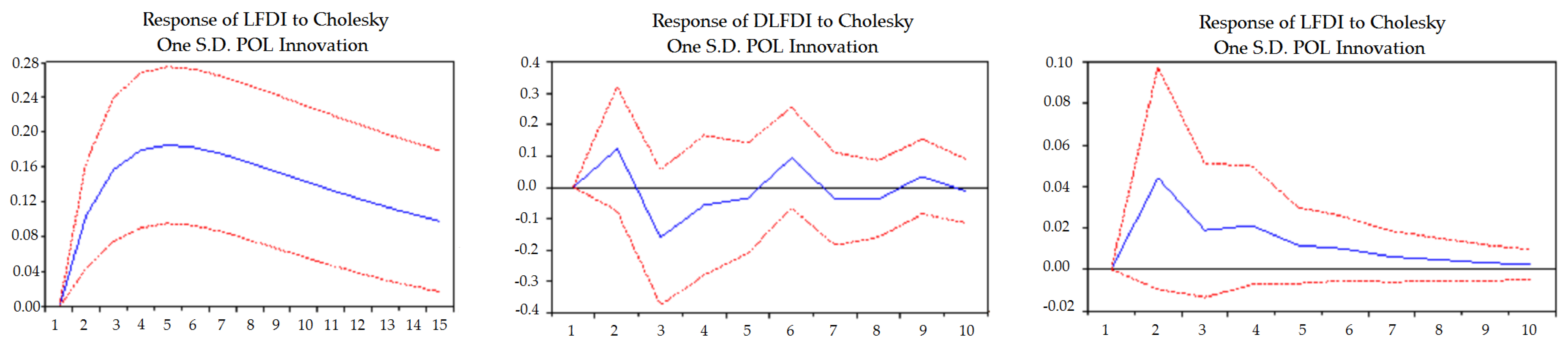
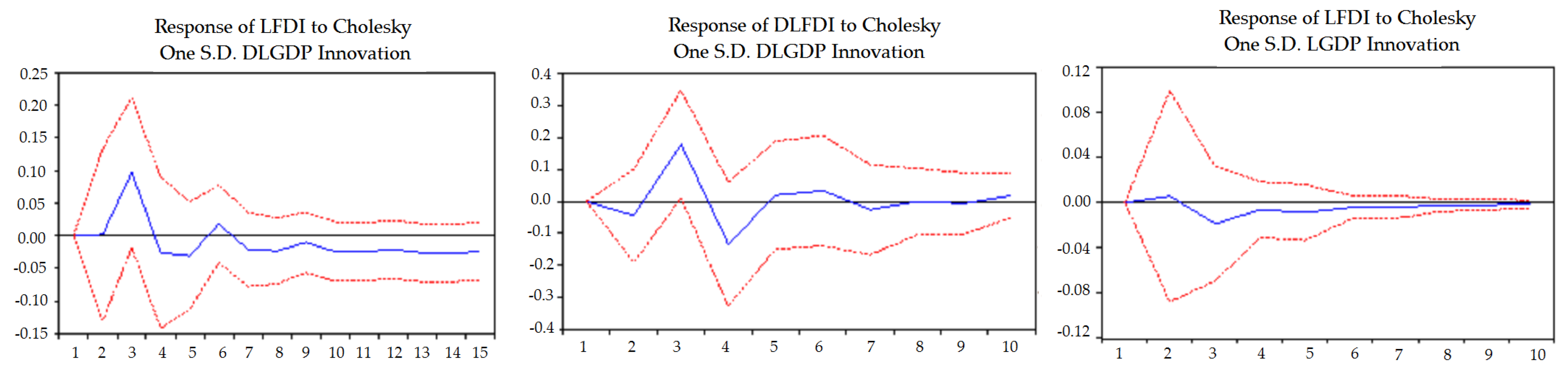
4.1. VAR Model Approach
4.2. ARDL Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Panel A | Panel A—Continued | Panel B | Panel C |
|---|---|---|---|
| Seychelles | Burundi | Australia | Mexico |
| Guinea-Bissau | Vanuatu | Canada | Israel |
| Lesotho | St. Kitts and Nevis | France | Russian Federation |
| Dominica | St. Vincent and the Grenadines | United Kingdom | Turkey |
| Grenada | Antigua and Barbuda | United States | |
| St. Lucia |
| Variable | Mean | Median | Maximum | Minimum | Std. Deviation | Skewness | Kurtosis | Observations | |
|---|---|---|---|---|---|---|---|---|---|
| GDP | Panel A | 1.22 × 109 | 8.64 × 108 | 9.50 × 109 | 4662335 | 1.16 × 109 | 3.145 | 24.916 | 373 |
| Panel B | 3.67 × 1012 | 1.77 × 1012 | 1.74 × 1013 | 4.43 × 1011 | 4.6 × 1012 | 1.769 | 4.72 | 170 | |
| Panel C | 5.81 × 1013 | 1.38 × 1012 | 1.28 × 1015 | 1.47 × 1011 | 1.99 × 1014 | 4.37 | 22.47 | 122 | |
| FDI | Panel A | 99575186 | 68421638 | 9.89 × 108 | 1093.496 | 1.22 × 108 | 4.023 | 24.916 | 363 |
| Panel B | 6.34 × 1010 | 3.4 × 1010 | 4.25 × 1011 | −3.36 × 1010 | 8.49 × 1010 | 2.332 | 8.16 | 170 | |
| Panel C | 2.17 × 1011 | 2.99 × 1010 | 3.85 × 1012 | 5.57 × 108 | 5.97 × 1011 | 3.919 | 19.605 | 122 | |
| Export | Panel A | 4.78 × 108 | 2.68 × 108 | 1.94 × 109 | 82674120 | 4.13 × 108 | 1.619 | 4.951 | 373 |
| Panel B | 5.97 × 1011 | 4.71 × 1011 | 2.34 × 1012 | 9.27 × 1010 | 4.72 × 1011 | 1.816 | 6.394 | 162 | |
| Panel C | 1.69 × 1013 | 3.91 × 1011 | 2.36 × 1014 | 4.59 × 1010 | 5.04 × 1013 | 3.364 | 13.247 | 120 | |
| Political stability | Panel A | 0.424 | 0.81 | 1.42 | −2.51 | 0.895 | −1.6 | 4.77 | 172 |
| Panel B | 0.501 | 0.55 | 1.01 | −0.2 | 0.276 | −0.533 | 3.491 | 31 | |
| Panel C | −0.539 | −0.68 | −0.1 | −0.8 | 0.249 | 0.714 | 1.888 | 15 | |
| Population | Panel A | 975517.4 | 108039.5 | 108116860 | 40833 | 2031449 | 2.888 | 10.961 | 374 |
| Panel B | 88451488 | 57453744 | 3.19 × 108 | 14927000 | 95128226 | 1.451 | 3.394 | 170 | |
| Panel C | 77479077 | 74116316 | 1.49 × 108 | 3956000 | 5203898 | −0.072 | 1.681 | 136 | |
| Area | Panel A | 144206.3 | 5000 | 1200000 | 80 | 279664.6 | 2.19 | 6.697 | 363 |
| Panel B | 58114336 | 45112000 | 1.89 × 108 | 5651000 | 60940263 | 1.289 | 3.065 | 165 | |
| Panel C | 35038522 | 22975000 | 1.32 × 108 | 285800 | 43234777 | 1.453 | 3.46 | 121 | |
| Null Hypothesis | Test statistic Value | ||
|---|---|---|---|
| 3 lags | 4 lags | 5 lags | |
| GDP does not Granger cause FDI | 6.82 *** (0.0003) | 5.554 *** (0.0005) | 5.554 ** (0.0005) |
| FDI does not Granger cause GDP | 2.622 * (0.0546) | 0.679 (0.6083) | 0.679 (0.6083) |
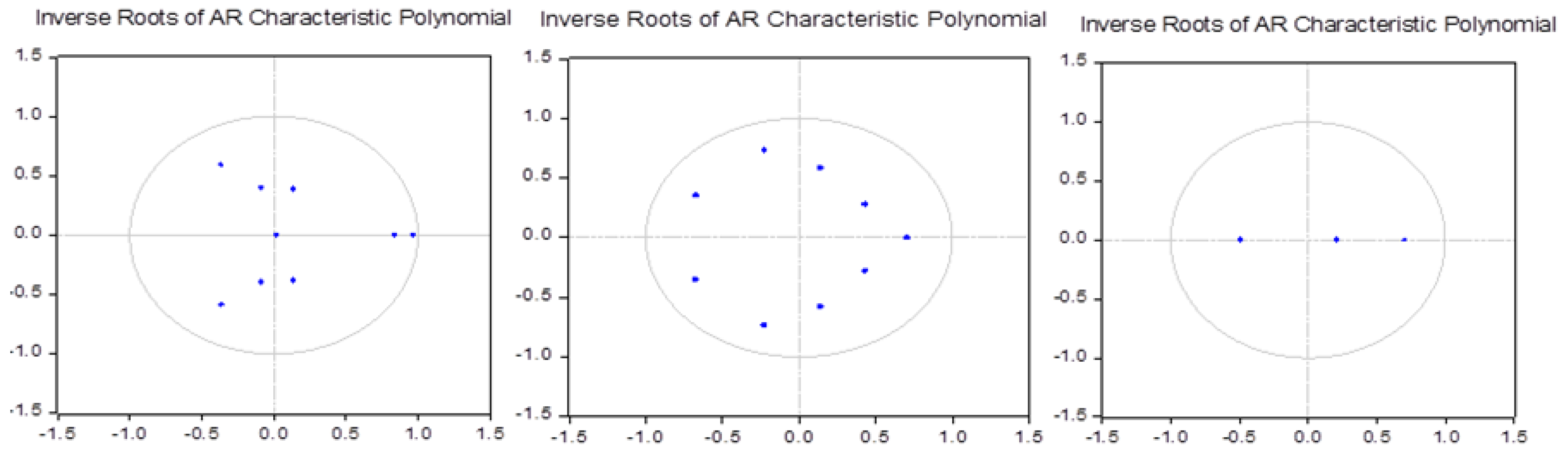
| Lags | Panel A LM-Stat | Panel B LM-Stat | Panel C LM-Stat |
|---|---|---|---|
| 1 | 13.404 (0.1452) | 13.49 (0.1417) | 14.366 (0.1099) |
| 2 | 12.45 (0.1891) | 10.71 (0.2963) | 16.411 (0.0518) |
| 3 | 16.49 (0.0513) | 9.458 (0.3202) | 10.457 (0.3147) |
| 4 | 5.319 (0.8056) | 9.459 (0.3961) | 13.717 (0.1327) |
| Country | Variable | ADF Test Statistic | ADF Test Statistic in First Difference | KPSS Test Statistic | KPSS Test Statistic in First Difference | Conclusion |
|---|---|---|---|---|---|---|
| Seychelles | GDP | −1.104 (0.6903) | −3.134 *** (0.0429) | 0.41 * | 0.101 | I(1) |
| FDI | −4.314 *** (0.04) | −7.235 *** (0.0000) | 0.142 | 0.23 | I(0) | |
| POL | −1.499 (0.5107) | −6.207 *** (0.0002) | 0.436 * | 0.122 | I(1) | |
| Guinea-Bissau | GDP | −1.211 (0.6455) | −2.932 * (0.0623) | 0.341 | 0.323 | I(1) |
| FDI | −2.107 (0.2444) | −4.663 *** (0.0022) | 0.349 * | 0.09 | I(1) | |
| POL | −4.554 ** (0.0122) | −7.964 *** (0.0001) | 0.353 * | 0.263 | I(1) | |
| Lesotho | GDP | −2.708 * (0.093) | −3.074 ** (0.0492) | 0.1663 | 0.127 | I(1) |
| FDI | −2.499 (0.1321) | −7.667 (0.0000) | 0.443 * | 0.207 | I(1) | |
| POL | −3.027 * (0.0523) | −3.995 *** (0.0087) | 0.2099 | 0.094 | I(1) | |
| Burundi | GDP | −4.94 *** (0.0011) | −1.645 (0.4372) | 0.323 | 0.423 * | I(0) |
| FDI | −3.655 ** (0.0176) | −3.099 * (0.0628) | 0.064 | 0.04 | I(0) | |
| POL | −0.755 (0.8076) | −4.24 *** (0.05) | 0.61 ** | 0.113 | I(1) | |
| Vanuatu | GDP | −1.49 (0.5099) | −2.395 (0.3684) | 0.52 ** | 0.207 | I(2) |
| FDI | −1.97 (0.2951) | −4.061 *** (0.0004) | 0.1772 | 0.151 | I(1) | |
| POL | −2.37 (0.1633) | −3.63 ** (0.0166) | 0.191 | 0.327 | I(1) | |
| St. Kitts and Nevis | GDP | −1.887 (0.3252) | −1.696 (0.4035) | 0.44 * | 0.18 | I(2) |
| FDI | −1.809 (0.3573) | −3.817 ** (0.0203) | 0.139 | 0.129 | I(1) | |
| POL | −0.697 (0.8075) | −2.73 (0.102) | 0.493 ** | 0.485 ** | I(2) | |
| Dominica | GDP | −0.767 (0.8044) | −3.54 ** (0.0197) | 0.566 ** | 0.106 | I(1) |
| FDI | −3.009 * (0.0531) | −5.312 *** (0.0006) | 0.164 | 0.107 | I(1) | |
| POL | −1.14 (0.674) | −4.916 (0.0013) | 0.483 ** | 0.0902 | I(1) | |
| St. Vincent and the Grenadines | GDP | −1.992 (0.2871) | −3.396 ** (0.0261) | 0.539 ** | 0.333 | I(1) |
| FDI | −1.968 (0.2966) | −4.434 *** (0.0034) | 0.315 * | 0.0657 | I(1) | |
| POL | −4.141 *** (0.006) | −3.974 *** (0.009) | 0.065 | 0.243 | I(0) | |
| Grenada | GDP | −2.172 (0.2219) | −4.439 *** (0.0034) | 0.528 ** | 0.304 | I(1) |
| FDI | −2.498 (0.1322) | −4.59 *** (0.0025) | 0.156 | 0.27 | I(1) | |
| POL | −1.496 (0.5128) | −4.246 *** (0.0049) | 0.409 * | 0.157 | I(1) | |
| Antigua and Barbuda | GDP | −1.692 (0.4173) | −2.319 (0.2815) | 0.4634 ** | 0.176 | I(2) |
| FDI | −1.888 (0.3341) | −2.16 (0.225) | 0.308 | 0.132 | I(2) | |
| POL | −1.555 (0.4827) | −3.418 ** (0.026) | 0.535 ** | 0.232 | I(1) | |
| St. Lucia | GDP | −2,187 (0.2172) | −4.346 *** (0.004) | 0.545 ** | 0.258 | I(1) |
| FDI | −3.0007 * (0.0539) | −4.029 *** (0.0076) | 0.21 | 0.32 | I(1) | |
| POL | −4.218 *** (0.0052) | −6.638 *** (0.0001) | 0.197 | 0.349 * | I(0) | |
| UK | GDP | −1.61 (0.4567) | −3.319 ** (0.0314) | 0.409 * | 0.115 | I(1) |
| FDI | −2.6886 * (0.0934) | −5.48 *** (0.004) | 0.13 | 0.067 | I(1) | |
| POL | −1.822 (0.3586) | −4.02 *** (0.0077) | 0.438* | 0.094 | I(1) | |
| Canada | GDP | −0.768 (0.804) | −3.05 * (0.0505) | 0.551 ** | 0.138 | I(1) |
| FDI | −3.835 ** (0.0387) | −6.123 *** (0.0007) | 0.1022 | 0.50 ** | I(0) | |
| POL | −2.79 * (0.0786) | −4.126 *** (0.0081) | 0.147 | 0.422 * | I(1) | |
| Australia | GDP | −0.303 (0.9065) | −3.738 ** (0.0134) | 0.526 ** | 0.143 | I(1) |
| FDI | −4.372 *** (0.0035) | −6.932 *** (0.0000) | 0.114 | 0.50 ** | I(0) | |
| POL | −2.582 (0.1146) | −3.741 ** (0.0133) | 0.423 * | 0.259 | I(1) | |
| USA | GDP | −2.986* (0.053) | −2.441 (0.1462) | 0.58 ** | 0.332 | I(2) |
| FDI | −2.512 (0.1292) | −3.422 ** (0.0248) | 0.098 | 0.122 | I(1) | |
| POL | −1.619 (0.4532) | −3.235 *** (0.0355) | 0.183 | 0.156 | I(1) | |
| France | GDP | −0.616 (0.8438) | −3.322 ** (0.0301) | 0.473 * | 0.177 | I(1) |
| FDI | −1.408 (0.5553) | −3.57 ** (0.0187) | 0.248 | 0.336 | I(1) | |
| POL | −2.487 (0.1348) | −4.96 *** (0.0012) | 0.361* | 0.139 | I(1) | |
| Turkey | GDP | −3.167 ** (0.0404) | −2.166 (0.2241) | 0.312 | 0.418 * | I(0) |
| FDI | −2.301 (0.1821) | −3.611 ** (0.0172) | 0.113 | 0.154 | I(1) | |
| POL | −1.77 (0.3821) | −3.396 ** (0.0261) | 0.192 | 0.262 | I(1) | |
| Russian Federation | GDP | −3.045 ** (0.0496) | −2.594 (0.2865) | 0.172 | 0.239 | I(0) |
| FDI | −1.508 (0.5069) | −3.234 ** (0.0355) | 0.2397 | 0.138 | I(1) | |
| POL | −1.094 (0.6909) | −5.364 *** (0.0007) | 0.529 ** | 0.059 | I(1) | |
| Israel | GDP | 0.121 (0.9569) | −4.33 *** (0.005) | 0.619 ** | 0.259 | I(1) |
| FDI | −2.713 * (0.0934) | −3.365 *** (0.0047) | 0.379 * | 0.11 | I(1) | |
| POL | −1.526 (0.4954) | −3.284 ** (0.0347) | 0.165 | 0.172 | I(1) | |
| Mexico | GDP | −3.108 ** (0.044) | −4.582 *** (0.0025) | 0.274 | 0.084 | I(0) |
| FDI | −3.793 ** (0.0114) | −3.333 ** (0.0332) | 0.38 * | 0.167 | I(1) | |
| POL | −2.369 (0.1647) | −2.068 (0.2584) | 0.252 | 0.312 | I(2) |
| Country | LM Test Statistic for GDP/FDI | LM Observed R-Squared for GDP/FDI | LM Test Statistic for FDI/POL | LM Observed R-Squared for FDI/POL |
|---|---|---|---|---|
| Seychelles | 0.447 (0.772) | 1.278 (0.528) | 0.102 (0.904) | 0.398 (0.8196) |
| Guinea-Bissau | 1.787 (0.2495) | 7.55 (0.0563) | 1.917 (0.2168) | 5.66 (0.0589) |
| Lesotho | 0.2856 (0.7612) | 1.304 (0.521) | 0.206 (0.8245) | 1.81 (0.4044) |
| Burundi | 1.914 (0.2173) | 5.3 (0.0706) | 0.128 (0.8842) | 1.103 (0.5762) |
| Vanuatu | / | 0.8197 (0.4638) | 2.164 (0.339) | |
| Dominica | 0.297 (0.751) | 1.105 (0.5754) | 0.125 (0.8834) | 0.3401 (0.8436) |
| St. Vincent and the Grenadines | 0.271 (0.7758) | 1.789 (0.4089) | 0.915 (0.4247) | 2.222 (0.3292) |
| Grenada | 0.081 (0.9228) | 0.396 (0.8203) | 1.184 (0.2685) | 4.246 (0.1197) |
| St. Lucia | 0.313 (0.7526) | 2.5895 (0.274) | 0.822 (0.4835) | 3.227 (0.1992) |
| UK | 0.16 (0.6965) | 0.244 (0.6211) | 0.9597 (0.4762) | 5.852 (0.0536) |
| Canada | 0.329 (0.7258) | 0.866 (0.6486) | 0.131 (0.881) | 0.921 (0.6311) |
| Australia | 0.061 (0.9407) | 0.168 (0.9191) | 2.2086 (0.1808) | 3.598 (0.0579) |
| USA | / | 0.597 (0.5799) | 2.491 (0.2878) | |
| France | 0.8667 (0.4433) | 2.118 (0.3469) | 0.101 (0.9045) | 0.276 (0.8712) |
| Turkey | 0.102 (0.9034) | 0.279 (0.8698) | 0.0045 (0.9955) | 0.012 (0.9938) |
| Russian Federation | 1.504 (0.2955) | 5.008 (0.0817) | 0.732 (0.4996) | 1.823 (0.402) |
| Israel | 0.345 (0.7435) | 3.334 (0.1888) | 0.594 (0.6759) | 5.44 (0.0593) |
| Mexico | 0.334 (0.7229) | 0.973 (0.6145) | ||
| Country | Heteroscedasticity F-Statistic for GDP/FDI | Heteroscedasticity Observed R-Squared for GDP/FDI | Heteroscedasticity F-Statistic for FDI/POL | Heteroscedasticity Observed R-Squared for FDI/POL |
|---|---|---|---|---|
| Seychelles | 0.629 (0.6824) | 3.83 (0.5745) | 1.23 (0.3637) | 6.094 (0.2972) |
| Guinea-Bissau | 0.654 (0.6883) | 4.858 (0.5622) | 0.486 (0.746) | 2.37 (0.668) |
| Lesotho | 1.173 (0.4055) | 7.02 (0.319) | 0.149 (0.9929) | 3.167 (0.9573) |
| Burundi | 0.309 (0.8955) | 2.198 (0.8212) | 0.688 (0.6966) | 7.335 (0.5009) |
| Vanuatu | / | 2.934 (0.0701) | 6.948 (0.0736) | |
| Dominica | 0.3835 (0.6879) | 0.8757 (0.6454) | 0.072 (0.9952) | 0.557 (0.9899) |
| St. Vincent and the Grenadines | 0.693 (0.6924) | 7.204 (0.5148) | 2.41 (0.1236) | 4.379 (0.112) |
| Grenada | 1.354 (0.3366) | 7.558 (0.2723) | 0.508 (0.7877) | 4.138 (0.658) |
| St. Lucia | 0.288 (0.9496) | 5.121 (0.8236) | 0.631 (0.7039) | 4.8198 (0.5671) |
| UK | 2.528 (0.0956) | 7.775 (0.1002) | 0.584 (0.7722) | 7.6895 (0.5657) |
| Canada | 0.419 (0.6654) | 0.952 (0.6214) | 3.152 (0.0896) | 12.117 (0.1461) |
| Australia | 0.315 (0.7347) | 0.725 (0.696) | 1.896 (0.1975) | 8.807 (0.1847) |
| USA | / | 0.1606 (0.9807) | 1.613 (0.9517) | |
| France | 1.2557 (0.3132) | 2.582 (0.2751) | 2.248 (0.140) | 4.1504 (0.1255) |
| Turkey | 0.016 (0.9842) | 0.038 (0.981) | 0.173 (0.8431) | 0.405 (0.8167) |
| Russian Federation | 1.338 (0.3422) | 7.513 (0.276) | 0.032 (0.9682) | 0.078 (0.962) |
| Israel | 2.647 (0.1814) | 10.934 (0.2054) | 0.387 (0.8823) | 6.98 (0.6392) |
| Mexico | 1.769 (0.2026) | 4.928 (0.1771) | / | |
References
- Aga, Ahmed Abdulrahman Khder. 2014. The Impact of Foreign Direct Investment on Economic Growth: A Case Study of Turkey 1980–2012. International Journal of Economics and Finance 6: 71–84. [Google Scholar]
- Akaike, H. 1974. A new look at the statistical model identification. IEEE Transactions on Automatic Control 19: 716–23. [Google Scholar] [CrossRef]
- Akande, Emmanuel, and Ola-David Oluyomi. 2010. The Two-Gap Model of Economic Growth in Nigeria: Vector Auto regression (VAR) Approach. Available online: https://www.gtap.agecon.purdue.edu/resources/res_display.asp?RecordID=3225 (accessed on 28 April 2016).
- Al-Eitan, Ghaith. 2013. A Dynamic Model for Determining Inward Foreign Direct Investment in Jordan. Perth: School of Economics and Finance, Curtin University. [Google Scholar]
- Almfraji, Mohammad Amin, and Mahmoud Khalid Almsafir. 2014. Foreign Direct Investment and Economic Growth Literature Review from 1994 to 2012. Procedia—Social and Behavioral Sciences 129: 206–13. [Google Scholar] [CrossRef]
- Asteriou, Dimitrios, Xeni Dassiou, and Dionysius Glycopantis. 2005. FDI and Growth: Evidence from a Panel of European Transition Countries. Spoudai 55: 9–30. [Google Scholar]
- Bačić, Katarina, Domagoj Račić, and Amina Ahec–Šonje. 2004. The effects of FDI on recipient countries in Central and Eastern Europe. Privredna Kretanja i Ekonomska Politika 14: 59–96. [Google Scholar]
- Balasubramanyam, Vudayagiri N., Mohammad Salisu, and David Sapsford. 1996. Foreign direct investment and growth in EP and IS countries. Economic Journal 106: 92–105. [Google Scholar] [CrossRef]
- Barnard, George. 1959. Control charts and stochastic processes. Journal of the Royal Statistical Society 21: 239–71. [Google Scholar]
- Bisson, Ourvashi. 2011. Can Better Institutions Attract More Foreign Direct Investment (FDI)? Evidence from Developing Countries. International Conference on Applied Economics. Available online: http://kastoria.teikoz.gr/icoae2/wordpress/wp-content/uploads/2011/10/007.pdf (accessed on 19 April 2016).
- Brada, Josef C., Ali M. Kutan, and Taner M. Yigit. 2005. The Effects of Transition and Political Instability on Foreign Direct Investment in ECE Emerging Markets. New York: United Nations Documents Index. [Google Scholar]
- Breusch, Trevor. 1978. Testing for Autocorrelation in Dynamic Linear Models. Australian Economic Papers 17: 334–55. [Google Scholar] [CrossRef]
- Breusch, Trevor, and Adrian Pagan. 1979. A Simple Test for Heteroscedasticity and Random Coefficient Variation. Econometrica 47: 1287–94. [Google Scholar] [CrossRef]
- Busse, Matthias, and Carsten Hefeker. 2005. Political Risk, Institutions and Foreign Direct Investment. Hamburgisches Welt-Wirtschafts-Archiv Discussion Paper 315. Available online: http://ageconsearch.umn.edu/bitstream/26388/1/dp050315.pdf (accessed on 19 April 2016).
- Büthe, Tim, and Helen V. Milner. 2008. The Politics of Foreign Direct Investment into Developing Countries: Increasing FDI through International Trade Agreements? American Journal of Political Science 52: 741–62. [Google Scholar] [CrossRef]
- Čičak, Krešimir, and Petar Sorić. 2015. The Interrelationship of FDI and GDP in European Transition Countries. International Journal of Management Science and Business Administration 1: 41–58. [Google Scholar] [CrossRef]
- Dickey, David A., and Wayne A. Fuller. 1979. Distribution of the Estimators for Autoregressive Time Series with a Unit Root. Journal of the American Statistical Association 74: 427–31. [Google Scholar] [CrossRef]
- Elkomy, Shimaa, Hilary Ingham, and Robert Read. 2016. Economic and Political Determinants of the Effects of FDI on Growth in Transition and Developing Countries. Thunderbird International Business Review 58: 347–62. [Google Scholar] [CrossRef]
- Gilboa, Eytan. 2005. The CNN Effect: The Search for a Communication Theory of International Relations. Political Communication 22: 27–44. [Google Scholar] [CrossRef]
- Godfrey, Leslie G. 1978. Testing Against General Autoregressive and Moving Average Error Models when the Regressors Include Lagged Dependent Variables. Econometrica 46: 1293–301. [Google Scholar] [CrossRef]
- Granger, Clive W.J. 1969. Investigating Causal Relations by Econometric Models and Cross-spectral Methods. Econometrica 37: 424–38. [Google Scholar] [CrossRef]
- Haksoon, Kim. 2010. Political Stability and Foreign Direct Investment. International Journal of Economics and Finance 2: 59–71. [Google Scholar]
- Iamsiraroj, Sasi, and Hristos Doucouliagos. 2015. Does Growth Attract FDI? Economics Journal. Available online: http://www.economics-ejournal.org/economics/journalarticles/2015–19 (accessed on 28 April 2016).
- Im, Kyung So, Mohammad Hashem Pesaran, and Yongcheol Shin. 2003. Testing for Unit Roots in Heterogeneous Panels. Journal of Econometrics 115: 53–74. [Google Scholar] [CrossRef]
- Jadhav, Pravin. 2012. Determinants of foreign direct investment in BRICS economies: Analysis of economic, institutional and political factor. Procedia - Social and Behavioral Sciences 37: 5–14. [Google Scholar] [CrossRef]
- Kaufmann, Daniel, Aart Kraay, and Massimo Mastruzzi. 2010. The Worldwide Governance Indicators: Methodology and Analytical Issues. Available online: www.govindicators.org (accessed on 19 April 2016).
- Khan, Mashrur Mustaque, and Ibne Akbar Mashque. 2013. The Impact of Political Risk on Foreign Direct Investment. MPRA Paper No. 47283. Available online: http://mpra.ub.uni-muenchen.de/47283/ (accessed on 28 April 2016).
- Kholdy, Shady. 1995. Causality between foreign investment and spillover efficiency. Applied Economics 27: 745–49. [Google Scholar] [CrossRef]
- Krugman, Paul. 2009. The Return of Depression Economics and the Crisis of 2008. New York: Norton & Company. [Google Scholar]
- Kwiatkowski, Denis, Peter C. B. Phillips, Peter Schmidt, and Yongcheol Shin. 1992. Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? Journal of Econometrics 54: 159–78. [Google Scholar] [CrossRef]
- Levin, Andrew, Chien-Fu Lin, and Chia-Shang James Chu. 2002. Unit Root Tests in Panel Data: Asymptotic and finite-sample properties. Journal of Econometrics 108: 1–24. [Google Scholar] [CrossRef]
- Livingston, Steven, and Todd Eachus. 1995. Humanitarian crises and U.S. foreign policy: Somalia and the CNN effect reconsidered. Political Communication 12: 413–29. [Google Scholar] [CrossRef]
- Lucas, Robert E., Jr. 1990. Why does not Capital Flow from Rich to Poor Countries. American Economic Review 80: 92–6. [Google Scholar]
- Maziarz, Mariusz. 2015. A review of the Granger-causality fallacy. The Journal of Philosophical Economics: Reflections on Economic and Social Issues 8: 86–105. [Google Scholar]
- McMillan, Susan M. 1999. Foreign Direct Investment in Three Regions of the South at the End of the 20th Century. Basingstoke: McMillan Ltd. [Google Scholar]
- Mehrara, Mohsen, Amin Haghnejad, Jalal Dehnavi, and Fereshteh Jandaghi Meybodi. 2010. Foreign Direct Investment, Exports, and Economic Growth in the Developing Countries: A Panel Data Approach. Journal of Academic Research in Economics 2: 259–80. [Google Scholar]
- Onwuka, Kevin, and Kutlu Yasar Zoral. 2009. Foreign Direct Investment and Imports Growth in Turkey. Journal of Yasar University 4: 2357–80. [Google Scholar]
- Page, E. S. 1954. Continuous Inspection Schemes. Biometrika 41: 100–15. [Google Scholar] [CrossRef]
- Pandya, Sonal S. 2016. Political Economy of Foreign Direct Investment: Globalized Production in the Twenty-First Century. Annual Review of Political Science 19: 455–75. [Google Scholar] [CrossRef]
- Pesaran, Mohammad Hashem H., Yongcheol Shin, and Richard J. Smith. 2001. Bounds Testing Approaches to the Analysis of Level Relationships. Journal of Applied Econometrics 16: 289–326. [Google Scholar] [CrossRef]
- Pesaran, Mohammad Hashem, and Yongcheol Shin. 1999. An Autoregressive Distributed Lag Modelling Approach to Cointegration Analysis. In Econometrics and Economic Theory in the 20th Century: The Ragnar Frisch Centennial Symposium. Edited by S. Strom. Cambridge: Cambridge University Press, chp. 11. [Google Scholar]
- Phillips, Peter C., and Pierre Perron. 1988. Testing for a Unit Root in Time Series Regression. Biometrika 75: 335–46. [Google Scholar] [CrossRef]
- Ray, Sarbapriya. 2012. Impact of Foreign Direct Investment on Economic Growth in India: A Co integration Analysis. Advances in Information Technology and Management 2: 187–201. [Google Scholar]
- Robinson, Piers. 2005. The CNN Effect Revisited. Critical Studies in Media Communication 22: 344–9. [Google Scholar] [CrossRef]
- Schwarz, Gideon. 1978. Estimating the Dimension of a Model. The Annals of Statistics 6: 461–4. [Google Scholar] [CrossRef]
- Thakur, Ramesh. 2006. The United Nations, Peace and Security: From Collective Security to the Responsibility to Protect. Cambridge: Cambridge University Press. [Google Scholar]
- Wooldridge, Jeffrey M. 2002. Econometric Analysis of Cross-Section and Panel Data. Cambridge: MIT Press. [Google Scholar]
- World Bank. 2016. World Development Indicators. Available online: http://data.worldbank.org/ (accessed on 12 April 2016).
| 1 | Simply stated, the CNN effect states that there is a strong connection between the news that is covered and policy-making (Gilboa 2005). This can be extended to the sphere of global economics, despite the primary field of the CNN effect being journalism and political science, where the impact of TV coverage on policy-making is discussed. The way we attempt to do so is through understanding whether negative coverage of political events decreases investor confidence into these countries and thus, investments. |
| 2 | Using the formula GDP t × GDP deflator base year/GDP deflator t where the base year was the value of the GDP deflator for the last year where the data was available—in most cases, 2014 and t are the years for which the GDP data was available. |
| 3 | There are two possible solutions when considering negative FDI inflows. Not using logged versions of the variables probably results in heteroscedasticity issues, amongst others. Thus, two solutions are possible: considering the negative values as NA-s or adding an arbitrary constant. As we find, the first approach unacceptable and accept that the second is not considered adequate universally, the suggested panel specification seems like the best approach to focus on the substantial issues of this paper. |
| 4 | In the case of our model, we examine causality between three variables—FDI, GDP and political stability and absence of violence/terrorism. |
| 5 | The data for the years 1997, 1999 and 2001 was generated by averaging the values of the values for t − 1 and t + 1, meaning that for the year 1997 the average value of the index for 1996 and 1998 was calculated. |
| 6 | This is also the only variable to which no log transformation, or any other statistical transformation, had been applied. |
| 7 | Test results for the panel C Granger causality test with three lags, as well as a short discussion about the results, are available in the Appendix A. |

| Variable | Levin, Lin and Chu t | Im, Pesaran and Schin W-stat | ADF-Fischer Chi Square | PP-Fischer Chi Square | Conclusion | |
|---|---|---|---|---|---|---|
| GDP | Panel A | −5.796 ** (0.0000) | −1.886 * (0.0297) | 35.471 * (0.0346) | 33.55 (0.0545) | I(1) |
| In first difference | −9.604 ** (0.0000) | −9.206 ** (0.0000) | 125.55 ** (0.0000) | 143.425 ** (0.0000) | ||
| Panel B | 0.078 (0.5311) | 3.215 (0.9993) | 1.147 (0.9997) | 0.9334 (0.9999) | I(1) | |
| In first difference | −8.158 ** (0.0000) | −7.446 (0.0000) | 67.342 (0.0000) | 65.938 (0.0000) | ||
| Panel C | −8.705 ** (0.0000) | −12.653 ** (0.0000) | 117.31 ** (0.0000) | 108.929 ** (0.0000) | I(0) | |
| FDI | Panel A | −5.421 ** (0.0000) | −5.001 ** (0.0000) | 63.3486 ** (0.0000) | 72.883 ** (0.0000) | I(0) |
| Panel B | −2.021 * (0.0216) | −1.565 (0.0588) | 15.54 (0.1136) | 14.113 (0.1679) | I(1) | |
| In first difference | −11.932 ** (0.0000) | −12.618 ** (0.0000) | 118.22 ** (0.0000) | 107.06 ** (0.0000) | ||
| Panel C | −3.958 ** (0.0000) | −4.647 ** (0.0000) | 37.947 ** (0.0000) | 43.809 ** (0.0000) | I(0) | |
| Exp | Panel A | −3.175 ** (0.0007) | −2.529 ** (0.0057) | 42.838 ** (0.0049) | 45.155 ** (0.0025) | I(0) |
| Panel B | 0.7669 (0.7784) | 3.112 (0.9991) | 0.9644 (0.9999) | 0.87092 (0.9999) | I(1) | |
| In first difference | −9.961 ** (0.0000) | −9.58 ** (0.0000) | 89.2926 ** (0.0000) | 116.361 ** (0.0000) | ||
| Panel C | −8.723 ** (0.0000) | −7.386 ** (0.0000) | 64.405 ** (0.0000) | 57.447 ** (0.0000) | I(0) | |
| Pol | Panel A | −2.9711 ** (0.0015) | −2.7115 ** (0.0033) | 41.521 ** (0.0071) | 39.909 * (0.0111) | I(0) |
| Panel B | −1.761 * (0.0391) | −1.679 * (0.0466) | 10.44 * (0.0336) | 9.636 * (0.047) | I(0) | |
| Panel C | −5.0694 ** (0.0000) | −2.692 ** (0.0036) | 28.21 ** (0.0004) | 271.71 ** (0.0000) | I(0) | |
| Pop | Panel A | 0.0599 (0.5239) | 1.0002 (0.8414) | 22.141 (0.4515) | 56.4981 ** (0.0001) | I(2) |
| In second difference | −6.474 ** (0.0000) | −5.566 ** (0.0000) | 83.12 ** (0.0000) | 48.604 ** (0.0000) | ||
| Panel B | −0.3597 (0.3595) | 4.557 (1.000) | 3.796 (0.9561) | 1.56 (0.9987) | I(2) | |
| In second difference | −9.787 ** (0.0000) | −9.488 ** (0.0000) | 91.967 ** (0.0000) | 94.309 (0.0000) | ||
| Panel C | −4.713 ** (0.0000) | −3.217 ** (0.0006) | 31.882 ** (0.0001) | 65.426 ** (0.0000) | I(0) | |
| Land | Panel A | 0.043 (0.5173) | −0.501 (0.3081) | 13.965 (0.6013) | 13.598 (0.6287) | I(1) |
| In first difference | −9.091 ** (0.0000) | −10.813 ** (0.0000) | 128.805 ** (0.0000) | 129.657 (0.0000) | ||
| Panel B | 1.67 (0.9525) | 0.421 (0.6632) | 11.43 (0.325) | 14.137 (0.1668) | I(1) | |
| In first difference | ||||||
| Panel C | −1.537 (0.0621) | 0.244 (0.5964) | 11.154 (0.1931) | 10.834 (0.2113) | I(1) | |
| In first difference | −6.416 ** (0.0000) | −7.379 ** (0.0000) | 60.041 ** (0.0000) | 59.721 ** (0.0000) | ||
| Null Hypothesis | Test Statistic Value | Number of Lags | ||
|---|---|---|---|---|
| Panel A | Panel B | Panel C | ||
| Pol does not Granger cause FDI | 4.656 ** (0.0114) | 3.561 * (0.0764) | 2.214 (0.1905) | 2 |
| Pol does not Granger cause FDI | 12.582 *** (0.0005) | 2.252 (0.1483) | 1.3 (0.4171) | 1 |
| Pol does not Granger cause GDP | 1.682 (0.1906) | 0.197 (0.823) | 0.418 (0.6759) | 2 |
| Pol does not Granger cause GDP | 0.066 (0.4747) | 0.391 (0.5383) | 0.093 (0.7669) | 1 |
| FDI does not Granger cause POL | 0.909 (0.4058) | 1.141 (0.3429) | 0.269 (0.7725) | 2 |
| FDI does not Granger cause POL | 1.13 (0.2897) | 0.0396 (0.5383) | 0.0029 (0.9582) | 1 |
| FDI does not Granger cause GDP | 0.202 (0.8171) | 0.226 (0.7982) | 1.659 (0.195) | 2 |
| FDI does not Granger cause GDP | 2.142 (0.1442) | 0.294 (0.5888) | 12.6812 *** (0.0005) | 1 |
| GDP does not Granger cause FDI | 6.394 *** (0.0019) | 2.62 * (0.0764) | 15.167 *** (0.000) | 2 |
| GDP does not Granger cause FDI | 8.065 *** (0.0048) | 3.634 * (0.0586) | 0.057 (0.811) | 1 |
| GDP does not Granger cause POL | 2.431 * (0.0924) | 0.211 (0.812) | 0.342 (0.7233) | 2 |
| GDP does not Granger cause POL | 0.514 (0.4747) | 0.264 (0.6126) | 0.114 (0.7434) | 1 |
| Dependant Variable | R-Squared | Adjusted R-Squared | S.E. Equation | F-Statistic | Akaike AIC | Number of Lags |
|---|---|---|---|---|---|---|
| Panel A | ||||||
| GDP | 0.17 | 0.08 | 0.586 | 1.95 | −2.15 | 3 |
| FDI | 0.816 | 0.796 | 0.649 | 42.051 | 2.07 | |
| POL | 0.944 | 0.939 | 0.195 | 161.34 | −0.33 | |
| Panel B | ||||||
| GDP | 0.801 | 0.581 | 0.029 | 3.63 | −3.92 | 3 |
| FDI | 0.778 | 0.532 | 0.424 | 3.158 | 1.422 | |
| POL | 0.616 | 0.19 | 0.199 | 0.149 | −0.671 | |
| Panel C | ||||||
| GDP | 0.34 | −0.04 | 0.271 | 4.683 | −1.937 | 1 |
| FDI | 0.728 | 0.573 | 0.045 | 0.901 | 0.519 | |
| POL | 0.916 | 0.868 | 0.079 | 19.105 | −3.048 | |
| Country | GDP and FDI ARDL Bounds Test | Null Hypothesis of No Long-Run Relationship | FDI and POL ARDL Bounds Test | Null Hypothesis of No Long-Run Relationship |
|---|---|---|---|---|
| Seychelles | 12.88 **** | Rejected | 6.237 **** | Rejected |
| Guinea-Bissau | 2.33 | Failed to reject | 6.467 **** | Rejected |
| Lesotho | 5.021 *** | Rejected | 38.865 **** | Rejected |
| Burundi | 14.391 **** | Rejected | 5.016 *** | Rejected |
| Vanuatu | / | 5.37 **** | Rejected | |
| Dominica | 7.738 **** | Rejected | 3.56 * | Rejected |
| St. Vincent and the Grenadines | 8.151 **** | Rejected | 1.63 | Failed to reject |
| Grenada | 2.432 | Failed to reject | 3.214 * | Rejected |
| St. Lucia | 8.037 **** | Rejected | 0.785 | Failed to reject |
| UK | 1.276 | Failed to reject | 2.903 | Failed to reject |
| Canada | 2.67 | Failed to reject | 2.8003 | Failed to reject |
| Australia | 0.759 | Failed to reject | 3.112 * | Rejected |
| USA | / | 4.012 ** | Rejected | |
| France | 1.056 | Failed to reject | 0.747 | Failed to reject |
| Turkey | 13.738 **** | Rejected | 2.956 | Failed to reject |
| Russian Federation | 6.442 **** | Rejected | 0.763 | Failed to reject |
| Israel | 11.39 **** | Rejected | 2.874 | Failed to reject |
| Mexico | 4.402 *** | Rejected | / | |
| Country | FDI Long Run Coefficient | POL Long Run Coefficient |
|---|---|---|
| Seychelles | −1.18 *** (0.0001) | −1.717 (0.1049) |
| Guinea-Bissau | / | 7.84 (0.1432) |
| Lesotho | 0.1003 (0.4456) | −0.696 (0.3738) |
| Burundi | −0.009 (0.7238) | 1.835 ** (0.028) |
| Vanuatu | / | 2.39 ** (0.0308) |
| Dominica | 1.106 (0.1539) | 0.098 (0.8642) |
| St. Vincent and the Grenadines | −0.224 (0.2259) | / |
| Grenada | / | 0.691 (0.295) |
| St. Lucia | 0.278 (0.1519) | / |
| UK | / | / |
| Canada | / | |
| Australia | 5.46 (0.7219) | |
| USA | 0.482 (0.1643) | |
| France | / | |
| Turkey | 0.294 (0.1669) | / |
| Russian Federation | 0.3304 *** (0.0000) | |
| Israel | 1.003 *** (0.0093) | |
| Mexico | 0.123 ** (0.0139) | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurecic, P.; Kokotovic, F. The Relevance of Political Stability on FDI: A VAR Analysis and ARDL Models for Selected Small, Developed, and Instability Threatened Economies. Economies 2017, 5, 22. https://doi.org/10.3390/economies5030022
Kurecic P, Kokotovic F. The Relevance of Political Stability on FDI: A VAR Analysis and ARDL Models for Selected Small, Developed, and Instability Threatened Economies. Economies. 2017; 5(3):22. https://doi.org/10.3390/economies5030022
Chicago/Turabian StyleKurecic, Petar, and Filip Kokotovic. 2017. "The Relevance of Political Stability on FDI: A VAR Analysis and ARDL Models for Selected Small, Developed, and Instability Threatened Economies" Economies 5, no. 3: 22. https://doi.org/10.3390/economies5030022
APA StyleKurecic, P., & Kokotovic, F. (2017). The Relevance of Political Stability on FDI: A VAR Analysis and ARDL Models for Selected Small, Developed, and Instability Threatened Economies. Economies, 5(3), 22. https://doi.org/10.3390/economies5030022





