Sources of Economic Growth in Zambia, 1970–2013: A Growth Accounting Approach
Abstract
:1. Introduction
2. Background
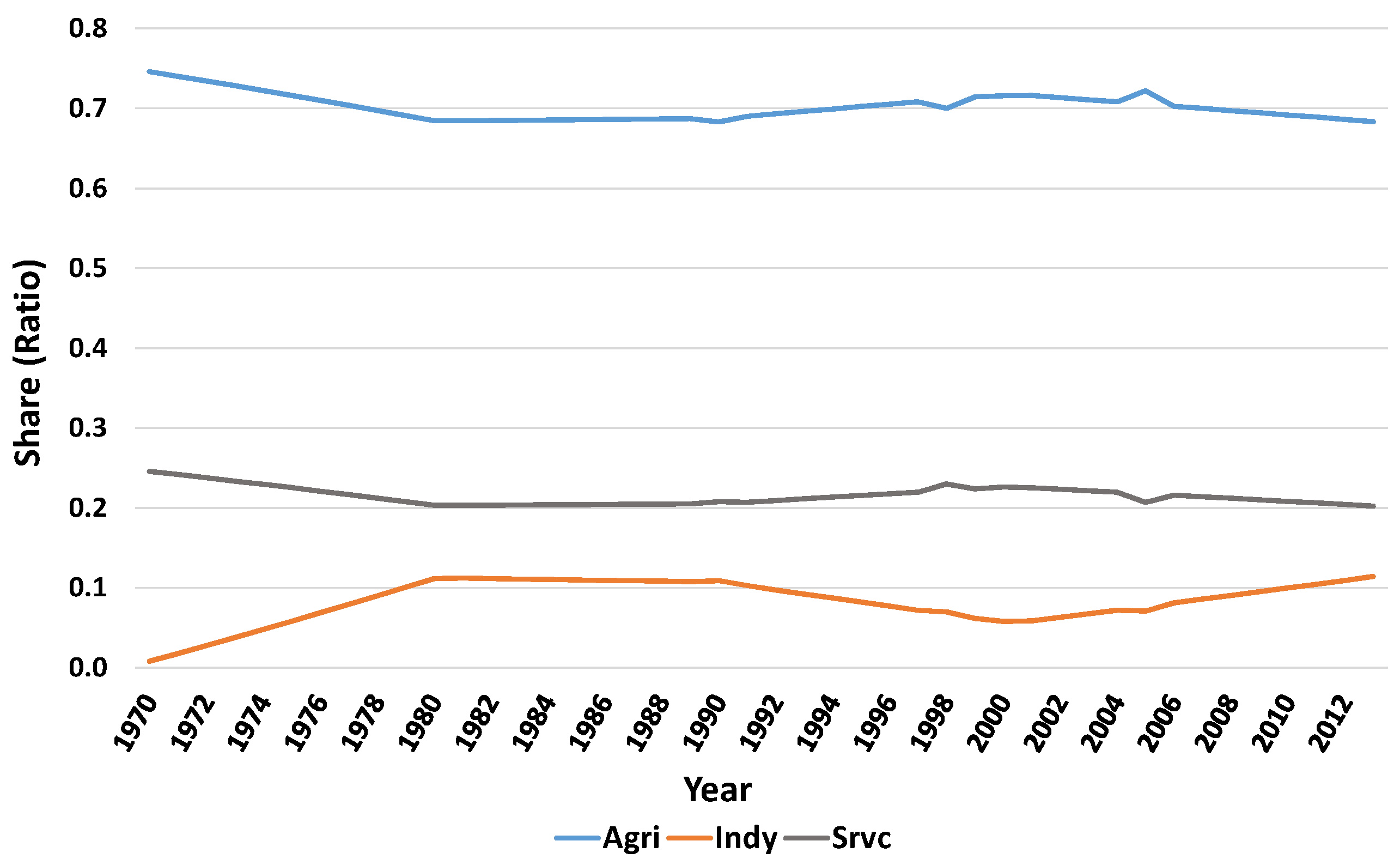
2.1. Agricultural Sector
2.2. Industry Sector
2.3. Services Sector
3. Methodology
3.1. Alternative TFP Estimation Methods
3.2. Neo-Classical Theory and TFP Estimation
4. Data
Data Issues
5. Results and Discussion
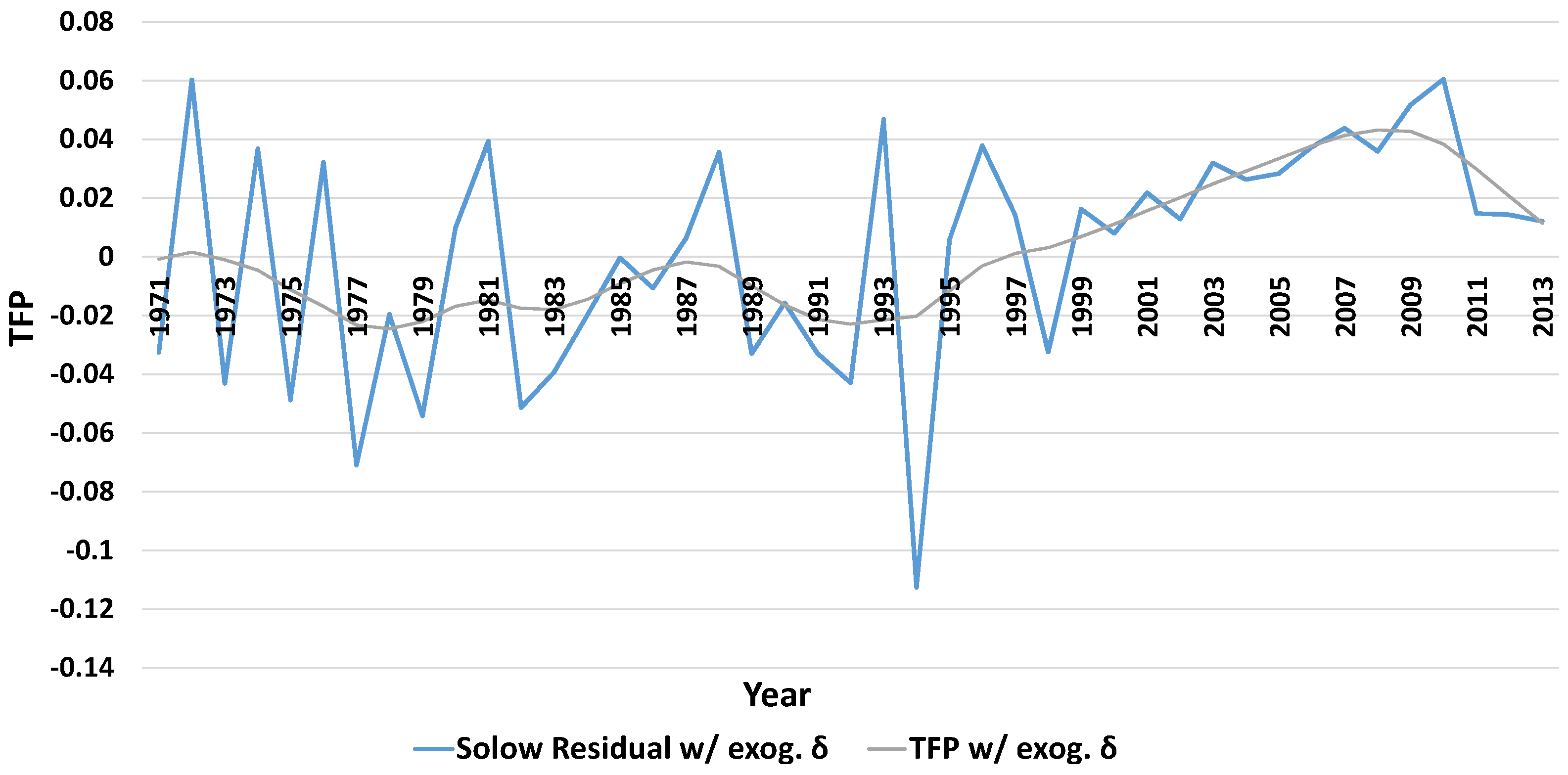
5.1. Economy-Wide Analysis
5.2. Sectoral Analysis
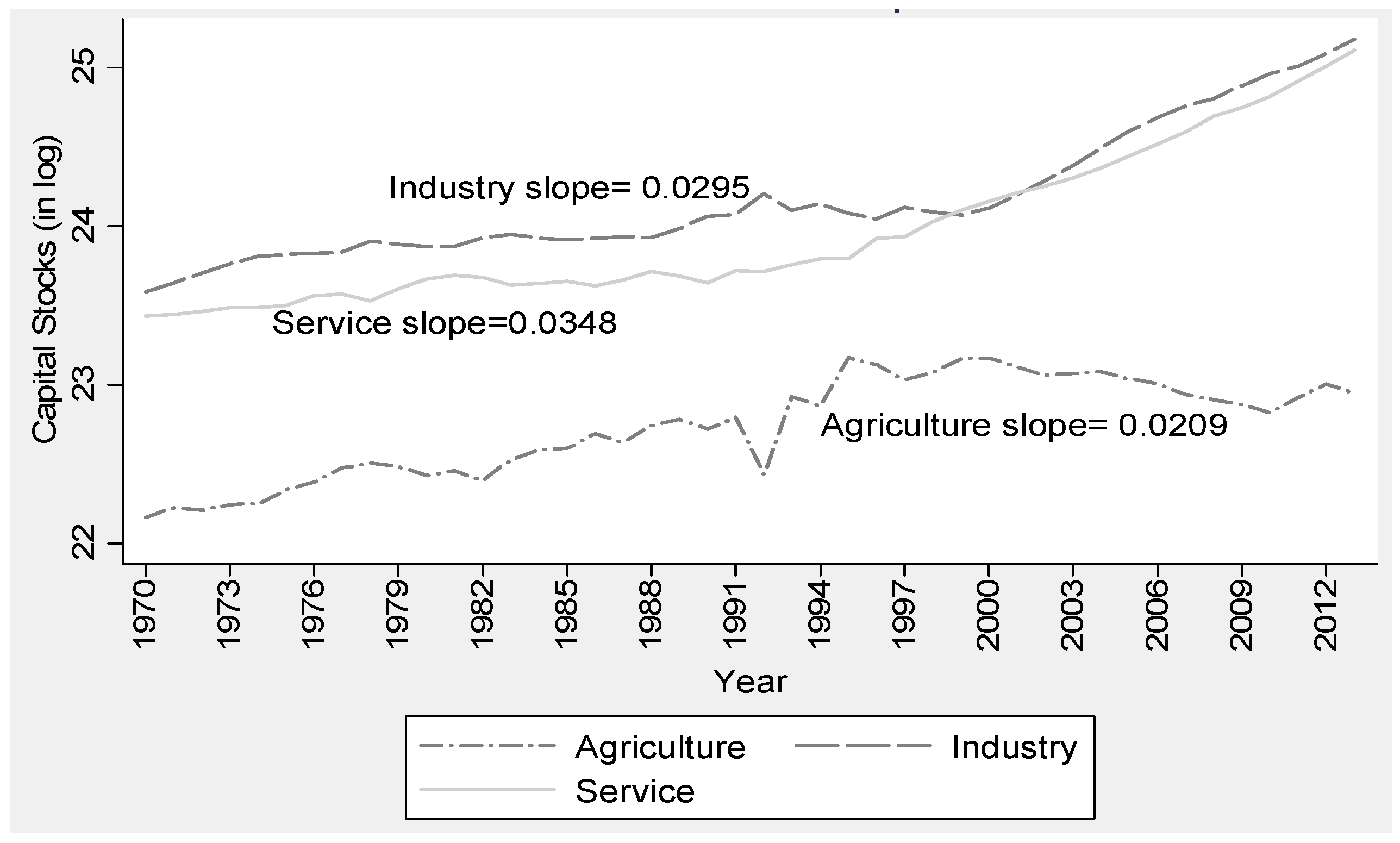
5.3. Sectoral TFP Analysis
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Sectoral Output Contributions to GDP and TFPs adapted from Roe et al. (2014)
A.2. Estimation of Sectoral TFP
References
- Abdulai, Abdul Nafeo, and Awudu Abdulai. 2015. Allocative and scale efficiency among maize farmers in Zambia: A zero efficiency stochastic frontier approach. Applied Economics 48: 5364–78. [Google Scholar] [CrossRef]
- Abel, Andrew B., Ben S. Bernanke, and Dean Croushore. 2008. Macroeconomics, 6th ed. New York: Addison Wesley Longman. [Google Scholar]
- Adamopoulos, T., and D. Restuccia. 2014. The size distribution of farms and international productivity differences. The American Economic Review 104: 1667–97. [Google Scholar] [CrossRef]
- Adams, Martin. 2003. Land Tenure Policy and Practice in Zambia: Issues Relating to the Development of the Agricultural Sector. Draft Document for DFID. Lusaka: DFID. [Google Scholar]
- Aghion, Philippe, and Peter Howitt. 1992. A Model of Growth through Creative Destruction. Econometrica 60: 323–51. [Google Scholar] [CrossRef]
- Aguiar, Diana, Leonardo Costa, and Elvira Silva. 2016. An Attempt to Explain Differences in Economic Growth: A Stochastic Frontier Approach. Bulletin of Economic Research. [Google Scholar] [CrossRef]
- Aigner, Dennis J., C. A. Knox Lovell, and Peter Schmidt. 1977. Formulation and Estimation of Stochastic Frontier Production Function Models. Journal of Econometrics 6: 21–37. [Google Scholar] [CrossRef]
- Altug, Sumru, Alpay Filiztekin, and Pamuk Sevket. 2008. Sources of Long-Term Economic Growth for Turkey, 1880–2005. European Review of Economic History 12: 393–430. [Google Scholar] [CrossRef]
- Anyanwu, John C. 2014. Factors Affecting Economic Growth in Africa: Are There Any Lessons from China? African Development Review 26: 468–93. [Google Scholar] [CrossRef]
- Bigsten, Arne, and Sven Tengstam. 2008. Smallholder Income Diversification in Zambia: The Way Out of Poverty. Lusaka: Food Security Research Project. [Google Scholar]
- Byerlee, Derek, and Carl K. Eicher. 1997. Africa’s Emerging Maize Revolution. Boulder: Lynne Rienner Publishers. [Google Scholar]
- Derek Byerlee, Alain de Janvry, and Elisabeth Sadoulet. 2009. Agriculture for Development: Toward a New Paradigm. Annual Review of Resource Economics 1: 15–35. [Google Scholar] [CrossRef]
- Carmody, Brendan Patrick. 2004. The Evolution of Education in Zambia. Lusaka: Bookworld Publishers. [Google Scholar]
- Carmody, Brendan Patrick. 2009. An Asian-driven economic recovery in Africa? The Zambian case. World Development 37: 1197–207. [Google Scholar] [CrossRef]
- Central Statistical Office. 2016. Zambia’s 2015 Living Conditions and Monetary Survey; Lusaka: Ministry of Finance.
- Cervantes-Godoy, Dalila, and Jonathan Brooks. 2008. Smallholder Adjustment in Middle-Income Countries: Issues and Policy Responses. OECD Food, Agriculture and Fisheries Working Papers No. 12. Paris: OECD. [Google Scholar]
- Chiona, Susan, Thomson Kalinda, and Gelson Tembo. 2014. Stochastic Frontier Analysis of the Technical Efficiency of Smallholder Maize Farmers in Central Province, Zambia. Journal of Agricultural Science 6: 108–18. [Google Scholar] [CrossRef]
- Chirwa, Themba G., and Nicholas M. Odhiambo. 2016. Sources of Economic Growth in Zambia: An Empirical Investigation. Pretoria: University of South Africa. [Google Scholar]
- Coelli, Tim J., and D. S. Prasada Rao. 2005. Total Factor Productivity Growth in Agriculture: A Malmquist Index Analysis of 93 Countries, 1980–2000. Agricultural Economics 32: 115–34. [Google Scholar] [CrossRef]
- Consumer Unit Trust Society (CUTS). 2008. Evolution of Service Sector in Zambia towards Greater Trade Orientation: An Overview. Briefing Paper No. 1/2008. Jaipur: CUTS. [Google Scholar]
- De Janvry, Alain, Kyle Emerick, Marco Gonzalez-Navarro, and Elisabeth Sadoulet. 2015. Delinking land rights from land use: Certification and migration in Mexico. The American Economic Review 105: 3125–49. [Google Scholar] [CrossRef]
- DiJohn, Jonathan. 2010. The Political Economy of Taxation and State Resilience in Zambia since 1990. London: Crisis States Research Centre, DESTIN, LSE. [Google Scholar]
- El-Hadj, M. Bah. 2013. Sectoral Productivity in Developing Countries. Available online: http://www.iariw.org/papers/2013/BahPaper.pdf (accessed on 17 December 2016).
- Greene, William H. 2008. The Econometric Approach to Efficiency Analysis. In The Measurement of Productive Efficiency and Productivity Change. Oxford: Oxford University Press, pp. 92–250. [Google Scholar]
- Haacker, Markus. 2002. The Economic Consequences of HIV/AIDS in Southern Africa. IMF Working Paper. Available online: https://ssrn.com/abstract=879415 (accessed on 14 December 2016).
- Hayami, Yujiro, and Vernon W. Ruttan. 1985. Population Growth and Agricultural Productivity. In Population Growth and Economic Development: Issues and Evidence. Edited by D. Gale Jonson and Ronald D. Lee. Madison: University of Wisconsin Press, pp. 57–101. [Google Scholar]
- Herrendorf, Berthold, Richard Rogerson, and Ákos Valentinyi. 2013. Growth and Structural Transformation (No. w18996). Cambridge: National Bureau of Economic Research. [Google Scholar]
- Isaksson, Anders. 2007. Determinants of Total Factor Productivity: A literature Review. Vienna: Research and Statistics Branch UNIDO. [Google Scholar]
- Jerven, Morten. 2010. Random Growth in Africa? Lessons from an Evaluation of the Growth Evidence on Botswana, Kenya, Tanzania and Zambia, 1965–1995. The Journal of Development Studies 46: 274–94. [Google Scholar] [CrossRef]
- Johnston, Bruce F. 1970. Agriculture and Structural Transformation in Developing Countries: A Survey of Research. Journal of Economic Literature 8: 369–404. [Google Scholar]
- Koo, Won W., and Jianqiang Lou. 1997. The Relationship between the Agricultural and Industrial Sectors in Chinese Economic Development. Fargo: Department of Agricultural Economics, Agricultural Experiment Station, North Dakota State University. [Google Scholar]
- Ministry of Agriculture and Co-Operatives. 2004. National Agricultural Policy; Lusaka: Ministry of Agriculture and Co-Operatives.
- Mankiw, N. Gregory, David Romer, and David N. Weil. 1992. A Contribution to the Empirics of Economic Growth. The Quarterly Journal of Economics 107: 407–37. [Google Scholar] [CrossRef]
- Manyika, James, Lenny Mendonca, Jaana Remes, Stefan Klubmann, Richard Dobbs, Kuntala Karkun, Vitaly Klintsov, Christina Kükenshöner, Mikhail Nikomarov, Charles Roxburgh, and et al. 2010. How to Compete and Grow: A Sector Guide to Policy. San Francisco: McKinsey Global Institute. [Google Scholar]
- Mason, Nicole M., and Robert J. Myers. 2013. The effects of the Food Reserve Agency on maize market prices in Zambia. Agricultural Economics 44: 203–16. [Google Scholar] [CrossRef]
- Mattoo, Aaditya, and Lucy Payton. 2007. Services Trade and Development: The Experience of Zambia. Washington: World Bank Publications. [Google Scholar]
- Meeusen, Wim, and Julien van Den Broeck. 1977. Efficiency Estimation from Cobb-Douglas Production Functions with Composed Error. International Economic Review 18: 435–44. [Google Scholar] [CrossRef]
- Ministry of Agriculture. 2017. CAADP in Zambia. Available online: http://www.agriculture.gov.zm/index.php?option=com_content&view=article&id=127:caadp-in-zambia&catid=88&Itemid=1626 (accessed on 8 May 2017).
- Mukherjee, A. 2013. The Service Sector in India. Asian Development Bank Economics Working Paper Series 352; Mandaluyong City: Asian Development Bank. [Google Scholar]
- Mulungu, Kelvin, and Natasha Chilundika. 2016. Zambia Food Reserve Agency Pricing Mechanisms and the Impact on Maize Markets. Jaipur: CUTS. [Google Scholar]
- Musaba, Emmanuel, and Isaac Bwacha. 2014. Technical Efficiency of Small Scale Maize Production in Masaiti District, Zambia: A Stochastic Frontier Approach. Journal of Economics and Sustainable Development 5: 104–11. [Google Scholar]
- Mwanakatwe, J. M. 1971. The Growth of Education in Zambia since Independence. Lusaka: Zambia Education Publishing House. [Google Scholar]
- Ndulo, Manenga, and Dale Mudenda. 2010. Trade Policy Reform and Adjustment in Zambia. In United Nations Conference on Trade and Development. Geneva: United Nations Conference on Trade and Development, Available online: http://www.saipar.org:8080/eprc/handle/123456789/224 (accessed on 20 October 2016).
- Ng’ombe, John, and Thomson Kalinda. 2015. A Stochastic Frontier Analysis of Technical Efficiency of Maize Production under Minimum Tillage in Zambia. Sustainable Agriculture Research 4: 31. [Google Scholar] [CrossRef]
- Ogundari, Kolawole. 2014. The paradigm of agricultural efficiency and its implication on food security in Africa: What does meta-analysis reveal? World Development 64: 690–702. [Google Scholar] [CrossRef]
- Ranis, Gustav, and John C. H. Fei. 1961. A theory of economic development. The American Economic Review 51: 533–65. [Google Scholar]
- Resnick, Danielle, and James Thurlow. 2014. The Political Economy of Zambia’s Recovery: Structural Change without Transformation? IFPRI Discussion Paper Number 01320. Washington: IFPRI. [Google Scholar]
- Rodrik, Dani. 2015. From welfare state to innovation state. Project Syndicate, January 14. [Google Scholar]
- Roe Terry, L., Rodney Smith, and Choi Donggul. 2014. Introduction to Growth Accounting as a Diagnostic. Minnesota: University of Minnesota. [Google Scholar]
- Romer, Paul M. 1986. Increasing Returns and Long-Run Growth. Journal of Political Economy 94: 1002–37. [Google Scholar] [CrossRef]
- Sachs, Jeffrey David, and Andrew M. Warner. 1997. Fundamental Sources of Long-Run Growth. The American Economic Review 87: 184–88. [Google Scholar]
- Solow, Robert M. 1956. A Contribution to the Theory of Economic Growth. The Quarterly Journal of Economics 70: 65–94. [Google Scholar] [CrossRef]
- Solow, Robert M. 1957. Technical Change and the Aggregate Production Function. The Review of Economics and Statistics 39: 312–20. [Google Scholar] [CrossRef]
- United Nations Development Programme. 2015. Human Development Report for Zambia 2015. Lusaka: United Nations Development Programme. [Google Scholar]
- Upreti, Parash. 2015. Factors Affecting Economic Growth in Developing Countries. Available online: http://business.uni.edu/economics/themes/Upreti.pdf (accessed on 29 December 2016).
- Wang, Jintian, Feng Gao, and Xuezhen Wang. 2009. Estimation of Agricultural Total Factor Productivity in China: A Panel Cointegration Approach. Paper presented at the International Association of Agricultural Economists Conference, Beijing, China, August 16–12; pp. 16–22. [Google Scholar]
- Wen, Guanzhong James. 1993. Total Factor Productivity Change in China’s Farming Sector: 1952–1989. Economic Development and Cultural Change 42: 1–41. [Google Scholar] [CrossRef]
- Woodland, A. D. 1982. International Trade and Resource Allocation. Amsterdam: Elsevier. [Google Scholar]
- World Bank. 1990. Adjustment Lending Policies for Sustainable Growth. Washington: World Bank. [Google Scholar]
| 1 | By “fair share”, we refer to the competitive rate of return on sector’s investment. |
| 2 | Upon this model, we build a three sector model and to reserve space, we present it in the appendix. |
| 3 | For more details on computation of percentage points, see Roe et al. (2014). |
| 4 | We are aware of the challenges arising from differences in national and WDI data. But Zambia, as shown by Jerven (2010) has more credible and highly correlated national and WDI data than most countries in SSA. This means we can combine CSO and WDI data without losing much accuracy. |
| 5 | The industry sector as considered in WDI data comprises manufacturing, mining, construction and utilities. Where necessary however, we use the terms industry and manufacturing interchangeably. |
| 6 | Former Zambia Republican President: Foreword to Mwanakatwe (1971), The Growth of Education in Zambia since Independence. |
| 7 | This could be as a result of the method we have used to estimate the labor shares in each sector, i.e. regressing the years for which data are available on urban population for industry and rural population for agriculture with the residual being service. |
| 8 | Again, we suspect this conspicuous contribution of labor could be rooted in the data problems. |
| 9 | See Roe et al. (2014) for cases where firms face different rk. |
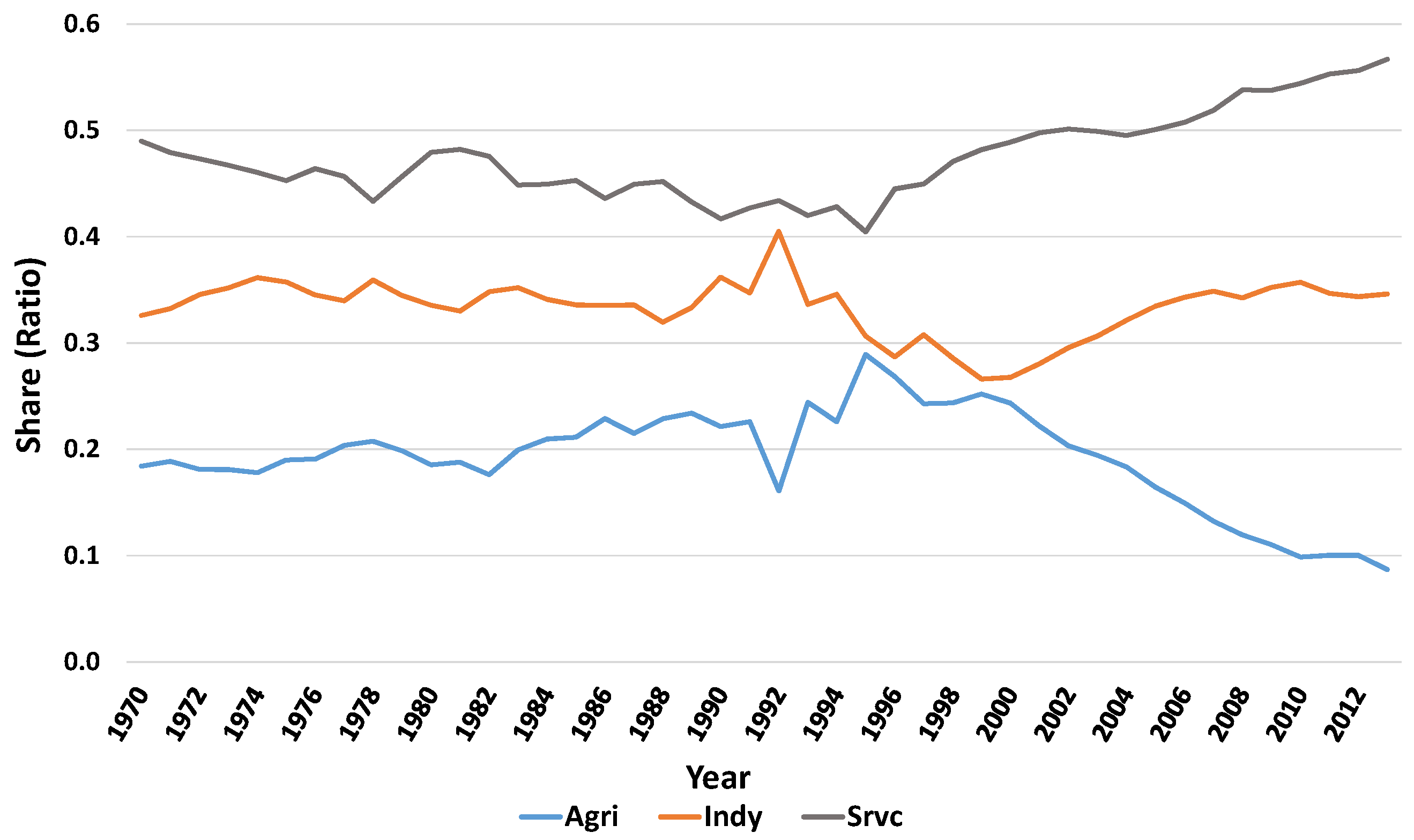
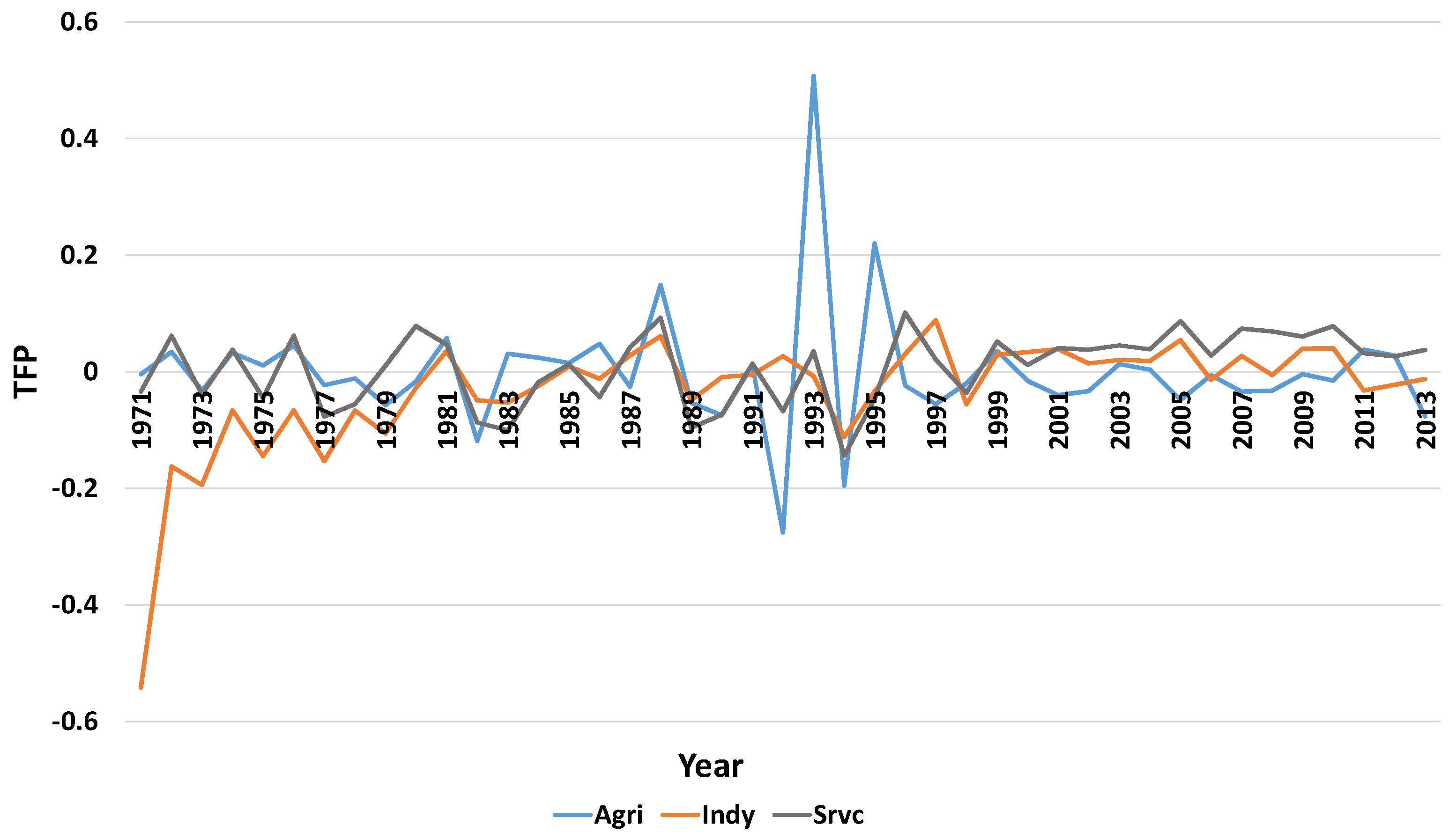
| Product | 1992 | 1995 | 2001 | 2005 | 2006 | 2007 | 2008 |
|---|---|---|---|---|---|---|---|
| Building materials (%) | 6.2 | 4.9 | 5.6 | 3.2 | 2.9 | 1.7 | 5.5 |
| Chemical products (%) | 3.2 | 1.9 | 4.7 | 7.9 | 4.1 | 8.3 | 14.3 |
| Engineering products (%) | 40.2 | 32.8 | 16.7 | 36.9 | 58.7 | 45.5 | 46.3 |
| Textiles and garments (%) | 24.3 | 29.0 | 27.0 | 10.5 | 4.0 | 4.8 | 4.1 |
| Leather (%) | 0.6 | 1.0 | 3.1 | 1.5 | 1.0 | 1.3 | 1.6 |
| Petroleum oils (%) | 1.8 | 9.0 | 1.3 | 5.5 | 2.7 | 4.4 | 4.0 |
| Processed foods (%) | 23.0 | 21.3 | 33.8 | 25.6 | 21.1 | 24.8 | 18.8 |
| Other manufactures (%) | 0.6 | 0.0 | 7.2 | 8.5 | 5.0 | 8.4 | 4.4 |
| Non-metallic (%) | 0.1 | 0.1 | 0.7 | 0.4 | 0.5 | 0.7 | 1.1 |
| Total manufactures (%) | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| 2007 Factor Share (from GTAP) | Economy | Agriculture | Industry5 | Services |
|---|---|---|---|---|
| Labor share | 0.590 | 0.577 | 0.425 | 0.672 |
| Capital share | 0.381 | 0.245 | 0.575 | 0.328 |
| Land share | 0.030 | 0.177 |
| 1971–1980 | 1981–1990 | 1991–2000 | 2001–2013 | 1971–2013 | |
|---|---|---|---|---|---|
| Mean | Mean | Mean | Mean | Mean | |
| GDP growth rate (%) | 1.45 | 1.08 | 1.75 | 7.26 | 3.19 |
| L force growth rate (%) | 2.96 | 2.54 | 2.64 | 2.63 | 2.69 |
| L contribution to growth (%) | 120.69 | 138.89 | 89.14 | 21.35 | 49.84 |
| K stock growth rate (%) | 2.66 | 1.27 | 2.93 | 7.09 | 3.74 |
| K contribution to growth (%) | 69.66 | 44.44 | 62.00 | 37.19 | 44.51 |
| Z growth (%) | −0.01 | 0.48 | 0.78 | 0.42 | 0.42 |
| Z contribution to growth (%) | 0.00 | 0.93 | 1.14 | 0.14 | 0.31 |
| Solow Residual (TFP) (%) | −90.34 | −83.33 | −53.14 | 41.46 | 5.64 |
| Sector | Arithmetic Mean |
|---|---|
| Sector Growth (%) | |
| GDP | 0.0323 |
| Agriculture | 0.0214 |
| Industry | 0.0344 |
| Services | 0.0367 |
| Sector Shares (%) | |
| Agriculture | 19.25 |
| Industry | 33.35 |
| Services | 47.40 |
| Sector % Point Contribution to GDP growth * | |
| Agriculture | 0.0060 (16.44) |
| Industry | 0.0116 (31.77) |
| Services | 0.0189 (51.78) |
| Sector Growth Contribution to GDP Growth in % | |
| Agriculture | 37.57 |
| Industry | 10.40 |
| Services | 0.86 |
| SUM | 48.84 |
| Contribution departure from share in % | |
| Agriculture | 75.2243 |
| Industry | −85.2911 |
| Services | −103.0619 |
| Annual Mean 1971–1991 | Annual Mean 1992–2013 | Annual Mean 1971–2013 | |
|---|---|---|---|
| Agriculture | |||
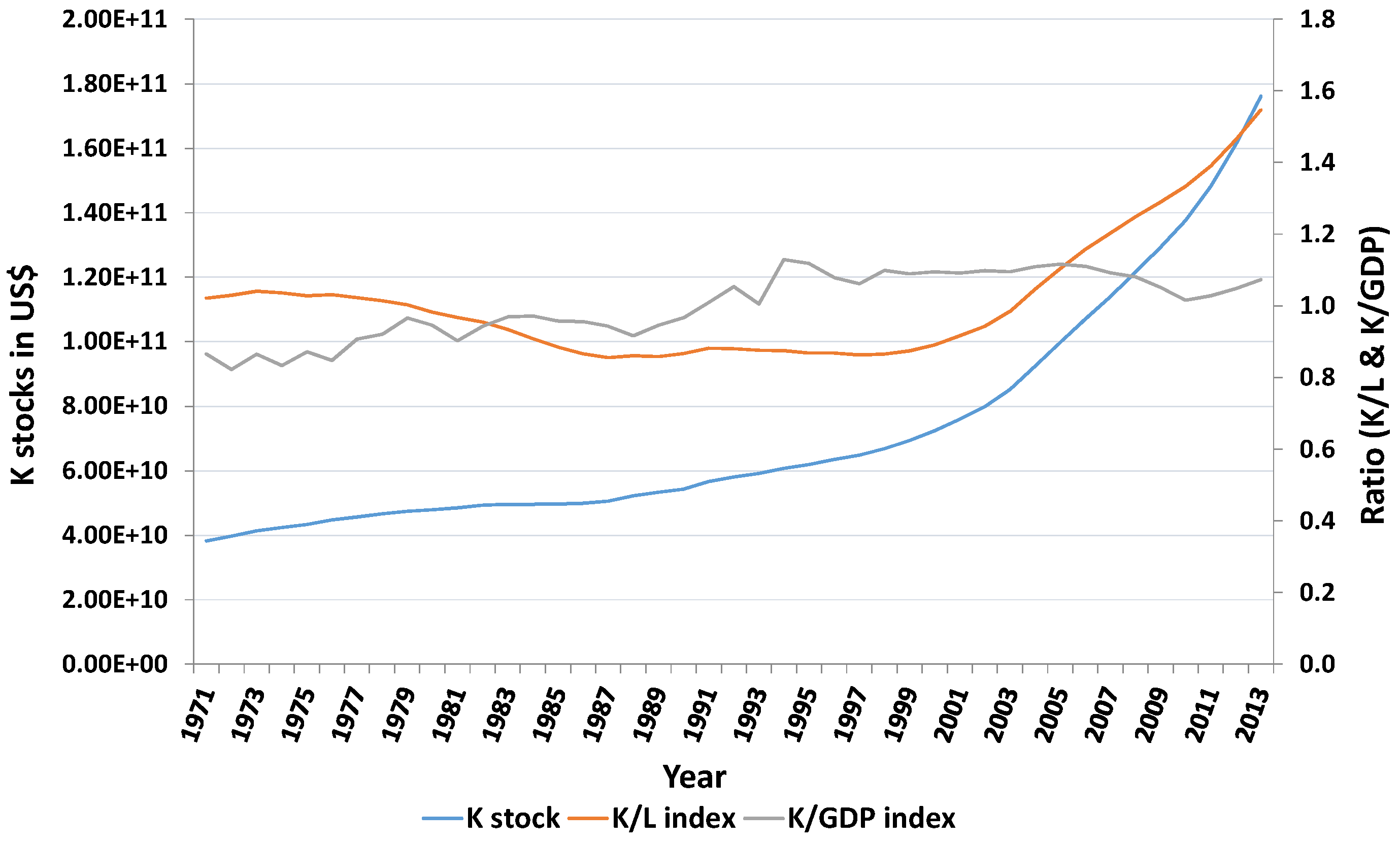
| K stock growth | 0.032 | 0.020 | 0.026 |
| L growth | 0.024 | 0.026 | 0.025 |
| Capital Deepening | 0.008 | −0.006 | 0.001 |
| Industry | |||
| K stock growth | 0.024 | 0.053 | 0.039 |
| L growth | 0.184 | 0.033 | 0.107 |
| Capital Deepening | −0.160 | 0.020 | −0.068 |
| Service | |||
| K stock growth | 0.015 | 0.066 | 0.041 |
| L growth | 0.019 | 0.026 | 0.022 |
| Capital Deepening | −0.005 | 0.040 | 0.018 |
| Period | 1971–1991 | 1992–2013 | 1971–2013 | |||
|---|---|---|---|---|---|---|
| Sector | Annual Mean Growth Rate (%) | Factor Contribution to Sector Growth (%) | Annual Mean Growth Rate | Factor Contribution to Sector Growth (%) | Annual Mean Growth Rate | Factor Contribution to Sector Growth (%) |
| Agriculture | ||||||
| Output growth | 0.0236 | 0.0192 | 0.0214 | |||
| L’s share | 0.0137 | 57.87 | 0.0150% | 77.85 | 0.0143 | 67.07 |
| K’s share | 0.0079 | 33.36 | 0.0049% | 25.42 | 0.064 | 29.71 |
| Z’s share | 0.0004 | 1.69 | 0.0011% | 5.52 | 0.007 | 3.46 |
| Solow residual | 0.0017 | 7.07 | −0.0017 | −8.79 | 0.00 | −0.23 |
| Industry | ||||||
| Output growth | 0.0157 | 0.0522 | 0.0344 | |||
| L’s share | 0.0781 | 498.75 | 0.0142 | 27.15 | 0.0454 | 132.13 |
| K’s share | 0.0138 | 88.37 | 0.0307 | 58.76 | 0.0224 | 65.35 |
| Solow residual | −0.0763 | −487.12 | 0.0074 | 14.09 | −0.0335 | −97.47 |
| Service | ||||||
| Output growth | 0.0073 | 0.0648 | 0.0367 | |||
| L’s share | 0.0129 | 176.39 | 0.0172 | 26.48 | 0.0151 | 41.06 |
| K’s share | 0.0048 | 65.41 | 0.0216 | 33.34 | 0.0134 | 36.46 |
| Solow residual | −0.0104 | −141.80 | 0.0260 | 40.18 | 0.0083 | 22.48 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mulungu, K.; Ng’ombe, J.N. Sources of Economic Growth in Zambia, 1970–2013: A Growth Accounting Approach. Economies 2017, 5, 15. https://doi.org/10.3390/economies5020015
Mulungu K, Ng’ombe JN. Sources of Economic Growth in Zambia, 1970–2013: A Growth Accounting Approach. Economies. 2017; 5(2):15. https://doi.org/10.3390/economies5020015
Chicago/Turabian StyleMulungu, Kelvin, and John N. Ng’ombe. 2017. "Sources of Economic Growth in Zambia, 1970–2013: A Growth Accounting Approach" Economies 5, no. 2: 15. https://doi.org/10.3390/economies5020015
APA StyleMulungu, K., & Ng’ombe, J. N. (2017). Sources of Economic Growth in Zambia, 1970–2013: A Growth Accounting Approach. Economies, 5(2), 15. https://doi.org/10.3390/economies5020015







