The Role of Oil Prices in Exchange Rate Movements: The CIS Oil Exporters
Abstract
:1. Introduction
2. Literature Review
3. Theoretical and Modeling Framework
3.1. Real Exchange Rate Equation
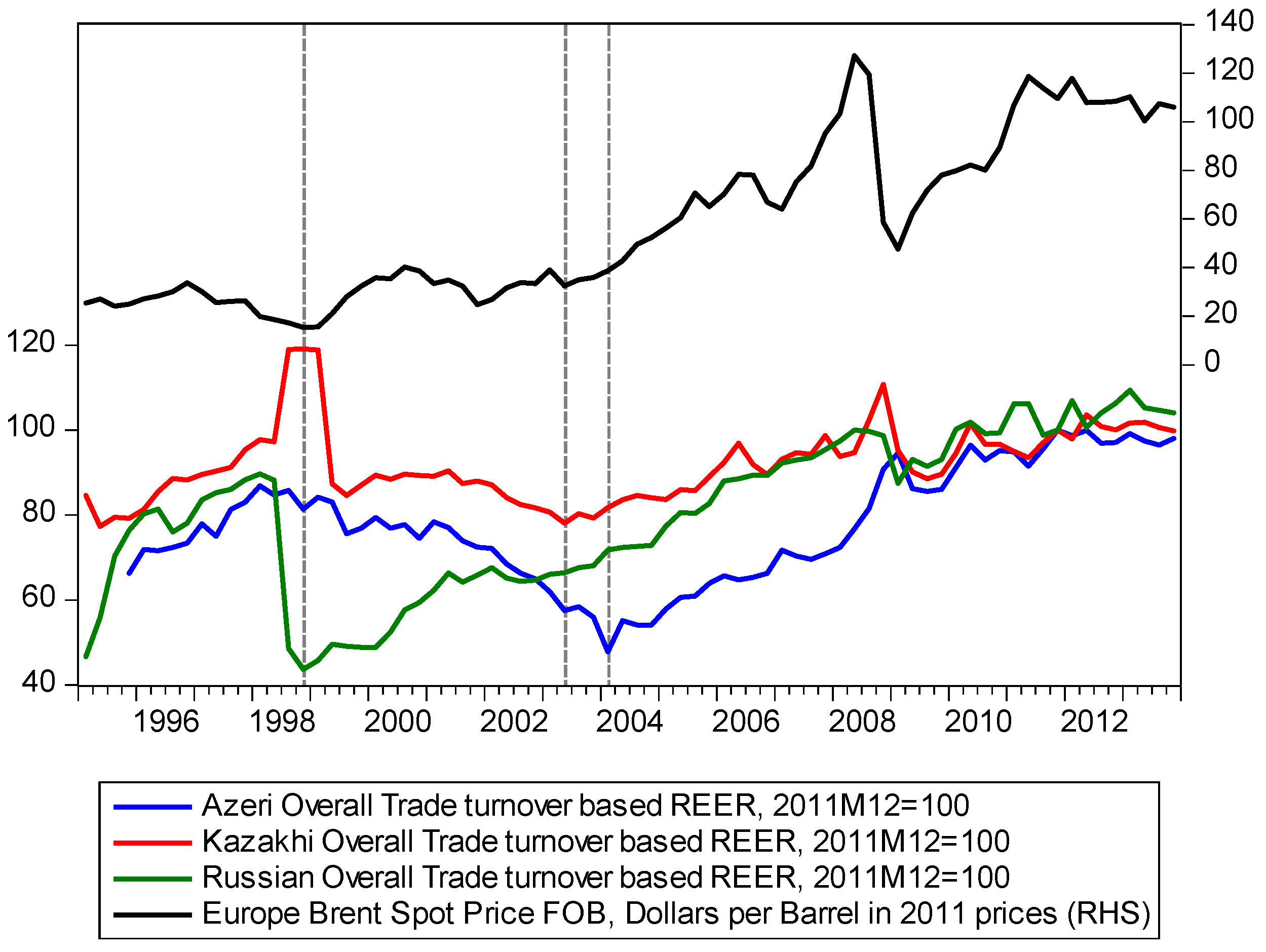
3.2. Movements of Oil Prices and REERs: Choosing the Period of Analysis
4. Data and Econometric Method
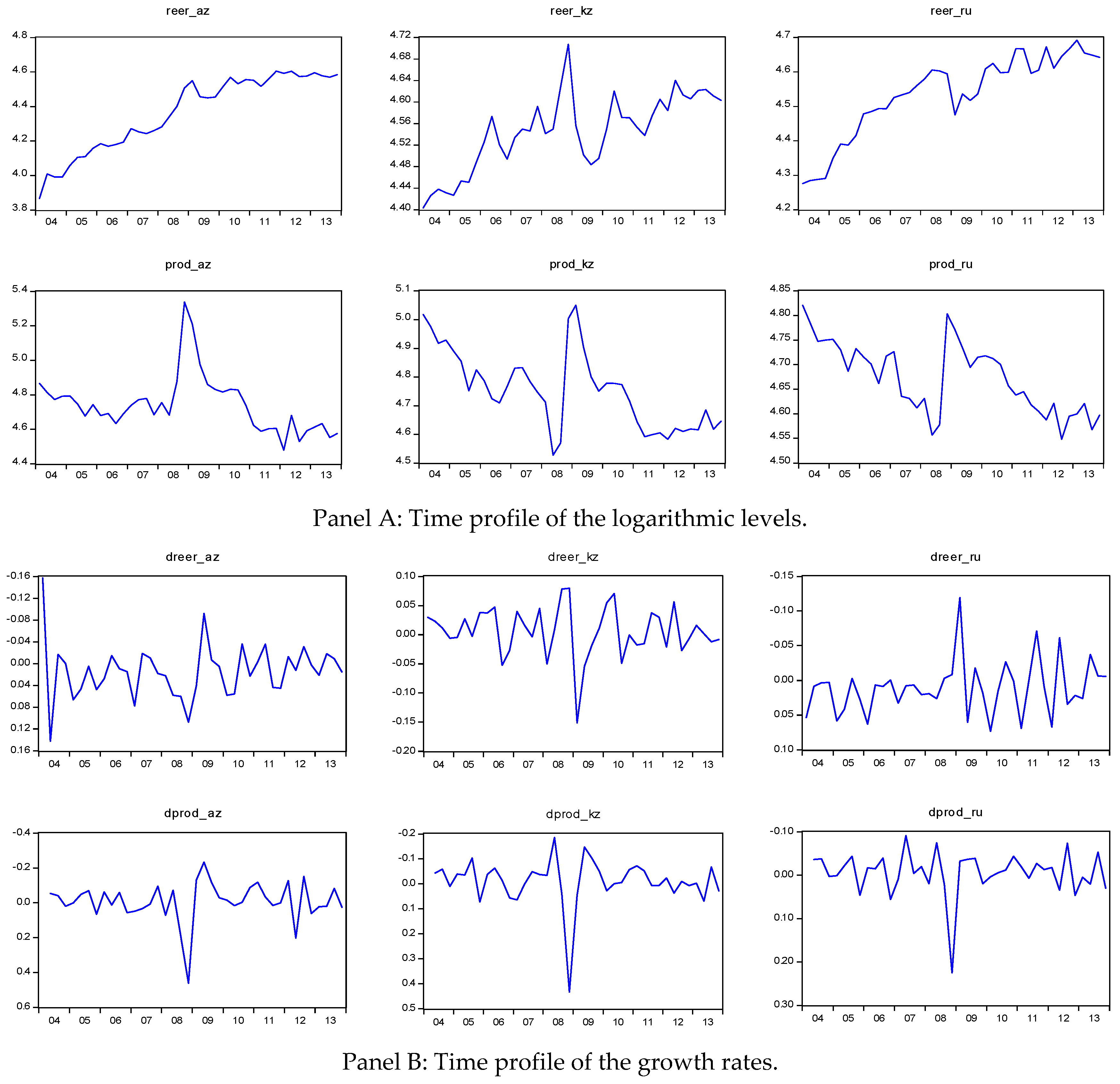
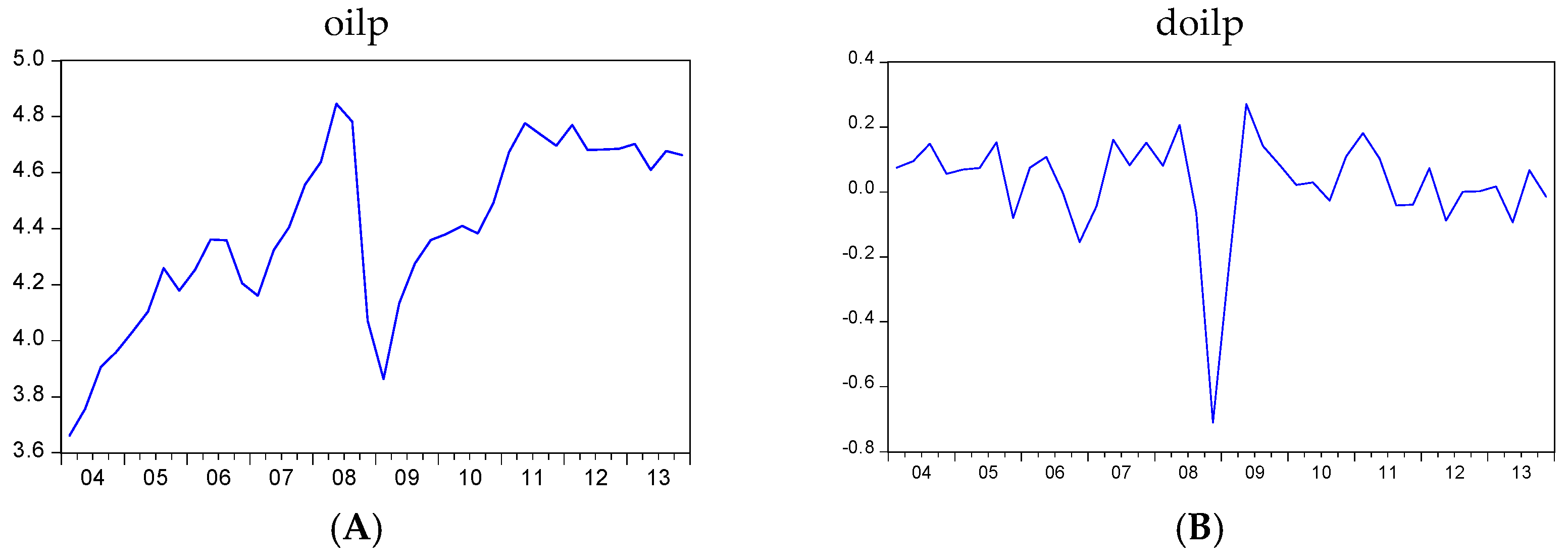
4.1. Data
4.2. Econometric Method
4.2.1. Unit Root Test
4.2.2. Autoregressive Distributed Lag Bounds Testing Approach
4.2.3. Small Sample Bias Correction in the ARDL Approach
5. Empirical Estimations and Discussion
5.1. Robustness Check
6. Concluding Remarks
Acknowledgment
Author Contributions
Conflicts of Interest
References
- Agazade, P., F. Hasanov, J. Mikayilov, and K. Aliyev. 2017. Testing Trilemma Hypothesis in case of Azerbaijan. The Journal of Economic Sciences: Theory and Practice. in press. [Google Scholar]
- Ahmad, A. H., and R. Moran Hernandez. 2013. Asymmetric adjustment between oil prices and exchange rates: Empirical evidence from major oil producers and consumers. Journal of International Financial Markets, Institutions and Money 27: 306–17. [Google Scholar] [CrossRef]
- Alberola, E., S. G. Cervero, H. Lopez, and A. Ubide. 1999. Global Equilibrium Exchange Rates: Euro, Dollar, “Ins,” “Outs,” and Other Major Currencies in a Panel Cointegration Framework. IMF Working Paper, No. 175. Washington: IMF. [Google Scholar]
- Aleksandrova, S. 2016. Impact of Oil Prices on Oil Exporting Countries in the Caucasus and Central Asia. Economic Alternatives 4: 447–60. [Google Scholar]
- Asian Development Bank. 2014. Asian Development Bank Report, Country Partnership Strategy: Azerbaijan, 2014–2018. Available online: https://www.adb.org/sites/default/files/linked-documents/cps-aze-2014-2018-sd-02.pdf (accessed on 22 February 2017).
- Babayev, M. 2010. The Impact of Oil Price on Economy: Evidence from Azerbaijan. Düsseldorf: VDM Verlag Dr. Müller. [Google Scholar]
- Basher, S. A., A. A. Haug, and P. Sadorsky. 2012. Oil prices, exchange rates and emerging stock markets. Energy Economics 34: 227–40. [Google Scholar] [CrossRef]
- Behar, A., and A. Fouejieu. 2016. External Adjustment in Oil Exporters: The Role of Fiscal Policy and the Exchange Rate. IMF Working Paper, WP/16/107. Washington: IMF. [Google Scholar]
- Benedictow, A., D. Fjærtoft, and O. Løfsnæs. 2010. Oil Dependency of the Russian Economy: An Econometric Analysis. Discussion Papers No. 617. Oslo: Statistics Norway, Research Department. [Google Scholar]
- Bewley, R. A. 1979. The Direct Estimation of the Equilibrium Response in a Linear Model. Economics Letters 3: 375–81. [Google Scholar] [CrossRef]
- Blokhina, T. K., O. A. Karpenko, and A. V. Guirinskiy. 2016. The Relationship between Oil Prices and Exchange Rate in Russia. International Journal of Energy Economics and Policy 6: 721–26. [Google Scholar]
- Bouoiyour, J., R. Selmi, A. K. Tiwari, and M. Shahbaz. 2015. The nexus between oil price and Russia’s real exchange rate: Better paths via unconditional vs conditional analysis. Energy Economics 51: 54–66. [Google Scholar] [CrossRef]
- Buiter, W., and D. Purvis. 1983. Oil, Disinflation and Export Competitiveness: A Model of the Dutch Disease. National Bureau of Economic Research Working Paper 592. Cambridge: NBER. [Google Scholar]
- Bruno, M., and J. Sachs. 1982. Energy and Resource Allocation: A Dynamic Model of the Dutch Disease. Review of Economic Studies 49: 845–59. [Google Scholar] [CrossRef]
- Cashin, P. F., R. Céspedes, and Sahay. 2007. Commodity currencies and the real exchange rate. Journal of Development Economics 75: 239–68. [Google Scholar] [CrossRef]
- Center for Social and Economic Research. 2008. The Economic Aspects of Energy Sector in CIS Countries. Economic Papers 327. Warsaw: European Communities, Available online: http://ec.europa.eu/economy_finance/publications/publication12678_en.pdf (accessed on 22 February 2017).
- Corden, W. M. 1984. Booming Sector and Dutch Disease Economics: Survey and Consolidation. Oxford Economic Papers 36: 359–80. [Google Scholar] [CrossRef]
- Corden, W. M., and J. P. Neary. 1982. Booming Sector and De-Industrialization in a Small Open Economy. Economic Journal 92: 825–48. [Google Scholar]
- De Broeck, M., and T. Slok. 2001. Interpreting Real Exchange Rate Movements in Transition Countries. IMF Working Paper WP/01/56. Washington: IMF. [Google Scholar]
- de Brouwer, G., and N. R. Ericsson. 1998. Modeling Inflation in Australia. Journal of Business and Economic Statistics 16: 433–49. [Google Scholar] [CrossRef]
- Dickey, D., and W. Fuller. 1981. Likelihood Ratio Statistics for Autoregressive Time Series with a Unit Root. Econometrica 49: 1057–72. [Google Scholar] [CrossRef]
- Dolado, Juan J., Tim Jenkinson, and Simon Sosvilla-Rivero. 1990. Cointegration and Unit Roots. Journal of Economic Surveys 4: 249–73. [Google Scholar] [CrossRef]
- Edwards, S. 1985. A Commodity Export Boom and the Real Exchange Rate: The Money-Inflation Link. NBER Working Paper Series, Working Paper No. 1741; Cambridge: NBER. [Google Scholar]
- Egert, Balázs. 2005. Equilibrium Exchange Rates in South Eastern Europe, Russia, Ukraine and Turkey: Healthy or (Dutch) Diseased? Economic Systems 29: 205–41. [Google Scholar] [CrossRef]
- Egert, Balázs, and Carol S. Leonard. 2007. The Dutch Disease in Kazakhstan: An Empirical Investigation. Focus on European Economic Integration 2: 85–108. [Google Scholar]
- Egert, B. 2009. Dutch Disease in Former Soviet Union: Witch-Hunting? BOFIT. Discussion Papers 4. Available online: http://papers.ssrn.com/sol3/papers.cfm?abstract_id¼1383522 (accessed on 22 February 2017).
- Enders, K., and H. Herberg. 1983. The Dutch Disease: Causes, Consequences, Cure and Calmatives. Welwirtschaftliches Archiv 119: 473–79. [Google Scholar] [CrossRef]
- EIA (Energy Information Administration). 2014. Available online: http://www.eia.gov/todayinenergy/detail.php?id=17231 (accessed on 22 February 2017).
- Enders, Walter. 2010. Applied Econometrics Time Series, 4th ed. Tuscaloosa: University of Alabama. [Google Scholar]
- Fatai, K., L. Oxley, and F. G. Scrimgeour. 2003. Modeling and Forecasting the demand for Electricity in New Zealand: A Comparison of Alternative Approaches. The Energy Journal 24: 75–102. [Google Scholar] [CrossRef]
- Habib, M., and M. Kalamova. 2007. Are There Oil Currencies? The Real Exchange Rate of Oil Exporting Countries. Working Paper Series No 839; Frankfurt: European Central Bank. [Google Scholar]
- Hasanov, Fakhri. 2010. The Impact of Real Oil Price on Real Effective Exchange Rate: The Case of Azerbaijan. Discussion Paper Series 1041; Berlin: DIW Berlin German Institute for Economic Research. [Google Scholar]
- Hasanov, Fakhri. 2011. Analyzing Price Level in a Booming Economy: The Case of Azerbaijan. Working Paper No 11/02E. Kyiv: Economics Education and Research Consortium. [Google Scholar]
- Hasanov, Fakhri. 2013. Dutch disease and the Azerbaijan economy. Communist and Post-Communist Studies 46: 463–80. [Google Scholar] [CrossRef]
- Hasanov, Fakhri, L. Hunt, and J. Mikayilov. 2016. Modeling and Forecasting Electricity Demand in Azerbaijan Using Cointegration Techniques. Energies 9: 1045. [Google Scholar] [CrossRef]
- Hsiao, Cheng. 2007. Benefits and limitations of panel data. Econometric Reviews 4: 121–74. [Google Scholar] [CrossRef]
- Hsiao, Cheng. 2003. Analysis of Panel Data, 2nd ed. Cambridge: Cambridge University Press. [Google Scholar]
- Issa, R., R. Lafrance, and J. Murray. 2006. The Turning Black Tide: Energy Prices and the Canadian Dollar. Working Paper 2006-29. Ottawa: Bank of Canada. [Google Scholar]
- Korhonen, Iikka, and Tuuli Juurikkala. 2009. Equilibrium exchange rates in oil-exporting countries. Journal of Economics and Finance 33: 71–79. [Google Scholar] [CrossRef]
- Ito, K. 2010. The Impact of Oil Price Volatility on Macroeconomic Activity in Russia. Economic Analysis Working Papers 9: 1–10. [Google Scholar]
- Kaplan, F., and A. R. Aktash. 2016. The Impact of Real Oil Price on Real Exchange Rate in Oil Dependent Countries. Business and Economics Research Journal 7: 103–13. [Google Scholar] [CrossRef]
- KCCG (Kazakhstan Country Commercial Guide). 2016. Kazakhstan―Oil and Gas Equipment and Services. Available online: https://www.export.gov/article?id=Kazakhstan-Oil-and-Gas-Equipment-and-Services (accessed on 22 February 2017).
- Koranchelian, T. 2005. The Equilibrium Real Exchange Rate in a Commodity Exporting Country: Algeria’s Experience. IMF Working Paper 05/135. Washington: IMF. [Google Scholar]
- Kose, N., and S. Baimaganbetov. 2015. The Asymmetric Impact of Oil Price Shocks on Kazakhstan Macroeconomic Dynamics: A Structural Vector Autoregression Approach. International Journal of Energy Economics and Policy 5: 1058–64. [Google Scholar]
- Kuralbayeva, Karlygash, Ali M. Kutan, and Michael L. Wyzan. 2001. Is Kazakhstan Vulnerable to the Dutch Disease? ZEI Working Paper, No. B 29-2001. Bonn: ZEI. [Google Scholar]
- MacKinnon, J. 1996. Numerical Distribution Functions for Unit Root and Cointegration Tests. Journal of Applied Econometrics 11: 601–18. [Google Scholar] [CrossRef]
- Mironov, V. V., and A. V. Petronevich. 2015. Discovering the Signs of Dutch Disease in Russia. BOFIT Discussion Papers 3/2015. Helsinki: BOFIT. [Google Scholar]
- Jahan-Parvar, Mohammad R., and Hassan Mohammadi. 2008. Oil Prices and Real Exchange Rates in Oil-Exporting Countries: A Bounds Testing Approach. The Journal of Developing Areas 45: 313–22. [Google Scholar] [CrossRef]
- Narayan, P. K. 2004. An Econometric Model of Tourism Demand and a Computable General Equilibrium Analysis of the Impact of Tourism: The Case of the Fiji Islands. Unpublished Ph.D. thesis, Department of Economics, Monash University, Melbourne, Australia. [Google Scholar]
- Narayan, P. K. 2005. The Saving and Investment Nexus for China: Evidence from Cointegration Tests. Applied Economics 37: 1979–90. [Google Scholar] [CrossRef]
- Nikbakht, L. 2010. Oil Prices and Exchange Rates: The Case of OPEC. Business Intelligence Journal 3: 83–92. [Google Scholar]
- Oteng-Abayie, E., and J. Frimpong. 2006. Bounds Testing Approach to Cointegration: An Examination of Foreign Direct Investment Trade and Growth Relationships. American Journal of Applied Sciences 3: 2079–85. [Google Scholar]
- Oomes, Nienke, and Katerina Kalcheva. 2007. Diagnosing Dutch Disease: Does Russia Have the Symptoms? IMF Working Paper No. 07/102. Washington: IMF. [Google Scholar]
- Perron, Pierre. 2006. Dealing with Structural Breaks. In Palgrave Handbook of Econometrics, Vol. 1: Econometric Theory. Edited by K. Patterson and T. C. Mills. Basingstoke: Palgrave Macmillan, pp. 278–352. [Google Scholar]
- Pesaran, H. M., and B. Pesaran. 1997. Microfit 4.0. Oxford: Oxford University Press. [Google Scholar]
- Pesaran, M. Hashem, and Y. Shin. 1999. An Autoregressive Distributed Lag Modelling Approach to Cointegration Analysis. Econometric Society Monographs 31: 371–413. [Google Scholar]
- Pesaran, M. H., Y. Shin, and R. J. Smith. 2001. Bound Testing Approaches to the Analysis of Level Relationships. Journal of Applied Econometrics 16: 289–326. [Google Scholar] [CrossRef]
- Rautava, Jouko. 2004. The role of oil prices and the real exchange rate in Russia’s economy—A cointegration approach. Journal of Comparative Economics 32: 315–27. [Google Scholar] [CrossRef]
- Saikkonen, P. 1992. Estimation and testing of cointegrated systems by an autoregressive approximation. Econometric Theory 8: 1–27. [Google Scholar] [CrossRef]
- Sosunov, Kirill, and Oleg Zamulin. 2006. Can Oil Prices Explain the Real Appreciation of the Russian Ruble in 1998-2005? Center for Economic and Financial Research at New Economic School (CEFIR/NES) working paper series, Working Paper No 83; Moscow: CEFIR. [Google Scholar]
- Spatafora, Nicola, and Emil Stavrev. 2003. The Equilibrium Exchange Rate in a Commodity Exporting Country: The Case of Russia. IMF Working Paper 03/93. Washington: IMF. [Google Scholar]
- Stock, J. H., and M. W. Watson. 1993. A simple estimator of cointegrating vectors in higher order integrated systems. Econometrica 61: 783–820. [Google Scholar] [CrossRef]
- Sturm, Michael, François Gurtner, and Juan Gonzalez Alegre. 2009. Fiscal Policy Challenges in Oil-Exporting Countries a Review of Key Issues. Occasional Paper Series No 104; Frankfurt: European Central Bank. [Google Scholar]
- Sulaiman, D. M., and U. Muhammad. 2010. The Bound Testing Approach for Co-Integration and Causality between Financial Development and Economic Growth in Case of Pakistan. European Journal of Social Sciences 13: 525–31. [Google Scholar]
- Utkulu, U. 1997. How to Estimate Long-Run Relationships in Economics, an Overview of Recent Development. DEÜIIBF Dergisi 12: 39–48. [Google Scholar]
- Wijnbergen, S. V. 1984. Inflation, Employment, and the Dutch Disease in Oil-Exporting Countries: A Short-Run Disequilibrium Analysis. The Quarterly Journal of Economics 99: 233–50. [Google Scholar] [CrossRef]
- Zalduendo, J. 2006. Determinants of Venezuela’s Equilibrium Real Exchange Rate. IMF Working Paper 06/74. Washington: IMF. [Google Scholar]
- Zivot, Eric, and Donald W. K. Andrews. 1992. Further Evidence on the Great Crash, the Oil-Price Shock, and the Unit-Root Hypothesis. Journal of Business & Economic Statistics 10: 251–70. [Google Scholar]
| 1 | Equation (3) is a transformed version of the unit root test equation (random walk with drift), where is equal to + 1. is an auto-regressive coefficient. If it is unity (or close to unity), it means that a given series has a unit root. By way of contrast, if it is zero (or close to zero), it means that the process does not have a unit root process. |
| 2 | The test results can be obtained from the authors upon request. |
| Study | Period | Country/Region | Methodology | Oil Price Coefficient | Productivity Coefficient |
|---|---|---|---|---|---|
| Kuralbayeva et al. (2001) | 1994M1–2000M4 | KZ | VECM | 0.23 | 0.36 |
| De Broeck and Slok (2001) | 1993–1998 | Panel of countries including AZ, KZ and RU | PMG | −0.55 * (for the group where AZ, KZ and RU were included) | 0.57 (for the group where AZ, KZ and RU were included) |
| Spatafora and Stavrev (2003) | 1995Q1–2002Q3 | RU | ECM | 0.31 | 1.3 |
| Egert (2005) | 1991M1–2003M11 | Country group (RU included) | DOLS, ARDL. Panel DOLS, MGE | −0.18 to −0.06 (for panel) | −1.1 (for RU) |
| Sosunov and Zamulin (2006) | 1998–2005 | RU | CGE | 0.25 | Not used |
| Habib and Kalamova (2007) | 1995Q1–2006Q2 (for RU) 1980Q1–2006Q2 (for other countries) | RU, Norway and Saudi Arabia | VECM | 0.50 | 0.82 |
| Oomes and Kalcheva (2007) | 1995M1–2005M12 | RU | VECM | 0.50 and 0.58 | 1.08 and 0.90 |
| Egert and Leonard (2007) | 1996–2005 | KZ | OLS, DOLS, ARDL | Not reported | Not reported |
| Jahan-Parvar and Mohammadi (2008) | 1970–2007 | 14 oil exporters, including RU | ARDL | 1.12 (for RU) | Not used |
| Egert (2009) | 1999–2006 | CIS (including AZ, KZ and RU) | Panel | Not reported | Not used |
| Benedictow et al. (2010) | 1995Q1–2008Q1 | RU | OLS | 0.19 | Not used |
| Hasanov (2010) | 2000Q4–2007Q4 | AZ | ARDL | 0.75 | 2.00 |
| Babayev (2010) | 1999–2009 | AZ | VAR | Not reported | Not reported |
| Ito (2010) | 1994Q1–2009Q3 | RU | VECM | 0.17 | Not used |
| Basher et al. (2012) | 1988M1–2008M12 | Group of countries, including KZ | SVAR | Not reported | Not reported |
| Mironov and Petronevich (2015) | 2002M5–2013M4 | RU | VECM | 0.2 | Not reported |
| Kose and Baimaganbetov (2015) | 2000M1–2013M12 | KZ | SVAR | Not reported | Not reported |
| Bouoiyour et al. (2015) | 1995Q1–2009Q3 | RU | ARDL, Wavelet and FDA | Not reported | Not reported |
| Kaplan and Aktash (2016) | 1995–2014 | Five countries (including RU) | CCEMG, CCEP | −0.16 | Not used |
| Aleksandrova (2016) | 2012–2016 | Caucasus and Central Asia, including AZ and KZ | Descriptive analyses | Not reported | Not reported |
| Blokhina et al. (2016) | 2000M1–2016M1 | RU | OLS | 0.1 | Not used |
| Variable | At the Level | At the First Difference | ||||||
|---|---|---|---|---|---|---|---|---|
| ADF | ZA | ADF | ZA | |||||
| k | Actual Value | k | Actual Value | k | Actual Value | k | Actual Value | |
| roilp | 1 | −3.91 ** | 1 | −4.60 | 1 | −5.89 *** | 1 | −8.01 *** |
| Panel A: Azerbaijan | ||||||||
| reer_az | 0 | −2.08 | 0 | −3.67 | 0 | −6.77 *** | 0 | −7.33 *** |
| prod_az | 0 | −2.34 | 0 | −3.89 | 0 | −5.88 *** | 2 | −8.31 *** |
| Panel B: Kazakhstan | ||||||||
| reer_kz | 0 | −3.37 * | 3 | −2.88 | 1 | −5.97 *** | 4 | −8.53 *** |
| prod_kz | 1 | −4.40 *** | 1 | −4.81 | 1 | −6.25 *** | 2 | −7.90 *** |
| Panel C: Russia | ||||||||
| reer_ru | 0 | −2.62 | 0 | −1.81 | 1 | −6.45 *** | 1 | −6.55 *** |
| prod_ru | 0 | −3.44 * | 0 | −1.66 | 0 | −6.89 *** | 2 | −7.24 *** |
| Panel A: Azerbaijan | Panel B: Kazakhstan | Panel C: Russia | |||
|---|---|---|---|---|---|
| = 6.412 | = 13.804 | = 4.907 | |||
| Lower and Upper Bound Critical Values in the Case of Two Lagged Level Regressors, Restricted Intercept and No Trend: | |||||
| Narayan (2005) * | Pesaran et al. (2001) ** | ||||
| At the 1% significance level: | 4.770 | 5.855 | 4.99 | 5.85 | |
| At the 5% significance level: | 3.435 | 4.260 | 3.88 | 4.61 | |
| At the 10% significance level: | 2.835 | 3.585 | 3.38 | 4.02 | |
| Azerbaijan | Kazakhstan | Russia | ||||
|---|---|---|---|---|---|---|
| Panel A: Estimated Long-Run Coefficients | ||||||
| Variables | ARDL | DOLS | ARDL | DOLS | ARDL | DOLS |
| roilp | 0.264 ** (0.099) | 0.262 *** (0.044) | 0.276 *** (0.083) | 0.285 *** (0.072) | 0.560 *** (0.103) | 0.570 *** (0.119) |
| prod | 0.581 *** (0.121) | 0.512 *** (0.052) | 0.237 (0.200) | 0.390 ** (0.149) | 1.150 ** (0.452) | 0.962 * (0.532) |
| Estimated Long-Run Coefficients with nfa variable | ||||||
| roilp | 0.458 *** (0.122) | 0.417 *** (0.080) | 0.266 ** (0.098) | 0.657 *** (0.142) | 0.240 *** (0.063) | 0.193 *** (0.067) |
| prod | 0.621 *** (0.114) | 0.577 *** (0.056) | 0.223 (0.206) | 1.073 *** (0.242) | 0.399 * (0.207) | 0.277 (0.247) |
| nfa | −0.124 * (0.069) | −0.149 (0.091) | 0.004 (0.022) | −0.128 (1.261) | 0.103 *** (0.022) | 0.121 *** (0.018) |
| ECT | −0.50 *** | −0.63 *** | −0.33 *** | |||
| Panel B: Residuals Diagnostics Tests Results | ||||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasanov, F.; Mikayilov, J.; Bulut, C.; Suleymanov, E.; Aliyev, F. The Role of Oil Prices in Exchange Rate Movements: The CIS Oil Exporters. Economies 2017, 5, 13. https://doi.org/10.3390/economies5020013
Hasanov F, Mikayilov J, Bulut C, Suleymanov E, Aliyev F. The Role of Oil Prices in Exchange Rate Movements: The CIS Oil Exporters. Economies. 2017; 5(2):13. https://doi.org/10.3390/economies5020013
Chicago/Turabian StyleHasanov, Fakhri, Jeyhun Mikayilov, Cihan Bulut, Elchin Suleymanov, and Fuzuli Aliyev. 2017. "The Role of Oil Prices in Exchange Rate Movements: The CIS Oil Exporters" Economies 5, no. 2: 13. https://doi.org/10.3390/economies5020013
APA StyleHasanov, F., Mikayilov, J., Bulut, C., Suleymanov, E., & Aliyev, F. (2017). The Role of Oil Prices in Exchange Rate Movements: The CIS Oil Exporters. Economies, 5(2), 13. https://doi.org/10.3390/economies5020013







